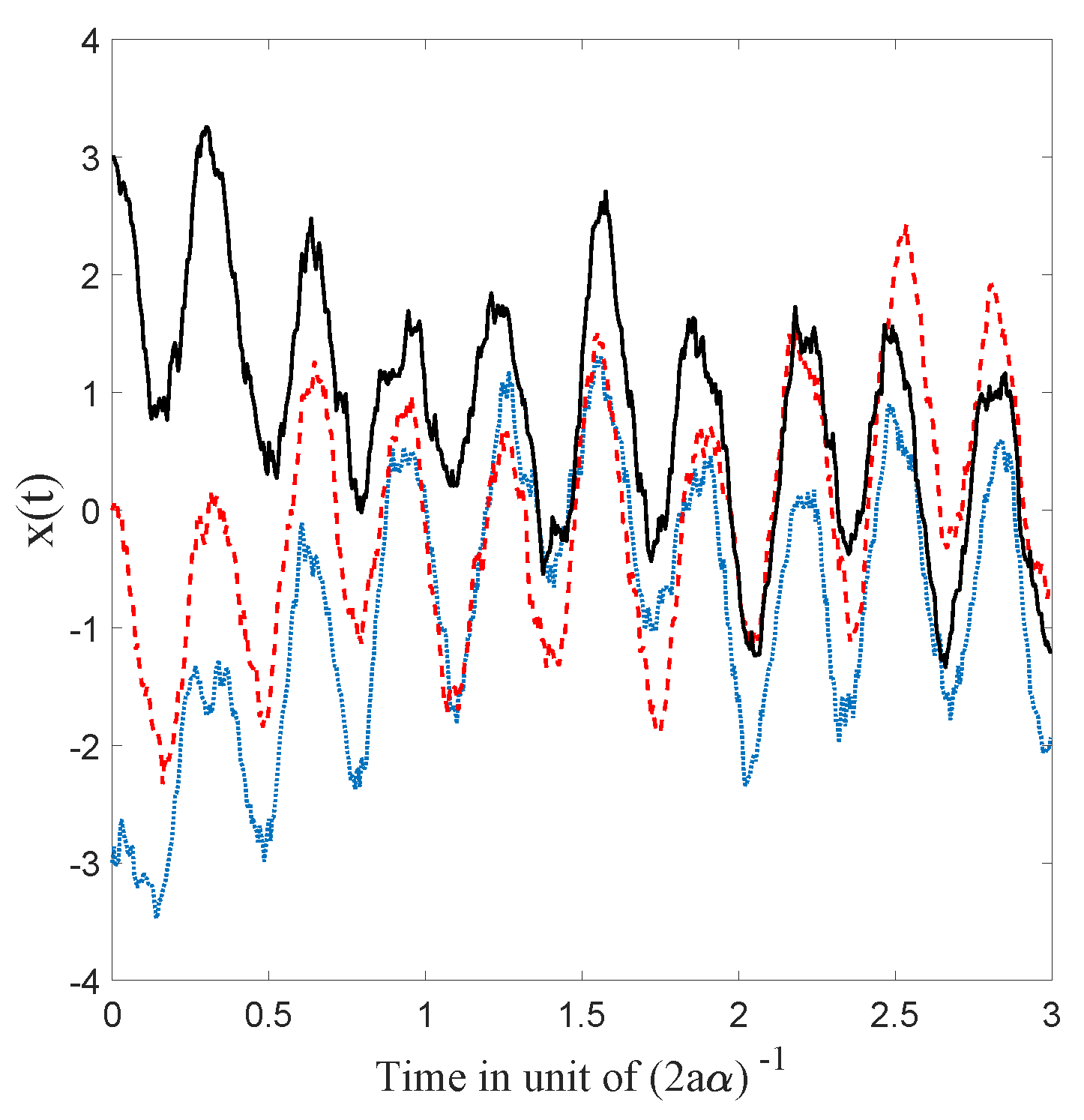
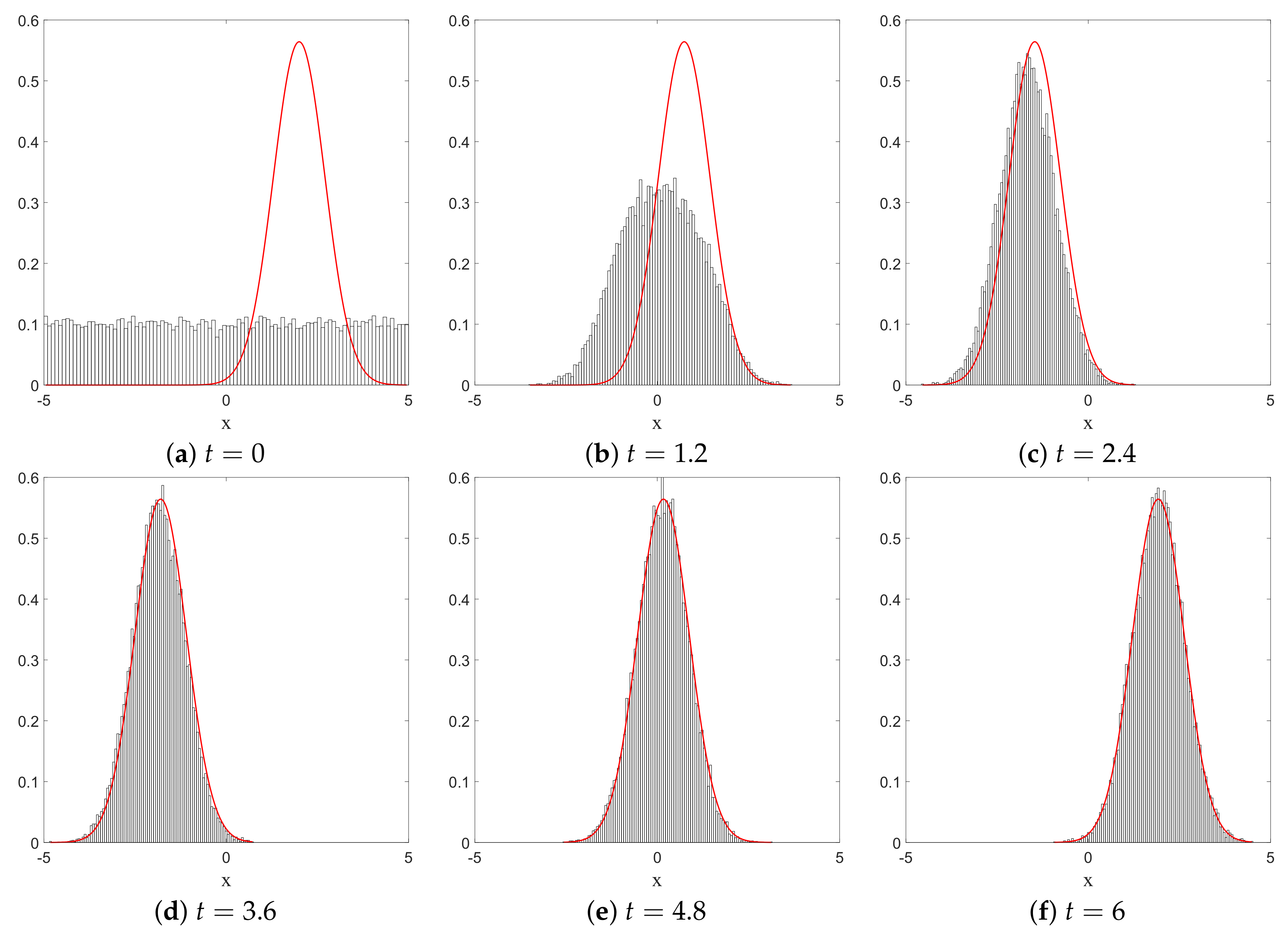
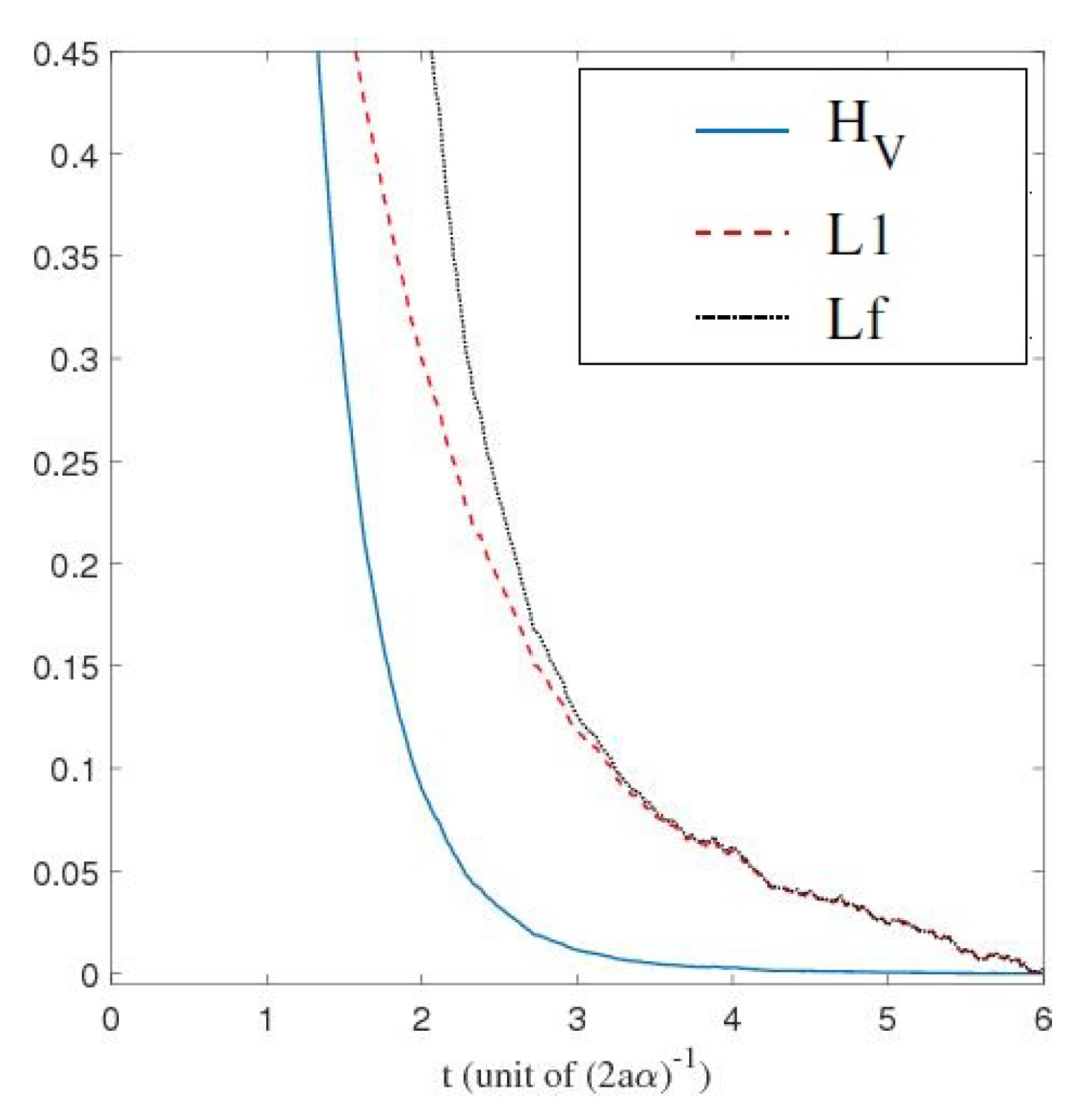
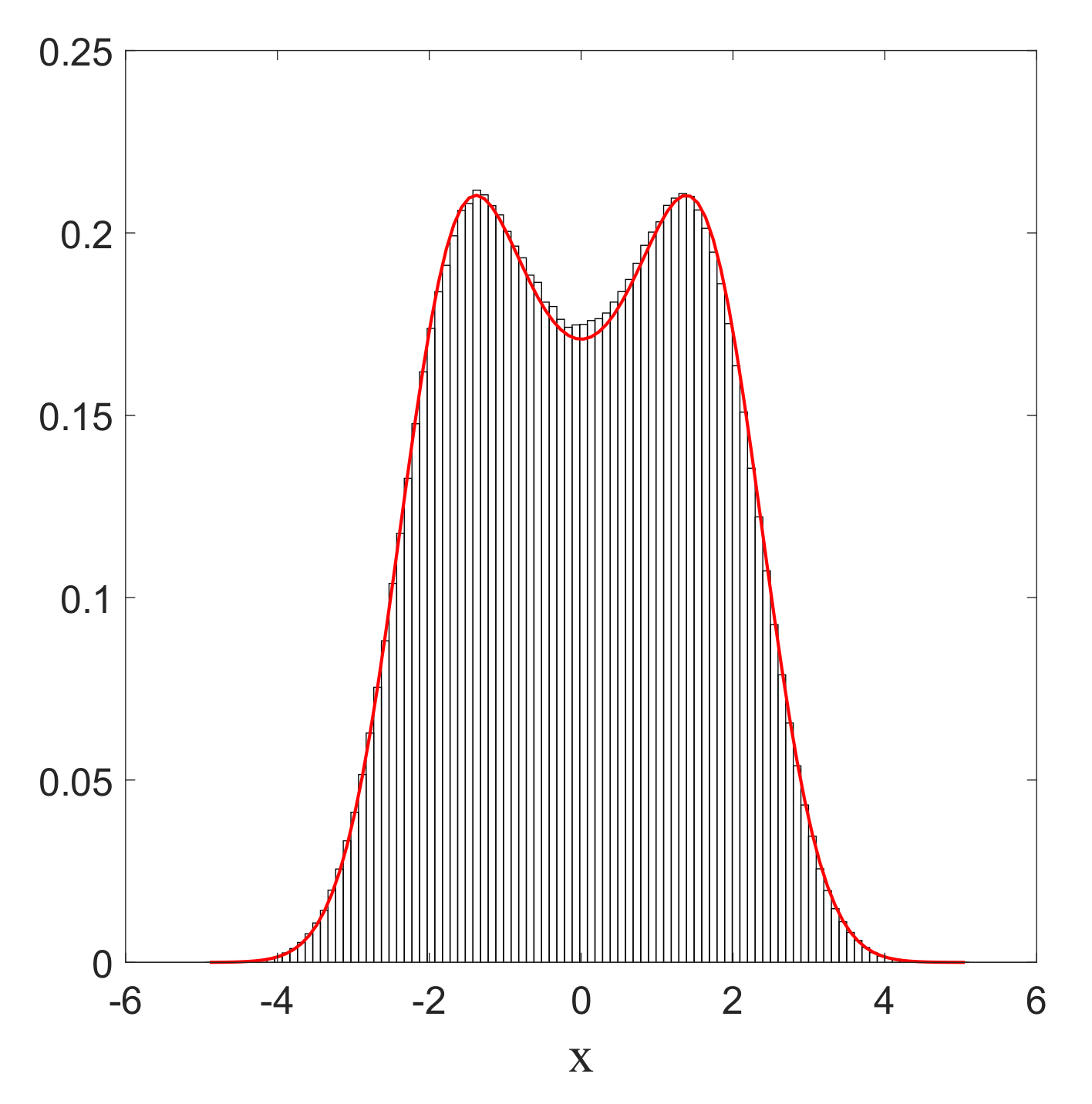
1. Introduction
“Walkers” are realized as oil droplets generated at the surface of a vibrating oil bath. As shown by Couder and Fort [
1,
2,
3], the vibration of the bath prevents the coalescence of the droplets with the surface, allowing them to remain stable for very long times. Moreover, the trajectories of the walkers are guided by an external wave [
4,
5] that they themselves generate at the surface of the oil bath. From this point of view, walkers are reminiscent of wave-particle duality [
2,
6], and they seem to offer deep analogies with de Broglie–Bohm particles [
7]. Up until now, different aspects of walker dynamics have been studied in a purely classical framework, typically in a hydrodynamical approach [
3,
5]. For instance, certain models address their deformations due to their bouncing off the surface of the bath, in function of the density and viscosity of the oil and other parameters [
5]. Other studies describe the dynamics of the surface waves that the walkers generate during the bouncing process, and how those waves in turn guide their trajectories. In these models, this complex behavior is characterized by a memory time which relates the dynamics of the walker bouncing at time
t to its successive bouncing positions in the past [
8,
9]. The presence of such a memory effect establishes a first difference with quantum mechanics. Normally, in quantum mechanics, it is assumed that all results of any possible future measurements to be performed on a quantum system are encapsulated in its present quantum state [
10]: its wave function at the present time
t.
Droplets also transcend the most common interpretations of quantum theory which prohibit any description of the system in terms of instantaneous, classical-like trajectories. Droplets and their trajectories are visible with the naked eye at any time and standard interpretations of quantum mechanics do not apply. This is why we believe that it is necessary and worthwhile to adapt realist (causal) formalisms such as de Broglie–Bohm (dBB) dynamics [
11,
12] or a stochastic version thereof à la Nelson [
13] to explore the analogy with quantum systems. This is the main motivation of the present paper.
Another difference between walker trajectories and quantum trajectories is that the quantum description is intrinsically probabilistic and non-classical, while there exist regimes in which the trajectory of the walkers is deterministic and classical (for example, when they bounce exactly in phase with the bath, they can be shown to follow straight lines at constant velocity [
14,
15,
16,
17]). However, there also exist regimes in which a Brownian motion is superimposed on their flow lines (e.g., above the Faraday threshold), and other regimes where the trajectories appear to be chaotic [
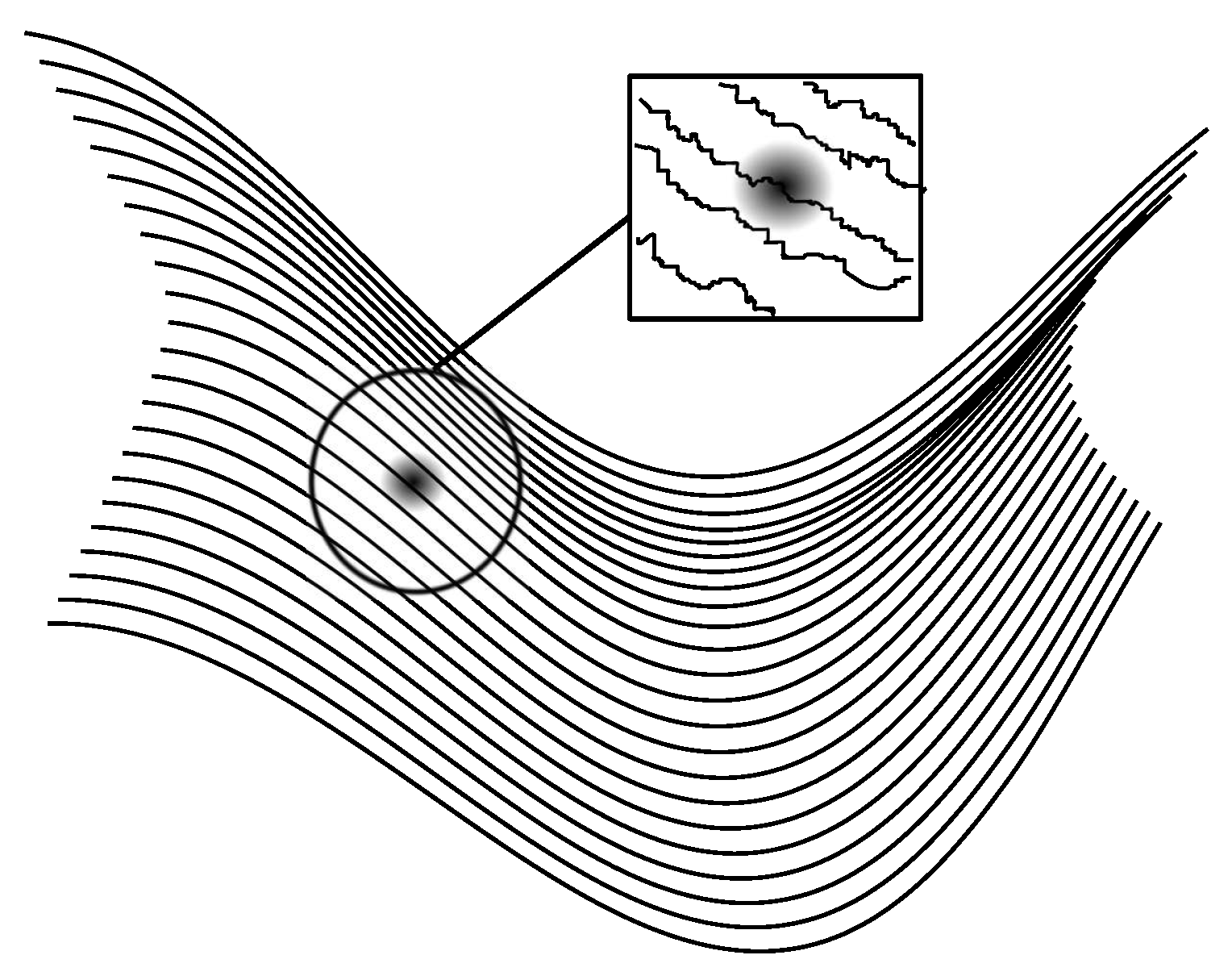
5]. In fact, in several regimes, droplets appear to exhibit ergodic behavior. In practice, ergodicity has been established on the basis of the following observations: if we prepare a walker at the surface of the liquid bath (a corral, for instance), it will progressively explore each part of the surface, following an apparently random motion [
4]. If one then visualizes the statistics of the sojourn time of the walker in each of these regions, a striking pattern emerges, bearing more than a simple resemblance to an interference pattern [
4,
7]. It is this, again remarkable, manifestation of wave-particle duality that first attracted our attention and which lies at the origin of this paper. The onset of quantum equilibrium in the framework of dBB dynamics and in stochastic versions thereof is an important foundational issue in itself, which has motivated numerous studies (see, e.g., [
13,
18,
19,
20,
21,
22,
23,
24] as well as [
25] and references therein). Several authors in the past have indeed tried to explain how the Born rule emerges from individual trajectories, which is a highly non-trivial problem. In the case of dBB dynamics, it is easy to show that in simple situations the relaxation to the Born statistical distribution does not occur at all, but recent studies [
26,
27,
28,
29,
30,
31] show that in sufficiently complex situations (several modes of different energies for instance) the system might exhibit mixing, which explains the onset of quantum equilibrium in such cases. As we shall show in the present paper, in the case of Nelson-type dynamics, the quantum Brownian motion imposed in such a model accelerates the relaxation to Born’s distribution, and in fact ensures that relaxation to the Born rule will almost always occur (as we shall also show). In our view, for the above reasons, de Broglie–Bohm and Nelson-type dynamics are good candidates for explaining how wavelike statistics emerge after averaging a set of apparently chaotic and/or stochastic trajectories.
Briefly summarized, our main goal is to explain the emergence of aforementioned interference patterns in the framework of the dynamical models of de Broglie–Bohm and of a stochastic version thereof which is based on the models of Bohm-Vigier [
18] and Bohm-Hiley [
19] but which is formally close to Nelson [
13]. Both models are introduced in
Section 2. Here, it is worth noting that thus far there is no experimental evidence that droplets indeed follow de Broglie–Bohm and/or Nelson trajectories. Our approach therefore differs radically from previous studies on droplets, in the sense that we impose a quantum dynamics by brute force, whereas, until now, the attempt to illustrate how chaos may underlie quantum stochasticity has been a pillar of the research on walkers/droplets. In fact, Nelson’s original goal, in proposing his dynamics, was to derive an effective wave equation from the properties of an underlying Brownian motion, as in classical statistical mechanics where a diffusion equation is derived from microscopic properties of the atoms. There actually exists an impressive number of attempts in that direction, as, e.g., stochastic electro-dynamics [
5,
32,
33]. However, there exists (as far as we know) no way to derive an effective Schrödinger equation from hydrodynamical models of droplets.
By choosing exactly the opposite approach, i.e., by imposing quantum-like dynamics on the droplets, we pursue three goals. The first one is to describe the onset of quantum equilibrium (and ergodicity). A second objective is to formulate precise quantitative predictions regarding this relaxation process, which can possibly be validated by future experiments. A third objective is to show, for the first time, that certain dBB trajectories present a deep structural resemblance with certain trajectories that have been reported in the literature for droplets trapped in a harmonic potential.
A short discussion of the onset of equilibrium in de Broglie–Bohm dynamics and the importance of coarse-graining is given in
Section 3. In the case of our stochastic, Nelson-type dynamics, we derive in
Section 4 a new H-theorem showing the relaxation to quantum equilibrium, which does not rely on coarse-graining and is valid at all scales. We pay particular attention to the ergodicity of trajectories in the case of our stochastic dynamics (which mix properties of the de Broglie–Bohm dynamics with Brownian motion). We apply these ideas to discuss ergodicity in the case of the stochastic treatment of a particle trapped in a harmonic potential (
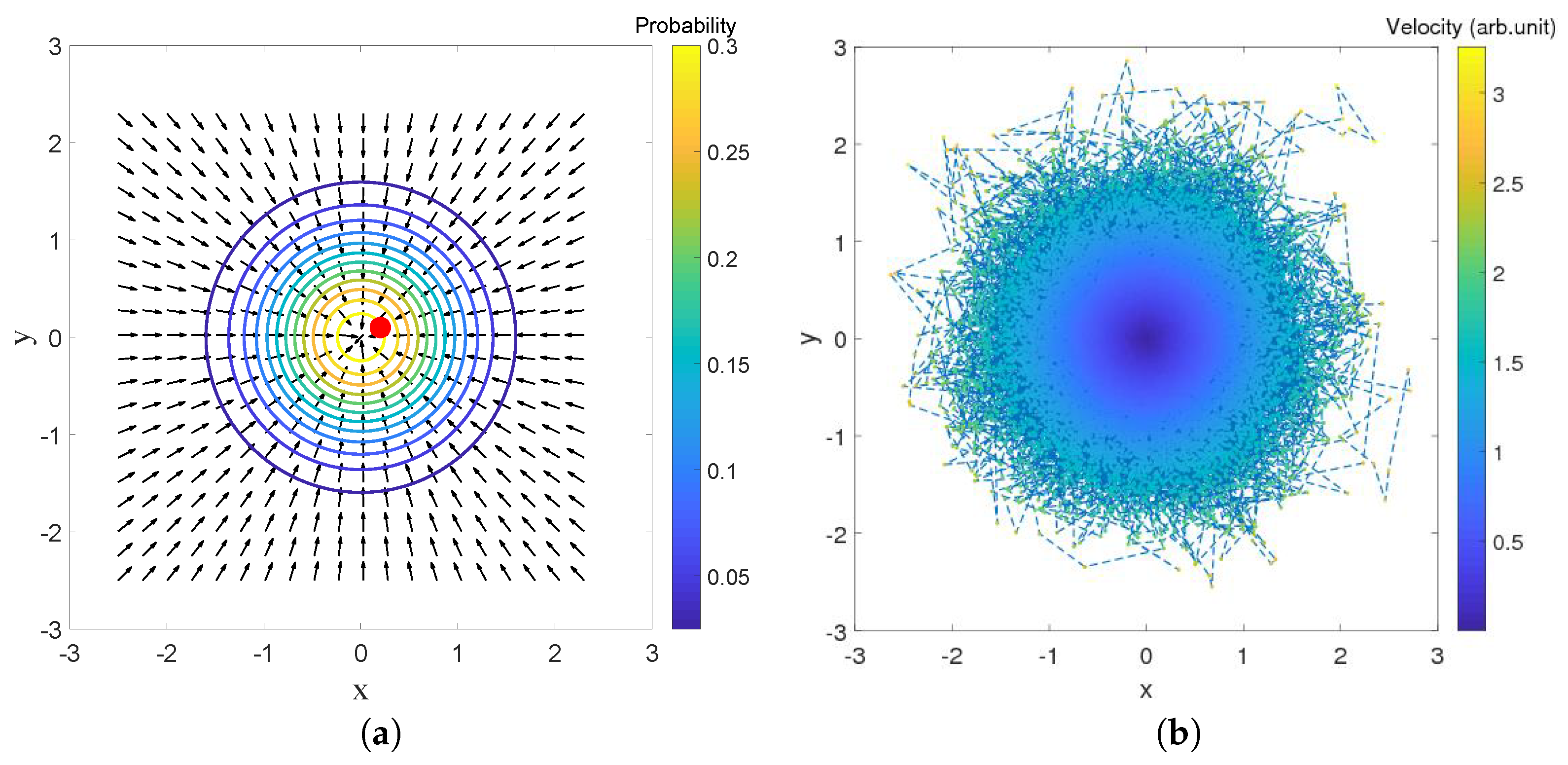
Section 5) and to describe the dynamics of a droplet trapped in a harmonic potential (
Section 6). In this latter section (in
Section 6.1), we also propose some simple experiments by which one can test the applicability of a Nelson-type dynamics to the context of bouncing oil droplets, and we briefly discuss the problems caused by the presence of zeros in the interference pattern that is encoded in the statistics of the trajectories. In
Section 7, we study a situation during which the attractor of the probability distribution is no longer a static eigenstate of the (static) Hamiltonian, and we compare the onset of equilibrium in the dBB and stochastic formalisms in that special framework. In
Section 8, we tackle the dynamics of droplets in a 2D harmonic potential through a simple model where the pilot wave is treated as a dynamical object. This constitutes a preliminary attempt, ultimately aimed at establishing a dynamics that would combine stochastic and/or dBB dynamics with a feedback of the trajectory on the wave, which is a fundamental feature of droplet phenomenology that has never been addressed in the framework of dBB or Nelson dynamics. The last section is devoted to conclusions and open questions. A short overview of the numerical methods used in the paper is given in the
Appendix A.
3. Relaxation to Quantum Equilibrium in the de Broglie–Bohm Theory
In our presentation of the dBB theory for a single particle, in
Section 2.1, we assumed that the particle positions are initially distributed according to Born’s law
over an ensemble. The dynamics then ensure that the same relation will hold for any later time. This is the assumption de Broglie and Bohm made in their original papers [
11,
12,
37]. Although Bohm tried, already in the 1950s (first on his own—see, e.g., [
11] (
Section 9)—and later with Vigier [
18]), to relax this assumption by modifying the dynamics, to many authors working today on the dBB theory it is still an assumption which has to be made (the final objective of de Broglie, Bohm, Vigier, and Nelson–and many other contributors to various realistic hidden variable interpretations in which quantum systems are assumed to be localized in space at any time–was to rationalize wave-like statistics in terms of individual trajectories; the same problem occurs in droplets phenomenology and, according to us, admits no fully satisfying solution yet).
According to Valentini [
21,
38,
39], however, there is no need to assume that the particle positions are initially distributed according to Born’s law or to modify the dynamics. His claim is that an ensemble in which Born’s law is not satisfied (so-called quantum non-equilibrium) will evolve naturally towards quantum equilibrium, provided that the wave function leads to sufficiently complex dynamics. This relaxation process has to take place on a coarse-grained level and can only occur if the initial distributions do not display any fine-grained micro structure.
Let us first explain the need for coarse-graining. Let us introduce the function
, as in [
26]. An important implication of (6) is that the function
f is conserved along the dBB trajectories:
Hence we have that
where
is the initial position of the particle which leads to
, when evolving from
to
t according to the dBB dynamics. If one assumes that
, relaxation to quantum equilibrium is clearly impossible, at least at the microscopic level. However, as argued by Valentini [
21], relaxation
is possible at the coarse-grained level, provided the initial distribution does not display any fine-grained microstructure.
The operational definition of the coarse-graining is as follows. We divide the domain of interest
into small cubes of equal edge length
(we call them coarse-graining cells, or CG cells for short). These CG cells do not overlap and their union is equal to
A. The coarse-grained densities, which we denote by
and
, are then defined as
where the domain of integration is the CG cell containing
.
We can now discuss the second assumption: the lack of a fine-grained microstructure in the initial distribution. Let us assume we have a non-equilibrium distribution which relaxes to quantum equilibrium at the coarse-grained level, under the dynamics generated by the wave function . As the dBB theory is time-reversal invariant, in the time-reversed situation, under the dynamics generated by , we would have a distribution that moves away from quantum equilibrium. Thus, it would seem that time-reversal invariance contradicts the possibility of relaxation to quantum equilibrium. This conclusion is unwarranted, however: as the initial distribution relaxes to quantum equilibrium, it retains information on the original values of f (which are constant in time) and thereby acquires a fine-grained microstructure, which means that at the final time , will differ significantly from . Therefore, in the time-reversed situation, the initial distribution would exhibit a fine-grained microstructure, which is prohibited under our assumption, thereby breaking the time-reversal invariance.
In order to quantify the difference between the distribution
and the quantum equilibrium condition
at the coarse-grained level, Valentini [
21,
38,
39] introduced the entropy-like function
where
and
as in Equations (
23) and (24), for which he has shown the (quantum) H-theorem,
under the assumption of no fine-grained microstructure. It should be stressed, however, that this is not necessarily a monotonic decay and therefore does not prove that quantum equilibrium will always be reached. It merely indicates a tendency towards relaxation. The strongest support for the idea of relaxation to quantum equilibrium comes from numerical simulations of the evolution of non-equilibrium distributions for various quantum systems [
26,
27,
28,
29,
30,
31] (see [
25] and references therein for a review). The first numerical simulations were performed by Valentini and Westman [
26] who showed, in the case of a 2D box, that relaxation quickly takes place for a wave function which is a superposition of the first 16 modes of energy (the superposition being equally weighted). It was also hinted that the nodes of the wave function, with their associated vorticity, play a crucial role in the relaxation process, as purveyors of chaos (or mixing) in the dynamics. This later claim was properly understood in [
40]. The dependence of the relaxation timescale on the coarse-graining length
and on the number of energy modes was studied in [
28]. In [
31], it was shown that quantum systems with a low number of modes are likely to never fully relax, in which case
reaches a non-zero residue value. However, such a scenario becomes unlikely as the number of modes increases.
According to the quantum non-equilibrium hypothesis, standard quantum mechanics is only one facet of the pilot-wave theory, that of quantum equilibrium, leaving the possibility for new physics: that of quantum non-equilibrium. One should assume of course that during our time we have only had (or can only have) access to systems for which quantum equilibrium has already been reached. But that does not mean that quantum non-equilibrium never existed in the early universe (which could be inferred from the observation of the remnants of the early fractions of seconds of the universe, just after the Big Bang [
41]), or that some, yet undetetected, exotic quantum systems cannot still be in quantum non-equilibrium today [
42]. This is why droplets are appealing, because if their dynamics do present analogies with dBB dynamics, their study will allow us to observe relaxation to (quantum) equilibrium “in real time” in the lab with the naked eye, which is not possible with quantum systems for which we have no direct access to individual trajectories.
4. An H-Theorem for Nelson Dynamics
Let us start by introducing an analog of Valentini’s entropy, Equation (
25), for the probability distribution
associated with our Nelson dynamics, as defined by Equations (
16)–(
19):
which is a special instance of a relative entropy known as the Kullback–Leibler divergence [
43].
We also define a second non-negative functional
where
Note that we always impose the boundary conditions and so as to avoid divergence of these integrals on the boundary of .
It should be noted that the entropy of Equation (
27) or the functional of Equation (
28) we shall use to quantify the relaxation to quantum equilibrium are very different from the entropies usually considered in the context of classical H-theorems (like e.g., the Boltzmann entropy). One should bear in mind, however, that
quantum equilibrium is radically different from classical equilibrium [
44] and has no connection whatsoever with relaxation to quantum
thermal equilibrium, for the simple reason that the Born distribution of positions reached by an ensemble of trajectories
à la Nelson or dBB is not a thermal distribution.
To understand why the functionals in Equations (
27) and (
28) are non-negative and why they are zero if and only if (quantum) equilibrium is reached (that is to say when
everywhere in space), it is important to note that the integrands of
and
satisfy the inequalities
for which any of the possible equalities only hold when
. (This is immediate from the trivial inequality:
.)
Now, since both
and
are probability distributions, i.e., since we have
, it follows from (
30) that whenever
and
are well-defined, they satisfy the following inequalities:
Moreover, for the same reason,
can be re-expressed as
, the integrand in which is non-negative due to Equation (
30). Therefore,
can only be zero if its integrand is zero, i.e., if
(if
P,
, and
f are sufficiently smooth, which is something we shall always assume unless otherwise stated). Similarly [
21], one also has that
can only be zero when
everywhere in
.
Let us now prove the relaxation to quantum equilibrium. Substituting
in the Fokker–Planck Equation (
18), and using Equations (
4) and (
10), it is easily verified that
Rewriting
as
its behavior in time can be calculated using Equations (
32), (
4), and (
10):
which is of course strictly negative, for all
t, as long as
and
are not identically zero. Hence, if
is not zero throughout
,
will decrease monotonically for as long as
f is not (identically) equal to 1 on
, and therefore necessarily converges to 0, a value it can only attain when
or, equivalently, when
. We have thus established a strong H-theorem showing that, in the case of Nelson dynamics, any probability distribution
P necessarily converges to
, if the latter does not become zero identically. Note that this excludes the case of a free particle for which
, for all
x, which means that
tends to zero even when
f does not converge to 1.
A result, similar to the above, is also easily established for
since
dominates the latter, or alternatively from the formula
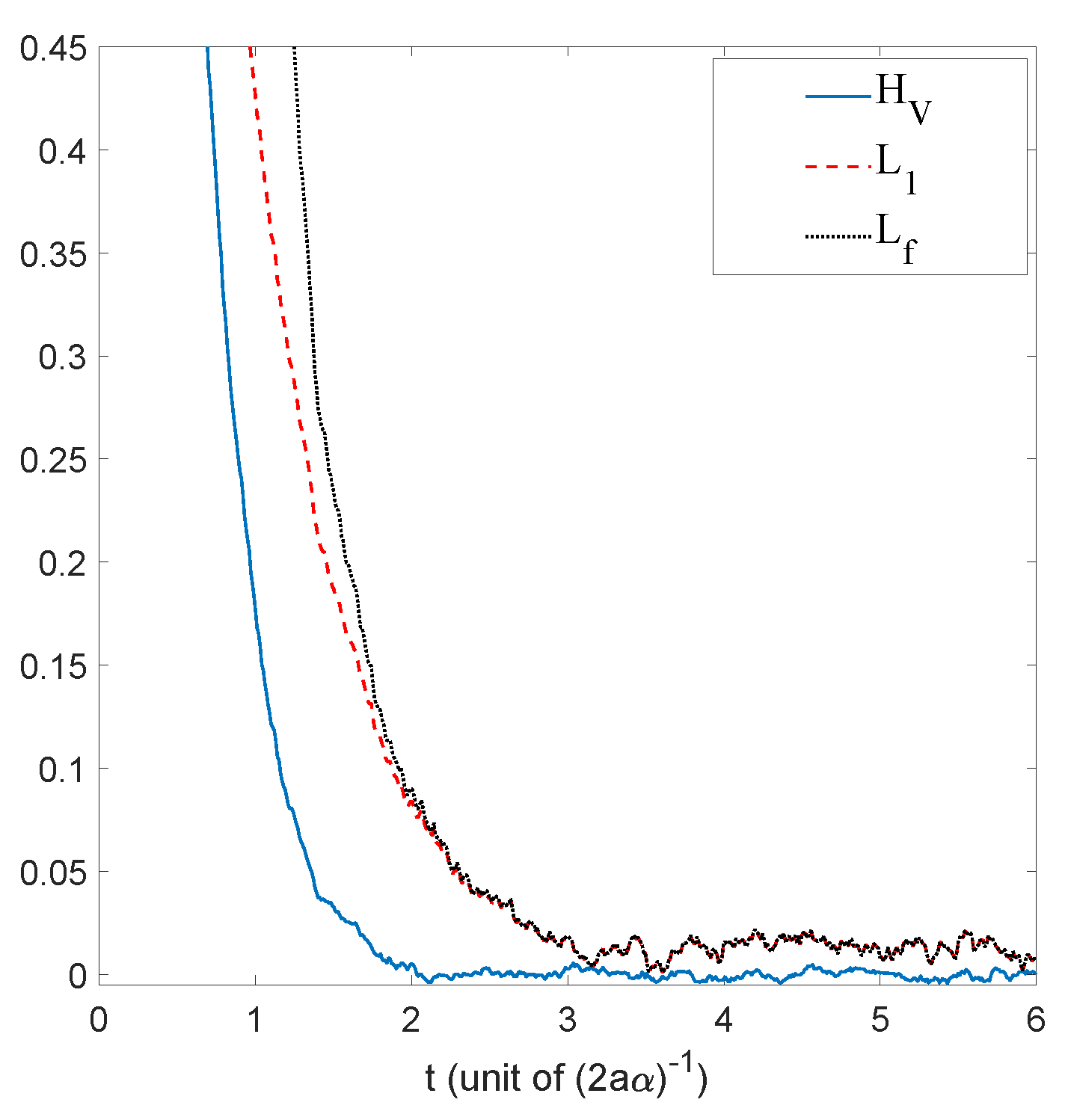
The above results show that (excluding the case of the free particle) Nelson dynamics, naturally, exhibits relaxation towards quantum equilibrium and that it does so for general initial probability distributions (at least, as long as the initial distribution is smooth enough). In this stochastic setting, there is therefore no need for any assumptions on the microstructure of the initial distributions, nor is there any need for the coarse-grained hypothesis when deriving an H-theorem.
Note that these results also show that we have, in fact, convergence of the distribution
P to the quantum equilibrium distribution
in the
norm. This is a consequence of the so-called Csiszár-Kullback-Pinsker inequality [
43]:
where
This generalizes the results by Petroni and Guerra [
22,
23] obtained in their study of the relaxation towards quantum equilibrium in the framework of the Nelson dynamics of a single particle in a harmonic potential. The
norm is also used by Efthymiopoulos et al. [
25] in the context of the dBB theory.
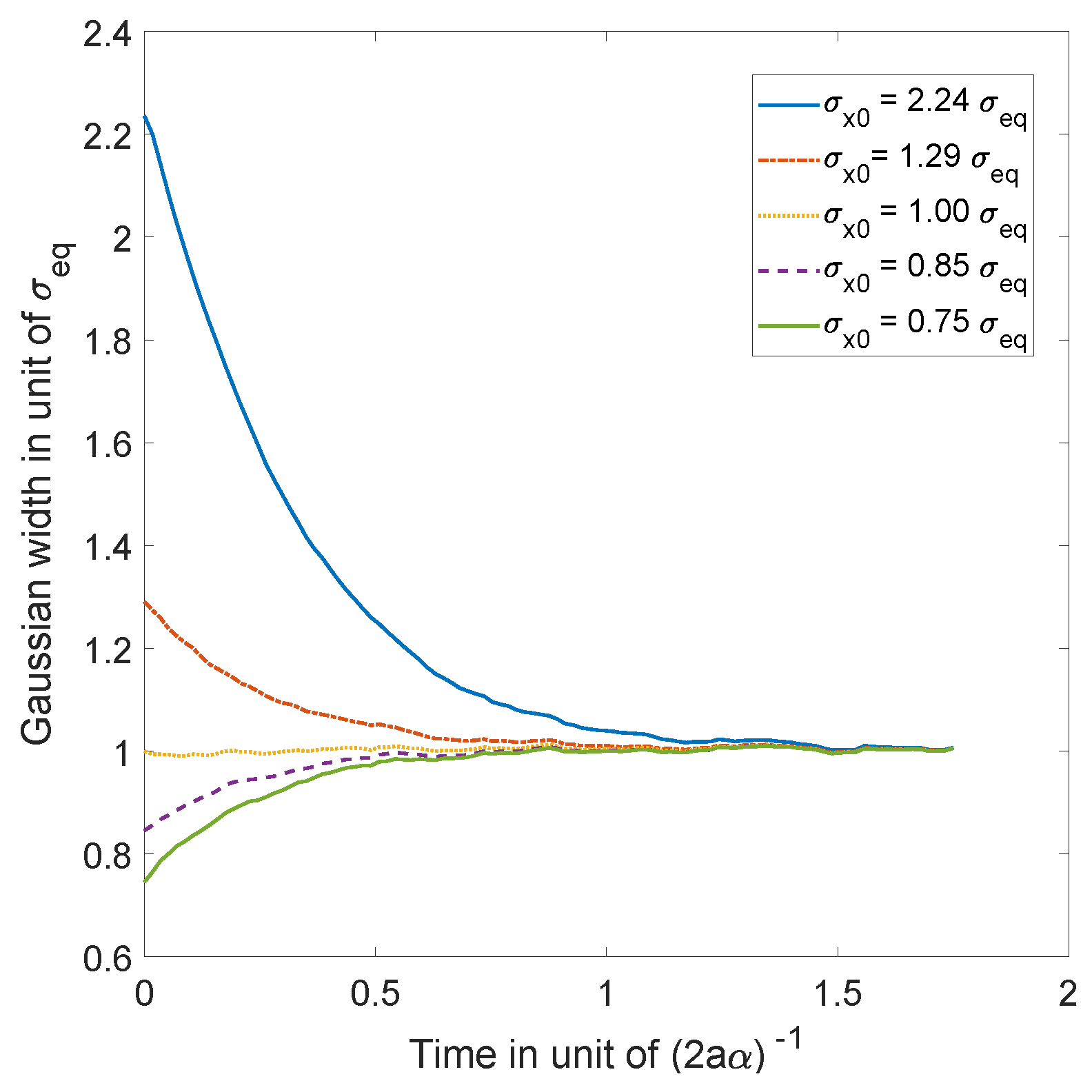
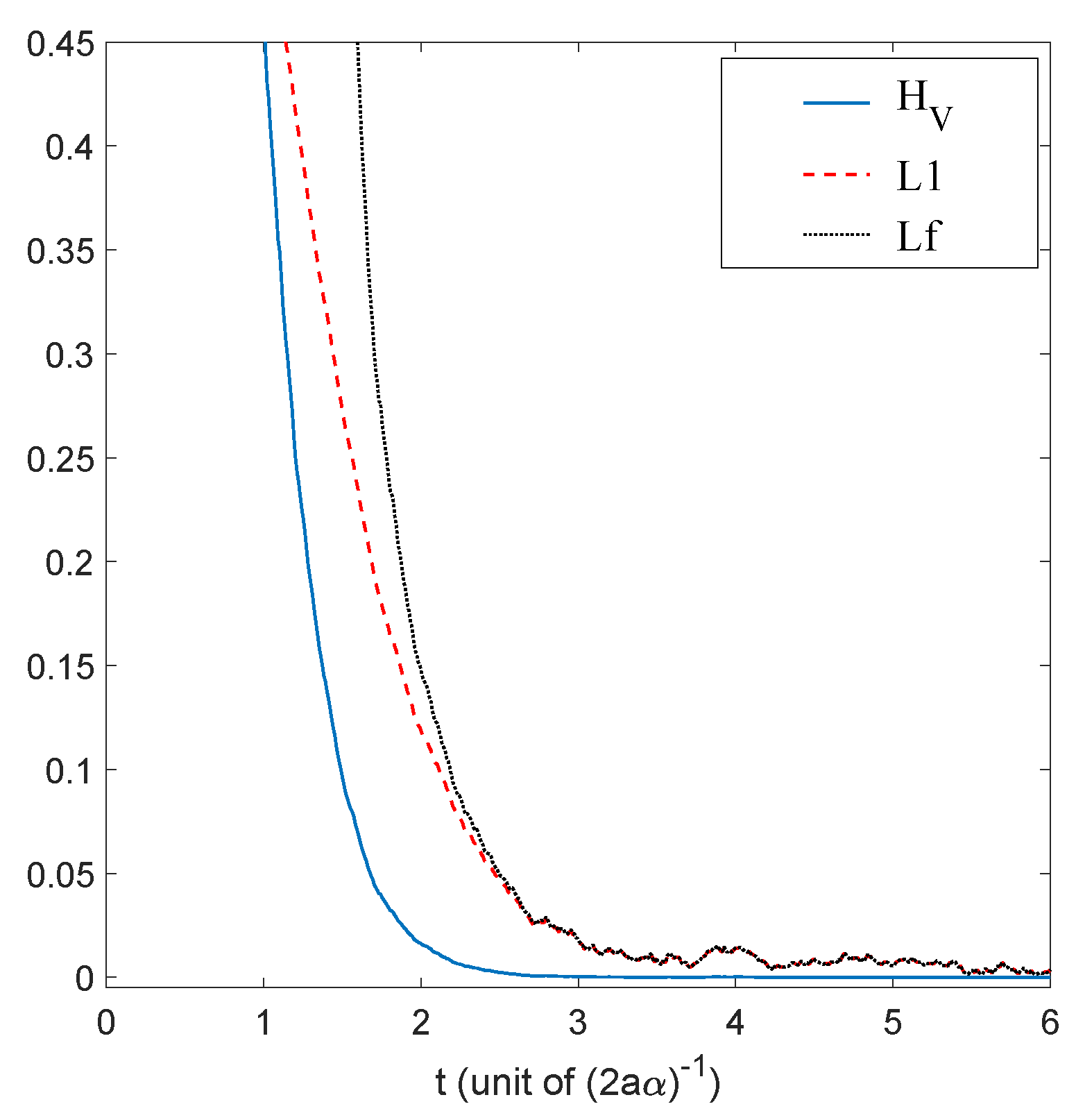
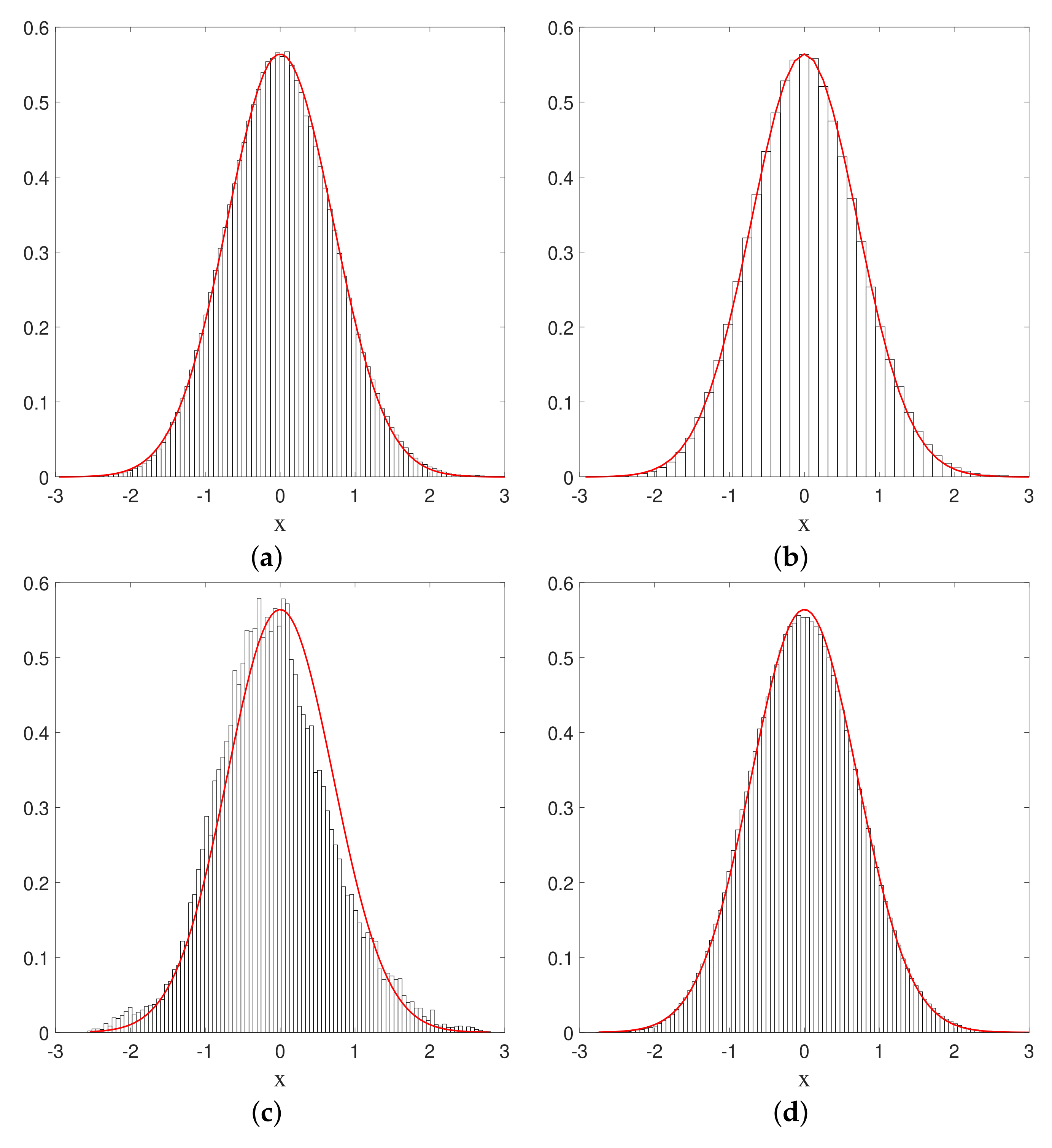
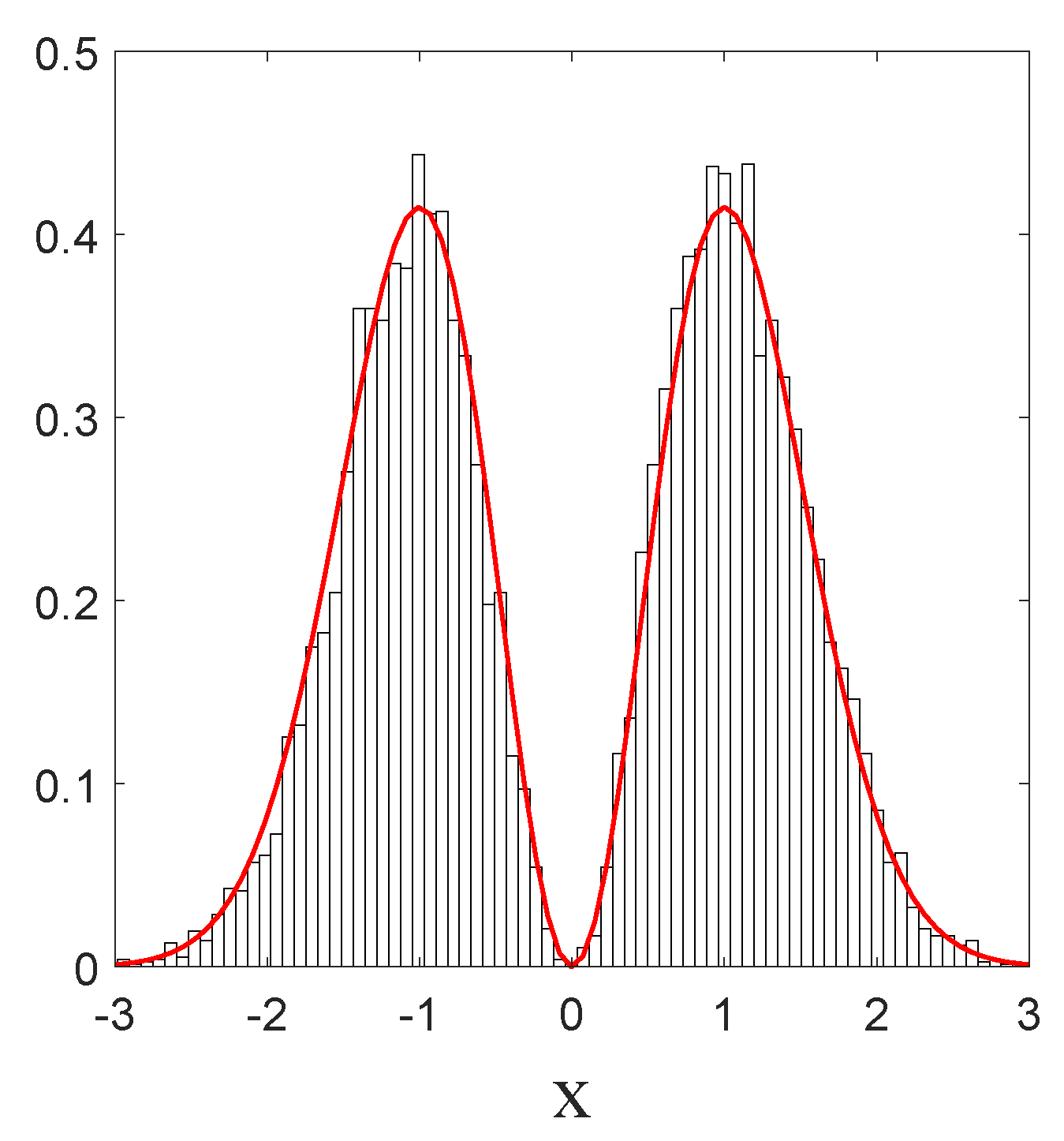
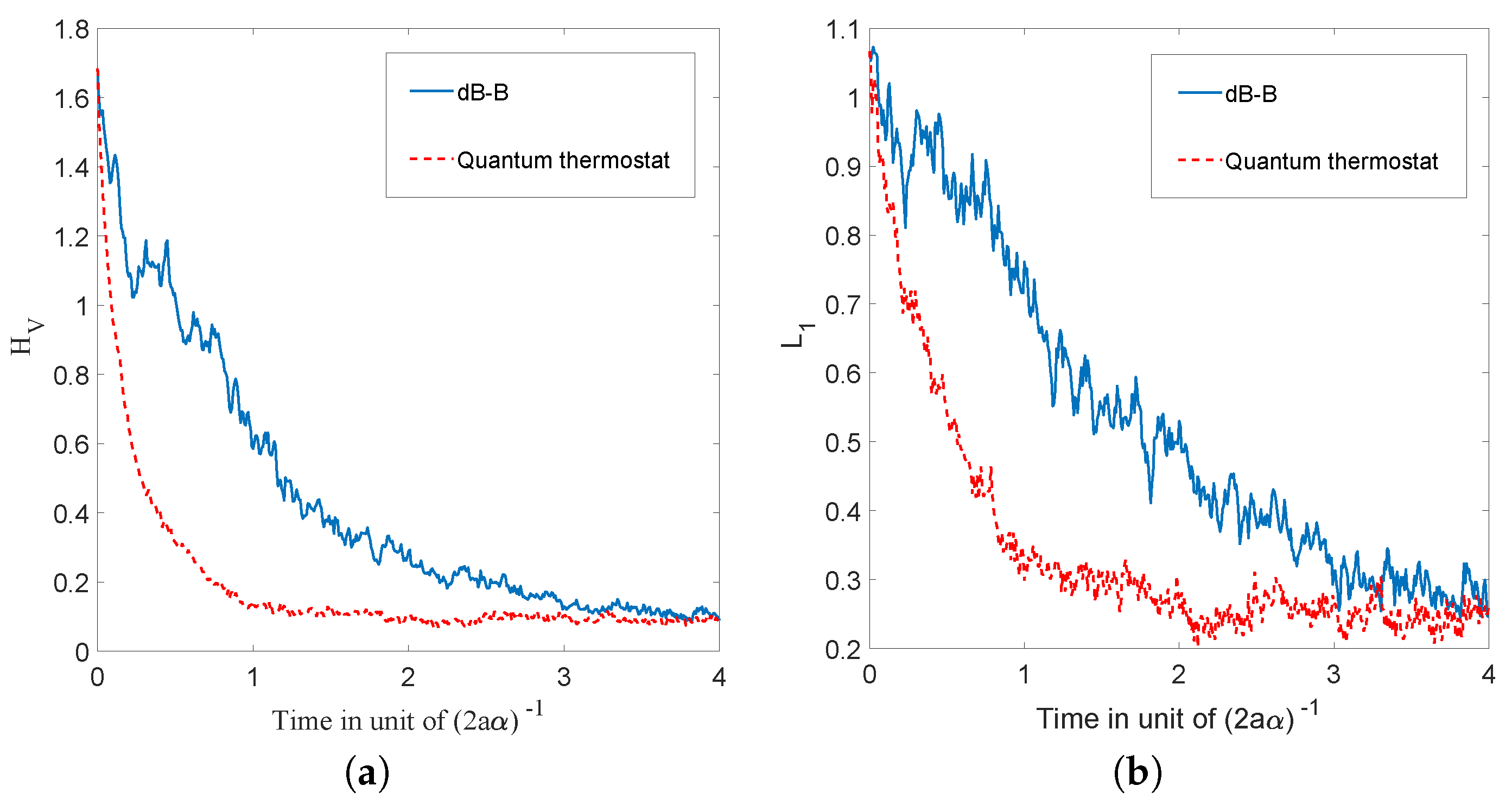
We shall illustrate these results by means of numerical simulations for the case of a ground state for the 1D-harmonic oscillator in
Section 5.4, for the case of the 2D-harmonic oscillator in
Section 6.2, and in the case of a coherent state in
Section 7.1.
A last important remark concerns the influence of possible zeros in the equilibrium distribution
, which would give rise to singularities in the osmotic velocity terms in the Ito equation, Equation (
16), or in the Fokker–Planck equation, Equation (
18) (or equivalently in Equation (
32)), and might make the functions
and
ill-defined. In
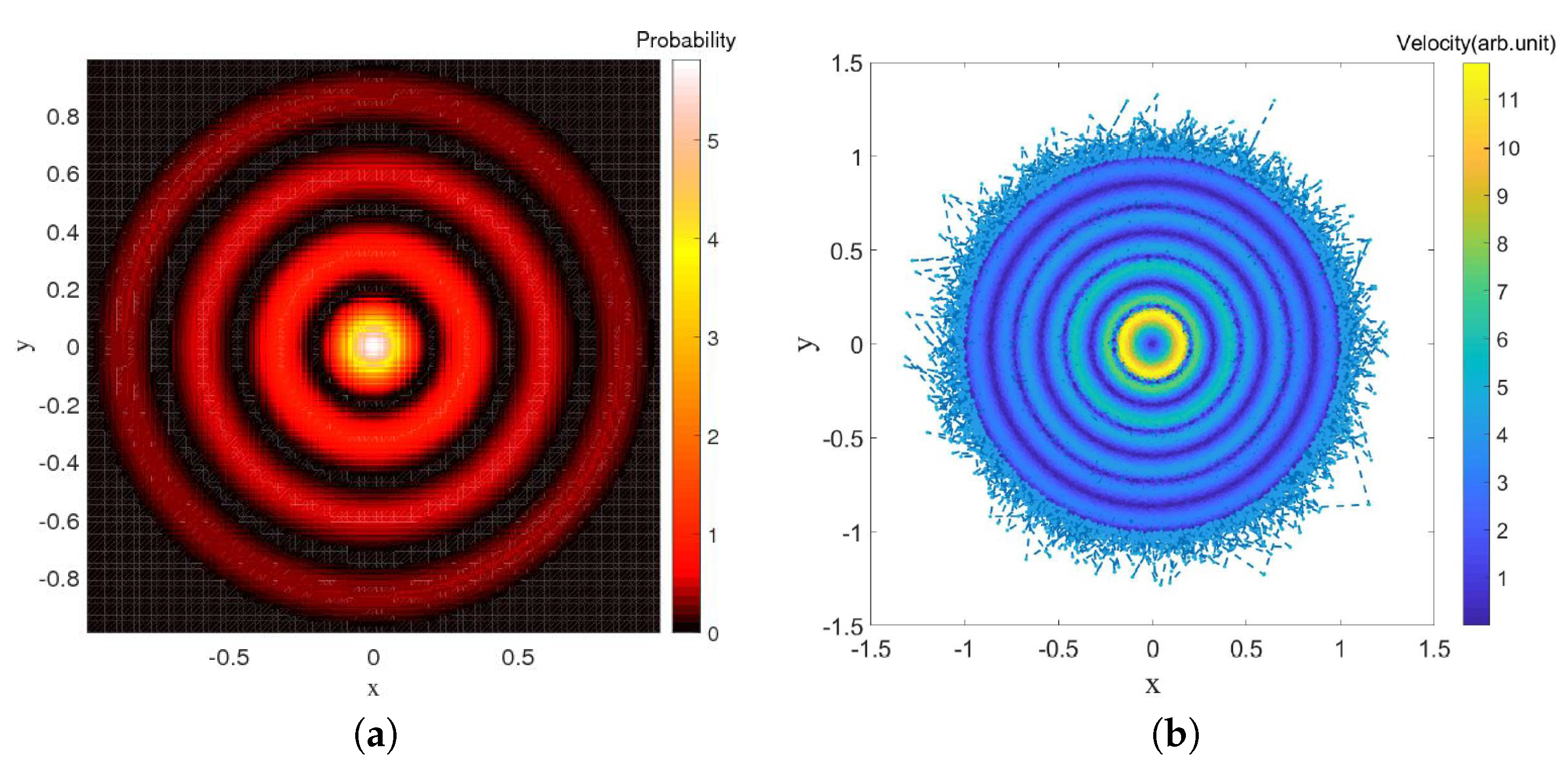
Section 6.2, we discuss the case of the first excited state of the 1D-harmonic oscillator, for which
has a node at
. One could in fact imagine studying higher excited states for which one has a finite number of nodes. In that case, the osmotic velocity of Equation (
15) will have simple poles at a finite number of positions in
x. At the level of the Ito equation, one would not expect a finite set of poles to cause any particular problems, not only because the probability of hitting a pole exactly in the stochastic evolution is zero but also because the osmotic term tends to move the particle away from the pole very quickly. Similarly, a finite number of simple poles in the convection-diffusion equation, Equation (
32), for
f only influence the velocity field in the convection term in a finite number of distinct places, and it is to be expected that this would have the effect of actually enhancing the mixing of information in the system.
Moreover, it is also clear that simple nodes in
only give rise to (a finite number of) logarithmic singularities in the integrand of
and that the integral in Equation (
27) therefore still converges. The H-theorem for
derived above is thus still valid, and an arbitrary distribution
P (sufficiently smooth) will still converge to quantum equilibrium, even in the presence of nodes for
. The same cannot be said, however, of the function
, as simple zeros in
give rise to double poles in the integrand and a possible divergence of the integral of Equation (
28). Hence, at the beginning of the evolution, for an arbitrary
P, the function
might take an infinitely large value (the integrand only diverges when
, i.e., when it is positive) but as soon as convergence sets in (which is guaranteed by the H-theorem for
), the divergent parts in its integrand will be smoothed out and the function
will take finite values that converge to zero as time goes on. Of course, when calculating these quantities for the results of numerical simulations, there is always some amount of coarse-graining going on and genuine infinities never occur.
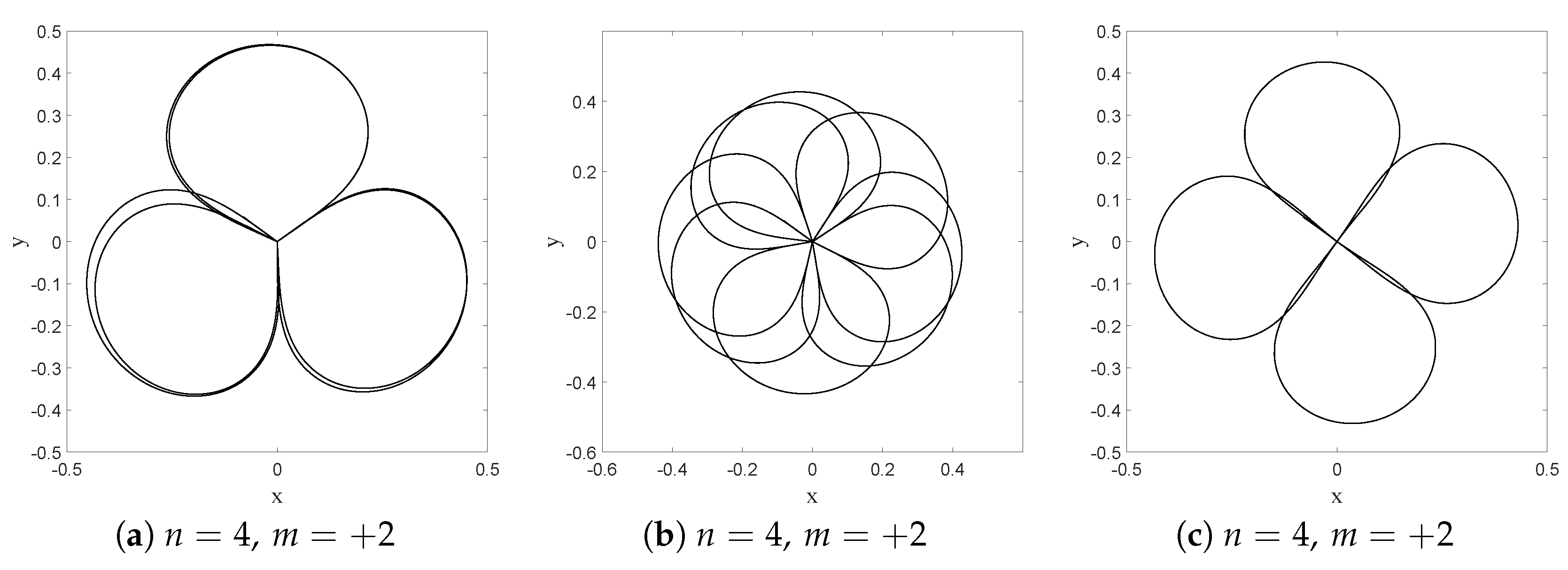
8. Dynamical Model for Droplets and Double Quantization of the 2-D Harmonic Oscillator
In this section we shall focus on the description of droplets dynamics as described in [
9,
52], for a magnetized droplet moving in an isotropic 2-D harmonic potential. We shall show that dBB dynamics allows us to reproduce some of the main features of the experimental observations. In [
9,
52], it is reported that stable structures appear in the droplets dynamics whenever a double quantisation condition is satisfied. The Hamiltonian of the isotropic 2-D harmonic oscillator being invariant under rotations, we may indeed impose a double quantisation constraint, requiring that the energy states of the 2D quantum harmonic oscillator are also eigenstates of the angular momentum. In polar coordinates, these states (which are parameterized by two quantum numbers, the energy number
n and the magnetic number
m) are expressed as follows [
58]:
where
are the generalized Laguerre polynomials and
. Note that these solutions are linear combinations of the product of Fock states in
x and
y.
A first experimental result reported in [
9] is the following: trajectories are chaotic and nearly unpredictable unless the spring constant of the harmonic potential takes quantized values that are strongly reminiscent of energy quantization (under the condition that, during the experiment, the size of the orbits is fixed once and for all). For quantized energies—in our case given by
, for some “effective” value of
ℏ to be determined from actual experiments—stable orbits, to which one can attribute yet another quantum number, appear, this time for the angular momentum, which is strongly reminiscent of the magnetic number (the eigenvalue of the orbital momentum, perpendicular to the surface of the vessel, is given by the product of
ℏ and
m). In [
9] it is shown, for instance, that for the first excitation (
n = 1,
) droplet orbits are circular or oval, turning clockwise or anti-clockwise depending on the sign of
m. At the second energy level (
n = 2,
), ovals appear again for
and lemniscates for an average value of the angular momentum
. At the fourth energy level (
n = 4,
), trefoils appear (for
).
We simulated dBB trajectories, always considering a superposition of one of the aforementioned doubly quantized eigenstates
with the ground state:
where
and
are real numbers with
. Computing the guidance relation of Equation (
11) for a single eigenstate (
74), one ends up with a value for
for which the trajectories are circles of radius
R around the origin, with tangential velocities proportional to
. In particular, the dynamics is frozen when
.
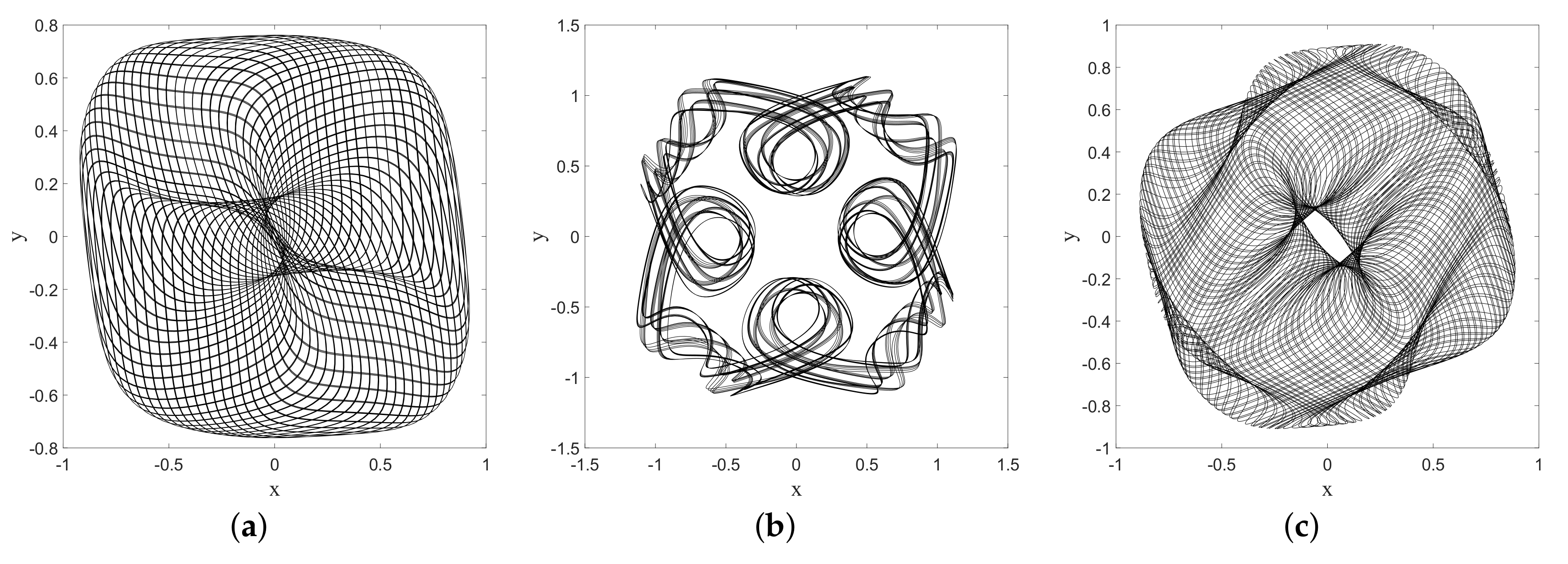
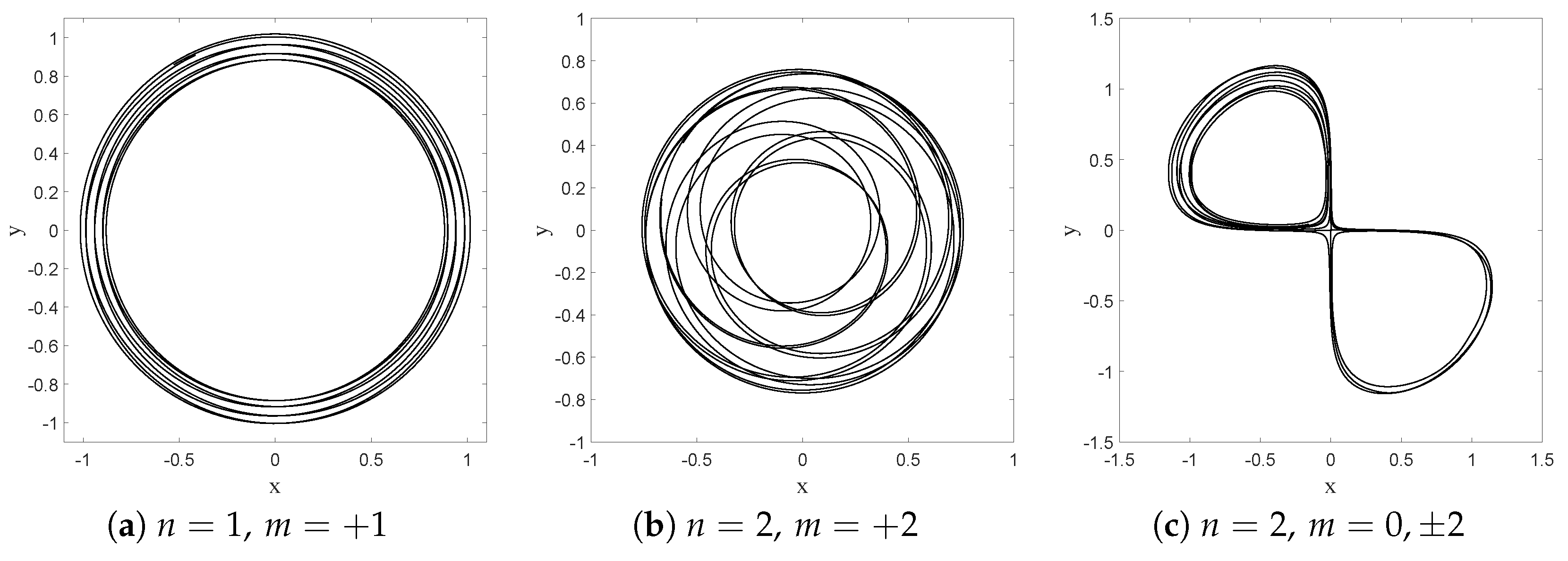
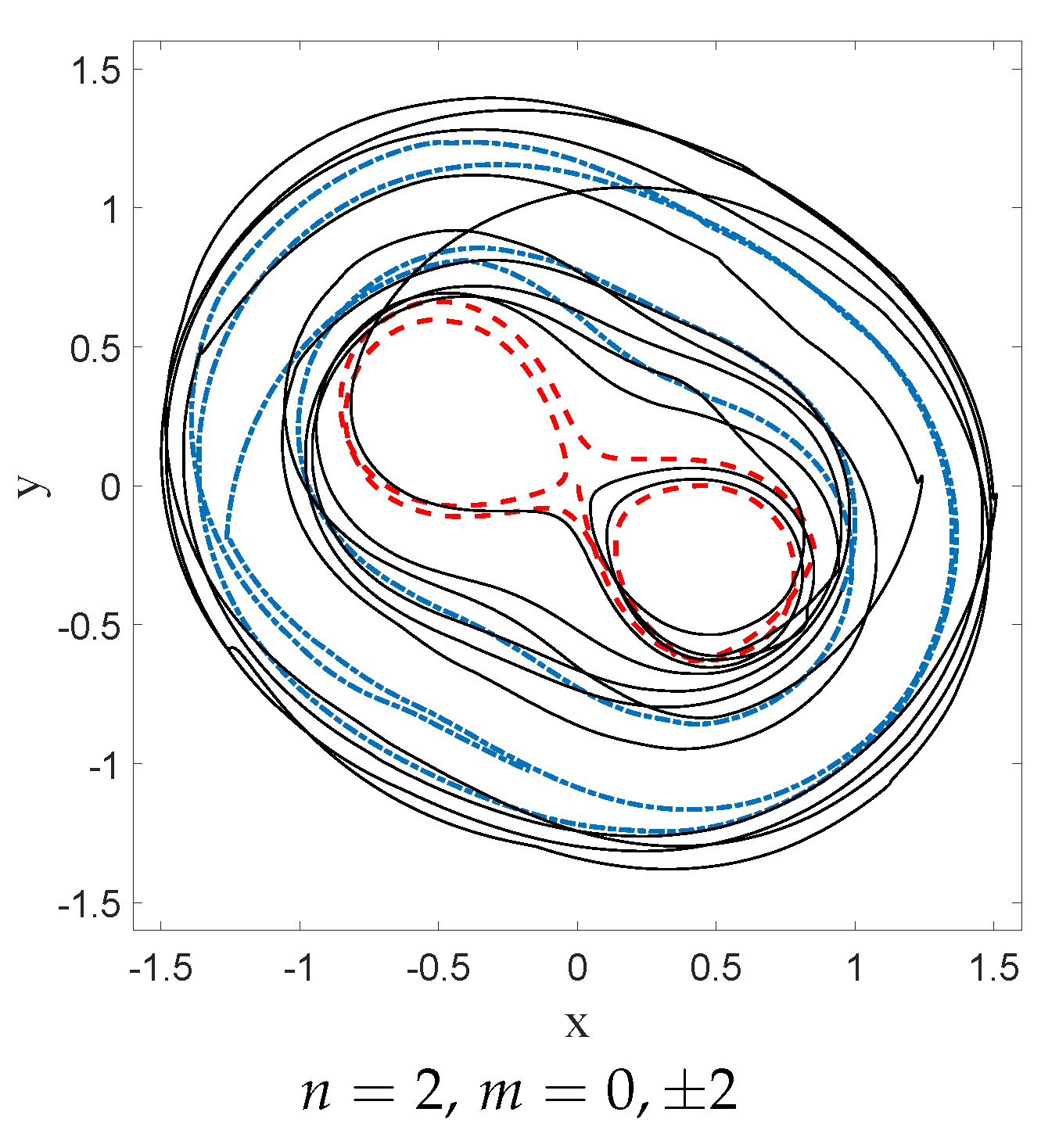
Mixing the wave function with the ground state, however, generates a periodic (in time) component in the dBB velocity field, which turns circular orbits into ovals when
is small enough, and eventually generates more complex structures, such as “rosaces” instead. We also tuned the energy difference between the ground state and the excited states such that two timescales characterize the dynamics. These are the “centrifugal” period, necessary for drawing a full circle around the origin, which varies as
, and the “Bohr” period which varies like
, where
T is the classical period of the oscillator. Tuning these parameters, we were able to simulate dBB trajectories very similar to those reported in [
9]. For instance, we found circles and ovals (see
Figure 15a,b) for
and
. Note that the lemniscate cannot be obtained with a superposition of the ground state and the
state for which dBB velocities are necessarily purely radial, contrary to the suggestion made in [
9]. Instead, it should be generated with a superposition of the ground state with
, and
in which the weights of the
and
components are slightly different (see
Figure 15c).
Figure 16 shows further detail of the evolution along this trajectory. Tuning the energy, we were also able to generate a trefoil and a “rosace” (see
Figure 17).
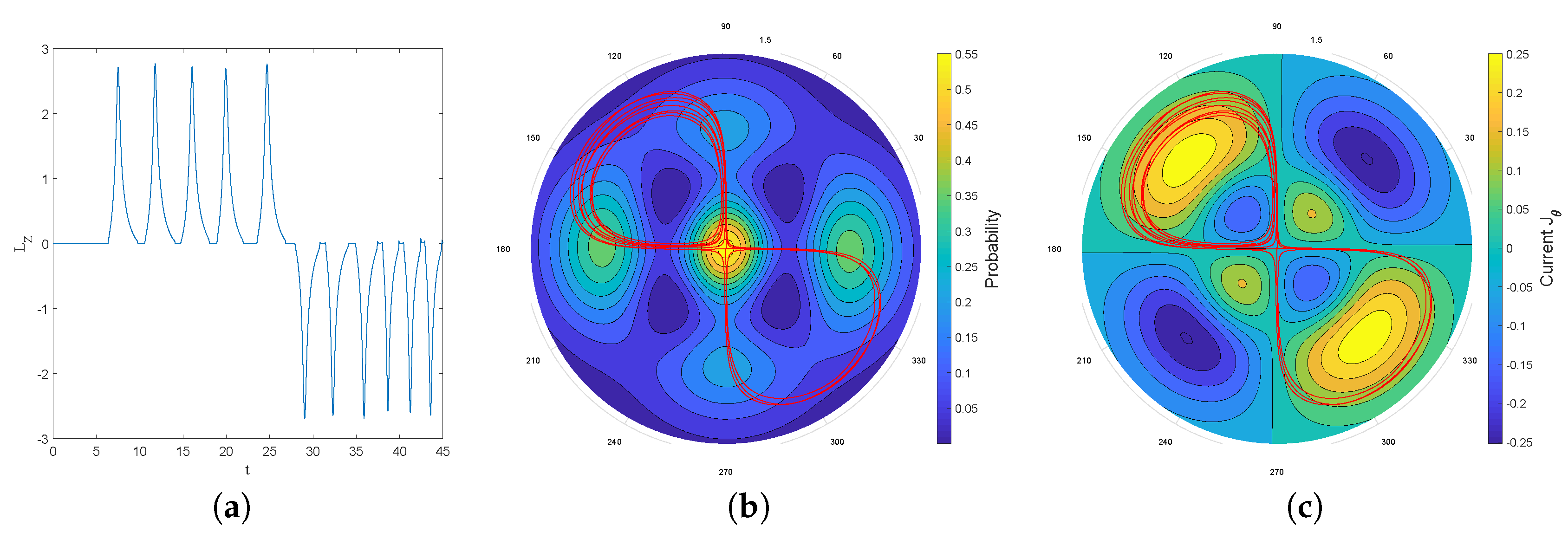
It is worth noting, however, that chaos is omnipresent in the dBB dynamics for this system, in the sense that the trajectories exhibit an extreme sensitivity to the initial conditions, which explains why these dBB orbits mimicking stable droplets orbits are in general unstable. For instance,
Figure 18 shows intermittent transitions between an oval trajectory and a lemniscate (as has also been reported in [
9]), for a superposition of the ground state with the
, and
states. Preliminary results furthermore show that the trajectories are also unstable under Nelson dynamics, i.e., in the presence of “noise,” whenever this noise (parameterized by
in (
16)) exceeds a critical value. Note that many experiments involving droplets are characterized by a lack of stability and predictability. For instance, the appearance of interferences similar to those obtained in a double slit experiment (see [
49,
59] for a description
à la Nelson of the double slit experiment) has been attributed to “air currents” in [
60]. Therefore, although our approach might not explain every detail of the double quantization reported in [
9], it does reproduce many of its essential features, and we believe it would be very interesting to deepen this analogy. For instance, having access to the empirical values of the weights of the ground state, or of the effective values of
ℏ and of the mass in the case of droplets [
56], would allow us to test our model in real detail.
Another experiment, reported in [
61], during which both the position of the droplet and the excitation of the bath are monitored, and where a superposition between two distinct modes of the bath is reported, could also provide more insight and might offer some means to test the validity of our model: using exactly the same observation device, but this time in the case where the droplet undergoes a 2-D isotropic potential, would allow one to check whether the modes of the bath are similar to the
quantum modes which we associate with the quantized droplets trajectories.
9. Conclusions and Open Questions
In this paper we studied stochastic, Nelson-like dynamics and dBB dynamics, with the aim of simulating the dynamics of droplets. The stochastic approach has the merit that it explicitly takes into account the influence of noise on the dynamics [
59,
62]. In contrast to experiments where noise is considered to be a parameter that should be minimized, here, noise is considered to be a relevant parameter for the dynamics (see also [
53]). For instance, as we have shown, it plays an essential role in the relaxation towards equilibrium and in the ergodicity of the dynamics. In the dBB approach, on the other hand, the main ingredient is the chaotic nature of the dynamics [
25]. Both models thus shed a different light on the dynamics and could possibly fit diverse sets of regimes in droplet dynamics. Note that in the limit where the amplitude of the Brownian motion in our Nelson dynamics tends to zero, the dynamics approaches dBB dynamics very closely. In sufficiently complex situations (e.g., when the mixing process due to the presence of zeros in the wave function becomes effective [
26,
40]), we expect the relaxation to equilibrium to be accompanied by chaotic rather than stochastic dynamics, as one has in Nelson dynamics (although Nelson dynamics with small but non-zero Brownian motion is hard to distinguish from dBB dynamics, it has the advantage that relaxation is guaranteed to occur, even in the absence of coarse graining and/or mixing).
Ultimately, experiments ought to indicate whether it is relevant, with respect to droplet phenomenology, to formalize the dynamical influence of noise à la Nelson (and/or dBB) as we did in the present paper. We have formulated several proposals in this sense in
Section 6.1 and
Section 8. As emphasized throughout the paper, however, our models should be seen as a first step in the direction of a dynamical model, which remains to be formulated, combining Nelson’s stochastic dynamics (and/or dBB dynamics) and memory effects. We think that the results of
Section 8 show that this is a promising program for future research.
Finally, it is worth recalling some of the problems that arose when first de Broglie and then Bohm and Nelson developed their theories aimed at deriving quantum dynamics (statistics) as an emergent property, i.e., resulting from an underlying “hidden” dynamics.
The most severe problem is undoubtedly non-locality, which was recognized by Bohm [
11,
12] to be an irreducible feature of dBB dynamics (see also [
19,
63] for similar conclusions concerning Nelson-type dynamics). Today, under the influence of the work of John Bell [
64] and his followers, it is widely recognized that quantum theory is irreducibly non-local, which makes it particularly difficult to mimic using classical models. Note that entanglement and non-locality (as well as decoherence, which is the corollary of entanglement [
65]) only appear if we consider more than one particle at a time, which explains why we did not address these fundamental questions in the core of the paper, where a single droplet is described. It would be interesting to enlarge our model such that the presence of the environment can be taken into account. This would require incorporating the description of open quantum systems, for which a generalization of Bohmian dynamics has been developed in the past [
66,
67,
68,
69], but obviously this is beyond the scope of the present paper.
Another problem concerns the fact that the pilot wave is a complex function. This poses still unresolved problems in the case of Nelson dynamics because Nelson’s diffusion process does not make it possible [
70,
71] to fix the phase of the wave function unequivocally (see [
72] for an interesting proposal involving a multivalued wave function, also based on Zitterbewegung). In our approach, which is mainly of quantum inspiration, complex wave functions and imaginary phases appear spontaneously, but if we wish to scrutinize the link with the empirically observed modes at the surface of oil baths [
9,
52,
56,
61], it will be important to interpret the exact meaning of this complex phase. In the framework of his double solution program [
73,
74] de Broglie, and others, showed how to derive the Schrödinger equation from a Klein–Gordon equation in the non-relativistic limit. This is only possible provided the real wave bounces at an extremely high frequency (of the order of
). A similar approach has been proposed in the context of droplets phenomenology in [
75], where a complex Schrödinger equation is derived from the Klein–Gordon equation along these lines. Although such (interesting and promising) alternative studies of droplets solve the problem of the appearance of a complex phase in a classical context, it is worth noting that the phenomenological results outlined in
Section 8, concerning the quantization of droplet orbits in the case of a harmonic potential [
9,
52], cannot be explained simply in terms of excited modes of the oil bath, because in these experiments only the droplet undergoes the harmonic potential, the oil bath being electromagnetically neutral. This difficulty actually concerns any classical model in which droplet dynamics is formulated in terms of classical modes of the bath only.
To conclude, in our view, the programs that aim at simulating droplet dynamics with quantum tools or at describing the emergence of quantum dynamics based on droplet dynamics, are still largely incomplete and raise challenging fundamental questions. This Pandora’s box is now open and it will not be closed any time soon, but this is not something to be feared as it offers new and stimulating perspectives for future research in the field.