Agent Inaccessibility as a Fundamental Principle in Quantum Mechanics: Objective Unpredictability and Formal Uncomputability
Abstract
1. Introduction
2. Many-World and Single-World Quantum Interpretations
3. Restricting Agent Access to Ontological Quantum States and Quantum Information
3.1. On the Reality of an Indefinite Quantum Ontology: Contextuality and Relationality
3.2. The Inaccessible Universe and the Limits of Science
3.2.1. On No-Hidden-Variables Theorems in Ontological Quantum Mechanics
3.3. Hidden-Variables in Quantum Mechanics are Agent-Inaccessible Variables
4. Defining the Experimenter Agent
4.1. The Quantum Measurement Problem
4.2. An Early Definition of the Experimenter Agent: “Maxwell’s Demon”
4.3. Recent Definition of the Experimenter Agent: “Epistemic Agency”
“Agency is generally defined as the capacity of humans or other entities to act in the world. Put differently, an agent is defined initially by possessing the capacity to influence causal flows in nature. By prefacing “agent” with the term “epistemic”, attention is drawn to the fact that a complete definition of agency represents more than the mere “capacity to influence causal flows”: an agent possesses knowledge-based, i.e., epistemic, capacity for predictably directing, and redirecting, causal flows, and thus for directing, and redirecting, information flows as well. That is, an epistemic agent holds the power to (statistically) control physical activity based upon an ability to predict the outcome of specific actions on targeted processes in reference to a known standard or goal. In short, an epistemic agent thus manifests in the world a genuine source of operational control”.
5. How does Nature Prohibit Access to the Experimenter Agent?
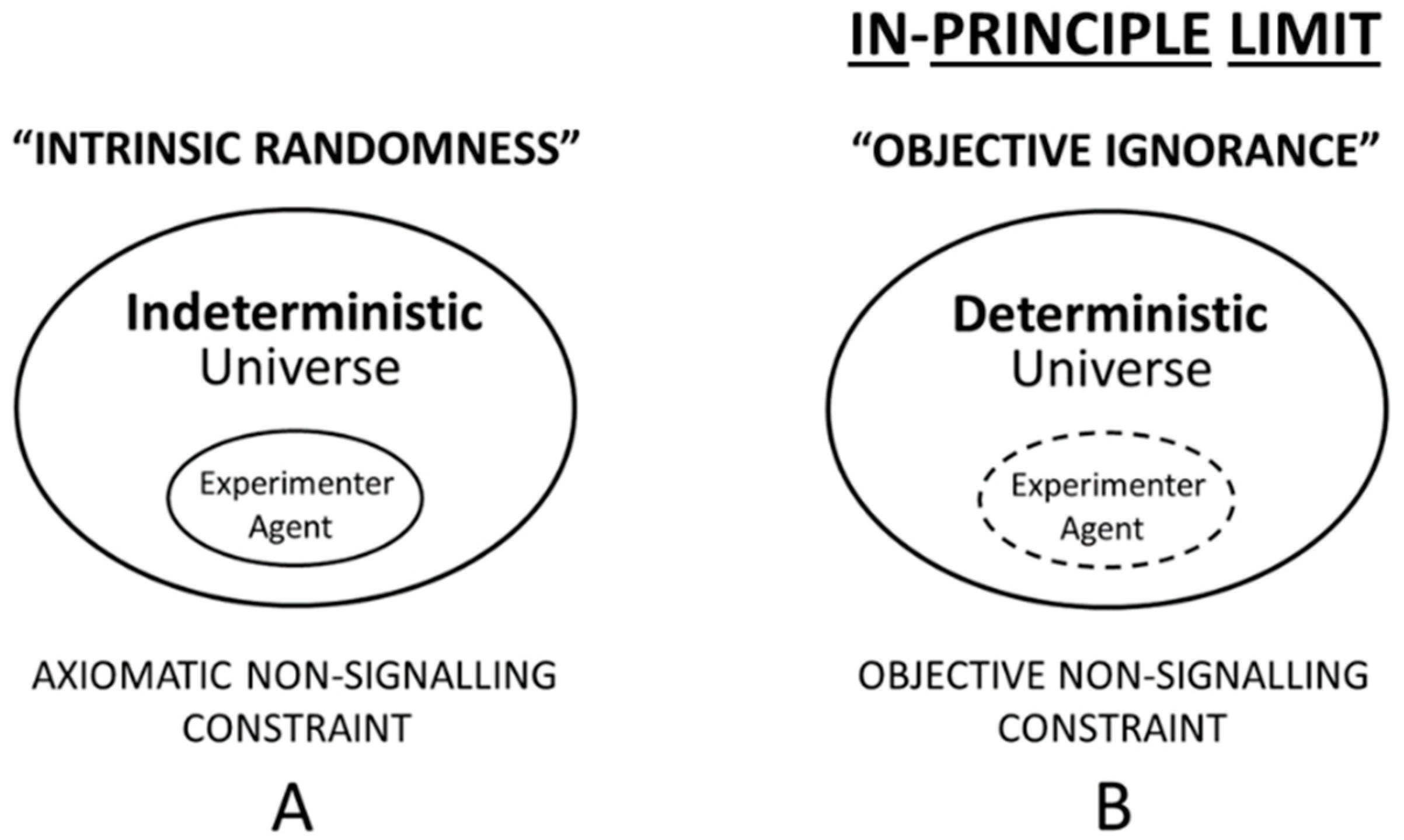
5.1. Orthodox Quantum Mechanics: “Universal Indeterminism”
5.1.1. On the Impossibility of Proving the Truth of Quantum Indeterminism
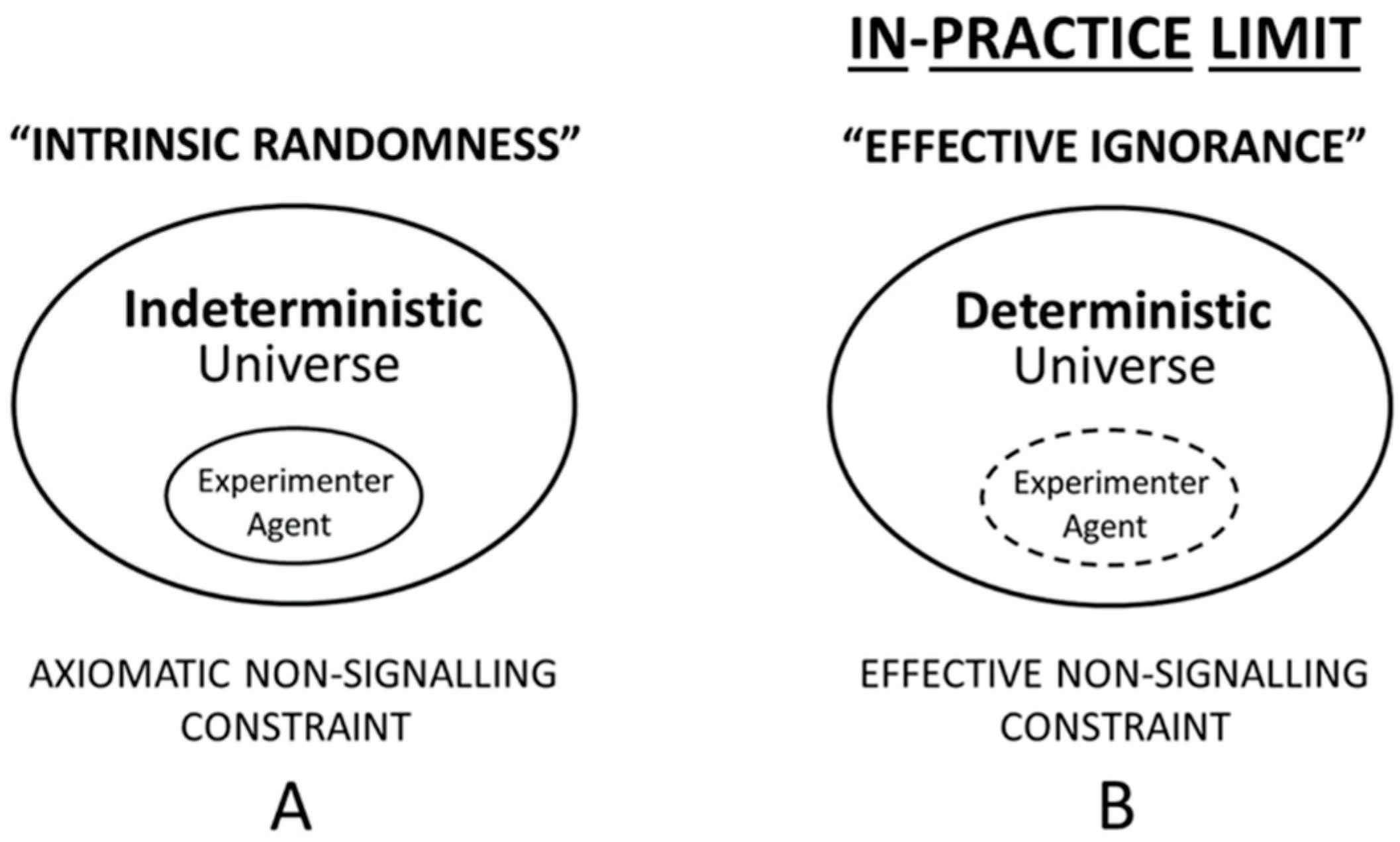
5.2. Ontological Quantum Mechanics: “Effective Ignorance in Global Determinism”
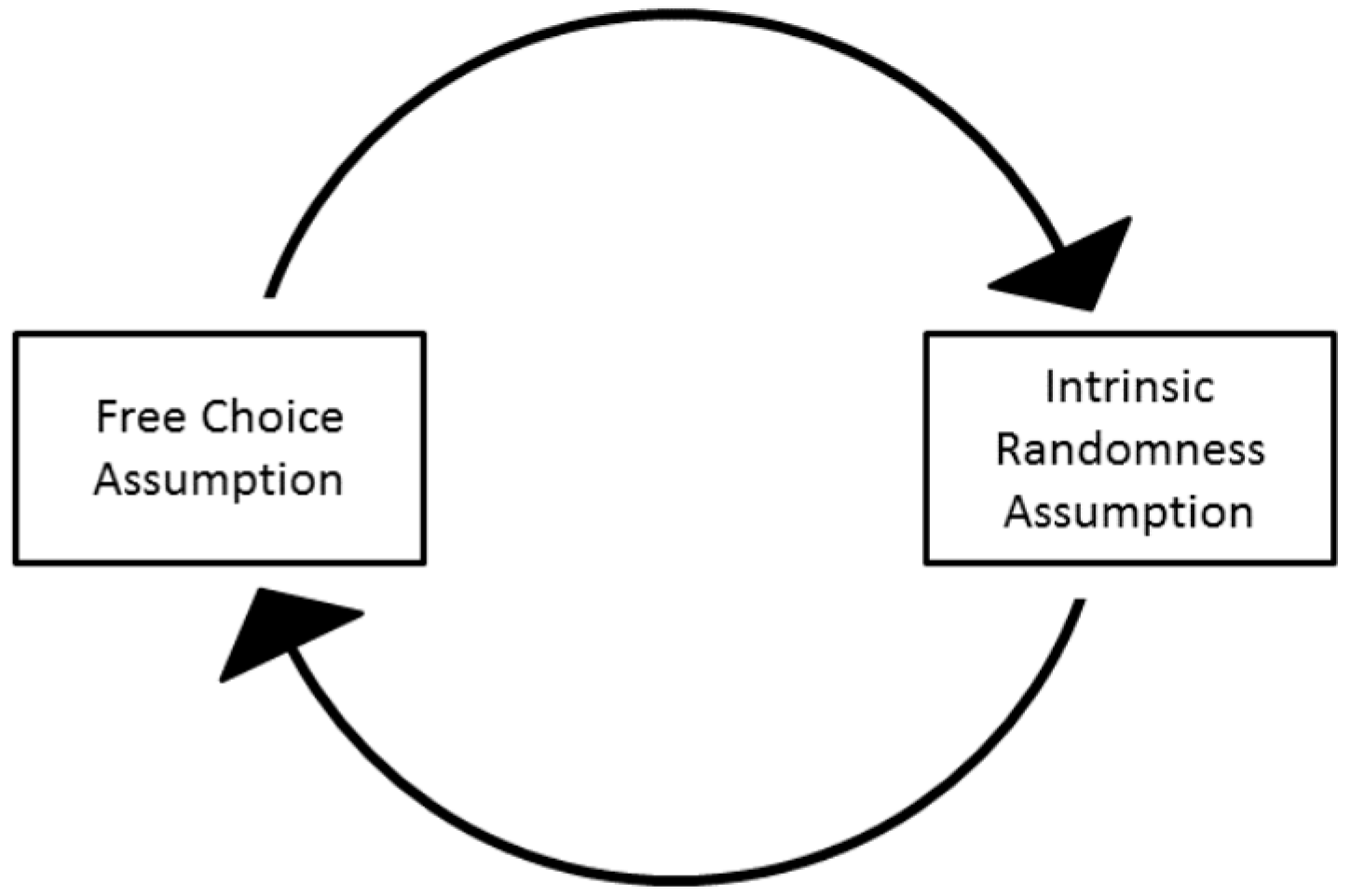
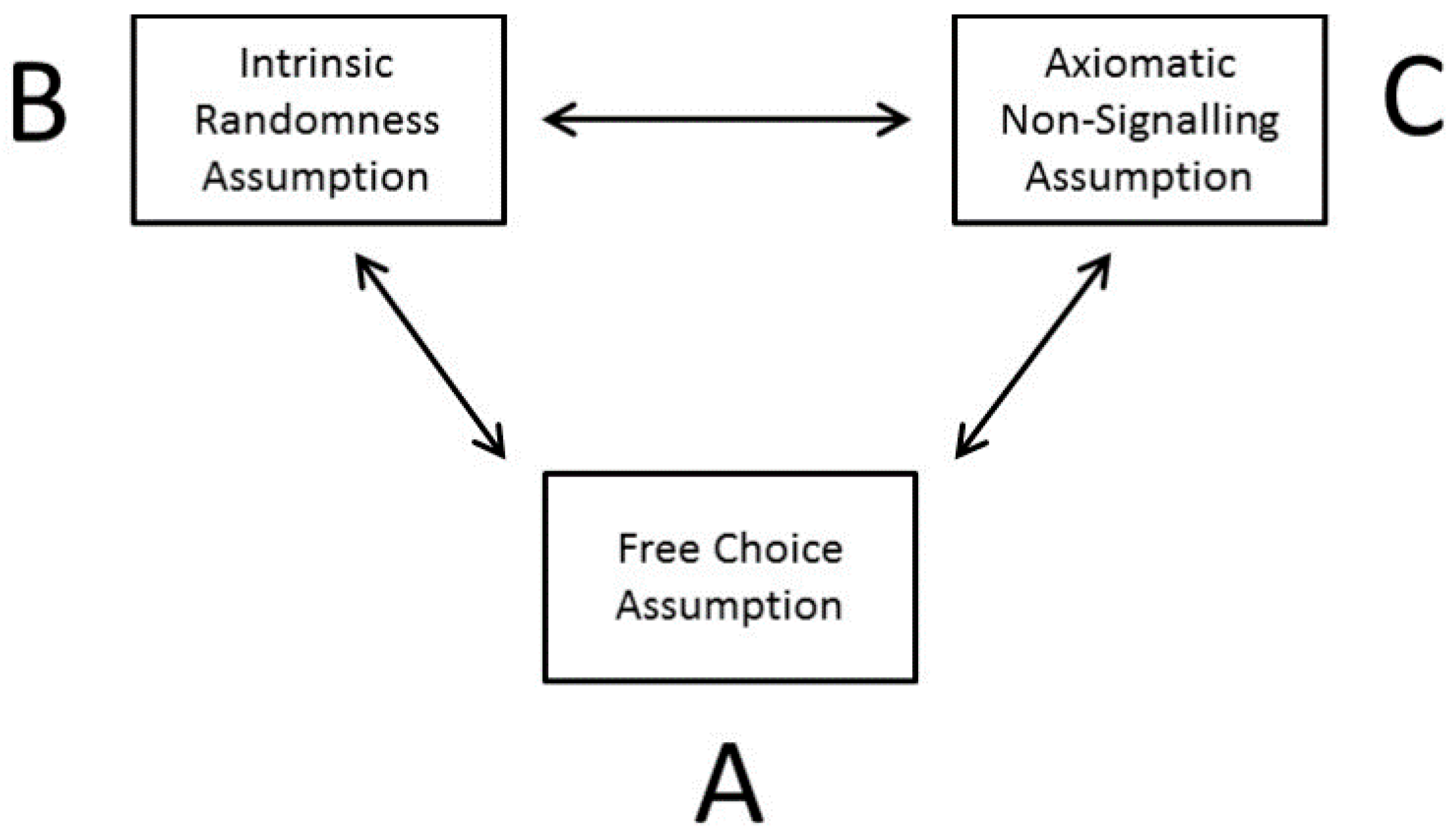
5.2.1. Understanding John Bell’s Concept of “Free Variables” for Quantum Mechanics
“Consider the extreme case of a ‘random’ generator which is in fact perfectly deterministic in nature—and, for simplicity, perfectly isolated. In such a device the complete final state perfectly determines the complete initial state—nothing is forgotten. And yet for many purposes, such a device is precisely a ‘forgetting machine’. A particular output is the result of combining so many factors, of such a lengthy and complicated dynamical chain, that it is quite extraordinarily sensitive to minute variations of any one of many initial conditions. It is the familiar paradox of classical statistical mechanics that such exquisite sensitivity to initial conditions is practically equivalent to complete forgetfulness of them.”
5.2.2. Criticizing the Weak Option Interpretation
5.3. Ontological Quantum Mechanics: “Objective Ignorance in Global Determinism”
6. In Search of Incomputable Nature: Quantum Reality and Quantum Randomness
6.1. Computational Approaches to Quantum Theory Invoking Nonlinear Interactions
6.2. Quantum Ontology and the Information-Theoretic Paradigm in Quantum Mechanics
6.3. Could Hidden Variables Represent Uncomputable Variables Such as Turing-Incomputable Variables?
6.4. The Non-Signaling Theorem and Effective versus Objective Computational Constraints
6.5. Quantum Randomness and Turing Incomputability
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys. Rev. 1952, 85, 166–179. [Google Scholar] [CrossRef]
- Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables. II. Phys. Rev. 1952, 85, 180–193. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. The Undivided Universe: An Ontological Interpretation of Quantum Theory; Routledge: London, UK, 1993. [Google Scholar]
- Holland, P.R. The Quantum Theory of Motion; Cambridge University Press: Cambridge, UK, 1993; ISBN 0-521-35404-8. [Google Scholar]
- Bricmont, J. Making Sense of Quantum Mechanics; Springer: Heidelberg, Germany, 2016. [Google Scholar]
- Norsen, T. Foundations of Quantum Mechanics; Springer: Heidelberg, Germany, 2018. [Google Scholar]
- Dürr, D.; Teufel, S. Bohmian Mechanics; Springer: Heidelberg, Germany, 2009. [Google Scholar]
- Tumulka, R. Bohmian mechanics. In The Routledge Companion to the Philosophy of Physics; Wilson, A., Ed.; Routledge: London, UK, 2018. [Google Scholar]
- Harrigan, N.; Spekkens, R.W. Einstein, incompleteness, and the epistemic view of quantum states. Found. Phys. 2010, 40, 125–157. [Google Scholar] [CrossRef]
- Pusey, M.F.; Barrett, J.; Rudolph, T. On the reality of the quantum state. Nat. Phys. 2012, 8, 475–478. [Google Scholar] [CrossRef]
- Leifer, M.S. Is the quantum state real? An extended review of ψ-ontology theorems. Quanta 2014, 3, 67–155. [Google Scholar] [CrossRef]
- Leifer, M.S.; Pusey, M.F. Is a time symmetric interpretation of quantum theory possible without retrocausality? Proc. R. Soc. A 2017, 473, 20160607. [Google Scholar] [CrossRef] [PubMed]
- Wharton, K. A new class of retrocausal models. Entropy 2018, 20, 410. [Google Scholar] [CrossRef]
- Adlam, E.C. Quantum mechanics and global determinism. Quanta 2018, 7, 40–53. [Google Scholar] [CrossRef]
- Adlam, E.C. Spooky action at a temporal distance. Entropy 2018, 20, 41. [Google Scholar] [CrossRef]
- Argaman, N. A lenient causal arrow of time? Entropy 2018, 20, 294. [Google Scholar] [CrossRef]
- Grössing, G.; Fussy, S.; Mesa Pascasio, J.; Schwabl, H. Vacuum landscaping: Cause of nonlocal influences without signaling. Entropy 2018, 20, 458. [Google Scholar] [CrossRef]
- Wolfram, S. Undecidability and intractability in theoretical physics. Phys. Rev. Lett. 1985, 54, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; ISBN 1-57955-008-8. [Google Scholar]
- Church, A. An unsolvable problem of elementary number theory. Am. J. Math. 1936, 58, 345–363. [Google Scholar] [CrossRef]
- Turing, A. On Computable Numbers, with an Application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1936, 42, 230–265. [Google Scholar]
- Everett, H. Relative state formulation of quantum mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Vaidman, L. All is ψ. J. Phys. Conf. Ser. 2016, 701, 012020. [Google Scholar] [CrossRef]
- Schiff, J.; Poirier, B. Quantum mechanics without wave functions. J. Chem. Phys. 2012, 136, 031102. [Google Scholar] [CrossRef] [PubMed]
- Hall, M.J.W.; Deckert, D.-A.; Wiseman, H.M. Quantum phenomena modeled by interactions between many classical worlds. Phys. Rev. X 2014, 4, 041013. [Google Scholar] [CrossRef]
- Ghadimi, M.; Hall, M.J.W.; Wiseman, H.M. Nonlocality in Bell’s theorem, in Bohm’s theory, and in many interacting worlds theorising. Entropy 2018, 20, 567. [Google Scholar] [CrossRef]
- Walleczek, J.; Grössing, G. Nonlocal quantum information transfer without superluminal signalling and communication. Found. Phys. 2016, 46, 1208–1228. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Sutherland, R.I. Bell’s theorem and backwards-in-time causality. Int. J. Theor. Phys. 1983, 22, 377–384. [Google Scholar] [CrossRef]
- Price, H. Time’s Arrow & Archimedes’ Point: New Directions for the Physics of Time; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Wharton, K. Quantum states as ordinary information. Information 2014, 5, 190–208. [Google Scholar] [CrossRef]
- Price, H.; Wharton, K. Disentangling the quantum world. Entropy 2015, 17, 7752–7767. [Google Scholar] [CrossRef]
- Frauchiger, D.; Renner, R. Quantum theory cannot consistently describe the use of itself. Nat. Commun. 2018, 9, 3711. [Google Scholar] [CrossRef] [PubMed]
- Brukner, C. A no-go theorem for observer-independent facts. Entropy 2018, 20, 350. [Google Scholar] [CrossRef]
- Bub, J. In defense of a “single-world” interpretation of quantum mechanics. arXiv, 2018; arXiv:quant-ph/1804.03267v1. [Google Scholar] [CrossRef]
- Lazarovici, D.; Hubert, M. How single-world quantum mechanics is consistent: Comment on Frauchiger and Renner. arXiv, 2018; arXiv:quant-ph/1809.08070v1. [Google Scholar]
- Zwolak, M.; Zurek, W. Complementarity of quantum discord and classically accessible information. Sci. Rep. 2013, 3, 1729. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Abbott, A.A.; Calude, C.S.; Conder, J.; Svozil, K. Strong Kochen-Specker theorem and incomputability of quantum randomness. Phys. Rev. A 2012, 86, 6. [Google Scholar] [CrossRef]
- Abbott, A.A.; Calude, C.S.; Svozil, K. Value-indefinite observables are almost everywhere. Phys. Rev. A 2014, 89, 032109. [Google Scholar] [CrossRef]
- Abbott, A.A.; Calude, C.S.; Svozil, K. A quantum random number generator certified by value indefiniteness. Math. Struct. Comput. Sci. 2014, 24, e240303. [Google Scholar] [CrossRef]
- Koberinski, A.; Müller, M.P. Quantum Theory as a Principle Theory: Insights from an Information-theoretic Reconstruction. In Physical Perspectives on Computation, Computational Perspectives on Physics; Fletcher, S.C., Cuffaro, M.E., Eds.; Cambridge University Press: Cambridge, UK, 2018; pp. 257–280. [Google Scholar]
- Fuchs, C. Quantum mechanics as quantum information, mostly. J. Mod. Opt. 2003, 50, 987–1023. [Google Scholar] [CrossRef]
- ’t Hooft, G. The Cellular Automaton Interpretation of Quantum Mechanics; Fundamental Theories of Physics; Springer: Berlin/Heidelberg, Germany, 2016; Volume 185. [Google Scholar]
- Elze, H.-T. Quantum features of natural cellular automata. J. Phys. Conf. Ser. 2016, 701, 012017. [Google Scholar] [CrossRef]
- Palmer, T.N. Experimental non-violation of the Bell inequality. Entropy 2018, 20, 356. [Google Scholar] [CrossRef]
- Mermin, N.D. Hidden variables and the two theorems of John Bell. Revs. Mod. Phys. 1993, 65, 803–815. [Google Scholar] [CrossRef]
- Maudlin, T. Quantum Non-locality and Relativity: Metaphysical Intimations of Modern Physics; Wiley-Blackwell: West Sussex, UK, 2011. [Google Scholar]
- Maudlin, T. Ontological clarity via canonical presentation: Electromagnetism and the Aharonov–Bohm effect. Entropy 2018, 20, 465. [Google Scholar] [CrossRef]
- Lazarovici, D.; Oldofredi, A.; Esfeld, M. Observables and unobservables in quantum mechanics: How the no-hidden-variables theorems support the Bohmian particle ontology. Entropy 2018, 20, 381. [Google Scholar] [CrossRef]
- Passon, O. On a common misconception regarding the de Broglie–Bohm theory. Entropy 2018, 20, 440. [Google Scholar] [CrossRef]
- Tumulka, R. On Bohmian mechanics, particle creation, and relativistic space-time: Happy 100th birthday, David Bohm! Entropy 2018, 20, 462. [Google Scholar] [CrossRef]
- Norsen, T. On the explanation of Born-rule statistics in the de Broglie-Bohm pilot-wave theory. Entropy 2018, 20, 422. [Google Scholar] [CrossRef]
- De Gosson, M.A. The symplectic camel and Poincaré superrecurrence: Open problems. Entropy 2018, 20, 499. [Google Scholar] [CrossRef]
- Khrennikov, A. Contextual Approach to Quantum Formalism; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2009. [Google Scholar]
- Khrennikov, A. Classical probability model for Bell inequality. J. Phys. Conf. Ser. 2014, 504, 012019. [Google Scholar] [CrossRef]
- Hiley, B.J.; Van Reeth, P. Quantum trajectories: Real or surreal? Entropy 2018, 20, 353. [Google Scholar] [CrossRef]
- Flack, R.; Hiley, B.J. Feynman paths and weak values. Entropy 2018, 20, 367. [Google Scholar] [CrossRef]
- Walleczek, J. The super-indeterminism in orthodox quantum mechanics does not implicate the reality of experimenter free will. J. Phys. Conf. Ser. 2016, 701, 012005. [Google Scholar] [CrossRef]
- Gisin, N. Why Bohmian mechanics? One- and two-time position measurements, Bell inequalities, philosophy, and physics. Entropy 2018, 20, 105. [Google Scholar] [CrossRef]
- Valentini, A. Signal-locality in hidden-variables theories. Phys. Lett. A 2002, 297, 273–278. [Google Scholar] [CrossRef]
- Bendersky, A.; Senno, G.; de la Torre, G.; Figueira, S.; Acin, A. Non-signaling deterministic models for non-local correlations have to be uncomputable. Phys. Rev. Lett. 2017, 118, 130401. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.S. Einstein-Podolsky-Rosen experiments. In Speakable and Unspeakable in Quantum Mechanics; Cambridge University Press: Cambridge, UK, 1987; pp. 81–92. [Google Scholar]
- Bell, J.S. La nouvelle cuisine. In Speakable and Unspeakable in Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2004; pp. 232–248. [Google Scholar]
- Bohm, D. Quantum Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1951. [Google Scholar]
- Fuchs, C.A.; Schack, R. QBism and the Greeks: Why a quantum state does not represent an element of physical reality. Phys. Scr. 2015, 90, 015104. [Google Scholar] [CrossRef]
- Maxwell, J.C. Theory of Heat; Reprinted Dover: New York, NY, USA, 2001. [Google Scholar]
- Szilard, L. Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen (On the reduction of entropy in a thermodynamic system by the intervention of intelligent beings). Zeitschrift für Physik 1929, 53, 840–856. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin, Germany, 1932. [Google Scholar]
- ‘t Hooft, G. Time, the arrow of time, and quantum mechanics. Front. Phys. 2018, 6, 81. [Google Scholar] [CrossRef]
- Colbeck, R.; Renner, R. A short note on the concept of free choice. arXiv, 2013; arXiv:quant-ph/1302.4446. [Google Scholar]
- Plotnitsky, A. What is complementarity? Niels Bohr and the architecture of quantum theory. Phys. Scr. 2014, 163, 014002. [Google Scholar] [CrossRef]
- Conway, J.; Kochen, S. The free will theorem. Found. Phys. 2006, 36, 1441–1473. [Google Scholar] [CrossRef]
- Conway, J.; Kochen, S. The strong free will theorem. Not. AMS 2009, 56, 226–232. [Google Scholar]
- Bera, M.N.; Acín, A.; Kuś, M.; Mitchell, M.; Lewenstein, M. Randomness in Quantum Mechanics: Philosophy, Physics, and Technology. Rep. Prog. Phys. 2017, 80, 124001. [Google Scholar] [CrossRef]
- Landsman, K. Foundations of Quantum Theory: From Classical Concepts to Operator Algebras; Fundamental Theories of Physics; Springer: Berlin/Heidelberg, Germany, 2017; Volume 188, ISBN 978-3-319-51777-3. [Google Scholar]
- Bell, J.S. The theory of local beables. Epistemol. Lett. 1976, 9, 11, reprinted in Dialectica 1985, 39, 85–96. [Google Scholar]
- Bell, J.S. Free variables and local causality. Epistemol. Lett. 1977, 15, 15, reprinted in Dialectica 1985, 39, 103–106. [Google Scholar]
- Bell, J.S. De Broglie-Bohm, delayed-choice, double-slit experiment, and density matrix. Int. J. Quantum Chem. 1980, 14, 155–159. [Google Scholar] [CrossRef]
- Bell, J.S. On the impossible pilot wave. Found. Phys. 1982, 12, 989–999. [Google Scholar] [CrossRef]
- Bell, J.S. Speakable and unspeakable in quantum mechanics. In Speakable and Unspeakable in Quantum Mechanics; Cambridge University Press: Cambridge, UK, 1987; pp. 169–172. [Google Scholar]
- Walleczek, J.; Grössing, G. The non-signalling theorem in generalizations of Bell’s theorem. J. Phys. Conf. Ser. 2014, 504, 012001. [Google Scholar] [CrossRef]
- Chaitin, G.J. Information, Randomness, and Incompleteness: Papers on Algorithmic Information Theory; Series in Computer Science; World Scientific: Singapore, 1987; Volume 8. [Google Scholar]
- Esfeld, M. Ontic structural realism and the interpretation of quantum mechanics. Eur. J. Philos. Sci. 2013, 3, 19–32. [Google Scholar] [CrossRef]
- Walleczek, J.; Grössing, G. Is the world local or nonlocal? Towards an emergent quantum mechanics in the 21st century. J. Phys. Conf. Ser. 2016, 701, 012001. [Google Scholar] [CrossRef]
- Shimony, A. Controllable and Uncontrollable Non-locality. In Foundations of Quantum Mechanics in Light of the New Technology; Kamefuchi, S., Butsuri Gakkai, N., Eds.; Physical Society of Japan: Tokyo, Japan, 1984; pp. 225–230. [Google Scholar]
- Aharonov, Y.; Cohen, E.; Shushi, T. Accommodating retrocausality with free will. Quanta 2016, 5, 53–60. [Google Scholar] [CrossRef]
- Rozema, L.A.; Darabi, A.; Mahler, D.H.; Hayat, A.; Soudagar, Y.; Steinberg, A.M. Violation of Heisenberg’s measurement-disturbance relationship by weak measurements. Phys. Rev. Lett. 2012, 109, 100404. [Google Scholar] [CrossRef]
- Walleczek, J. (Ed.) Self-Organized Biological Dynamics and Nonlinear Control; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bennett, C.H. Undecidable dynamics. Nature 1990, 346, 606–607. [Google Scholar] [CrossRef]
- Moore, C. Unpredictability and undecidability in dynamical systems. Phys. Rev. Lett. 1990, 64, 2354–2357. [Google Scholar] [CrossRef]
- Cooper, S.B.; Odifreddi, P. Incomputability in Nature. In Computability and Models; Cooper, S.B., Goncharov, S.S., Eds.; Kluwer Academic, Plenum Publishers: New York, NY, USA, 2003; pp. 137–160. [Google Scholar]
- Lloyd, S. Uncomputability and Physical Law. In The Incomputable: Journeys Beyond the Turing Barrier; Cooper, S.B., Soskova, M.I., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 95–104. [Google Scholar]
- Rucker, R. An Incompleteness Theorem for the Natural World. In Irreducibility and Computational Equivalence; Zenil, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 185–198. [Google Scholar]
- Cubitt, T.S.; Perez-Garcia, D.; Wolf, M.M. Undecidability of the spectral gap. Nature 2015, 528, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Cooper, S.B.; Soskova, M.I. (Eds.) The Incomputable: Journeys Beyond the Turing Barrier; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Fletcher, S.C.; Cuffaro, M.E. (Eds.) Physical Perspectives on Computation, Computational Perspectives on Physics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Franke, H.W. Cellular Automata: Models of the Physical World. In Irreducibility and Computational Equivalence; Zenil, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3–10. [Google Scholar]
- French, S. The Structure of the World: Metaphysics and Representation; Oxford University Press: Oxford, UK, 2014; ISBN 9780199684847. [Google Scholar]
- Tzemos, A.C.; Efthymiopoulos, C.; Contopoulos, G. Origin of chaos near three-dimensional quantum vortices: A general Bohmian theory. Phys. Rev. E 2018, 97, 042201. [Google Scholar] [CrossRef]
- Towler, M.D.; Russell, N.J.; Valentini, A. Time scales for dynamical relaxation to the Born rule. Proc. R. Soc. A 2012, 468, 990. [Google Scholar] [CrossRef]
- Efthymiopoulos, C.; Contopoulos, G.; Tzemos, A.C. Chaos in de Broglie-Bohm quantum mechanics and the dynamics of quantum relaxation. Ann. Fond. Louis Broglie 2017, 42, 133–160. [Google Scholar]
- Underwood, N.G. Extreme quantum nonequilibrium, nodes, vorticity, drift, and relaxation retarding states. arXiv, 2018; arXiv:quant-ph/1705.06757v2. [Google Scholar] [CrossRef]
- Islam, T.; Wehner, S. Computability limits non-local correlations. Phys. Rev. A 2012, 86, 042109. [Google Scholar] [CrossRef]
- Calude, C.S. Quantum Randomness: From Practice to Theory and Back. In The Incomputable: Journeys Beyond the Turing Barrier; Cooper, S.B., Soskova, M.I., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 169–181. [Google Scholar]
| Self-Referential Dynamics | Formal Uncomputability |
|---|---|
| Dynamical chaos | Infinite precision detection of initial conditions is impossible in-principle |
| Undecidable dynamics | Infinite computational resources are unavailable in-principle |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walleczek, J. Agent Inaccessibility as a Fundamental Principle in Quantum Mechanics: Objective Unpredictability and Formal Uncomputability. Entropy 2019, 21, 4. https://doi.org/10.3390/e21010004
Walleczek J. Agent Inaccessibility as a Fundamental Principle in Quantum Mechanics: Objective Unpredictability and Formal Uncomputability. Entropy. 2019; 21(1):4. https://doi.org/10.3390/e21010004
Chicago/Turabian StyleWalleczek, Jan. 2019. "Agent Inaccessibility as a Fundamental Principle in Quantum Mechanics: Objective Unpredictability and Formal Uncomputability" Entropy 21, no. 1: 4. https://doi.org/10.3390/e21010004
APA StyleWalleczek, J. (2019). Agent Inaccessibility as a Fundamental Principle in Quantum Mechanics: Objective Unpredictability and Formal Uncomputability. Entropy, 21(1), 4. https://doi.org/10.3390/e21010004




