On Quantum Superstatistics and the Critical Behavior of Nonextensive Ideal Bose Gases
Abstract
1. Introduction
2. Generalized Entropies
3. Ideal Extensive and Non-Extensive Quantum Bose Gases
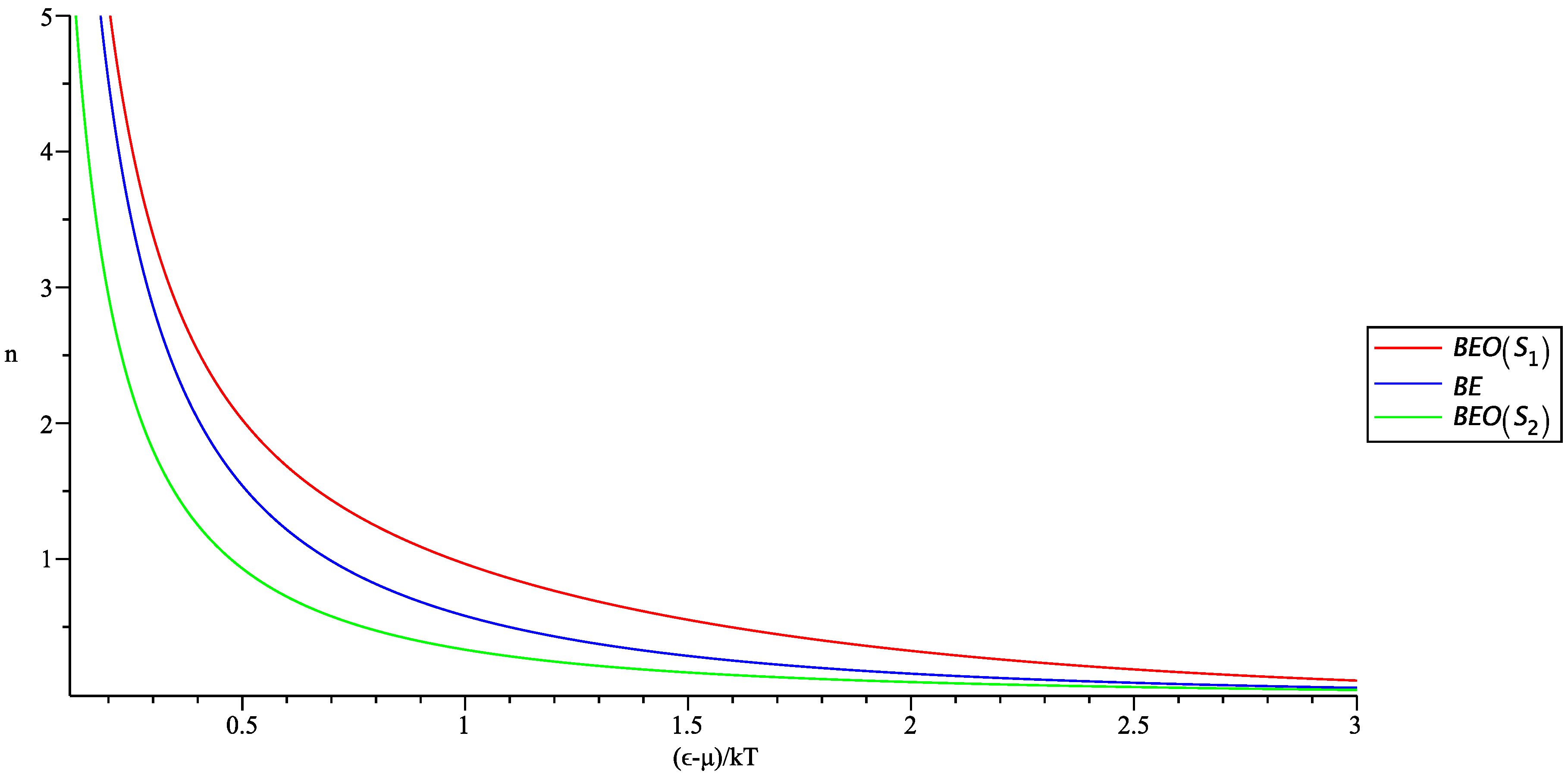
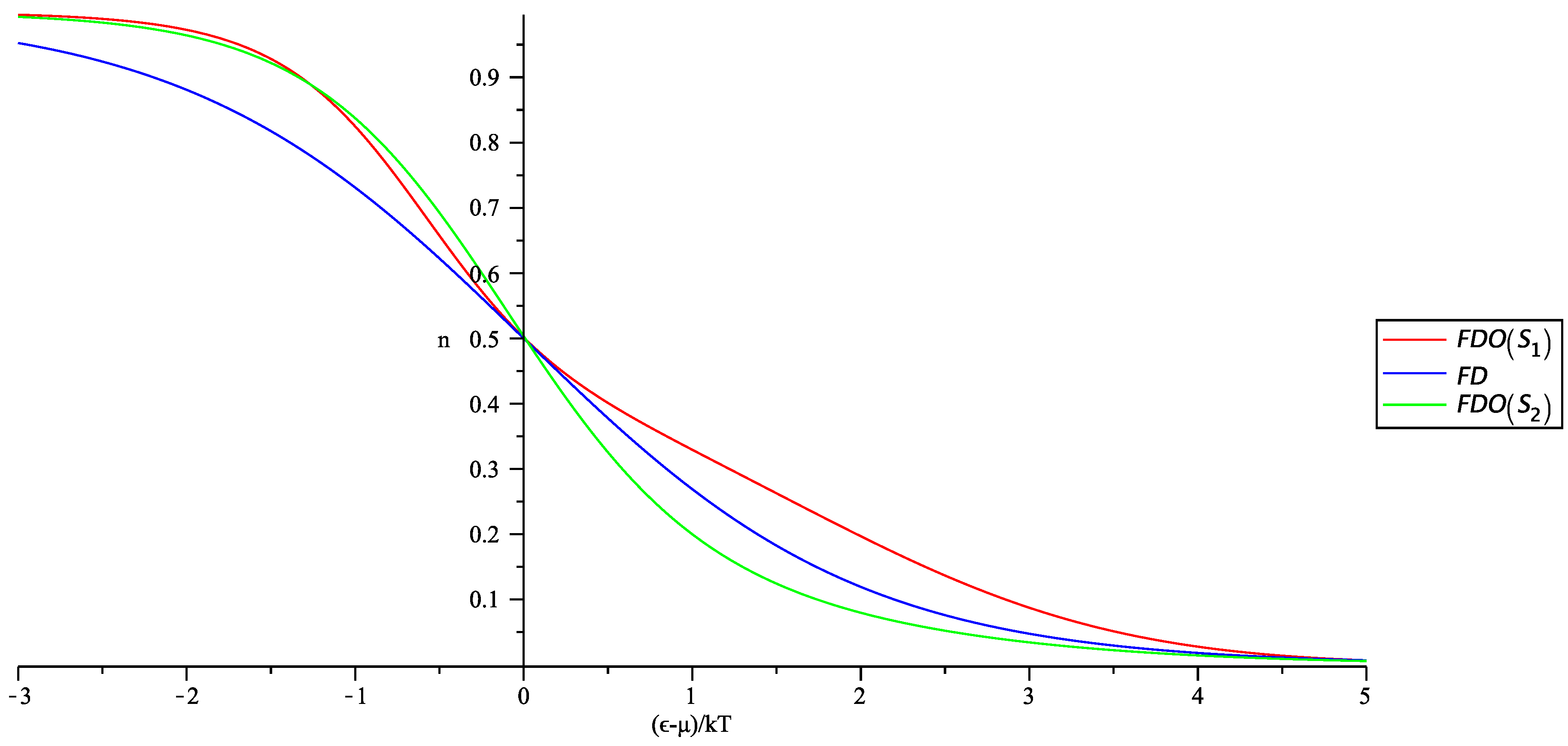
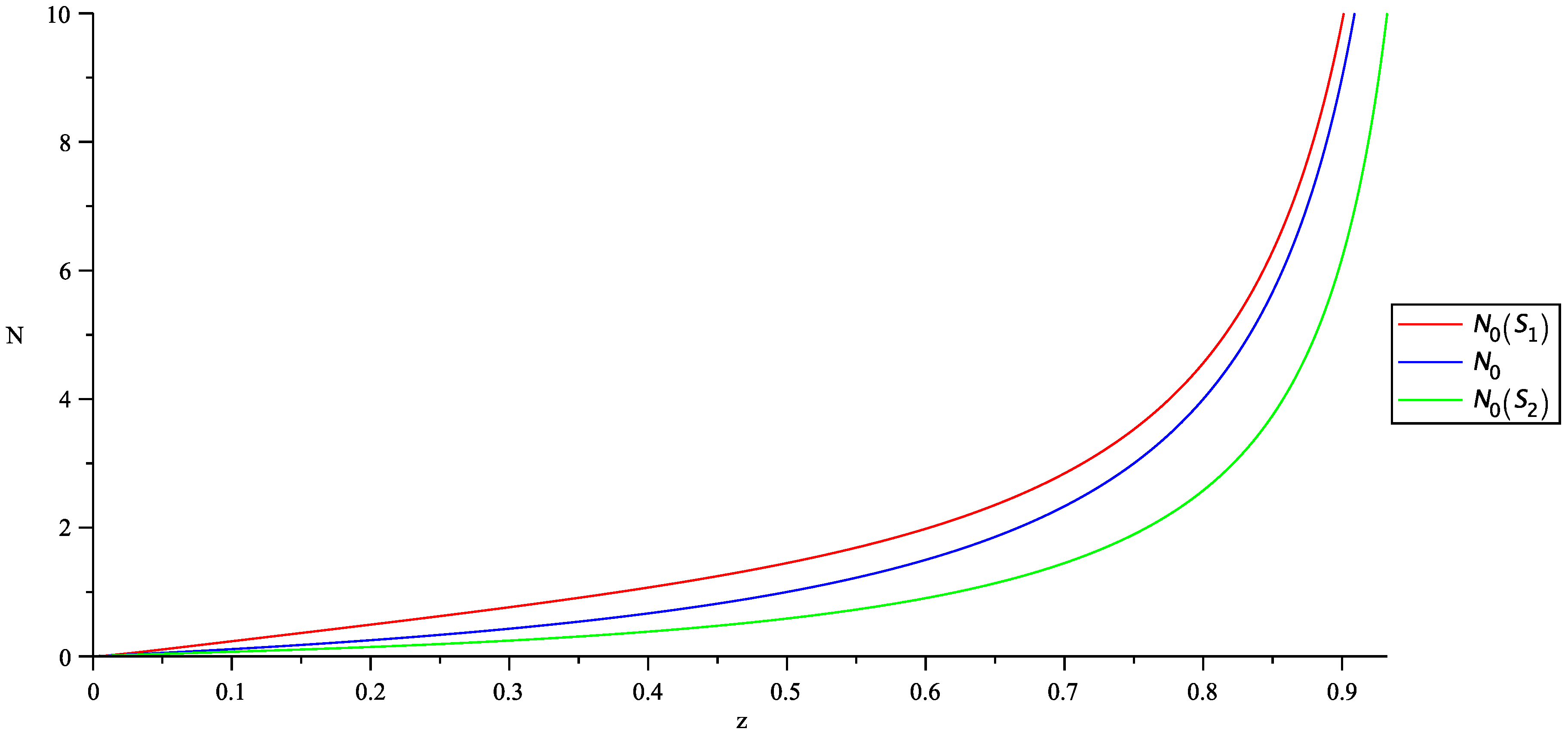
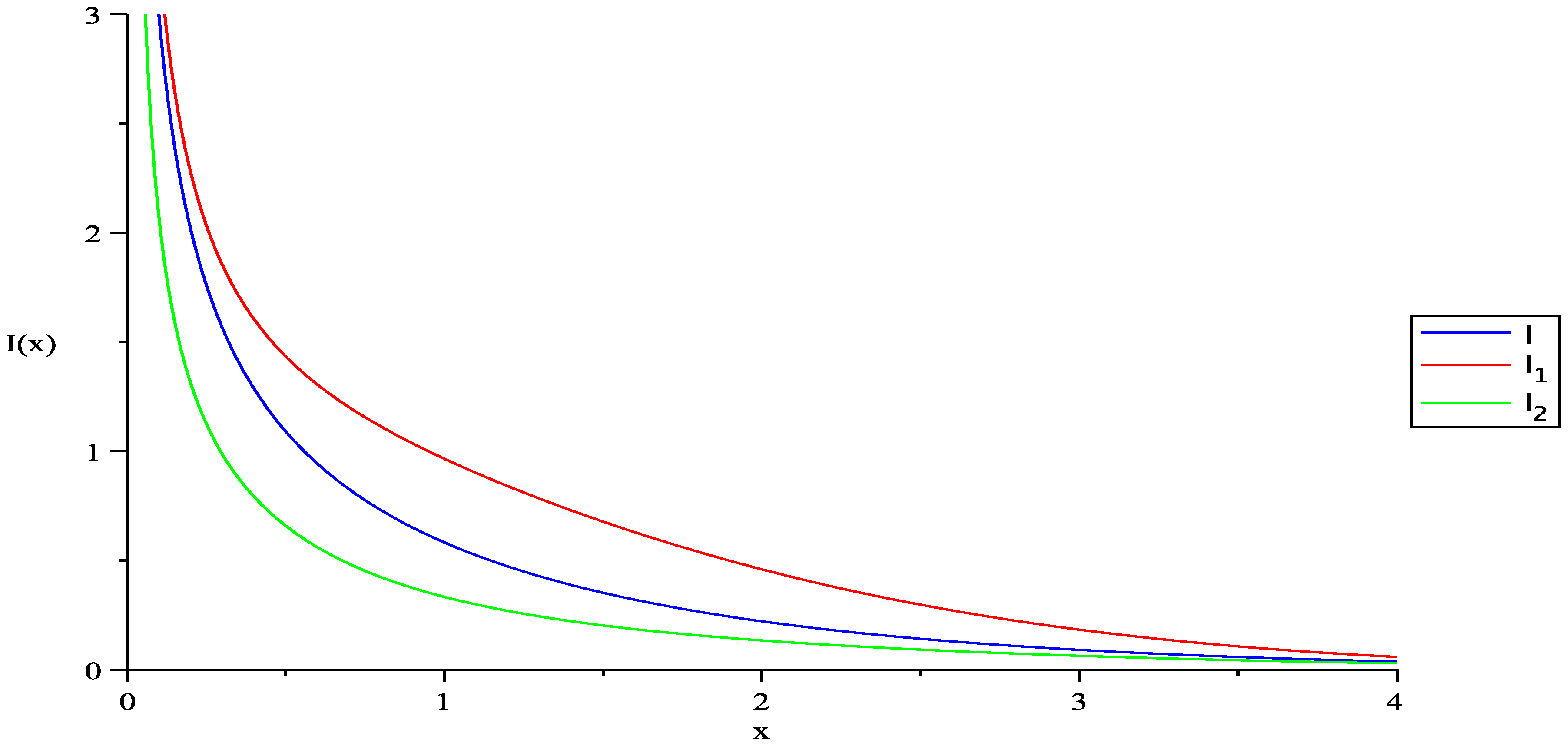
3.1. Usual Quantum Statistics
3.2. Generalized Quantum Statistics
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Fitting Parameters of the Generalized Probability Distributions
References
- Rényi, A. Probability Theory; North Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Kaniadakis, G.; Quarati, P. Generalized fractional statistics. Mod. Phys. Lett. B 1996, 10, 497–504. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1998, 52, 479–487. [Google Scholar] [CrossRef]
- Abe, S. A note on the q-deformation-theoretic aspect of the generalized entropies in nonextensive physics. Phys. Lett. A 1997, 224, 326–330. [Google Scholar] [CrossRef]
- Sharman, B.D.; Mittal, D.P. New nonadditive measures of entropy for discrete probability distributions. J. Math. Sci. 1975, 10, 28–40. [Google Scholar]
- Esteban, M.D.; Morales, D. A summary on entropy statistics. Kybernetica 1995, 31, 337–346. [Google Scholar]
- Gorban, A.N.; Gorban, P.A.; Judge, G. Entropy: The Markov ordering approach. Entropy 2010, 12, 1145–1193. [Google Scholar] [CrossRef]
- Beck, C. Generalized information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. On the interpretation of nonextensive parameter q in Tsallis statistics and Levy distributions. Phys. Rev. Lett. 2000, 84, 2770. [Google Scholar] [CrossRef] [PubMed]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Tsallis, C.; Souza, A.M.C. Constructing a statistical mechanics for Beck-Cohen superstatistics. Phys. Rev. E 2003, 67, 026106. [Google Scholar] [CrossRef] [PubMed]
- Obregón, O. Superstatistics and gravitation. Entropy 2010, 12, 2067–2076. [Google Scholar] [CrossRef]
- Obregón, O.; Gil-Villegas, A. Generalized information entropies depending only on the probability distribution. Phys. Rev. E 2013, 88, 062146. [Google Scholar] [CrossRef] [PubMed]
- Obregón, O.; Ortega-Cruz, M. Generalized entropies depending only on the probability and their quantum statistics. Proceedings 2018, 2, 169. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A.; Miller, H.G.; Uys, H. Foundations of Nonextensive Statistical Mechanics and Its Cosmological Applications. Astrophys. Space Sci. 2004, 290, 275–286. [Google Scholar] [CrossRef]
- Teweldeberhan, A.M.; Plastino, A.R.; Miller, H.G. On the cut-off prescriptions associated with power-law generalized thermostatistics. Phys. Lett. A 2005, 343, 71–78. [Google Scholar] [CrossRef]
- Shen, K.-M.; Zhang, B.-W.; Wang, E.K. Generalized ensemble theory with non-extensive statistics. Phys. A 2017, 487, 215–224. [Google Scholar] [CrossRef]
- Obregón, O. Generalized information and entanglement entropy, gravitation and holography. Int. J. Mod. Phys. A 2015, 30, 1530039. [Google Scholar] [CrossRef]
- Obregón, O.; Torres-Arenas, J.; Gil-Villegas, A. Computer simulation of effective potentials for generalized Boltzmann-Gibbs statistics. J. Mol. Liq. 2017, 248, 364. [Google Scholar]
- Bizet, N.C.; Obregón, O. Exploring gauge/gravity duality of a generalized von-Neumann entropy. Eur. Phys. J. Plus 2018, 133, 55. [Google Scholar] [CrossRef]
- López, J.L.; Obregón, O.; Torres-Arenas, J. Thermodynamic geometry for a non-extensive ideal gas. Phys. Lett. A 2018, 382, 1133–1139. [Google Scholar] [CrossRef]
- R-Monteiro, M.; Roditi, I.; Rodrigues, L.M. ν-Dimensional Ideal quantum q-gas Bose Einstein condensation and λ-point transition. Int. J. Mod. Phys. B 1994, 8, 3281–3298. [Google Scholar] [CrossRef]
- Buyukkilic, F.; Demirhan, D.; Gulec, A. A statistical mechanical approach to generalized statistics of quantum and classical gases. Phys. Lett. A 1995, 197, 209–220. [Google Scholar] [CrossRef]
- Curlief, S. On the Generalized Bose–Einstein condensation. Phys. Lett. A 1996, 218, 11. [Google Scholar] [CrossRef]
- Torres, D.F.; Tirnakli, U. Generalized quantal distribution functions within factorization approach: Some general results for bosons and fermions. Phys. A 1998, 26, 499–511. [Google Scholar] [CrossRef]
- Salasnich, L. BEC in Nonextensive statistical mechanics. Int. J. Mod. Phys. B 2000, 14, 405. [Google Scholar] [CrossRef]
- Sau Fa, K.; Lenzi, E.K. Note on BEC in nonextensive statistical mechanics. Br. J. Phys. 2001, 31, 317–321. [Google Scholar]
- Chen, J.; Zhang, Z.; Su, G.; Chen, L.; Shu, Y. q-Generalized Bose–Einstein condensation based on Tsallis entropy. Phys. Lett. A 2002, 300, 65–70. [Google Scholar] [CrossRef]
- Aragão-Rêgo, H.H.; Soares, D.J.; Lucena, L.S.; Da Silva, L.R.; Lenzi, E.K.; Sau Fa, K. Bose–Einstein and Fermi-Dirac distributions in nonextensive Tsallis statistics: An exact study. Phys. A 2003, 317, 199–208. [Google Scholar] [CrossRef]
- Aliano, G.; Kaniadakis, G.; Miraldi, E. Bose–Einstein condensation in the framework of κ-statistics. Phys. B Condens. Matter 2003, 325, 35. [Google Scholar] [CrossRef]
- Miller, H.G.; Khanna, F.C.; Teshina, R.; Plastino, A.R. Generalized thermostatistics and Bose–Einstein condensation. Phys. Lett. A 2006, 359, 357–358. [Google Scholar] [CrossRef]
- Biswas, S. More accurate theory of Bose–Einstein condensation fraction. Phys. Lett. A 2008, 372, 1574–1578. [Google Scholar] [CrossRef]
- Lawani, A.; Le Meur, J.; Tayurskii, D.; Kaabouchi, A.E.; Nivanen, L.; Minisini, B.; Tsobnang, F.; Pezeril, M.; Le Méhauté, A.; Wang, Q.A. A nonextensive approach to Bose–Einstein condensation of trapped interacting boson gas. J. Low. Temp. Phys. 2008, 150, 605–611. [Google Scholar] [CrossRef]
- Hasegawa, H. Bose–Einstein and Fermi-Dirac distributions in nonextensive quantum statistics: Exact and interpolation approaches. Phys. Rev. E 2009, 80, 011126. [Google Scholar] [CrossRef] [PubMed]
- Lavagno, A.; Narayana Swamy, P. Thermostatistics of deformed bosons and fermions. Found. Phys. 2010, 40, 814–828. [Google Scholar] [CrossRef]
- Wang, Y.; Kong, X.-M. Bose–Einstein condensation of a q-deformed Bose gas in a random box. Mod. Phys. Lett. B 2010, 24, 135. [Google Scholar] [CrossRef]
- Ishihara, M. Chiral phase transitions in the linear sigma model in the Tsallis nonextensive statistics. Int. J. Mod. Phys. E 2016, 25, 1650066. [Google Scholar] [CrossRef]
- Shen, K.M.; Zhang, H.; Hou, D.F.; Zhang, B.W.; Wang, E.K. Chiral phase transition in linear sigma model with nonextensive statistical mechanics. Adv. High Energy Phys. 2017, 2017, 4135329. [Google Scholar] [CrossRef]
- Guha, A.; Kumar Das, P. An extensive study of Bose–Einstein condensation in liquid helium using Tsallis statistics. Phys. A 2018, 497, 272–284. [Google Scholar] [CrossRef]
- Pathria, R.K. Statistical Mechanics; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Goodstein, D.L. States of Matter; Dover Publications: New York, NY, USA, 1985. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obregón, O.; López, J.L.; Ortega-Cruz, M. On Quantum Superstatistics and the Critical Behavior of Nonextensive Ideal Bose Gases. Entropy 2018, 20, 773. https://doi.org/10.3390/e20100773
Obregón O, López JL, Ortega-Cruz M. On Quantum Superstatistics and the Critical Behavior of Nonextensive Ideal Bose Gases. Entropy. 2018; 20(10):773. https://doi.org/10.3390/e20100773
Chicago/Turabian StyleObregón, Octavio, José Luis López, and Marco Ortega-Cruz. 2018. "On Quantum Superstatistics and the Critical Behavior of Nonextensive Ideal Bose Gases" Entropy 20, no. 10: 773. https://doi.org/10.3390/e20100773
APA StyleObregón, O., López, J. L., & Ortega-Cruz, M. (2018). On Quantum Superstatistics and the Critical Behavior of Nonextensive Ideal Bose Gases. Entropy, 20(10), 773. https://doi.org/10.3390/e20100773




