Entropy Signature for Crack Networks in Old Paintings: Saturation Prospectus
Abstract
:1. Introduction
2. Directional Entropy
3. Image Treatment
4. Experiments on Entropy Growth and Saturation Condition
4.1. Experiments on Tapes
4.2. A Two-Interacting-Peak Model
5. Crack Networks in Girl with A Pearl Earring and Other Paintings
5.1. Entropy Cracks in the Girl’s Front and Cheeks
5.2. Portrait of A Young Woman by Petrus Christus
5.3. Portrait of A Lady by Rogier Van Der Weyden
6. Comparing Results for Old Paintings and Experiments
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bucklow, S. The description and classification of craquelure. Stud. Conserv. 1999, 44, 233–244. [Google Scholar]
- Marthelot, J.; Roman, B.; Bico, J.; Teisseire, J.; Dalmas, D.; Melo, F. Self-replicating cracks: A collaborative fracture mode in thin films. Phys. Rev. Lett. 2014, 113, 085502. [Google Scholar] [CrossRef] [PubMed]
- Goehring, L.; Nakahara, A.; Dutta, T.; Kitsunezaki, S.; Tarafdar, S. Desiccation Cracks and Their Patterns: Formation and Modeling in Science and Nature; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Bao, T.F.; Peng, Y.; Cong, P.J.; Wang, J.L. Analysis of crack propagation in concrete structures with structural information entropy. Sci. China Technol. Sci. 2010, 53, 1943–1948. [Google Scholar] [CrossRef]
- Fang, Z.; Li, A.Q.; Bao, H.Y.; Wang, H. Calculation of stress intensity factor in two-dimensional cracks by strain energy density factor procedure. Sci. China Technol. Sci. 2018, 61, 542–550. [Google Scholar] [CrossRef]
- Johnson, M.K.; Stork, D.G.; Biswas, S.; Yasuo, F. Inferring illumination direction estimated from disparate sources in paintings: An investigation into jan vermeer’s girl with a pearl earring. In Proceedings of the SPIE—The International Society for Optical Engineering, San Jose, CA, USA, 18 March 2008; p. 681001. [Google Scholar]
- Mecklenburg, M.F. Some Aspects of the Mechanical Behavior of Fabric-Supported Paintings; Report to the Smithsonian Institute: Washington, DC, USA, 1982. [Google Scholar]
- Karpowicz, A. A study on the development of cracks on paintings. J. Am. Inst. Conserv. 1990, 29, 169–180. [Google Scholar] [CrossRef]
- Cornelis, B.; Ružić, T.; Gezels, E.; Dooms, A.; Pižurica, A.; Platiša, L.; Cornelis, J.; Martens, M.; De Mey, M.; Daubechies, I. Crack detection and inpainting for virtual restoration of paintings: The case of the Ghent Altarpiece. Signal Process. 2013, 93, 605–619. [Google Scholar] [CrossRef]
- Flores, J.C. Mean-field crack networks on desiccated films and their applications: Girl with a Pearl Earring. Soft Matter 2017, 13, 1352–1356. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.L.; Burton, J.C. Universal scaling of polygonal desiccation crack patterns. arXiv, 2018; arXiv:1807.06126. [Google Scholar]
- Sengupta, R.; Tirumkudulu, M.S. Dynamics of cracking in drying colloidal sheets. Soft Matter 2016, 12, 3149–3155. [Google Scholar] [CrossRef] [PubMed]
- Lazarus, V.; Pauchard, L. From craquelures to spiral crack patterns: Influence of layer thickness on the crack patterns induced by desiccation. Soft Matter 2011, 7, 2552–2559. [Google Scholar] [CrossRef]
- Nandakishore, P.; Goehring, L. Crack pattern over uneven substrates. Soft Matter 2016, 12, 2253–2263. [Google Scholar] [CrossRef] [PubMed]
- Romero, V.; Roman, B.; Hamm, E.; Cerda, E. Spiral tearing on thin films. Soft Matter 2013, 9, 8282–8288. [Google Scholar] [CrossRef]
- Griffith, A.A. The Phenomena of rupture and flow in solids. Philos. Trans. Royal Soc. A 1921, 221, 163–198. [Google Scholar] [CrossRef]
- Irwin, G.R. Analysis of stresses and strains near the end of a crack traversing a plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Ludovic, P.; Véronique, L.; Abou, B.; Ken, S.; Geneviève, A.; Christian, L. Craquelures dans les couches picturales des peintures d’art. Reflets Phys. 2007, 3, 5–9. (In French) [Google Scholar]
- Giorgiutti–Dauphiné, F.; Pauchard, L. Painting cracks: A way to investigate the pictorial matter. J. Appl. Mech. 2016, 120, 065107. [Google Scholar] [CrossRef]
- Prigogine, I. From Being to Becoming, Time and Complexity in the Physical Sciences; W. H. Freeman and Company: New York, NY, USA, 1980. [Google Scholar]
- Careri, G. Order and Disorder in Matter; Benjamin-Cummings Publishing Company: San Francisco, CA, USA, 1984. [Google Scholar]
- Toda, M.; Kubo, R.; Saito, N. Statistical Physics I; Springer: New York, NY, USA, 1991. [Google Scholar]
- Huang, K. Statistical Mechanics; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Zeh, H.D. The Physical Basis of the Direction of Time; Springer: New York, NY, USA, 2001. [Google Scholar]
- Borda, M. Fundamentals in Information Theory and Coding; Springer: New York, NY, USA, 2011. [Google Scholar]
- Basu, M. Gaussian–based edge–detection methods: A survey. IEEE Trans. Syst. Man. Cybern. C Appl. Rev. 2002, 32, 252–260. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Rangayyan, R.M.; Frank, C.V. Directional analysis of images in scale space. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 1185–1192. [Google Scholar] [CrossRef]
- Boccara, N. Modeling Complex Systems; Springer: New York, NY, USA, 2010. [Google Scholar]
- Nakayama, T.; Yakubo, K. Fractal Concepts in Condensed Matter Physics; Springer: New York, NY, USA, 2003. [Google Scholar]
- Chen, J.; Xu, J.; Liu, B.; Yao, X.; Li, Y. Quantity effect of radial cracks on the cracking propagation behavior and the crack morphology. PLoS ONE 2014, 9, e98196. [Google Scholar] [CrossRef] [PubMed]
- Kattouf, B.; Warwar, C.; Balla, I.; Shasha, H.; Sherman, D.; Frey, G.L. Hexagonal patterns in thin films: Experiments and modeling. Extreme Mech. Lett. 2015, 2, 65–71. [Google Scholar] [CrossRef]




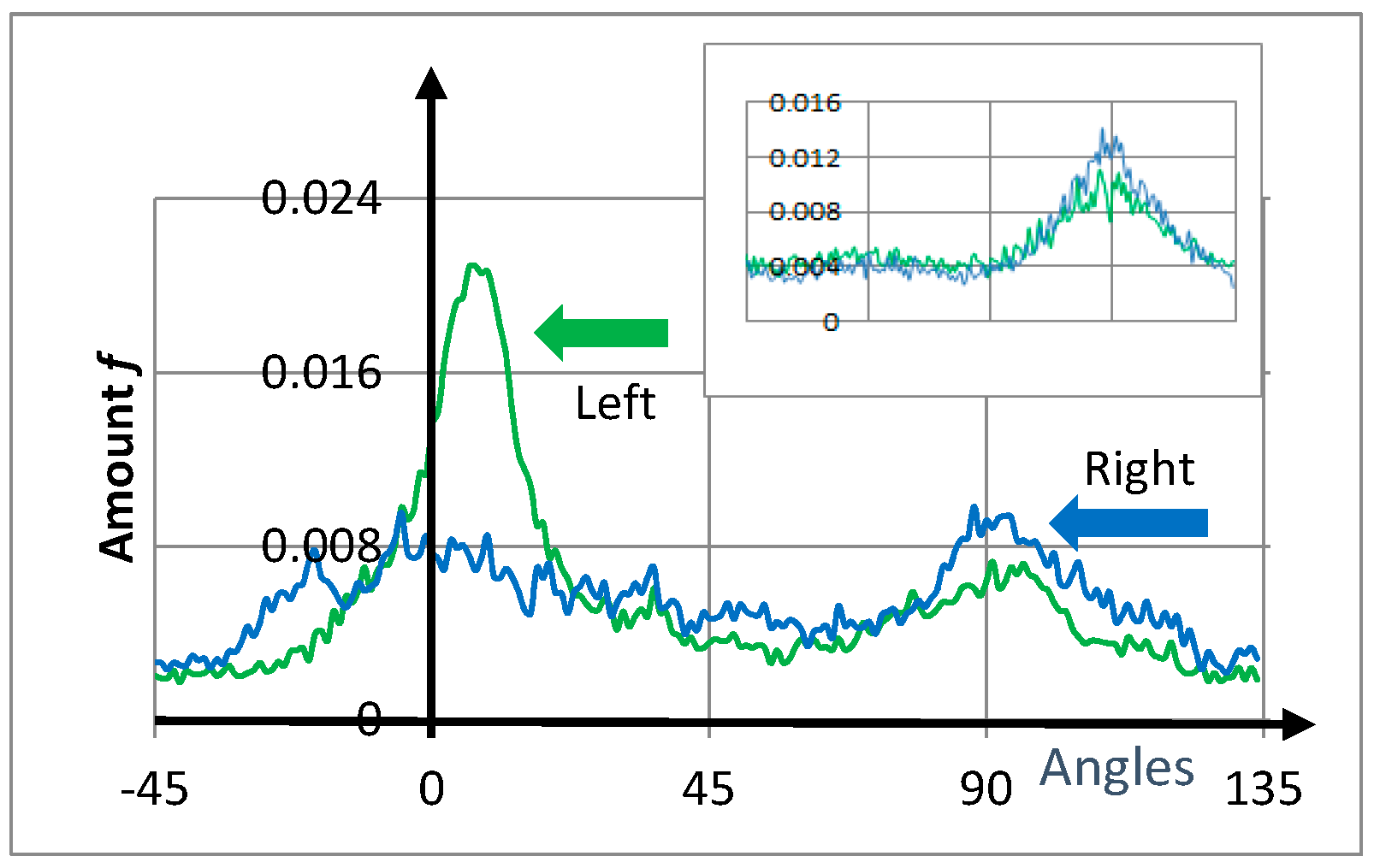
| Right Entropy | Comparison | Left Entropy | ||
|---|---|---|---|---|
| Girl’s front (canvas) | < | 0.015 | ||
| Girl’s cheeks (canvas) | < | 0.029 | ||
| Young Woman (wood) | > | 0.033 | ||
| Portrait of a Lady (wood) | < | 0.012 | ||
| Girl’s turban (canvas) | > | 0.001 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flores, J.C. Entropy Signature for Crack Networks in Old Paintings: Saturation Prospectus. Entropy 2018, 20, 772. https://doi.org/10.3390/e20100772
Flores JC. Entropy Signature for Crack Networks in Old Paintings: Saturation Prospectus. Entropy. 2018; 20(10):772. https://doi.org/10.3390/e20100772
Chicago/Turabian StyleFlores, Juan César. 2018. "Entropy Signature for Crack Networks in Old Paintings: Saturation Prospectus" Entropy 20, no. 10: 772. https://doi.org/10.3390/e20100772
APA StyleFlores, J. C. (2018). Entropy Signature for Crack Networks in Old Paintings: Saturation Prospectus. Entropy, 20(10), 772. https://doi.org/10.3390/e20100772





