1. Introduction
Network representations of complex interacting systems provide simple and powerful frameworks to characterize the topology of interactions and understand its impact on the emergence of collective phenomena [
1,
2]. Some topological properties are found in a wide variety of real networks, which has led scholars to investigate possible interaction mechanisms behind their emergence. An example is the heavy-tailed distribution of the number of links per node (degree); its ubiquity has motivated the study of various network growth mechanisms that can generate networks with that property [
2]. First conceived [
3] and measured [
4,
5] in biogeographic studies,
nestedness [
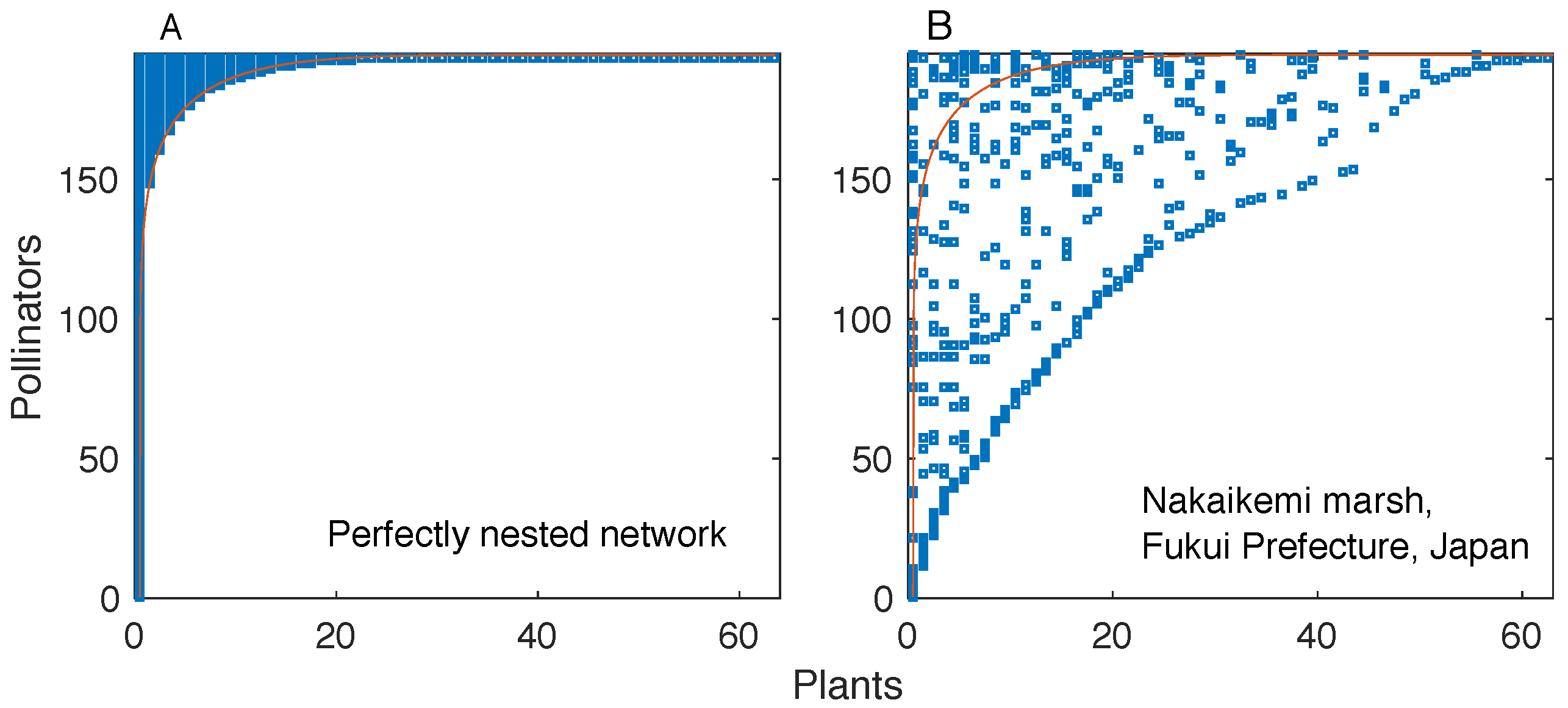
6] is one of such pervasive properties. In a perfectly nested bipartite network, the interaction partners of a given node are also partners of more generalist nodes. This property results in a “triangular” shape of the network’s interaction matrix (i.e., the binary matrix whose elements denote the presence or absence of a link, see
Figure 1).
While perfectly nested networks are unambiguously defined, they are also rarely found in real systems. However, many real networks exhibit a high degree of nestedness. The degree of nestedness of a bipartite network has not been uniquely defined in the literature [
6]. In the widely adopted definition by Atmar and Patterson [
5], which is the one we consider here, a network is highly nested if the rows and columns of its interaction matrix can be ordered in such a way that one can find a line that separates almost perfectly the filled and empty regions of the matrix. It is essential to notice that this definition involves a reordering of the interaction matrix’s rows and columns; alternative definitions of nestedness [
7,
8] (not considered here) do not involve any matrix reordering.
Based on various metrics and definitions, nestedness has indeed been found in systems as diverse as spatial patterns of species distribution [
4,
6], mutualistic plant-animal networks [
9], manufacturer-contractor networks [
10,
11], country-product export networks [
12,
13], spatial patterns of firm distribution [
12,
14], among others. The ubiquity of the pattern has naturally led scholars to investigate how nestedness relates to other network properties [
15,
16,
17], which mechanisms can possibly explain its emergence in ecological [
18,
19,
20] and socio-economic [
10,
21,
21] networks, and its implications for the stability and feasibility of ecological systems [
22,
23].
One of the most popular algorithms to quantify the degree of nestedness of a given network is the
Nestedness Temperature Calculator [
5]. Introduced by Atmar and Patterson in 1993 [
5], the algorithm first determines a line of perfect nestedness by defining a perfectly nested interaction matrix with the same number of links as the original matrix. Then, it seeks to find the ranking of rows and columns that minimizes the average distance (“temperature” [
5]) of observed “unexpected” matrix elements from the line of perfect nestedness; the unexpected matrix elements are those that are different from the corresponding ones in a perfectly nested matrix with the same number of links as the original matrix. Lower temperatures correspond to more nested topologies.
While the original Nestedness Temperature Calculator (NTC) by Atmar and Patterson [
5] has been widely used in ecology [
6], it exhibits some shortcomings that have been later overcome by the BINMATNEST algorithm [
24]. BINMATNEST minimizes nestedness temperature through a genetic algorithm that confers higher chance to reproduce upon lower-temperature orderings [
24]. The optimal matrices by BINMATNEST exhibit substantially lower temperature than those ranked by the NTC [
24], which is why BINMATNEST can be considered as the state-of-the-art approach for nestedness temperature minimization in ecology.
Here, we explore an alternative approach to nestedness temperature minimization inspired by the recent Economic Complexity literature [
25,
26]. Originally introduced to rank countries and products in the country-product export network [
25], the fitness-complexity algorithm ranks the countries and products in such a way that the resulting incidence matrix exhibits a (typically imperfect) “triangular” shape [
25,
26,
27,
28]. In World Trade, this suggests that the most competitive countries tend to diversify their export baskets, whereas the most sophisticated products can be only fabricated by the most competitive countries [
25,
26]. The country score produced by the algorithm, referred to as country fitness, is positively correlated with country GDP per capita [
25,
26]. Importantly, deviations from the linear-regressed trend are highly informative about the future economic development of the country [
29,
30], resulting in GDP predictions often more accurate than those by the International Monetary Fund [
31,
32].
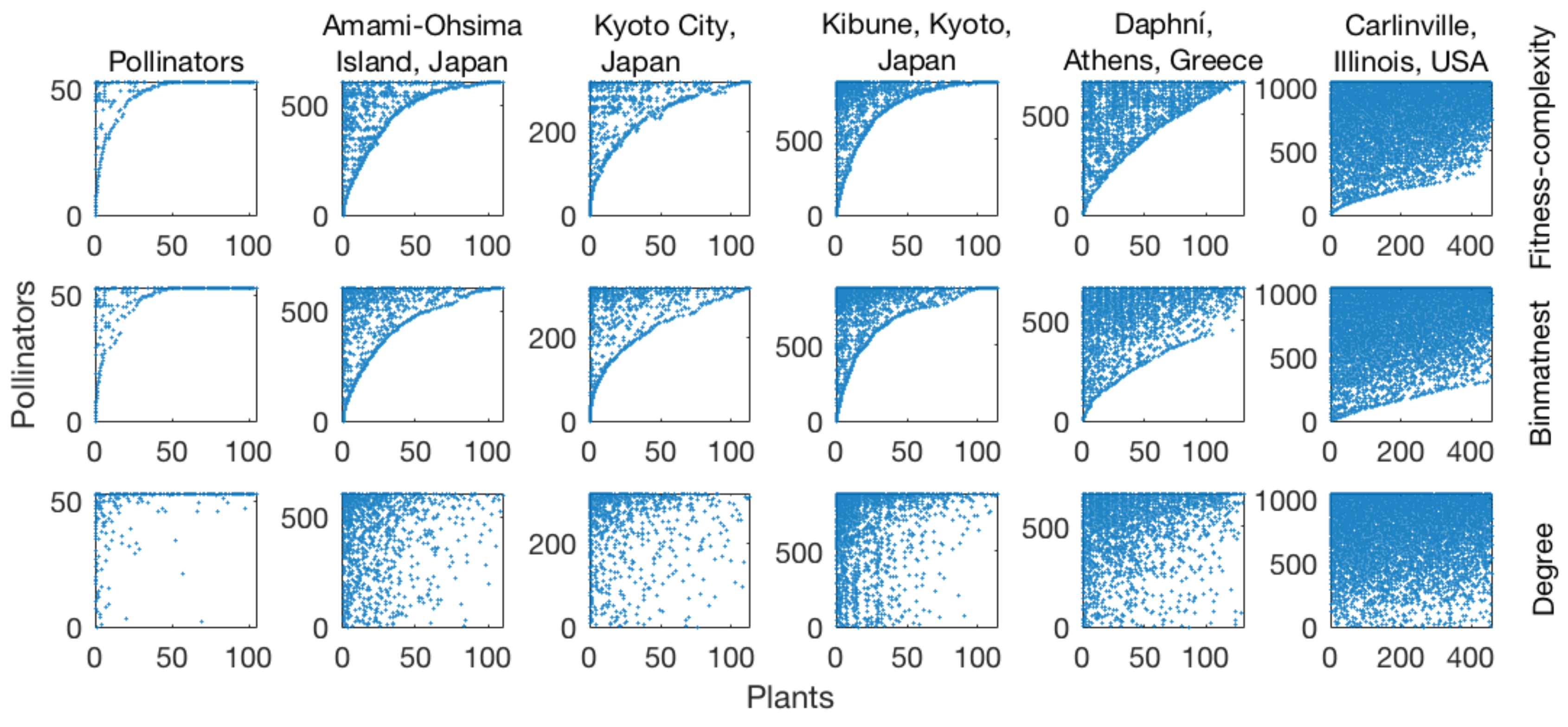
The fact that matrices sorted according to the fitness-complexity algorithm exhibit a neater “triangular” shape than those sorted by degree [
27] suggests that the algorithm might be competitive with algorithms typically adopted in ecology for nestedness temperature minimization [
33]. The main goal of this article is to extensively compare the fitness-complexity algorithm and BINMATNEST according to their ability to minimize nestedness temperature. To this end, we analyze 142 mutualistic networks from
http://www.web-of-life.es/ and 14 years of World Trade country-product networks from
https://atlas.media.mit.edu/ en/resources/data/. We compare the nestedness temperature of the matrices as ranked by BINMATNEST with those of the same matrices as ranked by the fitness-complexity algorithm.
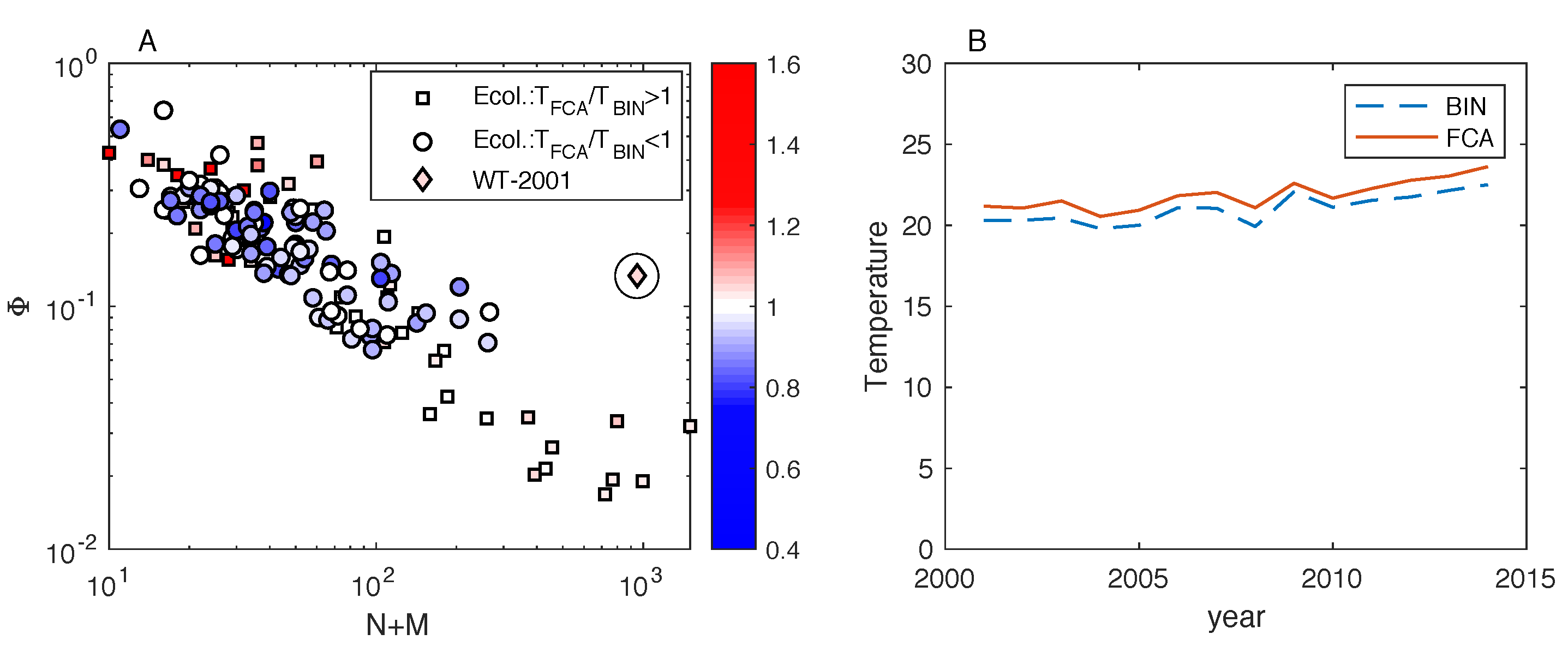
We find that the fitness-complexity algorithm generates sorted matrices that exhibit a lower temperature than the optimal matrices by BINMATNEST for the of the analyzed ecological networks. The only matrices where BINMATNEST outperforms substantially the fitness-complexity algorithm are low-size and high-density ones. The FCA is marginally outperformed by BINMATNEST for World Trade networks which exhibit higher density than mutualistic networks of similar size. Our findings suggest that while originally introduced as a ranking algorithm in economic production networks, the fitness-complexity algorithm has the potential to become a standard tool for nestedness detection in complex networks.
2. Materials and Methods
This paper focuses on binary bipartite networks. We label row-nodes (countries/pollinators) and column-nodes (products/plants) through Latin (
) and Greek (
) letters, respectively. The total number of row-nodes and column-nodes is denoted as
N and
M, respectively, whereas the total number of links is denoted as
L. The
network’s
incidence matrix [
1] is denoted as
: its element
is equal to one (“filled” element) if link
is observed, zero (“empty” element) otherwise. We refer to the incidence matrix of mutualistic networks as
interaction matrix [
9]. The density
of the network is defined as
.
2.1. Nestedness Temperature Minimization (NTM) Problem
Nestedness temperature is determined through three steps: determination of the line of perfect nestedness, node ranking, and temperature calculation. We provide below the details of the three steps, and state the NTM problem.
First, to compute the nestedness temperature of a given matrix, one needs to determine its
line of perfect nestedness. In this work, we use the definition provided by Rodríguez-Gironés and Santamaría [
24] which overcomes some of the shortcomings of the original geometrical construction by Atmar and Patterson [
5]. By rescaling the row and columns labels in such a way that they range from 0 to 1, the line of perfect nestedness is determined through the following shape function [
24]
This function depends on a single parameter, p, which is determined by imposing that the area above the curve in the interval equals the fill of the matrix .
Second, matrix temperature depends on the order of rows and columns. The
nestedness temperature minimization (NTM) problem (or, equivalently, the
nestedness maximization problem) consists in determining the ranking of rows and columns that produces a ranked matrix of minimal temperature
T (defined below). The output of this step is, therefore, a pair of rankings, one for rows and one for columns. Equivalently, we can say that the output of the ranking is a
ranked matrix. Due to the large number of possible permutations of rows and columns, a combinatorial search is infeasible [
24], which has motivated ecologists to search for fast ranking methods [
5,
24,
34]. The main goal of this paper is to compare two alternative ranking algorithms, the one adopted by BINMATNEST (details in
Section 2.2) and the fitness-complexity algorithm (details in
Section 2.3).
Third, for a given network and a given ranking of its row-nodes and column-nodes, one calculates nestedness temperature
T as follows. The unexpected elements of the ranked matrix are the the empty elements above and the filled elements below the line of perfect nestedness (as determined through Equation (
1)). We denote by
the set of unexpected elements. For each unexpected element
, one draws a straight line of slope
in the interaction matrix (after having normalized to one the column and row labels, as described above). On this line, one compute the distance
of unexpected element
from the line of perfect nestedness, and the distance
between the intersection points of this line with the
x-axis and
y-axis (see
Figure 1 in [
24] for an illustration). The total unexpectedness
U of the ranked matrix is given by [
5,
24]
Matrix temperature is defined as
, where
[
5,
24]. A perfectly nested matrix has zero temperature (“perfect order” [
5]), whereas random, noisy matrices have large temperature.
We stress that the key point in our analysis is that the calculation of nestedness temperature T requires a ranked matrix as input: different rankings of rows and columns lead to different matrix temperatures. This allows us to compare different ranking algorithms with respect to the nestedness temperature they produce. We expect the rankings by effective algorithms for NTM to produce ranked matrices that exhibit lower temperature than the ranked matrices by other algorithms.
2.2. Genetic Algorithm Approach: BINMATNEST (BIN)
The BINMATNEST algorithm [
24] adopts a genetic-algorithm approach [
35] to the NTM problem. As the computational steps of the ranking algorithm are detailed in [
24], we only discuss here the main ideas behind the algorithm. The goal is to find a “solution” to the NTM problem, i.e., the minimal-temperature ranking of the nodes. The algorithm starts with a set of candidate solutions (“chromosomes” in the genetic-algorithm language [
35]); among these solutions, the rankings by degree and by the Nestedness Temperature Calculator by Atmar and Patterson [
5]. In each generation, the algorithm considers a well-performing solution, and it generates an “offspring” solution
by probabilistically combining elements of the well-performing solution
with elements of a randomly selected “partner” solution
.
More specifically, let us consider the ranking of the row-nodes. Given a well-performing solution and a partner solution , the each element of the offspring solution is given by the corresponding element of with probability ; otherwise, it is determined by the following steps:
We randomly select an integer k between 1 and N.
We set for .
We set for , if and only if .
If , we assign one of the ranking positions that have not yet appeared in to .
One applies the same steps to the ranking of the column-nodes.Besides, after these steps are performed, the offspring solution can undergo a mutation with a given probability (set to
in [
24]). If the mutation happens, in the case of row-nodes, one extracts uniformly at random two integers
(
), and cyclically permutes the elements
. The process described above is iterated for a given number of generations, and the minimal-temperature solution is eventually selected to determine the network nestedness temperature.
The output of the BINMATNEST algorithm is therefore a ranking of the rows and columns that minimizes nestedness temperature
T. Importantly, the optimal rankings by BINMATNEST lead to temperature values that are substantially lower than those determined by the widely used Nestedness Temperature Calculator [
5]; see Figs. 4–5 in [
24], for example. Based on those results, BINMATNEST can be considered as the state-of-the-art approach for NTM in ecological networks. In this paper, we implement the BINMATNEST algorithm by using the function nestedrank (
https://www.rdocumentation.org/packages/bipartite/versions/2.11/topics/nestedrank) from the R package bipartite with argument method = “binmatnest”. This function gives as output the ranking of row-nodes and column-nodes by the BINMATNEST algorithm.
2.3. Non-Linear Iterative Algorithms: Fitness-Complexity Algorithm (FCA)
Originally introduced to rank countries and products in the bipartite country-product export network [
25], the fitness-complexity algorithm has been applied to diverse systems including ecological mutualistic networks [
33], knowledge production networks [
36], food production networks [
37]. In its formulation for countries and products [
25], the algorithm aims to find a vector of “fitness” scores
for countries and “complexity” scores
for products, respectively. The algorithm starts from a uniform initial condition [
25]
and it subsequently refines the fitness and complexity scores according to the following non-linear iterative equations:
After each iterative step, the scores are normalized by their mean:
Differently from widely used spectral ranking algorithms (see [
30] for a review), the second line of Equation (
4) is markedly non-linear. Such non-linearity is motivated by economic-complexity considerations. Empirical evidence indicates indeed that competitive countries tend to diversify their export baskets, which makes it reasonable to quantify the score of a given country as the sum over the scores of its exported products. At the same time, the fact that a product is exported by many countries (in particular, developing countries) suggests that the product might require few productive capabilities to be made and it is unlikely to be a sophisticated one. This motivates the non-linear dependence of product score
on country score
:
is heavily penalized if
is exported by a low-fitness country.
Do the iterations above converge to a unique fixed point? Scholars have found that while the answer is positive, the scores of several nodes can potentially converge to a zero value, which reduces the discriminative power of the ranking based on the fixed point of the map [
38]. Besides, this convergence to zero tends to be relatively slow, and it strongly depends on the density and shape of the incidence matrix [
28,
38]. To prevent this potential issue, we adopt a convergence criterion based on ranking: we stop the iterations at step
if and only if the ranking of countries and products at step
is almost exactly the same as the ranking at step
, i.e., if few ranking variations occurred in the subsequent
steps. In practice, the stopping iteration
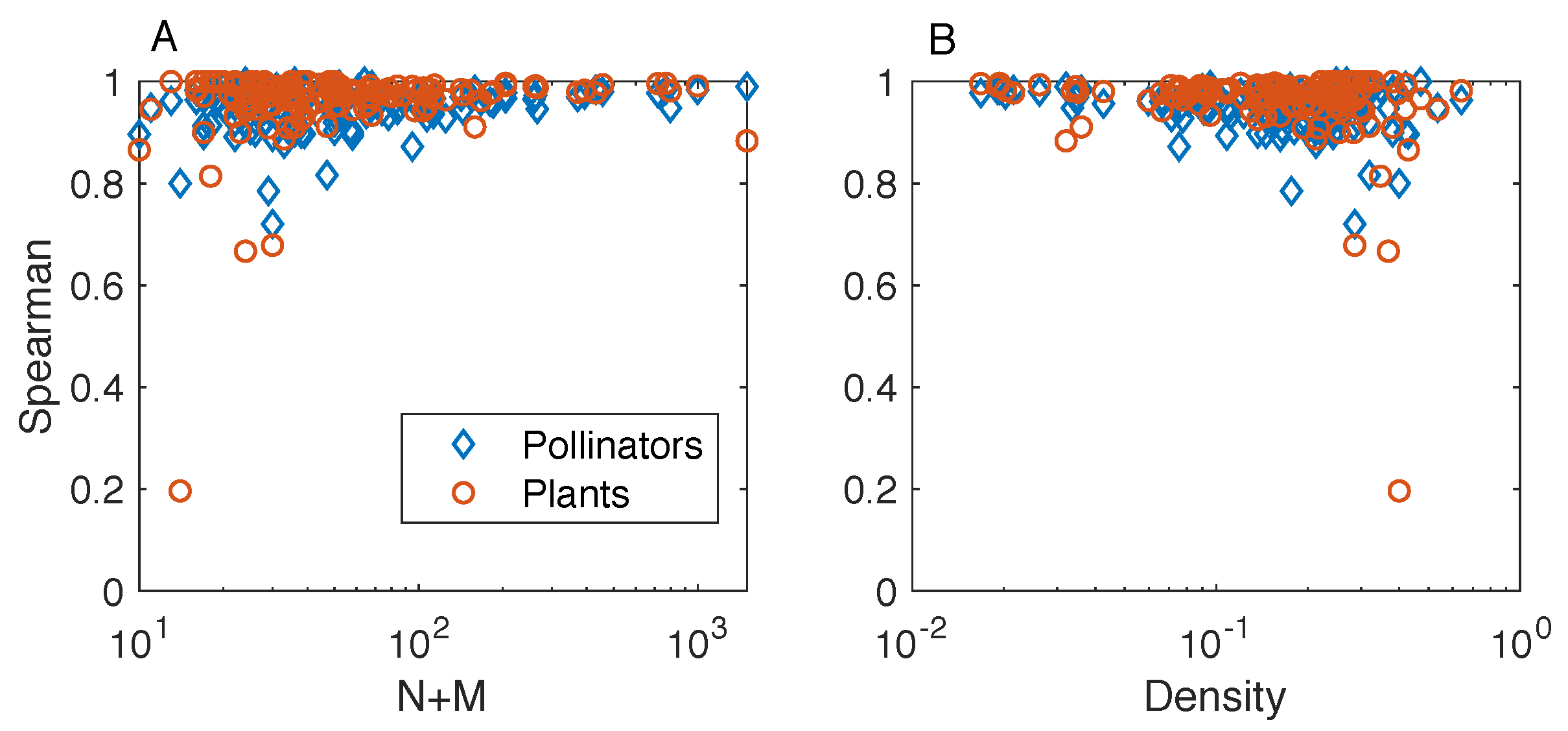
is defined as the smallest iteration such that both Spearman’s correlation coefficients
and
are larger than
. Unless otherwise stated, the results presented in this manuscript refer to
– the criterion allows us to stop the algorithm after a finite number of iteration for all the analyzed networks. We find that results for
and
are in qualitative agreement with those obtained with
; the same holds for results obtained by running a fixed number
of iterations of the FCA – details are provided in the Results section.
While we formulated the algorithm for the country-product network, the algorithm can be applied to any bipartite network by replacing “countries” with the system’s row-nodes (e.g., animals in mutualistic networks [
33]) and “products” with the system’s column-nodes (e.g., plants). In this paper, we apply it not only to the country-product network, but also to mutualistic networks: the fitness score of animal and plant species represents their importance and vulnerability, respectively [
33].
4. Discussion
We showed that the fitness-complexity ranking algorithm [
25] is a highly effective method to “pack” the incidence matrix of a given bipartite network in order to maximize its nestedness. In particular, an extensive comparison with BINMATNEST, the state-of-the-art nestedness maximization method in ecology, revealed that the FCA produces ranked matrices with temperature values substantially lower than those of the optimal matrices by BINMATNEST for the majority of analyzed datasets. Small-size and high-density ecological matrices are those where the rankings by the two methods differ the most, and where BINMATNEST has a chance to produce matrices of significantly smaller temperature than those ranked by the fitness-complexity algorithm.
Importantly, the Nestedness Temperature Minimization problem is not only a theoretical one, but it has also implications for the important problem of forecasting of the secondary effects of species’ extinctions [
33]. More specifically, recent works [
27,
33] have pointed out that the rankings of active and passive species (countries and products, in World Trade analysis [
27]) that result in the most packed matrices are also those that best reproduce the rankings of the nodes according to their structural importance and vulnerability (as determined by numerical simulations of ranking-based targeted attacks to the network). Maximizing nestedness is therefore highly informative on the structural importance of active species and vulnerability of passive species.
Finally, recent literature has reinterpreted nestedness as a mesoscopic property instead of a macroscopic one [
17,
41,
42]. This means that nestedness can be interpreted not as a hierarchical organization of interactions between all pairs of nodes (as in
Figure 1), but as a property of subcomponents of the network. While our results show that the fitness-complexity algorithm can be used as a nestedness detection tool, whether it can be exploited (and arguably, generalized) to detect network compartments that exhibit an internal nested topology remains an intriguing open question.