Constructal Optimizations for Heat and Mass Transfers Based on the Entransy Dissipation Extremum Principle, Performed at the Naval University of Engineering: A Review
Abstract
:1. Introduction
2. Constructal Optimizations Based on the Entransy Dissipation Extremum Principle
2.1. Heat Conduction and Finned Cooling Problems
2.2. Cooling Channel and Steam Generator Problems
2.3. Porous Medium Mass Transfer Problems
3. Conclusions
- (1)
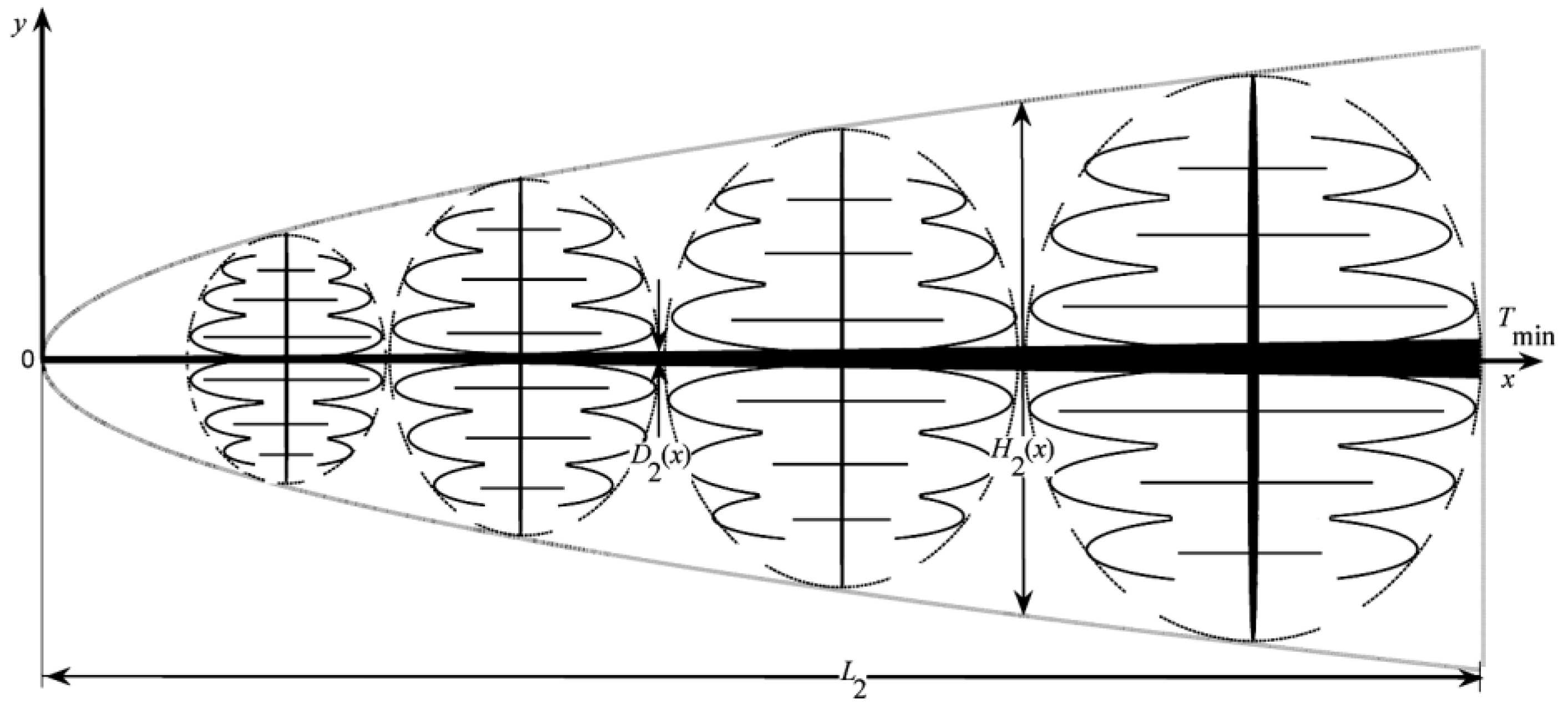
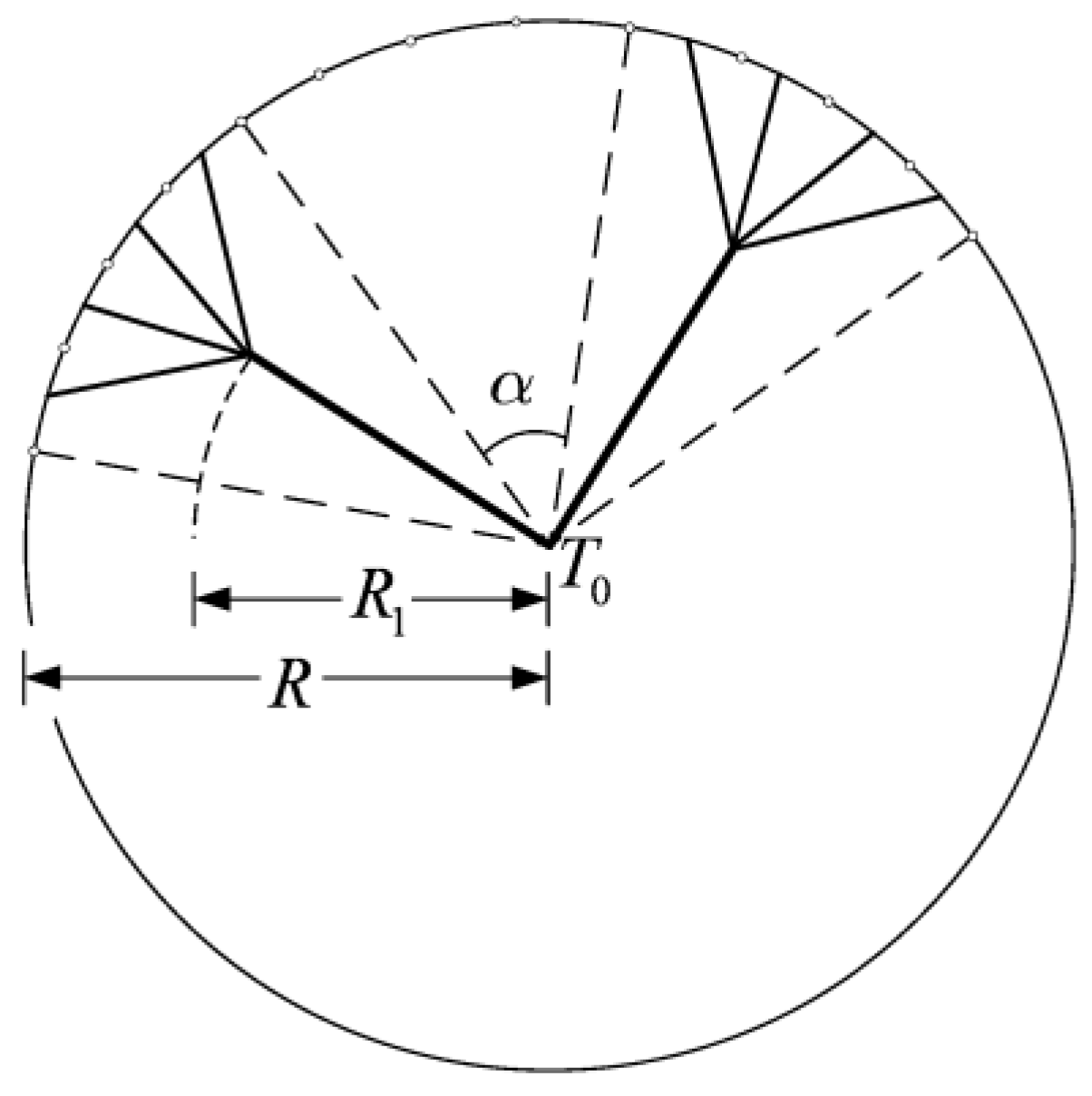
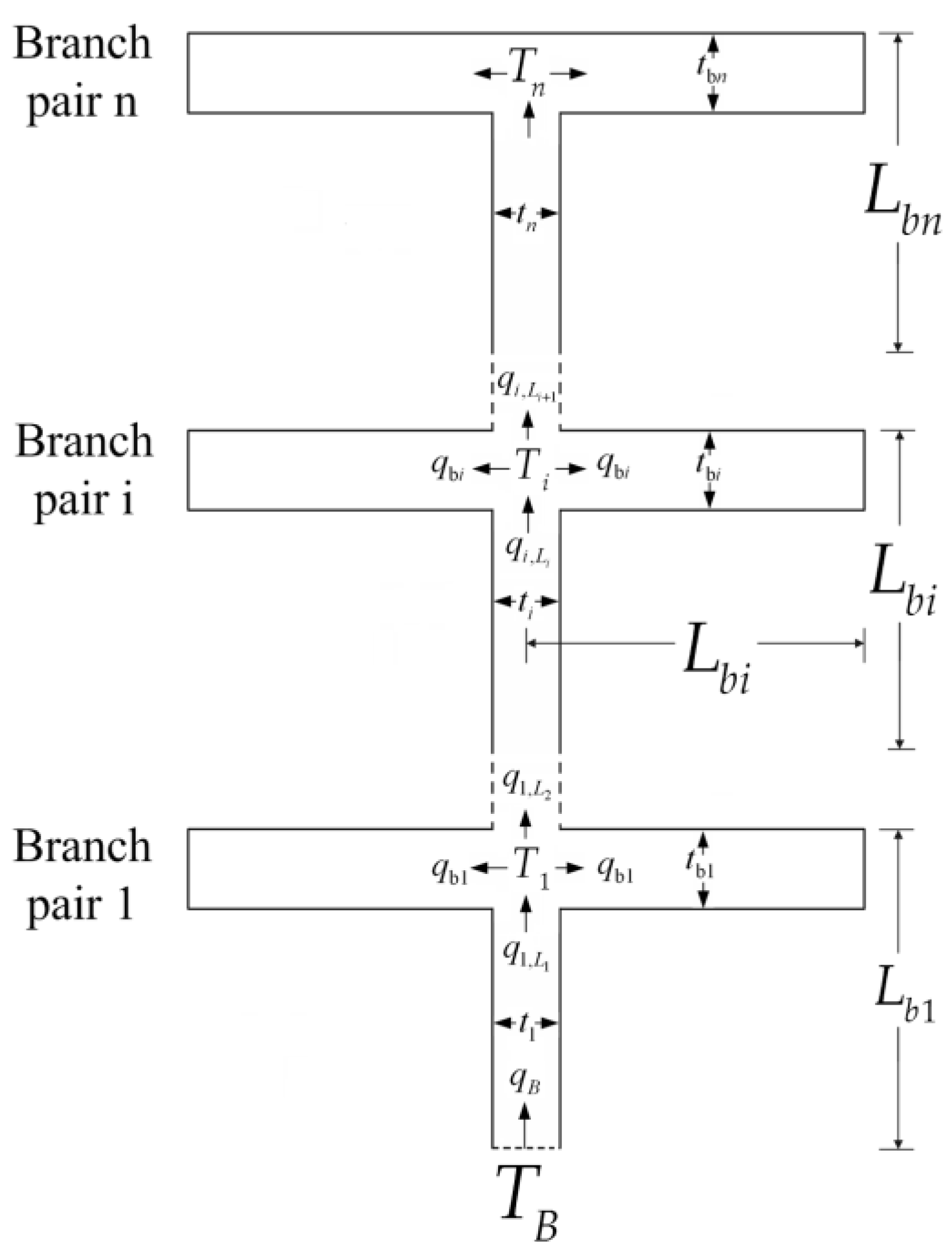
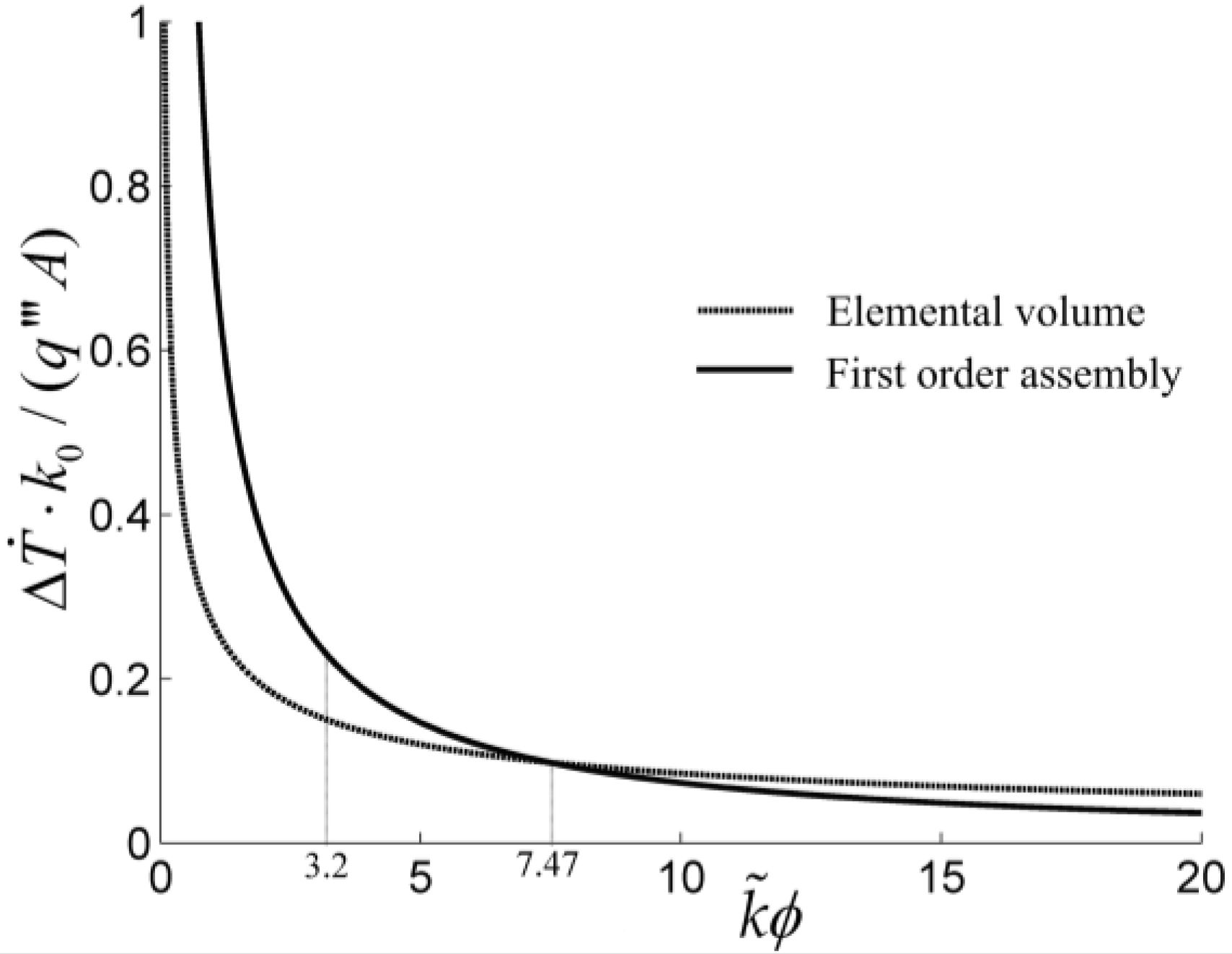
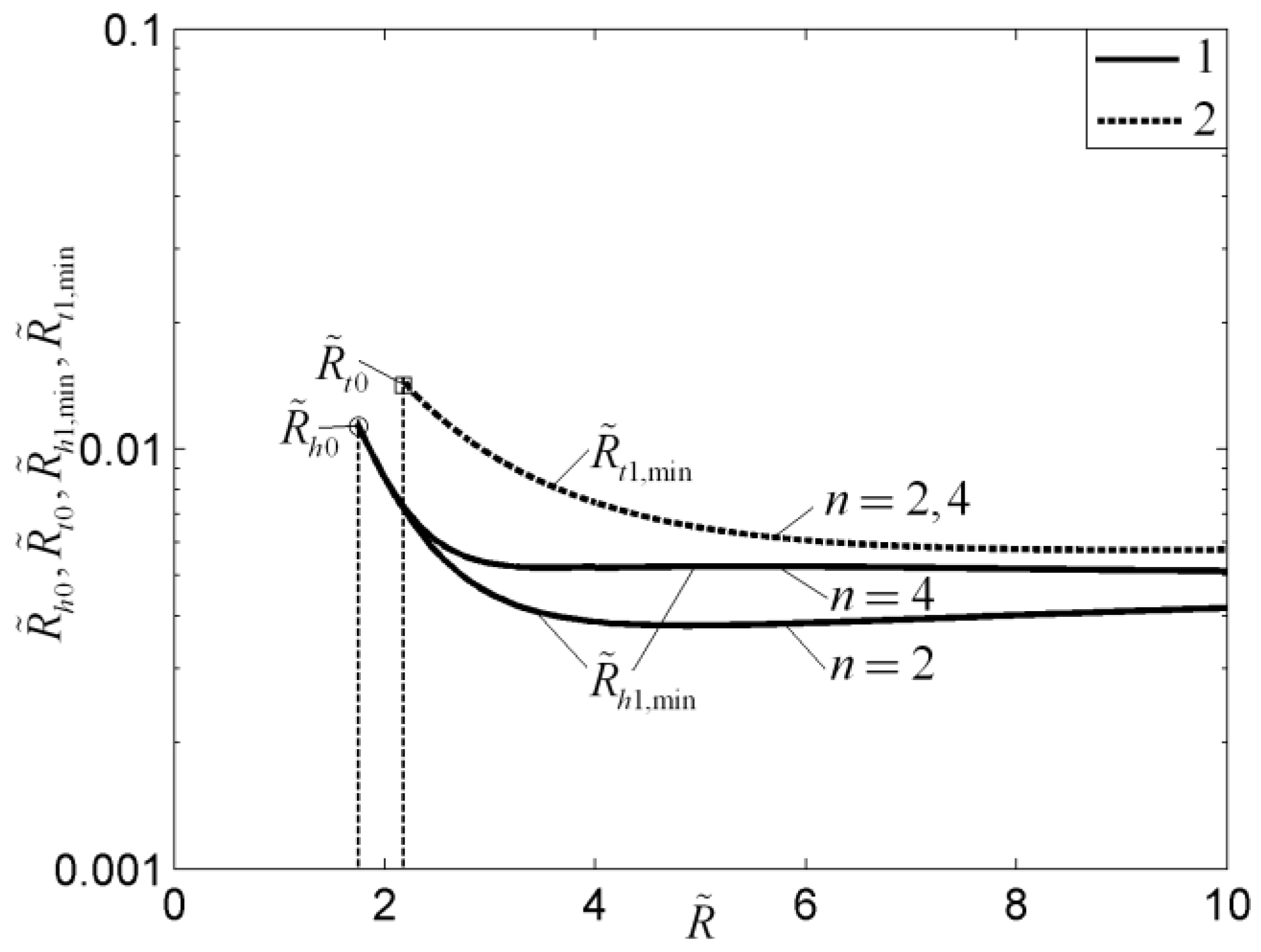
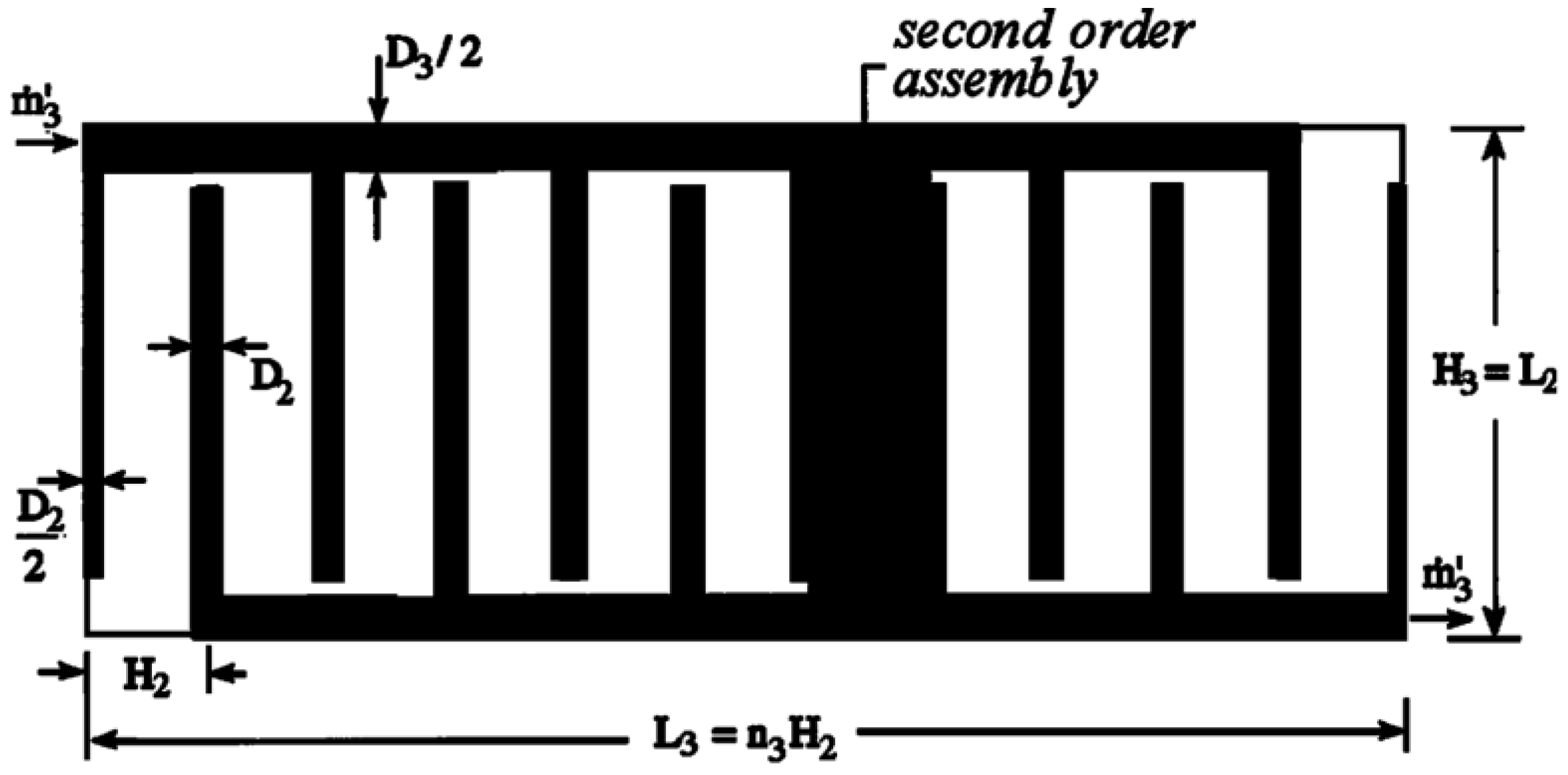
- For the heat conduction and finned cooling problems, the MHTTD of the tapered assembly is not always decreased when the internal complexity of the assembly increases, but there exists an optimal order of the assembly that leads to the minimum MHTTD. The critical radii of the disc-shaped assembly based on the minimizations of EDR and MTD, which determine whether the radial-patterned disc or tree-shaped disc is adopted, are different. The HCP of the disc-shaped assembly can be further improved by releasing the premise of an optimized last-order construct. The global HTPs of Y-shaped and tree-shaped fins are better than that of a T-shaped fin. The global HTP of a tree-shaped fin is not always better when the internal structure becomes more complex.
- (2)
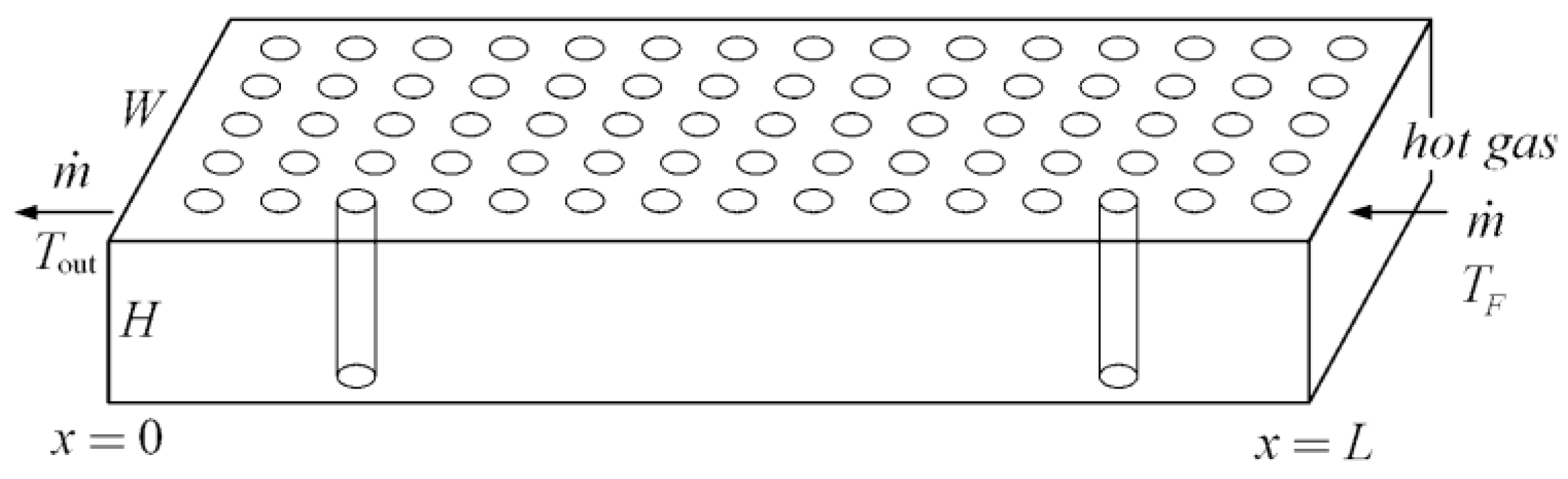
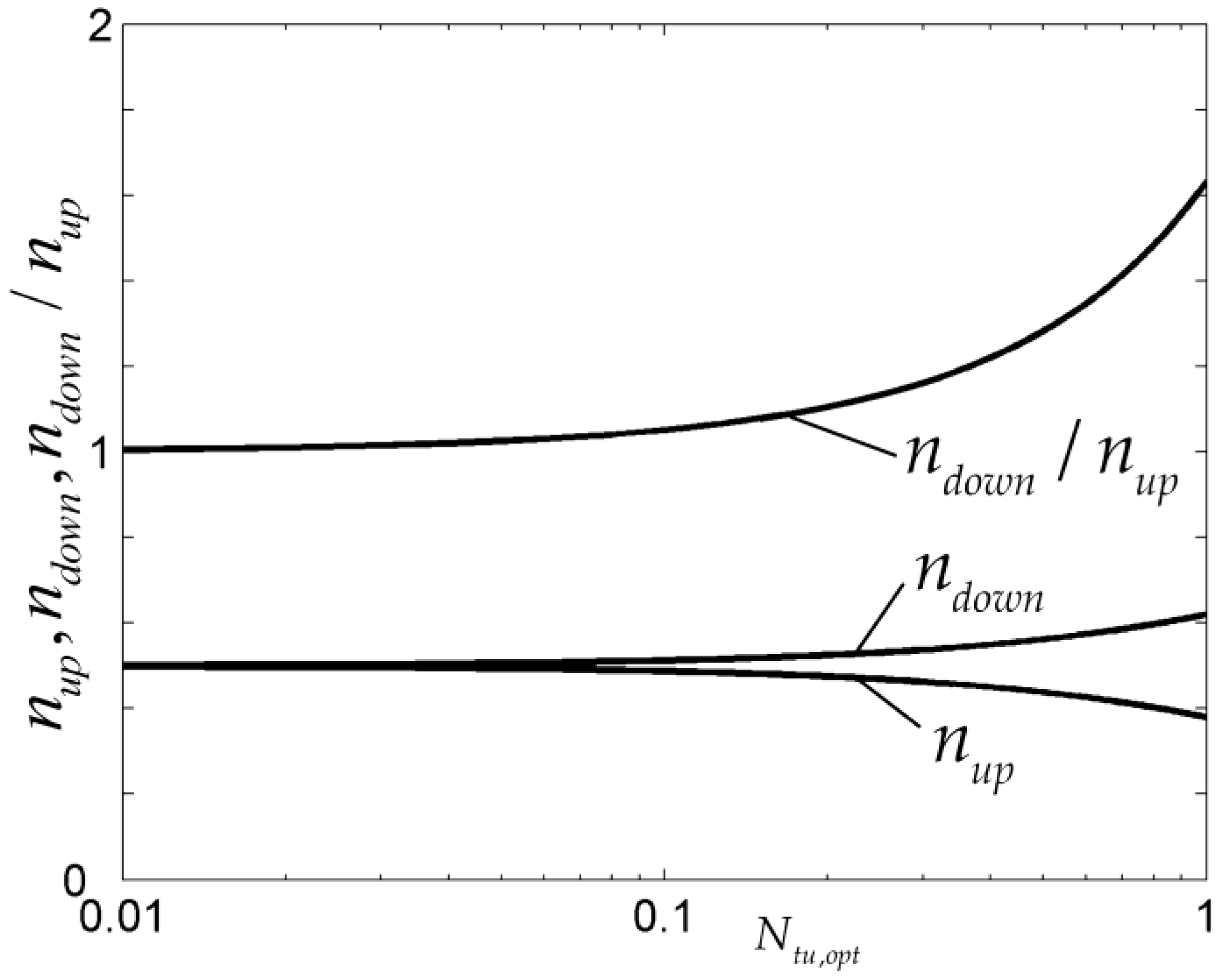
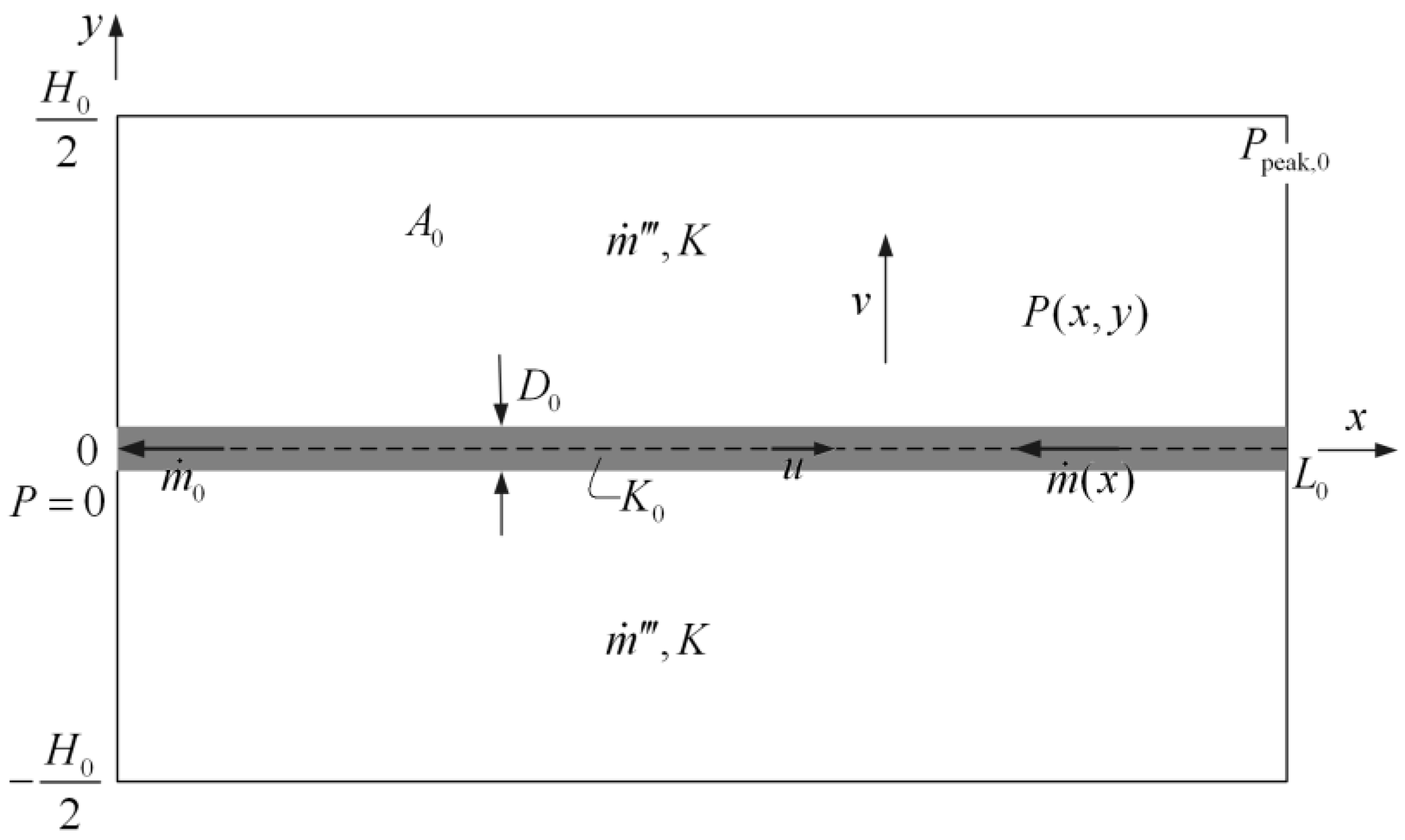
- For the cooling channel and steam generator problems, the optimal construct of cooling channels in rectangular and cuboid bodies based on the minimizations of EDR and MTD, as well as those of a steam generator based on the maximizations of EDR and HTR, are different. The flow resistance of the cooling channels in the rectangular body is evidently reduced when EDR minimization of the rectangular element is conducted, and it can be further reduced by adopting variable cross-sectional channels. There exists an optimal volume fraction of cooling channels in the cuboid when EDR minimization is conducted, but it does not exist in the MTD minimization. Compared with the optimal results obtained by MTD minimization, the ETR of the cuboid body obtained by EDR minimization is reduced by 23.12% and its global HTP is improved. The average HTR of a steam generator obtained by EDR maximization is increased by 58.7% compared with that by HTR maximization, which illustrates an evident improvement of the global HTP.
- (3)
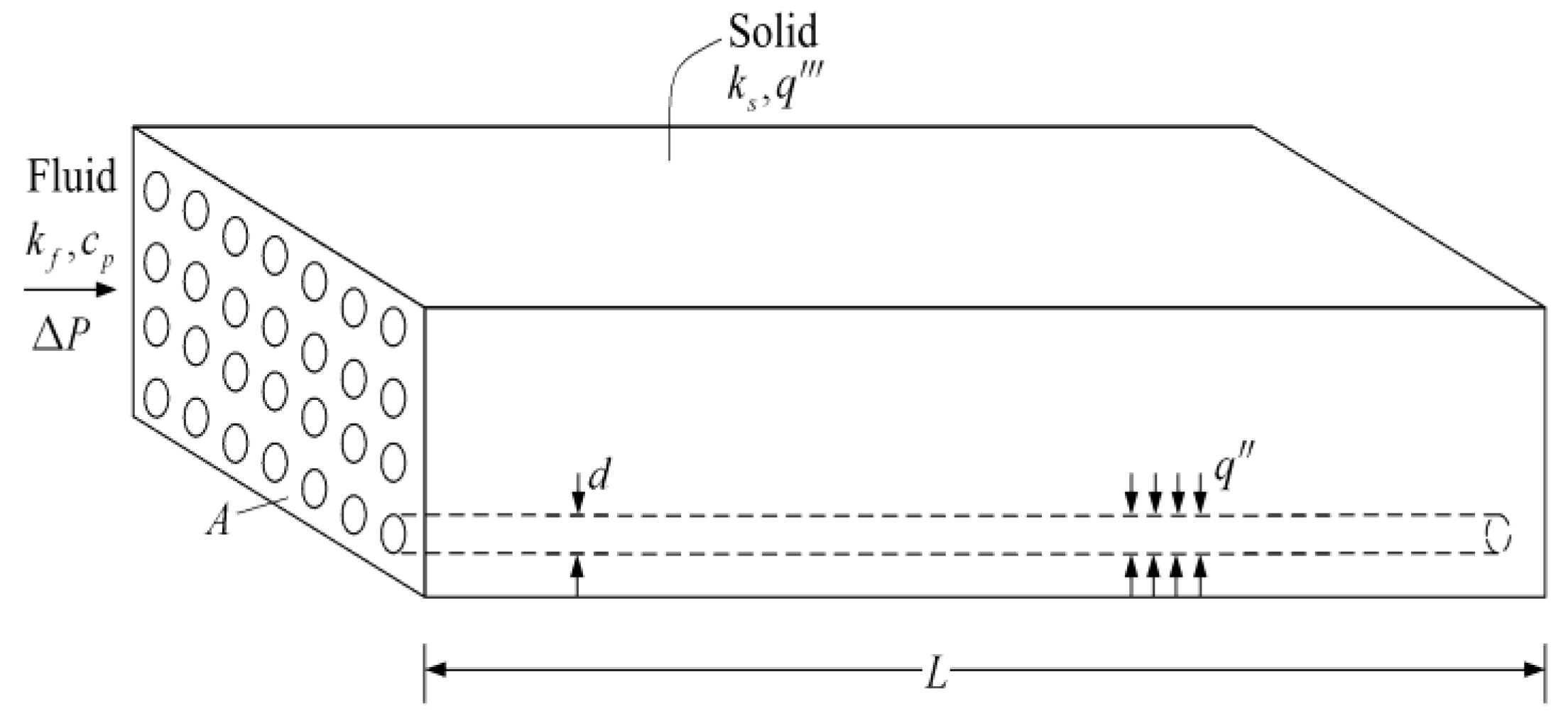
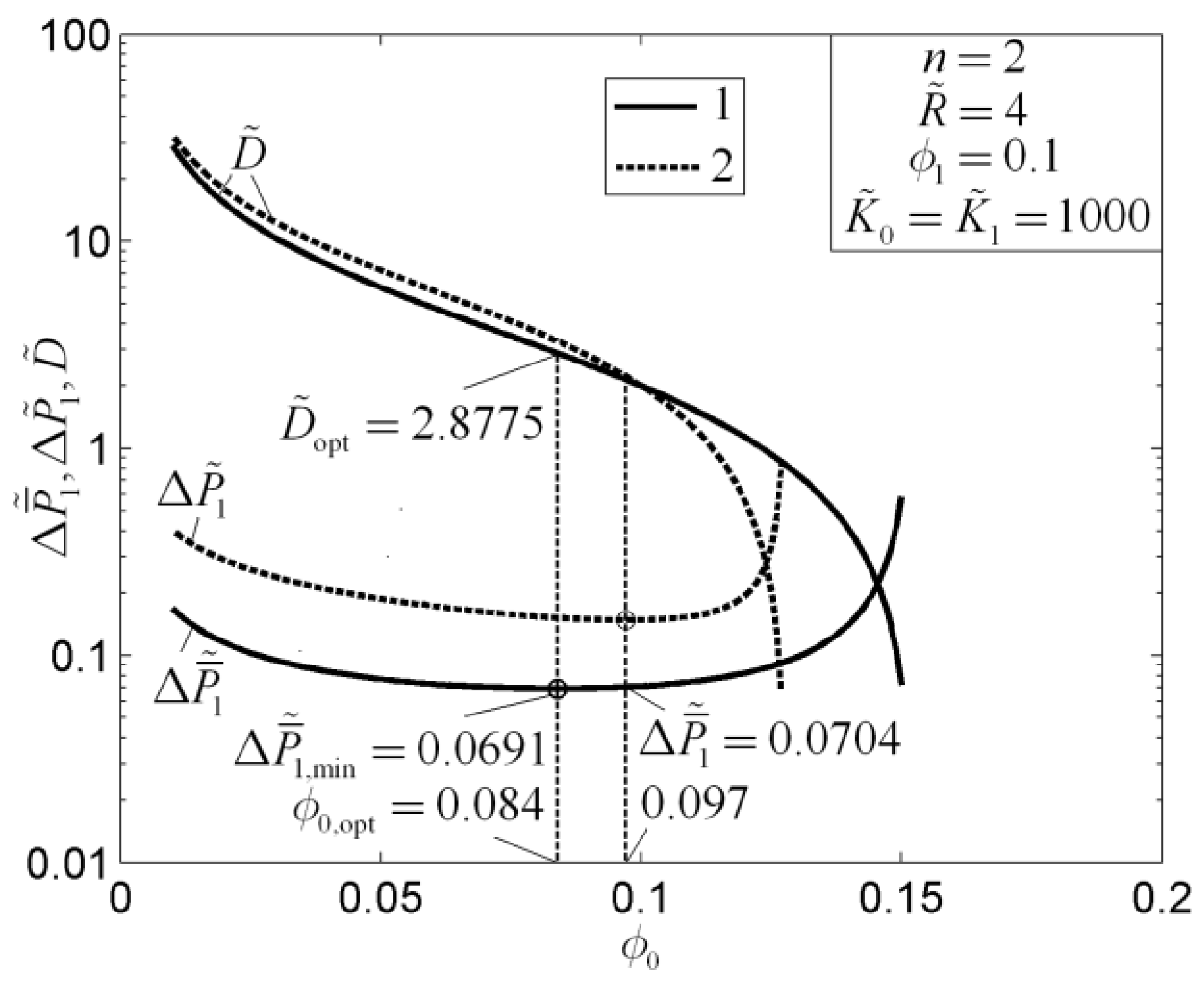
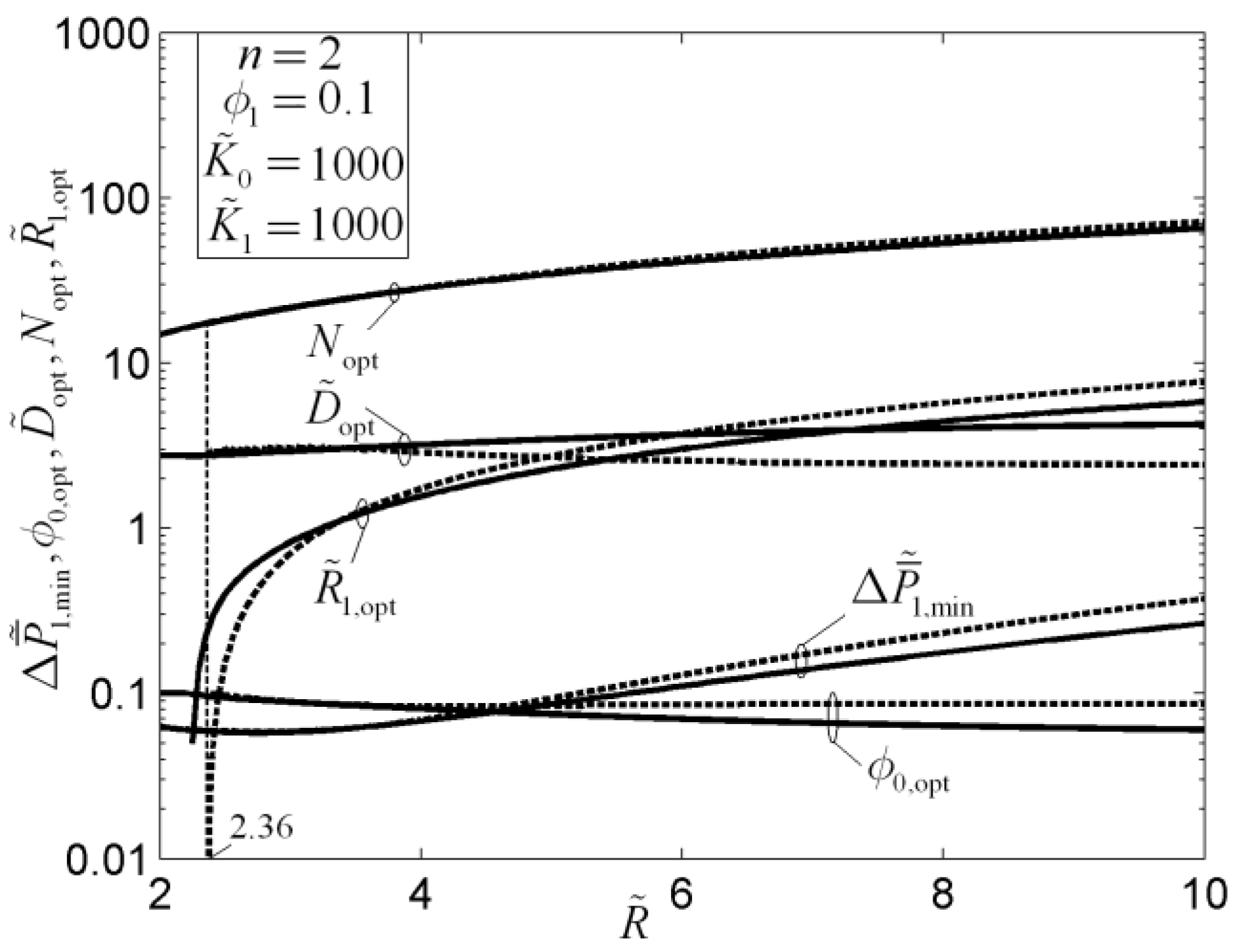
- For the porous medium mass transfer problems, the optimal constructs of rectangular mass transfer assembly with tapered HPP obtained by the minimizations of MPD and mass EDR are different. Compared with the rectangular mass transfer assembly with constant HPP, the MPDs of the element and first-order assembly with tapered HPPs are decreased by 6% and 11%, respectively, and the MTPs of the assemblies are improved. When the premise of an optimized last-order construct is adopted, the optimal constructs of a disc-shaped mass transfer assembly obtained based on the minimizations of MPD and mass EDR are different. The latter construct reduces the APD of the disc-shaped assembly evidently, which reflects the essential requirement of MTP optimization. Moreover, the APD can be further decreased by releasing the premise of an optimized last-order construct.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sheikholeslami, M.; Ellahi, R. Electrohydrodynamic nanofluid hydrothermal treatment in an enclosure with sinusoidal upper wall. Appl. Sci. 2015, 5, 294–306. [Google Scholar] [CrossRef]
- Eger, T.; Bol, T.; Thanu, A.R.; Daroczy, L.; Janiga, G.; Schroth, R.; Thevenin, D. Application of entropy generation to improve heat transfer of heat sinks in electric machines. Entropy 2016, 19, 255. [Google Scholar] [CrossRef]
- Laskowski, R.; Smyk, A.; Rusowicz, A.; Grzebielec, A. Determining the optimum inner diameter of condenser tubes based on thermodynamic objective functions and an economic analysis. Entropy 2016, 18, 444. [Google Scholar] [CrossRef]
- Li, P.; Xie, Y.H.; Zhang, D.; Xie, G.N. Heat transfer enhancement and entropy generation of nanofluids laminar convection in microchannels with flow control devices. Entropy 2016, 18, 134. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Zia, Q.M.Z.; Ellahi, R. Influence of induced magnetic field on free convection of nanofluid considering Koo-Kleinstreuer (KKL) correlation. Appl. Sci. 2016, 6, 324. [Google Scholar] [CrossRef]
- Rashidi, S.; Esfahani, J.A.; Ellahi, R. Convective heat transfer and particle motion in an obstructed duct with two side-by-side obstacles by means of DPM model. Appl. Sci. 2017, 7, 431. [Google Scholar] [CrossRef]
- Liu, W.; Fan, A.W.; Huang, X.M. Heat and Mass Transfer Theory and Application in Porous Media; Science Press: Beijing, China, 2006. [Google Scholar]
- Xu, P.; Sasmito, A.P.; Yu, B.M.; Mujumdar, A.S. Transport phenomena and properties in treelike networks. Appl. Mech. Rev. 2016, 68, 040802. [Google Scholar] [CrossRef]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Int. J. Heat Mass Transf. 1997, 40, 799–816. [Google Scholar] [CrossRef]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bejan, A.; Lorente, S. Design with Constructal Theory; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chen, L.G. Progress in study on constructal theory and its application. Sci. China Technol. Sci. 2012, 55, 802–820. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J. Multi-Objective Constructal Optimizations for Fluid Flow, Heat and Mass Transfer Processes; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Chen, L.G.; Feng, H.J.; Xie, Z.H. Generalized thermodynamic optimization for iron and steel production processes: A theoretical exploration and application cases. Entropy 2016, 18, 353. [Google Scholar] [CrossRef]
- Bejan, A. Evolution in thermodynamics. Appl. Phys. Rev. 2017, 4, 011305. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Zhu, H.Y.; Liang, X.G. Entransy—A physical quantity describing heat transfer ability. Int. J. Heat Mass Transf. 2007, 50, 2545–2556. [Google Scholar] [CrossRef]
- Li, Z.X.; Guo, Z.Y. Field Synergy Principle of Heat Convection Optimization; Science Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Chen, L.G. Progress in entransy theory and its applications. Chin. Sci. Bull. 2012, 57, 4404–4426. [Google Scholar] [CrossRef]
- Chen, Q.; Liang, X.G.; Guo, Z.Y. Entransy theory for the optimization of heat transfer—A review and update. Int. J. Heat Mass Transf. 2013, 63, 65–81. [Google Scholar] [CrossRef]
- Chen, L.G. Progress in optimization of mass transfer processes based on mass entransy dissipation extremum principle. Sci. China Technol. Sci. 2014, 57, 2305–2327. [Google Scholar] [CrossRef]
- Cheng, X.T.; Zhao, J.M.; Liang, X.G. Discussion on the extensions of the entransy theory. Sci. China Technol. Sci. 2017, 60, 363–373. [Google Scholar] [CrossRef]
- Ghodoossi, L.; Egrican, N. Exact solution for cooling of electronics using constructal theory. J. Appl. Phys. 2003, 93, 4922–4929. [Google Scholar] [CrossRef]
- Wu, W.J.; Chen, L.G.; Sun, F.R. On the “area to point” flow problem based on constructal theory. Energy Convers. Manag. 2007, 48, 101–105. [Google Scholar] [CrossRef]
- Wei, S.H.; Chen, L.G.; Sun, F.R. The area-point constructal optimization for discrete variable cross-section conducting path. Appl. Energy 2009, 86, 1111–1118. [Google Scholar] [CrossRef]
- Lorenzini, G.; Biserni, C.; Rocha, L.A.O. Constructal design of X-shaped conductive pathways for cooling a heat-generating body. Int. J. Heat Mass Transf. 2013, 58, 513–520. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Lorenzini, G.; Shariatzadeh, O.J.; Biserni, C. Evolution in the design of V-shaped highly conductive pathways embedded in a heat-generating piece. J. Heat Transf. 2015, 137, 061001. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal design for “+” shaped high conductive pathways over a square body. Int. J. Heat Mass Transf. 2015, 91, 162–169. [Google Scholar] [CrossRef]
- Lorenzini, G.; Barreto, E.X.; Beckel, C.C.; Schneider, P.S. Constructal design of I-shaped high conductive pathway for cooling a heat-generating medium considering the thermal contact resistance. Int. J. Heat Mass Transf. 2016, 93, 770–777. [Google Scholar] [CrossRef]
- Lorenzini, G.; Barreto, E.X.; Beckel, C.C.; Schneider, P.S.; Isoldi, L.A.; Santos, E.D.; Rocha, L.A.O. Geometrical evaluation of T-shaped high conductive pathway with thermal contact resistance for cooling of heat-generating medium. Int. J. Heat Mass Transf. 2017, 108, 1884–1893. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal design for a rectangular body with nonuniform heat generation. Eur. Phys. J. Plus 2016, 131, 274. [Google Scholar] [CrossRef]
- Ghodoossi, S.; Egrican, N. Conductive cooling of triangular shaped electronics using constructal theory. Energy Convers. Manag. 2004, 45, 811–828. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. “Volume-point” heat conduction constructal optimization based on minimization of maximum thermal resistance with triangular element at micro and nanoscales. J. Energy Inst. 2016, 89, 302–312. [Google Scholar] [CrossRef]
- Rocha, L.A.O.; Lorente, S.; Bejan, A. Contructal design for cooling a disc-shaped area by conduction. Int. J. Heat Mass Transf. 2002, 45, 1643–1652. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Xie, Z.H.; Sun, F.R. Constructal optimization for “disc-point” heat conduction at micro and nanoscales. Int. J. Heat Mass Transf. 2013, 67, 704–711. [Google Scholar] [CrossRef]
- Neagu, M.; Bejan, A. Constructal-theory tree networks of “constant” thermal resistance. J. Appl. Phys. 1999, 86, 1136–1144. [Google Scholar] [CrossRef]
- Wu, W.J.; Chen, L.G.; Sun, F.R. Heat-conduction optimization based on constructal theory. Appl. Energy 2007, 84, 39–47. [Google Scholar] [CrossRef]
- Chen, L.G.; Wei, S.H.; Sun, F.R. Constructal entransy dissipation minimization for “volume-point” heat conduction. J. Phys. D Appl. Phys. 2008, 41, 195506. [Google Scholar] [CrossRef]
- Ghodoossi, L. Entropy generation rate in uniform heat generating area cooled by conducting paths: Criterion for rating the performance of constructal designs. Energy Convers. Manag. 2004, 45, 2951–2969. [Google Scholar] [CrossRef]
- Tescari, S.; Mazet, N.; Neveu, P. Constructal theory through thermodynamics of irreversible processes framework. Energy Convers. Manag. 2011, 52, 3176–3188. [Google Scholar] [CrossRef]
- Chen, L.G.; Wei, S.H.; Sun, F.R. Constructal entransy dissipation rate minimization of a disc. Int. J. Heat Mass Transf. 2011, 54, 210–216. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Sun, F.R. “Volume-point” heat conduction constructal optimization based on entransy dissipation rate minimization with three-dimensional cylindrical element and rectangular and triangular elements at micro and nanoscales. Sci. China Technol. Sci. 2012, 55, 779–794. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal entransy dissipation rate minimization of a rectangular body with nonuniform heat generation. Sci. China Technol. Sci. 2016, 59, 1352–1359. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H. Constructal optimizations for “+” shaped high conductivity channels based on entransy dissipation rate minimization. Int. J. Heat Mass Transf. 2018, 119, 640–646. [Google Scholar] [CrossRef]
- Lorenzini, G.; Moretti, S.; Conti, A. Fin Shape Thermal Optimization Using Bejan’s Constructal Theory; Morgan & Claypool Publishers: San Rafael, CA, USA, 2011. [Google Scholar]
- Bejan, A.; Almogbel, M. Constructal T-shaped fins. Int. J. Heat Mass Transf. 2000, 43, 2101–2115. [Google Scholar] [CrossRef]
- Almogbel, M. Constructal tree-shaped fins. Int. J. Therm. Sci. 2005, 44, 342–348. [Google Scholar] [CrossRef]
- Xie, Z.H.; Chen, L.G.; Sun, F.R. Comparative study on constructal optimizations of T-shaped fin based on entransy dissipation rate minimization and maximum thermal resistance minimization. Sci. China Technol. Sci. 2011, 54, 1249–1258. [Google Scholar] [CrossRef]
- Lorenzini, G.; Rocha, L.A.O. Constructal design of Y-shaped assembly of fins. Int. J. Heat Mass Transf. 2006, 49, 4552–4557. [Google Scholar] [CrossRef]
- Lorenzini, G.; Rocha, L.A.O. Constructal design of T-Y assembly of fins for an optimized heat removal. Int. J. Heat Mass Transf. 2009, 52, 1458–1463. [Google Scholar] [CrossRef]
- Xie, Z.H.; Chen, L.G.; Sun, F.R. Constructal optimization of twice level Y-shaped assemblies of fins by taking maximum thermal resistance minimization as objective. Sci. China Technol. Sci. 2010, 53, 2756–2764. [Google Scholar] [CrossRef]
- Yang, A.B.; Chen, L.G.; Xie, Z.H.; Feng, H.J.; Sun, F.R. Constructal heat transfer rate maximization for cylindrical pin-fin heat sinks. Appl. Therm. Eng. 2016, 108, 427–435. [Google Scholar] [CrossRef]
- Chen, L.G.; Yang, A.B.; Xie, Z.H.; Sun, F.R. Constructal entropy generation rate minimization for cylindrical pin-fin heat sinks. Int. J. Therm. Sci. 2017, 111, 168–174. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal entransy dissipation rate minimization for helm-shaped fin with inner heat sources. Sci. China Technol. Sci. 2015, 58, 1084–1090. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal design for helm-shaped fin with inner heat sources. Int. J. Heat Mass Transf. 2017, 110, 1–6. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Chen, L.G.; Sun, F.R. Constructal entransy dissipation rate minimization for heat conduction based on a tapered element. Chin. Sci. Bull. 2011, 56, 2400–2410. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Chen, L.G.; Sun, F.R. Constructal entransy dissipation rate minimization for “disc-point” heat conduction. Chin. Sci. Bull. 2011, 56, 102–112. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Chen, L.G.; Sun, F.R. Constructal optimization for “disc-to-point” heat conduction without the premise of optimized last-order construct. Int. J. Therm. Sci. 2011, 50, 1031–1036. [Google Scholar] [CrossRef]
- Chen, L.G.; Xiao, Q.H.; Xie, Z.H.; Sun, F.R. T-shaped assembly of fins with constructal entransy dissipation rate minimization. Int. Comm. Heat Mass Transf. 2012, 39, 1556–1562. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Chen, L.G.; Xie, Z.H.; Feng, H.J.; Sun, F.R. Constructal entransy dissipation rate minimization for Y-shaped assembly of fins. J. Eng. Thermophys. 2012, 33, 1465–1470. (In Chinese) [Google Scholar]
- Xiao, Q.H.; Chen, L.G.; Sun, F.R. Constructal entransy dissipation rate minimization for umbrella-shaped assembly of cylindrical fins. Sci. China Technol. Sci. 2011, 54, 211–219. [Google Scholar] [CrossRef]
- Chen, L.G.; Xiao, Q.H.; Xie, Z.H.; Sun, F.R. Constructal entransy dissipation rate minimization for tree-shaped assembly of fins. Int. J. Heat Mass Transf. 2013, 67, 506–513. [Google Scholar] [CrossRef]
- Bejan, A.; Errera, M.R. Convective trees of fluid channels for volumetric cooling. Int. J. Heat Mass Transf. 2000, 43, 3105–3118. [Google Scholar] [CrossRef]
- Ordonez, J.C. Integrative Energy-Systems Design: System Structure from Thermodynamic Optimization; Duke University: Durham, NC, USA, 2003. [Google Scholar]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal optimization of a disc-shaped body with cooling channels for specified power pumping. Int. J. Low-Carbon Technol. 2015, 10, 229–237. [Google Scholar] [CrossRef]
- Xie, G.N.; Zhang, F.L.; Sundén, B.; Zhang, W.H. Constructal design and thermal analysis of microchannel heat sinks with multistage bifurcations in single-phase liquid flow. Appl. Therm. Eng. 2014, 62, 791–802. [Google Scholar] [CrossRef]
- Xie, G.N.; Shen, H.; Wang, C.C. Parametric study on thermal performance of microchannel heat sinks with internal vertical Y-shaped bifurcations. Int. J. Heat Mass Transf. 2015, 90, 948–958. [Google Scholar] [CrossRef]
- Song, Y.D.; Asadi, M.; Xie, G.N.; Rocha, L.A.O. Constructal wavy-fin channels of a compact heat exchanger with heat transfer rate maximization and pressure losses minimization. Appl. Therm. Eng. 2015, 75, 24–32. [Google Scholar] [CrossRef]
- Adewumi, O.O.; Bello-Ochende, T.; Meyer, J.P. Numerical investigation into the thermal performance of single microchannels with varying axial length and different shapes of micro pin-fin inserts. Heat Transf. Eng. 2017, 38, 1157–1170. [Google Scholar] [CrossRef]
- Adewumi, O.O.; Bello-Ochende, T.; Meyer, J.P. Constructal design of single microchannel heat sink with varying axial length and temperature-dependent fluid properties. Int. J. Heat Technol. 2016, 34, S167–S172. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lorente, S.; Bejan, A. Constructal steam generator architecture. Int. J. Heat Mass Transf. 2009, 52, 2362–2369. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lorente, S.; Bejan, A. Steam generator structure: Continuous model and constructal design. Int. J. Energy Res. 2011, 35, 336–345. [Google Scholar] [CrossRef]
- Norouzi, E.; Mehrgoo, M.; Amidpour, M. Geometric and thermodynamic optimization of a heat recovery steam generator: A constructal design. J. Heat Transf. 2012, 134, 111801. [Google Scholar] [CrossRef]
- Mehrgoo, M.; Amidpour, M. Constructal design and optimization of a dual pressure heat recovery steam generator. Energy 2017, 124, 87–99. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Chen, L.G.; Sun, F.R. Constructal entransy dissipation rate and flow-resistance minimization for cooling channels. Sci. China Technol. Sci. 2010, 53, 2458–2468. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Chen, L.G.; Sun, F.R. Constructal entransy dissipation rate minimization for a heat generating volume cooled by forced convection. Chin. Sci. Bull. 2011, 56, 2966–2973. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Chen, L.G.; Sun, F.R. Constructal design for a steam generator based on entransy dissipation extremum principle. Sci. China Technol. Sci. 2011, 54, 1462–1468. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 4th ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Bejan, A. Constructal theory: From thermodynamic and geometric optimization to predicting shape in nature. Energy Convers. Manag. 1998, 39, 1705–1718. [Google Scholar] [CrossRef]
- Bejan, A.; Errera, M.R. Deterministic tree networks for fluid flow: Geometry for minimal flow resistance between a volume and one point. Fractals 1997, 5, 685–695. [Google Scholar] [CrossRef]
- Bejan, A. Constructal tree network for fluid flow between a finite-size volume and one source or sink. Rev. Gen. Therm. 1997, 36, 592–604. [Google Scholar] [CrossRef]
- Errera, M.R.; Bejan, A. Tree networks for flows in composite porous media. J. Porous Media 1999, 2, 1–18. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. “Volume-point” mass transfer constructal optimization based on triangular element. Arab. J. Sci. Eng. 2013, 38, 365–372. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal mass transfer optimization for cylindrical assembly with minimum mass entransy dissipation. J. Eng. Thermophys. 2013, 34, 947–951. (In Chinese) [Google Scholar]
- Chen, L.G.; Feng, H.J.; Xie, Z.H.; Sun, F.R. “Volume-point” mass transfer constructal optimization based on flow resistance minimization with cylindrical element. Int. J. Heat Mass Transf. 2015, 89, 1135–1140. [Google Scholar] [CrossRef]
- Chen, L.G.; Tian, F.H.; Xiao, Q.H.; Sun, F.R. Constructal entransy dissipation minimization for mass transfer based on rectangular element with constant channel. J. Therm. Sci. Technol. 2012, 11, 136–141. (In Chinese) [Google Scholar] [CrossRef]
- Xiao, Q.H. Constructal Optimizations for Heat and Mass Transfer Based on Entransy Dissipation Extremum Principle. Ph.D. Thesis, Naval University of Engineering, Wuhan, China, 2011. (In Chinese). [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Xiao, Q.; Feng, H. Constructal Optimizations for Heat and Mass Transfers Based on the Entransy Dissipation Extremum Principle, Performed at the Naval University of Engineering: A Review. Entropy 2018, 20, 74. https://doi.org/10.3390/e20010074
Chen L, Xiao Q, Feng H. Constructal Optimizations for Heat and Mass Transfers Based on the Entransy Dissipation Extremum Principle, Performed at the Naval University of Engineering: A Review. Entropy. 2018; 20(1):74. https://doi.org/10.3390/e20010074
Chicago/Turabian StyleChen, Lingen, Qinghua Xiao, and Huijun Feng. 2018. "Constructal Optimizations for Heat and Mass Transfers Based on the Entransy Dissipation Extremum Principle, Performed at the Naval University of Engineering: A Review" Entropy 20, no. 1: 74. https://doi.org/10.3390/e20010074
APA StyleChen, L., Xiao, Q., & Feng, H. (2018). Constructal Optimizations for Heat and Mass Transfers Based on the Entransy Dissipation Extremum Principle, Performed at the Naval University of Engineering: A Review. Entropy, 20(1), 74. https://doi.org/10.3390/e20010074




