Granger Causality and Jensen–Shannon Divergence to Determine Dominant Atrial Area in Atrial Fibrillation
Abstract
1. Introduction
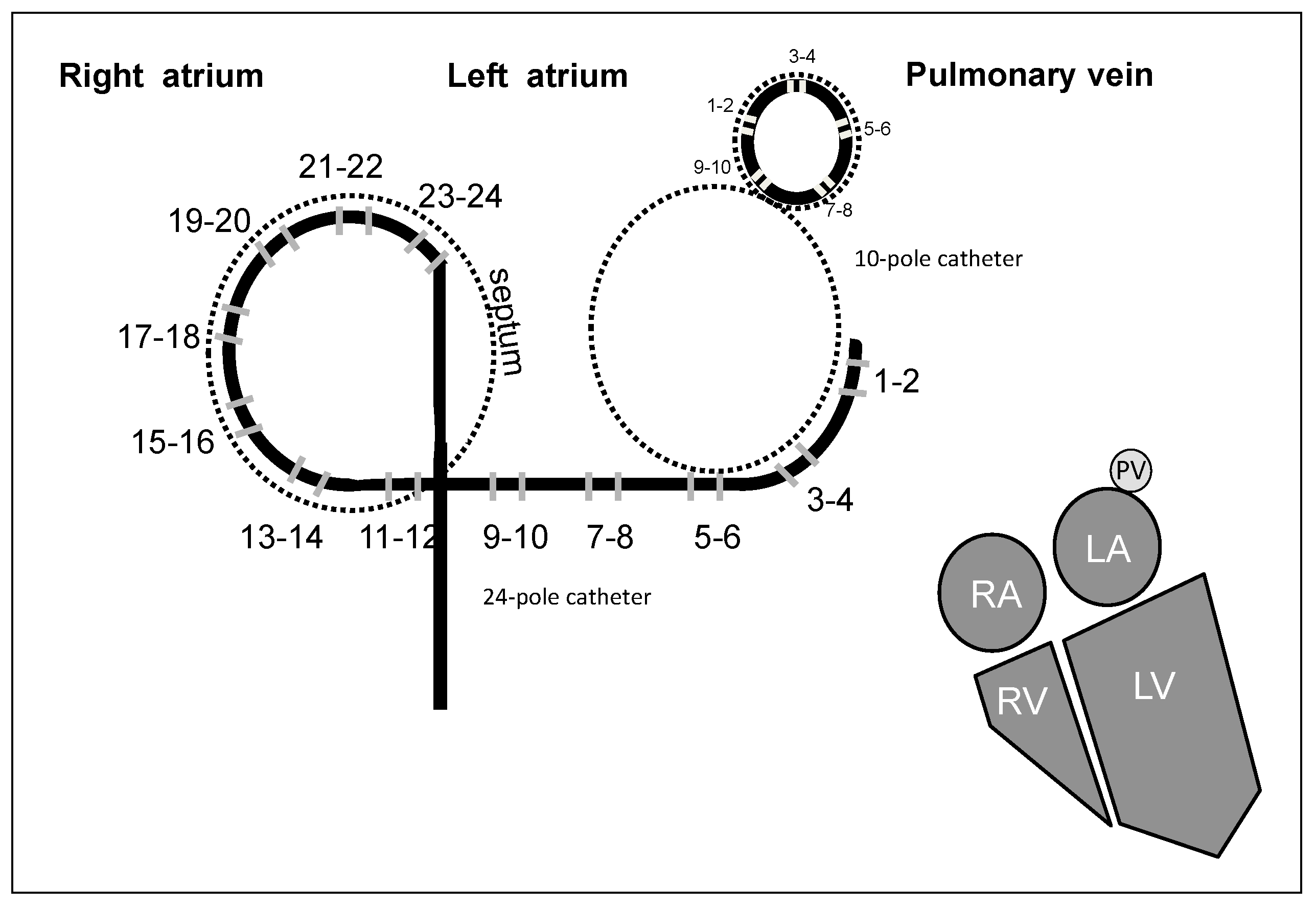
2. Materials
3. Methods
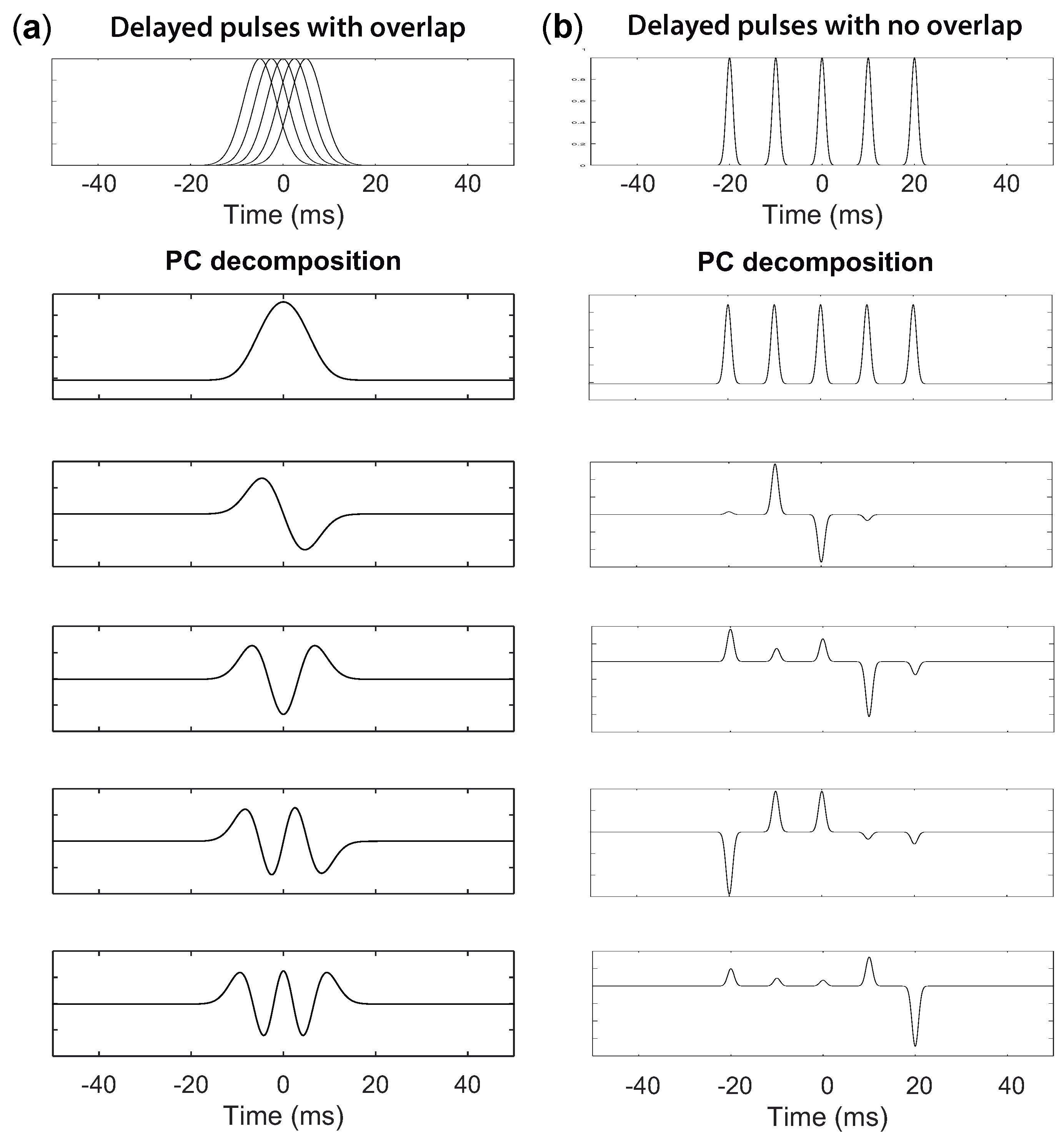
3.1. Principal Component Analysis
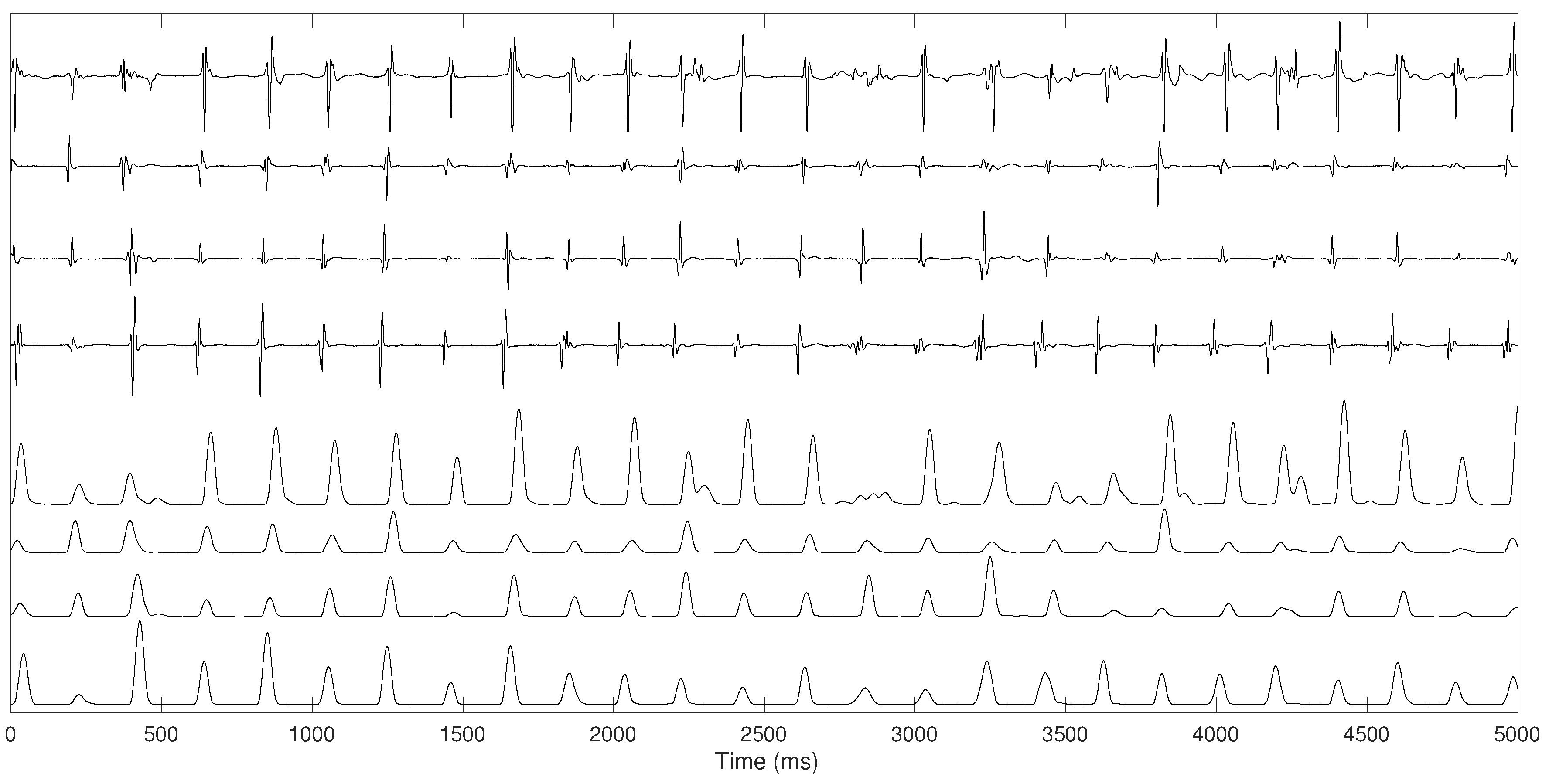
- Bipolar electrogram signals were pre-processed using several steps proposed by Botteron [30]. Initially, the signals were band-pass filtered between 40 and 250 Hz. Subsequently, they were rectified and, finally, the absolute value of the filtered waveforms were lowpass filtered with a 20-Hz cut-off filter. This filtering process extracts a time-varying waveform proportional to the amplitude of the high-frequency components of the original atrial electrograms, enhancing the atrial activations, simplifying their shape variations while reducing noise, as illustrated in Figure 2.
- PCA was applied to the pre-processed recordings on the RA and on the LA with Orbiter catheter and on the PVs with Lasso catheter before ablation procedure. We extract the first PC from the four electrograms recorded on the four PVs, simultaneous to the recordings from the LA and the RA, where the first PC was extracted in each area.
- PCA was applied to the recordings recorded on the LA and on the RA with the Orbiter catheter in four phases: in basal state, after right PVs’ isolation, after left PVs’ isolation and after the ablation procedure.
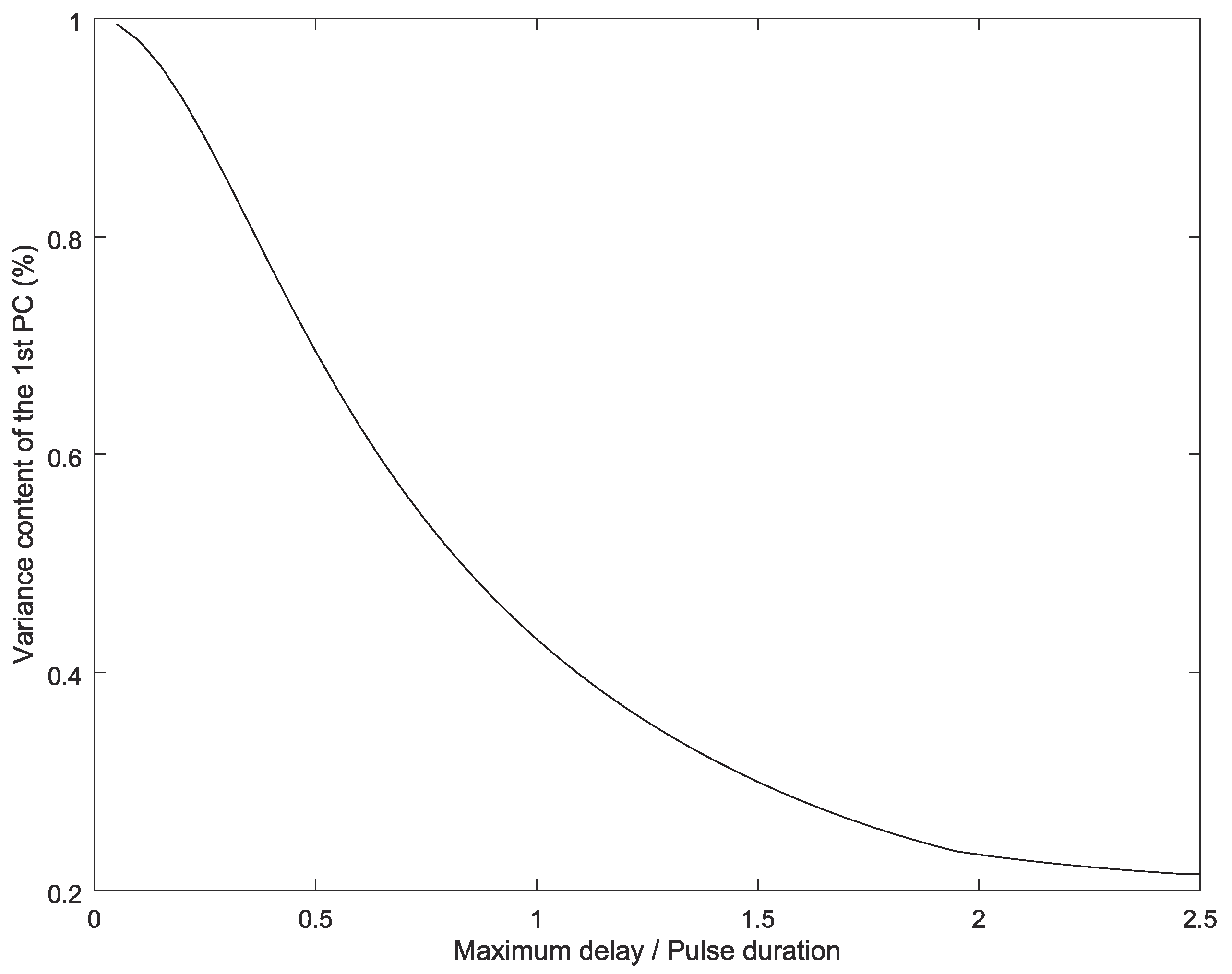
Suitability of PCA Decomposition
3.2. Granger Causality
3.3. Jensen–Shannon Divergence
3.4. Statistical Analysis
4. Results
4.1. Analysis Pre-Ablation Procedure
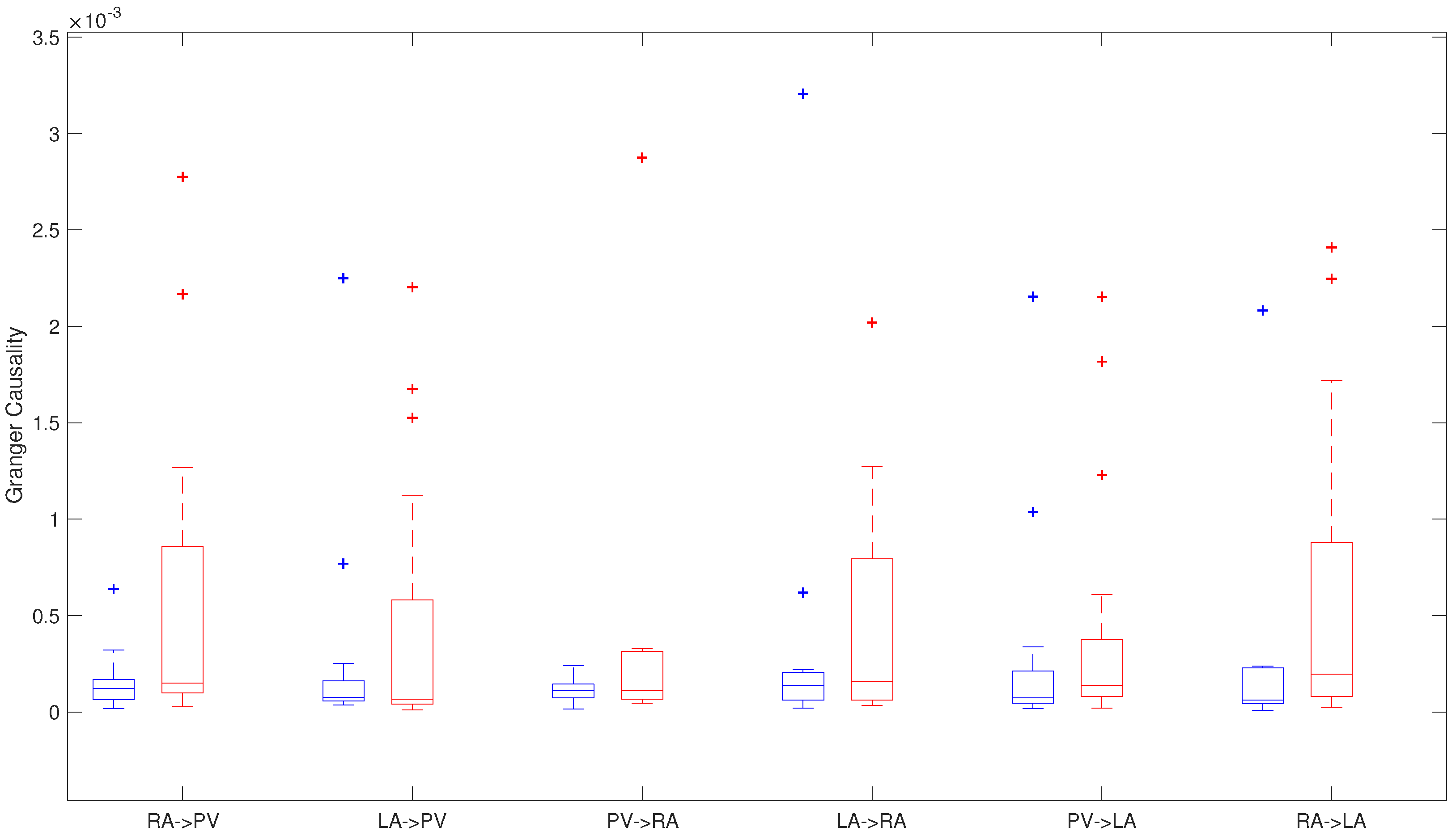
4.1.1. Granger Causality
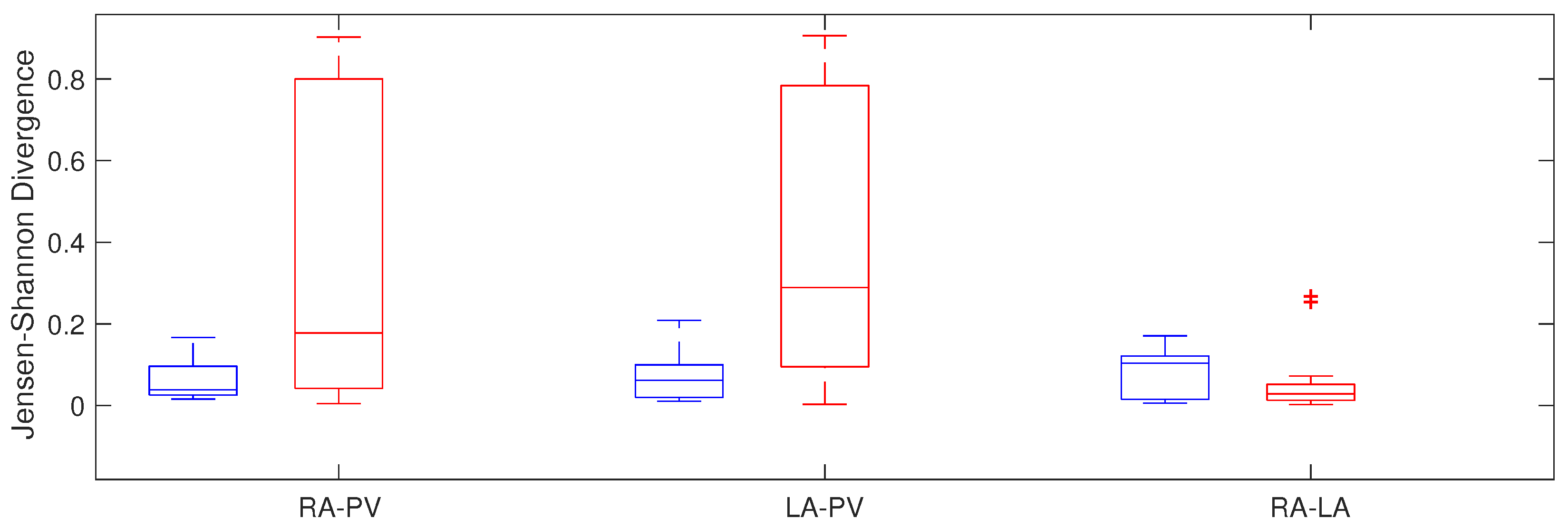
4.1.2. Jensen–Shannon Divergence
4.2. Analysis during the Ablation Procedure
- Phase 1: Basal state;
- Phase 2: After right PVs’ isolation;
- Phase 3: After left PVs’ isolation;
- Phase 4: After the procedure.
4.2.1. Granger Causality
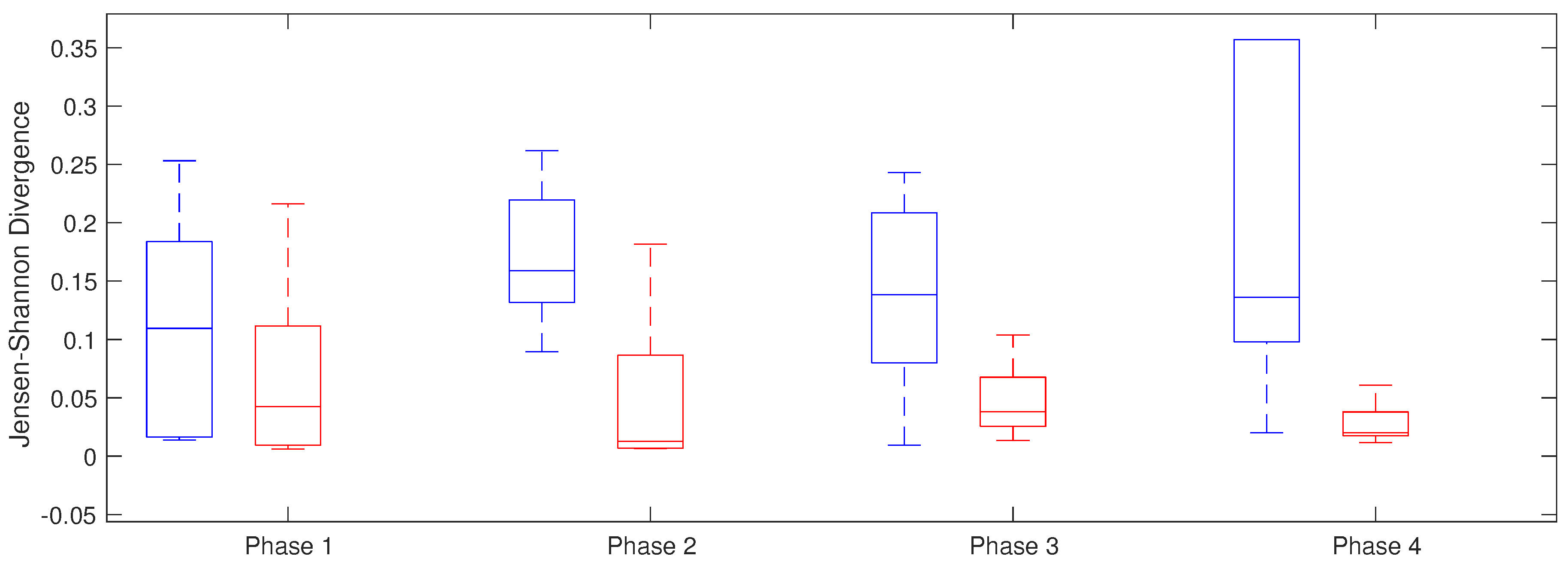
4.2.2. Jensen–Shannon Divergence
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AH | Arterial Hypertension |
| AF | Atrial Fibrillation |
| CS | Coronary Sinus |
| ECV | Electrical Cardioversion |
| G-Causality | Granger Causality |
| JSD | Jensen–Shannon Divergence |
| IQR | Interquartile Range |
| LA | Left Atrium |
| LIPV | Left Inferior Pulmonar Vein |
| LSPV | Left Superior Pulmonar Vein |
| PCA | Principal Component Analysis |
| PC | Principal Component |
| PV | Pulmonar Vein |
| RA | Right atrium |
| RIPV | Right Inferior Pulmonar Vein |
| RSPV | Right Superior Pulmonar Vein |
| SC | Structural Cardiopathology |
References
- Haim, M.; Hoshen, M.; Reges, O.; Rabi, Y.; Balicer, R.; Leibowitz, M. Prospective national study of the prevalence, incidence, management and outcome of a large contemporary cohort of patients with incident non-valvular atrial fibrillation. J. Am. Heart Assoc. 2015, 4, e001486. [Google Scholar] [CrossRef] [PubMed]
- Kirchhof, P.; Benussi, S.; Kotecha, D.; Ahlsson, A.; Atar, D.; Casadei, B.; Castellá, M.; Diener, H.C.; Heidbuchel, H.; Hendriks, J.; et al. 2016 ESC Guidelines for the Management of Atrial Fibrillation Developed in Collaboration With EACTS. Rev. Esp. Cardiol. 2017, 70, 50. [Google Scholar] [CrossRef] [PubMed]
- Chugh, S.S.; Havmoeller, R.; Narayanan, K.; Singh, D.; Rienstra, M.; Benjamin, E.J.; Gillum, R.F.; Kim, Y.H.; McAnulty, J.H., Jr.; Zheng, Z.J.; et al. Worldwide epidemiology of atrial fibrillation: A Global Burden of Disease 2010 Study. Circulation 2014, 129, 837–847. [Google Scholar] [CrossRef] [PubMed]
- Fuster, V.; Rydén, L.E.; Cannom, D.S.; Crijns, H.J.; Curtis, A.B.; Ellenbogen, K.A.; Halperin, J.L.; Kay, G.N.; Le Huezey, J.Y.; Lowe, J.E.; et al. 2011 ACCF/AHA/HRS focused updates incorporated into the ACC/AHA/ESC 2006 Guidelines for the management of patients with atrial fibrillation: A report of the American College of Cardiology Foundation/American Heart Association Task Force on Practice Guidelines developed in partnership with the European Society of Cardiology and in collaboration with the European Heart Rhythm Association and the Heart Rhythm Society. J. Am. Coll. Cardiol. 2011, 57, e101–e198. [Google Scholar] [PubMed]
- Krummen, D.E.; Narayan, S.M. Mechanisms for the initiation of human atrial fibrillation. Heart Rhythm 2009, 6, S12–S16. [Google Scholar] [CrossRef] [PubMed]
- Gerstenfeld, E.P.; Sahakian, A.V.; Swiryn, S. Evidence for transient linking of atrial excitation during atrial fibrillation in humans. Circulation 1992, 86, 375–382. [Google Scholar] [CrossRef] [PubMed]
- Narayan, S.M.; Krummen, D.E.; Shivkumar, K.; Clopton, P.; Rappel, W.J.; Miller, J.M. Treatment of atrial fibrillation by the ablation of localized sources: CONFIRM (Conventional Ablation for Atrial Fibrillation With or Without Focal Impulse and Rotor Modulation) trial. J. Am. Coll. Cardiol. 2012, 60, 628–636. [Google Scholar] [CrossRef] [PubMed]
- Shivkumar, K.; Ellenbogen, K.A.; Hummel, J.D.; Miller, J.M.; Steinberg, J.S. Acute termination of human atrial fibrillation by identification and catheter ablation of localized rotors and sources: First multicenter experience of focal impulse and rotor modulation (FIRM) ablation. J. Cardiovasc. Electrophysiol. 2012, 23, 1277–1285. [Google Scholar] [CrossRef] [PubMed]
- Haïssaguerre, M.; Jaïs, P.; Shah, D.C.; Takahashi, A.; Hocini, M.; Quiniou, G.; Garrigue, S.; Le Mouroux, A.; Le Métayer, P.; Clémenty, J. Spontaneous initiation of atrial fibrillation by ectopic beats originating in the pulmonary veins. N. Engl. J. Med. 1998, 339, 659–666. [Google Scholar] [CrossRef] [PubMed]
- Jalife, J.; Berenfeld, O.; Mansour, M. Mother rotors and fibrillatory conduction: A mechanism of atrial fibrillation. Cardiovasc. Res. 2002, 54, 204–216. [Google Scholar] [CrossRef]
- Arbelo, E.; Brugada, J.; Hindricks, G.; Maggioni, A.P.; Tavazzi, L.; Vardas, P.; Laroche, C.; Anselme, F.; Inama, G.; Jais, P.; et al. The atrial fibrillation ablation pilot study: a European Survey on Methodology and results of catheter ablation for atrial fibrillation conducted by the European Heart Rhythm Association. Eur. Heart J. 2014, 35, 1466–1478. [Google Scholar] [CrossRef] [PubMed]
- Walfridsson, H.; Walfridsson, U.; Nielsen, J.C.; Johannessen, A.; Raatikainen, P.; Janzon, M.; Levin, L.A.; Aronsson, M.; Hindricks, G.; Kongstad, O.; et al. Radiofrequency ablation as initial therapy in paroxysmal atrial fibrillation: Results on health-related quality of life and symptom burden. The MANTRA-PAF trial. Europace 2015, 17, 215–221. [Google Scholar] [CrossRef] [PubMed]
- Mont, L.; Bisbal, F.; Hernandez-Madrid, A.; Perez-Castellano, N.; Vinolas, X.; Arenal, A.; Arribas, F.; Fernandez-Lozano, I.; Bodegas, A.; Cobos, A.; et al. Catheter ablation vs. antiarrhythmic drug treatment of persistent atrial fibrillation: A multicentre, randomized, controlled trial (SARA study). Eur. Heart J. 2014, 35, 501–507. [Google Scholar] [CrossRef] [PubMed]
- Ganesan, A.N.; Shipp, N.J.; Brooks, A.G.; Kuklik, P.; Lau, D.H.; Lim, H.S.; Sullivan, T.; Roberts-Thomson, K.C.; Sanders, P. Long-term outcomes of catheter ablation of atrial fibrillation: A systematic review and meta-analysis. J. Am. Heart Assoc. 2013, 2, e004549. [Google Scholar]
- Verma, A.; Jiang, C.Y.; Betts, T.; Chen, J.; Deisenhofer, I.; Mantovan, R.; Macle, L.; Morillo, C.; Haverkamp, W.; Weerasooriya, R.; et al. Approaches to Catheter Ablation for Persistent Atrial Fibrillation. N. Engl. J. Med. 2015, 372, 1812–1822. [Google Scholar] [CrossRef] [PubMed]
- Seaburg, L.; Hess, E.P.; Coylewright, M.; Ting, H.H.; McLeod, C.J.; Montori, V.M. Shared decision making in atrial fibrillation: Where we are and where we should be going. Circulation 2014, 129, 704–710. [Google Scholar] [CrossRef] [PubMed]
- Lazar, S.; Dixit, S.; Marchlinski, F.E.; Callans, D.J.; Gerstenfeld, E.P. Presence of left-to-right atrial frequency gradient in paroxysmal but not persistent atrial fibrillation in humans. Circulation 2004, 110, 3181–3186. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, M.; Guillem, M.S.; Liberos, A.; Millet, J.; Berenfeld, O.; Climent, A.M. Identification of fibrillatory sources by measuring causal relationships. In Proceedings of the 2012 Computing in Cardiology, Krakow, Poland, 9–12 September 2012; pp. 705–708. [Google Scholar]
- Rodrigo, M.; Climent, A.M.; Liberos, A.; Calvo, D.; Fernández-Avilés, F.; Berenfeld, O.; Atienza, F.; Guillem, M.S. Identification of Dominant Excitation Patterns and Sources of Atrial Fibrillation by Causality Analysis. Ann. Biomed. Eng. 2016, 44, 2364–2376. [Google Scholar] [CrossRef] [PubMed]
- Luengo, D.; Munoz, G.R.; Elvira, V. Causality analysis of atrial fibrillation electrograms. In Proceedings of the 2015 Computing in Cardiology Conference (CinC), Nice, France, 6–9 September 2015; pp. 585–588. [Google Scholar]
- Luengo, D.; Rios-Munoz, G.; Elvira, V.; Artés-Rodríguez, A. A hierarchical algorithm for causality discovery among atrial fibrillation electrograms. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 774–778. [Google Scholar]
- Richter, U.; Faes, L.; Cristoforetti, A.; Masè, M.; Ravelli, F.; Stridh, M.; Sörnmo, L. A novel approach to propagation pattern analysis in intracardiac atrial fibrillation signals. Ann. Biomed. Eng. 2011, 39, 310–323. [Google Scholar] [CrossRef] [PubMed]
- Richter, U.; Faes, L.; Ravelli, F.; Sörnmo, L. Propagation pattern analysis during atrial fibrillation based on sparse modeling. IEEE Trans. Biomed. Eng. 2012, 59, 1319–1328. [Google Scholar] [CrossRef] [PubMed]
- Alcaine, A.; Mase, M.; Cristoforetti, A.; Ravelli, F.; Nollo, G.; Laguna, P.; Martinez, J.P.; Faes, L. A Multi-Variate Predictability Framework to Assess Invasive Cardiac Activity and Interactions During Atrial Fibrillation. IEEE Trans. Biomed. Eng. 2017, 64, 1157–1168. [Google Scholar] [CrossRef] [PubMed]
- Ré, M.A.; Azad, R.K. Generalization of entropy based divergence measures for symbolic sequence analysis. PLoS ONE 2014, 9, e93532. [Google Scholar] [CrossRef] [PubMed]
- Davies, A.; Brown, G.; Vigo, M.; Harper, S.; Horseman, L.; Splendiani, B.; Hill, E.; Jay, C. Exploring the Relationship Between Eye Movements and Electrocardiogram Interpretation Accuracy. Sci. Rep. 2016, 6, 38227. [Google Scholar] [CrossRef] [PubMed]
- Mateos, D.M.; Riveaud, L.E.; Lamberti, P.W. Detecting dynamical changes in time series by using the Jensen Shannon divergence. Chaos 2017, 27, 083118. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Wang, J. Complexity analysis of gait signal based on Jensen-Shannon divergence. J. Biomed. Eng. 2014, 31, 583–585. [Google Scholar]
- Jolliffe, I. Principal Component Analysis; Springer-Verlag: Berlin, Germany, 2002. [Google Scholar]
- Botteron, G.W.; Smith, J.M. A technique for measurement of the extent of spatial organization of atrial activation during atrial fibrillation in the intact human heart. IEEE Trans. Biomed. Eng. 1995, 42, 579–586. [Google Scholar] [CrossRef] [PubMed]
- Castells, F.; Cervigón, R.; Millet, J. On the preprocessing of atrial electrograms in atrial fibrillation: understanding Botteron’s approach. Pacing Clin. Electrophysiol. 2014, 37, 133–143. [Google Scholar] [CrossRef] [PubMed]
- Granger, C. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Gao, L.; Smielewski, P.; Czosnyka, M.; Ercole, A. Early Asymmetric Cardio-Cerebral Causality and Outcome after Severe Traumatic Brain Injury. J. Neurotrauma 2017, 34, 2743–2752. [Google Scholar] [CrossRef] [PubMed]
- Quinn, C.; Coleman, T.; Kiyavash, N.; Hatsopoulos, N. Estimating the directed information to infer causal relationships in ensemble neural spike train recordings. J. Comput. Neurosci. 2011, 30, 17–44. [Google Scholar] [CrossRef] [PubMed]
- Akaike, H. A Bayesian analysis of the minimum AIC procedure. Ann. Inst. Stat. Math. 1978, 30, 9–14. [Google Scholar] [CrossRef]
- Katatbeh, Q.; Martínez-Aroza, J.; Gómez-Lopera, J.; Blanco-Navarro, D. An Optimal Segmentation Method Using Jensen–Shannon Divergence via a Multi-Size Sliding Window Technique. Entropy 2015, 17, 7996–8006. [Google Scholar] [CrossRef]
- Rao, C. Differential Metrics in Probability Spaces. In Differential Geometry in Statistical Inference; Institute of Mathematical Statistics: Hayward, CA, USA, 1987; pp. 217–240. [Google Scholar]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Cover, T.; Thomas, J. Elements of Information Theory, 2nd ed.; Wiley Series in Telecommunications and Signal Processing; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Endres, D.; Schindelin, J. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar]
- Calkins, H.; Reynolds, M.R.; Spector, P.; Sondhi, M.; Xu, Y.; Martin, A.; Williams, C.J.; Sledge, I. Treatment of atrial fibrillation with antiarrhythmic drugs or radiofrequency ablation: Two systematic literature reviews and meta-analyses. Circ. Arrhythm. Electrophysiol. 2009, 2, 349–361. [Google Scholar] [CrossRef] [PubMed]
- Sotomi, Y.; Inoue, K.; Ito, N.; Kimura, R.; Toyoshima, Y.; Masuda, M.; Iwakura, K.; Fujii, K. Incidence and risk factors for very late recurrence of atrial fibrillation after radiofrequency catheter ablation. Europace 2013, 15, 1581–1586. [Google Scholar] [CrossRef] [PubMed]
- Andrade, J.G.; Khairy, P.; Macle, L.; Packer, D.L.; Lehmann, J.W.; Holcomb, R.G.; Ruskin, J.N.; Dubuc, M. Incidence and significance of early recurrences of atrial fibrillation after cryoballoon ablation: Insights from the multicenter Sustained Treatment of Paroxysmal Atrial Fibrillation (STOP AF) Trial. Circ. Arrhythm. Electrophysiol. 2014, 7, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Arora, R.; Verheule, S.; Scott, L.; Navarrete, A.; Katari, V.; Wilson, E.; Vaz, D.; Olgin, J.E. Arrhythmogenic substrate of the pulmonary veins assessed by high-resolution optical mapping. Circulation 2003, 107, 1816–1821. [Google Scholar]
- Hsieh, M.H.; Tai, C.T.; Lee, S.H.; Lin, Y.K.; Tsao, H.M.; Chang, S.L.; Lin, Y.J.; Wongchaoen, W.; Lee, K.T.; Chen, S.A. The different mechanisms between late and very late recurrences of atrial fibrillation in patients undergoing a repeated catheter ablation. J. Cardiovasc. Electrophysiol. 2006, 17, 231–235. [Google Scholar] [CrossRef] [PubMed]
- Berenfeld, O.; Zaitsev, A.V.; Mironov, S.F.; Pertsov, A.M.; Jalife, J. Frequency-dependent breakdown of wave propagation into fibrillatory conduction across the pectinate muscle network in the isolated sheep right atrium. Circ. Res. 2002, 90, 1173–1180. [Google Scholar] [CrossRef] [PubMed]
- Cervigón, R.; Moreno, J.; García-Quintanilla, J.; Pérez-Villacastín, J.; Castells, F. Entropy at the right atrium as a predictor of atrial fibrillation recurrence outcome after pulmonary vein ablation. Biomed. Technol. 2016, 61, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Ho, S.Y.; Sánchez-Quintana, D.; Becker, A.E. A review of the coronary venous system: A road less travelled. Heart Rhythm 2004, 1, 107–112. [Google Scholar] [CrossRef] [PubMed]
- Karagueuzian, H.S. Triggered activity, coronary sinus, and atrial fibrillation. Heart Rhythm 2010, 7, e4. [Google Scholar] [CrossRef] [PubMed]

| Patient | Age | Sex | LA Size | SC | AH | AF > | ECV | Paroxysmal | Recurrence |
|---|---|---|---|---|---|---|---|---|---|
| (Years) | (mm) | 6 Months | AF | ||||||
| Pat 1 | 67 | Male | 42 | 0 | 0 | 0 | 1 | 0 | 0 |
| Pat 2 | 63 | Female | 48 | 0 | 1 | 0 | 1 | 1 | 1 |
| Pat 3 | 32 | Male | 42 | 0 | 0 | 0 | 0 | 1 | 0 |
| Pat 4 | 52 | Male | 45 | 0 | 1 | 0 | 0 | 0 | 0 |
| Pat 5 | 65 | Female | 45 | 0 | 0 | 1 | 1 | 0 | 0 |
| Pat 6 | 24 | Male | 36 | 0 | 0 | 0 | 1 | 1 | 1 |
| Pat 7 | 51 | Male | 54 | 0 | 1 | 1 | 1 | 0 | 1 |
| Pat 8 | 39 | Male | 35 | 0 | 0 | 0 | 1 | 1 | 0 |
| Pat 9 | 57 | Female | 50 | 0 | 0 | 0 | 0 | 1 | 1 |
| Pat 10 | 38 | Male | 41 | 0 | 0 | 1 | 1 | 0 | 1 |
| G-Causality | Recurrent AF | Non Recurrent AF | p |
|---|---|---|---|
| RA → VP | ± | ± | 0.099 |
| LA → VP | ± | ± | 0.433 |
| PV → RA | ± | ± | 0.499 |
| LA → RA | ± | ± | 0.499 |
| PV → LA | ± | ± | 0.181 |
| RA → LA | ± | ± | 0.047 |
| Phases | Non Recurrent AF | Recurrent AF | p |
|---|---|---|---|
| RA-LA JSD | RA-LA JSD | ||
| Phase 1 | 0.11 ± 0.17 | 0.04 ± 0.10 | 0.420 |
| Phase 2 | 0.16 ± 0.09 | 0.012 ± 0.08 | 0.042 |
| Phase 3 | 0.14 ± 0.13 | 0.04 ± 0.04 | 0.122 |
| Phase 4 | 0.14 ± 0.26 | 0.02 ± 0.02 | 0.044 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cervigón, R.; Castells, F.; Gómez-Pulido, J.M.; Pérez-Villacastín, J.; Moreno, J. Granger Causality and Jensen–Shannon Divergence to Determine Dominant Atrial Area in Atrial Fibrillation. Entropy 2018, 20, 57. https://doi.org/10.3390/e20010057
Cervigón R, Castells F, Gómez-Pulido JM, Pérez-Villacastín J, Moreno J. Granger Causality and Jensen–Shannon Divergence to Determine Dominant Atrial Area in Atrial Fibrillation. Entropy. 2018; 20(1):57. https://doi.org/10.3390/e20010057
Chicago/Turabian StyleCervigón, Raquel, Francisco Castells, José Manuel Gómez-Pulido, Julián Pérez-Villacastín, and Javier Moreno. 2018. "Granger Causality and Jensen–Shannon Divergence to Determine Dominant Atrial Area in Atrial Fibrillation" Entropy 20, no. 1: 57. https://doi.org/10.3390/e20010057
APA StyleCervigón, R., Castells, F., Gómez-Pulido, J. M., Pérez-Villacastín, J., & Moreno, J. (2018). Granger Causality and Jensen–Shannon Divergence to Determine Dominant Atrial Area in Atrial Fibrillation. Entropy, 20(1), 57. https://doi.org/10.3390/e20010057





