Characterizing Complex Dynamics in the Classical and Semi-Classical Duffing Oscillator Using Ordinal Patterns Analysis
Abstract
1. Introduction
2. The Duffing Oscillator
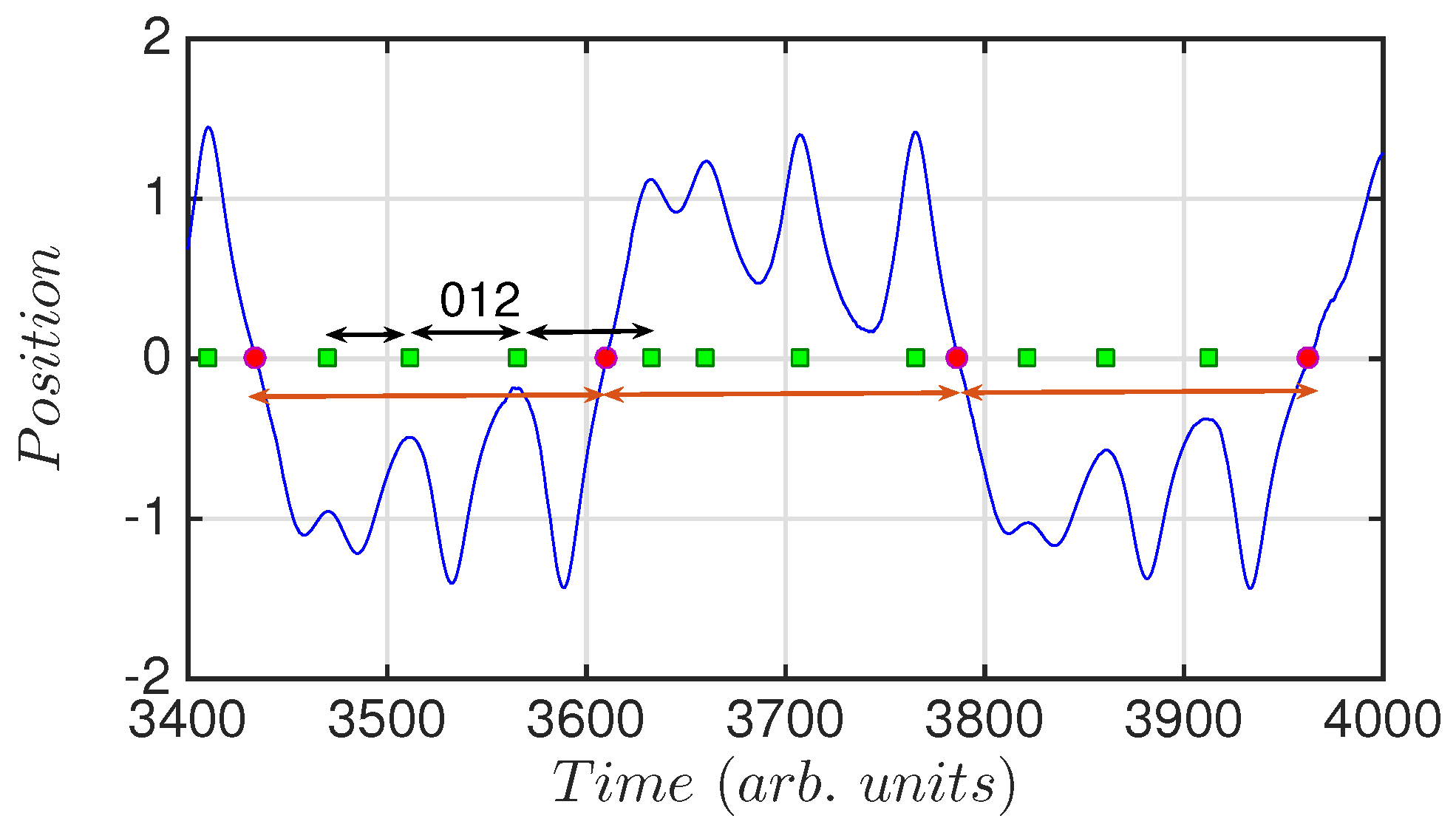
3. Ordinal Patterns Analysis and Permutation Entropy
4. Lyapunov Exponent and Poincaré Sections
5. Results and Discussion
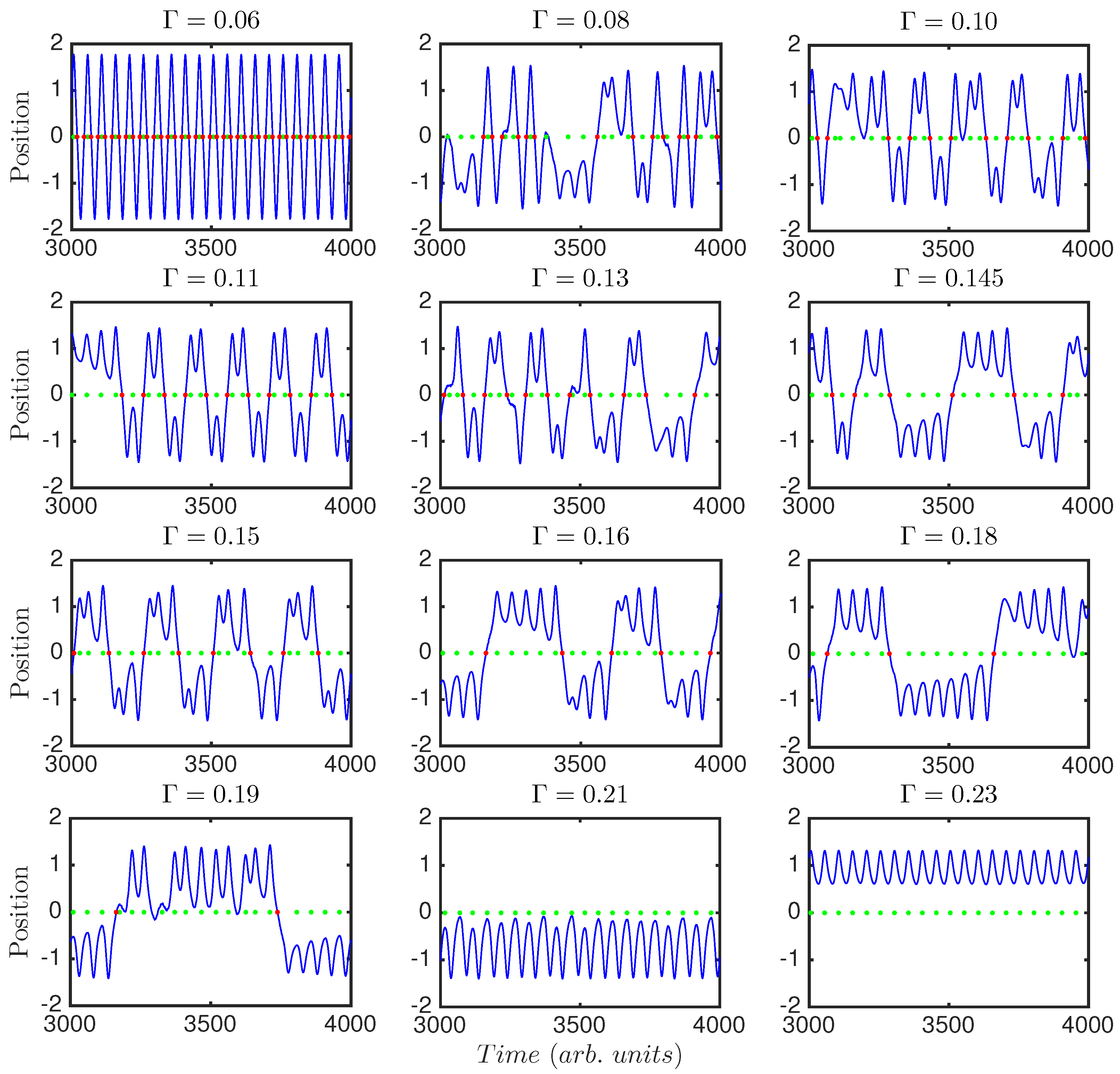
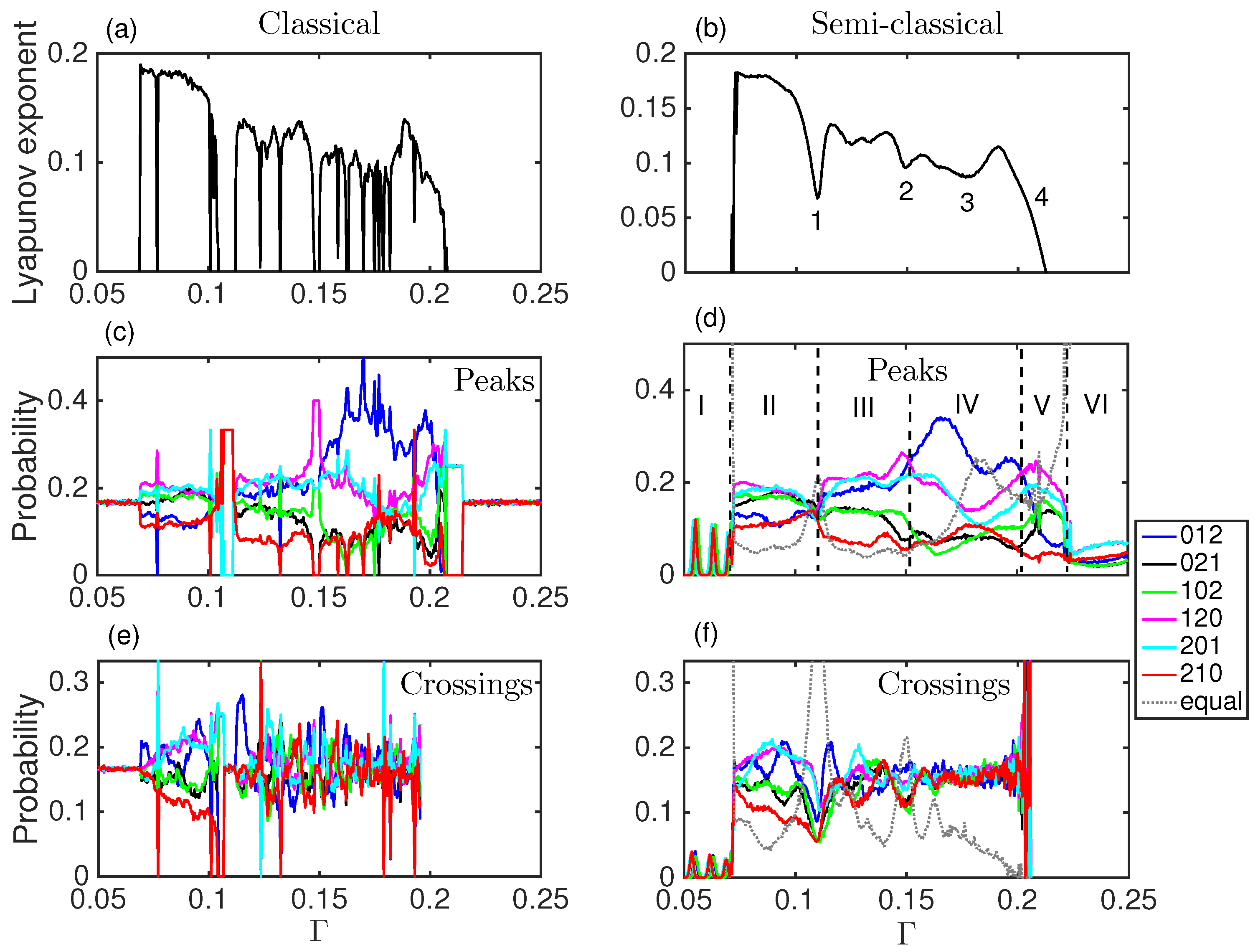
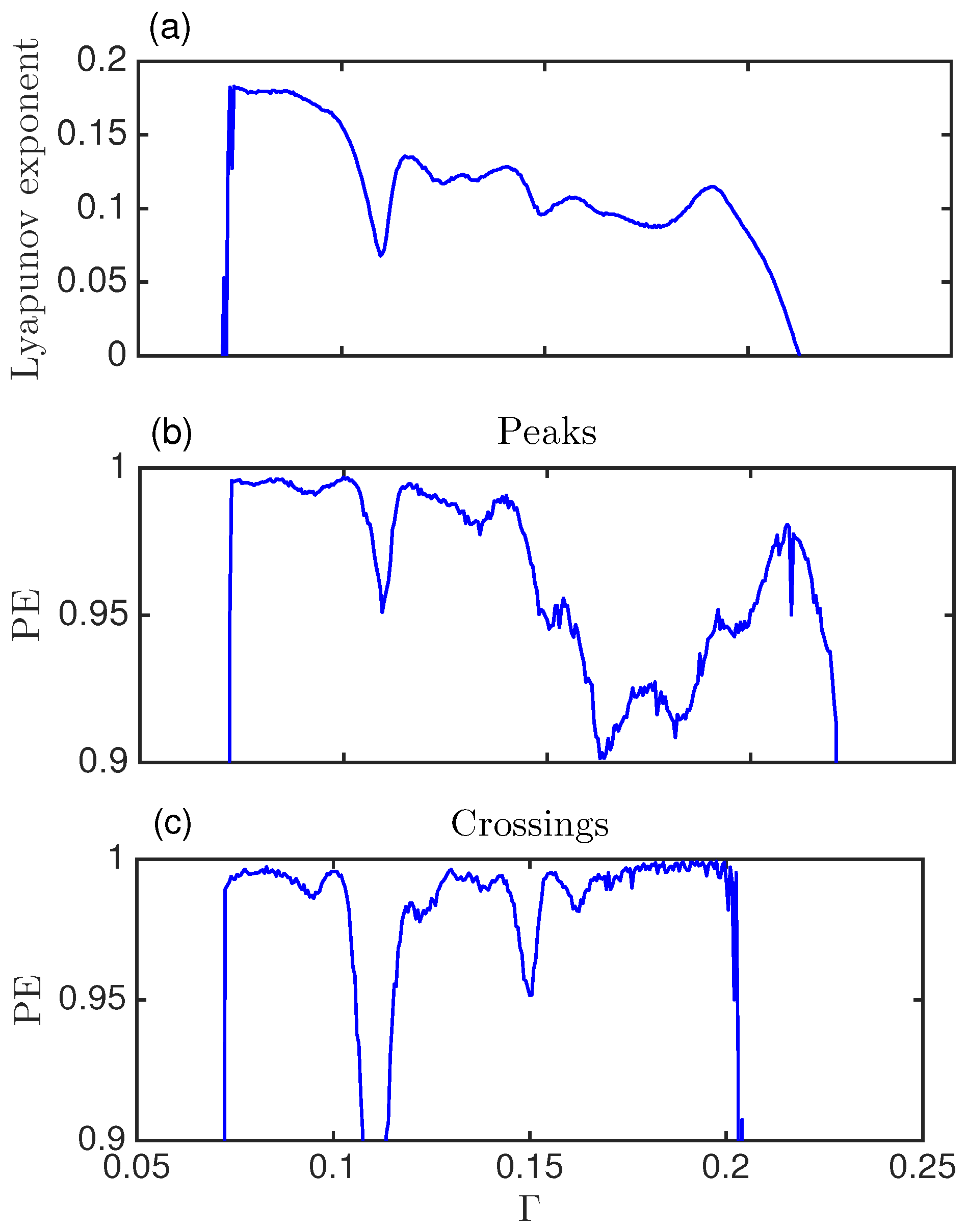
5.1. The Lyapunov Exponent
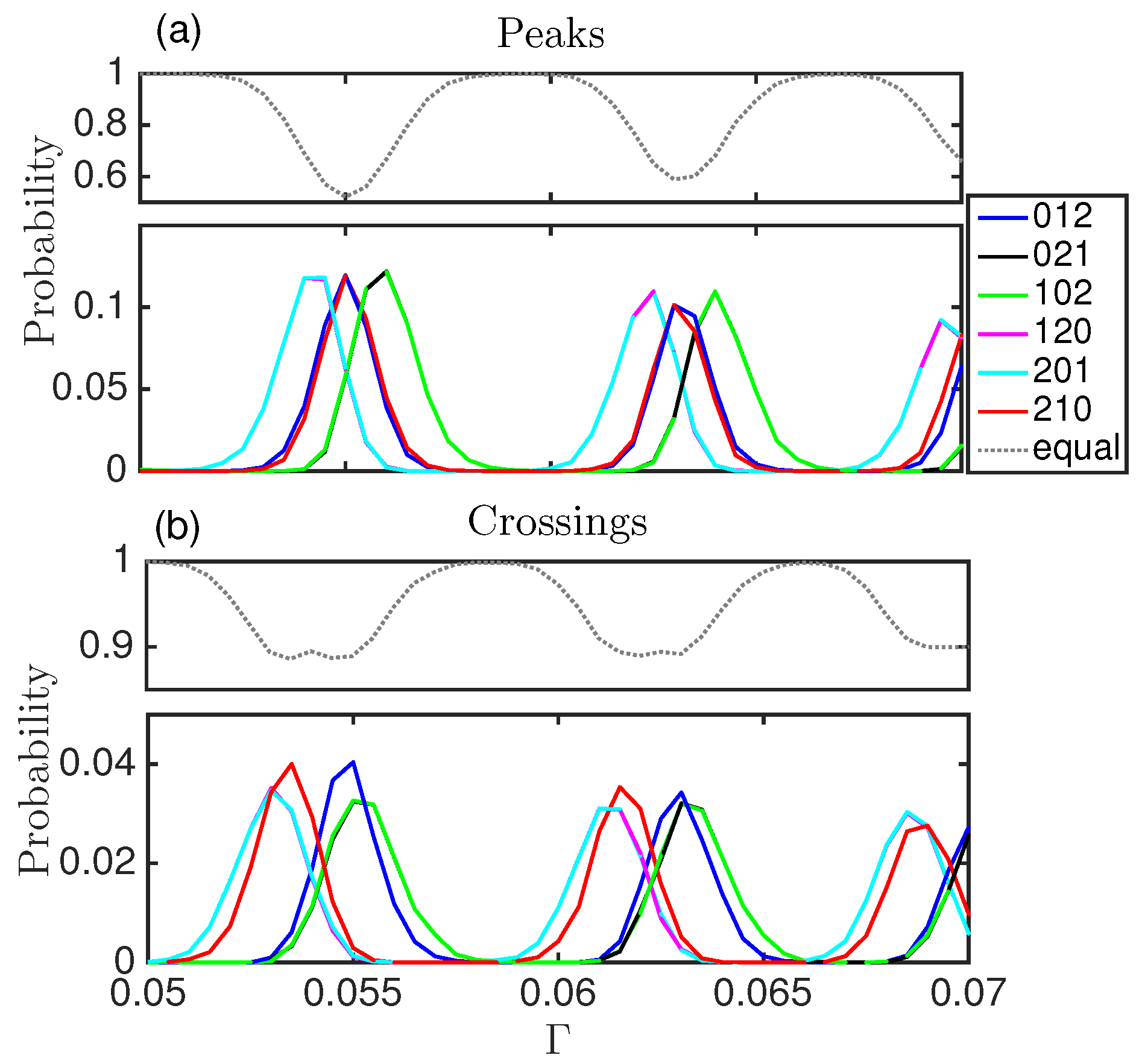
5.2. Ordinal Pattern Analysis of the Classical Duffing Oscillator
5.3. Ordinal Pattern Analysis of the Semi-Classical Duffing Oscillator
5.4. Permutation Entropy and Relation with Lyapunov Exponent
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Spiller, T.; Ralph, J. The emergence of chaos in an open quantum system. Phys. Lett. A 1994, 194, 235–240. [Google Scholar] [CrossRef]
- Brun, T.; Percival, I.; Schack, R. Quantum chaos in open systems: A quantum state diffusion analysis. J. Phys. A 1996, 29, 2077–2090. [Google Scholar] [CrossRef]
- Pokharel, B.; Duggins, P.; Misplon, M.; Lynn, W.; Hallman, K.; Anderson, D.; Kapulkin, A.; Pattanayak, A.K. Dynamical complexity in the quantum to classical transition. Scientific Reports accepted to appear 2018.
- Boffetta, G.; Cencini, M.; Falcioni, M.; Vulpiani, A. Predictability: A way to characterize complexity. Phys. Rep. 2002, 356, 367–474. [Google Scholar] [CrossRef]
- Ralph, J.; Jacobs, K.; Everitt, M. Observing quantum chaos with noisy measurements and highly mixed states. Phys. Rev. A 2017, 95, 12135. [Google Scholar] [CrossRef]
- Li, Q.; Kapulkin, A.; Anderson, D.; Tan, S.; Pattanayak, A. Experimental signatures of the quantum-classical transition in a nanomechanical oscillator modeled as a damped-driven double-well problem. Phys. Scr. 2012, T151, 14055. [Google Scholar] [CrossRef]
- Beugnon, J.; Jones, M.P.; Dingjan, J.; Darquié, B.; Messin, G.; Browaeys, A.; Grangier, P. Quantum interference between two single photons emitted by independently trapped atoms. Nature 2012, 440, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M.; Keller, K.; Kurths, J. Recent Progress in Symbolic Dynamics and Permutation Complexity: Ten Years of Permutation Entropy; EDP Sciences: Les Ulis, France, 2013; Volume 222. [Google Scholar]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Littlele, D.J.; Kane, D.M. Variance of permutation entropy and the influence of ordinal pattern selection. Phys. Rev. E 2017, 95, 52116. [Google Scholar]
- Ribeiro, H.V.; Jauregui, M.; Zunino, L.; Lenzi, E.K. Characterizing time series via complexity-entropy curves. Phys. Rev. E 2017, 95, 62106. [Google Scholar] [CrossRef] [PubMed]
- Parlitz, U.; Berg, S.; Luther, S.; Schirdewan, A.; Kurths, J.; Wessel, N. Classifying cardiac biosignals using ordinal pattern statistics and symbolic dynamics. Comput. Biol. Med. 2012, 42, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C. A new kind of permutation entropy used to classify sleep stages from invisible EEG microstructure. Entropy 2017, 19, 197. [Google Scholar] [CrossRef]
- Keller, K.; Mangold, T.; Stolz, I.; Werner, J. Permutation entropy: New ideas and challenges. Entropy 2017, 19, 134. [Google Scholar] [CrossRef]
- Aragoneses, A.; Perrone, S.; Sorrentino, T.; Torrent, M.C.; Masoller, C. Unveiling the complex organization of recurrent patterns in spiking dynamical systems. Sci. Rep. 2014, 4, 4696. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Soriano, M.C.; Fischer, I.; Rosso, O.A.; Mirasso, C.R. Permutation-information-theory approach to unveil delay dynamics from time-series analysis. Phys. Rev. E 2010, 82, 46212. [Google Scholar] [CrossRef] [PubMed]
- Aragoneses, A.; Carpi, L.; Tarasov, N.; Churkin, D.V.; Torrent, M.C.; Masoller, C.; Turitsyn, S.K. Unveiling temporal correlations characteristic to phase transition in the intensity of a fibre laser radiation. Phys. Rev. Lett. 2016, 116, 33902. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trostel, M.L.; Misplon, M.Z.R.; Aragoneses, A.; Pattanayak, A.K. Characterizing Complex Dynamics in the Classical and Semi-Classical Duffing Oscillator Using Ordinal Patterns Analysis. Entropy 2018, 20, 40. https://doi.org/10.3390/e20010040
Trostel ML, Misplon MZR, Aragoneses A, Pattanayak AK. Characterizing Complex Dynamics in the Classical and Semi-Classical Duffing Oscillator Using Ordinal Patterns Analysis. Entropy. 2018; 20(1):40. https://doi.org/10.3390/e20010040
Chicago/Turabian StyleTrostel, Max L., Moses Z. R. Misplon, Andrés Aragoneses, and Arjendu K. Pattanayak. 2018. "Characterizing Complex Dynamics in the Classical and Semi-Classical Duffing Oscillator Using Ordinal Patterns Analysis" Entropy 20, no. 1: 40. https://doi.org/10.3390/e20010040
APA StyleTrostel, M. L., Misplon, M. Z. R., Aragoneses, A., & Pattanayak, A. K. (2018). Characterizing Complex Dynamics in the Classical and Semi-Classical Duffing Oscillator Using Ordinal Patterns Analysis. Entropy, 20(1), 40. https://doi.org/10.3390/e20010040




