High Density Nodes in the Chaotic Region of 1D Discrete Maps
Abstract
:1. Introduction
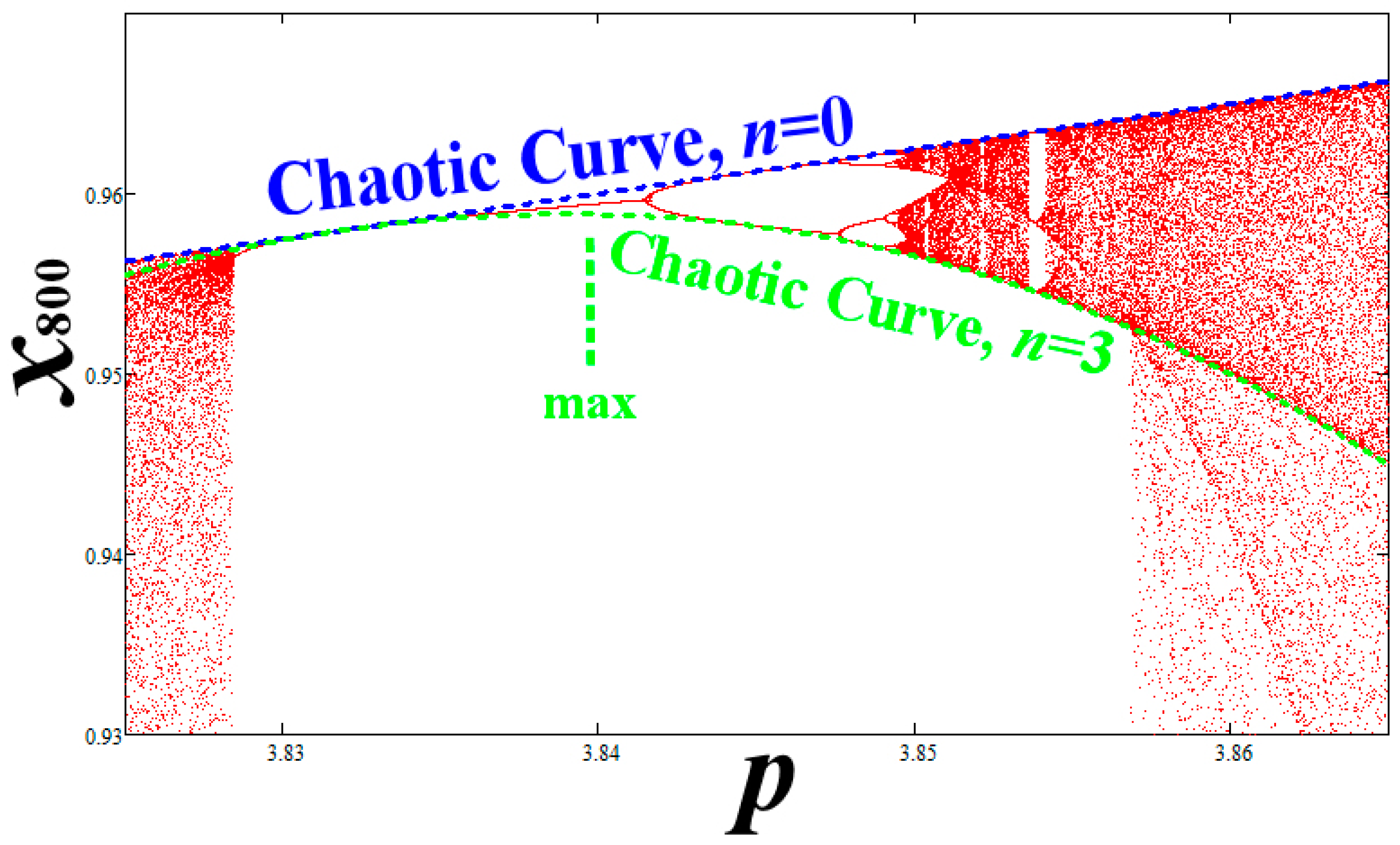
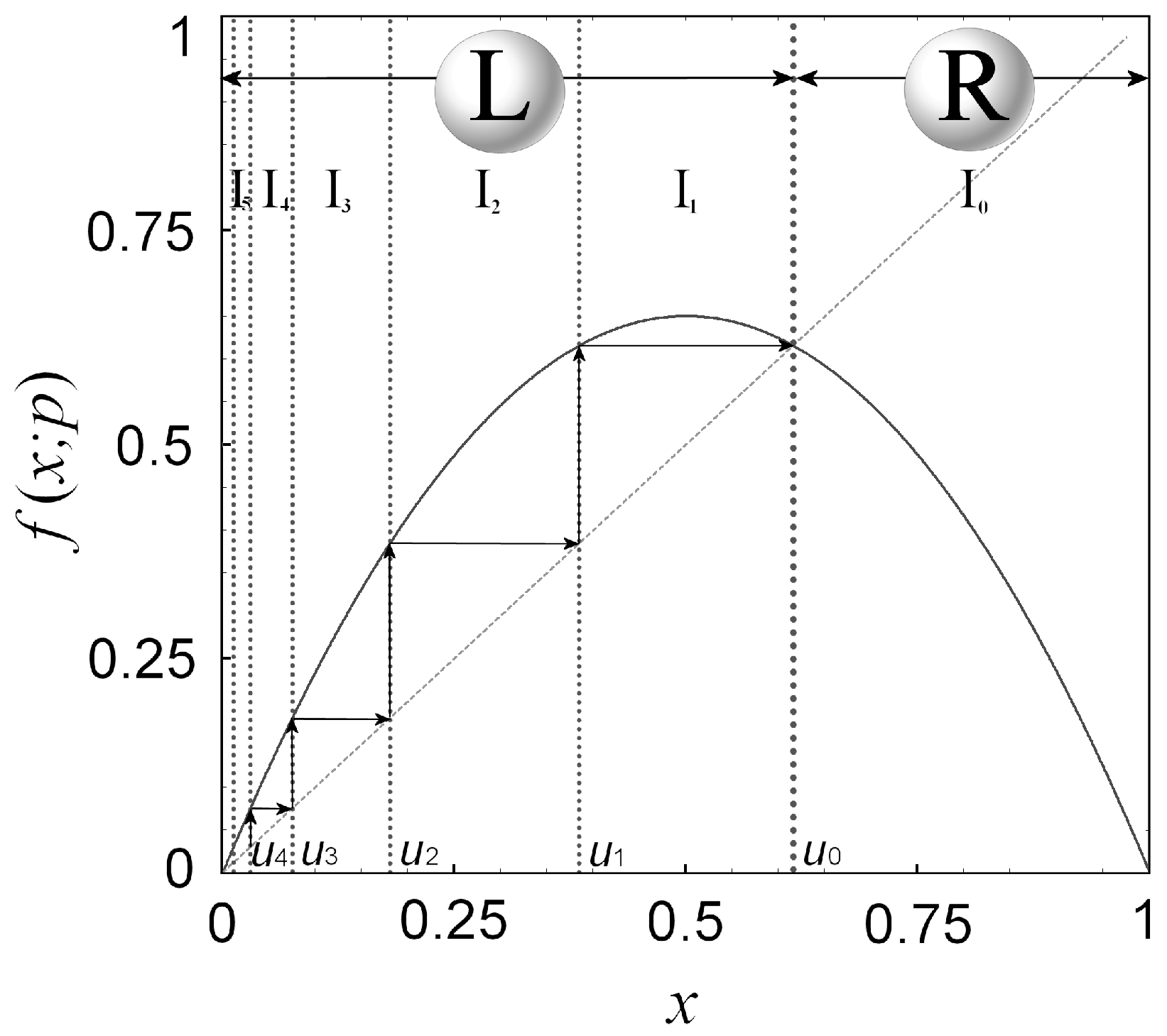
2. Critical Lines in the Chaotic Zone
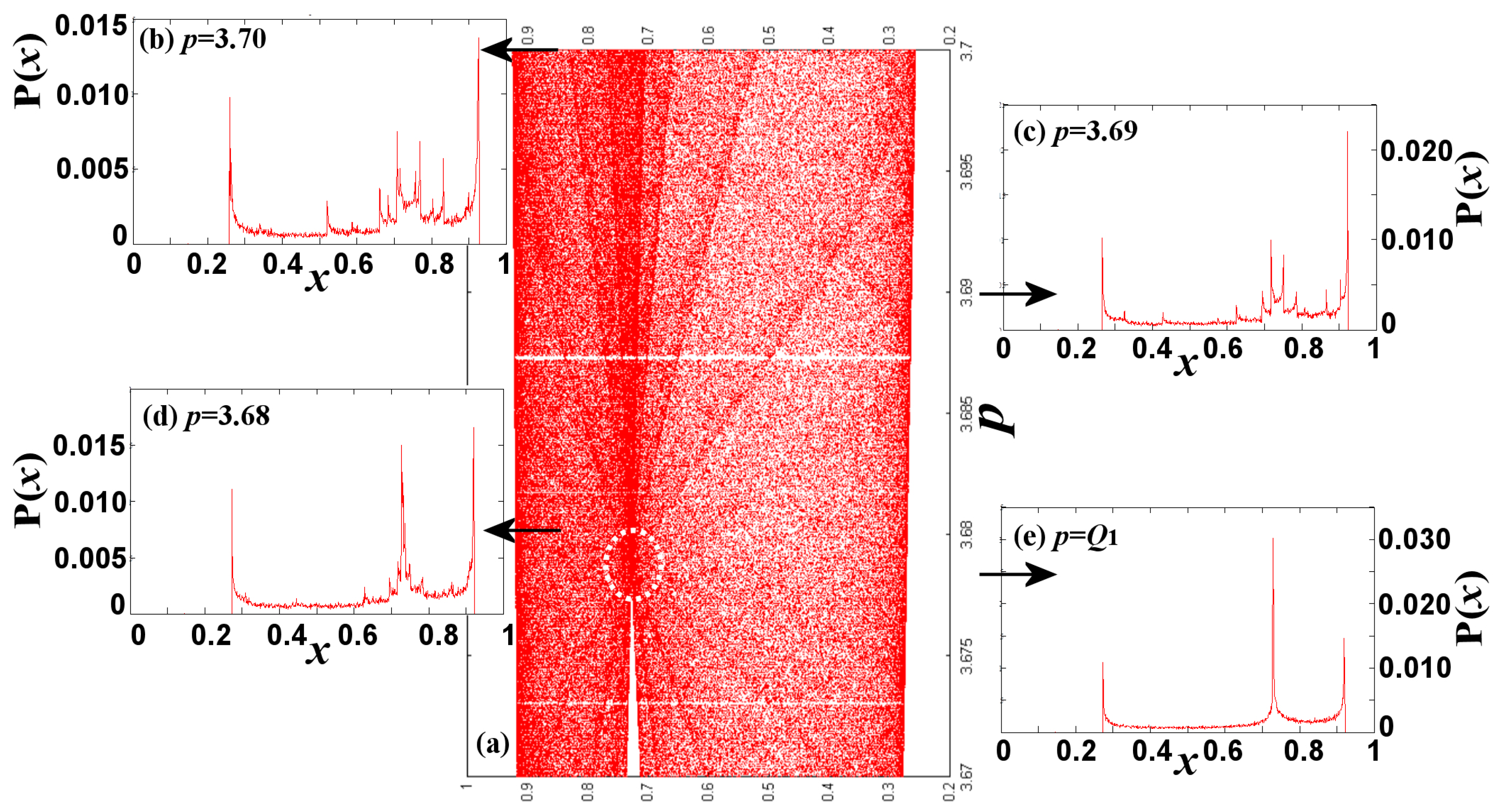
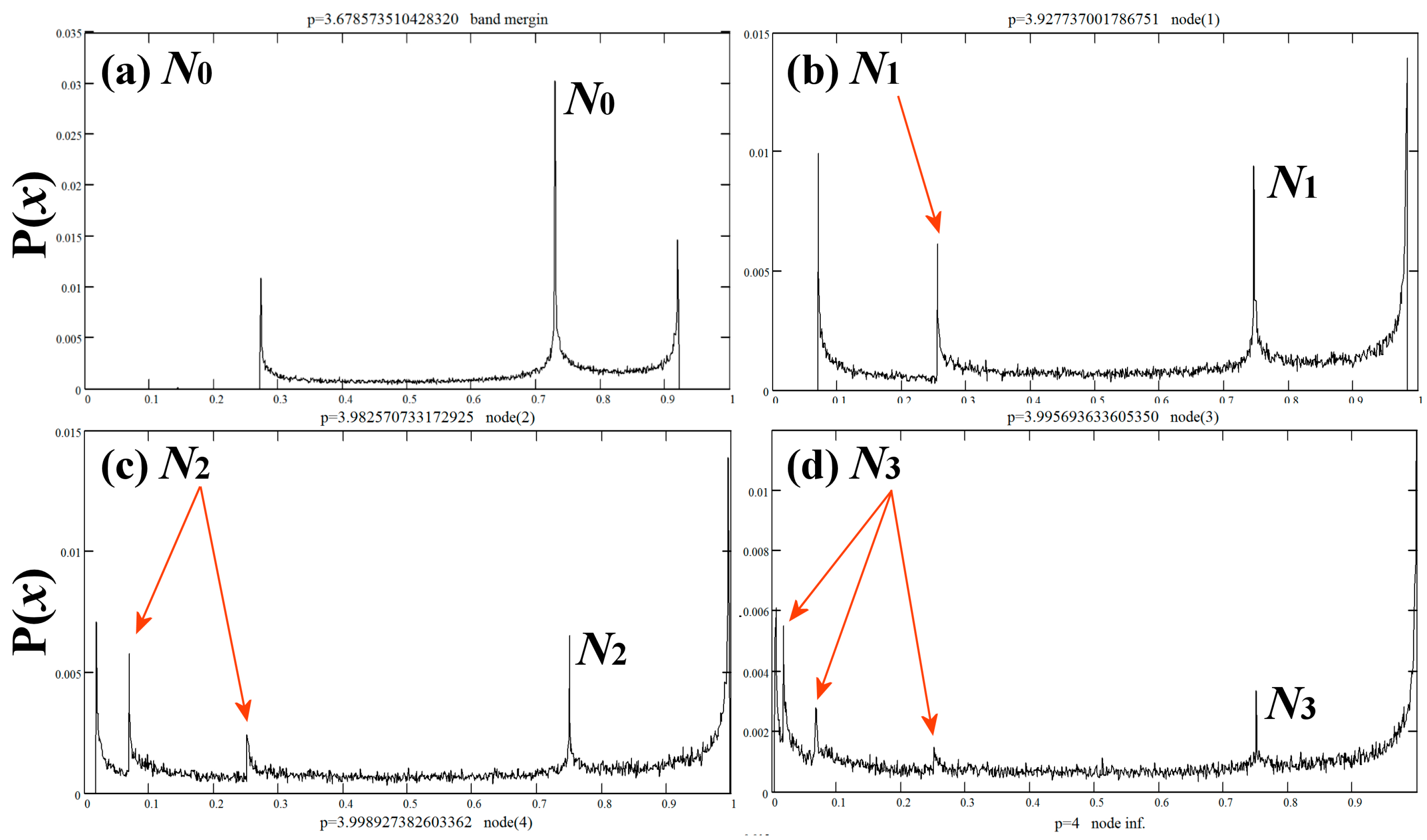
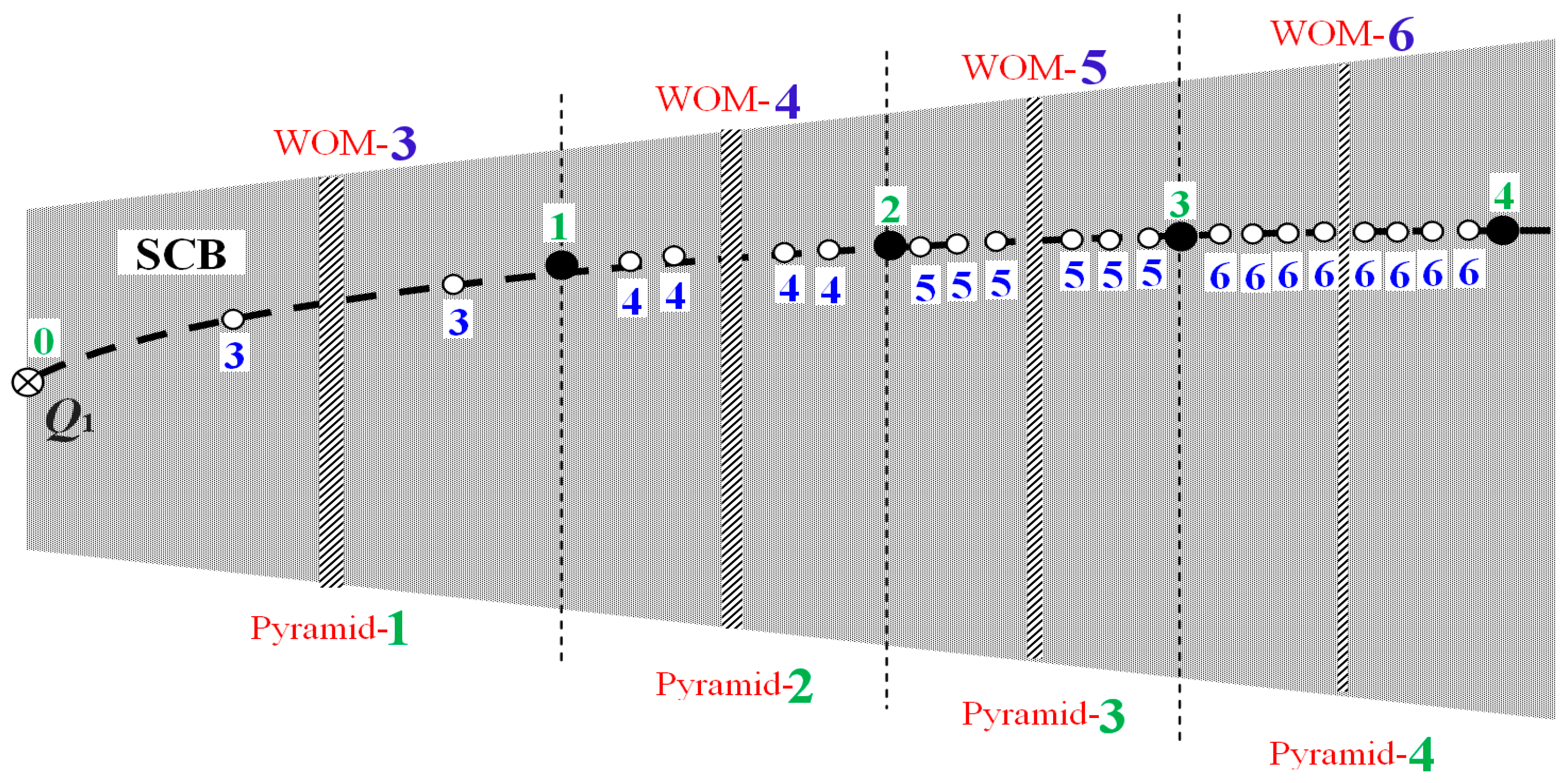
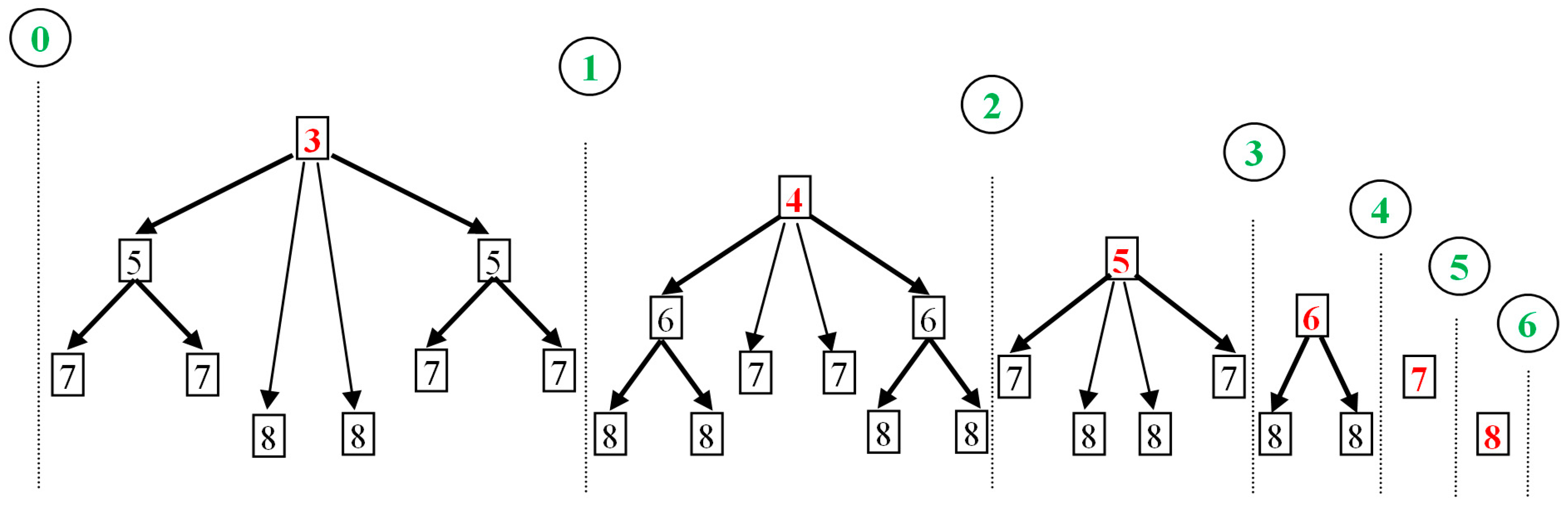
3. Identification and Arrangement of Nodes in the Chaotic Zone
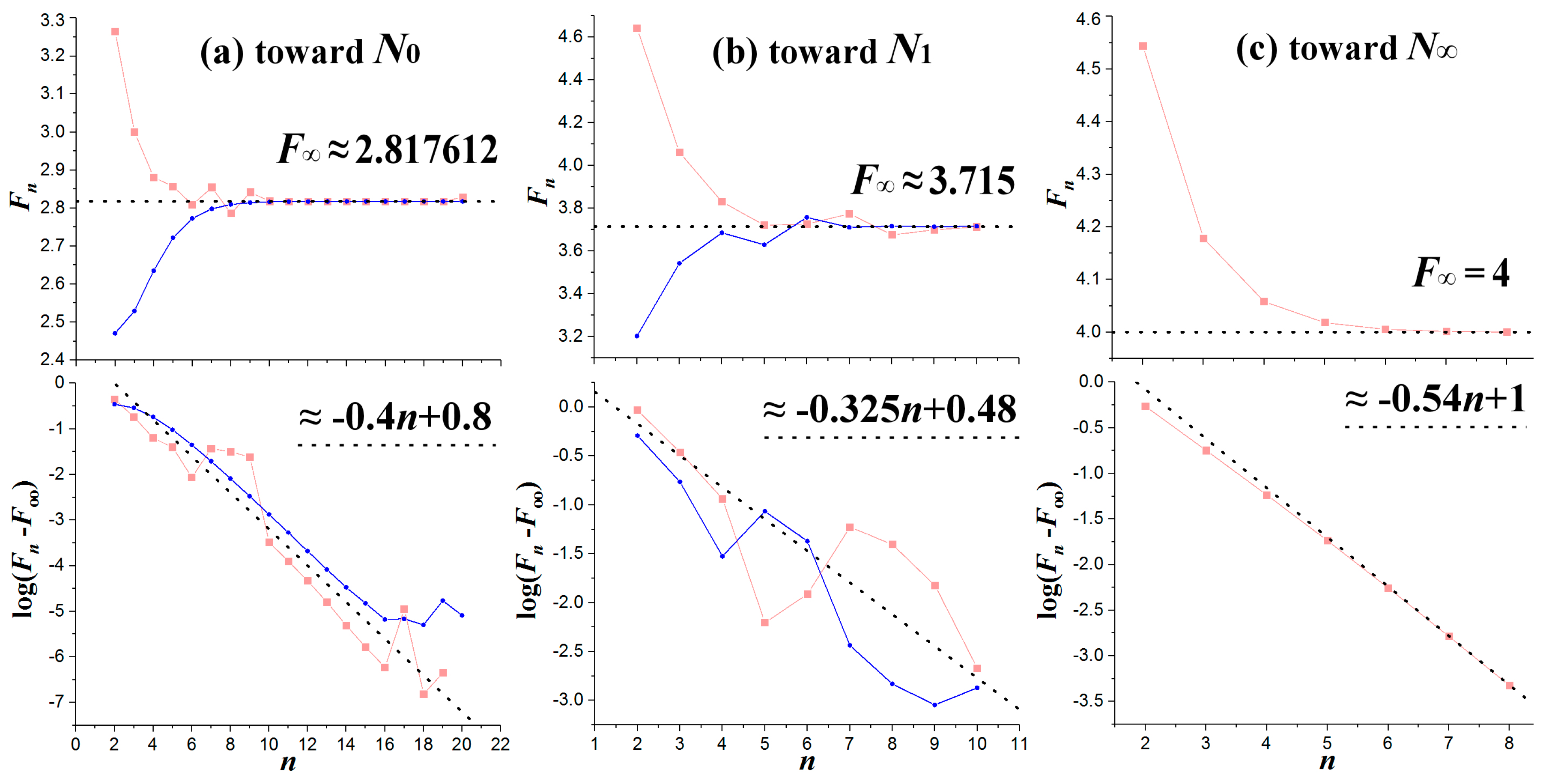
4. Mathematical Formulae of Critical Curves and Nodes
5. Connection between WOMs and Nodes
6. Features of Nodes
7. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Tables
| Order | p |
|---|---|
| 0 * | 3.678573510428329 |
| 1 | 3.927737001786751 |
| 2 | 3.982570733172925 |
| 3 | 3.995693633605350 |
| 4 | 3.998927382603362 |
| 5 | 3.999732146052877 |
| 6 | 3.999933058608207 |
| 7 | 3.999983266242305 |
| 8 | 3.999995816673156 |
| 3 Order | 4 Order | 5 Order | 6 Order |
|---|---|---|---|
| 3.791097, 3.876540 | 3.946550, 3.972211 | 3.727254, 3.752684 | 3.933204, 3.941763 |
| - | - | 3.894663, 3.915998 | 3.9751854, 3.9801912 |
| - | - | 3.9867746, 3.9929707 | 3.9967110, 3.9983206 |
| 3 | 4 | 7 | 8 | 9 | (Cont.) |
|---|---|---|---|---|---|
| 3.82843 | 3.960102 | 3.70164 | 3.80074 | 3.6872 | 3.975919 |
| 5 | 6 | 3.77413 | 3.87053 | 3.7171 | 3.979543 |
| 3.73817 | 3.93752 | 3.88602 | 3.89946 | 3.76124 | 3.983140 |
| 3.90557 | 3.977765 | 3.922186 | 3.91205 | 3.78577 | 3.986274 |
| 3.99026 | 3.9975826 | 3.951027 | 3.93047 | 3.87941 | 3.989188 |
| 3.968974 | 3.94421 | 3.89225 | 3.991324 | ||
| 3.984746 | 3.97372 | 3.917792 | 3.993577 | ||
| 3.9945375 | 3.981408 | 3.926277 | 3.995417 | ||
| 3.9993970 | 3.987746 | 3.9346999 | 3.996945 | ||
| 3.992519 | 3.94037 | 3.998148 | |||
| 3.9962195 | 3.947735 | 3.999058 | |||
| 3.9986417 | 3.954483 | 3.999661 | |||
| 3.9998495 | 3.966193 | 3.9999624 | |||
| 3.971413 |
| Left | p | Right | p |
|---|---|---|---|
| 2 × 3 | 3.62656 | 3 | 3.82842712 |
| 2 × 4 | 3.66211 | 5 | 3.73817237 |
| 2 × 5 | 3.67300 | 7 | 3.70164076 |
| 2 × 6 | 3.67663 | 9 | 3.68719687333 |
| 2 × 7 | 3.67789 | 11 | 3.68171601937 |
| 2 × 8 | 3.678331 | 13 | 3.67970245777 |
| 2 × 9 | 3.678488 | 15 | 3.67897629733 |
| 2 × 10 | 3.678543 | 17 | 3.678716777082 |
| 2 × 11 | 3.67856274217796 | 19 | 3.6786244025542 |
| 2 × 12 | 3.678569688994185 | 21 | 3.67859157901113 |
| 2 × 13 | 3.678572154206041 | 23 | 3.67857992406206 |
| 2 × 14 | 3.678573029096640 | 25 | 3.678575786820828 |
| 2 × 15 | 3.6785733395993465 | 27 | 3.6785743183617855 |
| 2 × 16 | 3.6785734497993825 | 29 | 3.6785737971749995 |
| 2 × 17 | 3.6785734889104695 | 31 | 3.6785736121981435 |
| 2 × 18 | 3.678573502791405 | 33 | 3.6785735465475785 |
| 2 × 19 | 3.678573507717898 | 35 | 3.6785735232474435 |
| 2 × 20 | 3.6785735094663632 | 37 | 3.678573514977968 |
| 2 × 21 | 3.678573510086913 | 39 | 3.678573512043041 |
| 2 × 22 | 3.678573510307152 | 41 | 3.678573511001403 |
| 2 × 23 | 3.678573510385 | 43 | 3.6785735106317145 |
| 2 × 24 | 3.678573510413 | 45 | 3.678573510500508 |
| 2 × 25 | 3.678573510423 | 47 | 3.678573510453941 |
| 2 × 26 | 3.6785735104264 | 49 | 3.6785735104374145 |
| 2 × 27 | 3.67857351042764 | 51 | 3.678573510431549 |
| 2 × 28 | 3.678573510428080 | 53 | 3.678573510429467 |
| 2 × 29 | 3.678573510428237 | 55 | 3.678573510428729 |
| 2 × 30 | 3.678573510428292 | 57 | 3.678573510428467 |
| 2 × 31 | 3.678573510428312 | 59 | 3.678573510428373 |
| 61 | 3.678573510428340 | ||
| 63 | 3.678573510428329 |
| Left WOMs | p | Right WOMs | p |
|---|---|---|---|
| 3 | 3.82843 | 4 | 3.96010 |
| 5 | 3.90557 | 6 | 3.93752 |
| 7 | 3.922186 | 8 | 3.93047 |
| 9 | 3.926277 | 10 | 3.92848 |
| 11 | 3.927345 | 12 | 3.92794 |
| 13 | 3.927632 | 14 | 3.9277912 |
| 15 | 3.927709 | 16 | 3.9277516 |
| 17 | 3.9277294 | 18 | 3.92774093 |
| 19 | 3.92773495 | 20 | 3.927738059 |
| 21 | 3.92773645 | 22 | 3.927737286 |
| 23 | 3.927736854 | 24 | 3.927737078 |
| 25 | 3.927736962 | 26 | 3.92773702239 |
| 27 | 3.927736991 | 28 | 3.92773700733 |
| 29 | 3.9277369989 | 30 | 3.92773700328 |
| 31 | 3.92773700101 | 32 | 3.9277370021882 |
| 33 | 3.92773700158 | 34 | 3.9277370018948 |
| 35 | 3.927737001731 | 36 | 3.9277370018158 |
| 37 | 3.927737001772 | 38 | 3.9277370017946 |
| 39 | 3.92773700178267 | 40 | 3.927737001788857 |
| 41 | 3.92773700178565 | 42 | 3.927737001787318 |
| 43 | 3.92773700178646 | 44 | 3.927737001786904 |
| 45 | 3.927737001786673 | 46 | 3.927737001786793 |
| 47 | 3.927737001786730 | 48 | 3.927737001786763 |
| 49 | 3.927737001786746 | 50 | 3.927737001786755 |
| 51 | 3.927737001786750 | 52 | 3.927737001786753 |
| 53 | 3.927737001786751 | 54 | 3.927737001786751 |
References
- May, R.M. Simple Mathematical Models with very Complicated Dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Grossman, S.; Thomae, S. Invariant Distributions and Stationary Correlation Functions of One-Dimensional Discrete Processes. Z. Naturforsch. 1977, 32, 1353–1363. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. Quantitative Universality for a Class of Nonlinear Transformations. J. Stat. Phys. 1978, 19, 25–52. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. The Universal Metric Properties of Nonlinear Transformations. J. Stat. Phys. 1979, 21, 669–706. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. Universal behavior in nonlinear systems. Los Alamos Sci. 1980, 1, 4–27. [Google Scholar]
- Ott, E. Strange attractors and chaotic motion of dynamical systems. Rev. Mod. Phys. 1981, 53, 655–671. [Google Scholar] [CrossRef]
- Thomae, S.; Grossmann, S. Correlations and Spectra of Periodic Chaos Generated by the Logistic Parabola. J. Stat. Phys. 1981, 26, 485–504. [Google Scholar] [CrossRef]
- Arrowsmith, D.K.; Place, C.M. Dynamical Systems, Differential Equations, Maps and Chaotic Behavior; Chapman & Hall/CRC: Boca Raton, FL, USA, 1992; Chapter 6.5.3; pp. 245–251. [Google Scholar]
- Peitgen, H.-O.; Jürgens, H.; Saupe, D. Chaos and fractals, New frontiers of Science; Springer: New York, NY, USA, 1992; Chapter 10.1, pp. 509–519; Chapter 11, pp. 585–653; Chapter 12.1, pp. 672–673. [Google Scholar]
- Philominathan, P.; Rajasekar, S. Dynamic behaviors of 2 attractor and q-phase transitions at bifurcations in logistic map. Physica A 1996, 229, 244–254. [Google Scholar] [CrossRef]
- Cavalcante, H.L.D.D.; Leite, J.R.R. Bifurcations and averages in the logistic map. Dyn. Stab. Syst. 2000, 15, 35–41. [Google Scholar] [CrossRef]
- Leonel, E.D.; Kamphorst Leal da Silva, J.; Oliffson Kamphorst, S. Relaxation and Transients in a Time-Dependent Logistic Map. Int. J. Bifurc. Chaos 2002, 12, 1667–1674. [Google Scholar] [CrossRef]
- Livadiotis, G. Numerical approximation of the percentage of order for one-dimensional maps. Adv. Complex Syst. 2005, 8, 15–32. [Google Scholar] [CrossRef]
- Elaydi, S. An Introduction to Difference Equations; Springer Science + Business Media, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Livadiotis, G.; Voglis, N. The rotation number in one-dimensional maps: Definition and applications. J. Phys. A 2006, 39, 15231–15244. [Google Scholar] [CrossRef]
- Livadiotis, G. Definition and applications of the ascent-probability distribution in 1-dimensional maps. Int. J. Bifurc. Chaos 2009, 19, 3567–3591. [Google Scholar] [CrossRef]
- Derrida, B.; Gervois, A.; Pomeau, Y. Iteration of Endomorphisms on the Real Axis and Representation of Numbers. Ann. Inst. Henri Poincaré 1978, 29, 305–356. [Google Scholar]
- Derrida, B.; Gervois, A.; Pomeau, Y. Universal metric Properties of Bifurcations and Endomorphisms. J. Phys. A 1979, 12, 269–296. [Google Scholar] [CrossRef]
- Collet, P.; Eckmann, J.-P. Iterated Maps on the Interval as Dynamical Systems; Birkhäuser: Basel, Switzerland, 1980. [Google Scholar]
- Collet, P.; Eckmann, J.-P.; Lanford, O.E. Universal Properties of Maps on an Interval. Commun. Math. Phys. 1980, 76, 211–254. [Google Scholar] [CrossRef]
- Yorke, J.A.; Alligood, K.T. Period doubling cascades of attractors: A prerequisite for horseshoes. Commun. Math. Phys. 1985, 101, 305–321. [Google Scholar] [CrossRef]
- Philominathan, P. Characterization of Bifurcations of Chaos, Weak and Strong Chaos in Certain Nonlinear Dynamical Systems; Department of Physics, AVVM Sri Pushpam College: Thanjavur, India, 2000; Chapter 2.2, pp. 21–24; Chapter 2.3, pp. 25–26; Chapter 2.4, pp. 31–34; Chapter 2.4, p. 37; Chapter 3.3, pp. 48–49. [Google Scholar]
- Sarkovskii, A.N. Coexistence of Cycles of a Continuous Map of a Line into Itself. Ukr. Math. Z. 1964, 16, 61–71. [Google Scholar]
- Metropolis, M.; Stein, M.L.; Stein, P.R. On Finite Limit Sets for Transformations of the Unit Interval. J. Comb. Theory A 1973, 15, 25–44. [Google Scholar] [CrossRef]
- Li, T.Y.; Yorke, J.A. Period Three implies Chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Guckenheimer, J. One Dimensional Dynamics. Ann. N. Y. Acad. Sci. 1979, 316, 76–85. [Google Scholar] [CrossRef]
- Geisel, T.; Nierwetberg, J. Universal Fine Structure of the Chaotic Region in Period-Doubling Systems. Phys. Rev. Lett. 1981, 47, 975–978. [Google Scholar] [CrossRef]
- Jacobson, M.V. Absolutely Continuous Invariant Measure for One-Parameter Families of One-Dimensional Maps. Commun. Math. Phys. 1981, 81, 39–88. [Google Scholar] [CrossRef]
- Farmer, J.D. Sensitive Dependence on Parameters in Nonlinear Dynamics. Phys. Rev. Lett. 1985, 55, 351–354. [Google Scholar] [CrossRef] [PubMed]
- Farmer, J.D. Dimensions and Entropies in Chaotic Systems; Mayer Kress, G., Ed.; Springer: Berlin, Germany, 1986; p. 54. [Google Scholar]
- Van der Weele, J.P.; Capel, H.W.; Kluiving, R. Period doubling in maps with a maximum of order z. Physica A 1987, 145, 425–460. [Google Scholar] [CrossRef]
- Post, T.; Capel, H.W.; Van der Weele, J.P. Phase-length distributions in intermittent band switching. Physica A 1989, 160, 321–350. [Google Scholar] [CrossRef]
- Lichtenberg, A.J.; Lieberman, M.A. Regular and Chaotic Dynamics; Springer: New York, NY, USA, 1992; Chapter 5.3, pp. 312–320; Chapter 7.1b, pp. 461–468; Chapter 7.2b, pp. 495–496; Chapter 7.2c, pp. 497–499; Chapter 8.5, p. 614. [Google Scholar]
- Cvitanović, P. Universality in Chaos; Hilger: Bristol, UK, 1984. [Google Scholar]
- Devaney, R.L. An Introduction to Chaotic Dynamical Systems; Benjamin/Cummings: Menlo Park, CA, USA, 1986. [Google Scholar]
- Hao, B.-L. Elementary Symbolic Dynamics and Chaos in Dissipative Systems; World Scientific: Singapore, 1989. [Google Scholar]
- Lorenz, E.N. Noisy periodicity and reverse bifurcation. Ann. N. Y. Acad. Sci. 1980, 357, 130–141. [Google Scholar] [CrossRef]
- Post, T.; Capel, H.W.; Van der Weele, J.P. Short-phase anomalies in intermittent band switching. Phys. Lett. A 1988, 133, 373–377. [Google Scholar] [CrossRef]
- Brown, R.; Grebogi, C.; Ott, E. Broadening of Spectral Peaks at the Merging of Chaotic Bands in Period Doubling Systems. Phys. Rev. A 1986, 34, 2248–2254. [Google Scholar] [CrossRef]
- Everson, R.M. Scaling of intermittency period with dimension of a partition boundary. Phys. Lett. A 1987, 122, 471–475. [Google Scholar] [CrossRef]
- Fujisaka, H.; Kamifukumoto, H.; Inoue, M. Intermittency Associated with the Breakdown of the Chaos Symmetry. Prog. Theor. Phys. Lett. 1983, 69, 333–337. [Google Scholar] [CrossRef]
- Grebogi, C.; Ott, E.; Yorke, J.A. Crises, sudden changes in chaotic attractors, and transient chaos. Physica D 1983, 7, 181–200. [Google Scholar] [CrossRef]
- Grebogi, C.; Ott, E.; Romeiras, F.; Yorke, J.A. Critical exponents for crisis induced intermittency. Phys. Rev. A 1987, 36, 5365–5380. [Google Scholar] [CrossRef]
- Ishii, H.; Fujisaka, H.; Inoue, M. Breakdown of Chaos Symmetry and Intermittency in the Double-Well Potential System. Phys. Lett. A 1986, 116, 257–263. [Google Scholar] [CrossRef]
- Kitano, M.; Yabuzaki, T.; Ogawa, T. Symmetry-recovering crises of chaos in polarization-related optical bistability. Phys. Lett. A 1984, 29, 1288–1296. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Nonlinear Dynamics; Helleman, R.H.G., Ed.; New York Academy of Sciences: New York, NY, USA, 1980; pp. 282–291. [Google Scholar]
- Schuster, H.G. Deterministic Chaos, An Introduction; VCH: Vancouver, BC, USA, 1989; Chapter 2.2, pp. 24–28; Chapter 3.1, pp. 39–41; Chapter 3.4, pp. 65–69; Chapter 4.1, pp. 82–83; Chapter 6.4, pp. 181–182. [Google Scholar]
- Shenker, S.J.; Kadanoff, L.P. Band to band hopping in one-dimensional maps. J. Phys. A 1981, 14, L23–L26. [Google Scholar] [CrossRef]
- Sporns, O.; Roth, S.; Seelig, F.F. Chaotic dynamics of two coupled biochemical oscillators. Physica D 1987, 26, 215–224. [Google Scholar] [CrossRef]
- Helleman, R.H.G. Nonequilibrium Problems in Statistical Mechanics 2; Horton, W., Reichl, L., Szebehely, V., Eds.; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Alligood, K.T.; Sauer, T.D.; Yorke, J.A. Chaos, an Introduction to Dynamical Systems; Springer: New York, NY, USA, 1996; Chapter 1.5, pp. 17–22; Chapter 1.8, pp. 32–35; Chapter 3.1, pp. 107–109; Chapter 3.2, p. 110; Chapter 3.3, pp. 121–123; Chapter 6.1, p. 237; Chapter 12.1, pp. 500–504; Chapter 12.4, pp. 525–527. [Google Scholar]
- Demir, B.; Koçak, Ş. A note on positive Lyapunov exponent and sensitive dependence on initial conditions. Chaos Solitons Fractals 2001, 12, 2119–2121. [Google Scholar] [CrossRef]
- Seydel, R. Practical Bifurcation and Stability Analysis, from Equilibrium to Chaos; Springer: New York, NY, USA, 1994; Chapter 9.6.1, pp. 346–347; Chapter 9.6.3, pp. 350–351. [Google Scholar]
- Dias de Deus, J.; Dilão, R.; Noronha da Costa, A. Scaling Behaviour of Windows and Intermittency in One-Dimensional Maps. Phys. Lett. A 1987, 124, 433–436. [Google Scholar] [CrossRef]
- Dias de Deus, J.; Dilão, R.; Noronha da Costa, A. CERN/SPS/88-11, 1988. Available online: https://cds.cern.ch/record/1599450/files/CERN-SPS-88.pdf (accessed on 3 January 2018).
- Hasler, M.J. Electrical circuits with chaotic behavior. Proc. IEEE 1987, 75, 1009–1021. [Google Scholar] [CrossRef]
- Matsumoto, T.; Chua, L.O.; Tanaka, S. Simplest chaotic nonautonomous circuit. Phys. Rev. A 1984, 30, 1155–1157. [Google Scholar] [CrossRef]
- Matsumoto, T. Chaos in electronic circuits. Proc. IEEE 1987, 75, 1033–1057. [Google Scholar] [CrossRef]
- Post, T.; Capel, H.W. Windows in one-dimensional maps. Physica A 1991, 178, 62–100. [Google Scholar] [CrossRef]
- Yorke, J.A.; Grebogi, C.; Ott, E.; Tedeschini-Lalli, L. Scaling Behavior of Windows in Dissipative Dynamical Systems. Phys. Rev. Lett. A 1985, 54, 1095–1098. [Google Scholar] [CrossRef] [PubMed]
- Post, T.; Capel, H.W.; Van der Weele, J.P. Window scaling in one-dimensional maps. Phys. Lett. A 1989, 136, 109–113. [Google Scholar] [CrossRef]
- Ge, Y.; Rusjan, E.; Zweifel, P. Renormalization of binary trees derived from one-dimensional unimodal maps. J. Stat. Phys. 1990, 59, 1265–1295. [Google Scholar] [CrossRef]
- Giorgilli, A.; Lazutkin, V.F. Some remarks on the problem of ergodicity of the Standard Map. Phys. Lett. A 2000, 272, 359–367. [Google Scholar] [CrossRef]
- Van der Weele, J.P.; Capel, H.W.; Kluiving, R. On the scaling factors α(z) and δ(z). Phys. Lett. A 1986, 119, 15–20. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Livadiotis, G. Lagrangian temperature: Derivation and physical meaning for systems described by kappa distributions. Entropy 2014, 16, 4290–4308. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa Distributions: Theory and Applications in Plasmas; Elsevier: Amsterdam, The Netherlands; Oxford/London, UK; Atlanta, GA, USA, 2017; Chapter 2. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Livadiotis, G.; McComas, D.J. Beyond kappa distributions: Exploiting Tsallis statistical mechanics in space plasmas. J. Geophys. Res. 2009, 114, A11105. [Google Scholar] [CrossRef]
- Field, R.J. Chaos in the Belousov-Zhabotinsky reaction. Mod. Phys. Lett. B 2015, 29, 1530015. [Google Scholar] [CrossRef]
- Livadiotis, G.; Moussas, X. The sunspot as an autonomous dynamical system: A model for the growth and decay phases of sunspots. Physica A 2007, 379, 436–458. [Google Scholar] [CrossRef]
- Livadiotis, G.; Elaydi, S. General Allee effect in two-species population biology. J. Biol. Dyn. 2012, 6, 959–973. [Google Scholar] [CrossRef] [PubMed]
- Livadiotis, G.; Assas, L.; Dennis, B.; Elaydi, S.; Kwessi, E. Kappa function as a unifying framework for discrete population modeling. Nat. Res. Mod. 2016, 29, 130–144. [Google Scholar] [CrossRef]











© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Livadiotis, G. High Density Nodes in the Chaotic Region of 1D Discrete Maps. Entropy 2018, 20, 24. https://doi.org/10.3390/e20010024
Livadiotis G. High Density Nodes in the Chaotic Region of 1D Discrete Maps. Entropy. 2018; 20(1):24. https://doi.org/10.3390/e20010024
Chicago/Turabian StyleLivadiotis, George. 2018. "High Density Nodes in the Chaotic Region of 1D Discrete Maps" Entropy 20, no. 1: 24. https://doi.org/10.3390/e20010024
APA StyleLivadiotis, G. (2018). High Density Nodes in the Chaotic Region of 1D Discrete Maps. Entropy, 20(1), 24. https://doi.org/10.3390/e20010024




