Liouvillian of the Open STIRAP Problem
Abstract
:1. Introduction
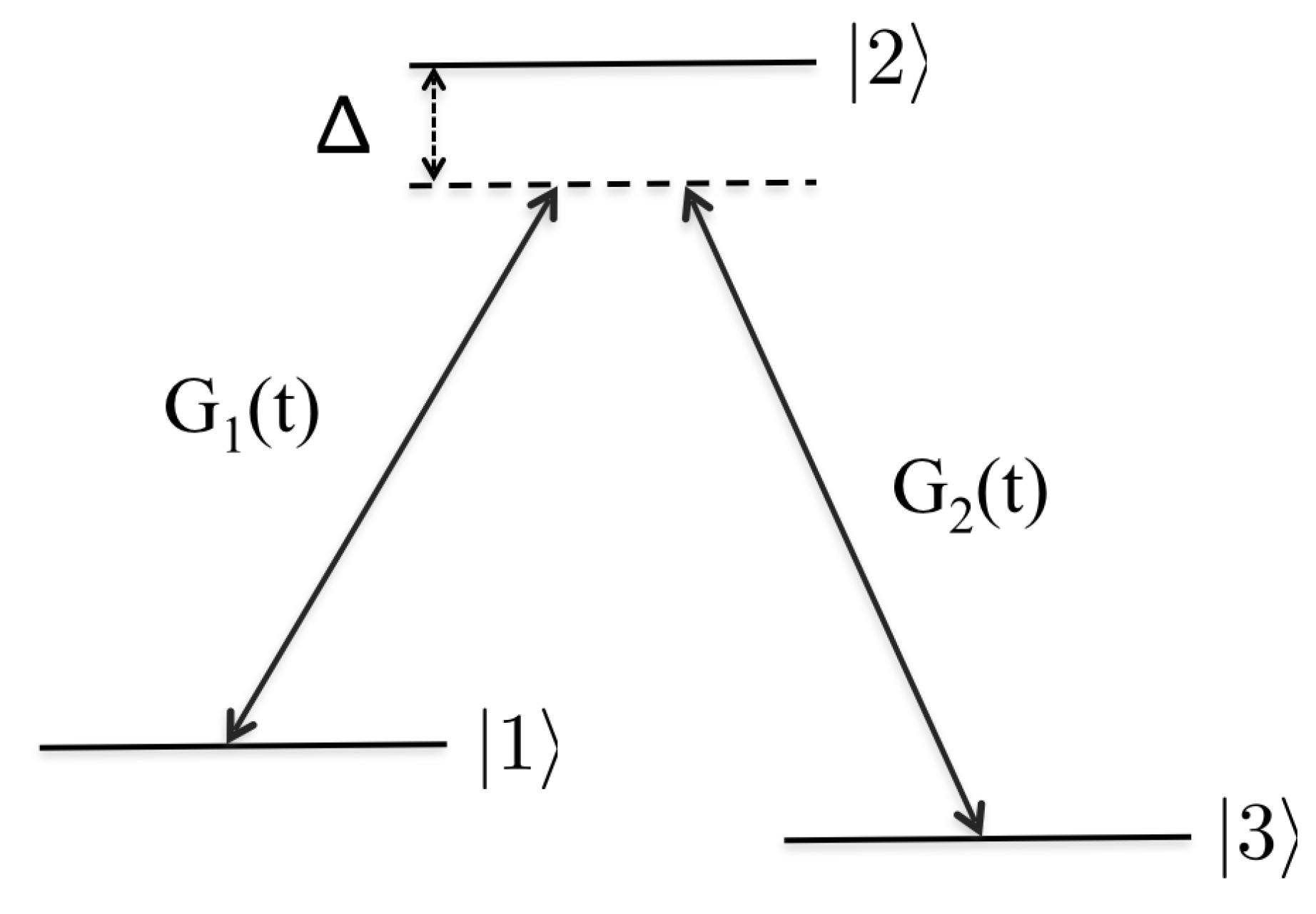
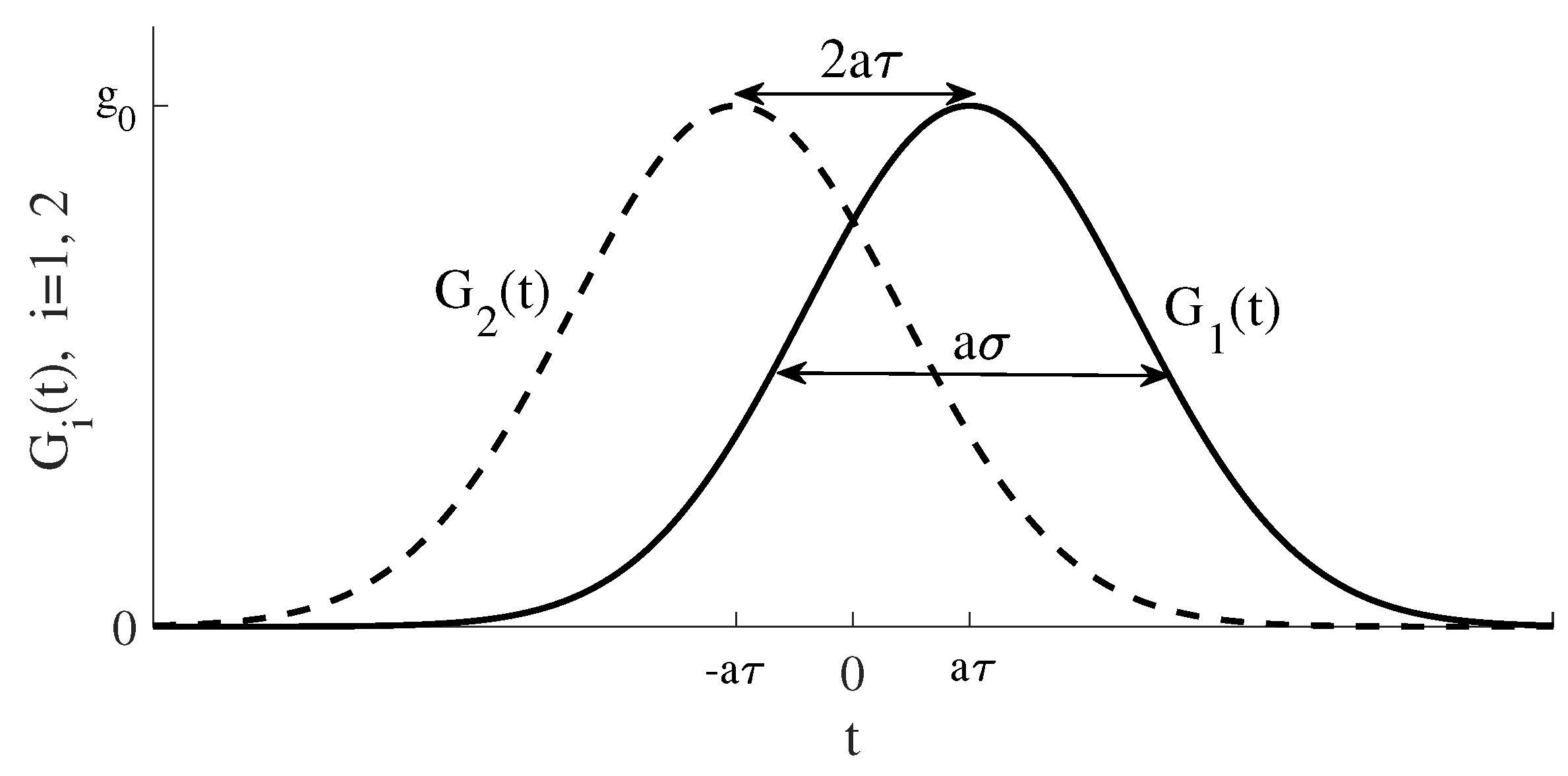
2. The Open STIRAP Model
STIRAP for Closed Systems
3. Results and Discussion
- (1)
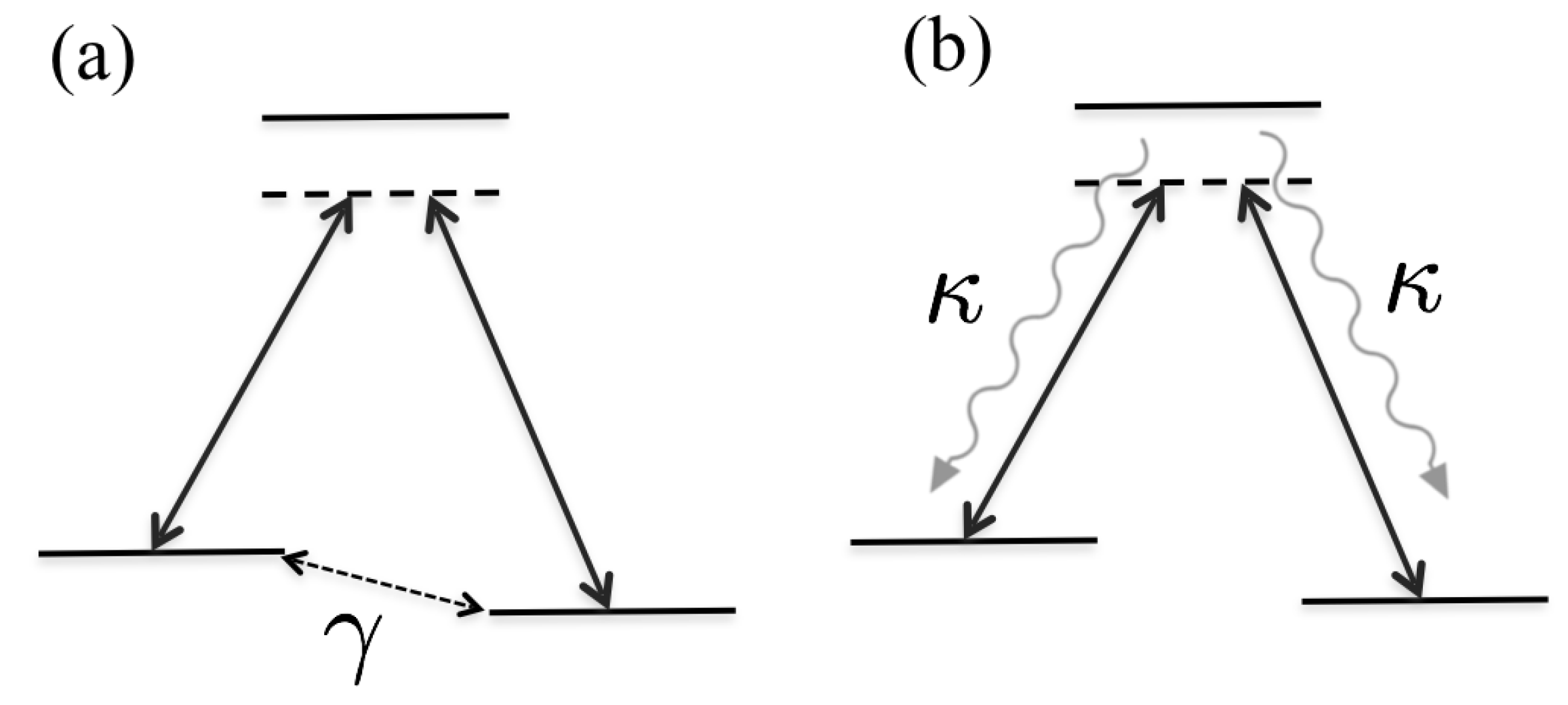
- Case (a). Dephasing of the lower states and implemented by the Lindblad jump operatorWe disregard any dephasing between the other levels as these are typically of less importance [9]. More precisely, once the dephasing arising from the jump operator (11) is taken into account, the additional dephasing occurring between the other levels do not qualitatively alter the results. This is especially true when the intermediate state is only slightly populated.
- (2)
- Case (b). Spontaneous emission of the excited state to the states and . The corresponding jump operators are
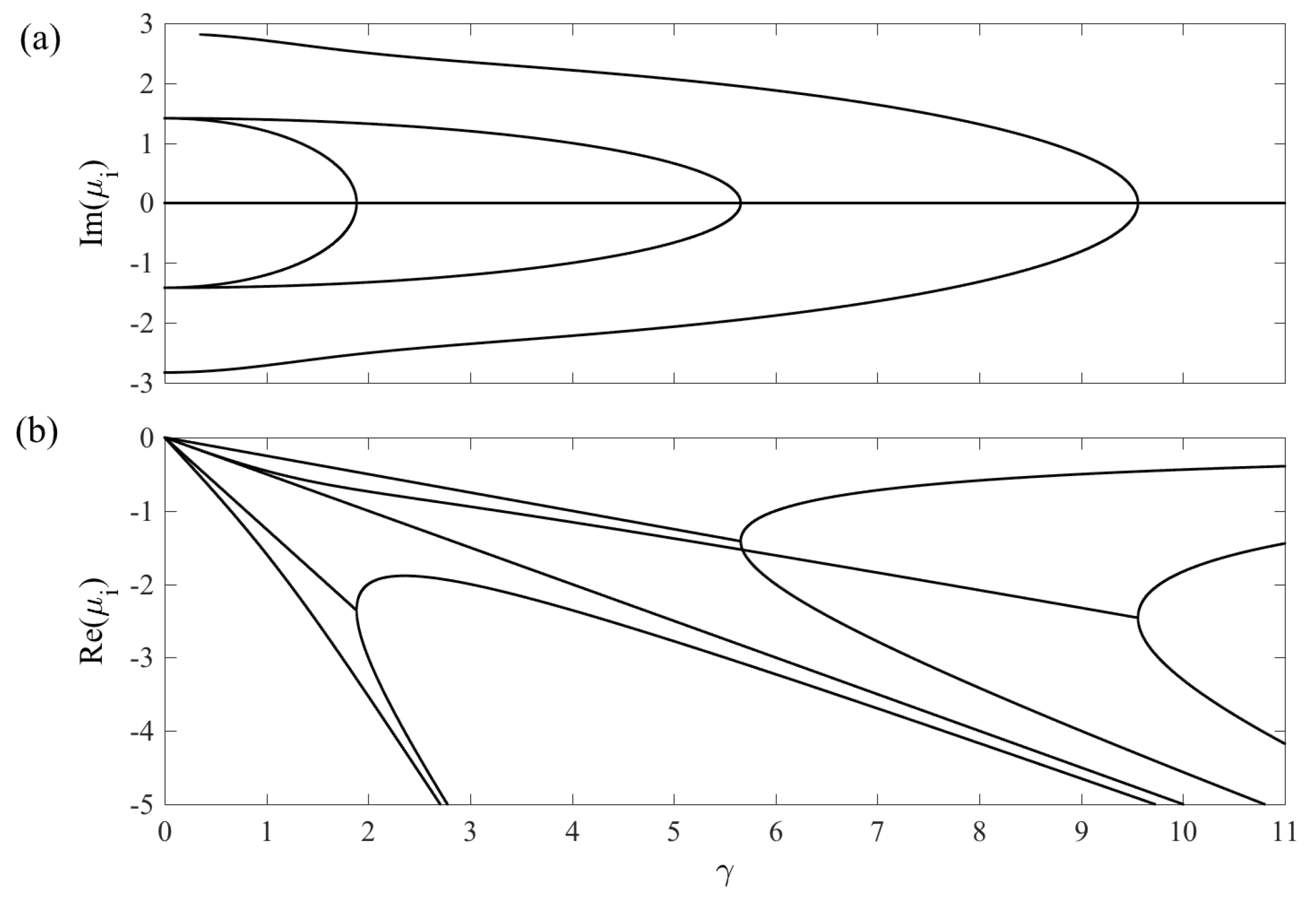
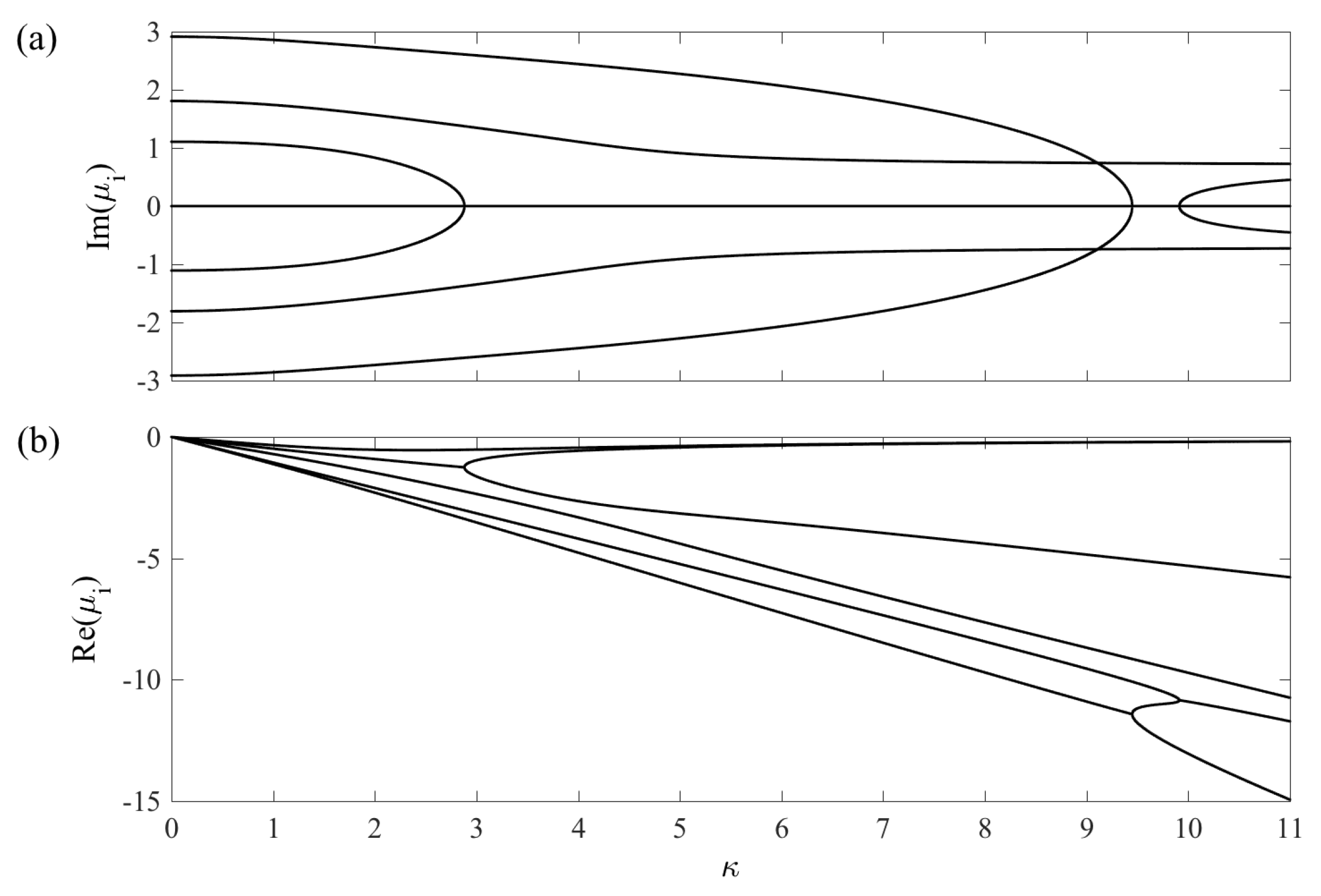
3.1. The Liouvillian Matrix for the System
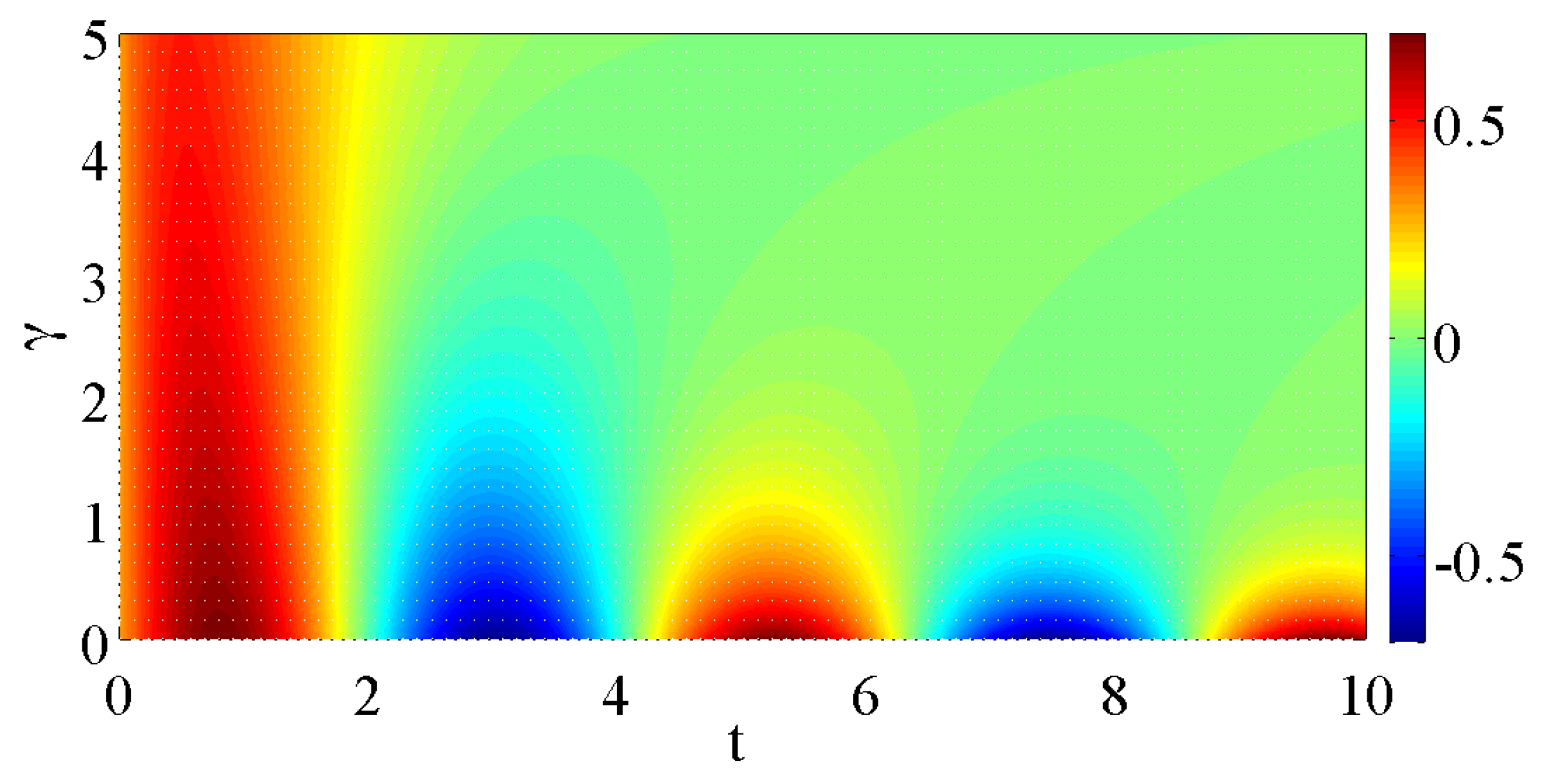
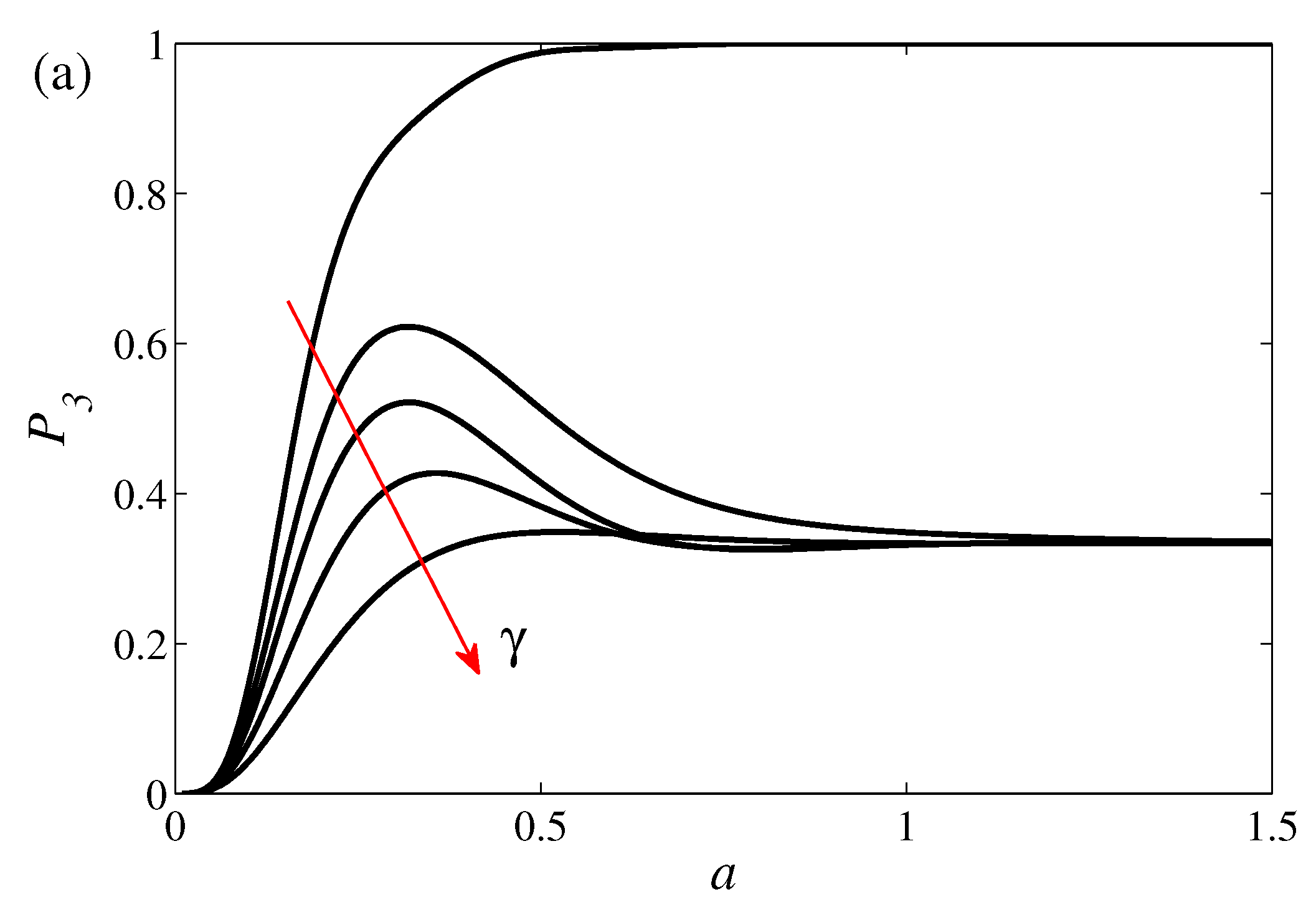
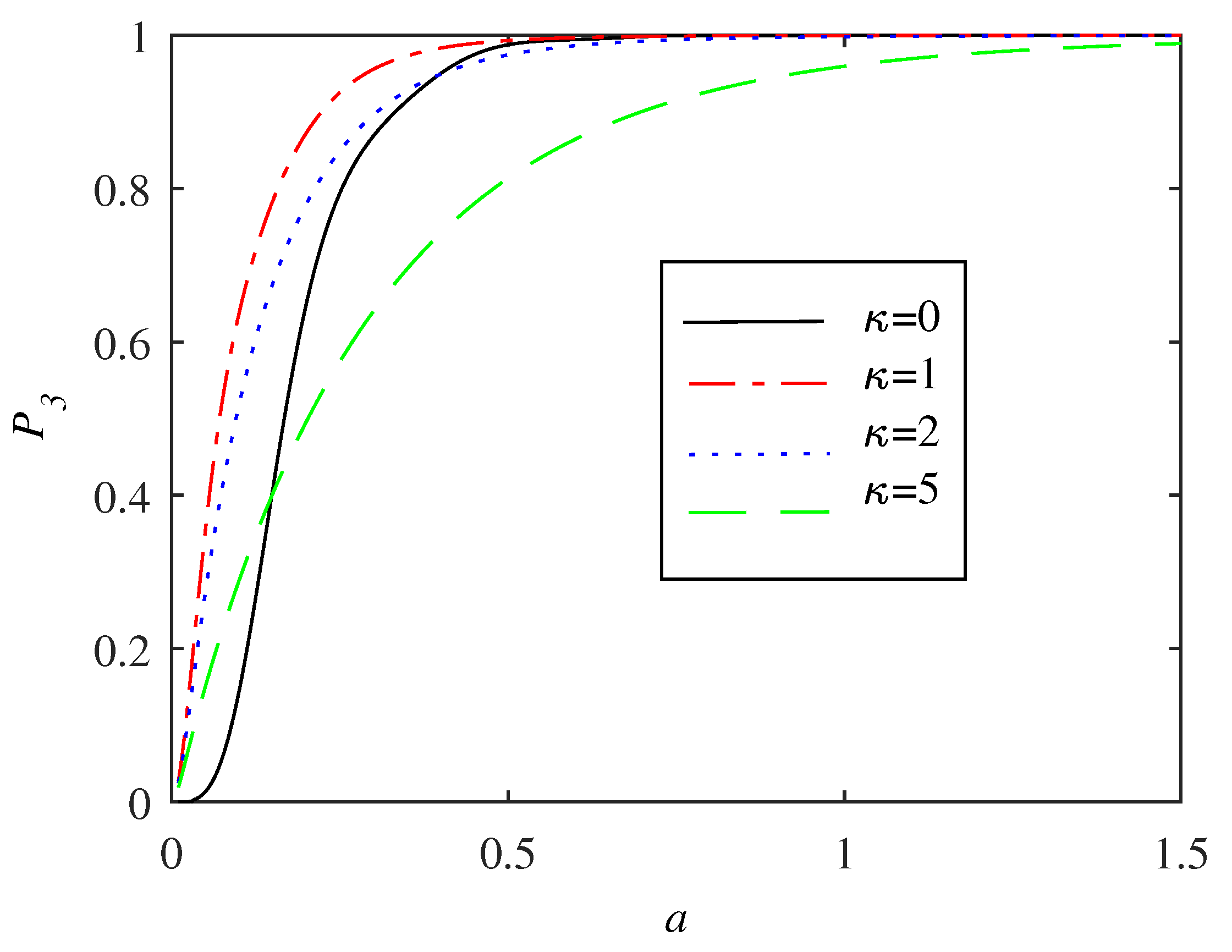
3.2. Dynamics—Numerical Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| STIRAP | Stimulated Raman Adiabatic Passage |
| AMO | Atomic, Molecular and Optical |
| EP | Exceptional Point |
Appendix A. Gell–Mann Matrices
Appendix B. Some General Properties of the Liuvillian
Appendix C. STIRAP Liouvillian Matrices
References
- Shore, B.W. Manipulating Quantum Structures Using Laser Pulses; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Nakamura, Y.; Pashkin, Y.A.; Tsai, J.S. Coherent control of macroscopic quantum states in a single-Cooper-pair box. Nature 1999, 398, 786–788. [Google Scholar] [CrossRef]
- Ginsberg, N.S.; Garner, S.R.; Hau, L.V. Coherent control of optical information with matter wave dynamics. Nature 2006, 445, 623–626. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, M.; Brumer, P. Principles of the Quantum Control of Molecular Processes; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Vitanov, N.V.; Halfmann, T.; Shore, B.W.; Bergmann, K. Laser-induced population transfer by adiabatic passage techniques. Rev. Phys. Chem. 2001, 52, 763–809. [Google Scholar] [CrossRef] [PubMed]
- Vitanov, N.V.; Rangelov, A.A.; Shore, B.W.; Bergmann, K. Stimulated Raman adiabatic passage in physics, chemistry and beyond. Rev. Mod. Phys. 2017, 89, 015006. [Google Scholar] [CrossRef]
- Vitanov, N.V.; Stenholm, S. Population transfer via a decaying state. Phys. Rev. A 1997, 56, 1463. [Google Scholar] [CrossRef]
- Ivanov, P.A.; Vitanov, N.V.; Bermann, K. Spontaneous emission in stimulated Raman adiabatic passage. Phys. Rev. A 2005, 72, 053412. [Google Scholar] [CrossRef]
- Ivanov, P.A.; Vitanov, N.V.; Bergmann, K. Effect of dephasing on stimulated Raman adiabatic passage. Phys. Rev. A 2004, 70, 063409. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Pen Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Scala, M.; Militello, B.; Messina, A.; Vitanov, N.V. Stimulated Raman adiabatic passage in an open quantum system: Master equation approach. Phys. Rev. A 2010, 81, 053847. [Google Scholar] [CrossRef]
- Heiss, W.D. Exceptional points of non-Hermitian operators. J. Phys. A Math. Theor. 2004, 37, 2455. [Google Scholar] [CrossRef]
- Heiss, W.D. The physics of exceptional points. J. Phys. A Math. Theor. 2012, 45, 444016. [Google Scholar] [CrossRef]
- Miesner, H.-J.; Stamper-Kurn, D.M.; Stenger, J.; Inouye, S.; Chikkatur, A.P.; Ketterle, W. Observation of Metastable States in Spinor Bose-Einstein Condensates. Phys. Rev. Lett. 1999, 82, 2228. [Google Scholar] [CrossRef]
- Gaudreau, L.; Granger, G.; Kam, A.; Aers, G.C.; Studenikin, S.A.; Zawadzki, P.; Pioro-Ladriere, M.; Wasilewski, Z.R.; Sachrajda, A.S. Coherent control of three-spin states in a triple quantum dot. Nat. Phys. 2012, 8, 54. [Google Scholar] [CrossRef]
- Scala, M.; Militello, B.; Messina, A.; Vitanov, N.V. Detuning effects in STIRAP processes in the presence of quantum noise. Opt. Spec. 2011, 111, 589. [Google Scholar] [CrossRef]
- Bear, M. Beyond Born-Oppenheimer; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Messiah, A. Quantum Mechanics; North-Holland Publishing Company: New York, NY, USA, 1961. [Google Scholar]
- Bloch, F. Nuclear Induction. Phys. Rev. 1946, 70, 460. [Google Scholar] [CrossRef]
- Kimura, G. The Bloch Vector for N-Level Systems. Phys. Lett. A 2003, 314, 339. [Google Scholar] [CrossRef]
- Bertlmann, R.A.; Krammer, P. Bloch vectors for qudits. J. Phys. A Math. Theor. 2008, 41, 235303. [Google Scholar] [CrossRef]
- Hioe, F.T.; Eberly, J.H. N-Level Coherence Vector and Higher Conservation Laws in Quantum Optics and Quantum Mechanics. Phys. Rev. Lett. 1981, 47, 838. [Google Scholar] [CrossRef]
- Sarandy, M.S.; Lidar, D.A. Adiabatic approximation in open quantum systems. Phys. Rev. A 2005, 71, 012331. [Google Scholar] [CrossRef]
- Sarandy, M.S.; Lidar, D.A. Adiabatic Quantum Computation in Open Systems. Phys. Rev. Lett. 2005, 95, 250503. [Google Scholar] [CrossRef] [PubMed]
- Schirmer, S.; Wang, X. Stabilizing open quantum systems by Markovian reservoir engineering. Phys. Rev. A 2010, 81, 062306. [Google Scholar] [CrossRef]
- Medvedyeva, M.V.; Kehrein, S. Power-law approach to steady state in open lattices of noninteracting electrons. Phys. Rev. B 2014, 90, 205410. [Google Scholar] [CrossRef]
- Cai, Z.; Barthel, T. Algebraic versus Exponential Decoherence in Dissipative Many-Particle Systems. Phys. Rev. Lett. 2013, 111, 150403. [Google Scholar] [CrossRef] [PubMed]
- Kessler, E.M.; Giedke, G.; Imamoglu, A.; Yelin, S.F.; Lukin, M.D.; Cirac, J.I. Dissipative phase transition in a central spin system. Phys. Rev. A 2012, 86, 012116. [Google Scholar] [CrossRef]
- Goyal, S.K.; Simon, B.N.; Singh, R.; Simon, S. Geometry of the generalized Bloch sphere for qutrits. J. Phys. A Math. Theor. 2016, 49, 165203. [Google Scholar] [CrossRef]
- Heiss, W.D.; Müller, M.; Rotter, I. Collectivity, phase transitions, and exceptional points in open quantum systems. Phys. Rev. E 1998, 58, 2894. [Google Scholar] [CrossRef]
- Rotter, I. A non-Hermitian Hamilton operator and the physics of open quantum systems. J. Phys. A Math. Theor. 2009, 42, 153001. [Google Scholar] [CrossRef]
- Hedvall, P.; Larson, J. Dynamics of non-equilibrium steady state quantum phase transitions. arXiv, 2017; arXiv:1712.01560. [Google Scholar]
- Dutta, A.; Rahmani, A.; del Campo, A. Anti-Kibble-Zurek Behavior in Crossing the Quantum Critical Point of a Thermally Isolated System Driven by a Noisy Control Field. Phys. Rev. Lett. 2016, 117, 080402. [Google Scholar] [CrossRef] [PubMed]
- Barreiro, J.T.; Müller, M.; Schindler, P.; Nigg, D.; Monz, T.; Chwalla, M.; Hennrich, M.; Roos, C.F.; Zoller, P.; Blatt, R. An open-system quantum simulator with trapped ions. Nature 2011, 470, 486–491. [Google Scholar] [CrossRef] [PubMed]
- Venuti, L.C.; Albash, T.; Lidar, D.A.; Zanardi, P. Adiabaticity in open quantum systems. Phys. Rev. A 2016, 93, 032118. [Google Scholar] [CrossRef]
- Thunström, P.; Åberg, J.; Sjöqvist, E. Adiabatic Approximation for weakly open systems. Phys. Rev. A 2005, 72, 022328. [Google Scholar] [CrossRef]
- Dziarmaga, J. Dynamics of a quantum phase transition in the random Ising model: Logarithmic dependence of the defect density on the transition rate. Phys. Rev. B 2006, 74, 064416. [Google Scholar] [CrossRef]
- Dziarmaga, J. Dynamics of a quantum phase transition and relaxation to a steady state. Adv. Phys. 2010, 59, 1063–1189. [Google Scholar] [CrossRef]
- Diehl, S.; Micheli, A.; Kantian, A.; Kraus, B.; Büchler, H.P.; Zoller, P. Quantum States and Phases in Driven Open Quantum Systems with Cold Atoms. Nat. Phys. 2008, 4, 878. [Google Scholar] [CrossRef]
- Clark, S.; Peng, A.; Gu, M.; Parkins, S. Unconditional Preparation of Entanglement between Atoms in Cascaded Optical Cavities. Phys. Rev. Lett. 2003, 91, 177901. [Google Scholar] [CrossRef] [PubMed]
- Leibfried, D.; Blatt, R.; Monroe, C.; Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 2003, 75, 281. [Google Scholar] [CrossRef]
- Sörensen1, J.L.; Möller, D.; Iversen, T.; Thomsen, J.B.; Jensen, F.; Staanum, P.; Voigt, D.; Drewsen, M. Efficient coherent internal state transfer in trapped ions using stimulated Raman adiabatic passage. New J. Phys. 2006, 8, 261. [Google Scholar] [CrossRef]
- Georgi, H. Lie Algebras in Particle Physics; Westview Press: Boulder, CO, USA, 1999. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Dasgupta, S.; Lidar, D.A. Decoherence-induced geometric phase in a multilevel atomic system. J. Phys. B 2007, 40, S127. [Google Scholar] [CrossRef]
- Mailybaev, A.A.; Kirillov, O.N.; Seyranian, A.P. Geometric phase around exceptional points. Phys. Rev. A 2005, 72, 014104. [Google Scholar] [CrossRef]
- Spohn, H. An algebraic condition for the approach to equilibrium of an open N-Level system. Lett. Math. Phys. 1977, 2, 33. [Google Scholar] [CrossRef]
- Mehri-Dehnavi, H.; Mostafazadeh, A. Geometric Phase for Non-Hermitian Hamiltonians and Its Holonomy Interpretation. J. Math. Phys. 2008, 49, 082105. [Google Scholar] [CrossRef]
- Bohm, A.; Mostafazadeh, A.; Koizumi, H.; Niu, Q.; Zwanziger, J. The Geometric Phase in Quantum Systems; Springer: Berlin, Germany, 2003. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathisen, T.; Larson, J. Liouvillian of the Open STIRAP Problem. Entropy 2018, 20, 20. https://doi.org/10.3390/e20010020
Mathisen T, Larson J. Liouvillian of the Open STIRAP Problem. Entropy. 2018; 20(1):20. https://doi.org/10.3390/e20010020
Chicago/Turabian StyleMathisen, Thomas, and Jonas Larson. 2018. "Liouvillian of the Open STIRAP Problem" Entropy 20, no. 1: 20. https://doi.org/10.3390/e20010020
APA StyleMathisen, T., & Larson, J. (2018). Liouvillian of the Open STIRAP Problem. Entropy, 20(1), 20. https://doi.org/10.3390/e20010020



