Born-Kothari Condensation for Fermions
Abstract
1. Introduction
- The principle of reciprocity originally proposed by Born can be observed in much, but not all, of the formalism of classical and quantum mechanics [19]. However, the idea was later taken up by Yukawa [20] in developing nonlocal quantum field theory [21,22,23] by recognizing “reciprocity principle as the leading heuristic idea in the theory of elementary particles” [24].
- It is important to point out that the theory of reciprocity is based on a demand for symmetry, requiring the fundamental laws of nature to remain unaltered as mentioned by Born in his letters to Einstein [24]. Although its universality as a general theory remains questionable not only in view of General Relativity which breaks this symmetry [25], but also, there is no extant empirical evidence that could confirm its validity. Current observations in high energy physics experiments suggest that if Born’s reciprocity would be valid, then its effect could only be present at energies of the order of TeV or higher.
- Yet, constructing a general theory defining Born reciprocity as an intrinsic symmetry [26], continued as an interesting field of research even in modern times by adapting group theoretical methods [27,28,29,30,31] which are employed to study a group, namely the quaplectic group. With the advent of renormalization theory and Higg’s mechanism in the last seventy years [32,33,34,35], both in theory as well as in experiments, it has also been suggested that Born’s reciprocity may be the underlying physical reason for the T-duality symmetry in string theory [25,35,36], and may be of relevance in developing a quantum geometry [37,38].
2. The Principle of Reciprocity: The Born-Green Formalism
3. “Condensation” in FD Statistics: The Kothari–Nath Approach
4. Fermionic Coherent States: The Cahill–Glauber Formulation
4.1. Properties of Anti-Commuting Numbers
4.2. Coherent States for Fermions
- As pointed out after Equation (19) that for fermionic field, every operator and Grassmann numbers anticommute with each other. Hence, special care must be taken for the ordering of all such fermionic quantities.
- Eigenstate of every fermionic creation operators, , stems from the characteristic upper bound exhibited by general system of fermions. Equation (24) will thus be shown to play the key role in our theoretical formulation which we explore in the next section.
5. BKC as Condensation-Like Coherence within Fermions
5.1. Comparative Study between BEC and BKC
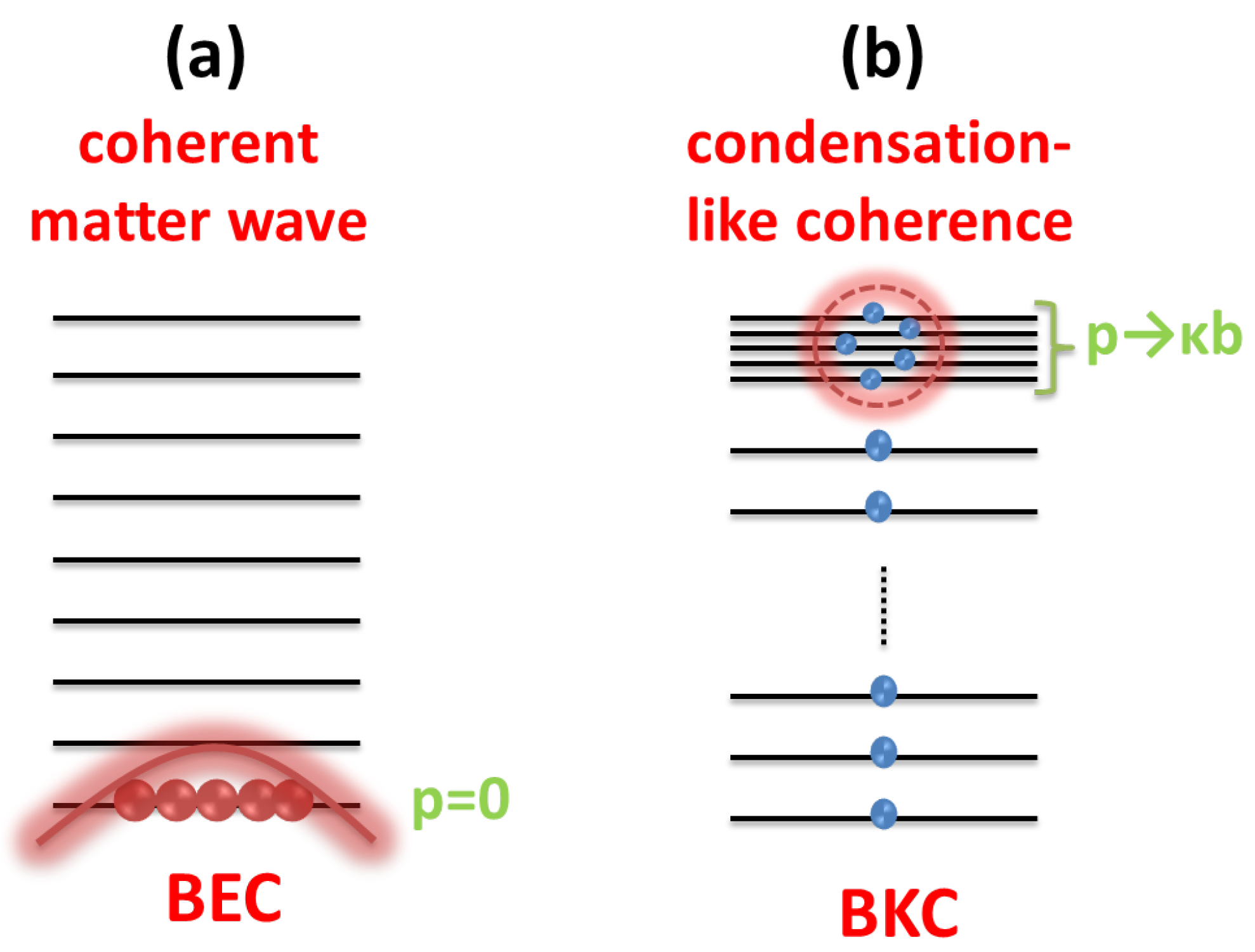
- In BEC, the condensed phase forms a coherent matter wave as the ground state of the many body system. Hence it is quite logical to delineate the giant matter wave in terms of a bosonic coherent state which is a displaced vacuum state , with, being the complex numbers (Figure 1a).
- On the other hand, as discussed in Section 2, the condensed phase for a FD gas occurs only at the highest energy state , characteristic of the reduced mass of the fermionic system. The reduced mass (rest mass) in case of BKC is analogous to for bosonic systems that dictates the existence of BEC below such critical temperatures.
- Due to Pauli exclusion principle, any eigenstate of fermions can accommodate only a single particle. Subsequently, by reciprocity principle the highest momentum state for any fermionic system, in principle contains an infinitely large number of eigenstates [14].
- Combining the points 2 and 3, unequivocally suggest that the condensed phase for each individual fermionic systems can occur only in the form of a single occupancy dense band at their respective highest accessible momentum (energy) state, (Figure 1b).
- Since, the eigenstate of the fermionic creation operator originates from the characteristic upper bound displayed by any general systems of fermions, our preliminary surmise is that the condensate of Reference [14] that appears at the highest energy state in the form of a dense band, is most appropriately described in light of our Equation (24), as a displaced state . As discussed in Section 3, that the Born reciprocity does not specify the modes, so an explanation of the exclusion principle focusing on the quantum numbers for the ad-hoc term of Equation (12), is not apparent. Therefore we resort to this end to fermionic coherent state in order to establish that the condensed phase at the highest energy is compatible with the exclusion principle. Since fermionic operator anticommutes, any creation operator can act only once on the vacuum, , thereby it creates only a single particle in each mode. As a result, which represents product state of all such large number of modes created by the single action of their creation operators, absolutely fulfils the exclusion principle. Thus, a unitary transformation of such state, here for instance, the displaced coherent state in Equation (24), automatically obeys the Pauli exclusion principle.
5.2. Characterization of the “Condensate” State
5.2.1. Thermodynamic Limit of Fermionic Operators
5.2.2. Fermionic Order Parameter
- One can argue that the fermionic order parameter does not bear any classical analogy, because it involves Grassmann variables. This may lead to misconception, hence needs further clarification. To be classically measurable, a field amplitude has to be large enough, like that of a strong electromagnetic (EM) field which can be produced and measured classically. This is possible when the particles obey BE statistics, as happens for light quanta in EM fields, where a large number of particles can accommodate a same state so that the fields get summed up coherently. On the other hand, for fermionic fields obeying FD statistics, quantities like energy, charge, current density which are bilinear in field variables, are only physically relevant entities. The reason is the number and energy operators do have classical limits even for fermionic fields, as they are bilinear in and . Extrapolating this idea, we may say that Grassmann fields and fermionic field operators are by nature fermionic, while an even product of these variables make them experimentally relevant [15,68,70,72,74,75]. A representation of correlation functions and construction of parent quadratic Hamiltonians in terms of such Grassmann variables can be found in recent review [59,60] and in the theory of fermionic analog of parametric amplifier developed by the present author [74,75].
- Therefore the order parameter which is linear in Grassmann variables (Equation (43)), represents the amplitude of the fermionic field and is not an experimentally viable quantity. On the contrary, the field intensity , is bilinear in Grassmann amplitudes, is an experimentally relevant quantity without any ambiguity [15]. Anticommutation in quantum mechanics is very special because it involves Pauli exclusion principle, which does not make sense at the classical level.
- Although the anticommuting nature of Grassmann variables preclude the possibility of interpreting them in experimental terms, we have shown [75] that unlike the bosonic field, fermionic fields are bound to satisfy fermionic analog of classical Liouville’s equation [61] and therefore most closely resemble to classical phase-space distribution functions. This is not surprising because of the simple fact that Grassmann algebra does not allow any derivative higher than second order. In this sense, the fermionic field operators being linear in their field variables, are always classical except for the effect that they incorporate Pauli exclusion principle. This is an important difference when compared with their bosonic counterparts since for the latter the Liouville’s equation is obtained only when the fields are either free or the quantum correction to the interaction are neglected [75].
5.2.3. Spontaneous Symmetry Breaking
- The microscopic Hamiltonian (Equation (28)) has global symmetry, since it is invariant under multiplication by a constant phase factor to the wavefunction of the system, .
- The specific macroscopic ground condense state of Reference [14], viewed as a fermionic coherent state, does not possess such symmetry. The phase factor to the state produces a different state altogether. This observation has a very fundamental consequence because the existence of BEC is always accompanied by spontaneous breaking of such symmetry [87,88].
6. Discussion
- In Section 2, we present basic idea behind the Born-Green reciprocity principle [12,13,16,17,18,19,20,21,22,23,24,40,41,42,43], the assumption of its validity is the hypothesis of our work. The main conclusion of this section is that the highest momentum of a particle allowed by the reciprocity principle is proportional to that of the reduced rest mass of the particle in appropriate units.
- In Section 3, we discuss the Kothari-Nath approach [14,48] which assesses the statistical and thermodynamical properties of an assembly of noninteracting gas of fermions. We emphasize thereafter, unlike BEC, the most conspicuous feature of BKC: The condensation is primarily guided by the density of states rather than only statistics itself.
- In Section 4, we outline the coherence theory for fermionic fields following Cahill and Glauber [39]. Like quantum theory of optical coherence [77,78,79,80,89] describes the statistical properties and coherence of photons in quantum optics, we discuss the fermionic coherence theory can be shown to play a similar role for the description of fermionic atom-counting experiments [64,74,75,85]. Most important result of this section is the fermionic coherent state which is the eigenstate of the fermionic creation operators: An unitary displaced state of all filled up modes which arises due to the very special property of fermionic fields.
- In Section 5, our formulation portrays that the condensed phase of BKC can be recognized by the fermionic coherent state where the unitary displacement operator displaces in principle an infinitely dense filled up modes. This is similar in spirit to that of harmonic oscillator coherent states defined as unitarily displaced vacuum state which are used to represent BEC as a coherent matter wave. Our formulation combined with thermodynamic consideration allows us to characterize the condensate in terms of fermionic order parameter. It forms an essential ingredient for the demonstration of thermodynamic limit and spontaneous breaking of guage symmetry of the state comprising FD statistics. Most remarkably, similar to their bosonic counterpart, the coherent and the rotated coherent state can be distinguished as macroscopically distinct ground states of the FD gas. This enables us to capture the essence of BKC as “condensation-like coherence” among fermions, likewise BEC is treated as “coherent matter wave” for bosons .
- The energy scale at which the physical evidence of the modification in the density of states should appear in terms of Compton’s wavelength for electrons (i.e., energy eV, estimated by Born [12]), has been achieved decades ago [47]; therefore, one has to conclude that the estimation of the critical density in terms of the Compton’s wavelength is far from realistic, and it was introduced into the discussion only for historical reasons.
- Present understanding in view of the last twenty years of experimental achievements on electrons energies reaching ∼200 GeV, implies that the effect of reciprocity principle could only be present at energies which are ≳1 TeV.
- It seems therefore that the initial proposal for such scales introduced by Born [12] in his original theory of reciprocity, needs to be updated in the light of last 70 years of theory and experimental progress in high energy physics.
- In our previous paper [15], we have given only the theoretical formulation that accounts for the condensation of FD gas as close equivalent to BE gas. However, the nature of the highest momentum state where condensation takes place was not looked into. More precisely we did not specify what determines the value of the highest momentum for a given system of fermionic particles and what is its physical significance.
- In this mini-review we address all these issues in more detail. We hope our approach based on an unified analysis of different aspects of formulation of quantum theory and relativity may shed more light on the condensation phenomena of elementary fermions of astrophysical significance.
7. Conclusions
- If the reciprocity theory remains valid, its effects should be observable only at energy scales ≳ TeV.
- In the BK model, a phenomenon like BKC could happen, and it could be modeled with our formalism based on coherent states with Grassmann variables.
- If a fermionic system presents a similar spectrum which is predicted by the BK theory, i.e., a high degeneracy around certain energy value inside a continuous band, then a similar phenomenon could appear only in the high density limit.
8. Open Issues
Acknowledgments
Conflicts of Interest
Abbreviations
| BEC | Bose–Einstein condensation |
| FD | Fermi–Dirac |
| BE | Bose–Einstein |
| BKC | Born-Kothari condensation |
| EM | Electromagnetic |
| BK | Born-Kothari |
Appendix A. Rest Masses of Particles from Reciprocity Principle
Appendix B. Properties of the Displacement Operator
References
- Einstein, A. Quantentheorie Des Einatomigen Idealen Gases; Wiley-VCH Verlag: Weinheim, Germany, 1925. [Google Scholar]
- Bose, S.N. Plancks Gesetz und Lichtquantenhypothese. Zeitschrift für Physik 1924, 26, 178–181. [Google Scholar] [CrossRef]
- London, F. The lambda-Phenomenon of Liquid Helium and the Bose–Einstein Degeneracy. Nature 1938, 141, 643–644. [Google Scholar] [CrossRef]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose–Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Davis, K.B.; Mewes, M.O.; Andrews, M.R.; van Druten, N.J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Bose–Einstein Condensation in a Gas of Sodium Atoms. Phys. Rev. Lett. 1995, 75, 3969–3973. [Google Scholar] [CrossRef] [PubMed]
- Bradley, C.C.; Sackett, C.A.; Tollett, J.J.; Hulet, R.G. Evidence of Bose–Einstein Condensation in an Atomic Gas with Attractive Interactions. Phys. Rev. Lett. 1995, 75, 1687–1690. [Google Scholar] [CrossRef] [PubMed]
- Leggett, A.J. Bose–Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307–356. [Google Scholar] [CrossRef]
- Pethick, C.J.; Smith, H. Bose–Einstein Condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Pitaevskii, L.P.; Stringari, S. Bose–Einstein Condensation; Clarendon Press: Oxford, UK, 2003. [Google Scholar]
- Casadio, R.; Giugno, A.; Micu, O.; Orlandi, A. Thermal BEC Black Holes. Entropy 2015, 17, 6893–6924. [Google Scholar] [CrossRef]
- Watanabe, G.; Venkatesh, B.P.; Dasgupta, R. Nonlinear Phenomena of Ultracold Atomic Gases in Optical Lattices: Emergence of Novel Features in Extended States. Entropy 2016, 18, 118. [Google Scholar] [CrossRef]
- Born, M. A Suggestion for Unifying Quantum Theory and Relativity. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1938, 165, 291–303. [Google Scholar] [CrossRef]
- Born, M. Relativity and quantum theory. Nature 1938, 141, 327–328. [Google Scholar] [CrossRef]
- Kothari, D.S.; Nath, B. ‘Condensation’ in Fermi–Dirac Statistics. Nature 1943, 151, 420–421. [Google Scholar] [CrossRef]
- Ghosh, A.; Ray, D.S. Born-Kothari condensation in an ideal Fermi gas. Phys. Rev. A 2017, 95, 022129. [Google Scholar] [CrossRef]
- Born, M.; Green, H.S.; Cheng, K.C.; Rodriguez, A.E. L.—Quantum Theory of Rest-Masses. Proc. R. Soc. Edinb. Sect. A Math. Phys. Sci. 1949, 62, 470–488. [Google Scholar] [CrossRef]
- Green, H.S. Quantized Field Theories and the Principle of Reciprocity. Nature 1949, 163, 208–209. [Google Scholar] [CrossRef]
- Born, M. Reciprocity Theory of Elementary Particles. Rev. Mod. Phys. 1949, 21, 463–473. [Google Scholar] [CrossRef]
- Wigner, E.P. Events, Laws of Nature, and Invariance Principles. Science 1964, 145, 995–999. [Google Scholar] [CrossRef] [PubMed]
- Yukawa, H. Quantum Theory of Non-Local Fields. Part I. Free Fields. Phys. Rev. 1950, 77, 219–226. [Google Scholar] [CrossRef]
- Born, M. Non-Localizable Fields and Reciprocity. Nature 1950, 165, 269–270. [Google Scholar] [CrossRef]
- Pais, A.; Uhlenbeck, G.E. On Field Theories with Non-Localized Action. Phys. Rev. 1950, 79, 145–165. [Google Scholar] [CrossRef]
- Yukawa, H. Structure and Mass Spectrum of Elementary Particles. II. Oscillator Model. Phys. Rev. 1953, 91, 416–417. [Google Scholar] [CrossRef]
- Born, M. The Born-Einstein Letters: Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955; Macmillan: New York, NY, USA, 1971. [Google Scholar]
- Freidel, L.; Leigh, R.G.; Minic, D. Born reciprocity in string theory and the nature of spacetime. Phys. Lett. B 2014, 730, 302–306. [Google Scholar] [CrossRef]
- Low, S.G. Reciprocal Relativity of Noninertial Frames and the Quaplectic Group. Found. Phys. 2006, 36, 1036–1069. [Google Scholar] [CrossRef]
- Wigner, E. On Unitary Representations of the Inhomogeneous Lorentz Group. Ann. Math. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- Bargmann, V.; Wigner, E.P. Group Theoretical Discussion of Relativistic Wave Equations. Proc. Natl. Acad. Sci. USA 1948, 34, 211–223. [Google Scholar] [CrossRef] [PubMed]
- Mackey, G.W. Induced Representations of Locally Compact Groups I. Ann. Math. 1952, 55, 101–139. [Google Scholar] [CrossRef]
- Mackey, G.W. Induced Representations of Locally Compact Groups II. The Frobenius Reciprocity Theorem. Ann. Math. 1953, 58, 193–221. [Google Scholar] [CrossRef]
- Mackey, G.W. Infinite-dimensional group representations. Bull. Am. Math. Soc. 1963, 69, 628–686. [Google Scholar] [CrossRef]
- Freidel, L.; Leigh, R.G.; Minic, D. Quantum gravity, dynamical phase-space and string theory. Int. J. Mod. Phys. D 2014, 23, 1442006. [Google Scholar] [CrossRef]
- Freidel, L.; Leigh, R.G.; Minic, D. Modular Spacetime and Metastring Theory. J. Phys. Conf. Ser. 2017, 804, 012032. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Herdeiro, C.A.R. Born-Infeld theory and stringy causality. Phys. Rev. D 2001, 63, 064006. [Google Scholar] [CrossRef]
- Castro, C. On Born’s deformed reciprocal complex gravitational theory and noncommutative gravity. Phys. Lett. B 2008, 668, 442–446. [Google Scholar] [CrossRef]
- Veneziano, G. A Stringy Nature Needs Just Two Constants. EPL Europhys. Lett. 1986, 2. [Google Scholar] [CrossRef]
- Prugovecki, E. Principles of Quantum General Relativity; World Scientific: Singapore, 1995. [Google Scholar]
- Connes, A. Noncommutative Geometry; Academic Press: London, UK, 1994. [Google Scholar]
- Cahill, K.E.; Glauber, R.J. Density operators for fermions. Phys. Rev. A 1999, 59, 1538–1555. [Google Scholar] [CrossRef]
- Born, M. Application of “Reciprocity” to Nuclei. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1938, 166, 552–557. [Google Scholar]
- Born, M. Some remarks on reciprocity. Proc. Indian Acad. Sci. Sect. A 1938, 8, 309–314. [Google Scholar]
- Born, M. Unification of the Theories of Photon and Meson. Nature 1944, 154, 764–765. [Google Scholar] [CrossRef]
- Born, M. Reciprocity Theory of Electrodynamics. Nature 1949, 164, 281–282. [Google Scholar] [CrossRef]
- Low, S.G. Canonically relativistic quantum mechanics: Representations of the unitary semidirect Heisenberg group, U(1,3)⊗sH(1,3). J. Math. Phys. 1997, 38, 2197–2209. [Google Scholar] [CrossRef]
- Morgan, S. Supersymmetric Born Reciprocity. Ph.D. Thesis, University of Tasmania, Hobart, Australia, 2003. [Google Scholar]
- Delbourgo, R.; Lashmar, D. Born Reciprocity and the 1/r Potential. Found. Phys. 2008, 38, 995–1010. [Google Scholar] [CrossRef]
- Jaeckel, J.; Spannowsky, M. Probing MeV to 90 GeV axion-like particles with LEP and LHC. Phys. Lett. B 2016, 753, 482–487. [Google Scholar] [CrossRef]
- Nath, B. Thermodynamics of a Fermi–Dirac gas obeying Born’s modified quantum statistics. Proc. Indian Acad. Sci. 1943, 9, 257–264. [Google Scholar]
- Greiner, W. Quantum Mechanics: Special Chapters; Springer: Heidelberg, Germany, 1998. [Google Scholar]
- Yang, C.N. Concept of Off-Diagonal Long-Range Order and the Quantum Phases of Liquid He and of Superconductors. Rev. Mod. Phys. 1962, 34, 694–704. [Google Scholar] [CrossRef]
- Schwinger, J. The Theory of Quantized Fields. IV. Phys. Rev. 1953, 92, 1283–1299. [Google Scholar] [CrossRef]
- Berezin, F.A. The Method of Second Quantization; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Amelino-Camelia, G.; Freidel, L.; Kowalski-Glikman, J.; Smolin, L. Principle of relative locality. Phys. Rev. D 2011, 84, 084010. [Google Scholar] [CrossRef]
- Chu, C.S.; Furuta, K.; Inami, T. Locality, Causality and Noncommutative Geometry. Int. J. Mod. Phys. A 2006, 21, 67–82. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Freidel, L.; Kowalski-Glikman, J.; Smolin, L. Relative locality: A deepening of the relativity principle. Gen. Relat. Gravit. 2011, 43, 2547–2553. [Google Scholar] [CrossRef]
- Brown, L. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Das, A. Field Theory: A Path Integral Approach; World Scientific: New Delhi, India, 2002. [Google Scholar]
- Zinn-Justin, J. Quantum Field Theory and Critical Phenomena; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Dalton, B.J.; Jeffers, J.; Barnett, S.M. Phase Space Methods for Degenerate Quantum Gases; Oxford University Press: New York, NY, USA, 2015. [Google Scholar]
- Dalton, B.; Jeffers, J.; Barnett, S. Grassmann phase space methods for fermions. II. Field Theory. Ann. Phys. 2017, 377, 268–310. [Google Scholar] [CrossRef]
- Mrówczyński, S. Wigner functional of fermionic fields. Phys. Rev. D 2013, 87, 065026. [Google Scholar] [CrossRef]
- Corney, J.F.; Drummond, P.D. Gaussian Quantum Monte Carlo Methods for Fermions and Bosons. Phys. Rev. Lett. 2004, 93, 260401. [Google Scholar] [CrossRef] [PubMed]
- Viennot, D.; Moro, O. Adiabatic transport of qubits around a black hole. Class. Quant. Gravity 2017, 34, 055005. [Google Scholar] [CrossRef]
- Braungardt, S.; Rodríguez, M.; Sen(De), A.; Sen, U.; Glauber, R.J.; Lewenstein, M. Counting of fermions and spins in strongly correlated systems in and out of thermal equilibrium. Phys. Rev. A 2011, 83, 013601. [Google Scholar] [CrossRef]
- Shen, H.Z.; Qin, M.; Xiu, X.M.; Yi, X.X. Exact non-Markovian master equation for a driven damped two-level system. Phys. Rev. A 2014, 89, 062113. [Google Scholar] [CrossRef]
- Efetov, K.B.; Pépin, C.; Meier, H. Exact Bosonization for an Interacting Fermi Gas in Arbitrary Dimensions. Phys. Rev. Lett. 2009, 103, 186403. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Jiang, L.; Liu, X.J.; Pu, H. Probing Anisotropic Superfluidity in Atomic Fermi Gases with Rashba Spin-Orbit Coupling. Phys. Rev. Lett. 2011, 107, 195304. [Google Scholar] [CrossRef] [PubMed]
- Plimak, L.I.; Collett, M.J.; Olsen, M.K. Langevin equations for interacting fermions and Cooper-like pairing in trapped one-dimensional fermions. Phys. Rev. A 2001, 64, 063409. [Google Scholar] [CrossRef]
- Tempere, J.; Klimin, S.N.; Devreese, J.T. Effect of population imbalance on the Berezinskii-Kosterlitz-Thouless phase transition in a superfluid Fermi gas. Phys. Rev. A 2009, 79, 053637. [Google Scholar] [CrossRef]
- Ghosh, A.; Sinha, S.S.; Ray, D.S. Fermionic oscillator in a fermionic bath. Phys. Rev. E 2012, 86, 011138. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Zhao, X.; Yu, T. Non-Markovian fermionic stochastic Schrodinger equation for open system dynamics. Phys. Rev. A 2013, 87, 052127. [Google Scholar] [CrossRef]
- Ghosh, A.; Sinha, S.S.; Ray, D.S. Canonical formulation of quantum dissipation and noise in a generalized spin bath. Phys. Rev. E 2012, 86, 011122. [Google Scholar] [CrossRef] [PubMed]
- Ho, S.H.; Li, W.; Lin, F.L.; Ning, B. Quantum decoherence with holography. J. High Energy Phys. 2014, 2014, 170. [Google Scholar] [CrossRef]
- Ghosh, A. Parametric control in coupled fermionic oscillators. Phys. Rev. A 2014, 90, 043820. [Google Scholar] [CrossRef]
- Ghosh, A. Parametrically coupled fermionic oscillators: Correlation functions and phase-space description. Phys. Rev. A 2015, 91, 013835. [Google Scholar] [CrossRef]
- Tyc, T.; Hamilton, B.; Sanders, B.C.; Oliver, W.D. No Approximate Complex Fermion Coherent States. Found. Phys. 2007, 37, 1519–1539. [Google Scholar] [CrossRef]
- Glauber, R.J. The Quantum Theory of Optical Coherence. Phys. Rev. 1963, 130, 2529–2539. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Cahill, K.E.; Glauber, R.J. Ordered Expansions in Boson Amplitude Operators. Phys. Rev. 1969, 177, 1857–1881. [Google Scholar] [CrossRef]
- Cahill, K.E.; Glauber, R.J. Density Operators and Quasiprobability Distributions. Phys. Rev. 1969, 177, 1882–1902. [Google Scholar] [CrossRef]
- Barik, D.; Banerjee, D.; Ray, D.S. Quantum Brownian Motion in c-Numbers: Theory and Application; Nova-Science: New York, NY, USA, 2009. [Google Scholar]
- Sinha, S.S.; Ghosh, A.; Ray, D.S. Quantum Smoluchowski equation for a spin bath. Phys. Rev. E 2011, 84, 031118. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Sinha, S.S.; Ray, D.S. Quantum Dissipation in a spin bath; Application to Chemical Dynamics. Proc. Indian Acad. Sci. Sect. A 2014, 80, 949–998. [Google Scholar] [CrossRef]
- Sinha, S.S.; Ghosh, A.; Ray, D.S. Decay of a metastable state induced by a spin bath. Phys. Rev. E 2011, 84, 041113. [Google Scholar] [CrossRef] [PubMed]
- Glauber, R.J. Quantum Theory of Optical Coherence: Selected Papers and Lectures; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Bogoliubov, N.N. On the theory of superfluidity. J. Phys. USSR 1947, 11, 23–32. [Google Scholar]
- Yukalov, V.I. Bose–Einstein condensation and gauge symmetry breaking. Laser Phys. Lett. 2007, 4, 632–647. [Google Scholar] [CrossRef]
- Yukalov, V.I. Basics of Bose–Einstein condensation. Phys. Part. Nucl. 2011, 42, 460–513. [Google Scholar] [CrossRef]
- Glauber, R.J. Quantum theory of coherence. In Quantum Optics; Kay, S.M., Maitland, A., Eds.; Academic Press: New York, NY, USA, 1970; Chapter 3; pp. 53–125. [Google Scholar]
- Dehmelt, H. A Single Atomic Particle Forever Floating at Rest in Free Space: New Value for Electron Radius. Phys. Scr. 1988, 1988, 102–110. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Drell, S.D. Anomalous magnetic moment and limits on fermion substructure. Phys. Rev. D 1980, 22, 2236–2243. [Google Scholar] [CrossRef]
- Dehmelt, H. Experiments with an isolated subatomic particle at rest. Rev. Mod. Phys. 1990, 62, 525–530. [Google Scholar] [CrossRef]
- Leggett, A.J. Quantum Liquids: Bose Condensation and Cooper Pairing in Condensed-Matter Systems; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Leggett, A.J.; Zhang, S. The BEC-BCS Crossover: Some History and Some General Observations; Springer: Berlin, Germany, 2012; pp. 33–47. [Google Scholar]
- Stoof, H.T.C.; Houbiers, M.; Sackett, C.A.; Hulet, R.G. Superfluidity of Spin-Polarized 6Li. Phys. Rev. Lett. 1996, 76, 10–13. [Google Scholar] [CrossRef] [PubMed]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215–1274. [Google Scholar] [CrossRef]
- Gurarie, V.; Radzihovsky, L. Resonantly paired fermionic superfluids. Ann. Phys. 2007, 322, 2–119. [Google Scholar] [CrossRef]
- Greiner, M.; Regal, C.A.; Jin, D.S. Atomic Physics 19: XIX International Conference on Atomic Physics; American Institute of Physics: College Park, MA, USA, 2004. [Google Scholar]
- Ketterle, W.; Inguscio, M.; Salomon, C. Proceedings of the Varenna “Enrico Fermi” Summer School; Societ Italiana di Fisica: Bologna, Italy, 2007. [Google Scholar]
- DeMarco, B.; Jin, D.S. Onset of Fermi Degeneracy in a Trapped Atomic Gas. Science 1999, 285, 1703–1706. [Google Scholar] [CrossRef] [PubMed]
- Regal, C.A.; Greiner, M.; Jin, D.S. Observation of Resonance Condensation of Fermionic Atom Pairs. Phys. Rev. Lett. 2004, 92, 040403. [Google Scholar] [CrossRef] [PubMed]
- Zwierlein, M.W.; Stan, C.A.; Schunck, C.H.; Raupach, S.M.F.; Kerman, A.J.; Ketterle, W. Condensation of Pairs of Fermionic Atoms near a Feshbach Resonance. Phys. Rev. Lett. 2004, 92, 120403. [Google Scholar] [CrossRef]
- Zwierlein, M.W.; Schunck, C.H.; Stan, C.A.; Raupach, S.M.F.; Ketterle, W. Formation Dynamics of a Fermion Pair Condensate. Phys. Rev. Lett. 2005, 94, 180401. [Google Scholar] [CrossRef] [PubMed]
- Landé, A. Sommerfeld’s Fine Structure Constant and Born’s Reciprocity. Phys. Rev. 1939, 56, 482–483. [Google Scholar] [CrossRef]
- Landé, A. The Structure of Electric Particles and the Number 137. Phys. Rev. 1939, 56, 486. [Google Scholar] [CrossRef]
- Born, M. XXI.—Reciprocity and the Number 137. Part I. Proc. R. Soc. Edinb. 1940, 59, 219–223. [Google Scholar] [CrossRef]
- Butts, D.A.; Rokhsar, D.S. Trapped Fermi gases. Phys. Rev. A 1997, 55, 4346–4350. [Google Scholar] [CrossRef]
- New Model to Unravel Mysteries of Elementary Particles. 2017. Available online: http://www.natureasia.com/en/nindia/article/10.1038/nindia.2017.45 (accessed on 7 September 2017).
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Mazin, I.I. Superconductivity: Extraordinarily conventional. Nature 2015, 525, 40–41. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, A. Born-Kothari Condensation for Fermions. Entropy 2017, 19, 479. https://doi.org/10.3390/e19090479
Ghosh A. Born-Kothari Condensation for Fermions. Entropy. 2017; 19(9):479. https://doi.org/10.3390/e19090479
Chicago/Turabian StyleGhosh, Arnab. 2017. "Born-Kothari Condensation for Fermions" Entropy 19, no. 9: 479. https://doi.org/10.3390/e19090479
APA StyleGhosh, A. (2017). Born-Kothari Condensation for Fermions. Entropy, 19(9), 479. https://doi.org/10.3390/e19090479



