Coupled Effects of Turing and Neimark-Sacker Bifurcations on Vegetation Pattern Self-Organization in a Discrete Vegetation-Sand Model
Abstract
1. Introduction
2. A Discrete Vegetation-Sand Model
3. Bifurcation Analysis
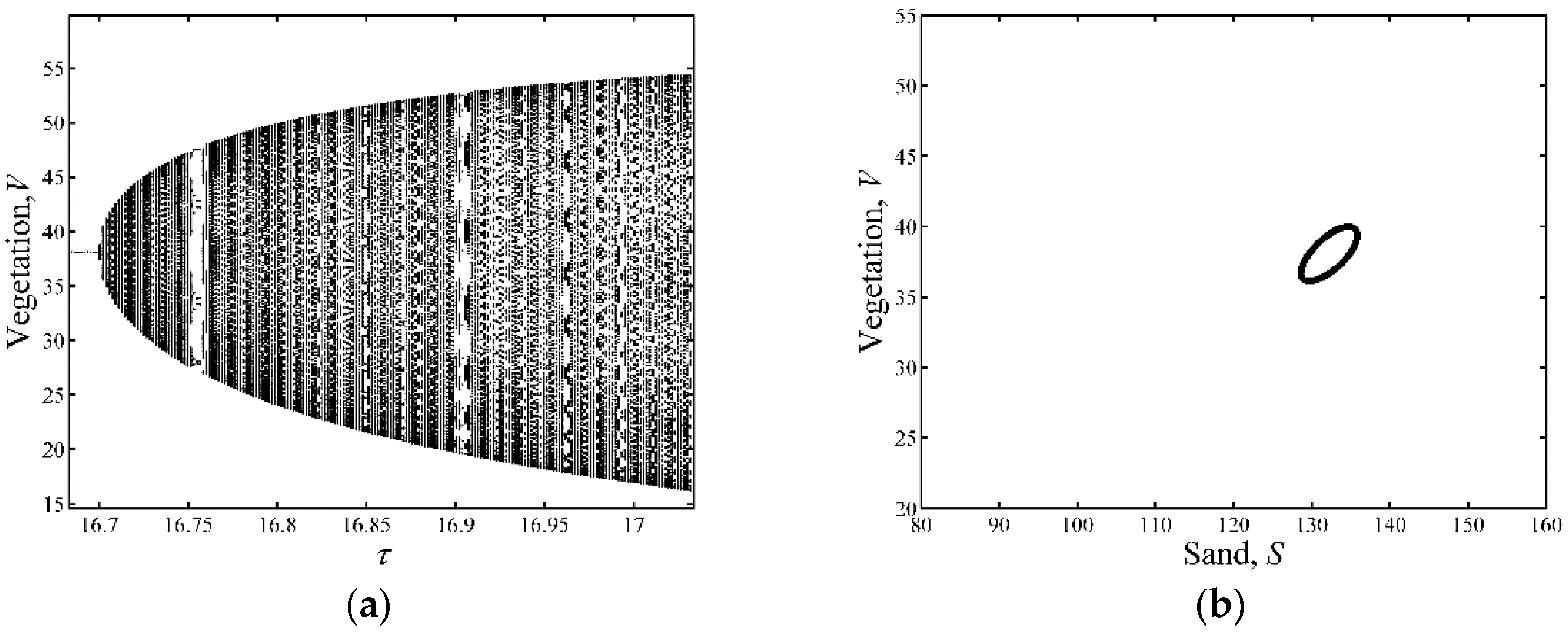
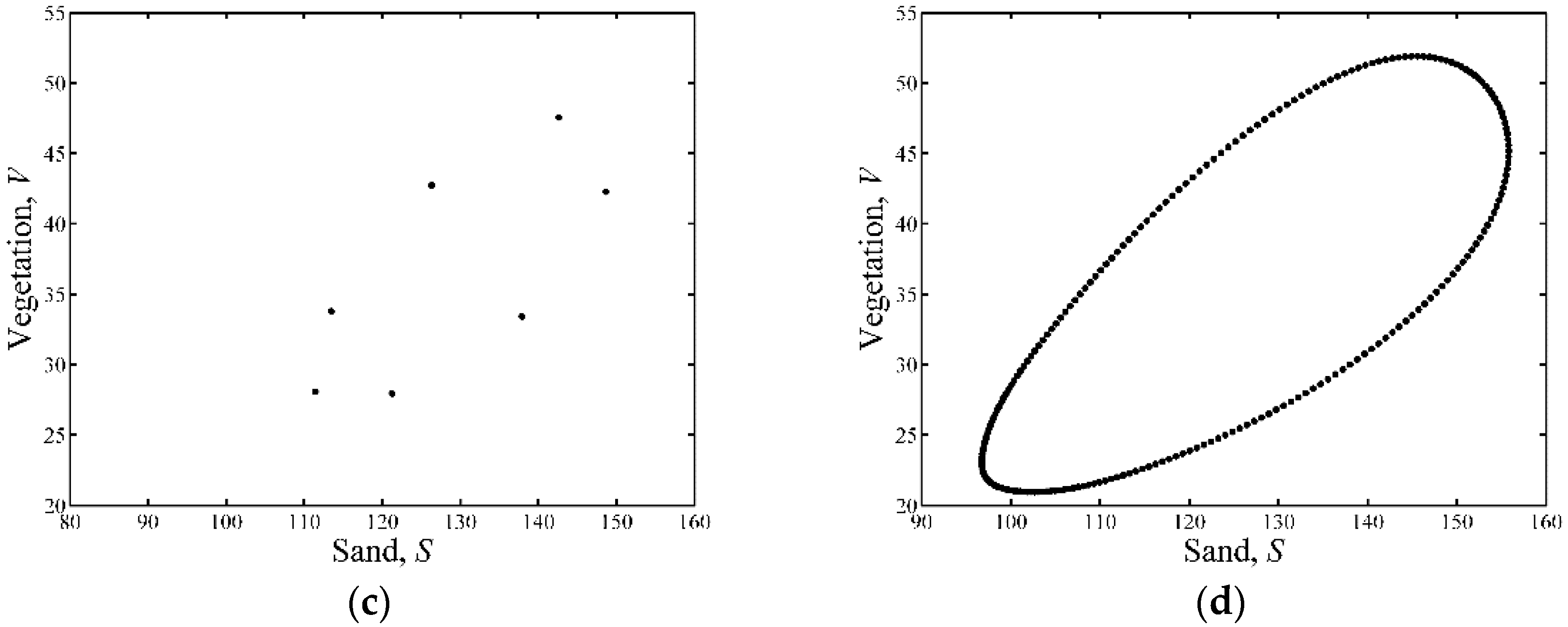
3.1. Neimark-Sacker Bifurcation Analysis
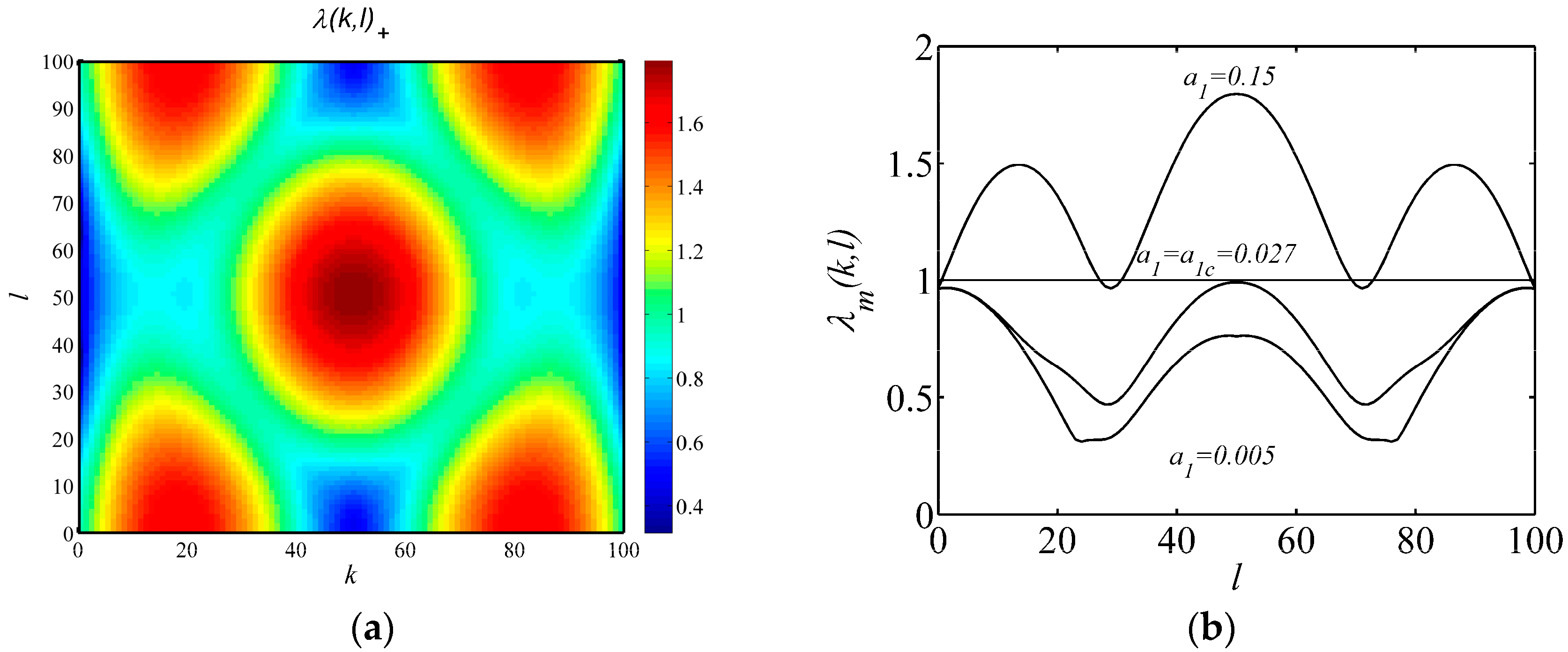
3.2. Turing Bifurcation Analysis
- In the absence of diffusion and advection, U0(μ) is asymptotically stable;
- With diffusion and advection, max(λ(μ)) > 0;
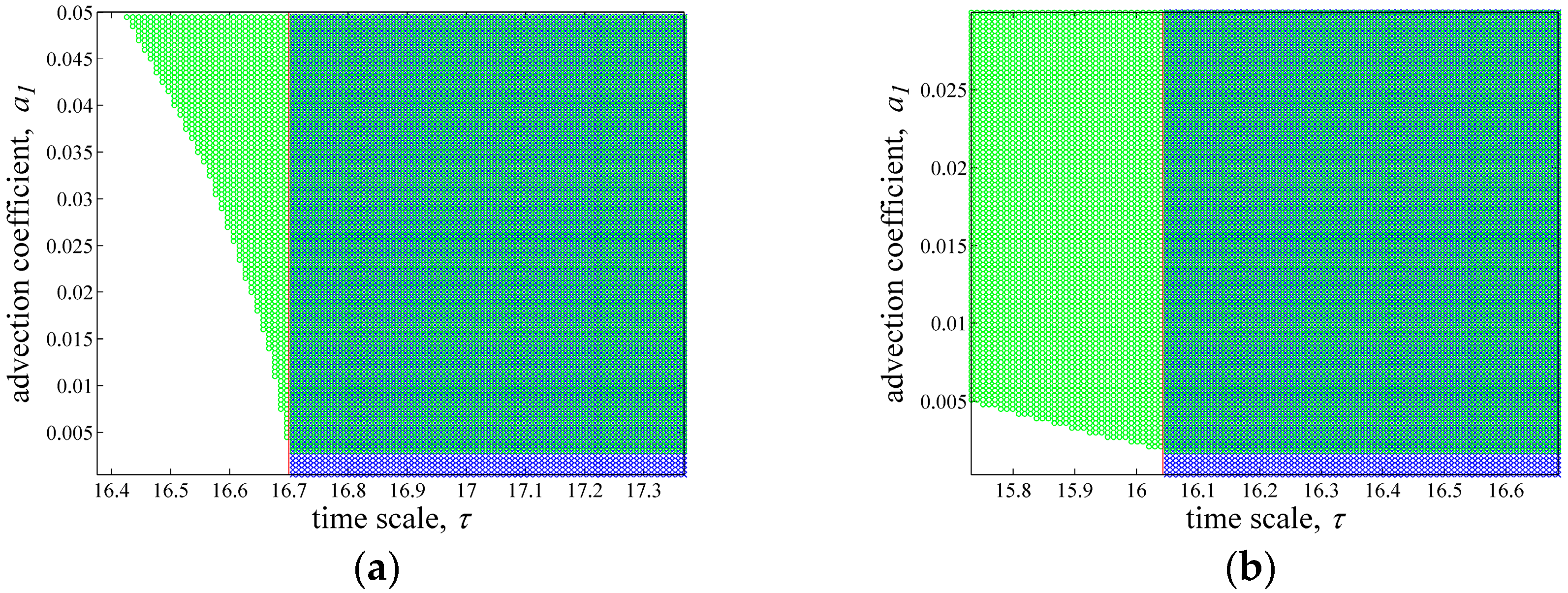
3.3. Parameter Space for Neimark-Sacker and Turing Bifurcation
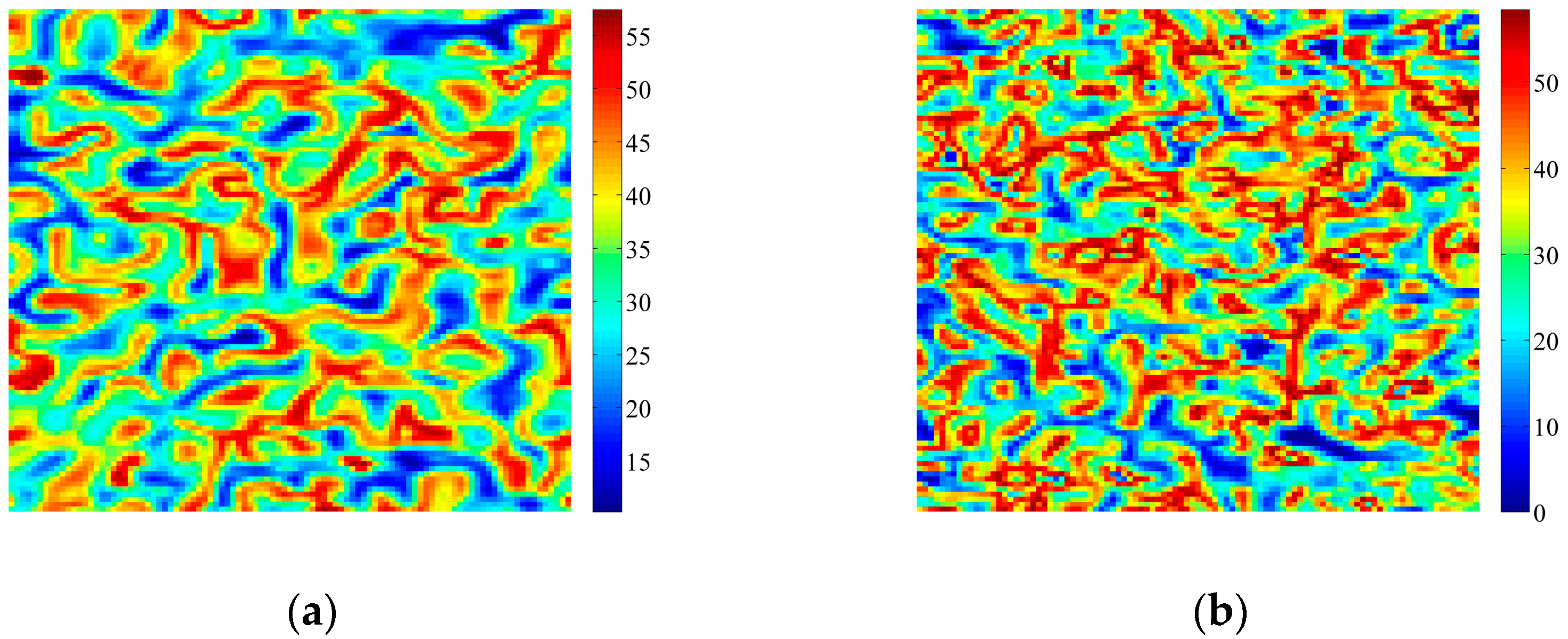
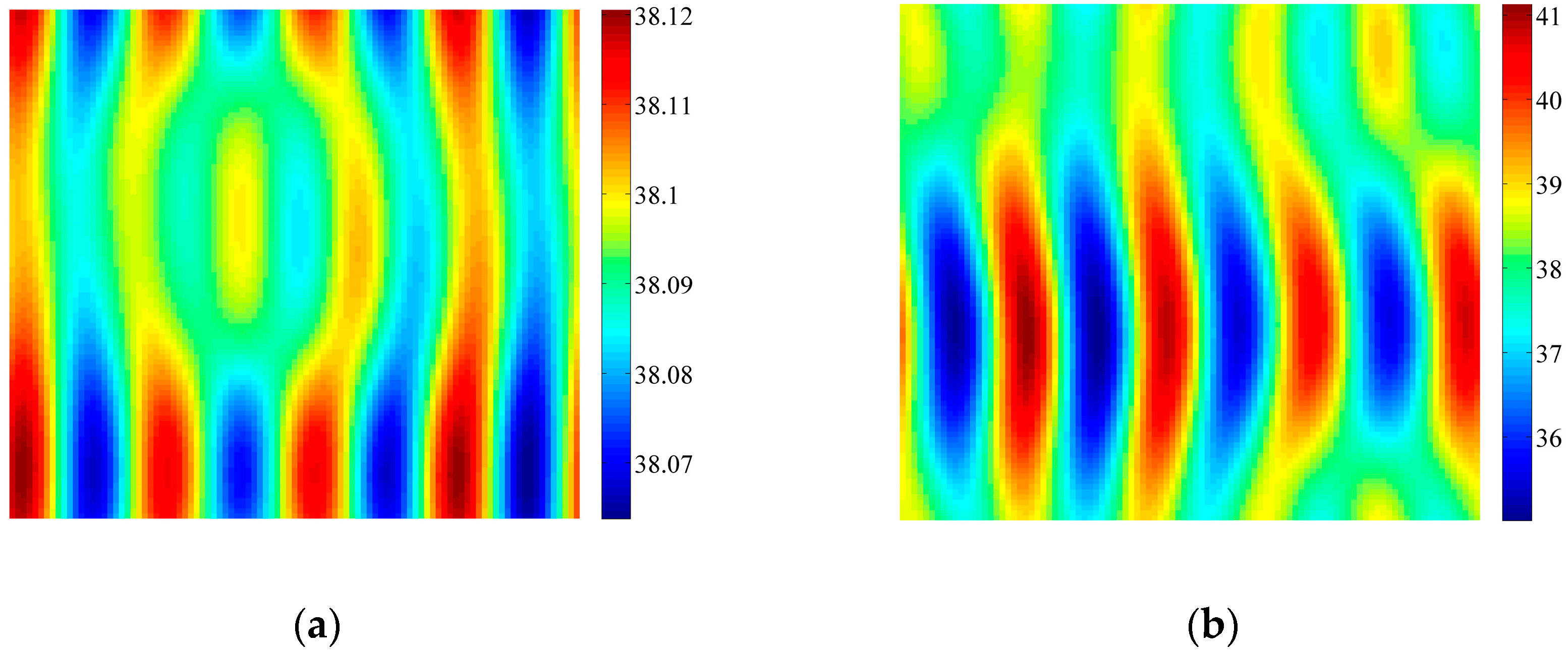
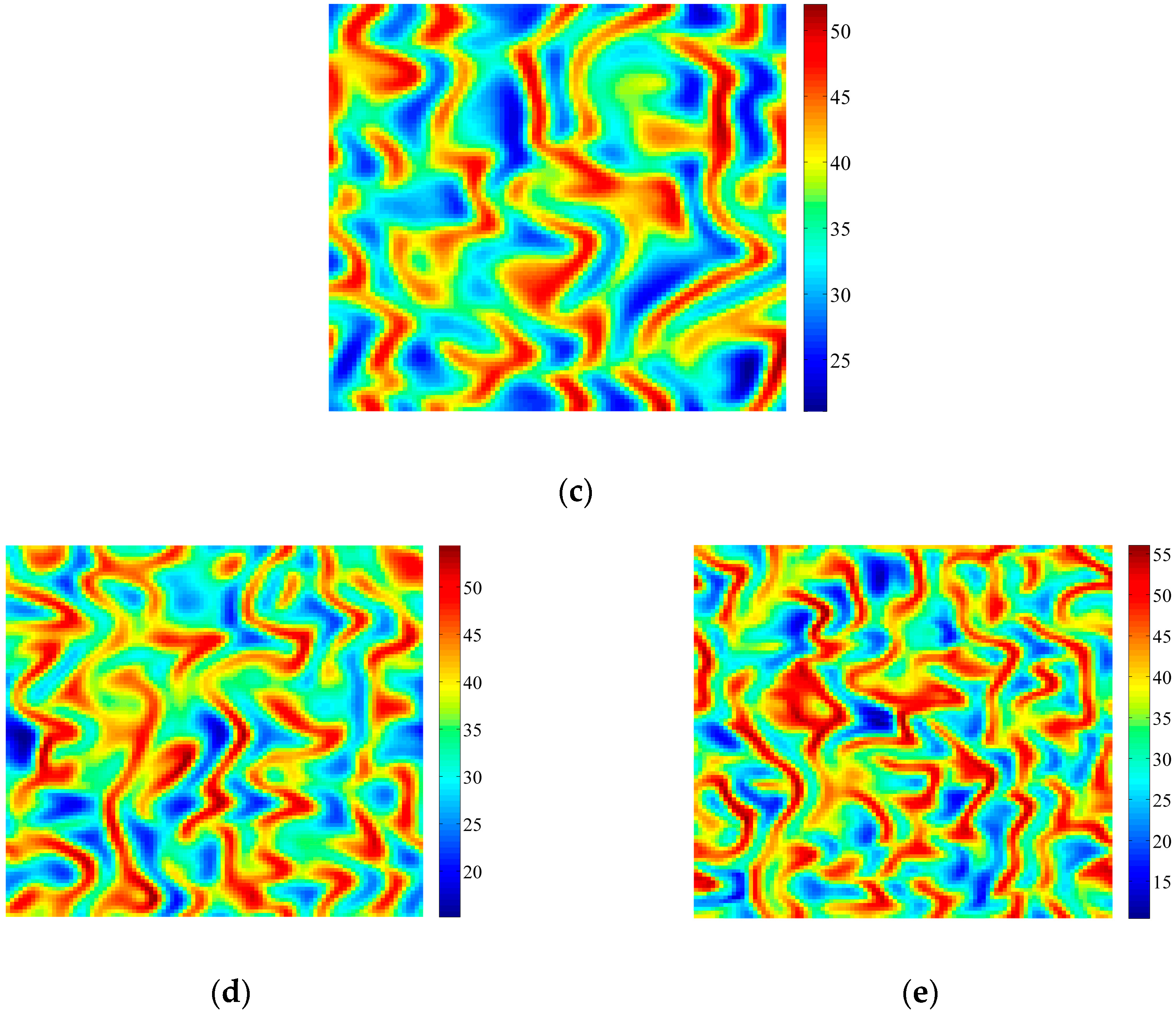
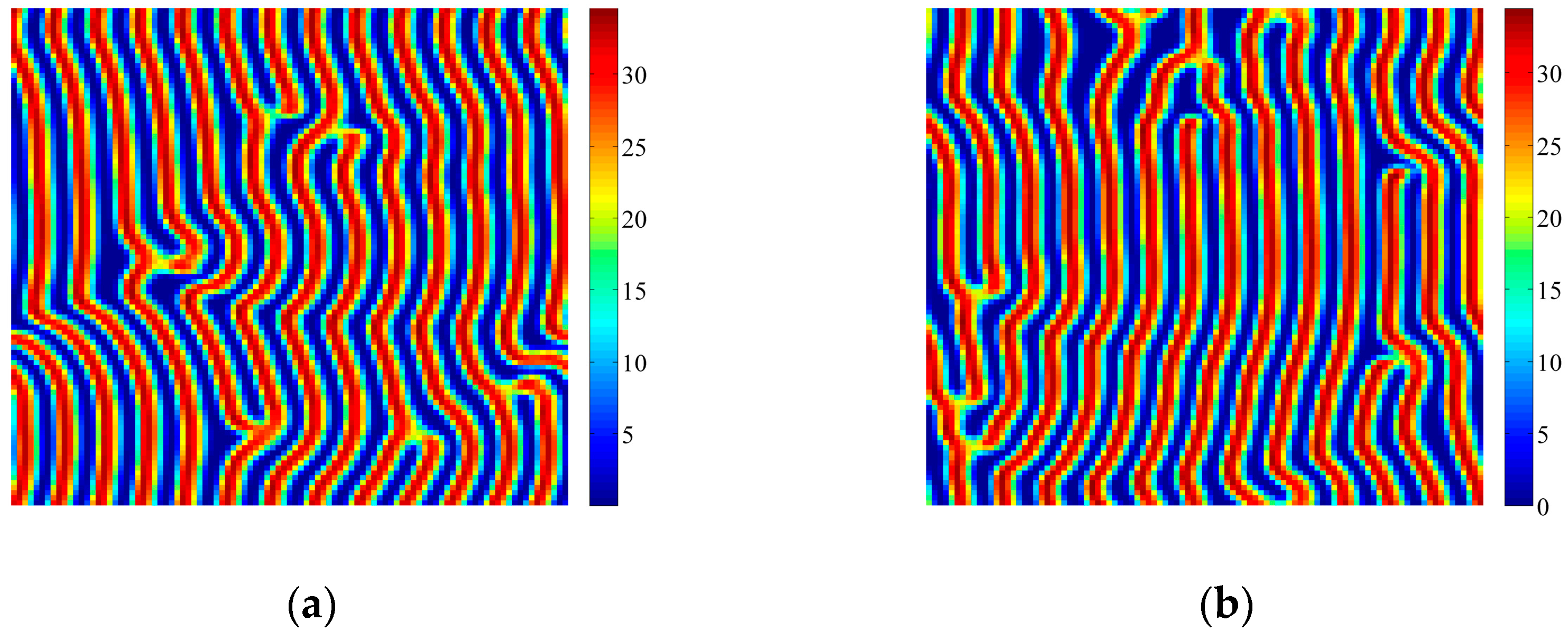
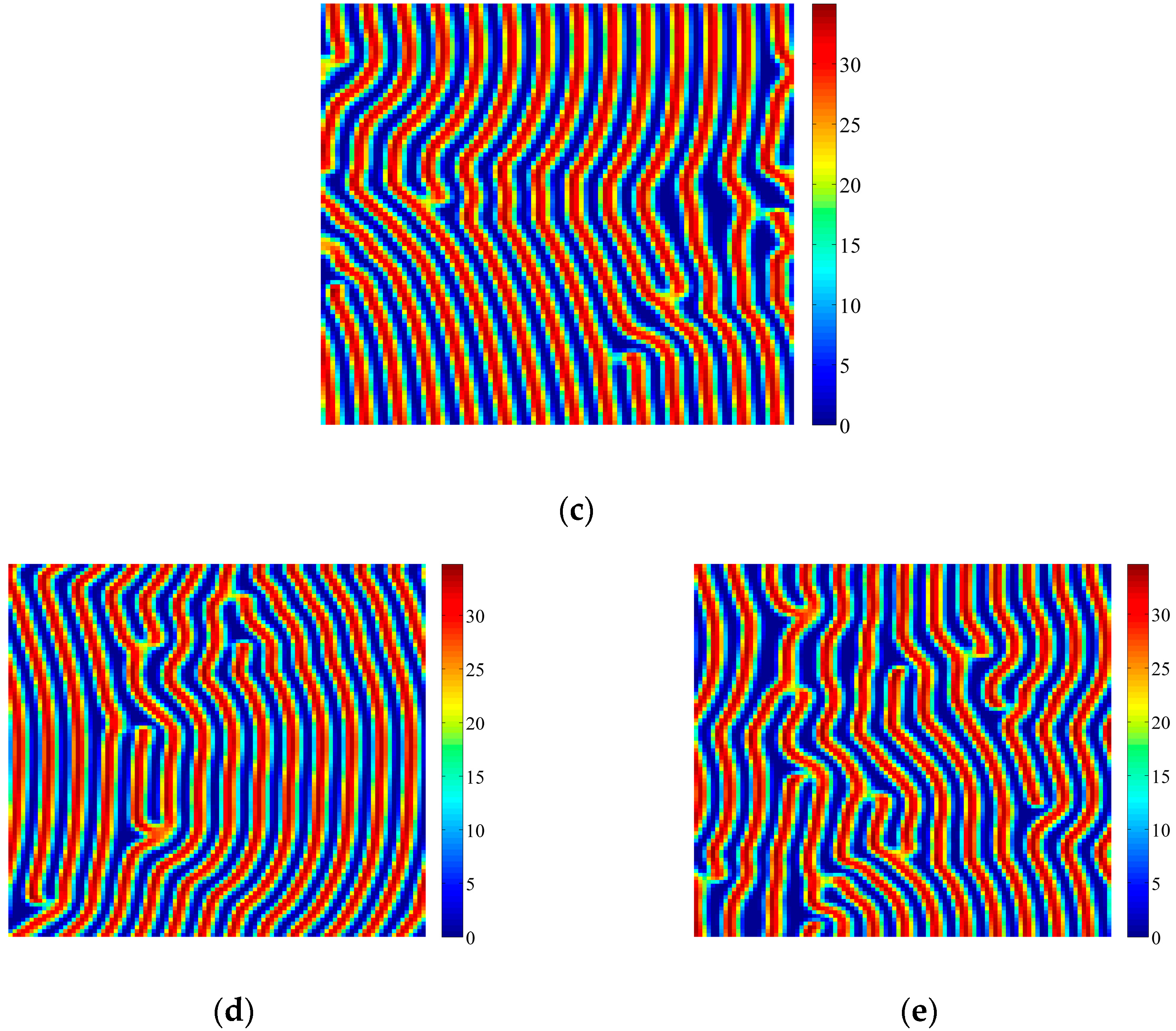
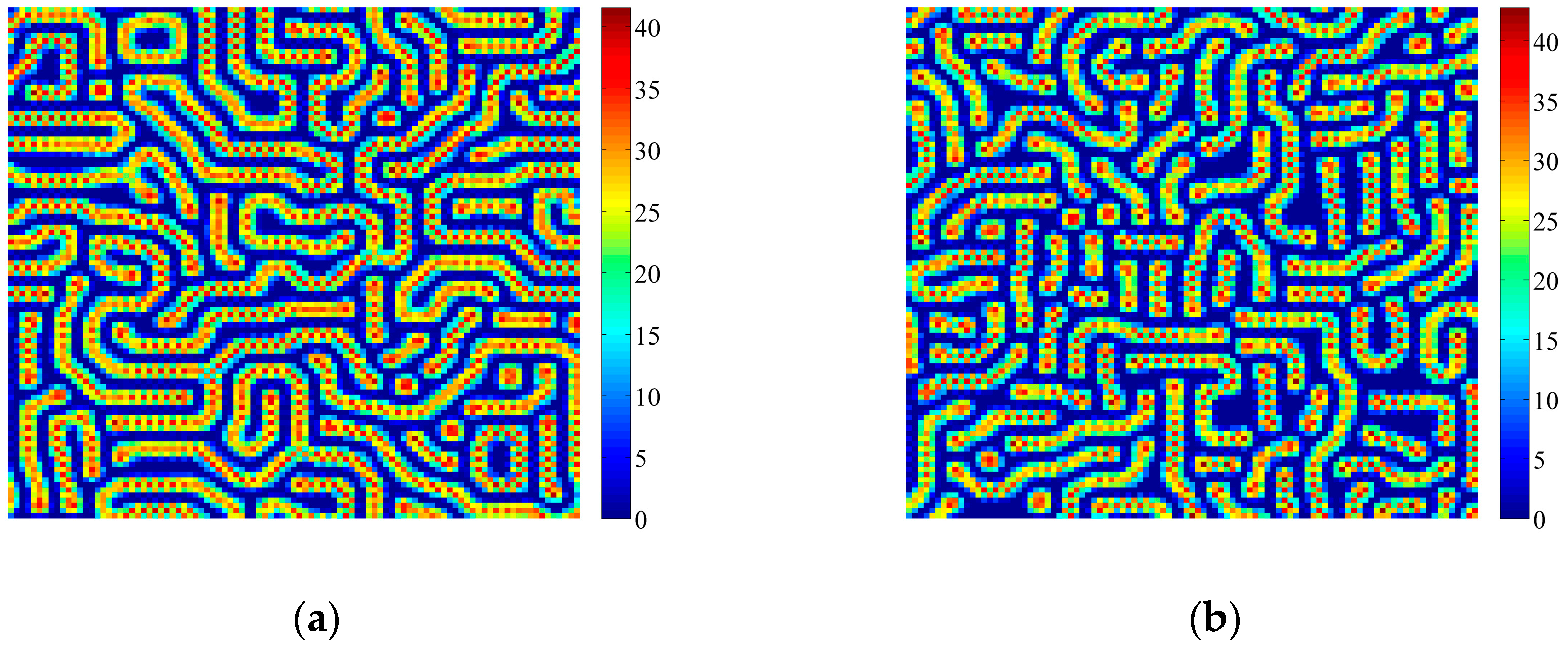
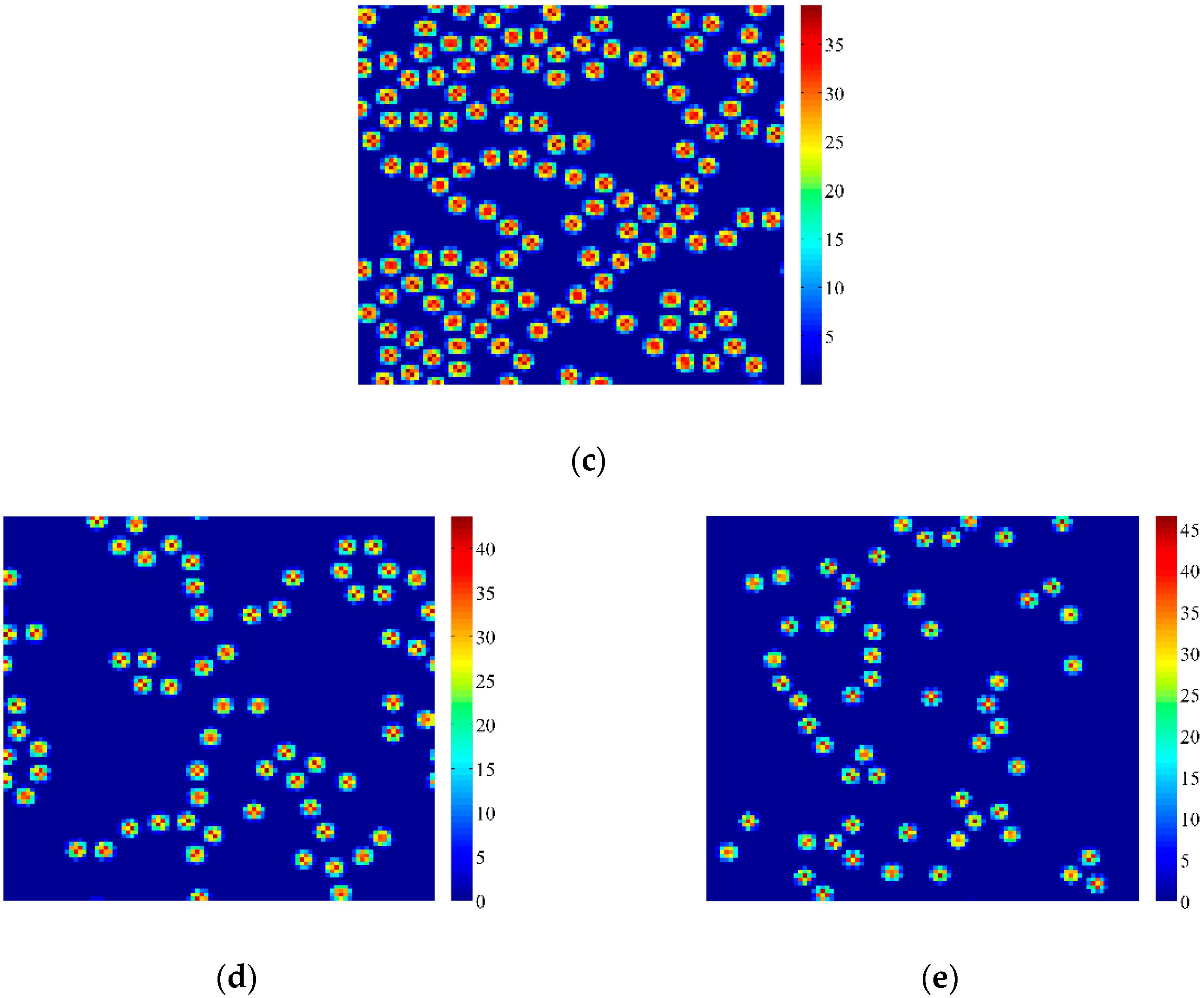
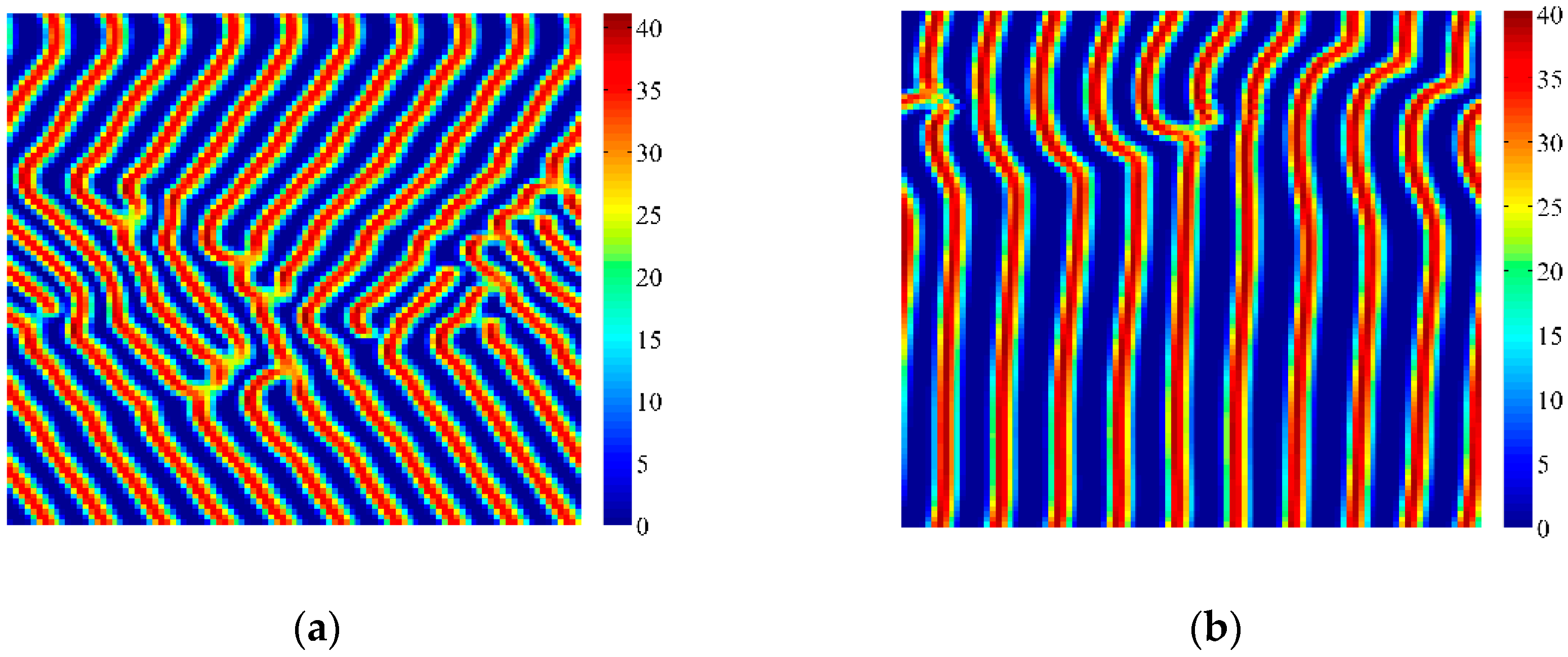
4. Coupled Effects of Turing and Neimark-Sacker Bifurcations on Vegetation Pattern Self-Organization
5. Conclusions
- (a)
- The method of discretization provides a new scenario in the study on wind-induced vegetation patterns. It preserves the patterns that can be obtained in [26].
- (b)
- After discretization, the variation of time scale becomes possible. This variation helps to understand pattern self-organization under different ecological scales.
- (c)
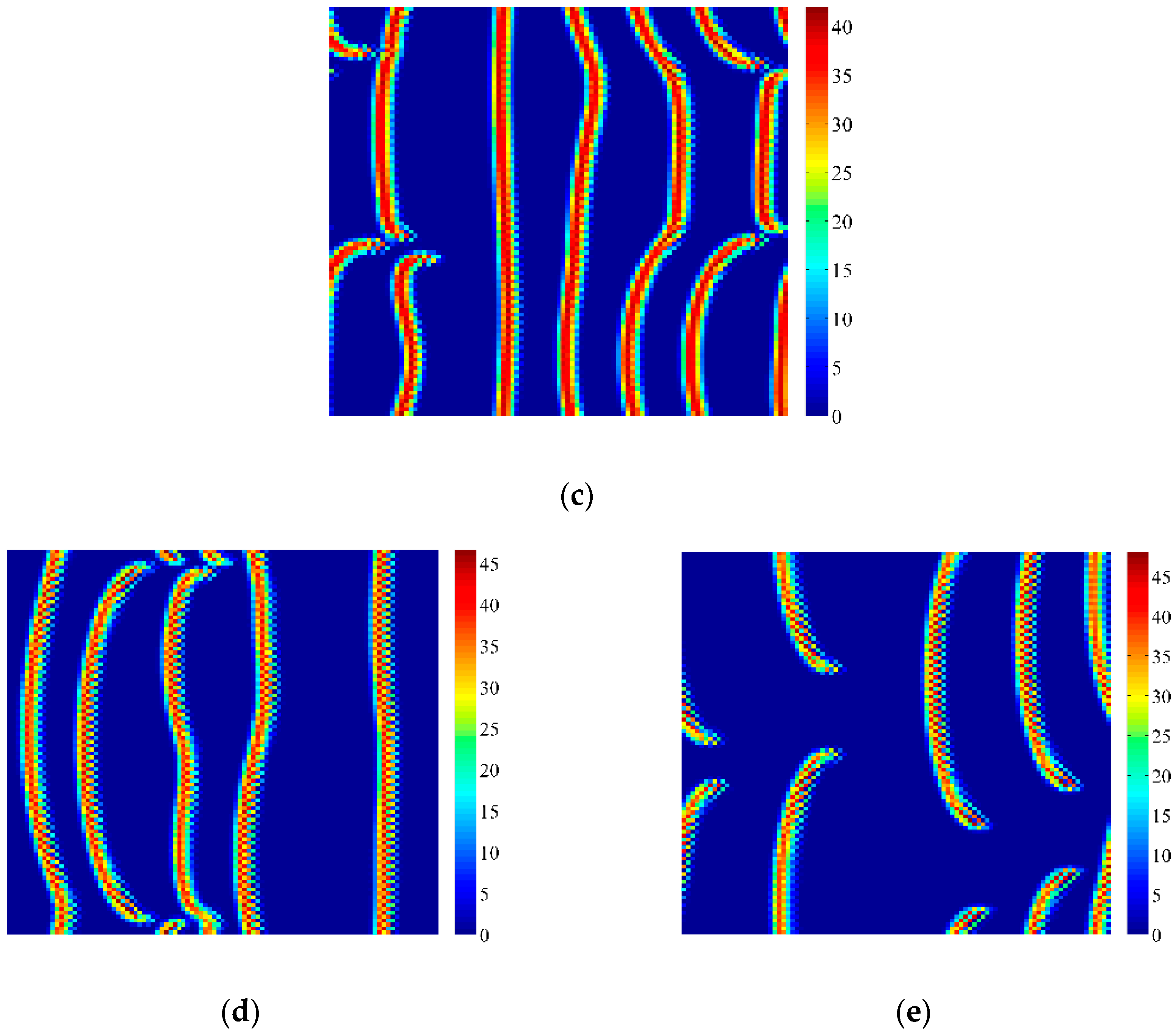
- With the discrete vegetation-sand model, we investigated the coupled effects of Turing and Neimark-Sacker bifurcations. Under both bifurcation conditions, the type of simulated patterns depends on the intensity of each bifurcation. Sometime one bifurcation effect dominates the self-organization of patterns, while specially they couple with each other and lead to pattern variation, which can also be supported by the variance of entropy in Figure 7 and Figure 8. However, the coupled effects of Turing and Neimark-Sacker bifurcations are so complex that new methods may be needed to assess the intensity of each bifurcation.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. Neimark-Sacker Bifurcation Analysis
Appendix A.2. Turing Bifurcation Analysis
References
- Klausmeier, C.A. Regular and irregular patterns in semiarid vegetation. Science 1999, 284, 1826–1828. [Google Scholar] [CrossRef] [PubMed]
- Deblauwe, V.; Couteron, P.; Bogaert, J.; Barbier, N. Determinants and dynamics of banded vegetation pattern migration in arid climates. Ecol. Monogr. 2012, 82, 3–21. [Google Scholar] [CrossRef]
- Muller, J. Floristic and structural pattern and current distribution of tiger bush vegetation in Burkina Faso (West Africa), assessed by means of belt transects and spatial analysis. Appl. Ecol. Environ. Res. 2013, 11, 153–171. [Google Scholar] [CrossRef]
- Berg, S.S.; Dunkerley, D.L. Patterned mulga near Alice Springs, central Australia, and the potential threat of firewood collection on this vegetation community. J. Arid Environ. 2004, 59, 313–350. [Google Scholar] [CrossRef]
- Moreno, M.L.H.; Saco, P.M.; Willgoose, G.R.; Tongway, D.J. Variations in hydrological connectivity of Australian semiarid landscapes indicate abrupt changes in rainfall-use efficiency of vegetation. J. Geophys. Res. 2012, 117, G03009. [Google Scholar] [CrossRef]
- Montan, C. The colonization of bare areas in two-phase mosaics of an arid ecosystem. J. Ecol. 1992, 80, 315–327. [Google Scholar] [CrossRef]
- McDonald, A.K.; Kinucan, R.J.; Loomis, L.E. Ecohydrological interactions within banded vegetation in the northeastern Chihuahuan Desert, USA. Ecohydrology 2009, 2, 66–71. [Google Scholar] [CrossRef]
- HilleRisLambers, R.; Rietkerk, M.; van den Bosch, F.; Prins, H.; de Kroon, H. Vegetation pattern formation in semi-arid grazing systems. Ecology 2001, 82, 50–61. [Google Scholar] [CrossRef]
- Rietkerk, M.; Boerlijst, M.C.; van Langevelde, F.; HilleRisLambers, R.; van de Koppel, J.; Kumar, L.; Prins, H.H.T.; de Roos, A.M. Self-organization of vegetation in arid ecosystems. Am. Nat. 2002, 160, 524–530. [Google Scholar] [PubMed]
- Lefever, R.; Lejeune, O. On the origin of tiger bush. Bull. Math. Biol. 1997, 59, 263–294. [Google Scholar] [CrossRef]
- D’Odorico, P.; Laio, F.; Ridolfi, L. Vegetation patterns induced by random climate fluctuations. Geophys. Res. Lett. 2006, 33, L19404. [Google Scholar] [CrossRef]
- D’Odorico, P.; Laio, F.; Porporato, A.; Ridolfi, L.; Barbier, N. Noise-induced vegetation patterns in fire-prone savannas. J. Geophys. Res. 2007, 112, G02021. [Google Scholar] [CrossRef]
- Sherratt, J.A. An analysis of vegetation stripe formation in semi-arid landscapes. J. Math. Biol. 2005, 51, 183–197. [Google Scholar] [CrossRef] [PubMed]
- Van de Koppel, J.; Rietkerk, M.; Van, L.F.; Kumar, L.; Klausmeier, C.A.; Fryxell, J.M.; Hearne, J.W.; van Andel, J.; de Ridder, N. Spatial heterogeneity and irreversible vegetation change in semiarid grazing systems. Am. Nat. 2002, 159, 209–218. [Google Scholar] [CrossRef] [PubMed]
- D’Odorico, P.; Laio, F.; Ridolfi, L. Patterns as indicators of productivity enhancement by facilitation and competition in dryland vegetation. J. Geophys. Res. 2006, 111, G03010. [Google Scholar] [CrossRef]
- Haken, H. Information and Self-Organization; Springer: Berlin, Germany, 1988. [Google Scholar]
- Nicolis, J.S. Chaos and Information Processing; World Scientific: Singapore, 1999. [Google Scholar]
- Mahara, H.; Yamaguchi, T. Calculation of the Entropy Balance Equation in a Non-equilibrium Reaction-diffusion System. Entropy 2010, 12, 2436–2449. [Google Scholar] [CrossRef]
- Nicolis, G.; Nicolis, C. Stochastic Resonance, Self-Organization and Information Dynamics in Multistable Systems. Entropy 2016, 18, 172. [Google Scholar] [CrossRef]
- Mezghani, N.; Mitiche, A.; Cheriet, M. Maximum Entropy Gibbs Density Modeling for Pattern Classification. Entropy 2012, 14, 2478–2491. [Google Scholar] [CrossRef]
- Clayton, W.D. Vegetation ripples near Gummi, Nigeria. J. Ecol. 1966, 54, 415–417. [Google Scholar] [CrossRef]
- Clayton, W.D. The vegetation of Katsina province, Nigeria. J. Ecol. 1969, 57, 445–451. [Google Scholar] [CrossRef]
- Zonneveld, I. A geomorphological based banded “tiger” pattern related to former dune fields in Ž. Sokoto, northern Nigeria. Catena 1999, 37, 45–56. [Google Scholar] [CrossRef]
- White, L.P. Vegetation arcs in Jordan. J. Ecol. 1969, 57, 461–464. [Google Scholar] [CrossRef]
- White, L.P. Vegetation stripes on sheet wash surfaces. J. Ecol. 1971, 59, 615–622. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, H.; Evans, M.R.; Huang, T. Vegetation patterns generated by a wind driven sand-vegetation system in arid and semi-arid areas. Ecol. Complex. 2017, 31, 21–33. [Google Scholar] [CrossRef]
- Okin, G.S.; Murray, B.; Schlesinger, W.H. Degradation of sandy arid shrubland environments: Observations, process modelling, and management implications. J. Arid Environ. 2001, 47, 123–144. [Google Scholar] [CrossRef]
- Eldridge, D.J.; Leys, J.F. Exploring some relationships between biological soil crusts, soil aggregation and wind erosion. J. Arid Environ. 2003, 53, 457–466. [Google Scholar] [CrossRef]
- Yan, Y.C.; Xu, X.L.; Xin, X.P.; Yang, G.X.; Wang, X.; Yan, R.R.; Chen, B.R. Effect of vegetation cover on aeolian dust accumulation in a semiarid steppe of northern China. Catena 2011, 87, 351–356. [Google Scholar] [CrossRef]
- Zhao, H.L.; Zhou, R.L.; Drake, S. Effects of aeolian deposition on soil properties and crop growth in sandy soils of northern China. Geoderma 2007, 142, 342–348. [Google Scholar] [CrossRef]
- Zhang, F.F.; Zhang, H.Y.; Huang, T.S. Dynamics on the interaction between vegetation growth and aeolian dust deposition. Adv. Mater. Res. 2012, 356–360, 2430–2433. [Google Scholar] [CrossRef]
- Wang, W.; Lin, Y.; Zhang, L.; Rao, F.; Tan, Y. Complex patterns in a predator–prey model with self and cross-diffusion. Commun. Nonlinear Sci. 2011, 16, 2006–2015. [Google Scholar] [CrossRef]
- Mistro, D.C.; Rodrigues, L.A.D.; Petrovskii, S. Spatiotemporal complexity of biological invasion in a space-and time-discrete predator-prey system with the strong Allee effect. Ecol. Complex. 2012, 9, 16–32. [Google Scholar] [CrossRef]
- Han, Y.T.; Han, B.; Zhang, L.; Xu, L.; Li, M.F.; Zhang, G. Turing instability and wave patterns for a symmetric discrete competitive Lotka-Volterra system. WSEAS Trans. Math. 2011, 10, 181–189. [Google Scholar]
- Punithan, D.; Kim, D.K.; McKay, R.I.B. Spatio-temporal dynamics and quantification of daisy world in two-dimensional coupled map lattices. Ecol. Complex. 2012, 12, 43–57. [Google Scholar] [CrossRef]
- Rodrigues, L.A.D.; Mistro, D.C.; Petrovskii, S. Pattern formation in a space- and time-discrete predator-prey system with a strong Allee effect. Theor. Ecol. 2012, 5, 341–362. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, H.; Yang, H.; Wang, N.; Zhang, F. Complex patterns in a space- and time-discrete predator-prey model with Beddington-DeAngelis functional response. Commun. Nonlinear Sci. Numer. Simul. 2017, 43, 182–199. [Google Scholar] [CrossRef]
- Yuan, S.; Xu, C.; Zhang, T. Spatial dynamics in a predator-prey model with herd behavior. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 033102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.H.; Xing, Y.P.; Zang, H.; Han, M. Spatio-temporal dynamics of a reaction–diffusion system for a predator–prey model with hyperbolic mortality. Nonlinear Dyn. 2014, 78, 265–277. [Google Scholar] [CrossRef]
- Zhang, T.; Zang, H. Delay-induced Turing instability in reaction-diffusion equations. Phys. Rev. E 2014, 90, 052908. [Google Scholar] [CrossRef] [PubMed]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Turing, A. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, G. Nontrivial solutions for a nonlinear discrete elliptic equation with periodic boundary conditions. Appl. Math. Comput. 2009, 210, 321–333. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Zhang, H.; Huang, T.; Meng, T.; Ma, S. Coupled Effects of Turing and Neimark-Sacker Bifurcations on Vegetation Pattern Self-Organization in a Discrete Vegetation-Sand Model. Entropy 2017, 19, 478. https://doi.org/10.3390/e19090478
Zhang F, Zhang H, Huang T, Meng T, Ma S. Coupled Effects of Turing and Neimark-Sacker Bifurcations on Vegetation Pattern Self-Organization in a Discrete Vegetation-Sand Model. Entropy. 2017; 19(9):478. https://doi.org/10.3390/e19090478
Chicago/Turabian StyleZhang, Feifan, Huayong Zhang, Tousheng Huang, Tianxiang Meng, and Shengnan Ma. 2017. "Coupled Effects of Turing and Neimark-Sacker Bifurcations on Vegetation Pattern Self-Organization in a Discrete Vegetation-Sand Model" Entropy 19, no. 9: 478. https://doi.org/10.3390/e19090478
APA StyleZhang, F., Zhang, H., Huang, T., Meng, T., & Ma, S. (2017). Coupled Effects of Turing and Neimark-Sacker Bifurcations on Vegetation Pattern Self-Organization in a Discrete Vegetation-Sand Model. Entropy, 19(9), 478. https://doi.org/10.3390/e19090478





