Twisted Soft Photon Hair Implants on Black Holes
Abstract
:1. Introduction
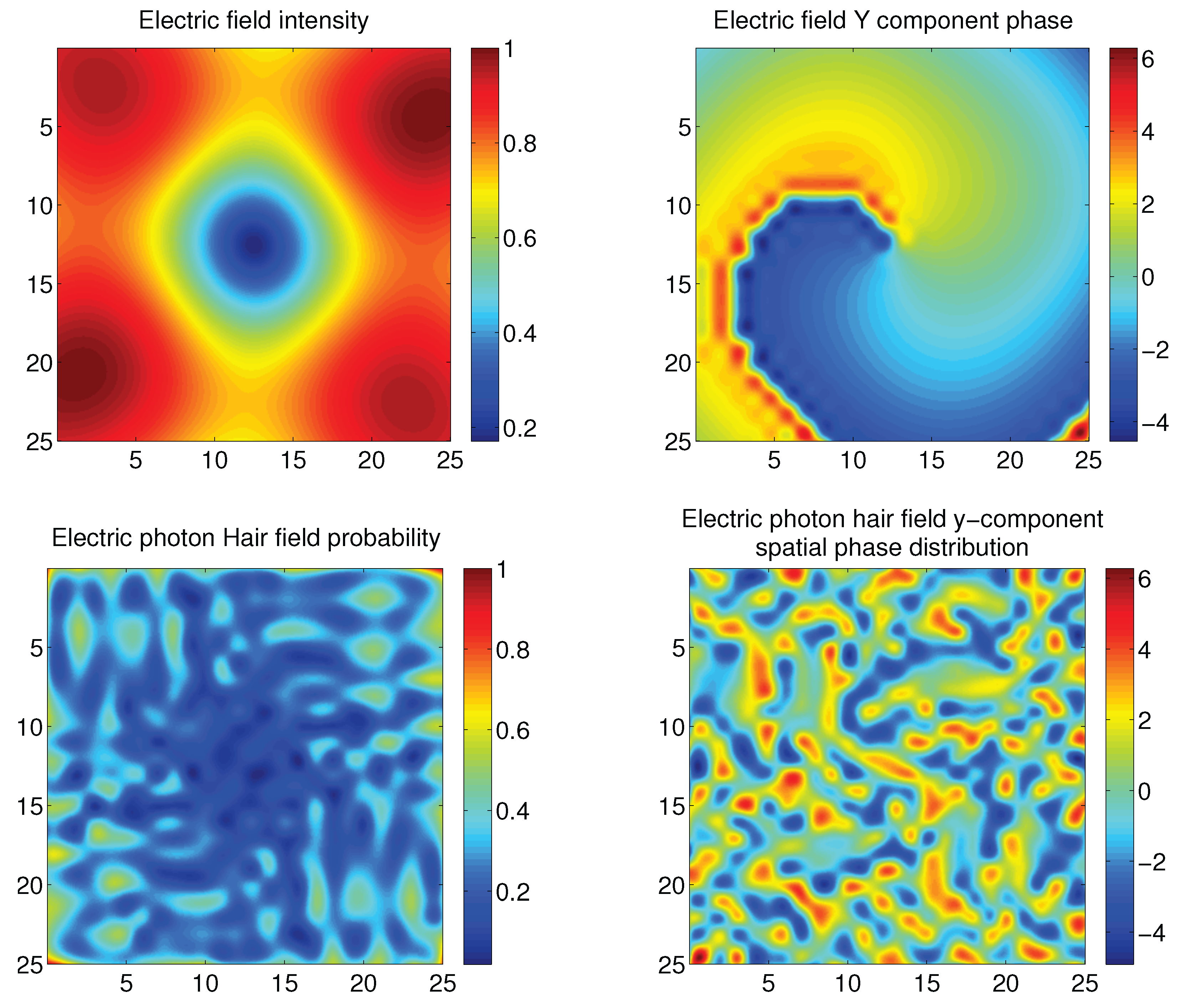
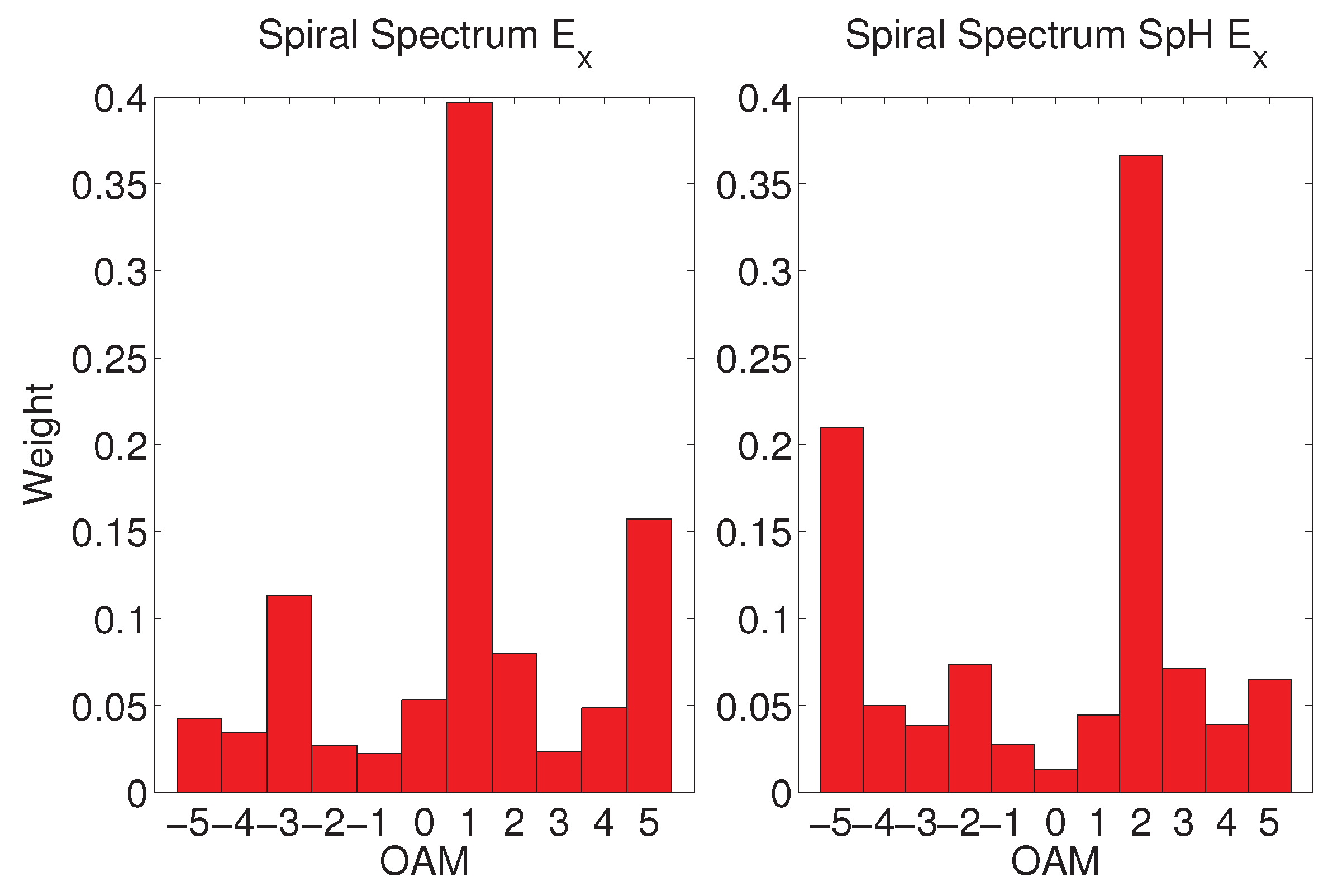
2. Results
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hawking, S.W.; Perry, M.J.; Strominger, A. Soft hair on black holes. Phys. Rev. Lett. 2016, 116, 231301. [Google Scholar] [CrossRef] [PubMed]
- Hawking, S.W. Black hole explosions. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460. [Google Scholar] [CrossRef]
- Page, D. Hawking radiation and black hole thermodynamics. New J. Phys. 2005, 7, 203. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Strominger, A. On BMS invariance of gravitational scattering. J. High Energy Phys. 2014, 2014, 152. [Google Scholar] [CrossRef] [Green Version]
- Mitra, T.; He, P.; Porfyriadis, A.P.; Strominger, A. New symmetries of massless QED. J. High Energy Phys. 2014, 2014, 112. [Google Scholar]
- Bondi, H.; van der Burg, M.G.J.; Metzner, A.W.K. Gravitational waves in general relativity. VII. Waves from axi-symmetric isolated systems. Proc. R. Soc. Lond. A 1962, 269, 21–52. [Google Scholar] [CrossRef]
- Donnay, L.; Giribet, G.; Gonzalez, H.A.; Pino, M. Supertranslations and superrotations at the black hole horizon. Phys. Rev. Lett. 2016, 116, 091101. [Google Scholar] [CrossRef] [PubMed]
- Mirbabayi, M.; Porrati, M. Dressed hard states and black hole soft hair. Phys. Rev. Lett. 2016, 117, 211301. [Google Scholar] [CrossRef] [PubMed]
- Compére, G. Bulk supertranslation memories: A concept reshaping the vacua and black holes of general relativity. Int. J. Mod. Phys. 2016, D25, 1644006. [Google Scholar] [CrossRef]
- Sheikh-Jabbari, M.M. Residual diffeomorphisms and symplectic soft hairs: The need to refine strict statement of equivalence principle. Int. J. Mod. Phys. 2016, 25, 1644019. [Google Scholar] [CrossRef]
- Fushchich, V.I.; Nikitin, A.G. Symmetries of Maxwell’s Equations; D. Reidel Publishing Company: Dordrecht, Holland, 1987. [Google Scholar]
- Thidé, B. Electromagnetic Field Theory, 2nd ed.; Dover Publications, Inc.: Mineola, NY, USA, 2011; in press. [Google Scholar]
- Thidé, B.; Tamburini, F.; Then, H.; Someda, C.G.; Ravanelli, R.A. The physics of angular momentum radio. arXiv, 2014; arXiv:1410.4268. [Google Scholar]
- Hawking, S.W.; Perry, M.J.; Strominger, A. Superrotation charge and supertranslation hair on black holes. High Energy Phys. 2017, 2017, 1–33. [Google Scholar] [CrossRef]
- Andrews, D.L. Structured Light and Its Applications: An Introduction to Phase-Structured Beams and Nanoscale Optical Forces; Academic Press: San Diego, CA, USA, 2011. [Google Scholar]
- Torres, P.; Torner, J.L. (Eds.) Twisted Photons: Applications of Light with Orbital Angular Momentum; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2011. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Leach, J.; Padgett, M.J.; Barnett, S.M.; Franke-Arnold, S.; Courtial, J. Measuring the orbital angular momentum of a single photon. Phys. Rev. Lett. 2002, 88, 257901. [Google Scholar] [CrossRef] [PubMed]
- Calvo, G.F.; Picòn, A.; Bagan, E. Quantum field theory of photons with orbital angular momentum. Phys. Rev. A 2006, 73, 013805. [Google Scholar] [CrossRef]
- Tamburini, F.; Vicino, D. Photon wave function: A covariant formulation and equivalence with QED. Phys. Rev. A, 2008, 78, 052116. [Google Scholar] [CrossRef]
- Speirits, F.C.; Barnett, S.M. Do waves carrying orbital angular momentum possess azimuthal linear momentum? Phys. Rev. Lett. 2013, 111, 103602. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef] [PubMed]
- Tamburini, F.; Mari, E.; Sponselli, A.; Thidé, B.; Bianchini, A.; Romanato, F. Encoding many channels on the same frequency through radio vorticity: first experimental test. New J. Phys. 2012, 14, 033001. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Tamburini, F.; Thidé, B.; Molina-Terriza, G.; Anzolin, G. Twisting of light around rotating black holes. Nat. Phys. 2011, 7, 195–197. [Google Scholar] [CrossRef]
- Soper, D.E. Classical Field Theory; John Wiley & Sons, Inc.: New York, NY, USA, 1976. [Google Scholar]
- Rose, M.E. Elementary Theory of Angular Momentum; Dover Publications, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Molina-Terriza, G. Determination of the total angular momentum of a paraxial beam. Phys. Rev. A 2008, 78, 053819. [Google Scholar] [CrossRef]
- Thidé, B.; Then, H.; Sjöholm, J.; Palmer, K.; Bergman, J.; Carozzi, T.D.; Istomin, Y.N.; Ibragimov, N.H.; Khamitova, R. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 2007, 99, 087701. [Google Scholar] [CrossRef] [PubMed]
- Rindler, W. Essential Relativity; Van Nostrand Reinhold Co.: New York, NY, USA, 1969. [Google Scholar]
- De Almeida, C.; Saa, A. The radiation of a uniformly accelerated charge is beyond the horizon: A simple derivation. Am. J. Phys. 2006, 74, 154–158. [Google Scholar] [CrossRef]
- Burke, G.; Poggio, A. NEC Part I: Program Description—Theory, Technical Report Lawrence Livermore Laboratory. 1981. Available online: http://www.radio-bip.qc.ca/NEC2/nec2prt1.pdf (accessed on 30 August 2017).
- Burke, G.; Poggio, A. NEC Part II: Program Description—Code, Technical Report Lawrence Livermore Laboratory. 1981. Available online: http://www.radio-bip.qc.ca/NEC2/nec2prt2.pdf (accessed on 30 August 2017).
- Burke, G.; Poggio, A. NEC Part I: Program Description—User’s Guide, Technical Report Lawrence Livermore Laboratory. 1992. Available online: http://www.radio-bip.qc.ca/NEC2/nec2prt3.pdf (accessed on 30 August 2017).
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields. In Course of Theoretical Physics; Elsevier: Pergamon, Turkey; Oxford, UK, 1975; Volume 2. [Google Scholar]
- Barcelo, C.; Liberati, S.; Visser, M. Analogue Gravity. Living Rev. Relativ. 2011, 14, 3. [Google Scholar] [CrossRef] [PubMed]
- Torner, L.; Torres, J.; Carrasco, S. Digital spiral imaging. Opt. Express 2005, 13, 873–881. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; 9th printing; Dover: New York, NY, USA, 1972; p. 17. [Google Scholar]
- Arfken, G. Mathematical Methods for Physicists, 3rd ed.; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamburini, F.; Laurentis, M.D.; Licata, I.; Thidé, B. Twisted Soft Photon Hair Implants on Black Holes. Entropy 2017, 19, 458. https://doi.org/10.3390/e19090458
Tamburini F, Laurentis MD, Licata I, Thidé B. Twisted Soft Photon Hair Implants on Black Holes. Entropy. 2017; 19(9):458. https://doi.org/10.3390/e19090458
Chicago/Turabian StyleTamburini, Fabrizio, Mariafelicia De Laurentis, Ignazio Licata, and Bo Thidé. 2017. "Twisted Soft Photon Hair Implants on Black Holes" Entropy 19, no. 9: 458. https://doi.org/10.3390/e19090458
APA StyleTamburini, F., Laurentis, M. D., Licata, I., & Thidé, B. (2017). Twisted Soft Photon Hair Implants on Black Holes. Entropy, 19(9), 458. https://doi.org/10.3390/e19090458






