Exact Negative Solutions for Guyer–Krumhansl Type Equation and the Maximum Principle Violation
Abstract
:1. Introduction
2. Heat Conduction Operator
3. Exact Operational Solution for Guyer–Krumhansl Equation
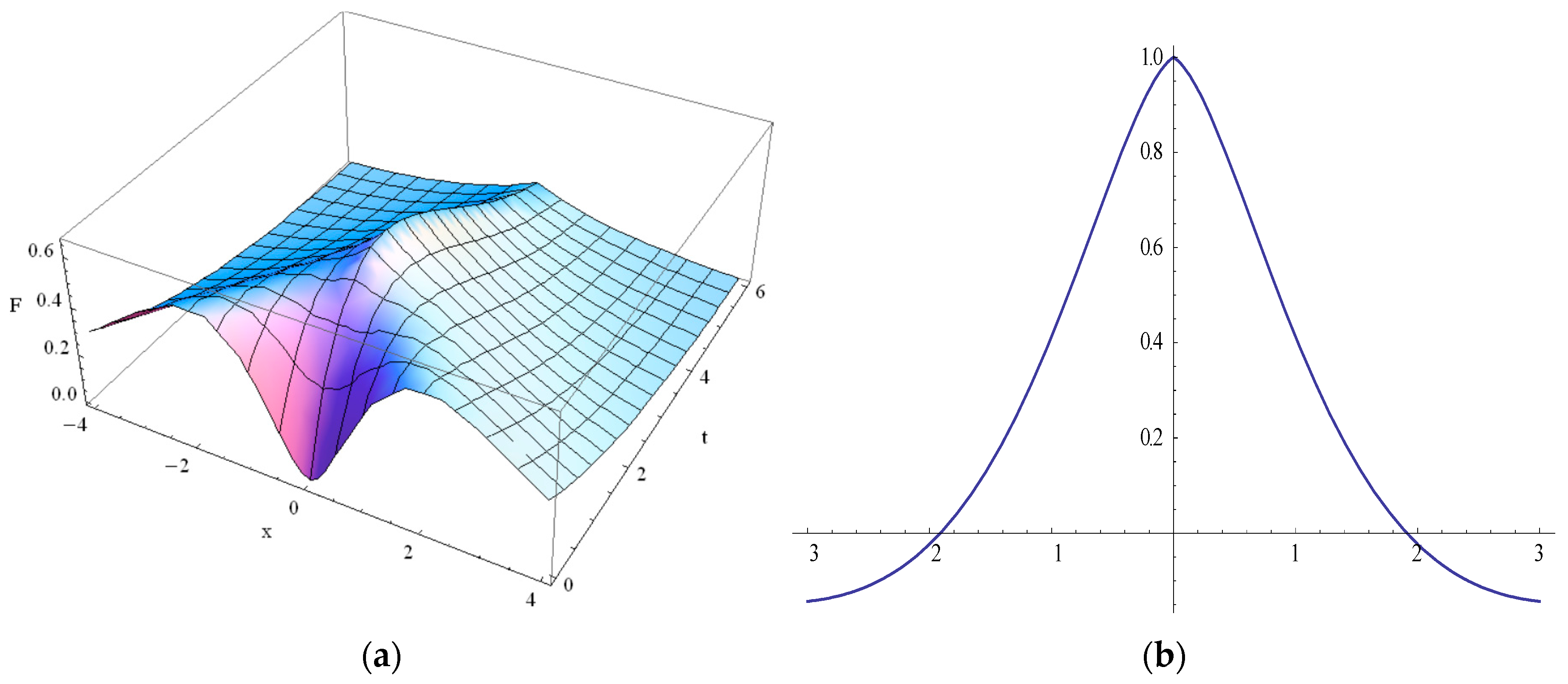
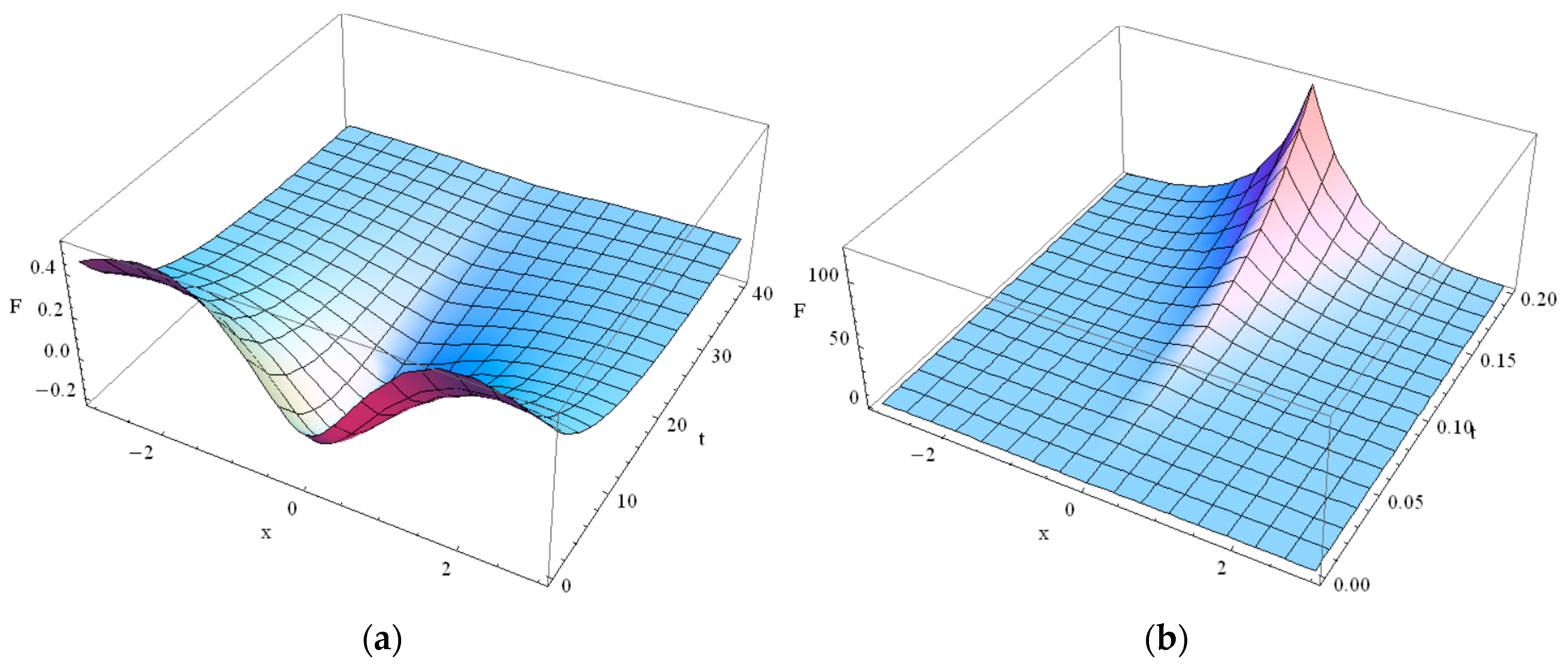
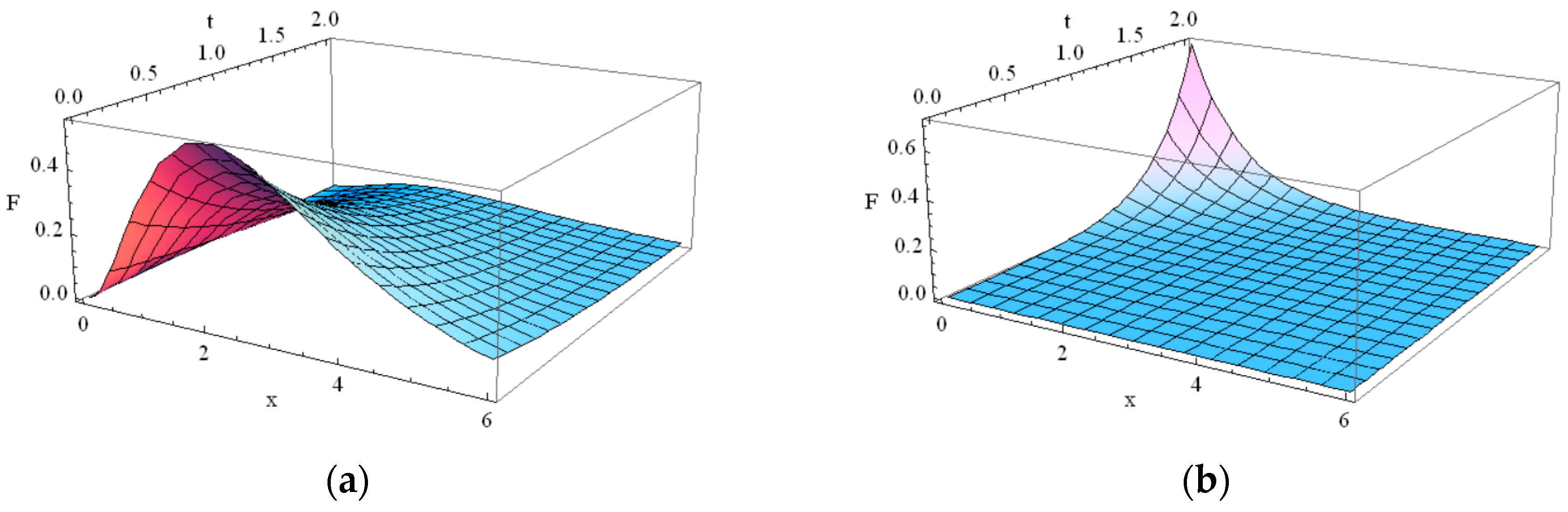
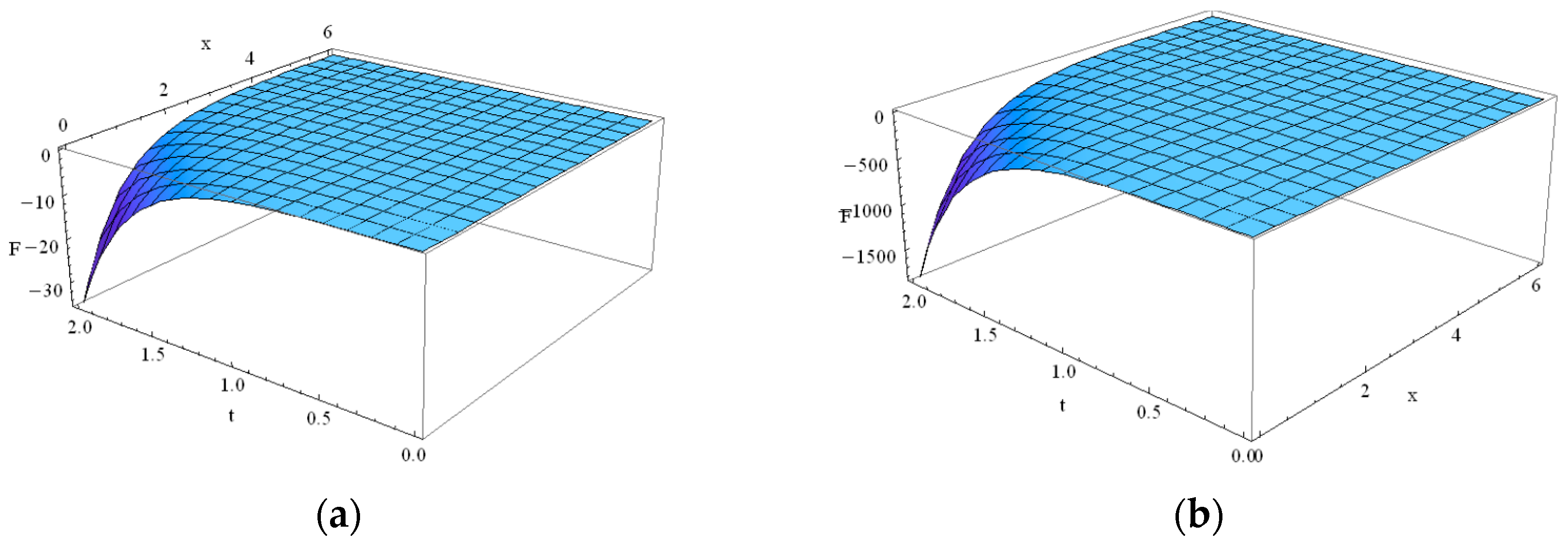
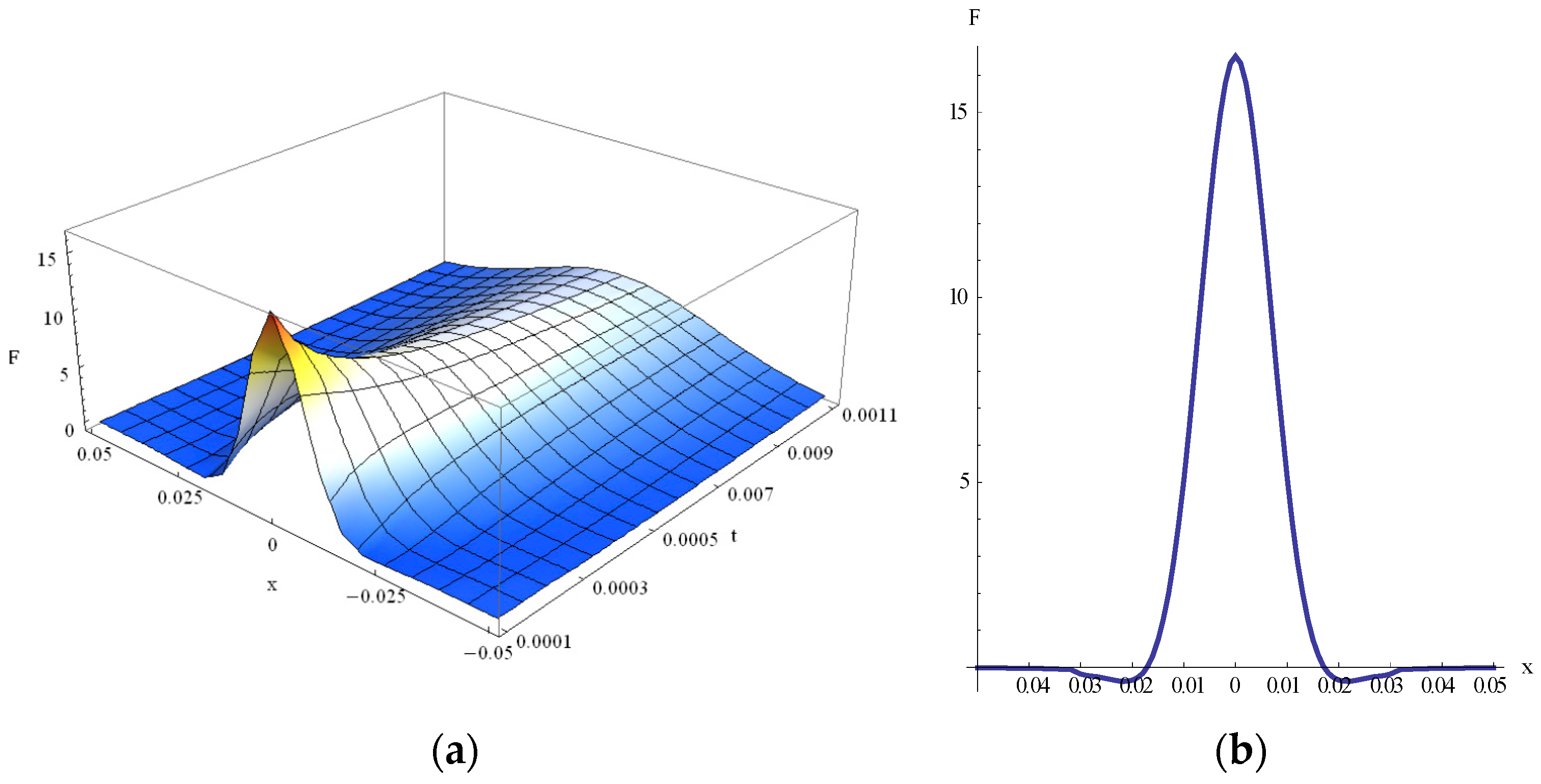
4. Violation of Maximum Principle and Negative Solutions in GK Equation
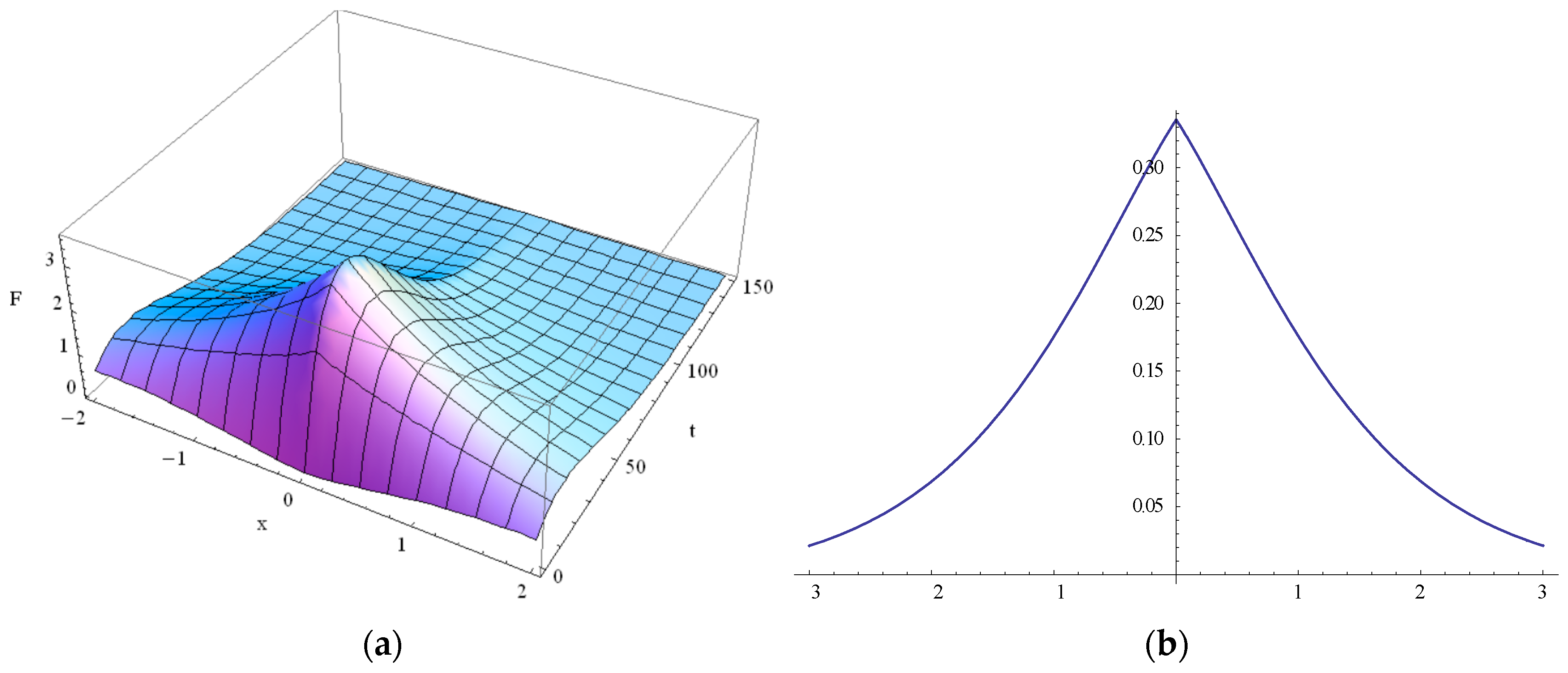
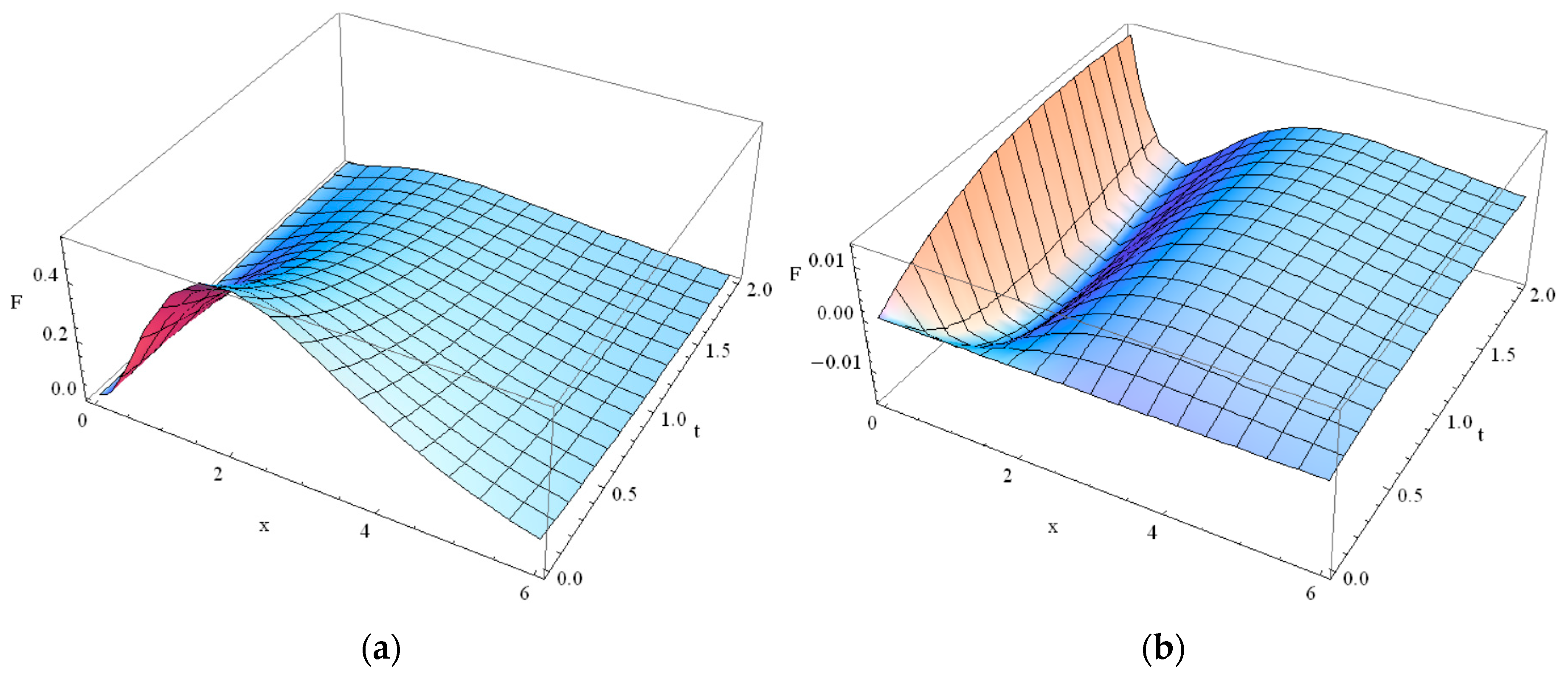
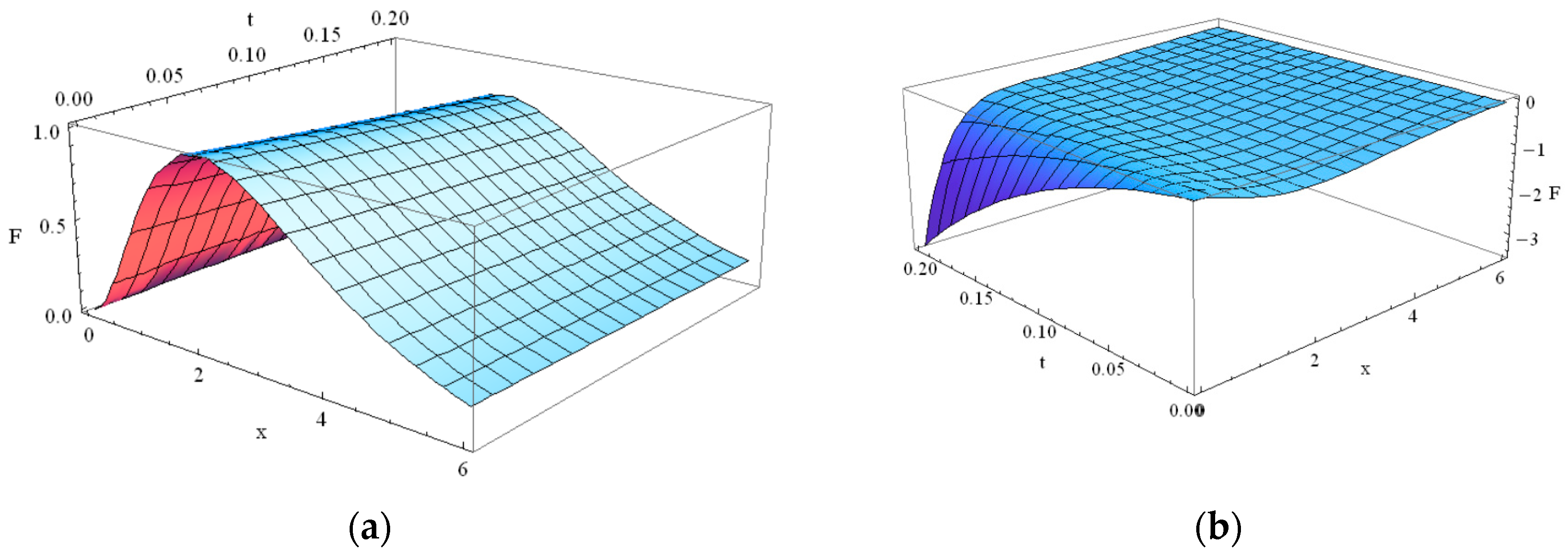
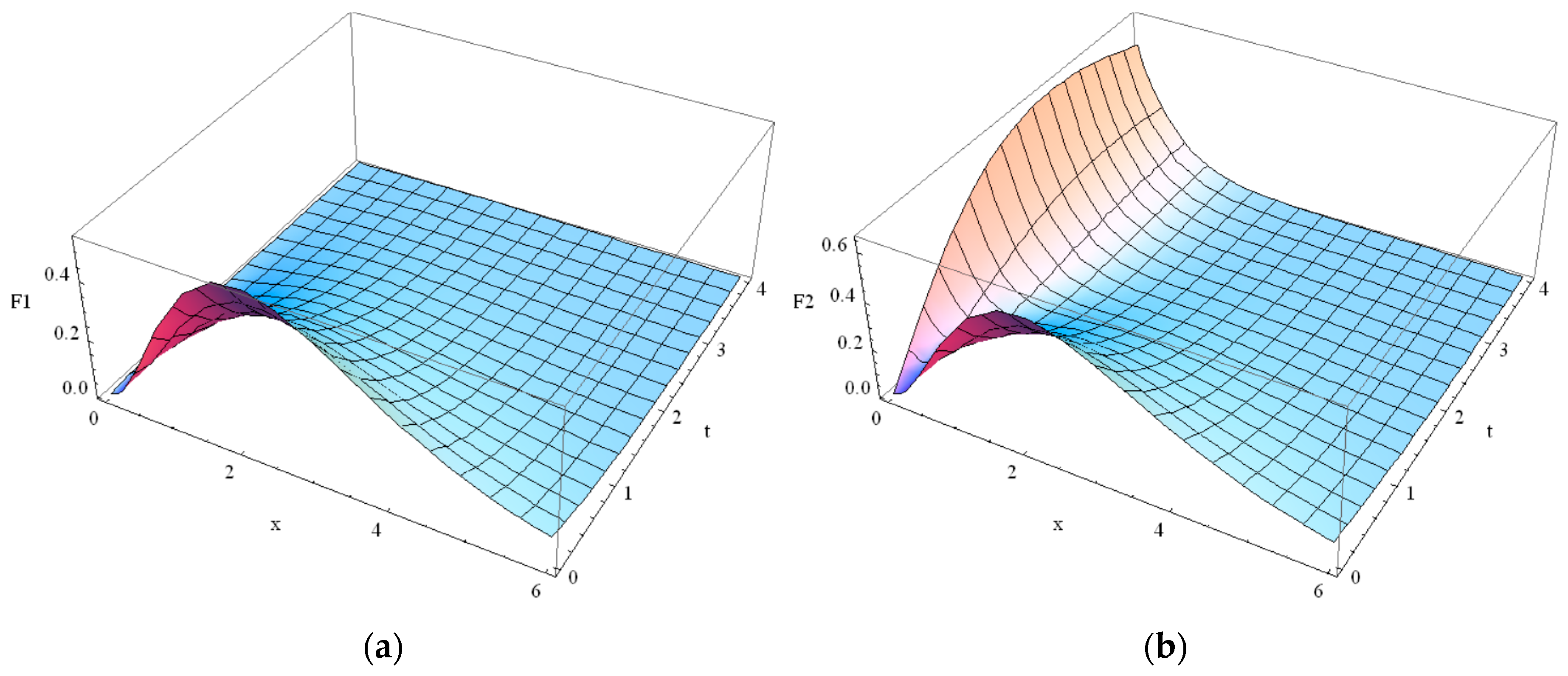
5. Solution for Guyer–Krumhansl Temperature Distribution in Thin Films
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Fourier, J. The Analytical Theory of Heat; Cambridge University Press: London, UK, 1878. [Google Scholar]
- Onsager, L. Reciprocal Relations in irreversible processes. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
- Peshkov, V. Helium 4: The Commonwealth and International Library: Selected Readings in Physics; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Ackerman, C.C.; Guyer, R.A. Temperature pulses in dielectric solids. Ann. Phys. 1968, 50, 128–185. [Google Scholar] [CrossRef]
- Ackerman, C.C.; Overton, W.C. Second sound in solid helium-3. Phys. Rev. Lett. 1969, 22, 764. [Google Scholar] [CrossRef]
- McNelly, T.F.; Rogers, S.J.; Channin, D.J.; Rollefson, R.; Goubau, W.M.; Schmidt, G.E.; Krumhansl, J.A.; Pohl, R.O. Heat pulses in NaF: Onset of second sound. Phys. Rev. Lett. 1970, 24, 100. [Google Scholar] [CrossRef]
- Narayanamurti, V.; Dynes, R.D. Observation of second sound in Bismuth. Phys. Rev. Lett. 1972, 26, 1461–1465. [Google Scholar] [CrossRef]
- Cattaneo, C. Sur une forme de l’équation de la chaleur éliminant le paradoxe d’une propagation instantanée. Compt. Rendu. 1958, 247, 431–433. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Bright, T.J.; Zhang, Z.M. Common misperceptions of the hyperbolic heat equation. J. Thermophys. Heat Transf. 2009, 23, 601–607. [Google Scholar] [CrossRef]
- Shiomi, J.; Maruyama, S. Non-Fourier heat conduction in a single-walled carbon nanotube: Classical molecular dynamics simulations. Phys. Rev. B 2006, 73, 205420. [Google Scholar] [CrossRef]
- Bai, C.; Lavine, A.S. On hyperbolic heat conduction and the second law of thermodynamics. J. Heat Transf. 1995, 117, 256–263. [Google Scholar] [CrossRef]
- Porrà, J.M.; Masoliver, J.; Weiss, G.H. When the telegrapher’s Equation furnishes a better approximation to the transport Equation than the diffusion approximation. Phys. Rev. E 1997, 55, 7771–7774. [Google Scholar] [CrossRef]
- Körner, C.; Bergmann, H.W. The physical defects of the hyperbolic heat conduction equation. Appl. Phys. A 1998, 67, 397–401. [Google Scholar] [CrossRef]
- Guyer, R.A.; Krumhansl, J.A. Thermal conductivity, second sound and phonon hydrodynamic phenomena in non-metallic crystals. Phys. Rev. 1966, 148, 778–788. [Google Scholar] [CrossRef]
- Guyer, R.A.; Krumhansl, J.A. Solution of the linearized phonon Boltzmann equation. Phys. Rev. 1966, 148, 766–778. [Google Scholar] [CrossRef]
- Lebon, G.; Machrafi, H.; Gremela, M.; Dubois, C. An extended thermodynamic model of transient heat conduction at sub-continuum scales. Proc. R. Soc. A 2011, 467, 3241–3256. [Google Scholar] [CrossRef]
- Minnich, J.; Johnson, J.A.; Schmidt, A.J.; Esfarjani, K.; Dresselhaus, M.S.; Nelson, K.A.; Chen, G. Thermal conductivity spectroscopy technique to measure phonon mean free paths. Phys. Rev. Lett. 2011, 107, 095901. [Google Scholar] [CrossRef] [PubMed]
- Casimir, H.B.G. Note on the Conduction of Heat in Crystals. Physica 1938, 5, 495–500. [Google Scholar] [CrossRef]
- Baringhaus, J.; Ruan, M.; Edler, F.; Tejeda, A.; Sicot, M.; Ibrahimi, A.T.; Jiang, Z.; Conrad, E.; Berger, C.; Tegenkamp, C.; et al. Exceptional ballistic transport in epitaxial graphene nanoribbons. Nature 2014, 506, 349–354. [Google Scholar] [CrossRef] [PubMed]
- Hochbaum, A.I.; Chen, R.; Delgado, R.D.; Liang, W.; Garnett, E.C.; Najarian, M.; Majumdar, A.; Yang, P. Enhanced thermoelectric performance of rough silicon nanowires. Nature 2008, 451, 163–167. [Google Scholar] [CrossRef] [PubMed]
- Boukai, A.I.; Bunimovich, Y.; Tahir-Kheli, J.; Yu, J.-K.; Goddard, W.A.; Heath, J.R. Silicon nanowires as efficient thermoelectric materials. Nature 2008, 451, 168. [Google Scholar] [CrossRef] [PubMed]
- Paddock, C.A.; Eesley, G.L. Transient thermoreflectance from thin metal films. J. Appl. Phys. 1986, 60, 285. [Google Scholar] [CrossRef]
- Maldovan, M. Transition between ballistic and diffusive heat transport regimes in silicon materials. Appl. Phys. Lett. 2012, 101, 113110. [Google Scholar] [CrossRef]
- Cahill, D.G. Thermal conductivity measurement from 30 to 750 K: The 3ω method. Rev. Sci. Instrum. 1990, 61, 802–808. [Google Scholar] [CrossRef]
- Van, P.; Berezovski, A.; Fulop, T.; Grof, G.; Kovacs, R.; Lovas, A.; Verhas, J. Guyer-Krumhansl-type heat conduction at room temperature. arXiv, 2017; arXiv:arXiv:1704.00341. [Google Scholar]
- Tang, D.W.; Araki, N. Non-Fourier heat conduction behaviour in finite mediums under pulse surface heating. Mater. Sci. Eng. 2000, 292, 173–178. [Google Scholar] [CrossRef]
- Kaminski, W. Hyperbolic heat conduction Equations for materials with a nonhomogeneous inner structure. J. Heat Transf. 1990, 112, 555–560. [Google Scholar] [CrossRef]
- Mitra, K.; Kumar, S.; Vedavarz, A.; Moallemi, M.K. Experimental evidence of hyperbolic heat conduction in processed meat. J. Heat Transf. 1995, 117, 568–573. [Google Scholar] [CrossRef]
- Herwig, H.; Beckert, K. Fourier versus non-Fourier heat conduction in materials with a nonhomogeneous inner structure. J. Heat Transf. 2000, 122, 363–365. [Google Scholar] [CrossRef]
- Roetzel, W.; Putra, N.; Das, S.K. Experiment and analysis for non-Fourier conduction in materials with non-homogeneous inner structure. Int. J. Therm. Sci. 2003, 42, 541–552. [Google Scholar] [CrossRef]
- Scott, E.P.; Tilahun, M.; Vick, B. The question of thermal waves in heterogeneous and biological materials. J. Biomech. Eng. 2009, 131, 074518. [Google Scholar] [CrossRef] [PubMed]
- Chen, G. Ballistic-Diffusive Heat-Conduction equations. Phys. Rev. Lett. 2001, 86, 2297–2300. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, T.; Chang, H.; Liou, S.; Chu, M.; Lee, S.; Chang, C. Observation of room-temperature ballistic thermal conduction persisting over 8.3 mm in SiGe nanowires. Nat. Nanotechnol. 2013, 8, 534–538. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ye, W. Modified ballistic–diffusive equations for transient non-continuum heat conduction. Int. J. Heat Mass Transf. 2015, 83, 51–63. [Google Scholar] [CrossRef]
- Kovacs, R.; Van, P. Generalized heat conduction in heat pulse experiments. Int. J. Heat Mass Transf. 2015, 83, 613–620. [Google Scholar] [CrossRef]
- Van, P.; Fulop, T. Universality in heat conduction theory: Weakly non-local thermodynamics. Ann. Phys. 2012, 524, 470–478. [Google Scholar] [CrossRef]
- Dattoli, G.; Srivastava, H.M.; Zhukovsky, K.V. Operational methods and Differential equations with Applications to Initial-Value problems. Appl. Math. Comput. 2007, 184, 979–1001. [Google Scholar] [CrossRef]
- Zhukovsky, K. Solution of Some Types of Differential equations: Operational Calculus and Inverse Differential Operators. Sci. World J. 2014, 2014, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zhukovsky, K.V. A method of inverse differential operators using ortogonal polynomials and special functions for solving some types of differential equations and physical problems. Mosc. Univ. Phys. Bull. 2015, 70, 93–100. [Google Scholar] [CrossRef]
- Dattoli, G.; Srivastava, H.M.; Zhukovsky, K. A new family of integral transforms and their applications. Integral Transform. Spec. Funct. 2006, 17, 31–37. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Manocha, H.L. A Treatise on Generating Functions; John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
- Sokolov, A.A.; Ternov, I.M.; Zhukovsky, V.C.; Borisov, A.V. Gauge Fields (Kalibrovochnye Polya); Moscow State University: Moscow, Russia, 1986; p. 264. (In Russian) [Google Scholar]
- Zhukovsky, K.V. Operational solution for some types of second order differential equations and for relevant physical problems. J. Math. Anal. Appl. 2017, 446, 628–647. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Operational method of solution of linear non-integer ordinary and partial differential equations. Springer Plus 2016, 5, 119. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, H.M.; Zhukovsky, K.V. Solutions of some types of differential equations and of their associated physical problems by means of inverse differential operators. In Mathematical Analysis, Approximation Theory and Their Applications; Springer Optimization and Its Applications Series; Rassias, H.M., Gupta, V., Eds.; Springer International Publishing: Cham, Switzerland, 2016; Volume 111, pp. 573–629. [Google Scholar]
- Zhukovsky, K.V. Operational solution of differential equations with derivatives of non-integer order, Black–Scholes type and heat conduction. Mosc. Univ. Phys. Bull. 2016, 71, 3237–3244. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Solving evolutionary-type differential equations and physical problems using the operator method. Theor. Math. Phys. 2017, 190, 52–68. [Google Scholar] [CrossRef]
- De Jagher, P.C. A hyperbolic “diffusion equation” taking a finite collision frequency into account. Physica A 1980, 101, 629–633. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Exact solution of Guyer-Krumhansl type heat Equation by operational method. Int. J. Heat Mass Transf. 2016, 96, 132–144. [Google Scholar] [CrossRef]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbott, G.L. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. J. Appl. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
- Zhukovsky, K.V.; Srivastava, H.M. Analytical solutions for heat diffusion beyond Fourier law. Appl. Math. Comput. 2017, 293, 423–437. [Google Scholar] [CrossRef]
- Zhukovsky, K. Operational approach and solutions of hyperbolic heat conduction equations. Axioms 2016, 5, 28. [Google Scholar] [CrossRef]
- Dattoli, G.; Górska, K.; Horzela, A.; Penson, K.A.; Sabia, E. Theory of relativistic heat polynomials and one-sided Lévy distributions. J. Math. Phys. 2017, 58, 063510. [Google Scholar] [CrossRef]
- Dattoli, G.; Srivastava, H.M.; Zhukovsky, K. Оrthogonality properties of the Hermite and related polynomials. J. Comput. Appl. Math. 2005, 182, 165–172. [Google Scholar] [CrossRef]
- Gould, H.W.; Hopper, A.T. Operational formulas connected with two generalizations of Hermite polynomials. Duke Math. J. 1962, 29, 51–63. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Violation of the maximum principle and negative solutions with pulse propagation in Guyer–Krumhansl model. Int. J. Heat Mass Transf. 2016, 98, 523–529. [Google Scholar] [CrossRef]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhukovsky, K. Exact Negative Solutions for Guyer–Krumhansl Type Equation and the Maximum Principle Violation. Entropy 2017, 19, 440. https://doi.org/10.3390/e19090440
Zhukovsky K. Exact Negative Solutions for Guyer–Krumhansl Type Equation and the Maximum Principle Violation. Entropy. 2017; 19(9):440. https://doi.org/10.3390/e19090440
Chicago/Turabian StyleZhukovsky, Konstantin. 2017. "Exact Negative Solutions for Guyer–Krumhansl Type Equation and the Maximum Principle Violation" Entropy 19, no. 9: 440. https://doi.org/10.3390/e19090440
APA StyleZhukovsky, K. (2017). Exact Negative Solutions for Guyer–Krumhansl Type Equation and the Maximum Principle Violation. Entropy, 19(9), 440. https://doi.org/10.3390/e19090440



