Entropy Generation Analysis of Wildfire Propagation
Abstract
1. Introduction
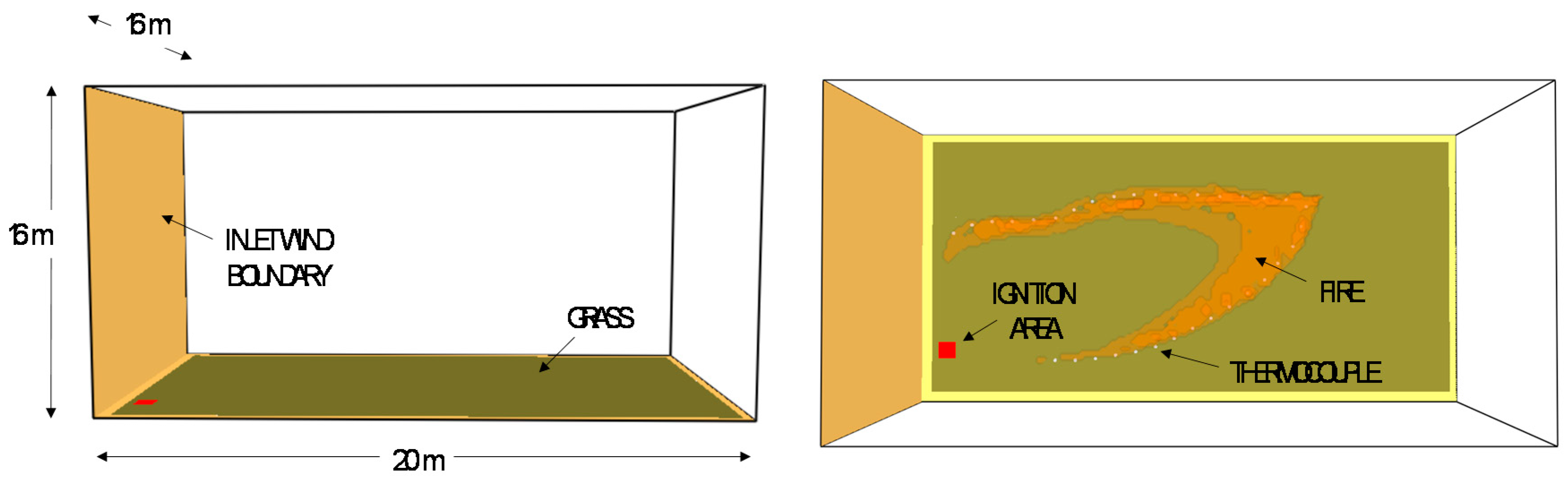
2. System Description
- height: 0.2 m (low/medium height)
- heat of combustion: 18,500 kJ/kg (typical value as indicated in [30])
- moisture content: 4% (very dry fuel)
- fuel load: 0.5 kg/m2 (medium/high load)
- char fraction: 10% (typical value)
- density of the vegetative fuel: 512 kg/m3 (typical value as indicated in [25])
- surface over volume ratio is 4950 m−1 (typical value for herbaceous fuel [31])
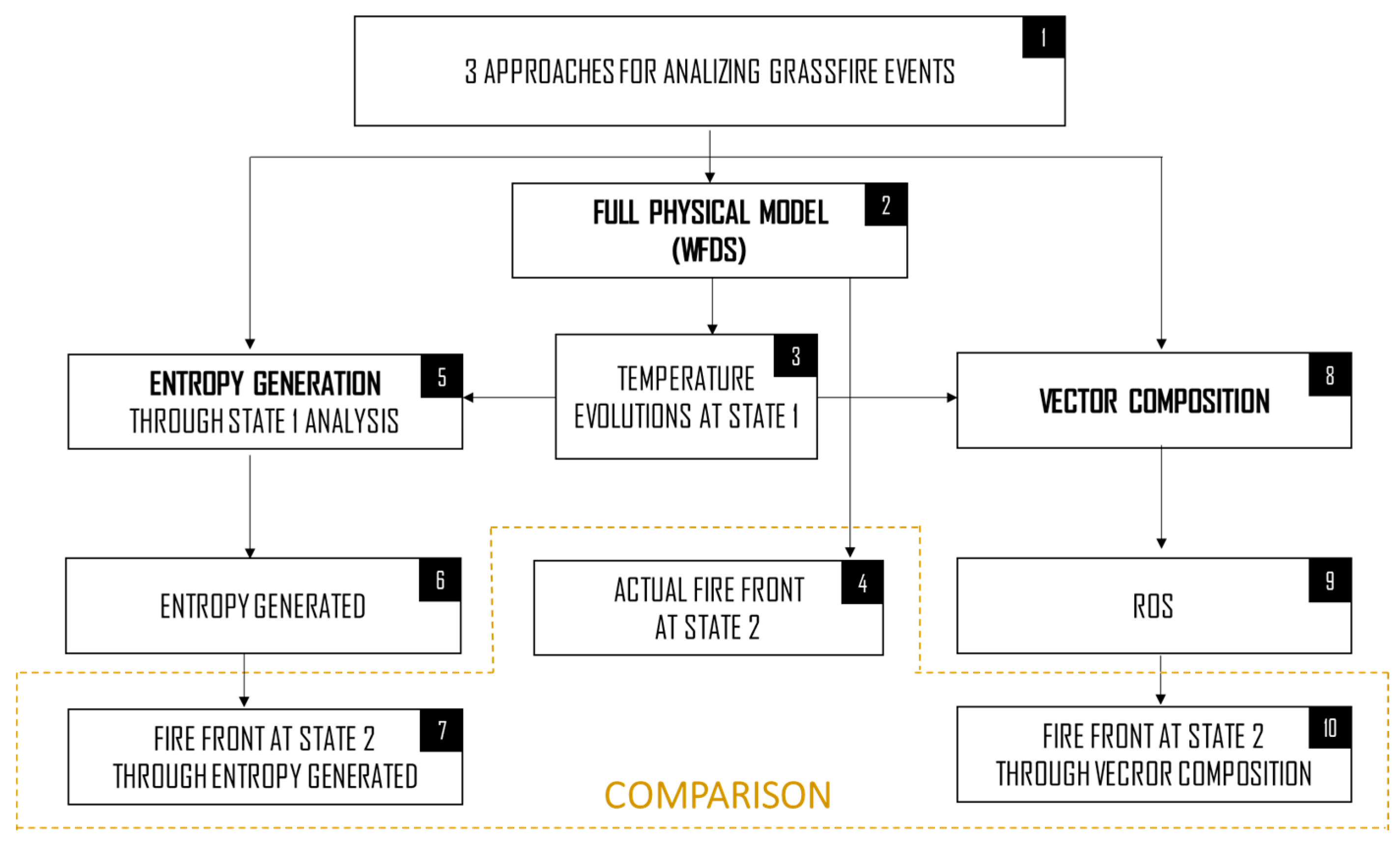
3. Method
- (a)
- 3D full physical model (block 2). This plays the role of a field experiment;
- (b)
- entropy generation analysis (block 5). This is the proposed approach;
- (c)
- 1D model with a vector composition approach (block 8). This is the reference for comparing the proposed approach to, as it is a commonly adopted prediction method.
- collect temperature evolutions and the other data which are needed for calculating the various terms of entropy generation and setting the coefficients for the vector composition analysis (block 3);
- generate the reference terms (the fire propagation velocity) for comparing the results obtained through the compact models, i.e., the entropy generation approach and the vector composition approach (block 4).
- STATE 1: the fire front after 185 s, i.e., when the fire front is fully developed, is used for gathering data for entropy generation analysis and the vector composition analysis.
- STATE 2: the fire front after 230 s is used for comparing the results obtained through the three approaches.
3.1. Entropy Generation Analysis of a Grassland Fire Event
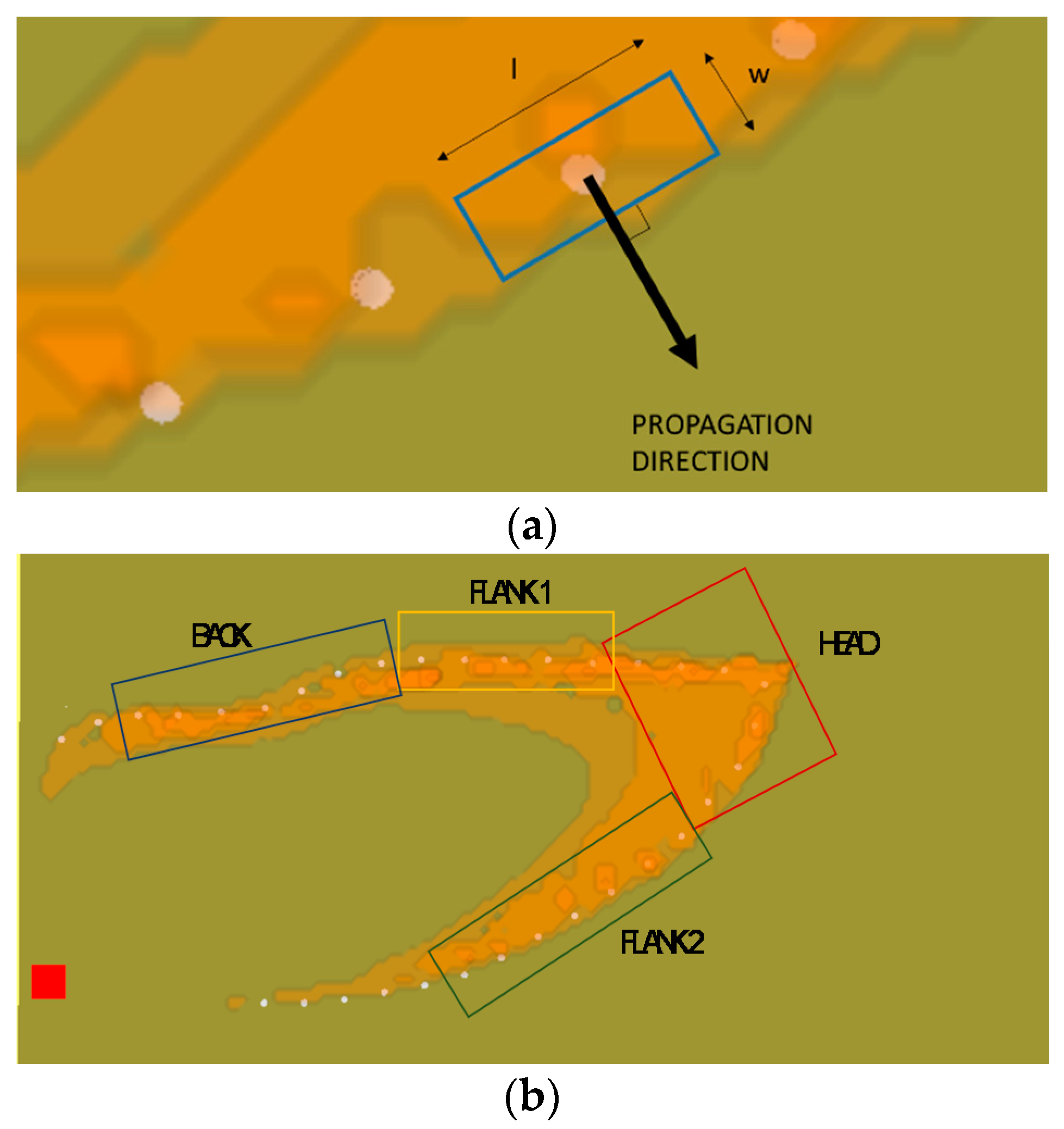
- It is oriented with two faces parallel to the fire front.
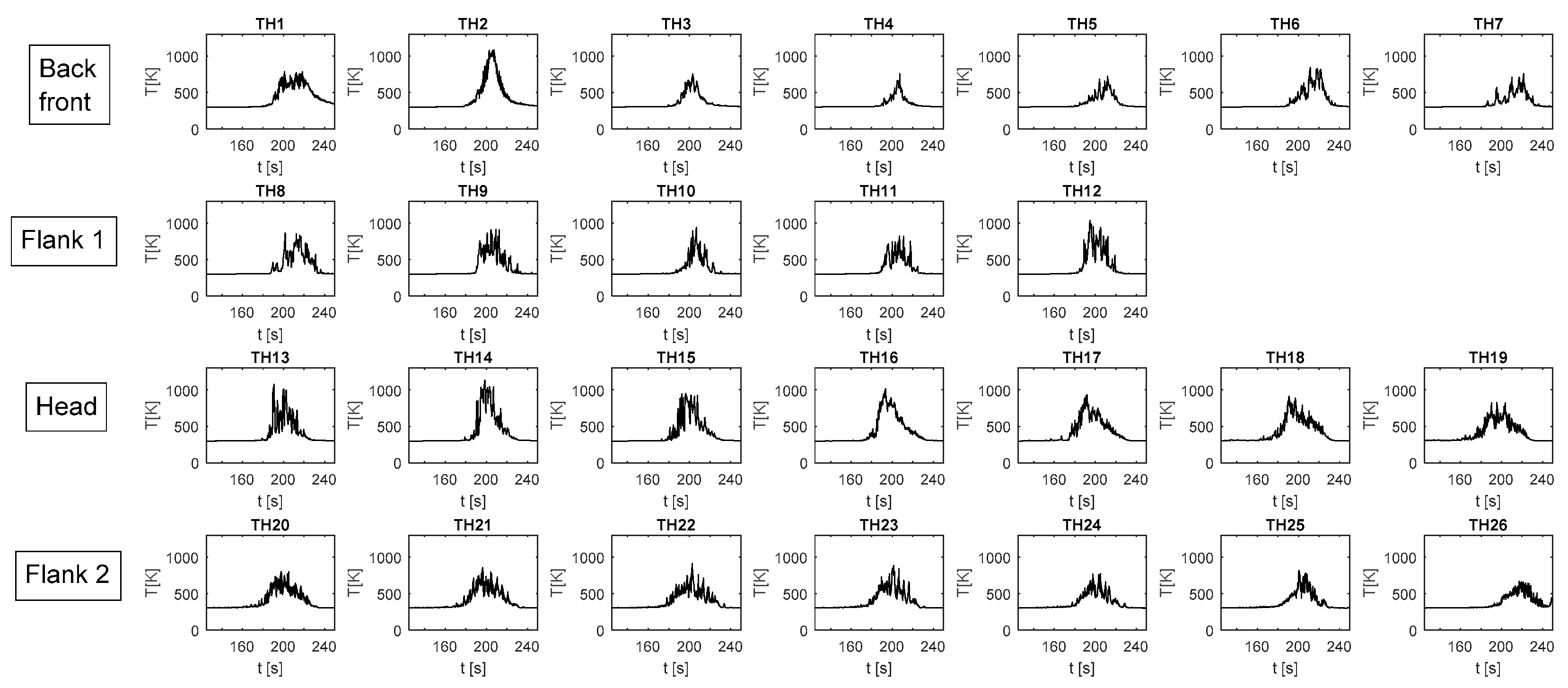
- In each volume, a fictitious thermocouple is installed. This allows the detection of the temperature during propagation, providing information in the same way that would be available from an experimental campaign. The thermocouple sampling time, dtTH, is 0.25 s.
- The length l is selected as the space the front travels in a time equal to dtTH.
- Each control volume exchanges mass and energy with the surrounding through five control surfaces: two lateral surfaces, two frontal surfaces and the top surface. The latter is considered only for balancing the mass transport through a contribution which is always exiting the volume.
- Head, where wind and slope influence are high and the fire front propagates faster;
- Flanks (in particular Flank 1 and Flank 2), which are the sectors where the wind and slope contributions are smaller than at head;
- Back, which is the sector where the influence of wind and slope is negligible and the fire front proceeds slowly.
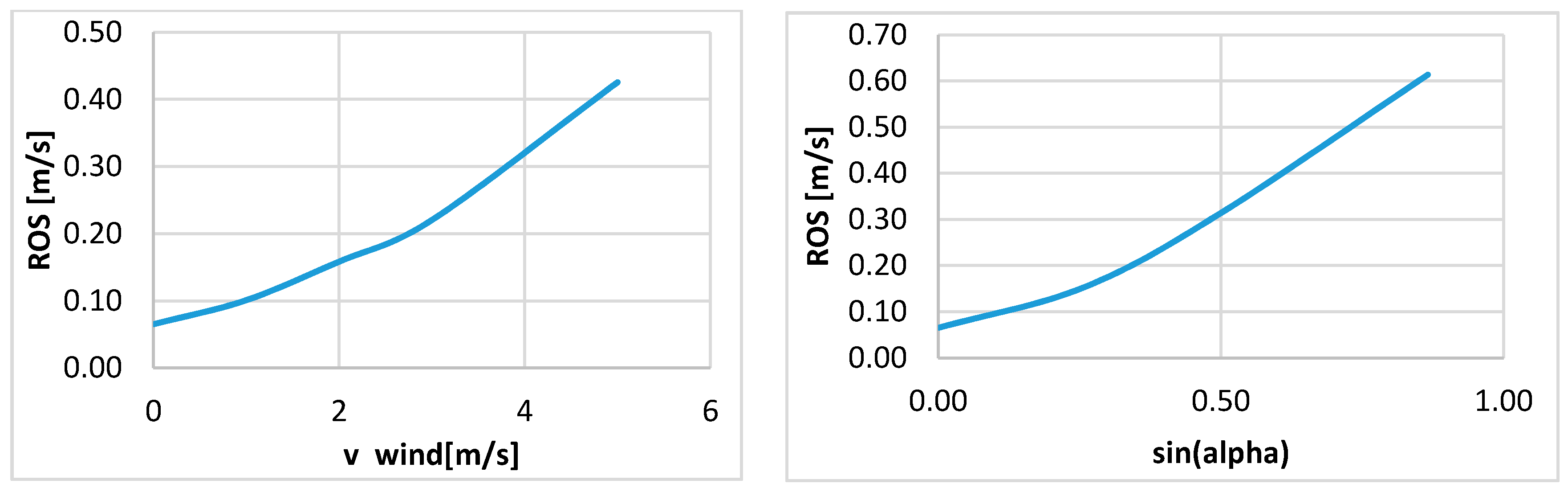
- no-slope condition and wind velocity equal to
- no-wind condition and slope equal to
- An upwind scheme is considered. This implies that the temperature at the boundaries are assumed as the temperature in the upstream control volume.
- Travelling wave assumption for the fire front, considering that an idle condition has been reached. Such assumption is acceptable in the case of fully developed fire in a sufficiently homogeneous fuel. Temperature evolution in a cell is the same recorded at the previous cell, just shifted ahead in time of the period spent by the front to travel the distance between two points. The same assumption is made for the following cell, shifting the time back.
3.2. WFDS
3.3. Vector Composition Propagation
3.4. Fire Evolution Comparison
4. Results
4.1. Pre-Processing Results
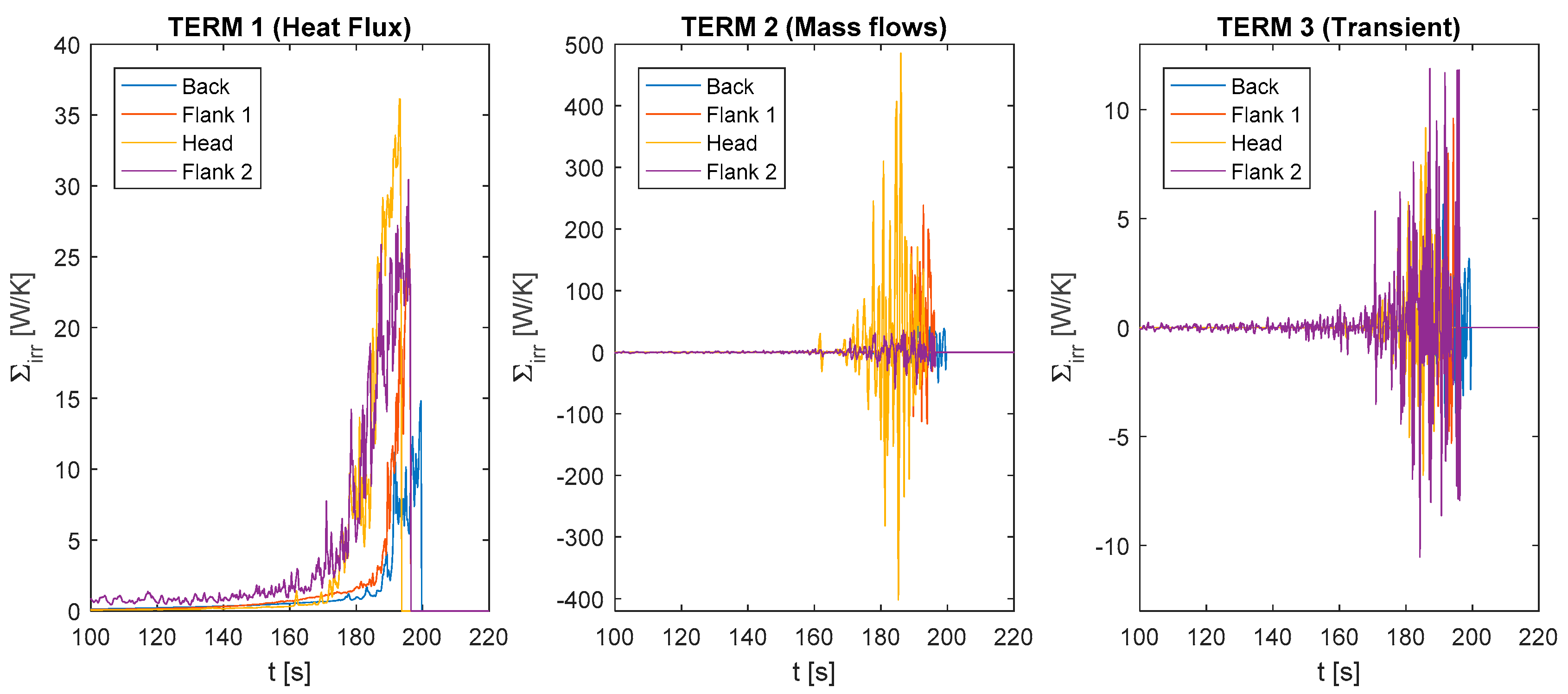
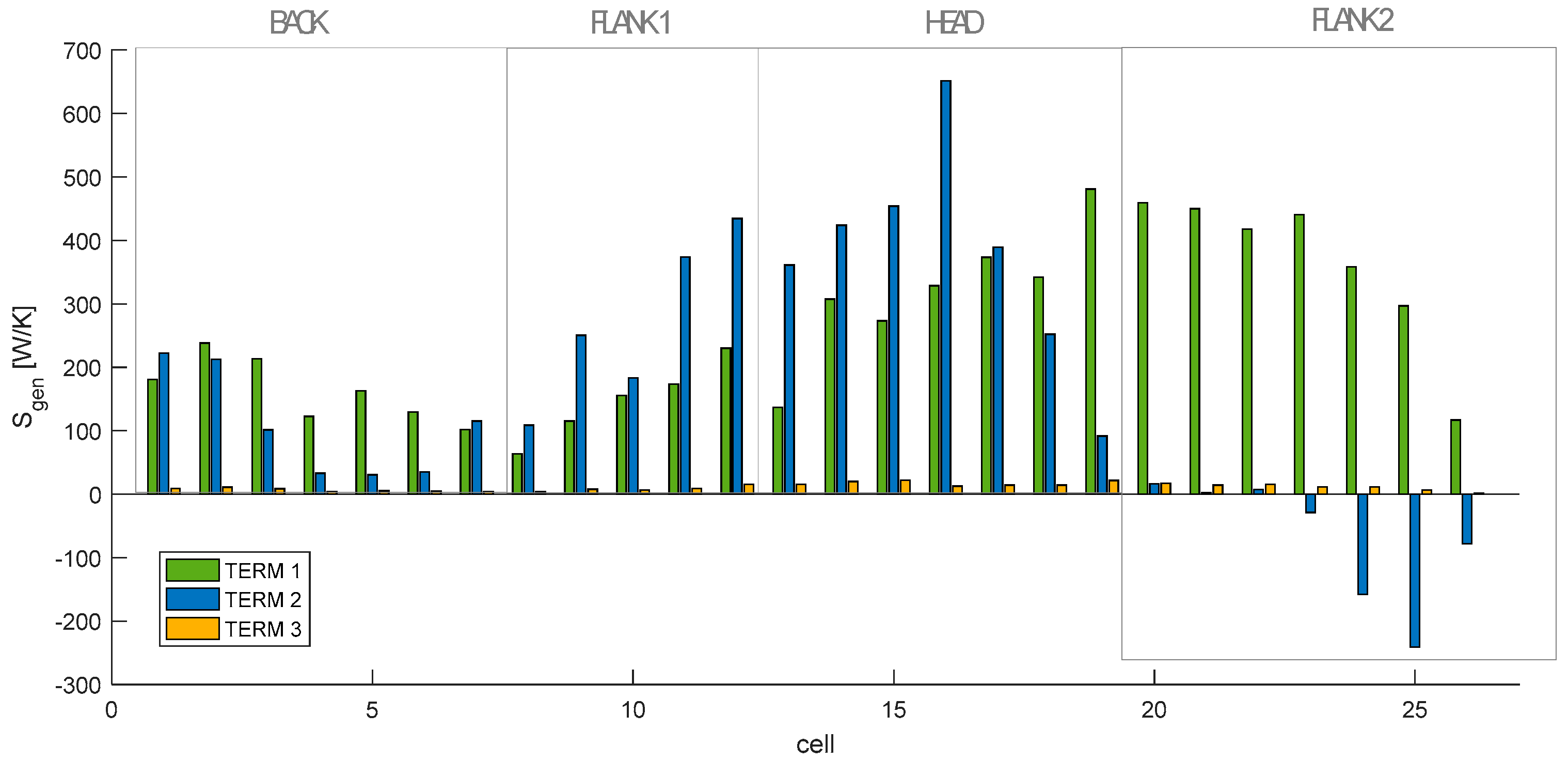
4.2. Main Entropy Generation Results
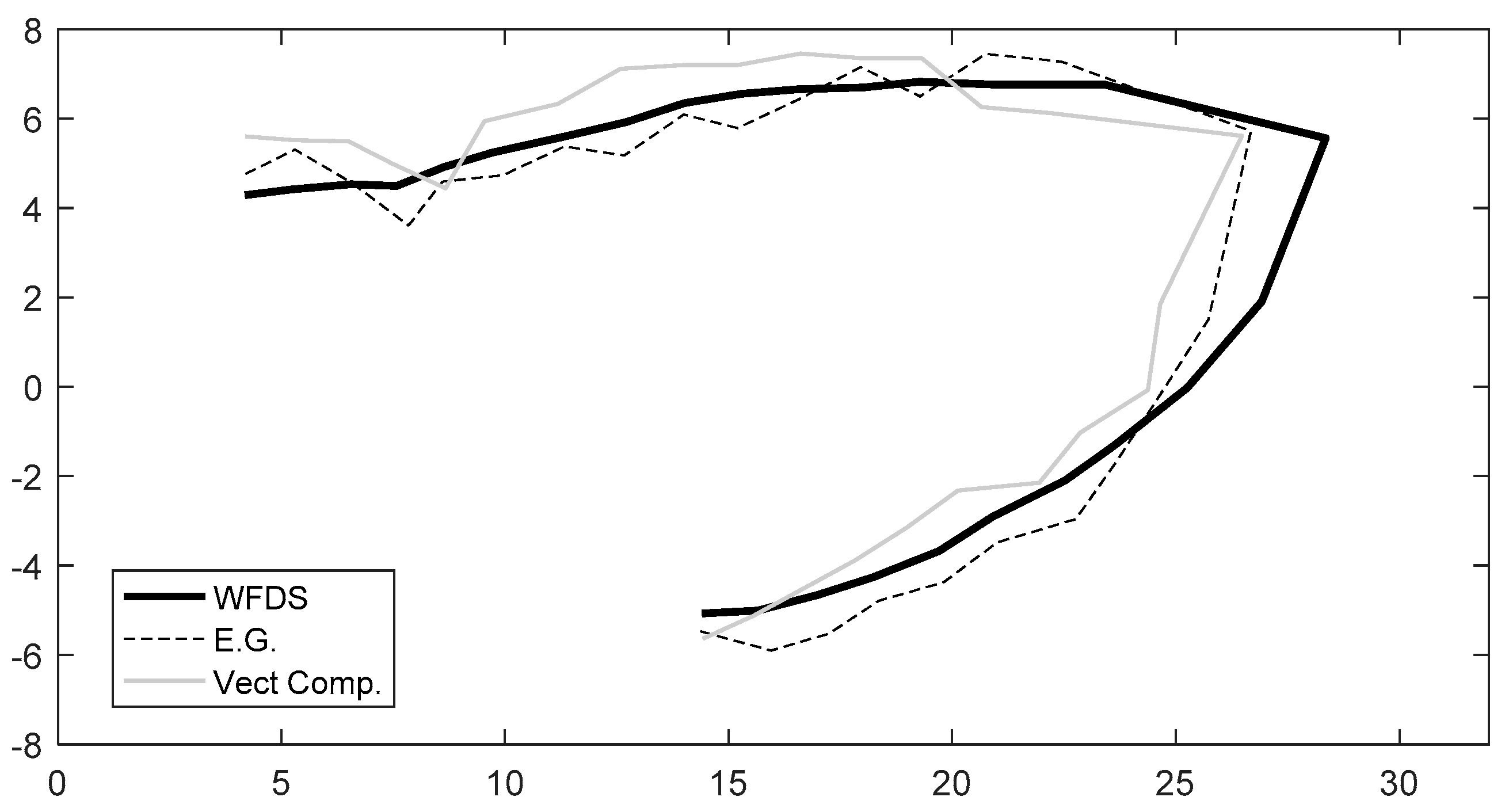
4.3. Propagation Prediction Comparison
4.4. Discussion
- (1)
- The fire propagation is considered as a travelling wave. This is a limitation in the case of significantly non homogenous fuels.
- (2)
- Each cell is described though the mean values of the thermodynamic quantities. This makes the results dependent on the size of the control volume. In particular, this is crucial when the tip of the fire front is examined.
5. Conclusions
- (a)
- A 3D model able to accurately predict the fire evolution. This model is used to provide the necessary data for tuning the parameters of other approaches. In addition, it provides the reference fire front propagation to be used as a term of comparison for the other approaches.
- (b)
- An entropy generation approach, which provides the entropy generated in all the control volumes along the propagating fire front.
- (c)
- A 1D model using, as the convective velocity, the vector resulting from the summation of the wind and slope contributions.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | area (m2) |
| c | specific heat (J∙kg−1∙K−1) |
| F | view factor |
| G | mass flow rate (kg∙s−1) |
| g | heat generation contribution (W∙m−3) |
| d | fuel height (m) |
| h | convective transfer coefficient, (W∙m−2∙K−1) |
| k | equivalent slope velocity coefficient (m) |
| l | length (m) |
| m | mass (kg) |
| N | number of cells |
| R | radiative heat exchange coefficient |
| r | equivalent propagation term |
| t | time (s) |
| T | temperature (°C) |
| s | specific entropy (J∙kg−1∙K−1) |
| S | entropy (W∙K−1) |
| u | equivalent slope velocity (m) |
| v | wind velocity (m∙s−1) |
| V | total velocity (m) |
| w | width (m) |
| Greek letters | |
| β | slope angle |
| γ | convective coefficient |
| ε | emissivity |
| λ | equivalent thermal conductivity |
| 𝜇 | equivalent ROS factor |
| ρ | density |
| σ | Stefan-Boltzmann (W∙m−2∙K−4) |
| ∑ | entropy flux (W∙K−1) |
| Φ | heat exchanged (W) |
| ω | convective wind speed |
| Subscripts | |
| max | maximum |
| env | environmental |
| 1 | related to the first fire front |
| 2 | related to the second fire front |
| rad | radiative |
| conv | convective |
References
- Sciacovelli, A.; Verda, V.; Sciubba, E. Entropy generation analysis as a design tool—A review. Renew. Sustain. Energy Rev. 2015, 43, 1167–1181. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Gouy, G. Sur l’énergie utilizable (on usable energy). J. Phys. 1889, 11, 501–518. [Google Scholar]
- Stodola, A. Die Kreisprozesse der Gasmaschine. Z. VDI 1898, 506, 1086–1091. [Google Scholar]
- Guelpa, E.; Sciacovelli, A.; Verda, V. Entropy generation analysis for the design improvement of a latent heat storage system. Energy 2013, 53, 128–138. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Guelpa, E.; Verda, V. Second law optimization of a PCM based latent heat thermal energy storage system with tree shaped fins. Int. J. Thermodyn. 2014, 17, 145–154. [Google Scholar] [CrossRef]
- Jegadheeswaran, S.; Pohekar, S.D.; Kousksou, T. Exergy based performance evaluation of latent heat thermal storage system: A review. Renew. Sustain. Energy Rev. 2010, 14, 2580–2595. [Google Scholar] [CrossRef]
- Sahin, A.Z.; Ben-Mansour, R. Entropy generation in laminar fluid flow through a circular pipe. Entropy 2003, 5, 404–416. [Google Scholar] [CrossRef]
- Schmandt, B.; Herwig, H. Diffuser and nozzle design optimization by entropy generation minimization. Entropy 2011, 13, 1380–1402. [Google Scholar] [CrossRef]
- Yapici, H.; Kayatas, N.; Kahraman, N.; Bastürk, G. Numerical study on local entropy generation in compressible flow through a suddenly expanding pipe. Entropy 2005, 7, 38–67. [Google Scholar] [CrossRef]
- Nakonieczny, K. Entropy generation in a diesel engine turbocharging system. Energy 2002, 27, 1027–1056. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Kyritsis, D.C. Comparative second-law analysis of internal combustion engine operation for methane, methanol, and dodecane fuels. Energy 2001, 26, 705–722. [Google Scholar] [CrossRef]
- Giangaspero, G.; Sciubba, E. Application of the entropy generation minimization method to a solar heat exchanger: A pseudo-optimization design process based on the analysis of the local entropy generation maps. Energy 2013, 58, 52–65. [Google Scholar] [CrossRef]
- Shiba, T.; Bejan, A. Thermodynamic optimization of geometric structure in the counterflow heat exchanger for an environmental control system. Energy 2001, 26, 493–512. [Google Scholar] [CrossRef]
- Mistry, K.H.; McGovern, R.K.; Thiel, G.P.; Summers, E.K.; Zubair, S.M.; Lienhard, J.H. Entropy generation analysis of desalination technologies. Entropy 2011, 13, 1829–1864. [Google Scholar] [CrossRef]
- Paulus, D.M.; Gaggioli, R.A. Some observations of entropy extrema in fluid flow. Energy 2004, 29, 2487–2500. [Google Scholar] [CrossRef]
- Baldwin, R.A. Use of maximum entropy modeling in wildlife research. Entropy 2009, 11, 854–866. [Google Scholar] [CrossRef]
- Bejan, A.; Lorente, S. The constructal law of design and evolution in nature. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 1335–1347. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A.; Lorente, S. Constructal law of design and evolution: Physics, biology, technology, and society. J. Appl. Phys. 2013, 113, 151301. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–4. [Google Scholar] [CrossRef]
- Lucia, U. Maximum or minimum entropy generation for open systems? Phys. A Stat. Mech. Appl. 2012, 391, 3392–3398. [Google Scholar] [CrossRef]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1972. [Google Scholar]
- McArthur, A.G. Weather and Grassland Fire Behaviour; Forestry and Timber: Canberra, Australia, 1966; p. 23. [Google Scholar]
- Morvan, D.; Méradji, S.; Accary, G. Physical modelling of fire spread in grasslands. Fire Saf. J. 2009, 44, 50–61. [Google Scholar] [CrossRef]
- Mell, W.; Jenkins, M.A.; Gould, J.; Cheney, P. A physics based approach to modeling grassland fires. Int. J. Wildland Fire 2007, 16, 1–22. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E. Uncertainty associated with model predictions of surface and crown fire rates of spread. Environ. Model. Softw. 2013, 47, 16–28. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 1: Physical and quasi-physical models. Int. J. Wildland Fire 2009, 18, 349–368. [Google Scholar] [CrossRef]
- Viegas, D.X. Slope and wind effects on fire propagation. Int. J. Wildland Fire 2004, 13, 143–156. [Google Scholar] [CrossRef]
- Viegas, D.X.; Simeoni, A. Eruptive behaviour of forest fires. Fire Technol. 2011, 47, 303–320. [Google Scholar] [CrossRef]
- Albini, F.A. Estimating Wildfire Behavior and Effects; U.S. Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1976.
- Scott, J.H.; Burgan, R.E. Standard Fire Behavior Fuel Models: A Comprehensive Set for Use with Rothermel’s Surface Fire Spread Model; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2005.
- Guelpa, E.; Sciacovelli, A.; Verda, V.; Ascoli, D. Faster prediction of wildfire behaviour by physical models through application of proper orthogonal decomposition. Int. J. Wildland Fire 2016, 25, 1181–1192. [Google Scholar] [CrossRef]
- Guelpa, E.; Verda, V. Second law analysis of wind and slope contributions in grassfires. In Proceedings of the 9th International Exergy, Energy and Environment Symposium, Split, Croatia, 14–17 May 2017. [Google Scholar]
- Mell, W.; Maranghides, A.; McDermott, R.; Manzello, S.L. Numerical simulation and experiments of burning douglas fir trees. Combust. Flame 2009, 156, 2023–2041. [Google Scholar] [CrossRef]
- Simeoni, A.; Santoni, P.A.; Larini, M.; Balbi, J.H. On the wind advection influence on the fire spread across a fuel bed: Modelling by a semi-physical approach and testing with experiments. Fire Saf. J. 2001, 36, 491–513. [Google Scholar] [CrossRef]
- Balbi, J.H.; Santoni, P.A.; Dupuy, J.L. Dynamic modelling of fire spread across a fuel bed. Int. J. Wildland Fire 2000, 9, 275–284. [Google Scholar] [CrossRef]
- Santoni, P.A.; Balbi, J.H.; Dupuy, J.L. Dynamic modelling of upslope fire growth. Int. J. Wildland Fire 2000, 9, 285–292. [Google Scholar] [CrossRef]
- Guelpa, E.; Sciacovelli, A.; Verda, V.; Ascoli, D. Model reduction approach for wildfire multi-scenario analysis. In Proceedings of the VII International Conference on Forest Fire Research, Coimbra, Portugal, Peninsula, 14–21 November 2014. [Google Scholar]
- Silvani, X.; Morandini, F. Fire spread experiments in the field: Temperature and heat fluxes measurements. Fire Saf. J. 2009, 44, 279–285. [Google Scholar] [CrossRef]
- Raposo, J.; Viegas, D.X.; Xie, X.; Almeida, M.; Naian, L. Analysis of the Jump Fire Produced by the Interaction of Two Oblique Fire Fronts: Comparison between Laboratory and Field Cases. 2014. Available online: http://hdl.handle.net/10316.2/34013 (accessed on 21 August 2017).

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guelpa, E.; Verda, V. Entropy Generation Analysis of Wildfire Propagation. Entropy 2017, 19, 433. https://doi.org/10.3390/e19080433
Guelpa E, Verda V. Entropy Generation Analysis of Wildfire Propagation. Entropy. 2017; 19(8):433. https://doi.org/10.3390/e19080433
Chicago/Turabian StyleGuelpa, Elisa, and Vittorio Verda. 2017. "Entropy Generation Analysis of Wildfire Propagation" Entropy 19, no. 8: 433. https://doi.org/10.3390/e19080433
APA StyleGuelpa, E., & Verda, V. (2017). Entropy Generation Analysis of Wildfire Propagation. Entropy, 19(8), 433. https://doi.org/10.3390/e19080433