Incipient Fault Diagnosis of Rolling Bearings Based on Impulse-Step Impact Dictionary and Re-Weighted Minimizing Nonconvex Penalty Lq Regular Technique
Abstract
:1. Introduction
- (1)
- When a spalling defect or pitting corrosion is induced, a series of successive impulses will be generated during subsequent operation. However, most dictionaries and optimal wavelet-basis constructed in the previous method only use single pulse or single impact frequencies, e.g., the optimal Laplace wavelet, single-side Morlet wavelet basis, transient impulse atoms, etc. Therefore there is no guarantee that the sparse-basis construction can match the natural waveform structure of the vibration signal well.
- (2)
- In practice, due to the fluctuation of the load and speed, and the interference of the harsh working environment, some random variations will be generated between an impulse and its neighboring impulses. The traditional sparse reconstruction methods such as greedy pursuit, orthogonal matching pursuit (OMP), L1-norm regularization and iterative shrinkage algorithm ignore those time-varying physical characteristics, which leads to a lower success rate of the transient impulse reconstruction. On the other hand, the traditional sparse reconstruction approaches also treat all vibration signal values equally and thus ignore the fact that the vibration peak value may have more useful information about periodical transient impulses and should be preserved at a larger weight value.
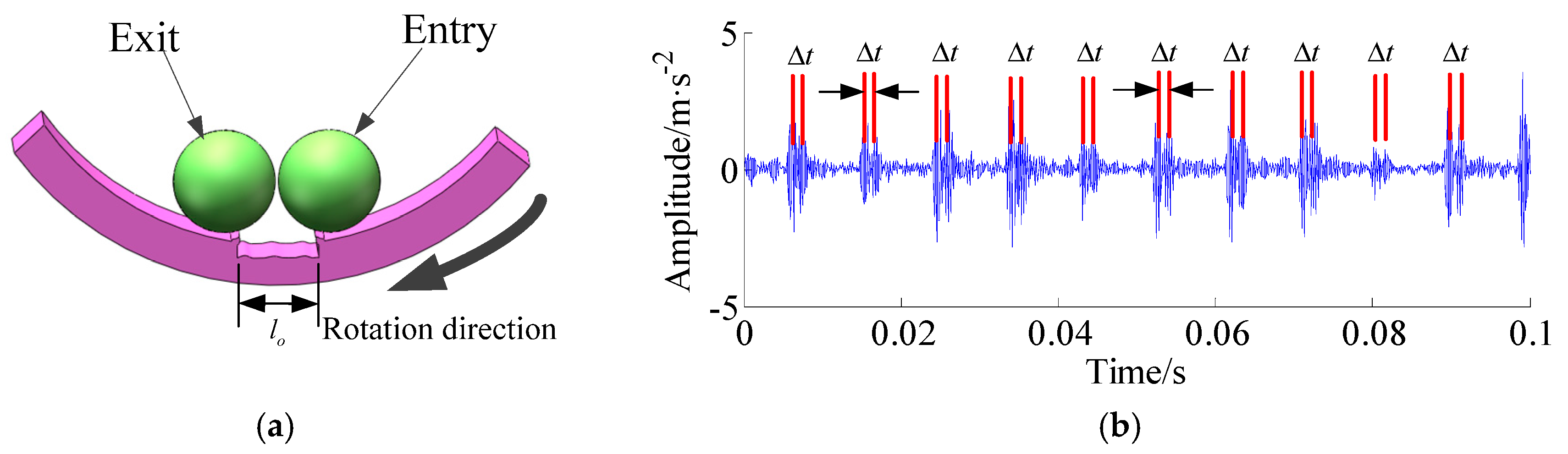
2. Impulse-Step Impact Dictionary and Its Simulation
3. Re-Weighted Minimizing Nonconvex Penalty Lq Regular Technique
3.1. Review of Sparse Representation
- (1)
- Designing a redundant dictionary D. The first important issue is how to construct a redundancy dictionary D that suitable for the transient behavior of fault impulse components.
- (2)
- Recovering sparse coefficients . Another important issue is how to design an optimization algorithm to calculate the sparse coefficients of vibration fault signal.
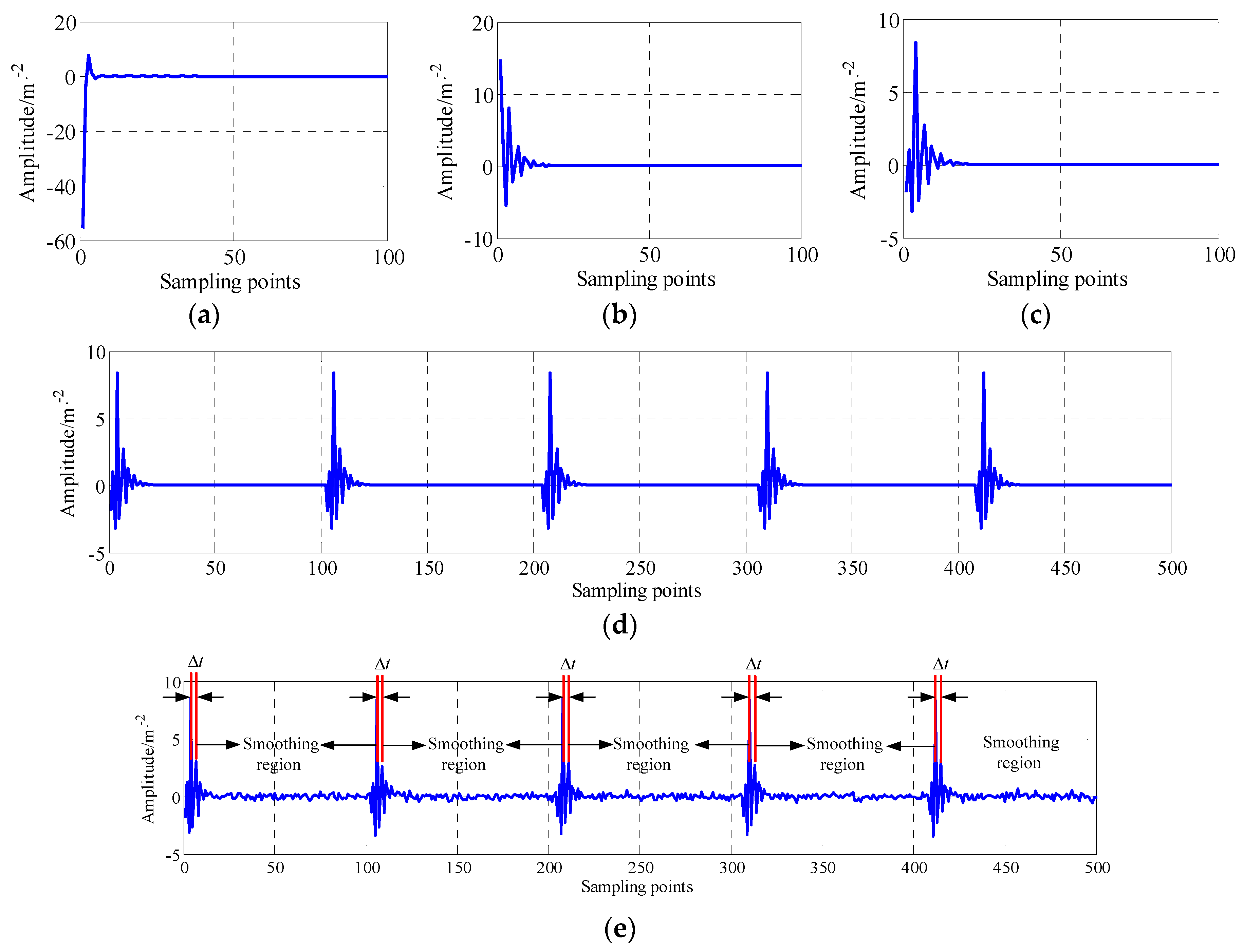
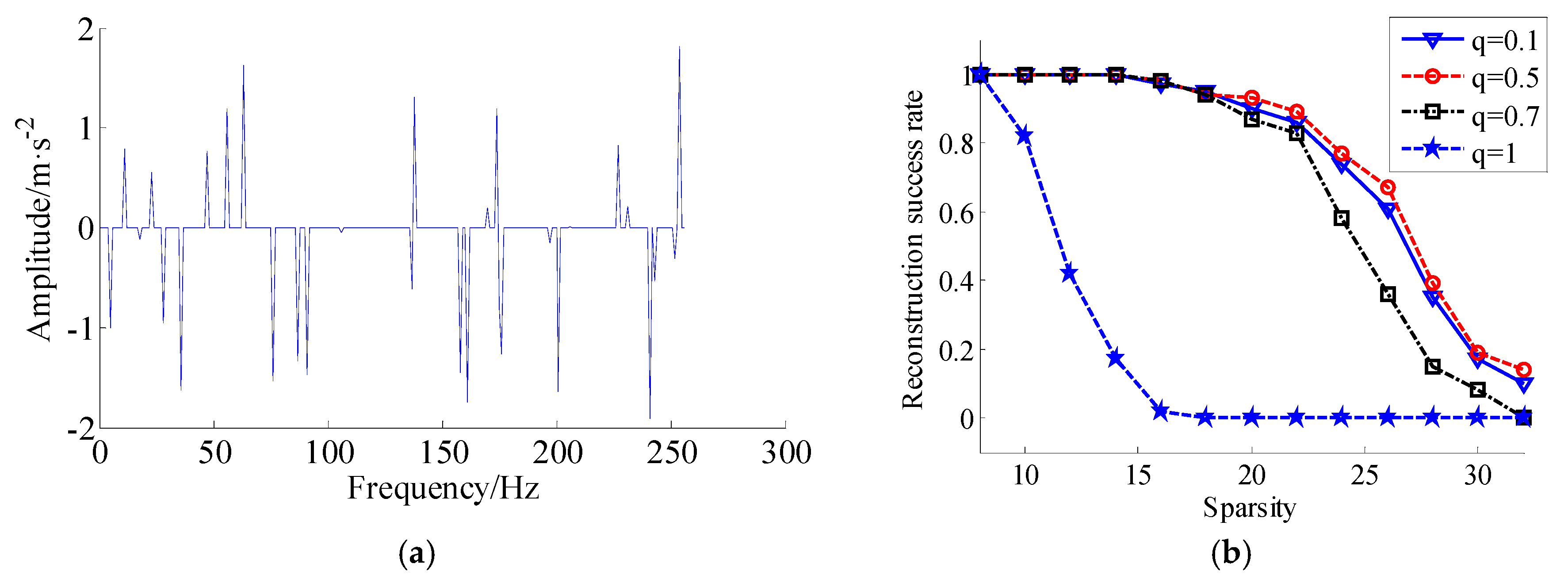
3.2. Re-Weighted Minimizing Nonconvex Penalty Lq Regular and Its Simulation Experiment
| Algorithm 1 Re-weighted minimizing nonconvex penalty Lq regular (R-NSMLq) | |
| 1: | Input: Matrix D, measurement vector b and estimated sparsity level s; |
| 2: | Choose appropriate parameters , q (0 < q ≤ 1); |
| 3: | Initialize such that , and ; |
| 4: | For k = 0; |
| 5: | Solve the following linear system for , |
| 6: | (11) |
| 7: | Or |
| 8: | (12) |
| 9: | When the required reconstruction precision is obtained, the coefficients will be considered as the output value assigned to , meanwhile end to this algorithm, otherwise execute next steps. |
| 10: | Let β be a constant, where 0 < β < 1. Update by formula , where represents the rearrangement of absolute values of in the decreasing order, and is the (s + 1) th component value of . Note that, if , choose to be an approximation of sparse solution and stop this iteration. |
| 11: | Let k = k + 1, and return to step 4 to continue. |
| 12: | Output: Sparse coefficients α; |
| 13: | End |
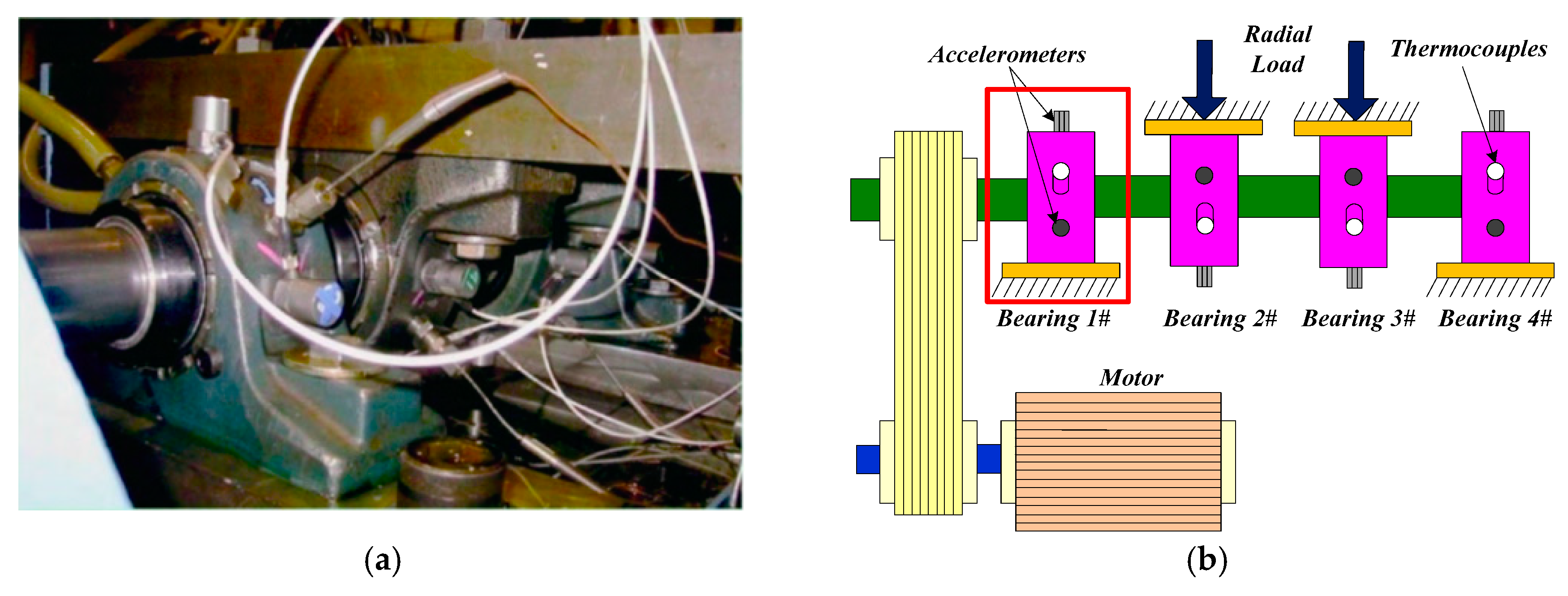
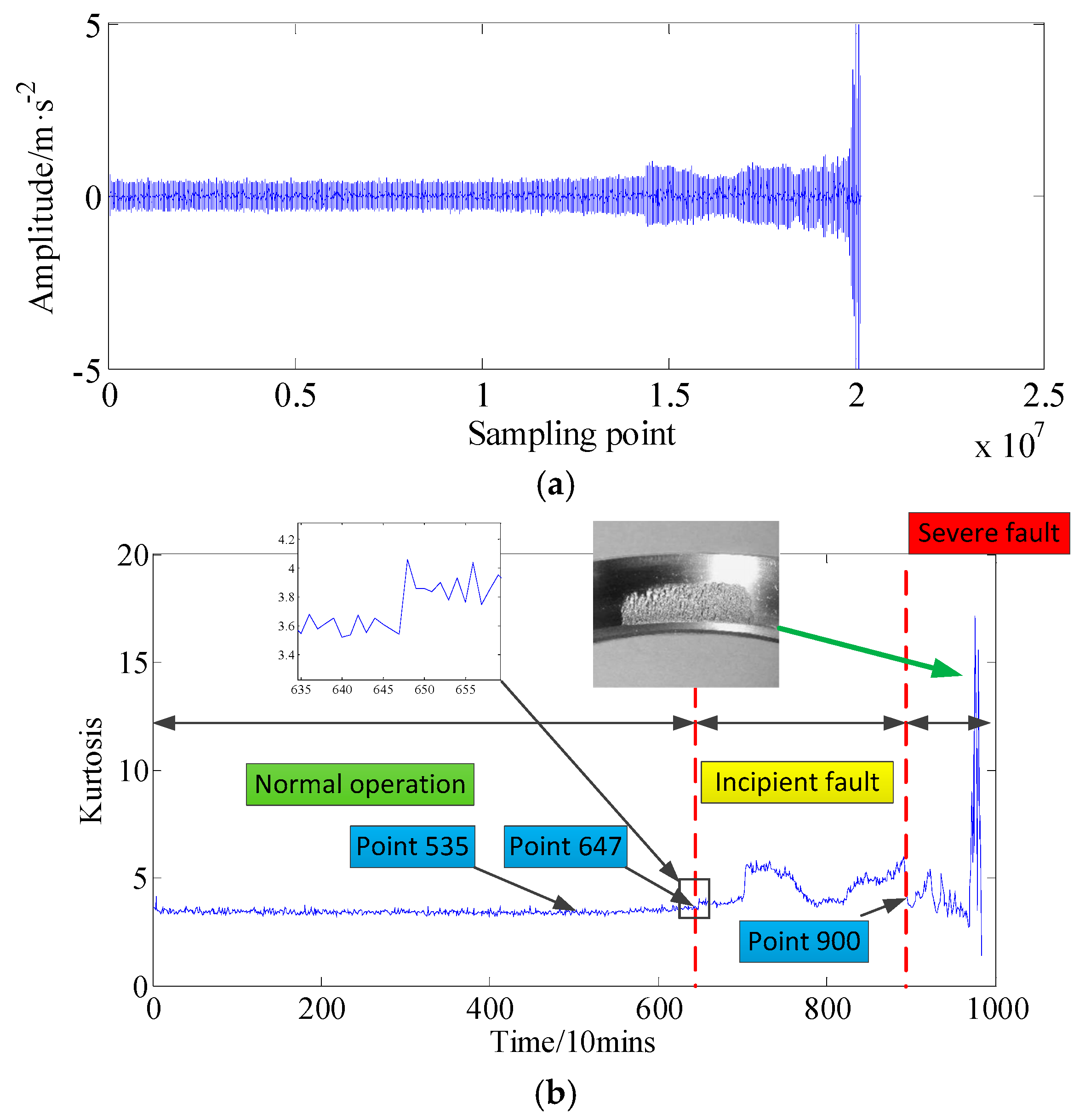
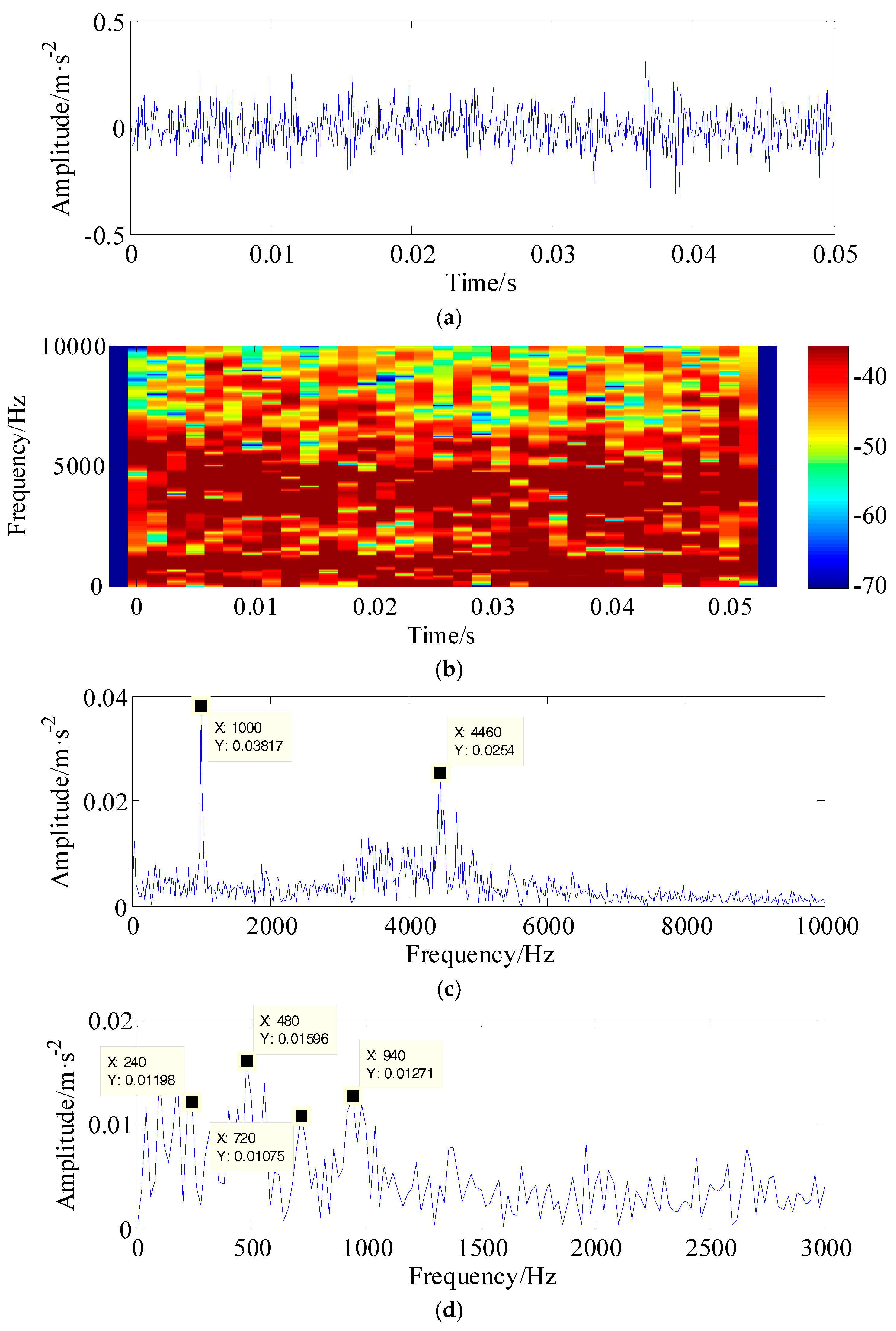
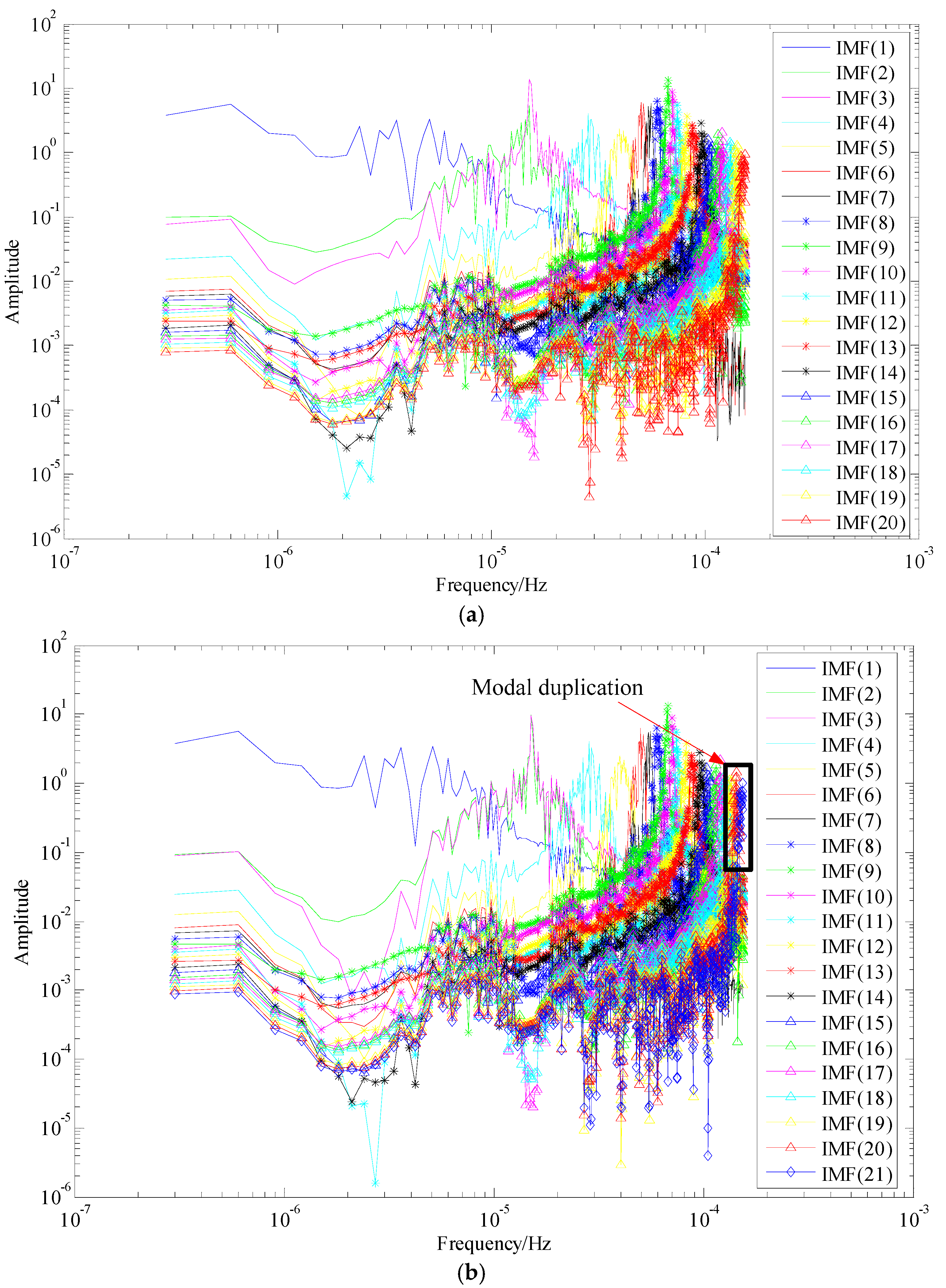
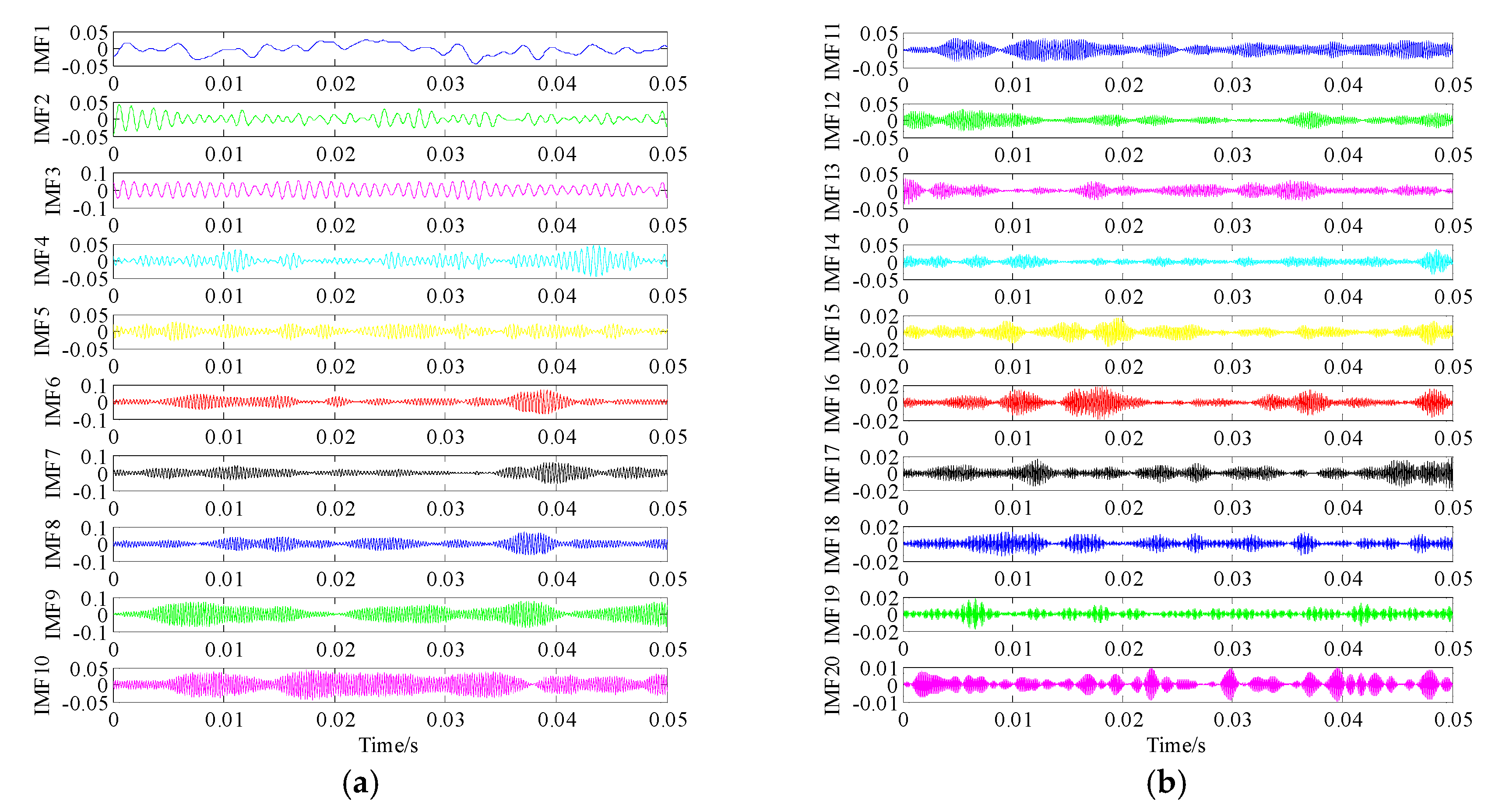
4. Experimental Evaluation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Chen, J.L.; Li, Z.P.; Pan, J.; Chen, G.; Zi, Y.Y.; Yuan, J.; Chen, B.Q.; He, Z.J. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal. Process. 2016, 70–71, 1–35. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.J.; Zhao, W.Y.; Ghaffari, M.; Liao, L.X.; Siegel, D. Prognostics and health management design for rotary machinery systems-reviews, methodology and applications. Mech. Syst. Signal. Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y.; Yang, J.G.; Li, B.Z. Long range dependence prognostics for bearing vibration intensity chaotic time series. Entropy 2016, 18, 23. [Google Scholar] [CrossRef]
- Mishra, C.; Samantaray, A.K.; Chakraborty, G. Rolling element bearing fault diagnosis under slow speed operation using wavelet de-noising. Measurement 2017, 103, 77–86. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y.; Song, W.Q. Revision of bearing fault characteristic spectrum using LMD and interpolation correction algorithm. Procedia CIRP 2016, 56, 182–187. [Google Scholar] [CrossRef]
- McDonald, G.L.; Zhao, Q. Multipoint optimal minimum entropy deconvolution and convolution fix: Application to vibration fault detection. Mech. Syst. Signal. Process. 2017, 82, 461–477. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B.; Endo, H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis. Mech. Syst. Signal. Process. 2007, 21, 2616–2633. [Google Scholar] [CrossRef]
- Jaouher, B.A.; Nader, F.; Lotfi, S.; Brigitte, C.M.; Farhat, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar]
- Mendonça, L.F.; Sousa, J.M.C.; Sá da Costa, J.M.G. An architecture for fault detection and isolation based on fuzzy methods. Expert Syst. Appl. 2009, 36, 1092–1104. [Google Scholar] [CrossRef]
- Sena, P.; Attianese, P.; Pappalardo, M.; Villecco, F. FIDELITY: Fuzzy inferential diagnostic engine for on-line support to physicians. In 4th International Conference on Biomedical Engineering in Vietnam; Springer: Berlin/Heidelberg, Germany, 2013; Volume 49, pp. 396–400. [Google Scholar]
- Sun, W.; Yang, G.A.; Chen, Q.; Palazoglu, A.; Feng, K. Fault diagnosis of rolling bearing based on wavelet transform and envelope spectrum correlation. J. Vib. Control. 2012, 19, 924–941. [Google Scholar] [CrossRef]
- Han, M.H.; Pan, J.L. A fault diagnosis method combined with LMD, sample entropy and energy ratio for roller bearings. Measurement 2015, 76, 7–19. [Google Scholar] [CrossRef]
- Gao, Y.D.; Villecco, F.; Li, M.; Song, W.Q. Multi-scale permutation entropy based on improved LMD and HMM for rolling bearing diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Ge, M.; Xiao, H.; Yu, X. Tensor singular spectrum decomposition algorithm based on permutation entropy for rolling bearing fault diagnosis. Entropy 2017, 19, 139. [Google Scholar] [CrossRef]
- Yang, D.M. The envelop-based bispectral analysis for motor bearing defect detection. In Proceedings of the IEEE International Conference on Applied System Innovation (ICASI), Sapporo, Japan, 13–17 May 2017; pp. 1646–1649. [Google Scholar]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. An improved data fusion technique for faults diagnosis in rotating machines. Measurement 2014, 58, 27–32. [Google Scholar]
- Tian, X.; Gu, J.X.; Rehab, I.; Abdalla, G.M.; Gu, F.; Ball, A.D. A robust detector for rolling element bearing condition monitoring based on the modulation signal bispectrum and its performance evaluation against the Kurtogram. Mech. Syst. Signal. Process. 2018, 100, 167–187. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Zuo, M.J. Diagonal slice spectrum assisted optimal scale morphological filter for rolling element bearing fault diagnosis. Mech. Syst. Signal. Process. 2017, 85, 146–161. [Google Scholar] [CrossRef]
- Wang, S.; Huang, W.; Zhu, Z.K. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis. Mech. Syst. Signal. Process. 2011, 25, 1299–1320. [Google Scholar] [CrossRef]
- Fan, W.; Cai, G.G.; Zhu, Z.K.; Shen, C.Q.; Huang, W.G.; Shang, L. Sparse representation of transients in wavelet basis and its application in gearbox fault feature extraction. Mech. Syst. Signal. Process. 2015, 56–57, 230–245. [Google Scholar] [CrossRef]
- Du, Z.H.; Chen, X.F.; Zhang, H.; Yang, B.Y.; Zhai, Z.; Yan, R.Q. Weighted low-rank sparse model via nuclear norm minimization for bearing fault detection. J. Sound Vib. 2017, 400, 270–287. [Google Scholar] [CrossRef]
- Cui, L.L.; Kang, C.H.; Wang, H.Q.; Chen, P. Application of composite dictionary multi-atom matching in gear fault diagnosis. Sensors 2011, 11, 5981–6002. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.L.; Wang, J.; Lee, S. Matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis. J. Sound Vib. 2014, 333, 2840–2862. [Google Scholar] [CrossRef]
- He, G.L.; Ding, K.; Lin, H.B. Fault feature extraction of rolling element bearings using sparse representation. J. Sound Vib. 2016, 366, 514–527. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.F.; Du, Z.H.; Yan, R.Q. Kurtosis based weighted sparse model with convex optimization technique for bearing fault diagnosis. Mech. Syst. Signal. Process. 2016, 80, 349–376. [Google Scholar] [CrossRef]
- He, Q.B.; Ding, X.X. Sparse representation based on local time–frequency template matching for bearing transient fault feature extraction. J. Sound Vib. 2016, 370, 424–443. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. Vibration response of spalled rolling element bearing: Observations, simulations and signal processing techniques to track the spall size. Mech. Syst. Signal Process. 2011, 25, 846–870. [Google Scholar] [CrossRef]
- Bearing Data Center. Available online: http://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website (accessed on 20 July 2017).
- Donoho, D.L. Compressed Sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969–985. [Google Scholar] [CrossRef]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. C. R. Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Natarajan, B.K. Sparse approximate solutions to linear systems. SIAM J. Comput. 1995, 24, 227–234. [Google Scholar] [CrossRef]
- Lai, M.J.; Wang, J.Y. An Unconstrained lq minimization with 0 < q ≤ 1 for sparse solution of underdetermined linear systems. SIAM J. Optim. 2011, 21, 82–101. [Google Scholar]
- Lai, M.J.; Xu, Y.Y.; Yin, W.T. Improved iteratively reweighted least squares for unconstrained smoothed lq minimization. SIAM J. Numer. Anal. 2013, 51, 927–957. [Google Scholar]
- Wang, Y.; Wang, J.; Xu, Z. On recovery of block-sparse signals via mixed l2/lq (0 < q ≤ 1) norm minimization. EURASIP J. Adv. Signal Process. 2013, 2013, 76. [Google Scholar]
- Hardy, G.; Littlewood, J.; Polya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Center for Intelligent Maintenance Systems. Available online: http://www.imscenter.net/ (accessed on 3 April 2017).
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its applicationon on roller bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Konstantin, D.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal. Process. 2014, 62, 531–544. [Google Scholar]
- Zhang, M.; Jiang, Z.N.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal. Process. 2017, 93, 460–493. [Google Scholar] [CrossRef]
- Li, Q.; Ji, X.; Liang, S.Y. Incipient fault feature extraction for rotating machinery based on improved AR-minimum entropy deconvolution combined with variational mode decomposition approach. Entropy 2017, 19, 317. [Google Scholar] [CrossRef]
- Singh, V.K.; Rai, A.K.; Kumar, M. Sparse data recovery using optimized orthogonal matching pursuit for WSNs. Procedia Comput. Sci. 2017, 109, 210–216. [Google Scholar] [CrossRef]
- Zhao, J.X.; Song, R.F.; Zhao, J.; Zhu, W.P. New conditions for uniformly recovering sparse signals via orthogonal matching pursuit. Signal Process. 2015, 106, 106–113. [Google Scholar] [CrossRef]
- Lin, J.H.; Li, S. Nonuniform support recovery from noisy random measurements by orthogonal matching pursuit. J. Approx. Theory 2013, 165, 20–40. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal. Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal. Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
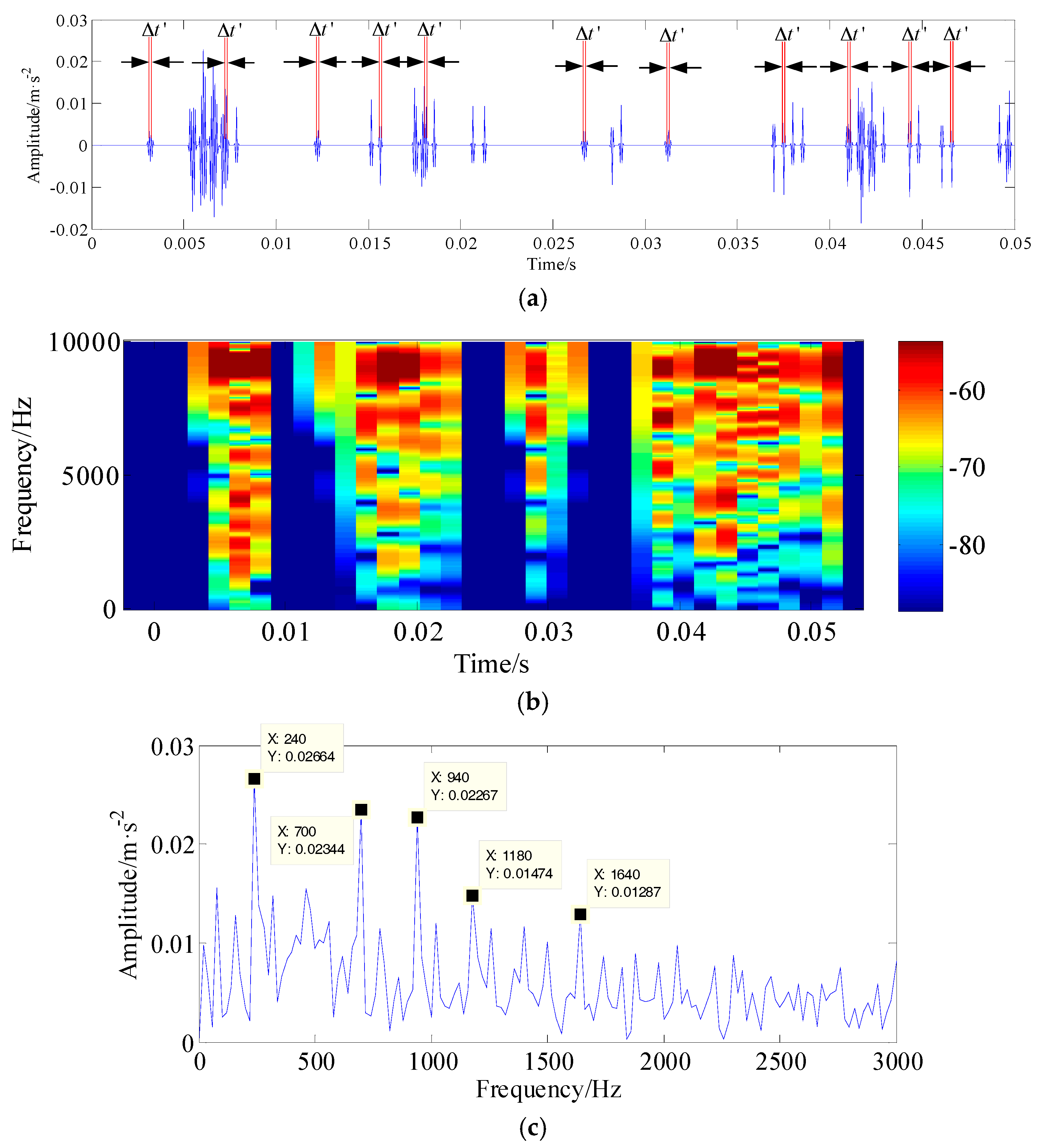
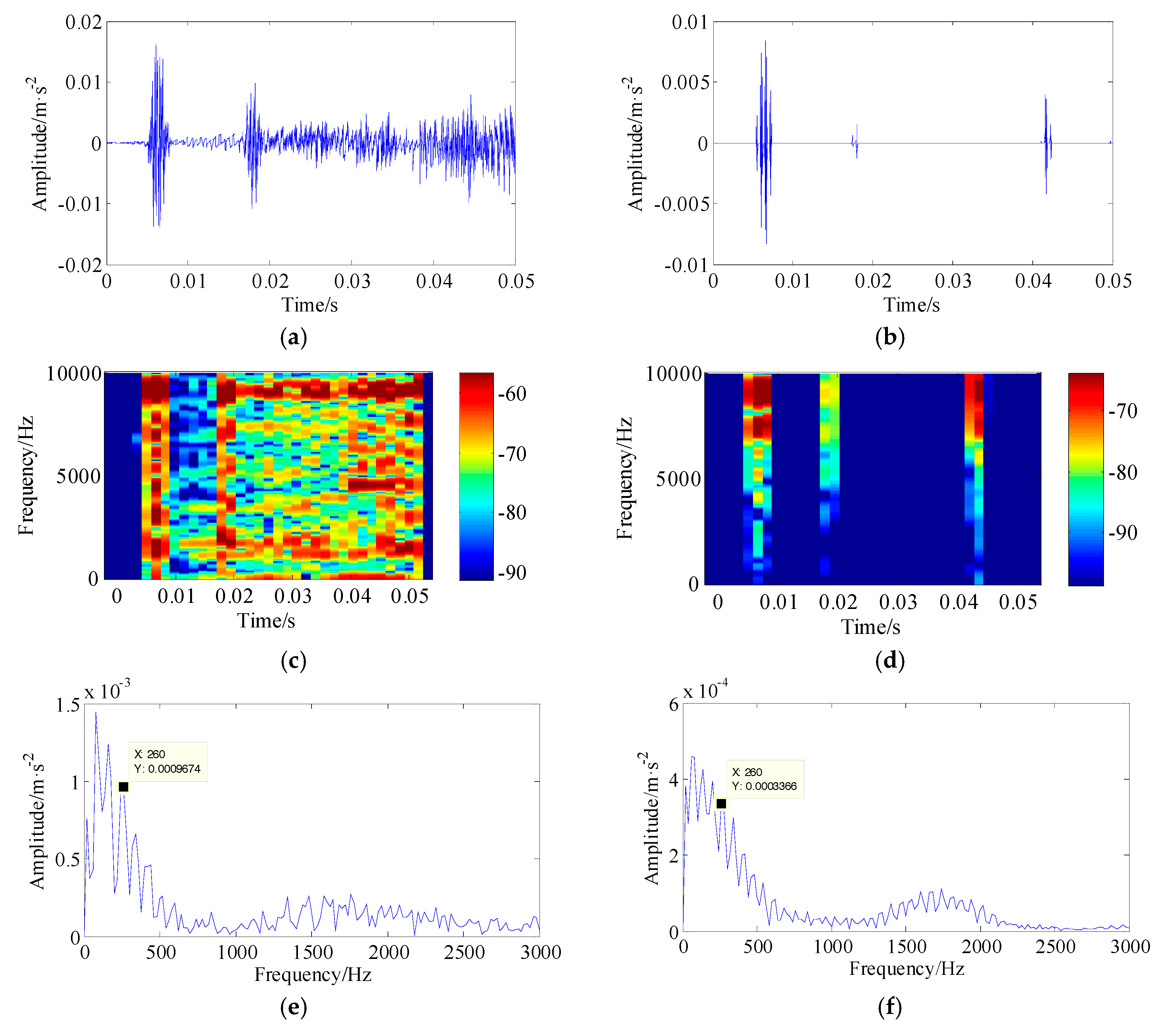
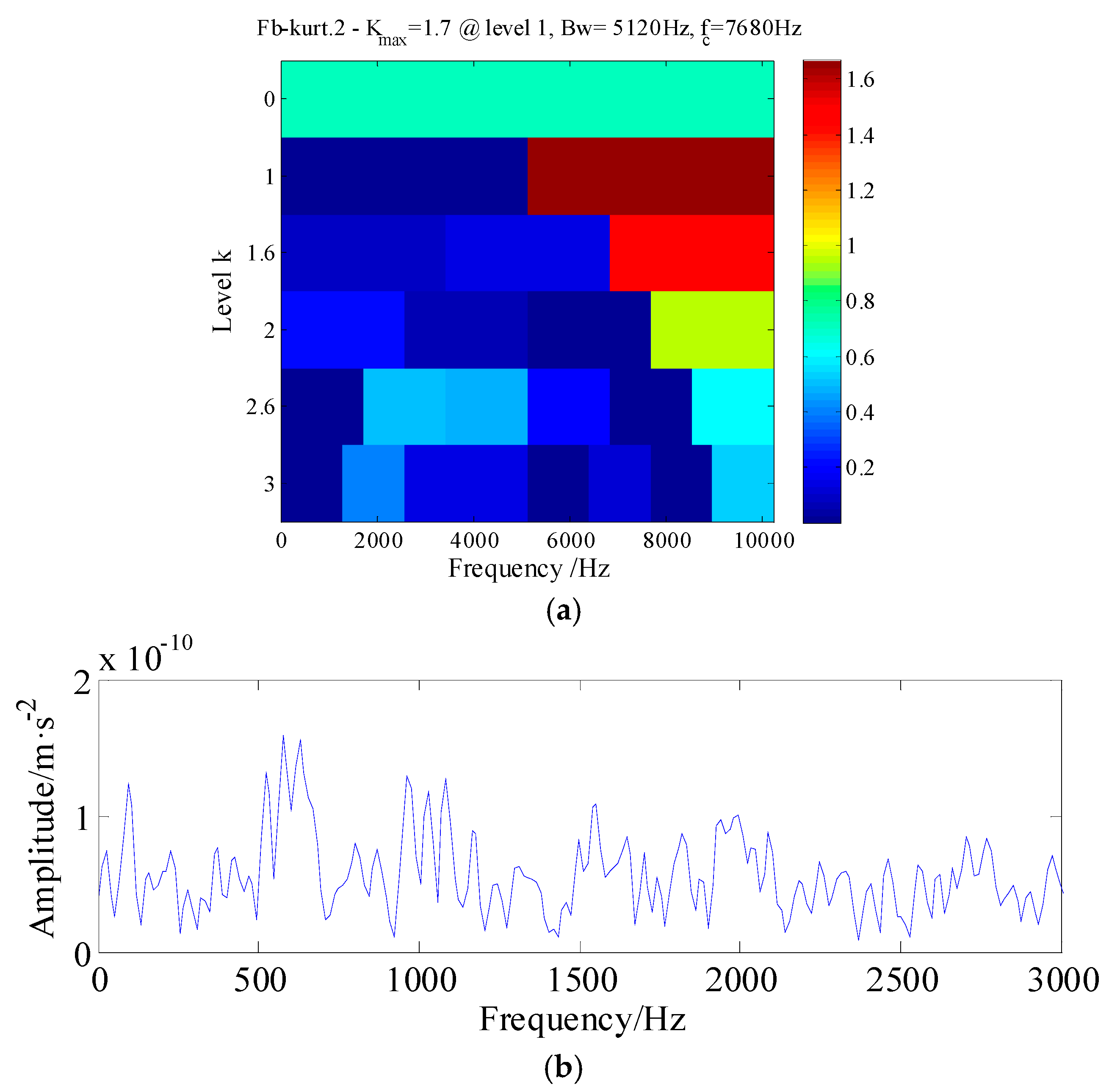
| Parameter | Outside Diameter (mm) | Pitch Diameter (mm) | Contact Angle | Element Number | Pitting Defect Size |
|---|---|---|---|---|---|
| Value | d0 = 7.95 | Dp = 45.14 | α = 0° | 14 | l0 = 1.28 |
| Regular Operator-q | Smoothing Parameter | Penalty Parameter | Maximum Iterations Number | Stopping Threshold |
|---|---|---|---|---|
| 0.5 | ε0 = 0 | 1000 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Liang, S.Y. Incipient Fault Diagnosis of Rolling Bearings Based on Impulse-Step Impact Dictionary and Re-Weighted Minimizing Nonconvex Penalty Lq Regular Technique. Entropy 2017, 19, 421. https://doi.org/10.3390/e19080421
Li Q, Liang SY. Incipient Fault Diagnosis of Rolling Bearings Based on Impulse-Step Impact Dictionary and Re-Weighted Minimizing Nonconvex Penalty Lq Regular Technique. Entropy. 2017; 19(8):421. https://doi.org/10.3390/e19080421
Chicago/Turabian StyleLi, Qing, and Steven Y. Liang. 2017. "Incipient Fault Diagnosis of Rolling Bearings Based on Impulse-Step Impact Dictionary and Re-Weighted Minimizing Nonconvex Penalty Lq Regular Technique" Entropy 19, no. 8: 421. https://doi.org/10.3390/e19080421
APA StyleLi, Q., & Liang, S. Y. (2017). Incipient Fault Diagnosis of Rolling Bearings Based on Impulse-Step Impact Dictionary and Re-Weighted Minimizing Nonconvex Penalty Lq Regular Technique. Entropy, 19(8), 421. https://doi.org/10.3390/e19080421






