Parameterization of Coarse-Grained Molecular Interactions through Potential of Mean Force Calculations and Cluster Expansion Techniques
Abstract
1. Introduction
- (a)
- In structural, or correlation-based, methods, the main goal is to find effective CG potentials that reproduce the pair radial distribution function , and the distribution functions of bonded degrees of freedom (e.g., bonds, angles, dihedrals) for CG systems with intramolecular interaction potential [6,7,9,10,21,22]. The CG effective interactions in such methods are obtained using the direct Boltzmann inversion, or reversible work, method [10,26,27,28], or iterative techniques, such as the iterative Boltzmann inversion (IBI) [7,29] and the inverse Monte Carlo (IMC); or inverse Newton approach [22,30].
- (b)
- (c)
- The relative entropy (RE) [8,18,34] method employs the minimization of the relative entropy, or Kullback–Leibler divergence, between the microscopic Gibbs measure and , representing approximations to the exact coarse space Gibbs measure. In this case, the microscopic probability distribution can be thought of as the observable. The minimization of the relative entropy is performed through Newton–Raphson approaches and/or stochastic optimization techniques [19,35].
2. Molecular Models
2.1. Atomistic and “Exact” Coarse-Grained Description
2.2. Coarse-Grained Approximations
- (a)
- The correlation-based (e.g., DBI, IBI and IMC) methods that use the pair radial distribution function , related to the two-body potential of mean force for the intermolecular interaction potential, as well as distribution functions of bonded degrees of freedom (e.g., bonds, angles, dihedrals) for CG systems with intramolecular interaction potential [6,7,9,10,21,22]. These methods will be further discussed below.
- (b)
- Force matching (FM) methods [5,16,31] in which the observable function is the average force acting on a CG particle. The CG potential is then determined from atomistic force information through a least-square minimization principle, to variationally project the force corresponding to the potential of mean force onto a force that is defined by the form of the approximate potential.
- (c)
- (a)
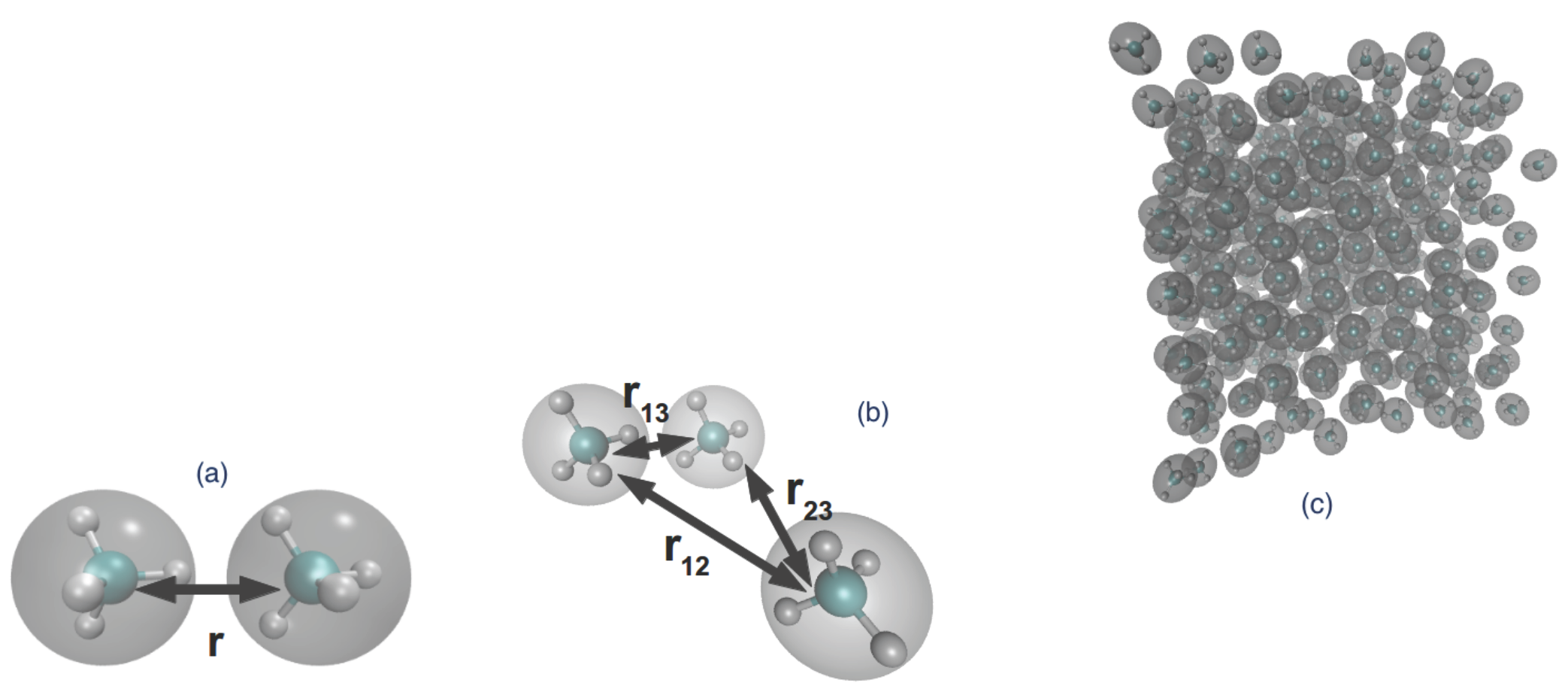
- One method is by fixing the distance between two molecules and performing molecular dynamics with such forces that maintain the fixed distance . In this way, we sample atomistic potential energy (and forces) over the constrained phase space and obtain the conditional partition function as the integral in (8). Alternatively, by integration of the constrained force (), the two-body effective potential can be obtained. These are the and terms, respectively. Note that we have not used any kind of fitting or projection over a basis as in [64,65]; the data are in tabulated form.
- (b)
- Upon inverting in (11) for two isolated molecules, the two-body effective potential can be directly obtained, since for such a system, ; i.e., the low regime. This method is only used for comparison with (a)as it uses the .
2.3. Thermodynamic Consistency
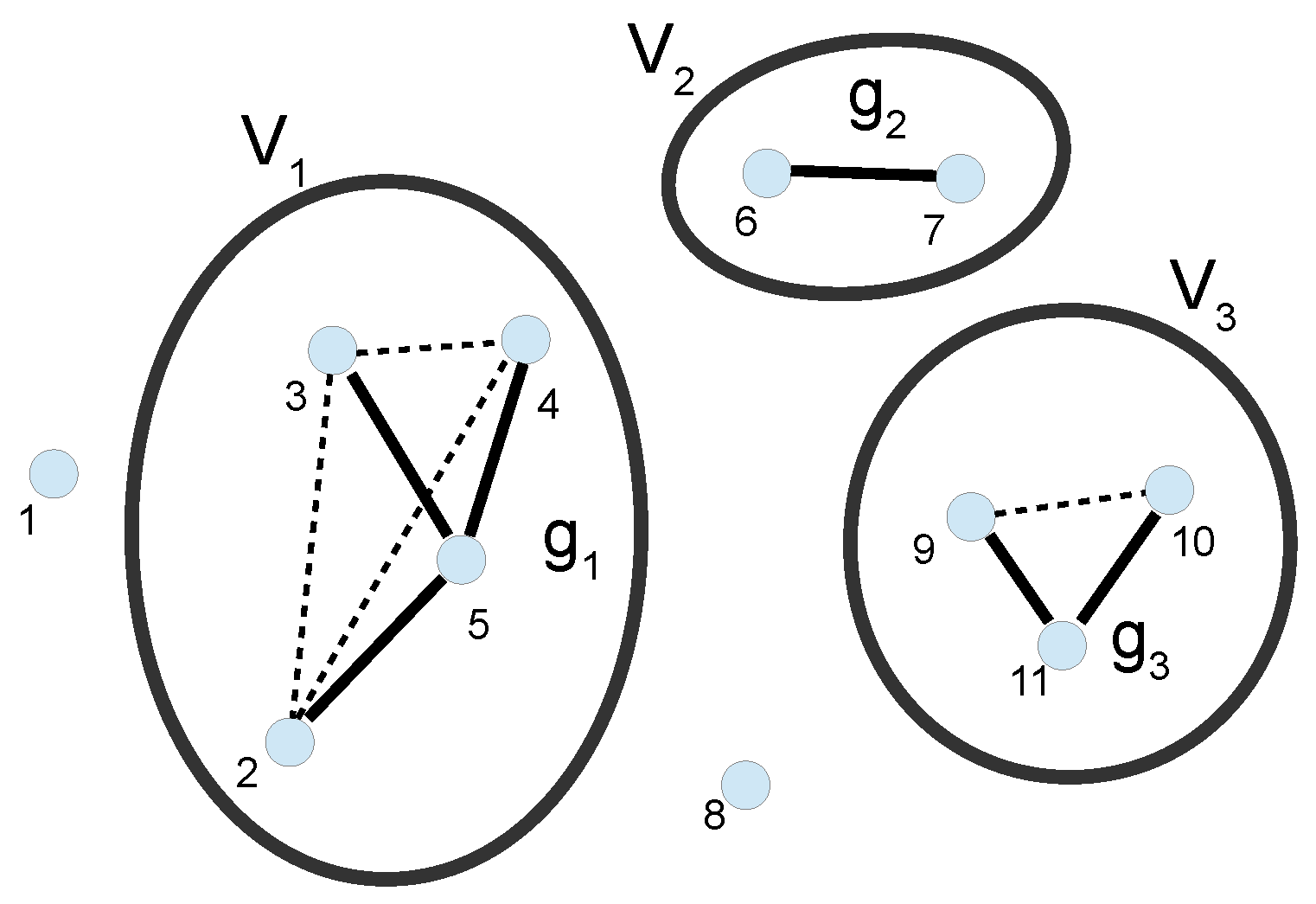
3. Cluster Expansion
3.1. Full Calculation of the PMF
4. Model and Simulations
4.1. The Model
4.2. Simulations
4.2.1. Constrained Runs
4.2.2. Geometric Direct Computation of PMF
5. Results
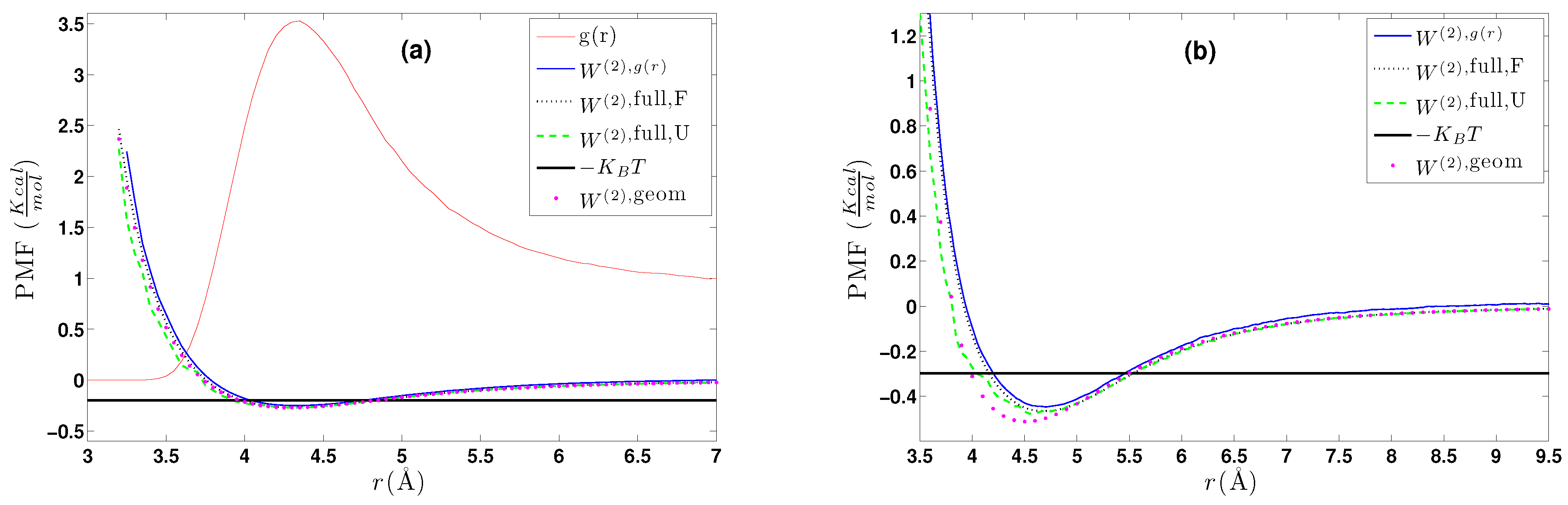
5.1. Calculation of the Effective Two-Body CG Potential
- (a)
- A calculation of the PMF using the constraint force approach, , as described in Section 4.2.1. Alternatively, through the same set of atomistic configurations, the two-body PMF, , can be directly calculated through Equation (24).
- (b)
- A direct calculation of the PMF, , using a geometrical approach as described in Section 4.2.2.
- (c)
- DBI method: The CG effective potential, , is obtained by inverting the pair (radial) correlation function, , computed through a stochastic LD run with only two methane (or ethane) molecules freely moving in the simulation box. The pair correlation function, , of the two methane molecules is also shown in Figure 3a.
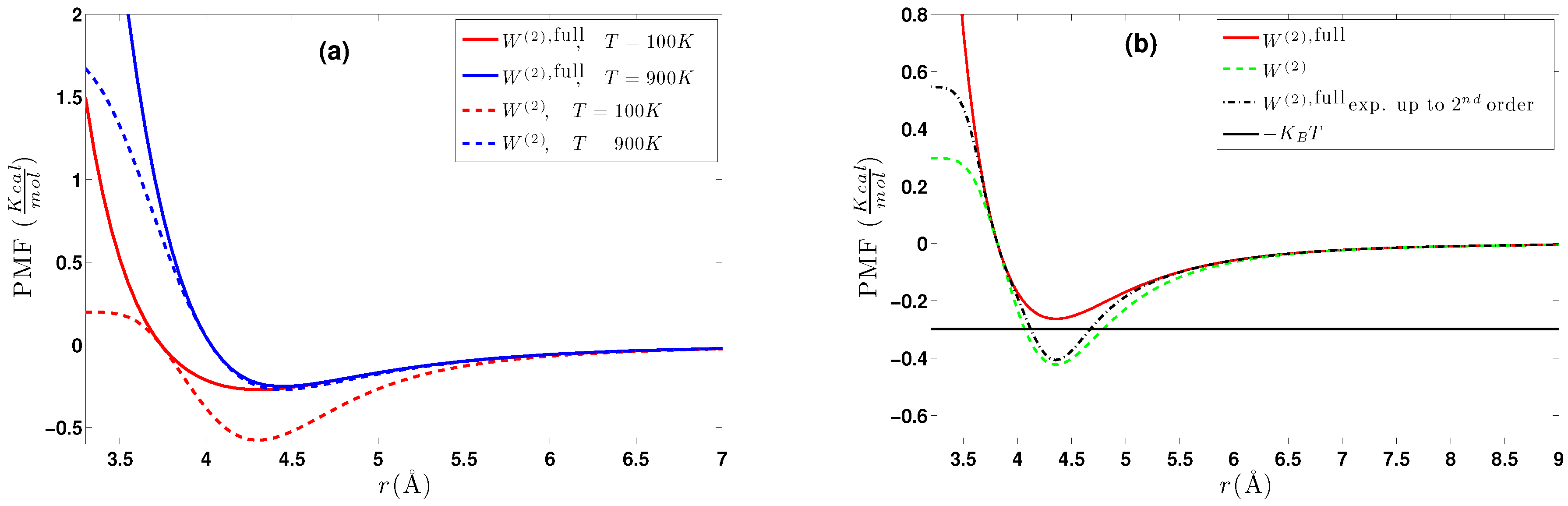
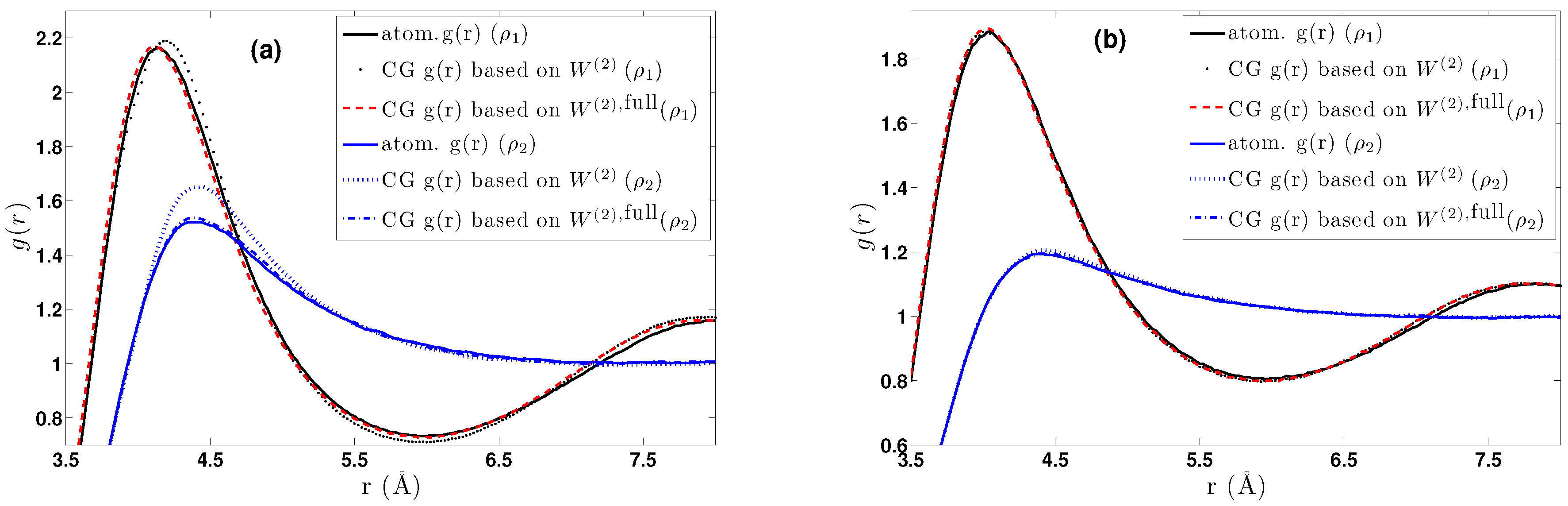
5.1.1. Effect of Temperature-Density
5.2. Bulk CG CH4 Runs Using a Pair Potential
5.2.1. Effect of Temperature-Density
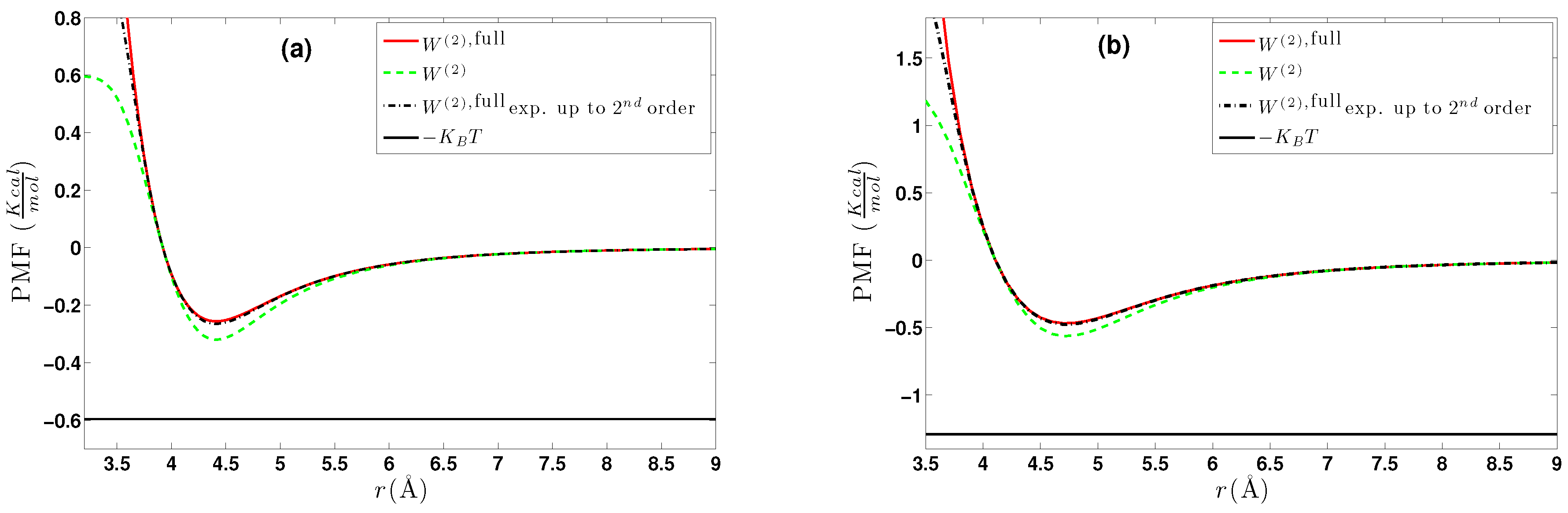
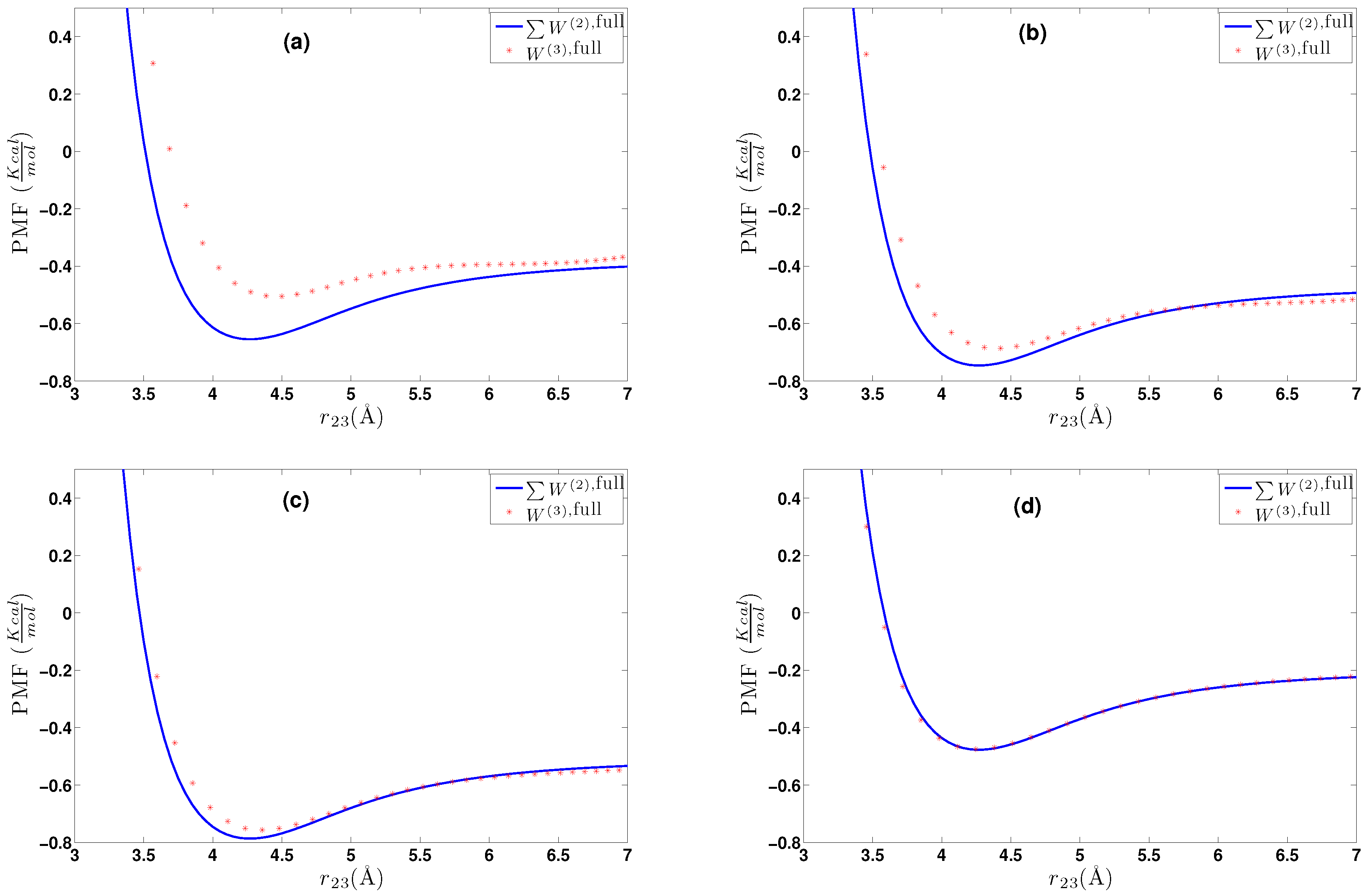
6. Effective Three-Body Potential
6.1. Calculation of the Effective Three-Body Potential
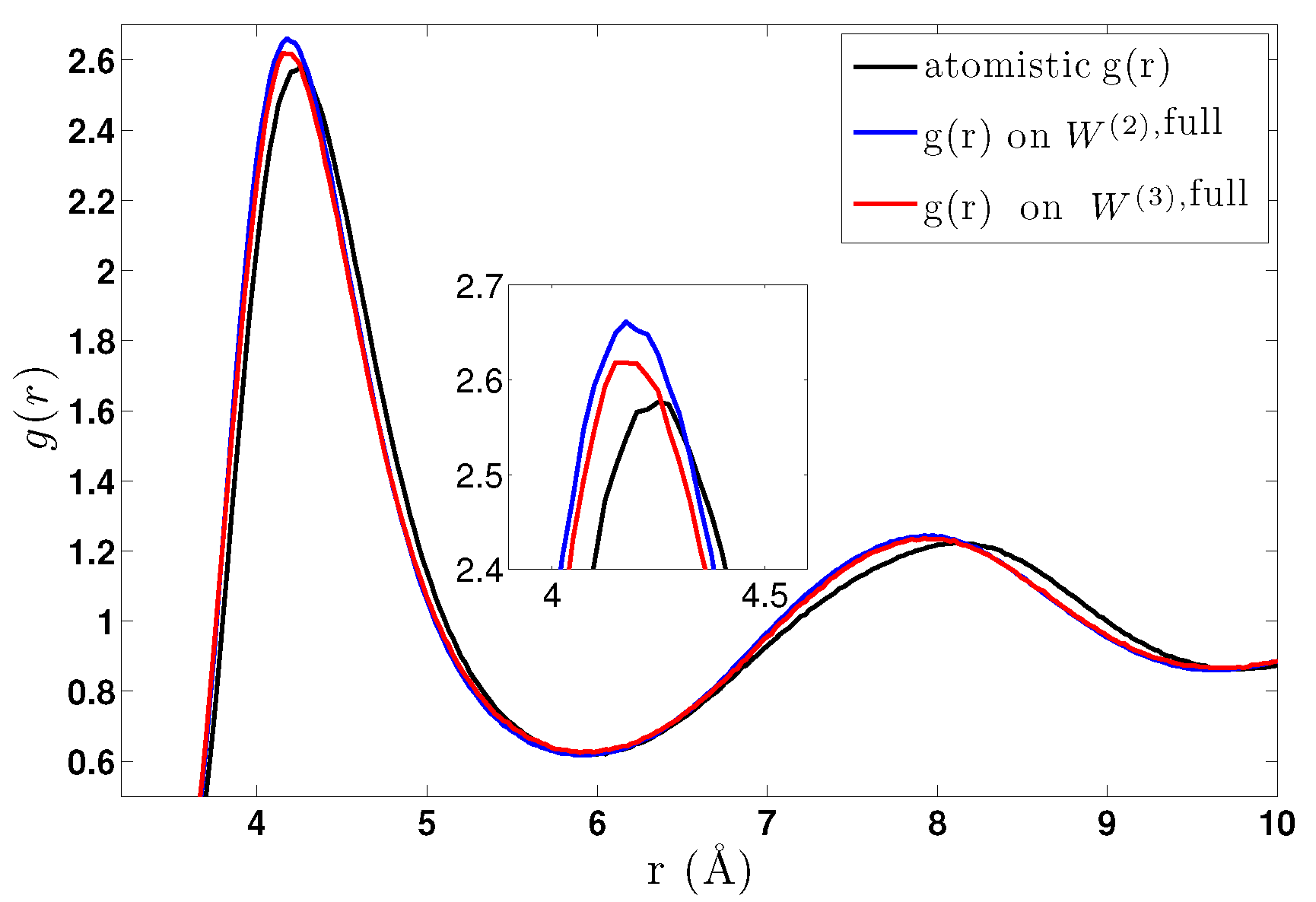
6.2. CG Runs with the Effective Three-Body Potential
7. Discussion and Conclusions
- (a)
- The hierarchy of the cluster expansion formalism allowed us to systematically define the CG effective interaction as a sum of pair, triplets, etc., interactions. Then, CG effective potentials can be computed as they arise from the cluster expansion. Note, that for this estimation, no information from long simulations of n-body (bulk) systems is required.
- (b)
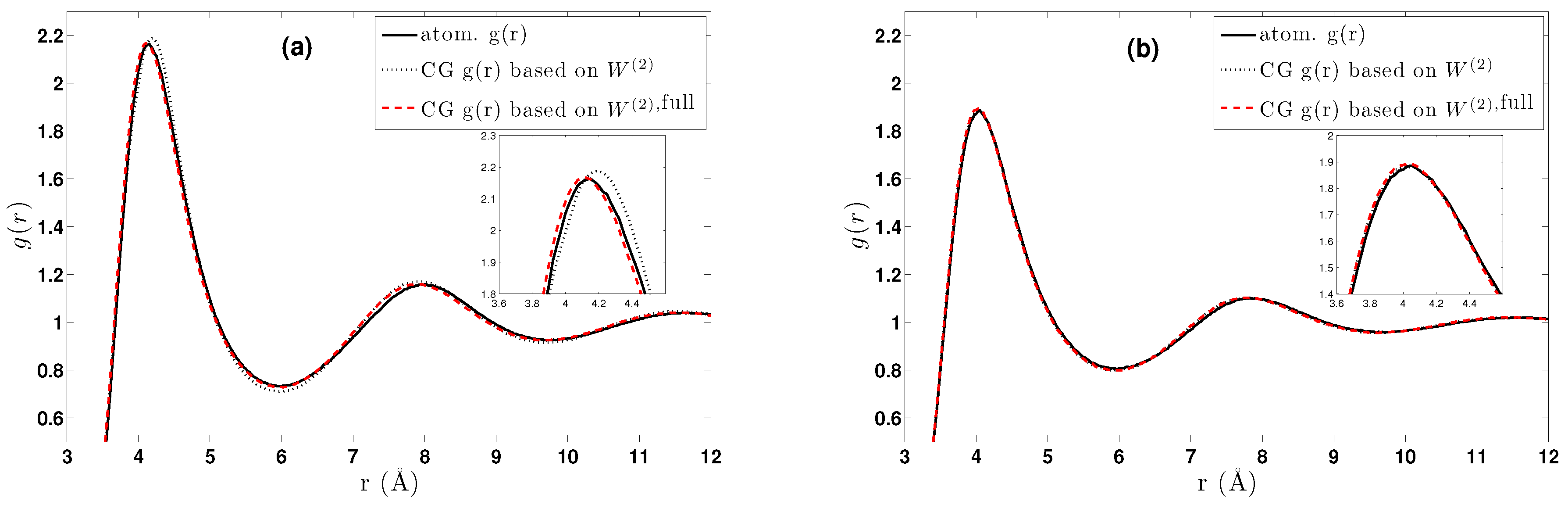
- The two-body coarse-grained potentials can be efficiently computed via the cluster expansion giving comparable results with the existing methods, such as the conditional reversible work. In addition, we present a more efficient direct geometric computation of the constrained partition function, which also alleviates sampling noise issues. No basis function is needed in any of these methods.
- (c)
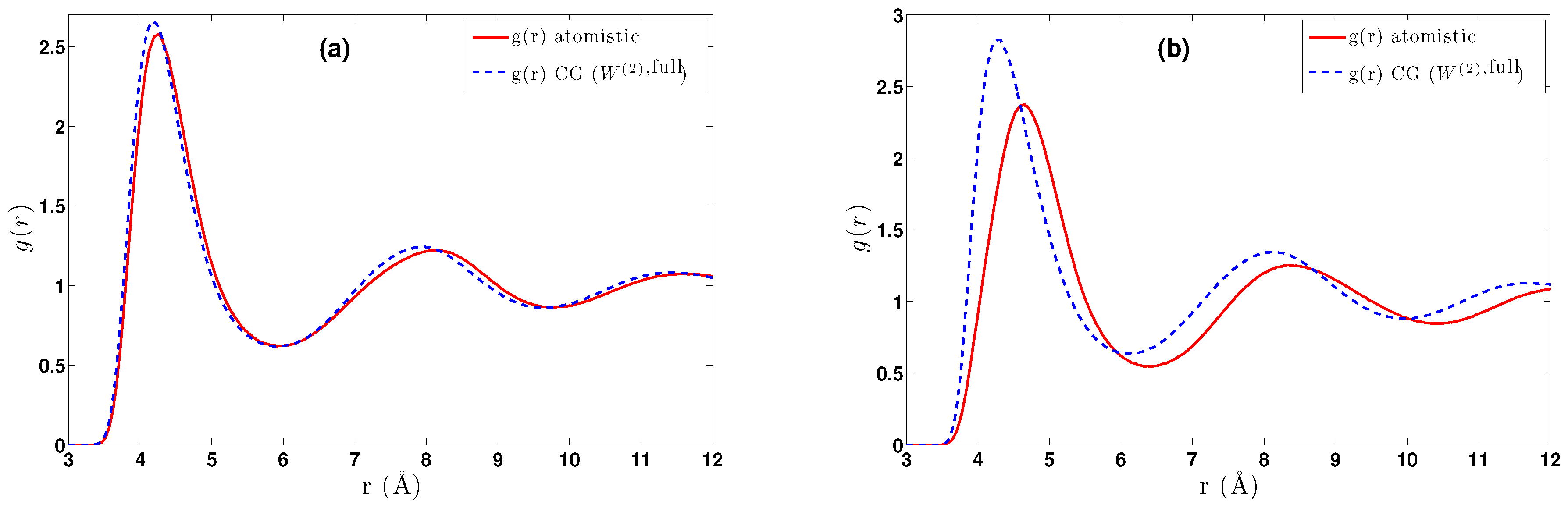
- The obtained pair CG potentials were used to model methane and ethane systems in various regimes. The derived data were compared against the all-atom ones. Clear differences between methane and ethane systems were observed; for the (almost spherical) methane, pair CG potentials seem to be a very good approximation, whereas much larger differences between CG and atomistic distribution functions were observed for ethane.
- (d)
- We further investigated different temperature and density regimes and in particular cases where the two-body approximations are not good enough compared to the atomistic simulations. In the latter case, we considered the next term in the cluster expansion, namely the three-body effective potentials, and we found that they give a small improvement over the pair ones in the liquid state.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Harmandaris, V.A.; Mavrantzas, V.G.; Theodorou, D.; Kröger, M.; Ramírez, J.; Öttinger, H.C.; Vlassopoulos, D. Dynamic crossover from Rouse to entangled polymer melt regime: Signals from long, detailed atomistic molecular dynamics simulations, supported by rheological experiments. Macromolecules 2003, 36, 1376–1387. [Google Scholar] [CrossRef]
- Kotelyanskii, M.; Theodorou, D.N. Simulation Methods for Polymers; Taylor & Francis: Abingdon, UK, 2004. [Google Scholar]
- Izvekov, S.; Voth, G.A. Multiscale coarse-graining of liquid-state systems. J. Chem. Phys. 2005, 123, 134105. [Google Scholar] [CrossRef] [PubMed]
- Tschöp, W.; Kremer, K.; Hahn, O.; Batoulis, J.; Bürger, T. Simulation of polymer melts. I. Coarse-graining procedure for polycarbonates. Acta Polym. 1998, 49, 61–74. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Coarse-Graining in Polymer Simulation: From the Atomistic to the Mesoscopic Scale and Back. ChemPhysChem 2002, 3, 754–769. [Google Scholar] [CrossRef]
- Shell, M.S. The relative entropy is fundamental to multiscale and inverse thermodynamic problems. J. Chem. Phys. 2008, 129, 144108. [Google Scholar] [CrossRef] [PubMed]
- Briels, W.J.; Akkermans, R.L.C. Coarse-grained interactions in polymer melts: A variational approach. J. Chem. Phys. 2001, 115, 6210. [Google Scholar]
- Harmandaris, V.A.; Adhikari, N.P.; van der Vegt, N.F.A.; Kremer, K. Hierarchical Modeling of Polystyrene: From Atomistic to Coarse-Grained Simulations. Macromolecules 2006, 39, 6708. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Kremer, K. Dynamics of Polystyrene Melts through Hierarchical Multiscale Simulations. Macromolecules 2009, 42, 791. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Kremer, K. Predicting polymer dynamics at multiple length and time scales. Soft Matter 2009, 5, 3920. [Google Scholar] [CrossRef]
- Johnston, K.; Harmandaris, V. Hierarchical simulations of hybrid polymer–solid materials. Soft Matter 2013, 9, 6696–6710. [Google Scholar] [CrossRef]
- Noid, W.G.; Chu, J.W.; Ayton, G.S.; Krishna, V.; Izvekov, S.; Voth, G.A.; Das, A.; Andersen, H.C. The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models. J. Chem. Phys. 2008, 128, 4114. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Izvekov, S.; Das, A.; Andersen, H.C.; Voth, G.A. Efficient, Regularized, and Scalable Algorithms for Multiscale Coarse-Graining. J. Chem. Theor. Comput. 2010, 6, 954–965. [Google Scholar] [CrossRef] [PubMed]
- Rudzinski, J.F.; Noid, W.G. Coarse-graining entropy, forces, and structures. J. Chem. Phys. 2011, 135, 214101. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.G. Perspective: Coarse-grained models for biomolecular systems. J. Chem. Phys. 2013, 139, 090901. [Google Scholar] [CrossRef] [PubMed]
- Chaimovich, A.; Shell, M.S. Anomalous waterlike behaviour in spherically-symmetric water models optimized with the relative entropy. Phys. Chem. Chem. Phys. 2009, 11, 1901–1915. [Google Scholar] [CrossRef] [PubMed]
- Bilionis, I.; Zabaras, N. A stochastic optimization approach to coarse-graining using a relative-entropy framework. J. Chem. Phys. 2013, 138, 044313. [Google Scholar] [CrossRef] [PubMed]
- Coifman, R.R.; Kevrekidis, I.G.; Lafon, S.; Maggioni, M.; Nadler, B. Diffusion Maps, Reduction Coordinates, and Low Dimensional Representation of Stochastic Systems. Multiscale Model. Simul. 2008, 7, 842–864. [Google Scholar] [CrossRef]
- Soper, A.K. Empirical potential Monte Carlo simulation of fluid structure. Chem. Phys. 1996, 202, 295–306. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Laaksonen, A. On the Reduction of Molecular Degrees of Freedom in Computer Simulations. In Novel Methods in Soft Matter Simulations; Karttunen, M., Lukkarinen, A., Vattulainen, I., Eds.; Springer: Berlin, Germany, 2004; Volume 640, pp. 219–244. [Google Scholar]
- Harmandaris, V.A. Quantitative study of equilibrium and non-equilibrium polymer dynamics through systematic hierarchical coarse-graining simulations. Korea Aust. Rheol. J. 2014, 26, 15–28. [Google Scholar] [CrossRef]
- Espanol, P.; Zuniga, I. Obtaining fully dynamic coarse-grained models from MD. Phys. Chem. Chem. Phys. 2011, 13, 10538–10545. [Google Scholar] [CrossRef] [PubMed]
- Padding, J.T.; Briels, W.J. Uncrossability constraints in mesoscopic polymer melt simulations: Non-Rouse behaviour of C120H242. J. Chem. Phys. 2001, 115, 2846–2859. [Google Scholar] [CrossRef]
- Deichmann, G.; Marcon, V.; van der Vegt, N.F.A. Bottom-up derivation of conservative and dissipative interactions for coarse-grained molecular liquids with the conditional reversible work method. J. Chem. Phys. 2014, 141, 224109. [Google Scholar] [CrossRef] [PubMed]
- Fritz, D.; Harmandaris, V.; Kremer, K.; van der Vegt, N. Coarse-grained polymer melts based on isolated atomistic chains: Simulation of polystyrene of different tacticities. Macromolecules 2009, 42, 7579–7588. [Google Scholar] [CrossRef]
- Brini, E.; Algaer, E.A.; Ganguly, P.; Li, C.; Rodriguez-Ropero, F.; van der Vegt, N.F.A. Systematic Coarse-Graining Methods for Soft Matter Simulations—A Review. Soft Matter 2013, 9, 2108–2119. [Google Scholar] [CrossRef]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef] [PubMed]
- Lyubartsev, A.P.; Laaksonen, A. Calculation of effective interaction potentials from radial distribution functions: A reverse Monte Carlo approach. Phys. Rev. E 1995, 52, 3730–3737. [Google Scholar] [CrossRef]
- Izvekov, S.; Voth, G.A. Effective force field for liquid hydrogen fluoride from ab initio molecular dynamics simulation using the force-matching method. J. Phys. Chem. B 2005, 109, 6573–6586. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.G.; Liu, P.; Wang, Y.; Chu, J.; Ayton, G.S.; Izvekov, S.; Andersen, H.C.; Voth, G.A. The multiscale coarse-graining method. II. Numerical implementation for coarse-grained molecular models. J. Chem. Phys. 2008, 128, 244115. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Dama, J.F.; Voth, G.A. Fitting coarse-grained distribution functions through an iterative force-matching method. J. Chem. Phys. 2013, 139, 121906. [Google Scholar] [CrossRef] [PubMed]
- Katsoulakis, M.A.; Plechac, P. Information-theoretic tools for parametrized coarse-graining of non-equilibrium extended systems. J. Chem. Phys. 2013, 139, 4852–4863. [Google Scholar]
- Chaimovich, A.; Shell, M.S. Coarse-graining errors and numerical optimization using a relative entropy framework. J. Chem. Phys. 2011, 134, 094112. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.M.; Chu, J.W. Inversion of radial distribution functions to pair forces by solving the Yvon–Born–Green equation iteratively. J. Chem. Phys. 2009, 131, 134107. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.G.; Chu, J.; Ayton, G.S.; Voth, G.A. Multiscale coarse-graining and structural correlations: Connections to liquid-state theory. J. Phys. Chem. B 2007, 111, 4116–4127. [Google Scholar] [CrossRef] [PubMed]
- Mullinax, J.W.; Noid, W.G. Generalized Yvon–Born–Green theory for molecular systems. Phys. Rev. Lett. 2009, 103, 198104. [Google Scholar] [CrossRef] [PubMed]
- Mullinax, J.W.; Noid, W.G. Generalized Yvon–Born–Green theory for determining coarse-grained interaction potentials. J. Phys. Chem. C 2010, 114, 5661–5674. [Google Scholar] [CrossRef]
- McCarty, J.; Clark, A.J.; Copperman, J.; Guenza, M.G. An analytical coarse-graining method which preserves the free energy, structural correlations, and thermodynamic state of polymer melts from the atomistic to the mesoscale. J. Chem. Phys. 2014, 140, 204913. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Bian, X.; Li, X.; Karniadakis, G.E. Incorporation of memory effects in coarse-grained modeling via the Mori-Zwanzig formalism. J. Chem. Phys. 2015, 143, 243128. [Google Scholar] [CrossRef] [PubMed]
- McCarty, J.; Clark, A.J.; Lyubimov, I.Y.; Guenza, M.G. Thermodynamic Consistency between Analytic Integral Equation Theory and Coarse-Grained Molecular Dynamics Simulations of Homopolymer Melts. Macromolecules 2012, 45, 8482–8493. [Google Scholar] [CrossRef]
- Clark, A.J.; McCarty, J.; Guenza, M.G. Effective potentials for representing polymers in melts as chains of interacting soft particles. J. Chem. Phys. 2013, 139, 124906. [Google Scholar] [CrossRef] [PubMed]
- Stell, G. The Percus-Yevick equation for the radial distribution function of a fluid. Physica 1963, 29, 517–534. [Google Scholar] [CrossRef]
- Kuna, T.; Tsagkarogiannis, D. Convergence of density expansions of correlation functions and the Ornstein-Zernike equation. arXiv, 2016; arXiv:1611.01716. [Google Scholar]
- Bolhuis, P.G.; Louis, A.A.; Hansen, J.P. Many-body interactions and correlations in coarse-grained descriptions of polymer solutions. Phys. Rev. E 2001, 64, 021801. [Google Scholar] [CrossRef] [PubMed]
- Mayer, J.E.; Mayer, M.G. Statistical Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1940. [Google Scholar]
- Morita, T.; Hiroike, K. The statistical mechanics of condensing systems. III. Prog. Theor. Phys. 1961, 25, 537. [Google Scholar] [CrossRef]
- Frisch, H.; Lebowitz, J. Equilibrium Theory of Classical Fluids; W.A. Benjamin: New York, NY, USA, 1964. [Google Scholar]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Lipquids; Academic Press: London, UK, 1986. [Google Scholar]
- Pulvirenti, E.; Tsagkarogiannis, D. Cluster expansion in the canonical ensemble. Commun. Math. Phys. 2012, 316, 289–306. [Google Scholar] [CrossRef]
- Louis, A.A. Beware of density dependent pair potentials. J. Phys. Condens. Matter 2002, 14, 9187–9206. [Google Scholar] [CrossRef]
- Katsoulakis, M.; Plecháč, P.; Rey-Bellet, L.; Tsagkarogiannis, D. Coarse-graining schemes and a posteriori error estimates for stochastic lattice systems. ESAIM Math. Model. Numer. Anal. 2007, 41, 627–660. [Google Scholar] [CrossRef]
- Katsoulakis, M.; Plecháč, P.; Rey-Bellet, L.; Tsagkarogiannis, D. Coarse-graining schemes for stochastic lattice systems with short and long range interactions. Math. Comput. 2014, 83, 1757–1793. [Google Scholar] [CrossRef]
- Katsoulakis, M.; Plecháč, P.; Rey-Bellet, L.; Tsagkarogiannis, D. Mathematical strategies and error quantification in coarse-graining of extended systems. J. Non Newton. Fluid Mech. 2008, 152, 101–112. [Google Scholar] [CrossRef]
- Trashorras, J.; Tsagkarogiannis, D. Reconstruction schemes for coarse-grained stochastic lattice systems. SIAM J. Numer. Anal. 2010, 48, 1647–1677. [Google Scholar] [CrossRef]
- Kremer, K.; Müller-Plathe, F. Multiscale problems in polymer science: Simulation approaches. MRS Bull. 2001, 26, 205–210. [Google Scholar] [CrossRef]
- McCoy, J.D.; Curro, J.G. Mapping of Explicit Atom onto United Atom Potentials. Macromolecules 1998, 31, 9352–9368. [Google Scholar] [CrossRef]
- Tsourtis, A.; Harmandaris, V.; Tsagkarogiannis, D. Effective coarse-grained interactions: The role of three-body terms through cluster expansions. under preparation.
- Kirkwood, J.G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- McQuarrie, D.A. Statistical Mechanics; University Science Books: Sausalito, CA, USA, 2000. [Google Scholar]
- Kalligiannaki, E.; Chazirakis, A.; Tsourtis, A.; Katsoulakis, M.; Plecháč, P.; Harmandaris, V. Parametrizing coarse grained models for molecular systems at equilibrium. Eur. Phys. J. 2016, 225, 1347–1372. [Google Scholar] [CrossRef]
- Henderson, R. A uniqueness theorem for fluid pair correlation functions. Phys. Lett. A 1974, 49, 197–198. [Google Scholar] [CrossRef]
- Larini, L.; Lu, L.; Voth, G.A. The multiscale coarse-graining method. VI. Implementation of three-body coarse-grained potentials. J. Chem. Phys. 2010, 132, 164107. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Andersen, H.C. The multiscale coarse-graining method. IX. A general method for construction of three body coarse-grained force fields. J. Chem. Phys. 2012, 136, 194114. [Google Scholar] [CrossRef] [PubMed]
- Lelièvre, T.; Rousset, M.; Stoltz, G. Free Energy Computations: A Mathematical Perspective; Imperial College Press: London, UK, 2010. [Google Scholar]
- Tsourtis, A.; Pantazis, Y.; Katsoulakis, M.A.; Harmandaris, V. Parametric sensitivity analysis for stochastic molecular systems using information theoretic metrics. J. Chem. Phys. 2015, 143, 014116. [Google Scholar] [CrossRef] [PubMed]
- Kuna, T.; Lebowitz, J.; Speer, E. Realizability of point processes. J. Stat. Phys. 2007, 129, 417–439. [Google Scholar] [CrossRef]

| System | N (Molecules) | T/K | Simulation Time/ns |
|---|---|---|---|
| CH4, CH3–CH3 | 2, 3 | 100–900 | 10–20 |
| CH4 | 512 | 80, 100, 120, 300, 900 | 100 |
| CH3–CH3 | 500 | 150, 300, 650 | 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsourtis, A.; Harmandaris, V.; Tsagkarogiannis, D. Parameterization of Coarse-Grained Molecular Interactions through Potential of Mean Force Calculations and Cluster Expansion Techniques. Entropy 2017, 19, 395. https://doi.org/10.3390/e19080395
Tsourtis A, Harmandaris V, Tsagkarogiannis D. Parameterization of Coarse-Grained Molecular Interactions through Potential of Mean Force Calculations and Cluster Expansion Techniques. Entropy. 2017; 19(8):395. https://doi.org/10.3390/e19080395
Chicago/Turabian StyleTsourtis, Anastasios, Vagelis Harmandaris, and Dimitrios Tsagkarogiannis. 2017. "Parameterization of Coarse-Grained Molecular Interactions through Potential of Mean Force Calculations and Cluster Expansion Techniques" Entropy 19, no. 8: 395. https://doi.org/10.3390/e19080395
APA StyleTsourtis, A., Harmandaris, V., & Tsagkarogiannis, D. (2017). Parameterization of Coarse-Grained Molecular Interactions through Potential of Mean Force Calculations and Cluster Expansion Techniques. Entropy, 19(8), 395. https://doi.org/10.3390/e19080395






