1. Introduction
An increasing number of applications in micro- and sub-micro-scale physics calls for the development of general techniques for engineered finite-time equilibration of systems operating in a thermally-fluctuating environment. Possible concrete examples are the design of nano-thermal engines [
1,
2] or of micro-mechanical oscillators used for high precision timing or sensing of mass and forces [
3].
A recent experiment [
4] exhibited the feasibility of driving a micro-system between two equilibria over a control time several orders of magnitude faster than the natural equilibration time. The system was a colloidal micro-sphere trapped in an optical potential. There is consensus that non-equilibrium thermodynamics (see, e.g., [
5]) of optically-trapped micron-sized beads is well captured by Langevin–Smoluchowski equations [
6]. In particular, the authors of [
4] took care of showing that it is accurate to conceptualize the outcome of their experiment as the evolution of a Gaussian probability density according to a controlled Langevin–Smoluchowski dynamics with gradient drift and constant diffusion coefficient. Finite time equilibration means that at the end of the control horizon, the probability density is the solution of the stationary Fokker–Planck equation. The experimental demonstration consisted of a compression of the confining potential. In such a case, the protocol steering the equilibration process is specified by the choice of the time evolution of the stiffness of the quadratic potential whose gradient yields the drift in the Langevin–Smoluchowski equation. As a result, the set of admissible controls is infinite. The selection of the control in [
4] was then based on simplicity of implementation considerations.
A compelling question is whether and how the selection of the protocol may stem from a notion of optimal efficiency. A natural indicator of efficiency in finite-time thermodynamics is entropy production. Transitions occurring at minimum entropy production set a lower bound in the Clausius inequality. Optimal control of these transitions is, thus, equivalent to a refinement of the second law of thermodynamics in the form of an equality.
In the Langevin–Smoluchowski framework, entropy production optimal control takes a particularly simple form if states at the end of the transition are specified by sufficiently regular probability densities [
7]. Namely, the problem admits an exact mapping into the well-known Monge–Kantorovich optimal mass transport [
8]. This feature is particularly useful because the dynamics of the Monge–Kantorovich problem is exactly solvable. Mass transport occurs along free-streaming Lagrangian particle trajectories. These trajectories satisfy boundary conditions determined by the map, called the Lagrangian map, transforming into each other the data of the problem, the initial and the final probability densities. Rigorous mathematical results [
9,
10,
11] preside over the existence, qualitative properties and reconstruction algorithms for the Lagrangian map.
The aforementioned results cannot be directly applied to optimal protocols for engineered equilibration. Optimal protocols in finite-time unavoidably attain minimum entropy by leaving the end probability densities out of equilibrium. The qualitative reason is that optimization is carried over the set of drifts sufficiently smooth to mimic all controllable degrees of freedom of the micro-system. Controllable degrees of freedom are defined as those varying over typical time scales much slower than the time scales of Brownian forces [
12]. The set of admissible protocols defined in this way is too large for optimal engineered equilibration. The set of admissible controls for equilibration must take into account also extra constraints coming from the characteristic time scales of the forces acting on the system. From the experimental slant, we expect these restrictions to be strongly contingent on the nature and configuration of peripherals in the laboratory setup. From the theoretical point of view, the self-consistence of Langevin–Smoluchowski modeling imposes a general restriction. The time variation of drift fields controlling the dynamics must be slow in comparison to Brownian and inertial forces.
In the present contribution, we propose a refinement of the entropy production optimal control adapted to engineered equilibration. We do this by restricting the set of admissible controls to those satisfying a non-holonomic constraint on accelerations. The constraint relates the bound on admissible accelerations to the path-wise displacement of the system degrees of freedom across the control horizon. Such displacement is a deterministic quantity, intrinsically stemming from the boundary conditions inasmuch as we determine it from the Lagrangian map.
This choice of the constraint has several inherent advantages. It yields an intuitive hold on the realizability of the optimal process. It also preserves the integrability properties of the optimal control problem specifying the lower bound to the second law. This is so because the constraint allows us to maintain protocols within the admissible set by exerting on them uniform accelerating or decelerating forces. On the technical side, the optimal control problem can be handled by a direct application of the Pontryagin maximum principle [
13]. For the same reasons as for the refinement of the second law [
7], the resulting optimal control is of the deterministic type. This circumstance yields a technical simplification, but it is not a necessary condition in view of extensions of our approach. We will return to this point in the conclusions.
The structure of the paper is as follows. In
Section 2 we briefly review the Langevin–Smoluchowski approach to non-equilibrium thermodynamics [
14]. This section can be skipped by readers familiar with the topic. In
Section 3, we introduce the problem of optimizing the entropy production. In particular we explain its relation with the Schrödinger diffusion problem [
15,
16]. This relation, already pointed out in [
17], has recently attracted the attention of mathematicians and probabilists interested in rigorous application of variational principles in hydrodynamics [
18]. In
Section 4, we formulate the Pontryagin principle for our problem. Our main result follows in
Section 5, where we solve in explicit form the optimal protocols.
Section 6 and
Section 7 are devoted to applications. In
Section 6, we revisit the theoretical model of the experiment [
4], the primary motivation of our work. In
Section 7, we apply our results to a stylized model of controlled nucleation obtained by manipulating a double-well potential. Landauer and Bennett availed themselves of this model to discuss the existence of an intrinsic thermodynamic cost of computing [
19,
20]. Optimal control of this model has motivated in more recent years in several theoretical [
21] and experimental works [
22,
23,
24].
Finally, in
Section 8, we compare the optimal control we found with those of [
25]. This reference applied a regularization technique coming from instanton calculus [
26] to give a precise meaning to otherwise ill-defined problems in non-equilibrium thermodynamics, where terminal cost seems to depend on the control rather than being a given function of the final state of the system.
In the conclusions, we discuss possible extensions of the present work. The style of the presentation is meant to be discursive, but relies on notions in between non-equilibrium physics, optimal control theory and probability theory. For this reason, we include in the Appendices some auxiliary information as a service to the interested reader.
2. Kinematics and Thermodynamics of the Model
We consider a physical process in a
d-dimensional Euclidean space (
) modeled by a Langevin–Smoluchowski dynamics:
The stochastic differential
stands here for the increment of a standard
d-dimensional Wiener process at time
t [
6].
denotes a smooth scalar potential, and
is a constant sharing the same canonical dimensions as
U. We also suppose that the initial state of the system is specified by a smooth probability density:
Under rather general hypotheses, the Langevin–Smoluchowski Equation (
1) can be derived as the scaling limit of the overdamped non-equilibrium dynamics of a classical system weakly coupled to a heat bath [
27]. The Wiener process in (
1) thus embodies thermal fluctuations of order
. The fundamental simplification entailed by (
1) is the possibility to establish a framework of elementary relations linking the dynamical to the statistical levels of description of a non-equilibrium process [
14,
28]. In fact, the kinematics of (
1) ensures that for any time-autonomous, confining potential, the dynamics tends to a unique Boltzmann equilibrium state.
Building on the foregoing observations [
14], we may then identify
U over a finite-time horizon with the internal energy of the system. The differential of
U:
yields the energy balance in the presence of thermal fluctuations due to interactions with the environment. We use the notation
for the Stratonovich differential [
6]. From (
3), we recover the first law of thermodynamics by averaging over the realizations of the Wiener process. In particular, we interpret:
as the average work done on the system. Correspondingly,
is the average heat discarded by the system into the heat bath, and therefore:
is the embodiment of the first law.
The kinematics of stochastic processes [
29] allows us also to write a meaningful expression for the second law of thermodynamics. The expectation value of a Stratonovich differential is in general amenable to the form:
where:
is the current velocity. For a potential drift, the current velocity vanishes identically at equilibrium. As is well known from stochastic mechanics [
30,
31], the current velocity permits couching the Fokker–Planck equation into the form of a deterministic mass transport equation (see also
Appendix B). Hence, upon observing that:
we can recast (
7) into the form:
which we interpret as the second law of thermodynamics (see, e.g., [
32]). Namely, if we define
as the total entropy change in
, (
10) states that the sum of the entropy generated by heat released into the environment plus the change of the Gibbs–Shannon entropy of the system is positive definite and vanishes only at equilibrium. The second law in the form (
10) immediately implies a bound on the average work done on the system. To evince this fact, we avail ourselves of the equality:
and define the current velocity potential:
In equilibrium thermodynamics, the Helmholtz free energy is defined as the difference:
between the internal energy
and entropy
of a system at temperature
. This relation admits a non-equilibrium extension by noticing that the information content [
33] of the system probability density:
weighs the contribution of individual realizations of (
1) to the Gibbs–Shannon entropy. We refer to [
29] for the kinematic and thermodynamic interpretation of the information content as the osmotic potential. We also emphasize that the notions above can be given an intrinsic meaning using the framework of stochastic differential geometry [
17,
31]. Finally, it is worth noticing that the above relations can be regarded as a special case of macroscopic fluctuation theory [
34].
3. Non-Equilibrium Thermodynamics and Schrödinger Diffusion
We are interested in thermodynamic transitions between an initial state (
2) at time
and a pre-assigned final state at time
also specified by a smooth probability density:
We also suppose that the cumulative distribution functions of (
2) and (
12) are related by a Lagrangian map
such that:
According to the Langevin–Smoluchowski dynamics (
1), the evolution of probability densities obeys a Fokker–Planck equation, a first order in time partial differential equation. As a consequence, the price we pay to steer transitions between assigned states is to regard the drift in (
1) not as an assigned quantity, but as a control. A priori, a control is only implicitly characterized by the set of conditions that make it admissible. Informally speaking, admissible controls are all those drifts steering the process
between the assigned end states (
2) and (
12) while ensuring that at any time
, the Langevin–Smoluchowski dynamics remains well defined.
Schrödinger [
15] considered already in 1931 the problem of controlling a diffusion process between assigned states. His work was motivated by the quest for a statistical interpretation of quantum mechanics. In modern language [
35,
36], the problem can be rephrased as follows. Given (
2) and (
12) and a reference diffusion process, determine the diffusion process interpolating between (
2) and (
12) while minimizing the value of its Kullback–Leibler divergence (relative entropy) [
37] with respect to the reference process. A standard application (
Appendix A) of the Girsanov formula [
6] shows that the Kullback–Leibler divergence of (
1) with respect to the Wiener process is:
and
denote respectively the measures of the process solution of (
1) with drift
and of the Wiener process
. The expectation value on the right-hand side is with respect to
as elsewhere in the text. A now well-established result in optimal control theory (see, e.g., [
35,
36]) is that the optimal value of the drift satisfies a backward Burgers equation with the terminal condition specified by the solution of the Beurling–Jamison integral equations. We refer to [
35,
36] for further details. What interests us here is to emphasize the analogy with the problem of minimizing the entropy production
in a transition between assigned states.
Several observations are in order at this stage.
The first observation is that also (
10) can be directly interpreted as a Kullback–Leibler divergence between two probability measures. Namely, we can write (
Appendix A):
for
the path-space measure of the process:
evolving backward in time from the final condition (
12) [
38,
39].
The second observation has more far reaching consequences for optimal control. The entropy production depends on the drift of (
1) exclusively through the current velocity (
8). Hence, we can treat the current velocity itself as the natural control quantity for (
15). This fact entails major simplifications [
7]. The current velocity can be thought of as deterministic rather than as a stochastic velocity field (see [
29] and
Appendix B). Thus, we can couch the optimal control of (
15) into the problem of minimizing the kinetic energy of a classical particle traveling from an initial position
at time
and a final position
at time
specified by the Lagrangian map
ℓ (
13). In other words, entropy production minimization in the Langevin–Smoluchowski framework is equivalent to solving a classical optimal transport problem [
8].
The third observation comes as a consequence of the second one. The optimal value of the entropy production is equal to the Wasserstein distance [
40] between the initial and final probability measures of the system; see [
41] for details. This fact yields a simple characterization of the Landauer bound and permits a fully-explicit analysis of the thermodynamics of stylized isochoric micro-engines (see [
42] and the references therein).
Finally, the construction of Schrödinger diffusions via optimal control of (
14) corresponds to a viscous regularization of the optimal control equations occasioned by the Schrödinger diffusion problem (
15).
4. Pontryagin’s Principle for Bounded Accelerations
An important qualitative feature of the solution of the optimal control of the entropy production is that the system starts from (
2) and reaches (
12) with non-vanishing current velocity. This means that the entropy production attains a minimum value when the end-states of the transition are out-of-equilibrium. We refer to this lower bound as the refinement of the second law.
Engineered equilibration transitions are, however, subject to at least two further types of constraints not taken into account in the derivation of the refined second law. The first type of constraint is on the set of admissible controls. For example, admissible controls cannot vary in an arbitrary manner: the fastest time scale in the Langevin–Smoluchowski dynamics is set by the Wiener process. The second type is that end-states are at equilibrium. In mathematical terms, this means that the current velocity must vanish identically at and .
We formalize a deterministic control problem modeling these constraints. Our goal is to minimize the functional:
over the set of trajectories generated for any given choice of the measurable control
by the differential equation:
satisfying the boundary conditions:
We dub the dynamical variable
the running Lagrangian map as it describes the evolution of the Lagrangian map within the control horizon. We restrict the set of admissible controls
to those enforcing equilibration at the boundaries of the control horizon:
whilst satisfying the bound:
We suppose that the
are strictly positive functions of the initial data
of the form:
The constraint is non-holonomic inasmuch as it depends on the initial data of a trajectory. The proportionality (
22) relates the bound on acceleration to the Lagrangian displacement needed to satisfy the control problem. Finally, we emphasize that the rate of change
of the running Lagrangian map is related to the current velocity (
8) by a standard change of hydrodynamic coordinates from Lagrangian to Eulerian, which we write explicitly in formula (
33) below.
We resort to the Pontryagin principle [
13] to find normal extremals of (
17). We defer the statement of the Pontryagin principle, as well as the discussion of abnormal extremals to
Appendix C. We proceed in two steps. We first avail ourselves of Lagrange multipliers to define the effective cost functional:
subject to the boundary conditions (
19) and (
20). Then, we couch the cost functional into an explicit Hamiltonian form:
with:
Pontryagin’s principle yields a rigorous proof of the intuition that extremals of the optimal control equations correspond to stationary curves of the action (
23) with Hamiltonian:
In view of the boundary conditions (
19), (
20), extremals satisfy the Hamilton system of equations formed by (
18a) and:
In writing (
24a), we adopt the convention:
5. Explicit Solution in the Case
The extremal Equations (
18a) and (
24) are time-autonomous and do not couple distinct vector components. It is therefore not too restrictive to focus on the
case in the time horizon
.
The Hamilton equations are compatible with two behaviors: a “push-region” where the running Lagrangian map variable evolves with constant acceleration:
and a “no-action” region specified by the conditions:
where
follows a free streaming trajectory:
We call switching times the values of
t corresponding to the boundary values of a no-action region. Switching times correspond to discontinuities of the acceleration
. Drawing from the intuition offered by the solution of the unbounded acceleration case, we compose push and no-action regions to construct a single solution trajectory satisfying the boundary conditions. If we surmise that during the control horizon, only two switching times occur, we obtain:
The self-consistence of the solution fixes the initial data in (
27):
whilst the requirement of vanishing velocity at
determines the relation between the switching times:
Self-consistence then dictates:
We are now ready to glean the information we unraveled by solving (
24), to write the solution of (
18a):
The terminal condition on
fixes the values of
and
:
The equation for
is well posed only if:
The only admissible solution is then of the form:
The switching time is independent of
q in view of (
22). It is realizable as long as:
The threshold value of corresponds to the acceleration needed to construct an optimal protocol consisting of two push regions matched at the half control horizon.
Qualitative Properties of the Solution
Equation (
28) complemented by (
29) and the realizability bound (
31) fully specify the solution of the optimization problem we set out to solve. The solution is optimal because it is obtained by composing locally-optimal solutions for a Markovian dynamics. Qualitatively, it states that transitions between equilibrium states are possible at the price of the formation of symmetric boundary layers determined by the occurrence of the switching times. For
, the relative size of the boundary layers is:
In the same limit, the behavior of the current velocity far from the boundaries tends to the optimal value of the refined second law [
7]. Namely, for
, we find:
More generally, for any
, we can couch (
28) into the form:
The use of the value of the switching time
to parametrize the bound simplifies the derivation of the Eulerian representation of the current velocity. Namely, in order to find the field
satisfying:
We can invert (
32) by taking advantage of the fact that all of the arguments of the curly brackets are independent of the position variable
q.
We also envisage that the representation (
32) may be of use to analyze experimental data when finite measurement resolution may affect the precision with which microscopic forces acting on the system are known.
6. Comparison with Experimental Swift Engineering Protocols
The experiment reported in [
4] showed that a micro-sphere immersed in water and trapped in an optical harmonic potential can be driven in finite-time from one equilibrium state to another. The probability distribution of the particle in and out of equilibrium remained Gaussian within the experimental accuracy.
It is therefore expedient to describe more in detail the solution of the optimal control problem in the case when the initial equilibrium distribution in one dimension is normal, i.e., Gaussian with zero mean and variance
. We also assume that the final equilibrium state is Gaussian and satisfies (
13) with Lagrangian map:
The parameters
h and
respectively describe a change of the mean and of the variance of the distribution. We apply (
13) and (
32) for any
to derive the minimum entropy production evolution of the probability density. As a consequence of (
22), the running Lagrangian map leaves Gaussian distributions invariant in form with mean value:
Finally, we find that the Eulerian representation (
33) of the current velocity at
is:
From (
34)–(
36), we can derive explicit expressions for all of the thermodynamic quantities governing the energetics of the optimal transition. In particular, we obtain the drift in the Langevin–Smoluchowski dynamics (
1) by inverting (
8) as in [
7]:
The minimum entropy production is:
with:
the value of the minimum entropy production appearing in the refinement of the second law [
7].
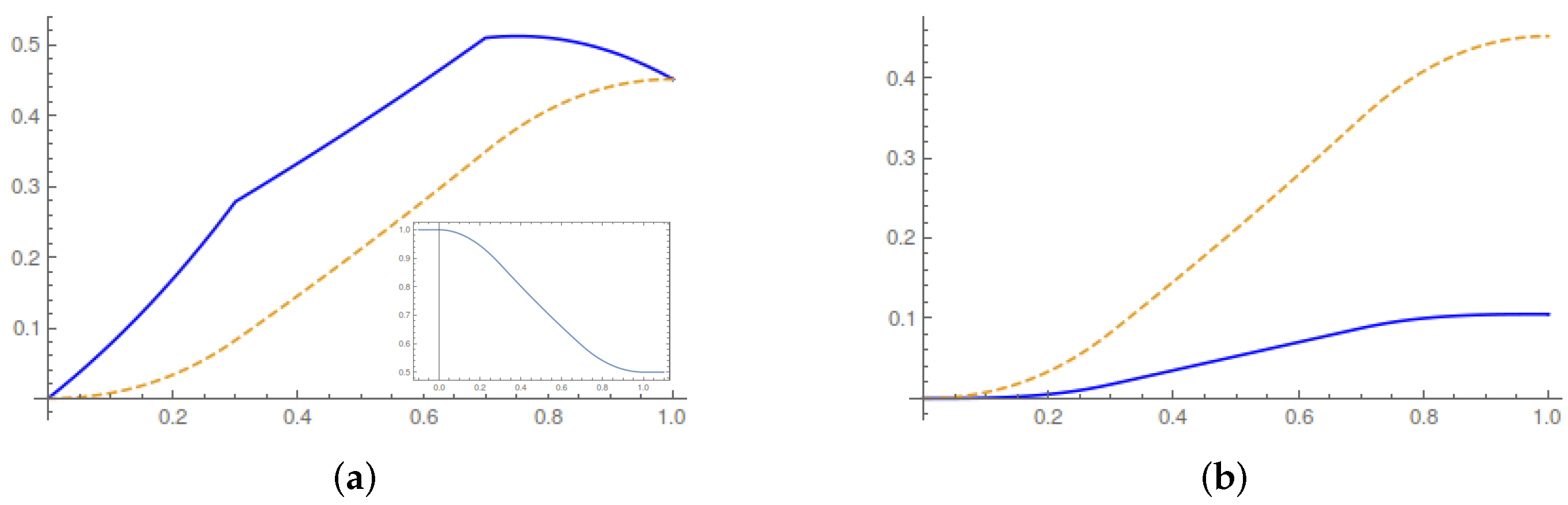
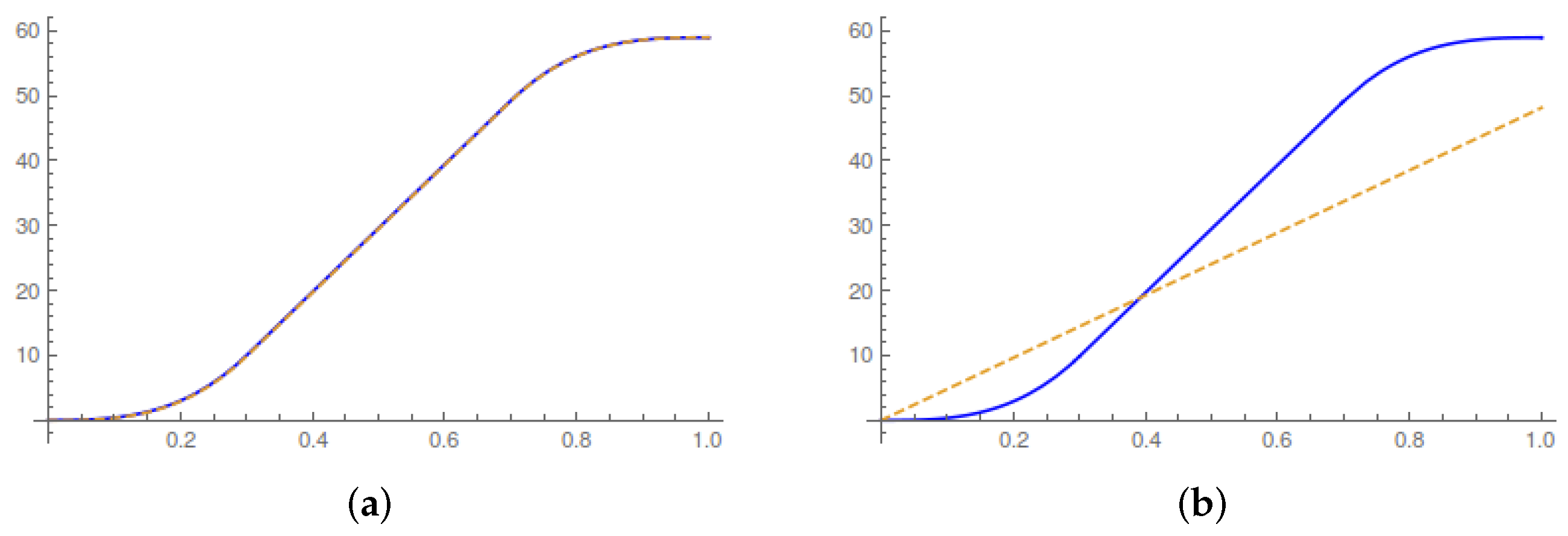
In
Figure 1, we plot the evolution of the running average values of the work done on the system, the heat released and the entropy production during the control horizon. In particular,
Figure 1a illustrates the first law of thermodynamics during the control horizon. A transition between Gaussian equilibrium states occurs without any change in the internal energy of the system. The average heat and work must therefore coincide at the end of the control horizon. The theoretical results are consistent with the experimental results of [
4].
7. Optimally-Controlled Nucleation and Landauer Bound
The form of the bound (
22) and running Lagrangian map Formula (
32) reduce the computational cost of the solution of the optimal entropy production control to the determination of the Lagrangian map (
13). In general, the conditions presiding over the qualitative properties of the Lagrangian map have been studied in depth in the context of optimal mass transport [
8]. We refer to [
11,
41] respectively for a self-contained overview from respectively the mathematics an physics slant.
For illustrative purposes, we revisit here the stylized model of nucleation analyzed in [
7]. Specifically, we consider the transition between two equilibria in one dimension. The initial state is described by the symmetric double well:
In the final state, the probability is concentrated around a single minimum of the potential:
In the foregoing expressions, is a constant ensuring the consistency of the canonical dimensions.
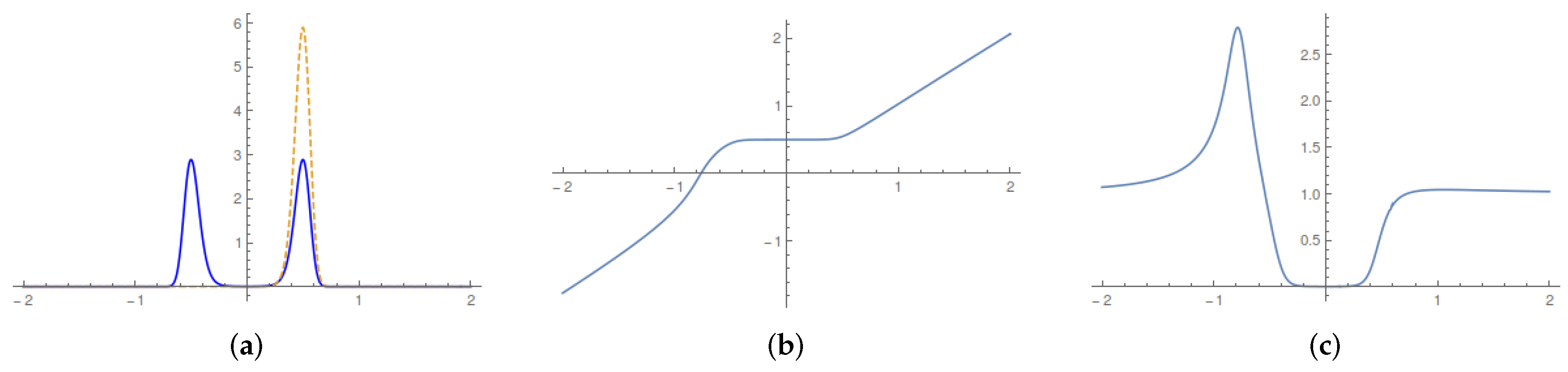
We used the ensuing elementary algorithm to numerically determine the Lagrangian map. We first computed the median of the assigned probability distributions and then evaluated first the left and then right branch of the Lagrangian map. For the left branch, we proceeded iteratively in as follows:
- Step 1
We renormalized the distribution restricted to .
- Step 2
We computed the quantile of the remaining distribution.
- Step 3
We skipped Step 3 whenever the difference
turned out to be smaller than a given threshold ‘resolution’. We plot the results of this computation in
Figure 2.
Once we know the Lagrangian map, we can numerically evaluate the running Lagrangian map (
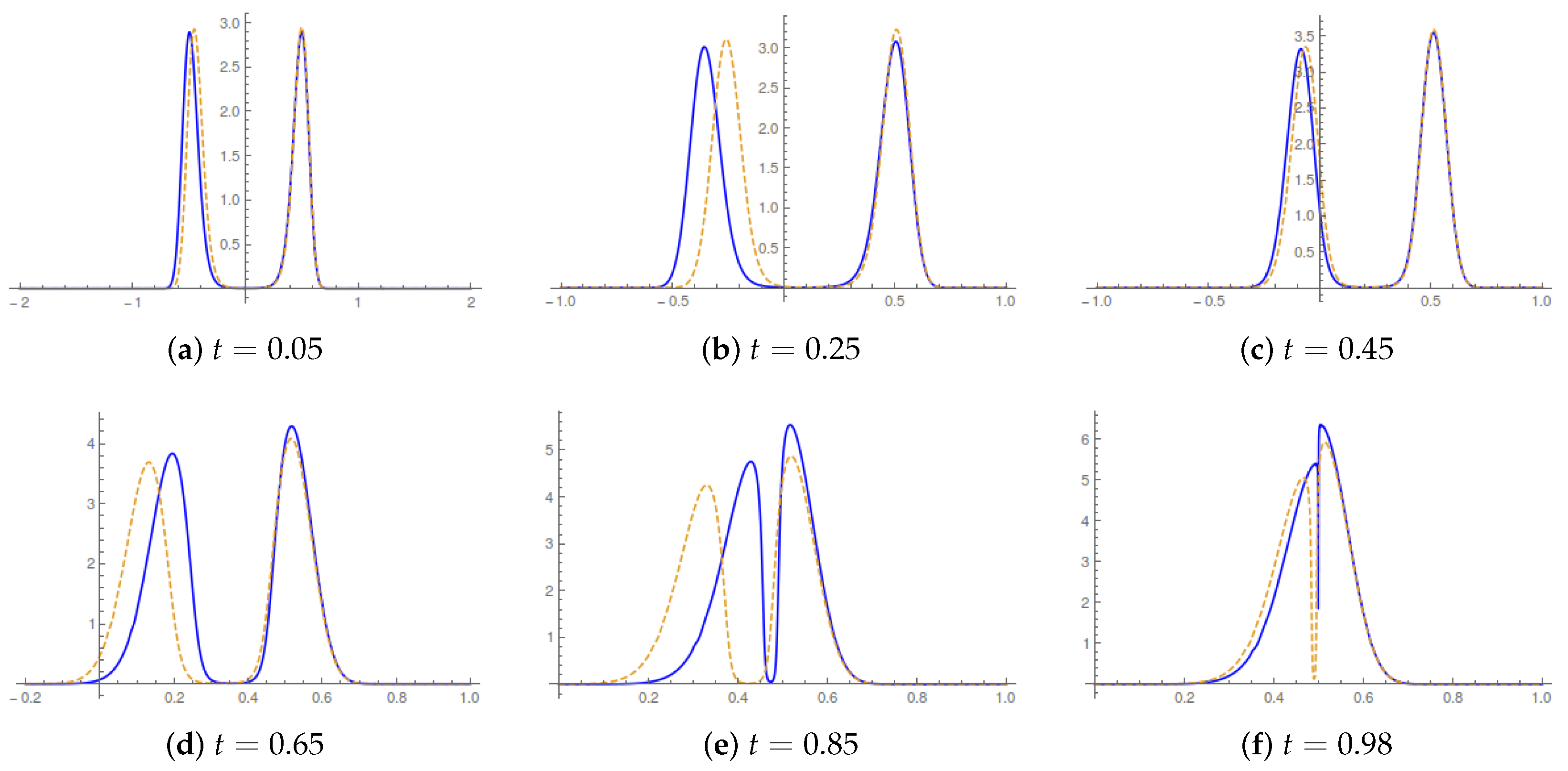
32) and its spatial derivatives. In
Figure 3, we report the evolution of the probability density in the control horizon for two reference values of the switching time.
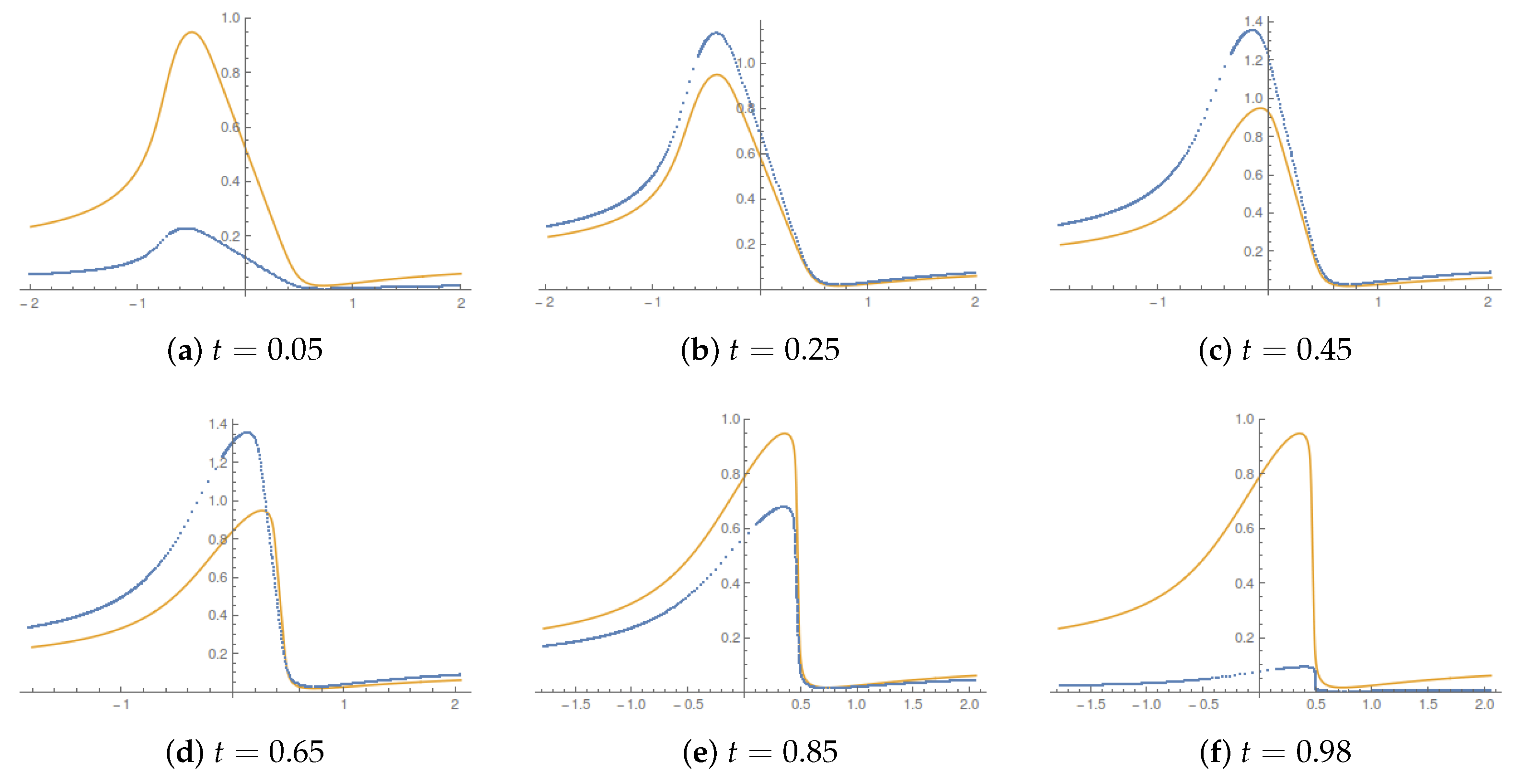
Figure 4 illustrates the the corresponding evolution of the current velocity.
The qualitative behavior is intuitive. The current velocity starts and ends with a vanishing value; it catches up with the value for
, i.e., when the bound on acceleration tends to infinity, in the bulk of the control horizon. There, the displacement described by the running Lagrangian map occurs at a speed higher than in the
case. The overall value of the entropy production is always higher than in the
limit. From (
32), we can also write the running values of average heat released by the system. The running average heat is:
and the running average work:
The second summand on the right-hand side of (
39) fixes the arbitrary constant in the Helmholtz potential in the same way as in the Gaussian case.
In
Figure 5, we plot the running average work, heat and entropy production.
8. Comparison with the Valley Method Regularization
An alternative formalism to study transitions between equilibrium states in the Langevin–Smoluchowski limit was previously proposed in [
25]. As in the present case, Ref. [
25] takes advantage of the possibility to map the stochastic optimal control problem into a deterministic one via the current velocity formalism. Physical constraints on admissible controls are, however, enforced by adding to the entropy production rate a penalty term proportional to the squared current acceleration. In terms of the entropy production functional (
17), we can couch the regularized functional of [
25] into the form:
stands for the variation of
with respect to the running Lagrangian map. The idea behind the approach is the “valley method” advocated by [
26] for instanton calculus. The upshot is to approximate field configurations satisfying boundary conditions incompatible with stationary values of classical variational principles by adding extra terms to the action functional. The extra term is proportional to the squared first variation of the classical action. Hence, it vanishes whenever there exists a classical field configurations matching the desired boundary conditions. It otherwise raises the order of the time derivative in the problem, thus permitting one to satisfy extra boundary conditions.
Optimal control problems are well posed if terminal costs are pure functionals of the boundary conditions. The rationale for considering valley method-regularized thermodynamic functionals is to give a non-ambiguous meaning to the optimization of functionals whenever naive formulations of the problem yield boundary conditions or terminal costs as the functional of the controls.
Contrasted with the approach proposed in the present work, [
25] has one evident drawback and one edge. The drawback is that the quantities actually minimized are no longer the original thermodynamic functionals. The edge is that the resulting optimal protocol has better analyticity properties. In particular, the running Lagrangian map takes the form:
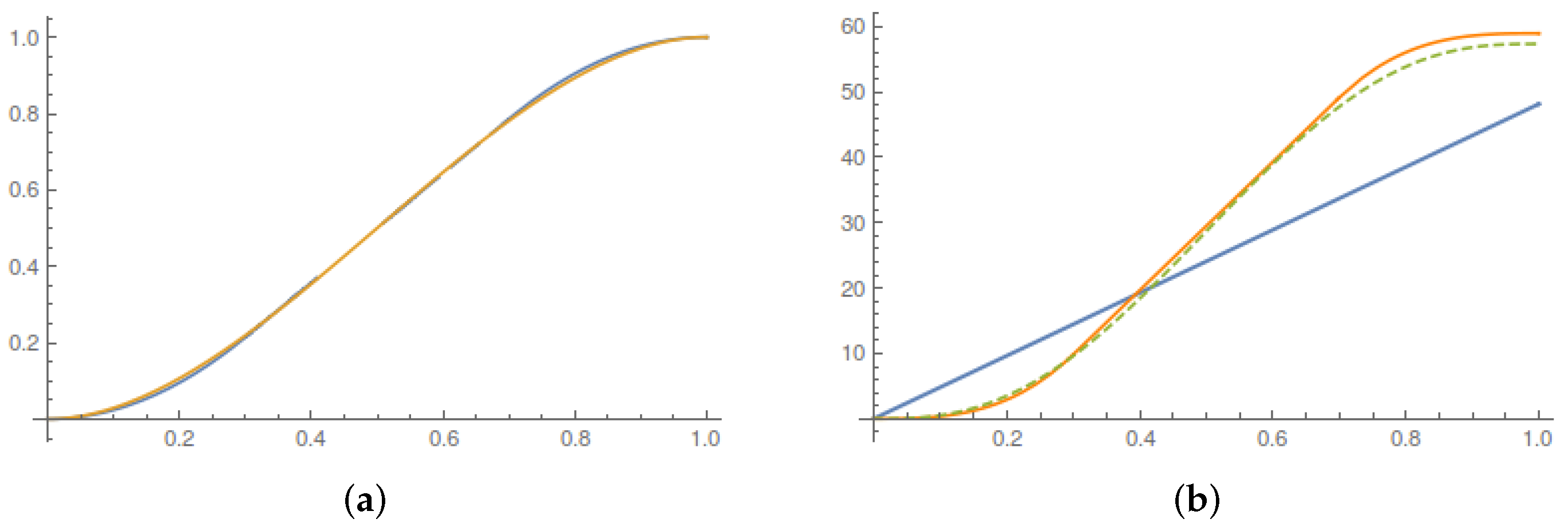
In
Figure 6a, we compare the qualitative behavior of the universal part of the running Lagrangian map predicted by the valley method and by the bound (
21) on admissible current accelerations. The corresponding values of the running average entropy production are in
Figure 6b.
The upshot of the comparison is the weak sensitivity of the optimal protocol to the detail of the optimization once the intensity of the constraint on the admissible control (i.e., the current acceleration) is fixed. We believe that this is an important observation for experimental applications (see, e.g., the discussion in the conclusions of [
24]), as the details of how control parameters can be turned on and off in general depend on the detailed laboratory setup and on the restrictions by the available peripherals.
9. Conclusions and Outlooks
We presented a stylized model of engineered equilibration of a micro-system. Owing to explicit integrability modulo numerical reconstruction of the Lagrangian map, we believe that our model may provide a useful benchmark for the devising of efficient experimental setups. Furthermore, extensions of the current model are possible, although at the price of some complications.
The first extension concerns the form of the constraint imposed on admissible protocols. Here, we showed that choosing the current acceleration constraint in the form of (
22) greatly simplifies the determination of the switching times. It also guarantees that optimal control with only two switching times exists for all boundary conditions if we allow accelerations to take sufficiently large values. The non-holonomic form of the constraint (
21) may turn out to be restrictive for the study of transitions for which admissible controls are specified by given forces. If the current velocity formalism is still applicable to these cases, then the design of optimal control still follows the steps we described here. In particular, uniformly-accelerated Lagrangian displacement at the end of the control horizon correspond to the first terms of the integration of the Newton law in Peano–Picard series. The local form of the acceleration may then occasion some qualitative differences in the form of the running Lagrangian map. Furthermore, the analysis of the realizability conditions of the optimal control may also become more involved.
A further extension is optimal control when constraints on admissible controls are imposed directly on the drift field appearing in the stochastic evolution equation. Constraints of this type are natural when inertial effects become important and the dynamics is governed by the Langevin–Kramers equation in the so-called under-damped approximation. In the Langevin–Kramers framework, finding minimum entropy production thermodynamic transitions requires instead a full-fledged formalism of stochastic optimal control [
42]. Nevertheless, it is possible also in that case to proceed in a way analogous to the one of the present paper by applying the stochastic version of the Pontryagin principle [
43,
44,
45].
We expect that considering these theoretical refinements will be of interest in view of the increasing available experimental resolution for the efficient design of atomic force microscopes [
3,
46].