Tidal Analysis Using Time–Frequency Signal Processing and Information Clustering
Abstract
1. Introduction
2. Mathematical Fundamentals
2.1. Multitaper Method
2.2. Fractional Fourier Transform
2.3. Wavelet Transform
2.4. Jensen–Shannon Divergence
2.5. Hierarchichal Clustering
3. Dataset
4. Analysis and Visualization of Tidal Data
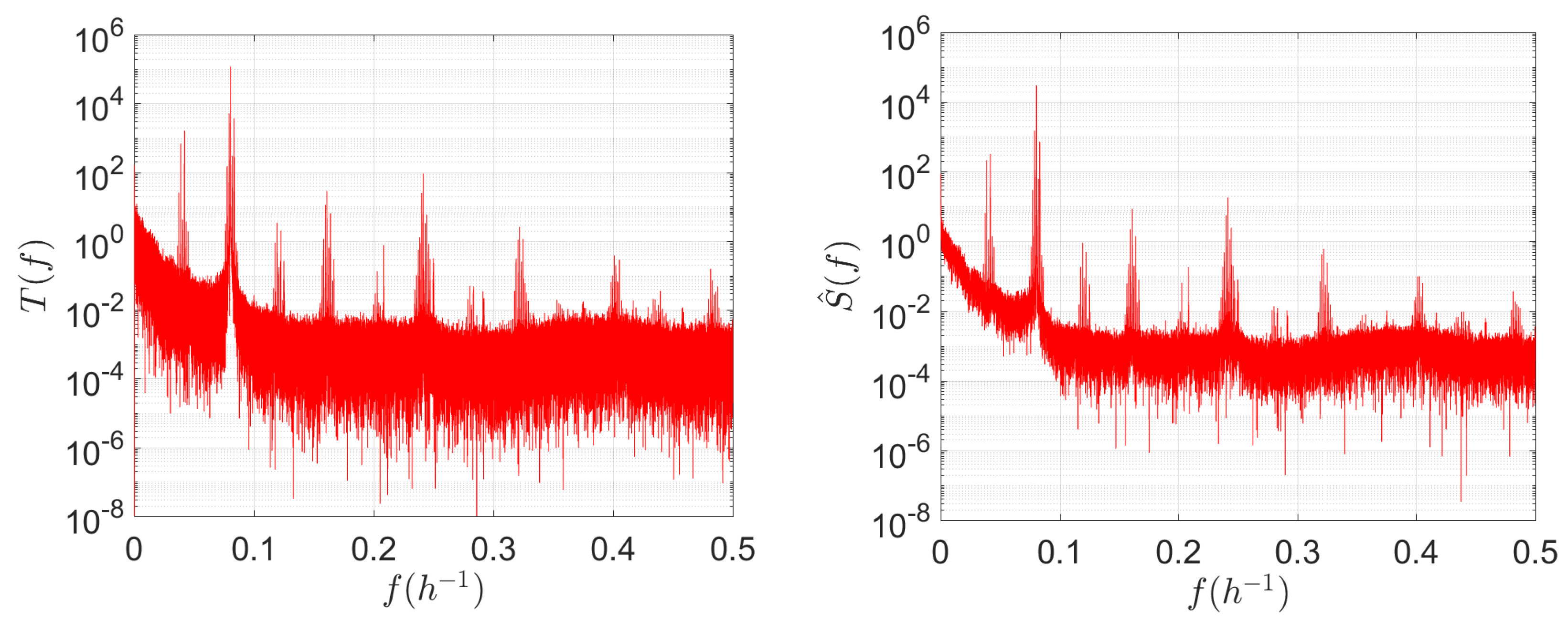
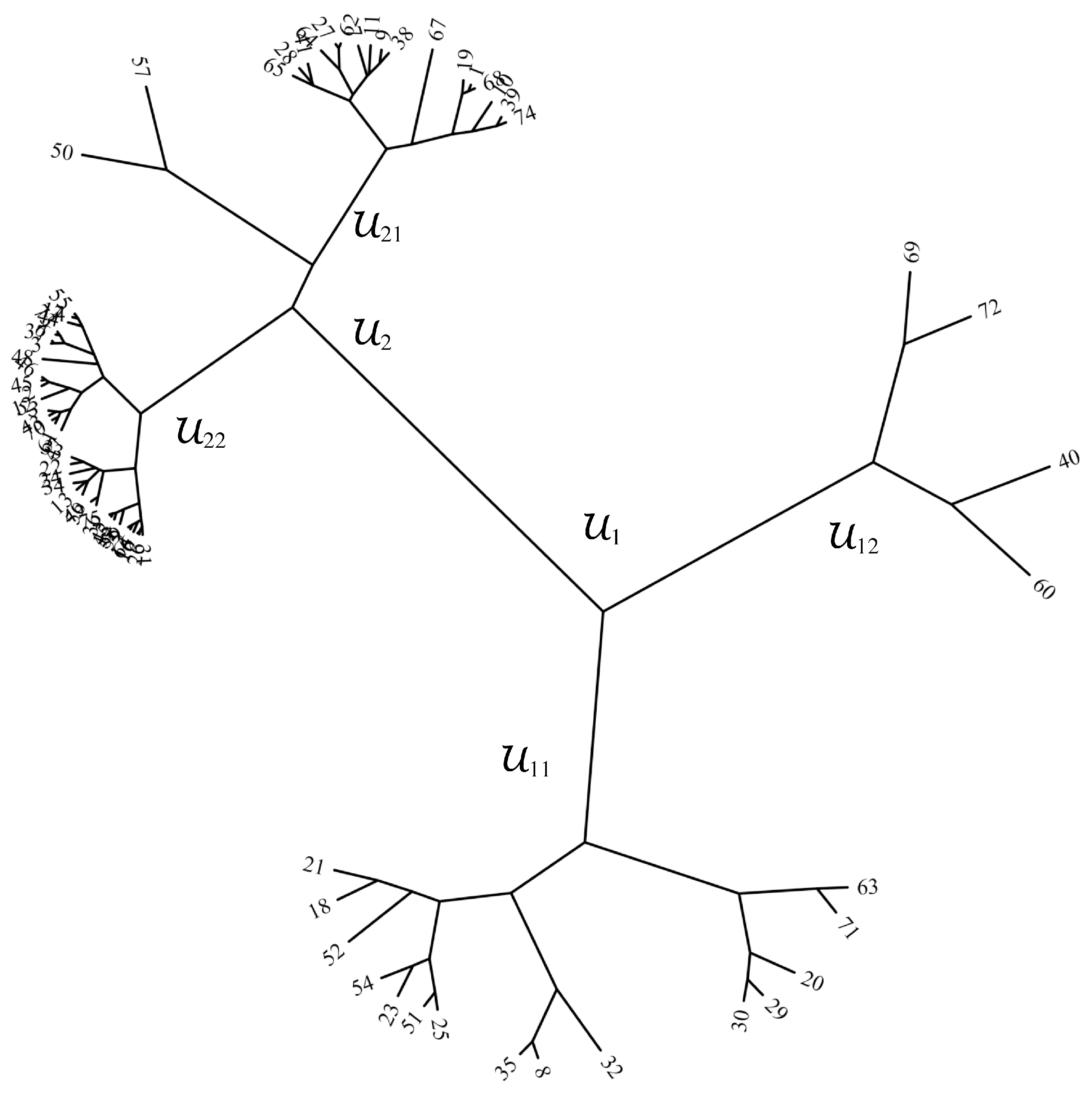
4.1. HC Analysis in the Frequency Domain
4.2. HC Analysis in the Time–Frequency Domain
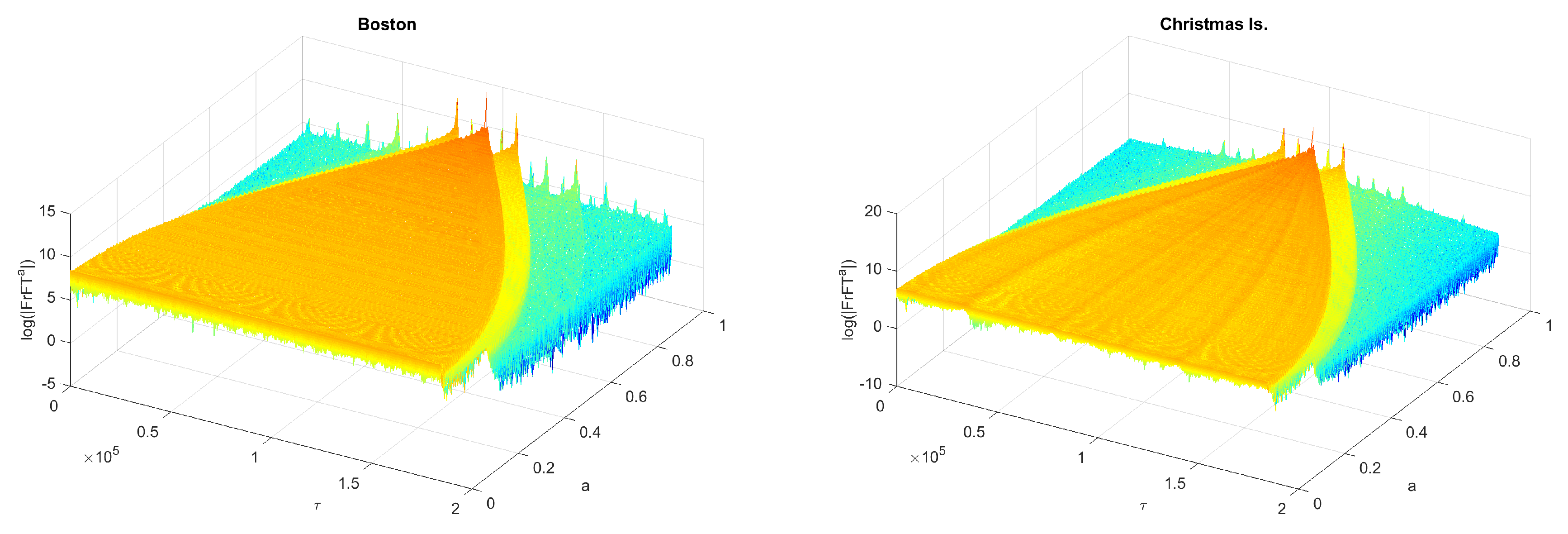
4.2.1. The FFrT-Based Approach
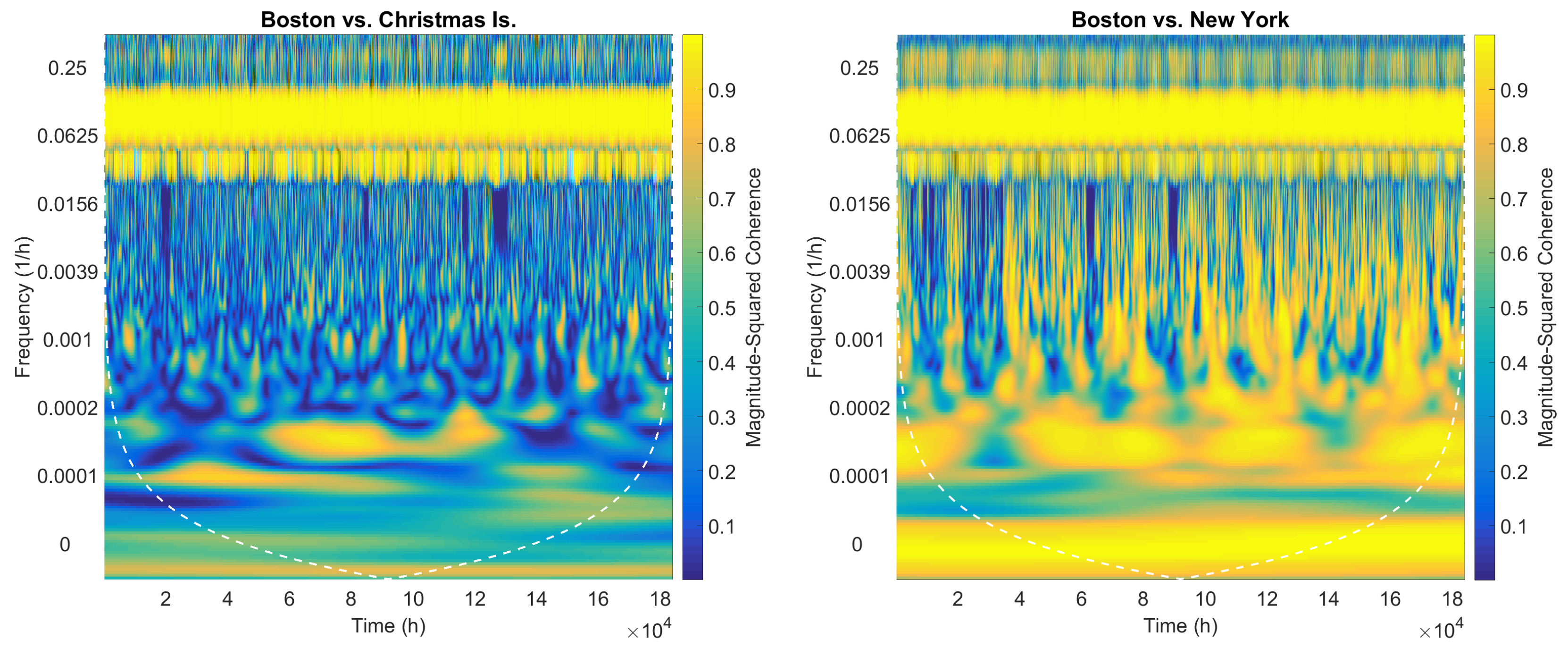
4.2.2. The CWT-Based Approach
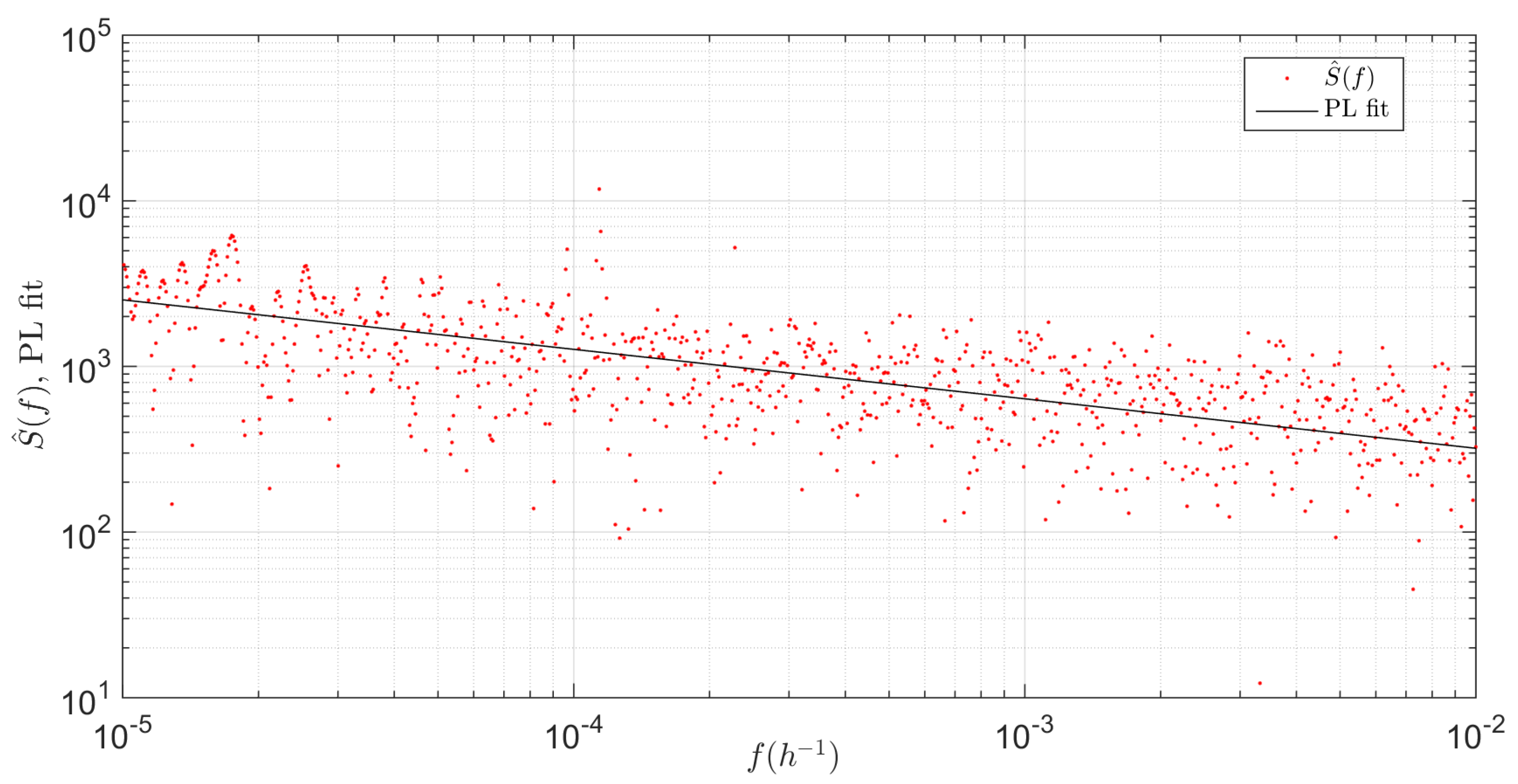
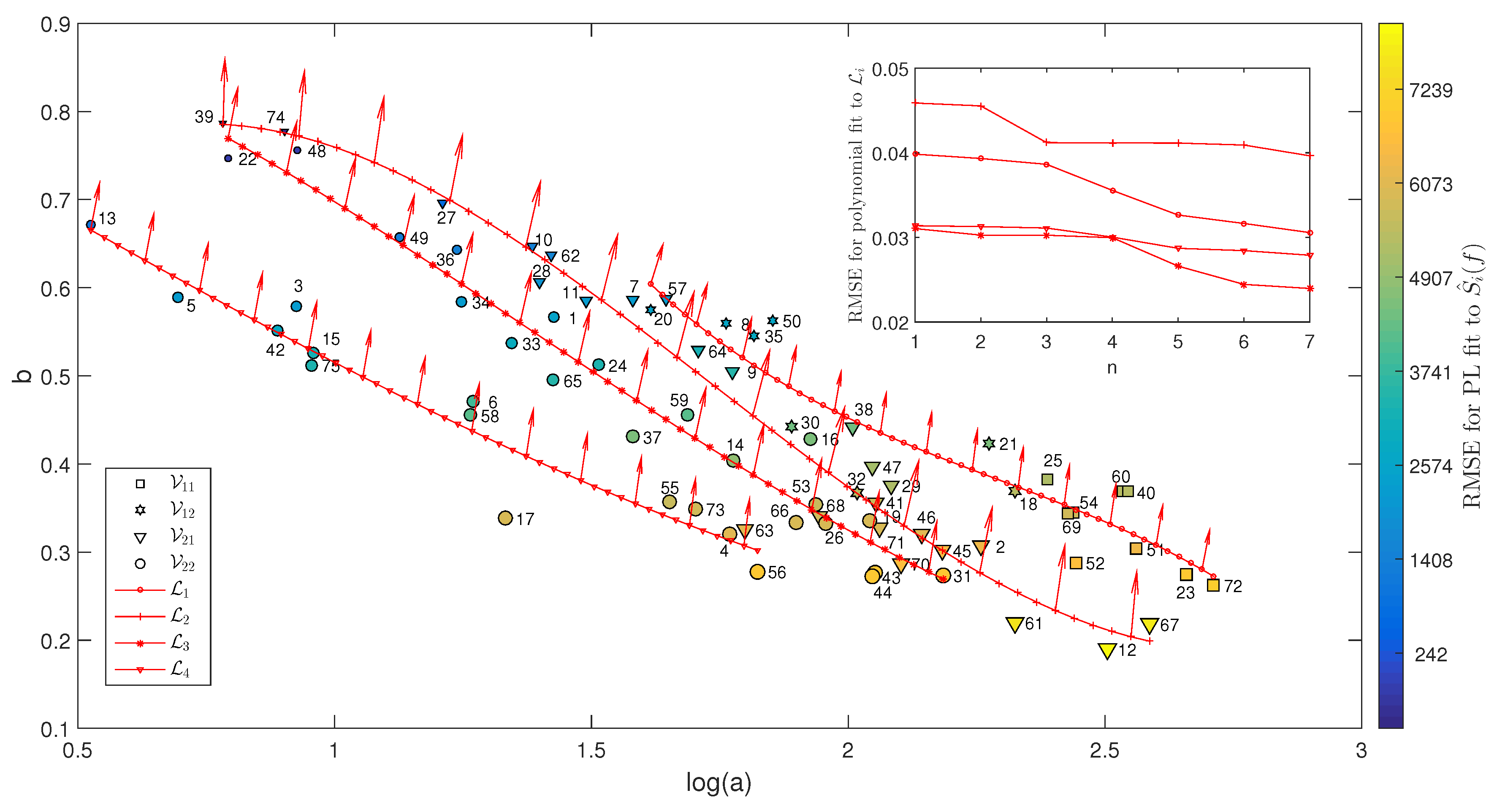
5. Long-Range Behavior of Tides
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin, Germany, 1981; pp. 366–381. [Google Scholar]
- Dergachev, V.A.; Gorban, A.; Rossiev, A.; Karimova, L.; Kuandykov, E.; Makarenko, N.; Steier, P. The filling of gaps in geophysical time series by artificial neural networks. Radiocarbon 2001, 43, 365–371. [Google Scholar]
- Ghil, M.; Allen, M.; Dettinger, M.; Ide, K.; Kondrashov, D.; Mann, M.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; Yiou, P. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 1–41. [Google Scholar]
- Stein, E.M.; Shakarchi, R. Fourier Analysis: An Introduction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Dym, H.; McKean, H. Fourier Series and Integrals; Academic Press: San Diego, CA, USA, 1972. [Google Scholar]
- Wu, D.L.; Hays, P.B.; Skinner, W.R. A least squares method for spectral analysis of space-time series. J. Atmos. Sci. 1995, 52, 3501–3511. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Phys. D Nonlinear Phenom. 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Thomson, D.J. Multitaper analysis of nonstationary and nonlinear time series data. In Nonlinear and Nonstationary Signal Processing; Cambridge University Press: London, UK, 2000; pp. 317–394. [Google Scholar]
- Ding, H.; Chao, B.F. Detecting harmonic signals in a noisy time-series: The z-domain Autoregressive (AR-z) spectrum. Geophys. J. Int. 2015, 201, 1287–1296. [Google Scholar] [CrossRef]
- Donelan, M.; Babanin, A.; Sanina, E.; Chalikov, D. A comparison of methods for estimating directional spectra of surface waves. J. Geophys. Res. Oceans 2015, 120, 5040–5053. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis; Prentice-Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Almeida, L.B. The fractional Fourier transform and time–frequency representations. IEEE Trans. Signal Process. 1994, 42, 3084–3091. [Google Scholar] [CrossRef]
- Sejdić, E.; Djurović, I.; Stanković, L. Fractional Fourier transform as a signal processing tool: An overview of recent developments. Signal Process. 2011, 91, 1351–1369. [Google Scholar]
- Portnoff, M. Time-frequency representation of digital signals and systems based on short-time Fourier analysis. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 55–69. [Google Scholar]
- Qian, S.; Chen, D. Joint time-frequency analysis. IEEE Signal Process. Mag. 1999, 16, 52–67. [Google Scholar]
- Kemao, Q. Windowed Fourier transform for fringe pattern analysis. Appl. Opt. 2004, 43, 2695–2702. [Google Scholar] [CrossRef] [PubMed]
- Hlubina, P.; Luňáček, J.; Ciprian, D.; Chlebus, R. Windowed Fourier transform applied in the wavelength domain to process the spectral interference signals. Opt. Commun. 2008, 281, 2349–2354. [Google Scholar] [CrossRef]
- Qian, S.; Chen, D. Discrete Gabor Transform. IEEE Trans. Signal Process. 1993, 41, 2429–2438. [Google Scholar] [CrossRef]
- Yao, J.; Krolak, P.; Steele, C. The generalized Gabor transform. IEEE Trans. Image Process. 1995, 4, 978–988. [Google Scholar] [PubMed]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: Burlington, VT, USA, 1999. [Google Scholar]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Zayed, A.I. Hilbert transform associated with the fractional Fourier transform. IEEE Signal Process. Lett. 1998, 5, 206–208. [Google Scholar] [CrossRef]
- Peng, Z.; Peter, W.T.; Chu, F. A comparison study of improved Hilbert–Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Process. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Olsson, J.; Niemczynowicz, J.; Berndtsson, R. Fractal analysis of high-resolution rainfall time series. J. Geophys. Res. Atmos. 1993, 98, 23265–23274. [Google Scholar] [CrossRef]
- Matsoukas, C.; Islam, S.; Rodriguez-Iturbe, I. Detrended fluctuation analysis of rainfall and streamflow time series. J. Geophys. Res. 2000, 105, 29165–29172. [Google Scholar] [CrossRef]
- Marwan, N.; Donges, J.F.; Zou, Y.; Donner, R.V.; Kurths, J. Complex network approach for recurrence analysis of time series. Phys. Lett. A 2009, 373, 4246–4254. [Google Scholar] [CrossRef]
- Donner, R.V.; Donges, J.F. Visibility graph analysis of geophysical time series: Potentials and possible pitfalls. Acta Geophys. 2012, 60, 589–623. [Google Scholar] [CrossRef]
- Machado, J.T. Fractional order description of DNA. Appl. Math. Model. 2015, 39, 4095–4102. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.T. Integer and fractional-order entropy analysis of earthquake data series. Nonlinear Dyn. 2016, 84, 79–90. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Lopes, A.M. Analysis and visualization of seismic data using mutual information. Entropy 2013, 15, 3892–3909. [Google Scholar] [CrossRef]
- Machado, J.A.; Mata, M.E.; Lopes, A.M. Fractional state space analysis of economic systems. Entropy 2015, 17, 5402–5421. [Google Scholar] [CrossRef]
- Jalón-Rojas, I.; Schmidt, S.; Sottolichio, A. Evaluation of spectral methods for high-frequency multiannual time series in coastal transitional waters: Advantages of combined analyses. Limnol. Oceanogr. Methods 2016, 14, 381–396. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L. Self-affine time series: I. Generation and analyses. Adv. Geophys. 1999, 40, 1–90. [Google Scholar]
- Gong, D.; Feng, L.; Li, X.T.; Zhao, J.-M.; Liu, H.-B.; Wang, X.; Ju, C.-H. The Application of S-transform Spectrum Decomposition Technique in Extraction of Weak Seismic Signals. Chin. J. Geophys. 2016, 59, 43–53. [Google Scholar] [CrossRef]
- Forootan, E.; Kusche, J. Separation of deterministic signals using independent component analysis (ICA). Stud. Geophys. Geod. 2013, 57, 17–26. [Google Scholar] [CrossRef]
- Donner, R.V.; Zou, Y.; Donges, J.F.; Marwan, N.; Kurths, J. Recurrence networks—A novel paradigm for nonlinear time series analysis. New J. Phys. 2010, 12, 033025. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.T. Analysis of temperature time-series: Embedding dynamics into the MDS method. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 851–871. [Google Scholar] [CrossRef]
- Machado, J.T.; Lopes, A.M. The persistence of memory. Nonlinear Dyn. 2015, 79, 63–82. [Google Scholar] [CrossRef]
- Pugh, D.; Woodworth, P. Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Shankar, D. Seasonal cycle of sea level and currents along the coast of India. Curr. Sci. 2000, 78, 279–288. [Google Scholar]
- Erol, S. Time-frequency analyses of tide-gauge sensor data. Sensors 2011, 11, 3939–3961. [Google Scholar] [CrossRef] [PubMed]
- Brigham, E.O. The Fast Fourier Transform and Its Applications; Number 517.443; Prentice Hall: Upper Sadlle River, NJ, USA, 1988. [Google Scholar]
- Prieto, G.; Parker, R.; Thomson, D.; Vernon, F.; Graham, R. Reducing the bias of multitaper spectrum estimates. Geophys. J. Int. 2007, 171, 1269–1281. [Google Scholar] [CrossRef]
- Thomson, D.J. Spectrum estimation and harmonic analysis. Proc. IEEE 1982, 70, 1055–1096. [Google Scholar] [CrossRef]
- Slepian, D. Prolate spheroidal wave functions, Fourier analysis, and uncertainty–V: The discrete case. Bell Labs Tech. J. 1978, 57, 1371–1430. [Google Scholar] [CrossRef]
- Fodor, I.K.; Stark, P.B. Multitaper spectrum estimation for time series with gaps. IEEE Trans. Signal Process. 2000, 48, 3472–3483. [Google Scholar]
- Smith-Boughner, L.; Constable, C. Spectral estimation for geophysical time-series with inconvenient gaps. Geophys. J. Int. 2012, 190, 1404–1422. [Google Scholar] [CrossRef]
- Bultheel, A.; Sulbaran, H.E.M. Computation of the fractional Fourier transform. Appl. Comput. Harmon. Anal. 2004, 16, 182–202. [Google Scholar] [CrossRef]
- Ozaktas, H.M.; Zalevsky, Z.; Kutay, M.A. The Fractional Fourier Transform; Wiley: Chichester, UK, 2001. [Google Scholar]
- Machado, J.T.; Costa, A.C.; Quelhas, M.D. Wavelet analysis of human DNA. Genomics 2011, 98, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Cattani, C. Wavelet and Wave Analysis as Applied to Materials with Micro or Nanostructure; World Scientific: Singapore, 2007; Volume 74. [Google Scholar]
- Stark, H.G. Wavelets and Signal Processing: An Application-Based Introduction; Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar]
- Ngui, W.K.; Leong, M.S.; Hee, L.M.; Abdelrhman, A.M. Wavelet analysis: Mother wavelet selection methods. Appl. Mech. Mater. 2013, 393, 953–958. [Google Scholar] [CrossRef]
- Cui, X.; Bryant, D.M.; Reiss, A.L. NIRS-based hyperscanning reveals increased interpersonal coherence in superior frontal cortex during cooperation. Neuroimage 2012, 59, 2430–2437. [Google Scholar] [CrossRef] [PubMed]
- Jeong, D.H.; Kim, Y.D.; Song, I.U.; Chung, Y.A.; Jeong, J. Wavelet Energy and Wavelet Coherence as EEG Biomarkers for the Diagnosis of Parkinson’s Disease-Related Dementia and Alzheimer’s Disease. Entropy 2015, 18, 8. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Sato, A.H. Frequency analysis of tick quotes on the foreign exchange market and agent-based modeling: A spectral distance approach. Phys. A Stat. Mech. Appl. 2007, 382, 258–270. [Google Scholar] [CrossRef]
- Felsenstein, J. PHYLIP (Phylogeny Inference Package) version 3.6. Distributed by the author. Department of Genome Sciences, University of Washington, Seattle. Available online: http://evolution.genetics.washington.edu/phylip.html (accessed on 29 July 2017).
- Tenreiro Machado, J.; Duarte, F.B.; Duarte, G.M. Analysis of stock market indices with multidimensional scaling and wavelets. Math. Probl. Eng. 2012, 2012, 819503. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.A.T. Fractional order models of leaves. J. Vib. Control 2014, 20, 998–1008. [Google Scholar] [CrossRef]
- Baleanu, D. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Keshner, M.S. 1/f noise. Proc. IEEE 1982, 70, 212–218. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Macmillan: London, UK, 1983; Volume 173. [Google Scholar]
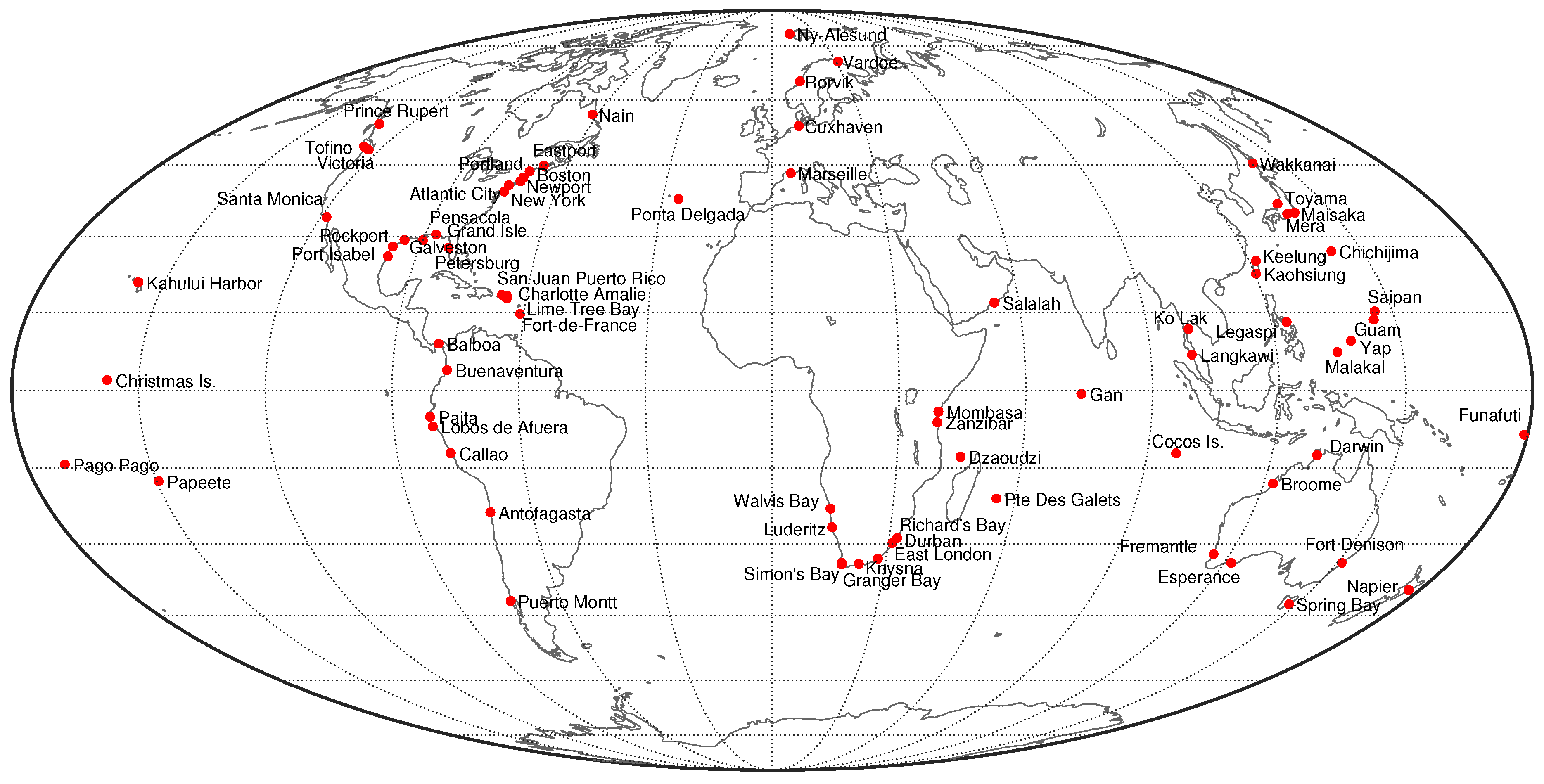




| Label | Name | Missing Data (%) | Label | Name | Missing Data (%) | Label | Name | Missing Data (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | Antofagasta | 5.4 | 26 | Granger Bay | 47.1 | 51 | Pensacola | 4.3 |
| 2 | Atlantic City | 3.5 | 27 | Guam | 11.4 | 52 | Petersburg | 0.6 |
| 3 | Balboa | 1.8 | 28 | Kahului Harbor | 0.3 | 53 | Ponta Delgada | 16.7 |
| 4 | Boston | 0.5 | 29 | Kaohsiung | 4.8 | 54 | Port Isabel | 0.4 |
| 5 | Broome | 1.7 | 30 | Keelung | 23.2 | 55 | Portland | 0.9 |
| 6 | Buenaventura | 12.9 | 31 | Knysna | 40.4 | 56 | Prince Rupert | 0.2 |
| 7 | Callao | 4.4 | 32 | Ko Lak | 5.3 | 57 | Pte Des Galets | 23.1 |
| 8 | Charlotte Amalie | 3.9 | 33 | Langkawi | 1.4 | 58 | Puerto Montt | 5.3 |
| 9 | Chichijima | 0 | 34 | Legaspi | 16.9 | 59 | Richard’s Bay | 36.4 |
| 10 | Christmas Is | 6.9 | 35 | Lime Tree Bay | 0.4 | 60 | Rockport | 0.1 |
| 11 | Cocos Is. | 0.9 | 36 | Lobos de Afuera | 14.8 | 61 | Rorvik | 15.2 |
| 12 | Cuxhaven | 0 | 37 | Luderitz | 63.8 | 62 | Saipan | 13.5 |
| 13 | Darwin | 0.2 | 38 | Maisaka | 0.1 | 63 | Salalah | 14.7 |
| 14 | Durban | 39.6 | 39 | Malakal | 1 | 64 | San Juan Puerto Rico | 1 |
| 15 | Dzaoudzi | 65.6 | 40 | Marseille | 31.5 | 65 | Santa Monica | 1.5 |
| 16 | East London | 37.6 | 41 | Mera | 0 | 66 | Simon’s Bay | 41.3 |
| 17 | Eastport | 2.4 | 42 | Mombasa | 30.5 | 67 | Spring Bay | 0.6 |
| 18 | Esperance | 2.5 | 43 | Nain | 50.8 | 68 | Tofino | 2.8 |
| 19 | Fort Denison | 1 | 44 | Napier | 19.4 | 69 | Toyama | 0 |
| 20 | Fort-de-France | 57.5 | 45 | New York | 13.1 | 70 | Vardoe | 1.3 |
| 21 | Fremantle | 0 | 46 | Newport | 0.3 | 71 | Victoria | 0.4 |
| 22 | Funafuti | 1.9 | 47 | Ny-Alesund | 0.3 | 72 | Wakkanai | 0 |
| 23 | Galveston | 2.2 | 48 | Pago Pago | 3.3 | 73 | Walvis Bay | 59 |
| 24 | Gan | 0.2 | 49 | Paita | 10.9 | 74 | Yap | 9 |
| 25 | Grand Isle | 3.1 | 50 | Papeete | 3.3 | 75 | Zanzibar | 5.3 |
| Name | Symbol | Period (h) | Speed (/h) |
|---|---|---|---|
| Higher Harmonics | |||
| Shallow water overtides of principal lunar | 6.210300601 | 57.9682084 | |
| Shallow water overtides of principal lunar | 4.140200401 | 86.9523127 | |
| Shallow water terdiurnal | 8.177140247 | 44.0251729 | |
| Shallow water overtides of principal solar | 6 | 60 | |
| Shallow water quarter diurnal | 6.269173724 | 57.4238337 | |
| Shallow water overtides of principal solar | 4 | 90 | |
| Lunar terdiurnal | 8.280400802 | 43.4761563 | |
| Shallow water terdiurnal | 8.38630265 | 42.9271398 | |
| Shallow water eighth diurnal | 3.105150301 | 115.9364166 | |
| Shallow water quarter diurnal | 6.103339275 | 58.9841042 | |
| Semi-Diurnal | |||
| Principal lunar semidiurnal | 12.4206012 | 28.9841042 | |
| Principal solar semidiurnal | 12 | 30 | |
| Larger lunar elliptic semidiurnal | 12.65834751 | 28.4397295 | |
| Larger lunar evectional | 12.62600509 | 28.5125831 | |
| Variational | 12.8717576 | 27.9682084 | |
| Lunar elliptical semidiurnal second-order | 12.90537297 | 27.8953548 | |
| Smaller lunar evectional | 12.22177348 | 29.4556253 | |
| Larger solar elliptic | 12.01644934 | 29.9589333 | |
| Smaller solar elliptic | 11.98359564 | 30.0410667 | |
| Shallow water semidiurnal | 11.60695157 | 31.0158958 | |
| Smaller lunar elliptic semidiurnal | 12.19162085 | 29.5284789 | |
| Lunisolar semidiurnal | 11.96723606 | 30.0821373 | |
| Diurnal | |||
| Lunar diurnal | 23.93447213 | 15.0410686 | |
| Lunar diurnal | 25.81933871 | 13.9430356 | |
| Lunar diurnal | 22.30608083 | 16.1391017 | |
| Solar diurnal | 24 | 15 | |
| Smaller lunar elliptic diurnal | 24.84120241 | 14.4920521 | |
| Smaller lunar elliptic diurnal | 23.09848146 | 15.5854433 | |
| Larger lunar evectional diurnal | 26.72305326 | 13.4715145 | |
| Larger lunar elliptic diurnal | 26.86835 | 13.3986609 | |
| Larger elliptic diurnal | 28.00621204 | 12.8542862 | |
| Solar diurnal | 24.06588766 | 14.9589314 | |
| Long Period | |||
| Lunar monthly | 661.3111655 | 0.5443747 | |
| Solar semiannual | 4383.076325 | 0.0821373 | |
| Solar annual | 8766.15265 | 0.0410686 | |
| Lunisolar synodic fortnightly | 354.3670666 | 1.0158958 | |
| Lunisolar fortnightly | 327.8599387 | 1.0980331 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
M. Lopes, A.; Tenreiro Machado, J.A. Tidal Analysis Using Time–Frequency Signal Processing and Information Clustering. Entropy 2017, 19, 390. https://doi.org/10.3390/e19080390
M. Lopes A, Tenreiro Machado JA. Tidal Analysis Using Time–Frequency Signal Processing and Information Clustering. Entropy. 2017; 19(8):390. https://doi.org/10.3390/e19080390
Chicago/Turabian StyleM. Lopes, Antonio, and Jose A. Tenreiro Machado. 2017. "Tidal Analysis Using Time–Frequency Signal Processing and Information Clustering" Entropy 19, no. 8: 390. https://doi.org/10.3390/e19080390
APA StyleM. Lopes, A., & Tenreiro Machado, J. A. (2017). Tidal Analysis Using Time–Frequency Signal Processing and Information Clustering. Entropy, 19(8), 390. https://doi.org/10.3390/e19080390






