Pretreatment and Wavelength Selection Method for Near-Infrared Spectra Signal Based on Improved CEEMDAN Energy Entropy and Permutation Entropy

Abstract

The noise of near-infrared spectra and spectral information redundancy can affect the accuracy of calibration and prediction models in near-infrared analytical technology. To address this problem, the improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) and permutation entropy (PE) were used to propose a new method for pretreatment and wavelength selection of near-infrared spectra signal. The near-infrared spectra of glucose solution was used as the research object, the improved CEEMDAN energy entropy was then used to reconstruct spectral data for removing noise, and the useful wavelengths are selected based on PE after spectra segmentation. Firstly, the intrinsic mode functions of original spectra are obtained by improved CEEMDAN algorithm. The useful signal modes and noisy signal modes were then identified by the energy entropy, and the reconstructed spectral signal is the sum of useful signal modes. Finally, the reconstructed spectra were segmented and the wavelengths with abundant glucose information were selected based on PE. To evaluate the performance of the proposed method, support vector regression and partial least square regression were used to build the calibration model using the wavelengths selected by the new method, mutual information, successive projection algorithm, principal component analysis, and full spectra data. The results of the model were evaluated by the correlation coefficient and root mean square error of prediction. The experimental results showed that the improved CEEMDAN energy entropy can effectively reconstruct near-infrared spectra signal and that the PE can effectively solve the wavelength selection. Therefore, the proposed method can improve the precision of spectral analysis and the stability of the model for near-infrared spectra analysis.

1. Introduction

Diabetes, which is a kind of blood glucose metabolism disorder, causes serious health problems [1]. According to the statistical data from the International Diabetes Federation (IDF), the number of people with diabetes will reach 592 million in 2025 [2]. The foundations of diabetes treatment are regular blood glucose detection, diet plans, and injected or oral insulin. Therefore, blood glucose detection is the key step to an effective diabetes treatment. The non-invasive blood glucose detection method is a painless, convenient, and affordable method. Given the development of computer technology and chemometrics in recent years, high efficiency and low-cost near-infrared spectra technologies that can perform fast analysis are widely used in non-invasive blood glucose detection [3]. The electromagnetic wavelength near-infrared light between visible light and medium infrared light ranges from 700 to 2500 nm [4]. For example, glucose molecules contain C–H, N–H, and O–H groups, and the stretching vibration of these hydrogen groups [5] forms certain strength absorption bands of frequency doubling and combined frequency in the near-infrared wavelength region. The different numbers of hydrogen groups in different concentrations of glucose will affect the intensity of the peak position. Therefore, the glucose concentration is quantitatively analyzed based on near-infrared spectra and Beer–Lambert’s law. However, different hydrogen groups have varying near-infrared characteristics. Some groups have no absorption or weak absorption capacity. The quality of the models will decline with the use of all wavelengths that build the calibration and prediction models. Moreover, the near-infrared spectra itself has some problems, such as the presence of wavelength points, overlap of spectral information, and low absorption intensity. Therefore, the pretreatment of spectra and wavelength selection method [6] are critical for simplifying and improving the predictive ability of the model before building the calibration model in near-infrared spectra analysis technology.

The acquired spectra contain not only useful information related to the glucose concentration, but also many uncorrelated noise signals. These noises will affect spectral quality and model accuracy. Thus, the removal of these useless noises is needed. At present, Empirical Mode Decomposition (EMD) is widely used in the signal denoising domain [7,8,9,10]. EMD decomposes time series to intrinsic mode functions (IMFs) and a residue that depends on time scale. EMD is an adaptive signal processing method that can effectively analyze stationary and non-stationary signals. Ensemble Empirical Mode Decomposition (EEMD) solves the mode mixing problem in the EMD method by adding white Gaussian noise; this approach also brings residue noise [11]. Complementary Ensemble Empirical Mode Decomposition (CEEMD) eliminates residue noise in the reconstructed signal by adding a pair of positive and negative signals [12]. However, this method will produce false modes. The CEEMDAN method, which has an iteration number that is half of the EEMD method, accurately completes signal reconstruction [13]. However, false modes in the early stage of CEEMDAN method and residue noise in the modes are still observed. Therefore, an improved CEEMDAN [14] method is used in denoising and reconstructing near-infrared spectra signals in this study.

The superior quantitative calibration model can be obtained through the characteristic wavelength or wavelength interval using specific method. Wavelength selection can simplify the model and reduce modeling time. Irrelevant or nonlinear variables should be eliminated to obtain an excellent calibration model with strong prediction and stability [15]. Therefore, wavelength selection procedures are particularly important when dealing with near-infrared spectra data. Common variable wavelength selection methods include correlation coefficient [16], uninformative variable elimination [17], interval partial least squares [18], successive projections algorithm (SPA) [19], simulated annealing, and genetic algorithms [20]. In this study, a wavelength selection method based on PE is proposed as a new method. C. Bandt and B. Pompe proposed a random detection method for time series, namely, permutation entropy (PE) [21,22,23,24,25,26].

This study proposed a new pretreatment and wavelength selection method. Firstly, the original near-infrared spectra signal is decomposed by using improved CEEMDAN to obtain IMFs. The critical point between useful signal modes and noisy signal modes can be identified through the value of energy entropy of each IMF. The reconstructed signal is the sum of useful signal mode and residue. The characteristic wavelengths are then selected by comparing the PE of the same wavelength interval spectra between glucose solution and pure water. Finally, the performance of the proposed method is verified by the quantitative model established with PLSR and SVR. The results show that the proposed pretreatment and wavelength selection method outperforms the other pretreatment and wavelength selection methods in near-infrared spectra analysis.

2. Related Theory

2.1. EMD Method

According to [27], the general steps of the EMD method are as follows:

(1)

Find all the maxima and minima for the signal, $s(t)$.

(2)

Obtain the upper envelope composed of all the maxima and the lower envelope composed of all the minima using the cubic spline interpolation, and define them as $u(t)$ and $v(t)$ respectively.

(3)

The mean of upper and lower envelope is $m(t)=\frac{u(t)+v(t)}{2}$.

(4)

The difference between original signal and mean of envelope is $h(t)=s(t)-m(t)$.

(5)

If $h(t)$ meet the nature of IMF, then the $h(t)$ is $c_1(t)$. Otherwise, repeat steps (1)–(4) until $c_1(t)$ is obtained. The IMF needs to meet two natures, one is that the number of extreme value points and passing zero points is equal or differs at most by one point, another one is that the mean of upper and lower envelope at any point is zero.

(6)

The $r_1(t)=s(t)-c_1(t)$, as a new signal to be analyzed, repeat the steps (1)–(5) to obtain the second IMF and the $r_2(t)=s(t)-c_2(t)$.

(7)

Repeat the above steps and the decomposition ends when the residue $r_n(t)$ is a monotonic function.

Finally, a set of IMF, $c_1(t)$, $c_2(t)$, …, $c_n(t)$ and the residue $r_n(t)$ are obtained. Therefore, the original signal is

$$s(t)={\displaystyle \sum }_{i=1}^n{c}_i(t)+r_n(t)$$

(1)

2.2. Improved CEEMDAN Method

According to Ref. [14], given $x^{(i)}=x+w^i$, the first mode for the CEEMDAN algorithm is

$${\mathrm{IMF}}_1=\langle E_1(x^{(i)})\rangle =\langle x^{(i)}-M(x^{(i)})\rangle =\langle x^{(i)}\rangle -\langle M(x^{(i)})\rangle$$

(2)

where, $x$ is the original signal, $w^i$ is a realization of zero mean unit variance white Gaussian noise, $E_1$ is a function to extract the first mode decomposed by EMD ($E_1(x)=x-M(x)$), $M(·)$ is the operator that produces the local mean of the applied signal, and $\langle ·\rangle$ is the action of averaging throughout the realization.

If only the local mean is estimated and subtracted from the original signal, ${\mathrm{IMF}}_1=x-\langle M(x^{(i)})\rangle$.

Based on the above content, the improved CEEMDAN method is described as follows:

(1)

Decompose signal $x^{(i)}=x+{\beta }_0{E}_1(w^i)$ to obtain the first residue and first mode using the EMD algorithm.

$$r_1=\langle M(x^{(i)})\rangle$$

(3)

$${\mathrm{IMF}}_1=x-r_1$$

(4)

where $x$ is the original signal, ${\beta }_0$ is the standard deviation of the added white Gaussian noise, and $E_k(·)$ is the operator that produces the k-th mode obtained by EMD algorithm (k = 1,2,…,N, N is the total ensemble number).

(2)

When $k=2,\cdots ,\mathrm{N}$, the k-th residue is

$$r_k=\langle M(r_{k-1}+{\beta }_{k-1}{E}_k(w^i))\rangle$$

(5)

(3)

The k-th mode is

$${\mathrm{IMF}}_k=r_{k-1}-r_k$$

(6)

2.3. Energy Entropy of IMF

Entropy is used to describe the irregular and complex evolution of time series. The composition changes of signal can be directly distinguished by comparing the transformation situation of some characteristics of signal entropy [28]. The IMF components decomposed by improved CEEMDAN contain the local characteristics of original signal and time scale information with different characteristics. The joint distribution of signal energy entropy with frequency and time can be accurately given through the characteristic information of signal expressed by different resolution. The concept of information entropy is introduced to the energy distribution analysis of the IMFs to describe the difference. Information entropy is a measure used to locate a system in a certain state. Information entropy is a measure of unknown degree of time series $(x_1,x_2,\cdots ,x_n)$, which can be used to estimate the complexity of the random signal. The entropy in this process is expressed by the following formula

$$\mathrm{H}=-{{\displaystyle \int }}_{-\infty }^{\infty }p(x)\ln p(x)dx$$

(7)

where $p(x)$ is the joint probability density function of $(x_1,x_2,\cdots ,x_n)$.

Each IMF component is equally divided into N segments along the time axis. The energy of each segment is $W_i(i=1,2,\cdots ,N)$ and the energy of the whole timeline is A. The energy of each segment is normalized to obtain energy normalized values $q_i=\raisebox{1ex}{$W_i$}\!\left/ \!\raisebox{-1ex}{$A$}\right.$. With reference to the information entropy calculation formula, the energy entropy of IMF is defined as [29]

$$\mathrm{H}(q)=-{\displaystyle \sum }_{i=1}^N{q}_i\ln q_i$$

(8)

2.4. Permutation Entropy

According to the [21], the definition of PE is:

Considering time series $\left\{x(i),i=1,2,\cdots ,N\right\}$ with the length N, it is reconstructed in phase space to obtain the time series,

$$\left[\begin{array}{c}X(1)=\left\{x(1),x(1+\tau ),\cdots ,x(1+(m-1)\tau )\right\}\\ ⋮\\ X(i)=\left\{x(i),x(i+\tau ),\cdots ,x(i+(m-1)\tau )\right\}\\ ⋮\\ X(N-(m-1)\tau )=\left\{x(N-(m-1)\tau ),x(N-(m-2)\tau ),\cdots ,x(N)\right\}\end{array}\right]$$

(9)

where $m$ and $\tau$ are the embedding dimension and delay time, respectively. Afterward, an ordinal pattern probability distribution, $\mathrm{P}=\left\{p_j,j=1,\cdots m!\right\}$ can be obtained from the time series by computing the relative frequencies of the m! possible permutations j. The PE is just the Shannon entropy estimated by using this ordinal pattern probability diatribution,

$$S_p=-{\displaystyle \sum }_{j=1}^{m!}{p}_{j}ln{p}_j$$

(10)

If some ordinal patterns appear more frequently than others, the PE decreases, indicating that the signal is less random and more predictable [30]. For convenience, $H_p$ is typically normalized with $\log m!$, namely,

$$H_p={\mathrm{S}}_p/S_{max}={\mathrm{S}}_p/\ln (m!)$$

(11)

$S_{max}=\ln (m!)$ is the value obtained from an equiprobable ordinal pattern probability distribution. Therefore, the $H_p$ ranges between 0 and 1. The magnitude of $H_p$ represents the randomness degree of the time series. The smaller the value of $H_p$ is, the more inerratic the time series will be, otherwise, the more stochastic the time series will be. The change in $H_p$ reflects and amplifies the minute details of the time series.

3. Reconstruction Methods

3.1. Selection of Relevant Mode

The noisy signal, $y(t)$, can be decomposed into several modes by improved CEEMDAN algorithm as

$$y(t)={\displaystyle \sum }_{i=1}^{I}IM{F}_i+r_I(t)$$

(12)

Equation (12) also can be expressed as the sum of noisy modes and useful signal modes as

$$y(t)={\displaystyle \sum }_{i=1}^{k-1}IM{F}_i+{\displaystyle \sum }_{i=k}^{I}IM{F}_i+r_I(t)$$

(13)

where the first (k − 1) modes are noisy modes, and the residual modes are the useful signal modes and residue. The critical task is to find $k$ to reconstruct the signal. The role of signal reconstruction can also be understood as a low-pass filter. The front several high frequency IMFs (noise modes) are removed, and the low frequency IMFs (useful signal modes) are kept and added to reconstruct the signal. Given that each IMF contains different frequency components and different energy, the energy of the IMFs is measured by energy entropy to select the relevant modes effectively. According to a large number of experimental results, it is found that the energy entropy of the noise modes is around a certain value, and that of useful signal modes is around another certain value. The difference of energy entropy of noise modes or useful signal modes is a small change. The maximum energy entropy appears when the first useful signal mode comes. Therefore, a mutational point exists, which is the maximum of all energy entropy of IMFs between two kinds of modes. The mutational point that corresponds to the mode index is $k$. The steps of the selection of relevant mode are as follows:

(1)

Noisy signal $y(t)$ is decomposed to obtain $IM{F}_i(i=1,2,\cdots ,I)$ by improved CEEMDAN algorithm.

(2)

The energy entropy of each $IM{F}_i$ is calculated, which is denoted as $E{E}_i(i=1,2,\cdots ,I)$, where I is the number of modes obtained by improved CEEMDAN algorithm.

(3)

The relevant mode is identified as

$$k=\mathrm{argmax}(E{E}_i)$$

(14)

(4)

The reconstructed signal is

$$\tilde{y}(t)={\displaystyle \sum }_{i=k}^{I}IM{F}_i+r_I(t)$$

(15)

3.2. Application

The periodic signal $y(t)=\sin (2\mathsf{\pi }{f}_{1}t)+\cos (2\mathsf{\pi }{f}_{2}t)$, which has a data length of 1024, composed by different frequencies $f_1$ and $f_2$, where $f_1=2$ Hz and $f_2=4$ Hz. The white Gaussian noise with 3 dB is added to signal $y(t)$ (Figure 1). The signal is decomposed by improved CEEMDAN, where the ratio of standard deviation of added white noise is 0.2 and the ensemble number is 50. To illustrate the stability of the proposed reconstructed method, the method is tested 10 times to prove the effect of reconstruction. Each time, the noisy signal $y(t)$ is decomposed by improved CEEMDAN algorithm. The energy entropy of each IMF is then calculated. Figure 2 shows that the noisy signal is decomposed into nine IMFs and one residue. The eighth and ninth modes are the useful signal modes, and the reconstructed signal is the sum of the last three modes (IMF8, IMF9, and IMF10). The energy entropy of each IMF is listed in

Table 1. The energy entropy of each IMF.

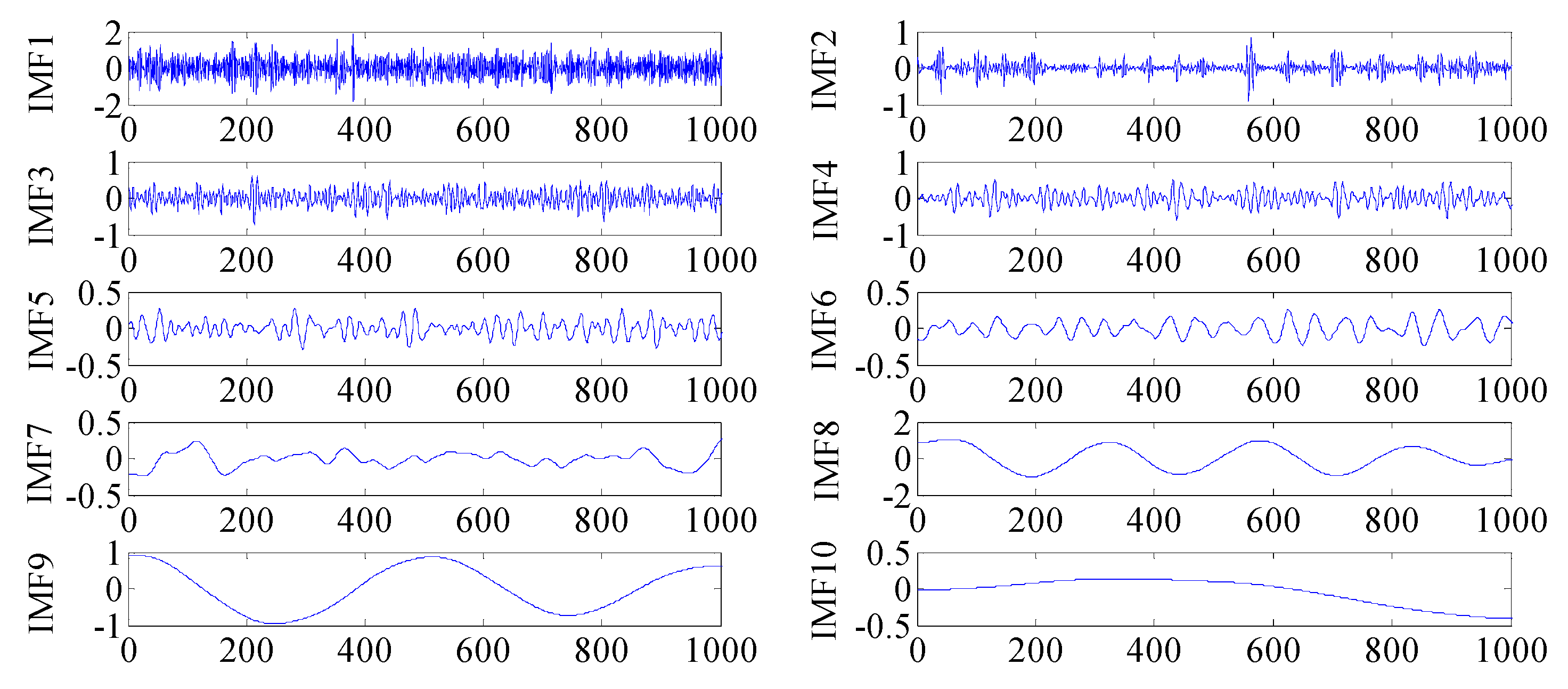
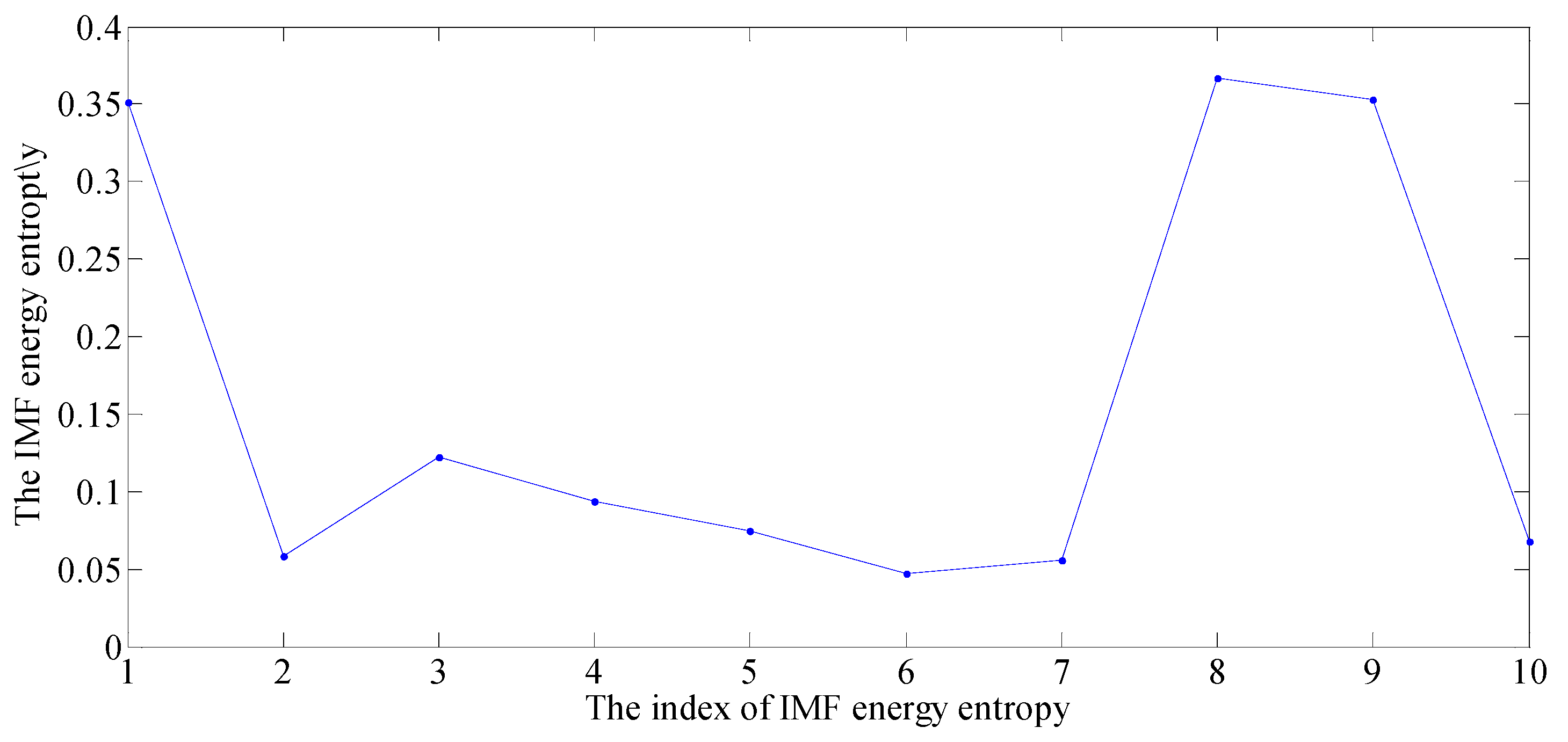
IMF	IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7	IMF8	IMF9	IMF10
Energy Entropy	0.3509	0.0586	0.1226	0.0939	0.0751	0.0471	0.0556	0.3664	0.3526	0.0680

. The maximum of energy entropy corresponds to IMF8. Therefore, the index $k$ of mutational point is 8 (Figure 3), and the useful modes start with the eighth mode. The results of other nine tests are similar to those of the first test. The reconstructed signal is shown in Figure 4, which illustrates the energy entropy can effectively identify the noisy modes and useful modes.

To compare the reconstruction result, improved CEEMDAN energy entropy, Fourier transform (the cut-off frequency is 70 Hz), wavelet transform (the mother wavelet is db3, and the level of decomposition is 5), moving averaging (the size of sliding window is 5), and median (the dim is 2) are used to reconstruct the signal. The reconstructed performance is evaluated at various input signal to noise ratios (SNR), which range from 1 to 10 dB with a fixed step of 1 dB. The output SNR and mean square error (MSE) are calculated to quantize the reconstructed result.

$$\mathrm{SNR}=10{\log }_{10}(\frac{{{\displaystyle \sum }}_{n=1}^N{(y(n))}^2}{{{\displaystyle \sum }}_{n=1}^N{(y(n)-\overline{y}(n))}^2})$$

(16)

$$\mathrm{MSE}=\frac{1}{N}{\displaystyle \sum }_{n=1}^N{(y(n)-\overline{y}(n))}^2$$

(17)

where the $y(n)$ is the pure signal, and the $\overline{y}(n)$ is the reconstructed signal.

Table 2. Value of SNR for different reconstructed signal methods.

Input SNR (dB)	Improved CEEMDAN	Fourier Transform	Wavelet	Moving Averaging	Median
1	17.8248	16.0560	15.0341	14.5787	12.2264
2	18.0438	17.3067	15.7924	15.5213	14.3009
3	18.4945	17.8271	16.6156	16.5692	15.5220
4	20.8505	18.7479	17.3508	17.0353	15.7923
5	20.9332	20.0900	19.3935	17.9618	15.9758
6	21.4840	20.9410	20.9280	20.5687	16.9514
7	22.0085	21.9528	21.2787	21.0124	17.8478
8	22.4068	22.0203	21.9441	21.0533	19.0951
9	23.3195	22.9087	22.8480	22.2636	19.3020
10	23.9494	23.6274	23.5810	23.2829	20.4236

and

Table 3. Value of MSE for different reconstructed signal methods.

Input SNR (dB)	Improved CEEMDAN	Fourier Transform	Wavelet	Moving Averaging	Median
1	0.0165	0.0234	0.0314	0.0348	0.0599
2	0.0157	0.0207	0.0263	0.0280	0.0371
3	0.0141	0.0187	0.0218	0.0220	0.0280
4	0.0082	0.0120	0.0184	0.0198	0.0263
5	0.0081	0.0102	0.0115	0.0160	0.0252
6	0.0071	0.0075	0.0081	0.0088	0.0202
7	0.0063	0.0069	0.0074	0.0079	0.0164
8	0.0057	0.0060	0.0064	0.0078	0.0123
9	0.0047	0.0049	0.0052	0.0059	0.0117
10	0.0040	0.0042	0.0044	0.0047	0.0091

are the SNR and MSE of different reconstructed signal methods. To effectively evaluate reconstructed result, the ratio of standard deviation of added white noise is 0.2 and the ensemble number is 100 in the improved CEEMDAN algorithm. The value of SNR and MSE are the average value of 10 test times. Based on the Table 2 and Table 3, we conclude that the SNR of the reconstructed method based on improved CEEMDAN energy entropy is larger than that of others. The MSE of the reconstructed method based on improved CEEMDAN with energy entropy is smaller than that of others. These results show that the proposed reconstructed method is superior to other methods.

To verify the validity of the proposed method, the non-stationary ECG signal (from the MIT-BIH normal Sinus Rhythm Database) and Blocks signal [31] with 5 dB white Gaussian noise is introduced into the experiments. The reconstructed results were then compared with Fourier transform (the cut-off frequency is 110 Hz), wavelet transform (the mother wavelet is db5, and the level of decomposition is 10), moving averaging (the size of the sliding window is 5), and median (the dim is 5).

Table 4. Values of SNR and MSE of different reconstructed methods for ECG signal and Blocks signal (input SNR = 5 dB).

Methods	ECG		Blocks
	SNR	MSE	SNR	MSE
Improved CEEMDAN	35.6925	0.4605	20.1445	0.0853
Wavelet	32.8187	0.8924	14.8604	0.2881
Median	31.5652	1.1910	17.5286	0.1558
Moving Averaging	30.7328	1.4427	19.6235	0.0962
Fourier Transform	30.3529	1.5744	16.3653	0.2037

shows the output SNR and MSE of the ECG signal and Block signal. In the table, the output SNR/MSE of the proposed method is higher/smaller than that of others. The structure of the ECG signal is different from that of the Blocks signal. These results demonstrate the extensive application of the proposed method based on improved CEEMDAN energy entropy.

To verify the validity of the proposed method for different noise distribution, the uniform distribution noise between 0 and 1 is added into the periodic signal $y(t)$, the ECG signal, and Blocks signal. The reconstructed results were then compared with Fourier transform (the cut-off frequency is 110 Hz), wavelet transform (the mother wavelet is db5, and the level of decomposition is 10), moving averaging (the size of the sliding window is 5), and median (the dim is 5).

Table 5. Values of SNR and MSE of different reconstructed methods for signals $y(t)$ , ECG and Blocks with uniform distribution noise.

Methods	$\mathit{y}(\mathit{t})$		ECG		Blocks
	SNR	MSE	SNR	MSE	SNR	MSE
Improved CEEMDAN	6.1669	0.2417	37.0801	0.3345	14.8196	0.2908
Wavelet	5.6590	0.2717	35.7799	0.4513	14.3990	0.3204
Moving Averaging	5.6052	0.2751	30.4034	1.5563	14.0942	0.3436
Fourier Transform	5.4867	0.2827	30.9340	1.3773	13.8094	0.3669
Median	5.0963	0.3093	32.1864	1.0323	14.5561	0.3090

shows the output SNR and MSE of the periodic signal $y(t)$, ECG signal, and Block signal. In the table, the output SNR/MSE of the proposed method is higher/smaller than that of others. These results demonstrate that the proposed method based on improved CEEMDAN energy entropy is effective for uniform distribution of noise.

Overall, the method of how to select the relevant mode to distinguish the noise mode and useful signal mode is explained in the Section 3.1. In Section 3.2, three kinds of signals are introduced to illustrate the effectiveness of the proposed method. The periodic signal y(t) is a stationary signal, and the two signals with different structures, ECG signal (Electrocardiogram) and Blocks signal, are non-stationary signals.

4. Results and Discussion

4.1. Near-Infrared Spectra Collection

The near-infrared spectra were measured on Antaris II FT-NIR instrument (America Thermo Company, Shanghai, China) in the spectral range of 833 nm to 2630 nm at 4 cm⁻¹ resolution. The diagram of measure system structure is shown in Figure 5. In the measurement experiments for glucose concentration of near-infrared spectra, all glucose solutions with concentrations ranging from 50 to 1000 mg/dL are continuous and equally distributed liquid that are uniformly configured under the same conditions. The collected near-infrared spectra data of the glucose solutions are measured five times with the same concentration to obtain a small statistical error and shown in Figure 6.

4.2. Reconstruction of Near-Infrared Spectra

The noise of the collected near-infrared spectral data is removed based on the improved CEEMDAN energy entropy method. This method is performed by adding a standard deviation of added white noise of 0.2 and the ensemble number of 100. The reconstructed efficiency was compared with the proposed method, wavelet filter method (the mother wavelet is db5, and the level of decomposition is 10), moving average filter method (the size of the sliding window is 5), and median filter method (the dim is 2).The reconstructed results of near-infrared spectra for a 700 mg/dL glucose solution are shown in Figure 7. To quantify the reconstructed results and verify the effectiveness of these methods, the SNR and MSE were calculated for different methods. Given that the noisy signal was used to replace the pure signal $\mathrm{y}(\mathrm{n})$ in Equations (16) and (17), the evaluated results are opposite to the simulation signals, i.e., the smaller the SNR (bigger MSE) is, the better the reconstructed effect. The values of SNR and MSE of different methods are shown in

Table 6. Value of SNR and MSE for different reconstructed signal methods.

Methods	SNR	MSE
Improved CEEMDAN	24.0355	0.0297
Wavelet	26.3136	0.0178
Moving Averaging	27.7917	0.0125
Median	28.0776	0.0117

. The SNR and MSE values generated by the improved CEEMDAN energy entropy method are 24.0355 and 0.0297, respectively. These values are better than those generated by other methods. The results show that the reconstructed signal based on the improved CEEMDAN energy entropy was smooth and presented the near-infrared spectra characteristics. The proposed method had excellent performance in de-noising and signal reconstruction.

4.3. Wavelength Selection of Near-Infrared Spectra

The characteristic wavelengths are selected from reconstructed near-infrared spectra data of the glucose solution. Full spectrum wavelength data have a total of 1867 points, which are divided into wavelength intervals with a rolling window. The rolling window size W is chosen according to the rule $W>5m!$ [32,33], where m is the order of ordinal patterns or embedding dimension. The permutation entropy of each wavelength interval is calculated with an embedding dimension of 4 and a delay time of 1 in this experiment. Therefore, the window size is larger than 120. However, some permutation entropy of the spectral absorption peak will be missed with an extremely large rolling window size. Given these conditions, the window size is chosen as 130 for the wavelength selection of near-infrared spectra. To illustrate the proposed method, the four different concentrations of glucose solutions are used in the calculation. The calculated results of glucose solutions with 50, 500, and 1000 mg/dL, and a pure water solution are shown in Figure 8. As shown in the figure, PE values in some wavelength intervals are substantially consistent and significantly different in other wavelength intervals. Therefore, the later wavelength intervals are the characteristic wavelengths that contained abundant glucose concentration information. All of the non-overlapping intervals are considered as the final characteristic wavelengths (

Table 7. Selection of characteristic wavelengths.

Number	Point Number	Wavenumber (cm−1)
1	218–301	5639–5959
2	701–791	7502–7849
3	942–1141	8431–9120

). By combining the Figure 6 and Table 7, the result shows that the selected characteristic wavelengths contain the peak position of near-infrared spectra, which correspond to the peak of glucose absorption.

To verify the effectiveness of the proposed method, the characteristic wavelength of the reconstructed spectral data of glucose solutions with the proposed method, mutual information method [34], SPA method [35], PCA method [36], and full spectral data are integrated into the calibration models established by PLSR [37] and SVR [38] ($\mathsf{\epsilon }=\left[0,0.2\right],\mathrm{C}=\left[1,{10}^8\right],\mathsf{\gamma }=\left[0.01,2\right]$). The correlation coefficient and root mean square error of prediction (RMSEP) of the model are evaluated.

$$R=\sqrt{1-\frac{{\displaystyle \sum }{({\widehat{y}}_i-y_i)}^2}{{\displaystyle \sum }{({\overline{\widehat{y}}}_i-y_i)}^2}}$$

(18)

$$RMSEP=\sqrt{\frac{{\displaystyle \sum }{({\widehat{y}}_i-y_i)}^2}{n-1}}$$

(19)

where, n is the sample quantity of the calibration set, $y_i$ is the true value of the ith sample, ${\widehat{y}}_i$ is the predicted value of the i-th sample, and ${\overline{\widehat{y}}}_i$ is the average value of ${\widehat{y}}_i$ of all the samples in the calibration set.

The characteristic wavelengths selected based on the permutation entropy are 375, which is lower than the points of full spectral wavelength. The smaller the selected characteristic wavelength points are, the shorter the established model time. The experimental results of PLSR and SVR calibration model (

Table 8. R and RMSEP of SVR model and PLSR model.

Methods	SVR		PLSR
	R	RMSEP	R	RMSEP
Improved CEEMDAN-FD	0.9999	0.9125	0.9998	0.9089
SPA	0.9892	0.8195	0.9878	0.8002
MI	0.9790	0.7604	0.9658	0.7019
PCA	0.9621	0.7542	0.9403	0.6958
Full wave bands	0.8988	0.5499	0.8147	0.5013

) show that the correlation coefficient (R) and RMSEP of established calibration model by characteristic wavelengths that were selected based on the improved CEEMDAN energy entropy method reach 0.9999/0.9998 and 0.9125/0.9089. This result is better than that of the established calibration model by characteristic wavelengths that were selected based on MI method, SPA method, PCA method, and full spectral data. The overall modeling results of SVR are more reliable than that of PLSR modeling. The errors between the predicted values and the true values are calculated and those between the predicted values and true values are provided in Figure 9.

5. Conclusions

This study proposed a novel pretreatment and wavelength selection method for near-infrared spectra signal using the improved CEEMDAN energy entropy and permutation entropy. In terms of signal reconstruction, Fourier transform, wavelet transform, moving averaging, and median are compared to remove noise with different input SNRs. The reconstructed results show that the proposed method based on the improved CEEMDAN energy entropy works best. By utilizing the near-infrared spectral data of glucose solutions as the object, full spectral data are reconstructed by the improved CEEMDAN energy entropy to remove noise. To select the characteristic wavelength, the reconstructed near-infrared spectra are divided with certain interval points. The PE values of wavelength intervals are then calculated. The PLSR and SVR models are introduced to establish the calibration model with characteristic wavelength selection using the PE method, MI method, SPA method, PCA method, and full spectral data. According to the correlation coefficient and RMSEP of the calibration models, the proposed wavelength selection method effectively solves the redundancy problem of near-infrared spectral data. This approach also improves the robustness and predictive ability of the regression model. Therefore, the proposed method can remove the useless noise information and reduce the effective range of data to establish stable, accurate, and practicable quantitative models.