Cognition and Cooperation in Interfered Multiple Access Channels †
Abstract
:1. Introduction
2. Channel Model and Preliminaries
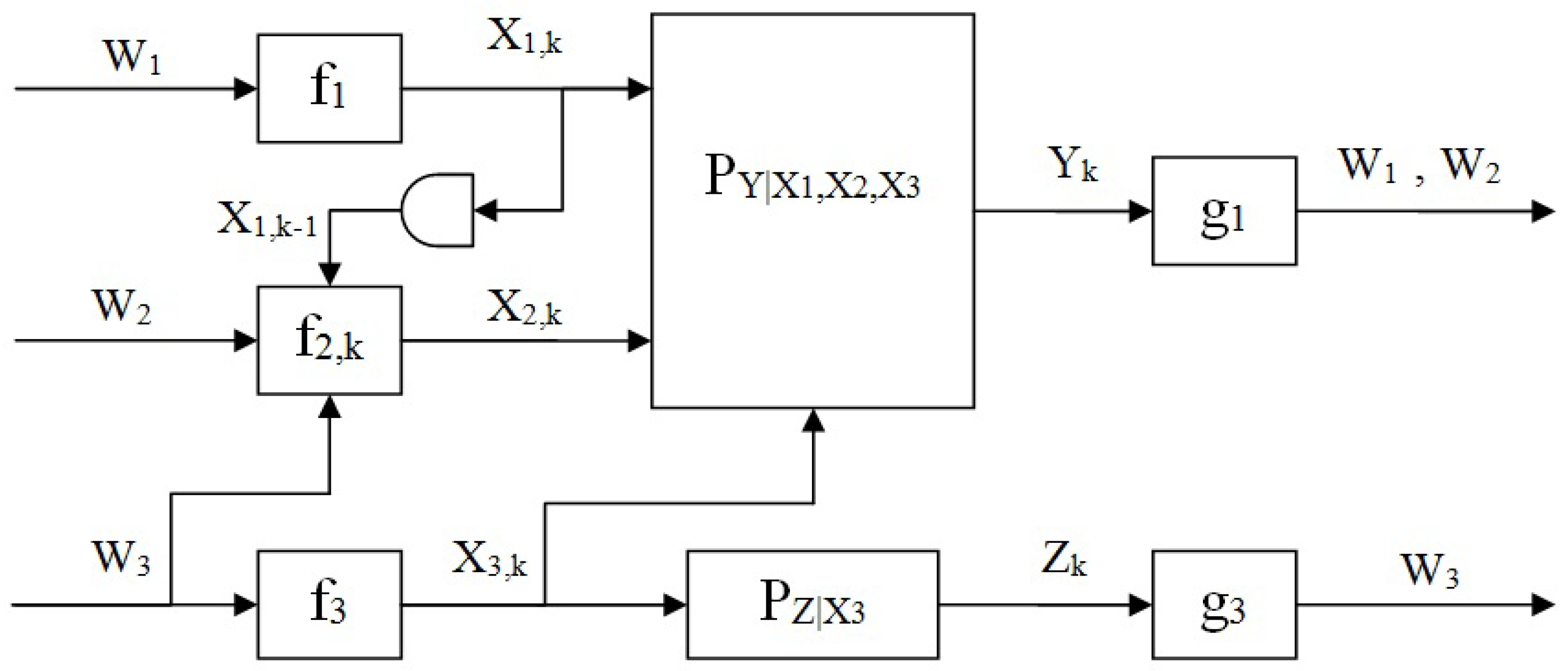
- Encoder 1 defined by a deterministic mappingwhich maps the message to a channel input codeword.
- Encoder 2 which observes and prior to transmitting , is defined by the mappings
- Encoder 3 is defined by a deterministic mapping
- The primary (main) decoder is defined by a mapping
- The secondary decoder is defined by a mapping
3. Main Results
3.1. Inner Bound
3.2. Outer Bound
3.3. Special Cases
4. Cooperative Encoding
5. Partial Cribbing
6. Discussion and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MAC | Multiple-Access Channel |
| IFC | Interference Channel |
| OFDMA | Orthogonal Frequency-Division Multiple Access |
| HK | Han-Kobayashi |
| QoS | Quality of Service |
| DF | Decode and Forward |
| AF | Amplify and Forward |
| CIFC | Cognitive Interference Channel |
| MA-CZIC | Multiple-Access Cognitive Z-Interference Channel |
| P2P | point-to-point |
| RV | Random Variable |
| AEP | Asymptotic Equipartition Property |
Appendix A
Appendix A.1. Encoder 3 and Decoder 3 Coding Scheme
Appendix A.1.1. Encoder 3 Codebook generation
Appendix A.1.2. Encoding Scheme of Encoder 3
Appendix A.1.3. Receiver 3 Decoding
Appendix A.2. Encoder 1, Encoder 2 and Main Decoder Coding Scheme
Appendix A.2.1. Encoder 1 Codebook generation
Appendix A.2.2. Encoding Scheme of Encoder 1
Appendix A.2.3. Encoder 2 Codebook Generation
Appendix A.2.4. Encoding Scheme of Encoder 2
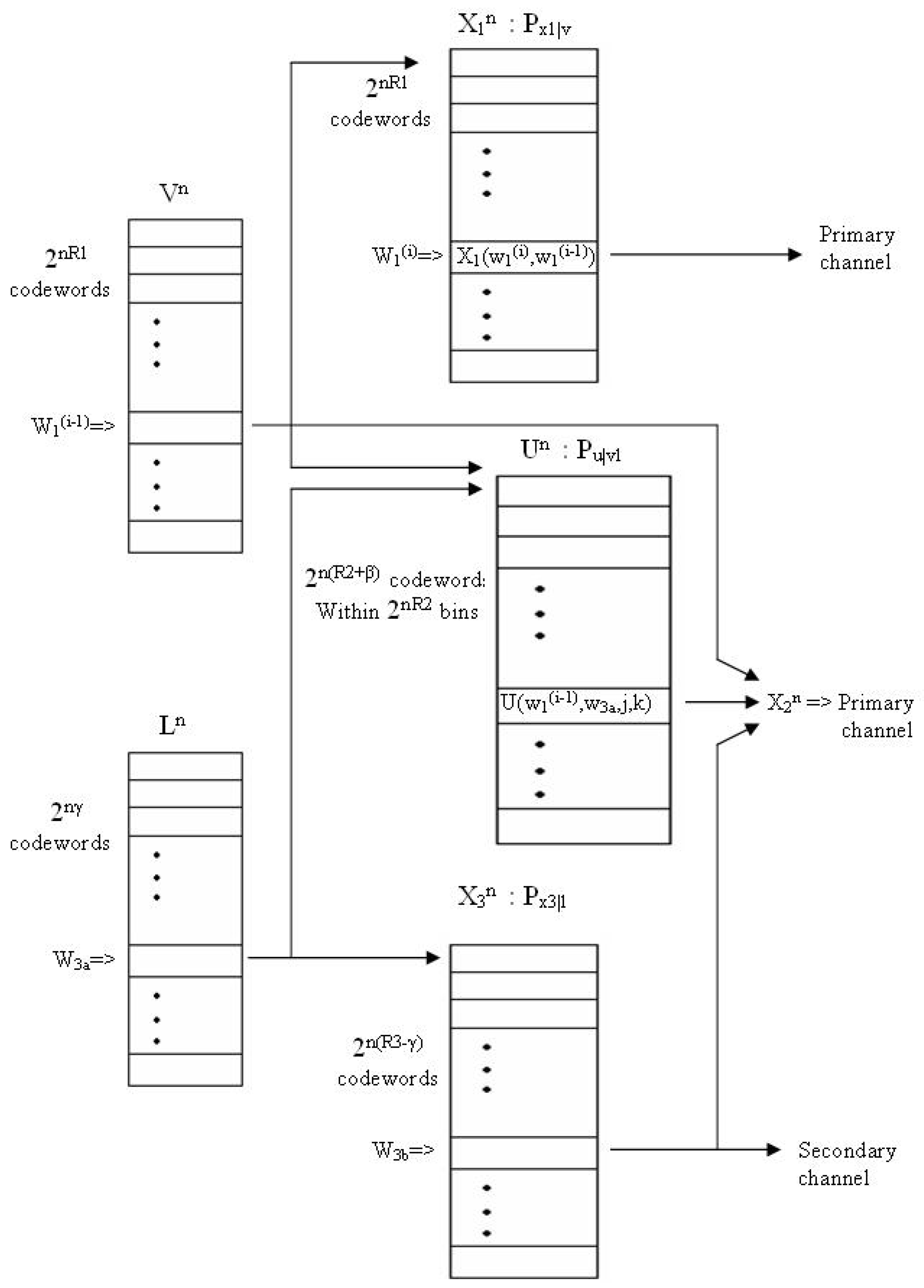
Appendix A.2.5. Decoding at the Primary Receiver ()
Appendix A.2.6. Decoding at Encoder 2
Appendix A.3. Bounding the Probability of Error
- : Codebook error, the codewords , , , are not jointly typical. That is
- : Error decoding at Encoder 2, that is, there exists such that
- : Encoding error at Encoder 2, no suitable encoding index t. That is, there is no such that
- : Channel error, one or more of the input signals is not jointly typical with the outputs and . That is
- : Codebook error in decoding at either one of the decoders, a false message was detected. That is, there exists such that
- : Codebook error in decoding . There exists such thatfor some pair , .
- : Codebook error in decoding . There exists a different bin , such thatfor some .
- : Codebook error in decoding . There exists such that
- By the Asymptotic Equipartition Property (AEP) [40], as .
- In the second summand, , the conditioning on insures that are jointly typical, and that Encoder 2 decoded correctly all the previous messages and specifically . Since each codeword is drawn i.i.d. given , from the strong typicality Lemma we getwhere is the eventAssuming, without loss of generality, that , we get by using the union boundHence forwe get as .
- Since the codewords are generated in an i.i.d. manner we havewhere is the eventfor a specific index t. Hence, we haveConditioning on V and L in ([41], Lemma 3) we getfor all , where as . HenceThe expression converges to 0 as for
- By the AEP as .
- Ifthen, from joint typicality decoding, as .
- We state thatwhere stands for the eventBy using the strong typicality Lemma we bound each of the summands aboveSumming over all codewords we getTherefore, ifthen as
- Similarly, using the same technique as the previous step, ifthen as .
- Finally, ifthen as .
Appendix B
Appendix C
Appendix D
Appendix E
- (a)
- (b)
- follows since conditioning reduces entropy, and
- (c)
- follows since is a Markov chain.
Appendix F
Appendix G
Appendix H
Appendix I
References
- Ahlswede, R. Multi-way communication channels. In Proceedings of the Second International Symposium on Information Theory, Tsahkadsor, Armenia, USSR, 2–8 September 1971; pp. 23–52. [Google Scholar]
- Liao, H. Multiple Access Channels. Ph.D. Thesis, Department of Electrical Engineering, University of Hawaii, Honolulu, HI, USA, 1972. [Google Scholar]
- Shannon, C.E. Two-way communication channels. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Statistical Laboratory of the University of California, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 611–644. [Google Scholar]
- Ahlswede, R. The capacity region of a channel with two senders and two receivers. Ann. Probab. 1974, 2, 805–814. [Google Scholar] [CrossRef]
- Han, T.; Kobayashi, K. A new achievable rate region for the interference channel. IEEE Trans. Inf. Theory 1981, 27, 49–60. [Google Scholar] [CrossRef]
- Chong, H.F.; Motani, M.; Garg, H.; El Gamal, H. On the Han-Kobayashi Region for the Interference Channel. IEEE Trans. Inf. Theory 2008, 54, 3188–3195. [Google Scholar] [CrossRef]
- Carleial, A.B. Interference channels. IEEE Trans. Inf. Theory 1978, IT-24, 60–70. [Google Scholar] [CrossRef]
- Sason, I. On achievable rate regions for the Gaussian interference channel. IEEE Trans. Inf. Theory 2004, 50, 1345–1356. [Google Scholar] [CrossRef]
- Kramer, G. Review of rate regions for interference channels. In Proceedings of the International Zurich Seminar on Communications, Zurich, Switzerland, 2–4 March 2006; pp. 152–165. [Google Scholar]
- Etkin, R.; Tse, D.; Wang, H. Gaussian Interference Channel Capacity to within One Bit. IEEE Trans. Inf. Theory 2008, 54, 5534–5562. [Google Scholar] [CrossRef]
- Telatar, E.; Tse, D. Bounds on the capacity region of a class of interference channels. In Proceedings of the IEEE International Symposium Information Theory (ISIT), Nice, France, 24–29 June 2007. [Google Scholar]
- Maric, I.; Goldsmith, A.; Kramer, G.; Shamai (Shitz), S. On the capacity of interference channels with one cooperating transmitter. Eur. Trans. Telecommun. 2008, 19, 329–495. [Google Scholar] [CrossRef]
- El Gamal, A.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2012; ISBN 1-107-00873-1. [Google Scholar]
- Gamal, A.E.; Costa, M. The capacity region of a class of deterministic interference channels (Corresp.). IEEE Trans. Inf. Theory 1982, 28, 343–346. [Google Scholar] [CrossRef]
- Goldsmith, A.; Jafar, S.A.; Maric, I.; Srinivasa, S. Breaking Spectrum Gridlock with Cognitive Radios: An Information Theoretic Perspective. Proc. IEEE 2009, 97, 894–914. [Google Scholar] [CrossRef]
- Jovicic, A.; Viswanath, P. Cognitive Radio: An Information-Theoretic Perspective. IEEE Trans. Inf. Theory 2009, 55, 3945–3958. [Google Scholar] [CrossRef]
- Wang, B.; Liu, K.J.R. Advances in cognitive radio networks: A survey. IEEE J. Sel. Top. Signal Process. 2011, 5, 5–23. [Google Scholar] [CrossRef]
- Zhao, Q.; Sadler, B.M. A Survey of Dynamic Spectrum Access. IEEE Signal Process. Mag. 2007, 3, 79–89. [Google Scholar] [CrossRef]
- Guzzon, E.; Benedetto, F.; Giunta, G. Performance Improvements of OFDM Signals Spectrum Sensing in Cognitive Radio. In Proceedings of the 2012 IEEE Vehicular Technology Conference (VTC Fall), Quebec City, QC, Canada, 3–6 September 2012; Volume 5, pp. 1–5. [Google Scholar]
- Devroye, N.; Mitran, P.; Tarokh, V. Achievable rates in cognitive radio channels. IEEE Trans. Inf. Theory 2006, 52, 1813–1827. [Google Scholar] [CrossRef]
- Rini, S.; Kurniawan, E.; Goldsmith, A. Primary Rate-Splitting Achieves Capacity for the Gaussian Cognitive Interference Channel. arXiv, 2012; arXiv:1204.2083. [Google Scholar]
- Rini, S.; Kurniawan, E.; Goldsmith, A. Combining superposition coding and binning achieves capacity for the Gaussian cognitive interference channel. In Proceedings of the 2012 IEEE Information Theory Workshop (ITW), Lausanne, Switzerland, 3–7 September 2012; pp. 227–231. [Google Scholar]
- Wu, Z.; Vu, M. Partial Decode-Forward Binning for Full-Duplex Causal Cognitive Interference Channels. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Cambridge, MA, USA, 1–6 July 2012; pp. 1331–1335. [Google Scholar]
- Duan, R.; Liang, Y. Bounds and Capacity Theorems for Cognitive Interference Channels with State. IEEE Trans. Inf. Theory 2015, 61, 280–304. [Google Scholar] [CrossRef]
- Rini, S.; Huppert, C. On the Capacity of the Cognitive Interference Channel with a Common Cognitive Message. IEEE Trans. Inf. Theory 2015, 26, 432–447. [Google Scholar] [CrossRef]
- Willems, F.; van der Meulen, E. The discrete memoryless multiple-access channel with cribbing encoders. IEEE Trans. Inf. Theory 1985, IT-31, 313–327. [Google Scholar] [CrossRef]
- Bross, S.; Lapidoth, A. The state-dependent multiple-access channel with states available at a cribbing encoder. In Proceedings of the 2010 IEEE 26th Convention of Electrical and Electronics Engineers in Israel (IEEEI), Eilat, Israel, 17–20 November 2010; pp. 665–669. [Google Scholar]
- Permuter, H.H.; Asnani, H. Multiple Access Channel with Partial and Controlled Cribbing Encoders. IEEE Trans. Inf. Theory 2013, 59, 2252–2266. [Google Scholar]
- Somekh-Baruch, A.; Shamai (Shitz), S.; Verdú, S. Cooperative Multiple-Access Encoding With States Available at One Transmitter. IEEE Trans. Inf. Theory 2008, 54, 4448–4469. [Google Scholar] [CrossRef]
- Kopetz, T.; Permuter, H.H.; Shamai (Shitz), S. Multiple Access Channels With Combined Cooperation and Partial Cribbing. IEEE Trans. Inf. Theory 2016, 62, 825–848. [Google Scholar] [CrossRef]
- Kolte, R.; Özgür, A.; Permuter, H. Cooperative Binning for Semideterministic Channels. IEEE Trans. Inf. Theory 2016, 62, 1231–1249. [Google Scholar] [CrossRef]
- Permuter, H.H.; Shamai (Shitz), S.; Somekh-Baruch, A. Message and State Cooperation in Multiple Access Channels. IEEE Trans. Inf. Theory 2011, 57, 6379–6396. [Google Scholar] [CrossRef]
- Mokari, N.; Saeedi, H.; Navaie, K. Channel Coding Increases the Achievable Rate of the Cognitive Networks. IEEE Commun. Lett. 2013, 17, 495–498. [Google Scholar] [CrossRef]
- Passiatore, C.; Camarda, P. A P2P Resource Sharing Algorithm (P2P-RSA) for 802.22b Networks. In Proceedings of the 3rd International Conference on Context-Aware Systems and Applications, Dubai, UAE, 15–16 October 2014. [Google Scholar]
- Costa, M.H.M. Writing on dirty paper. IEEE Trans. Inf. Theory 1983, 29, 439–441. [Google Scholar] [CrossRef]
- Liu, N.; Maric, I.; Goldsmith, A.; Shamai (Shitz), S. Capacity Bounds and Exact Results for the Cognitive Z-Interference Channel. IEEE Trans. Inf. Theory 2013, 59, 886–893. [Google Scholar] [CrossRef]
- Rini, S.; Tuninetti, D.; Devroye, N. Inner and Outer bounds for the Gaussian cognitive interference channel and new capacity results. IEEE Trans. Inf. Theory 2012, 58, 820–848. [Google Scholar] [CrossRef]
- Shimonovich, J.; Somekh-Baruch, A.; Shamai (Shitz), S. Cognitive cooperative communications on the Multiple Access Channel. In Proceedings of the 2013 IEEE Information Theory Workshop (ITW), Sevilla, Spain, 9–13 September 2013; pp. 1–5. [Google Scholar]
- Shimonovich, J.; Somekh-Baruch, A.; Shamai (Shitz), S. Cognitive aspects in a Multiple Access Channel. In Proceedings of the 2012 IEEE 27th Convention of Electrical and Electronics Engineers in Eilat, Israel, 14–17 November 2012; pp. 1–3. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory, 1st ed.; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Gel’fand, S.I.; Pinsker, M.S. Coding for Channels with Random Parameters. Probl. Contr. Inf. Theory 1980, 9, 19–31. [Google Scholar]
- Zaidi, A.; Kotagiri, S.; Laneman, J.; Vandendorpe, L. Cooperative Relaying with State Available Noncausally at the Relay. IEEE Trans. Inf. Theory 2010, 56, 2272–2298. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 1978, 24, 339–348. [Google Scholar] [CrossRef]
- Kotagiri, S.; Laneman, J.N. Multiple Access Channels with State Information Known at Some Encoders. EURASIP J. Wireless Commun. Netw. 2008, 2008. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimonovich, J.; Somekh-Baruch, A.; , S.S. Cognition and Cooperation in Interfered Multiple Access Channels. Entropy 2017, 19, 378. https://doi.org/10.3390/e19070378
Shimonovich J, Somekh-Baruch A, SS. Cognition and Cooperation in Interfered Multiple Access Channels. Entropy. 2017; 19(7):378. https://doi.org/10.3390/e19070378
Chicago/Turabian StyleShimonovich, Jonathan, Anelia Somekh-Baruch, and Shlomo Shamai (Shitz). 2017. "Cognition and Cooperation in Interfered Multiple Access Channels" Entropy 19, no. 7: 378. https://doi.org/10.3390/e19070378
APA StyleShimonovich, J., Somekh-Baruch, A., & , S. S. (2017). Cognition and Cooperation in Interfered Multiple Access Channels. Entropy, 19(7), 378. https://doi.org/10.3390/e19070378



.png)
