Study on the Business Cycle Model with Fractional-Order Time Delay under Random Excitation
Abstract
:1. Introduction
2. The Model
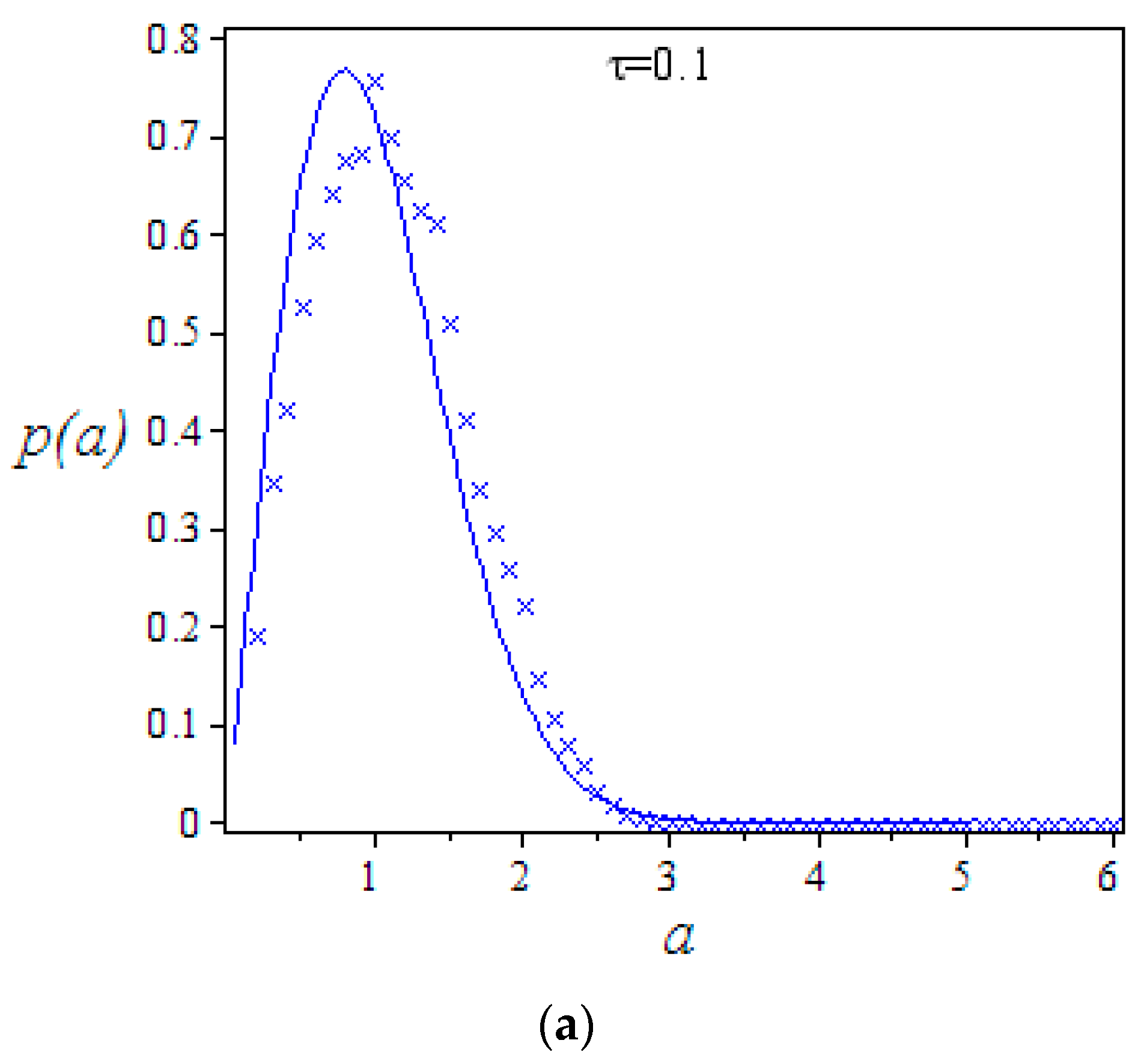
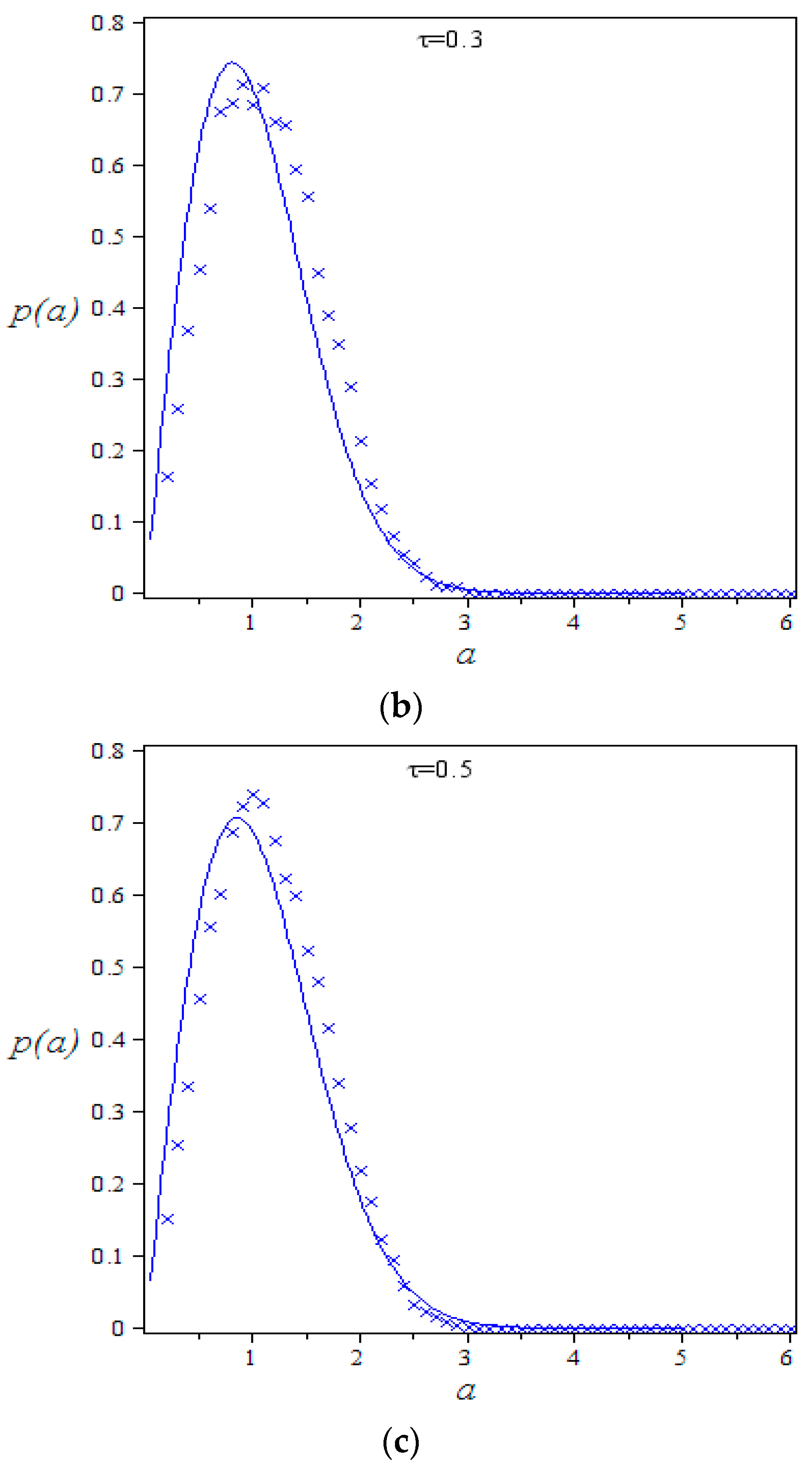
3. Stationary PDF of the Model with Random Excitation
Stochastic Averaging Method
4. Nonlinear Investment Function
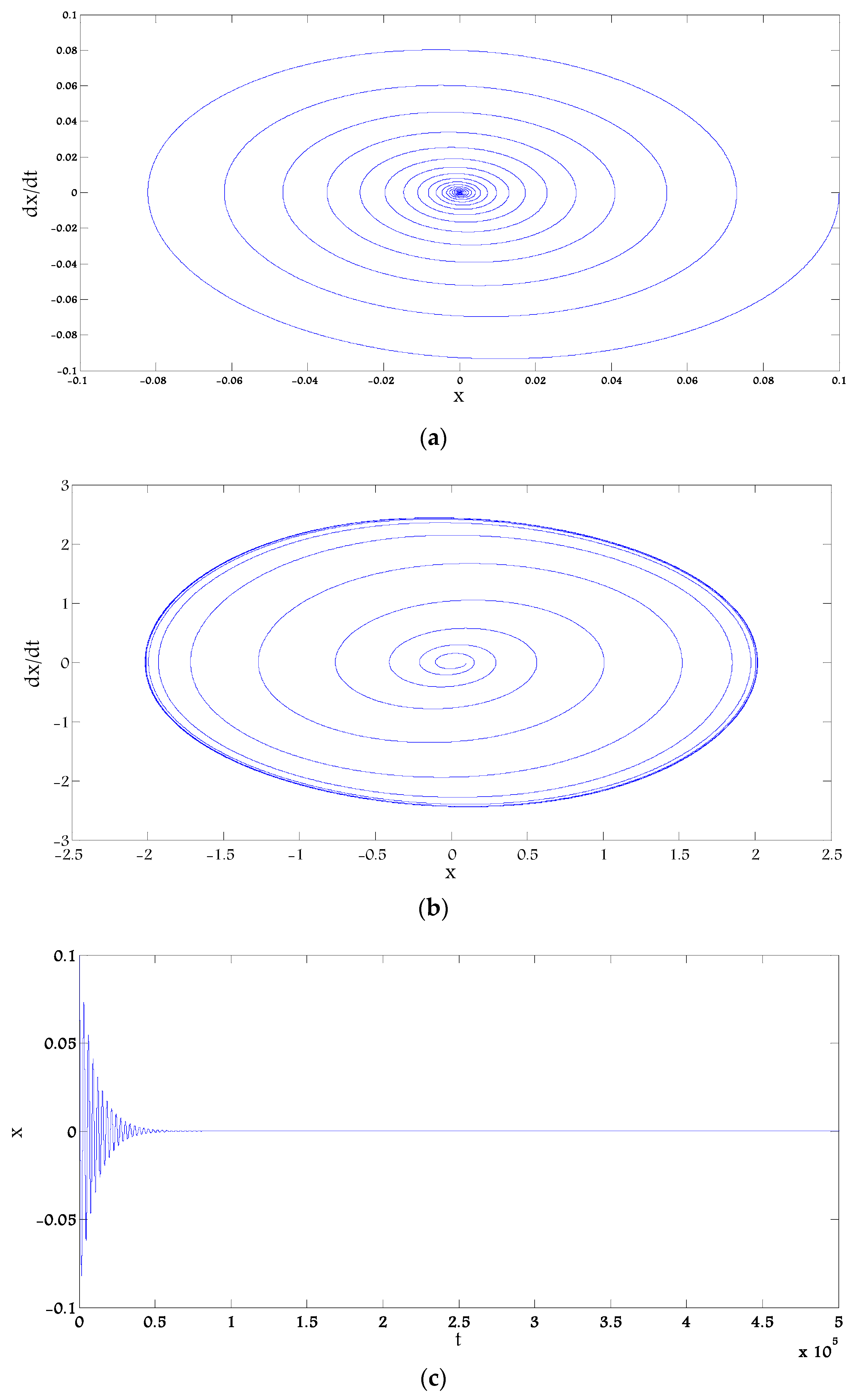
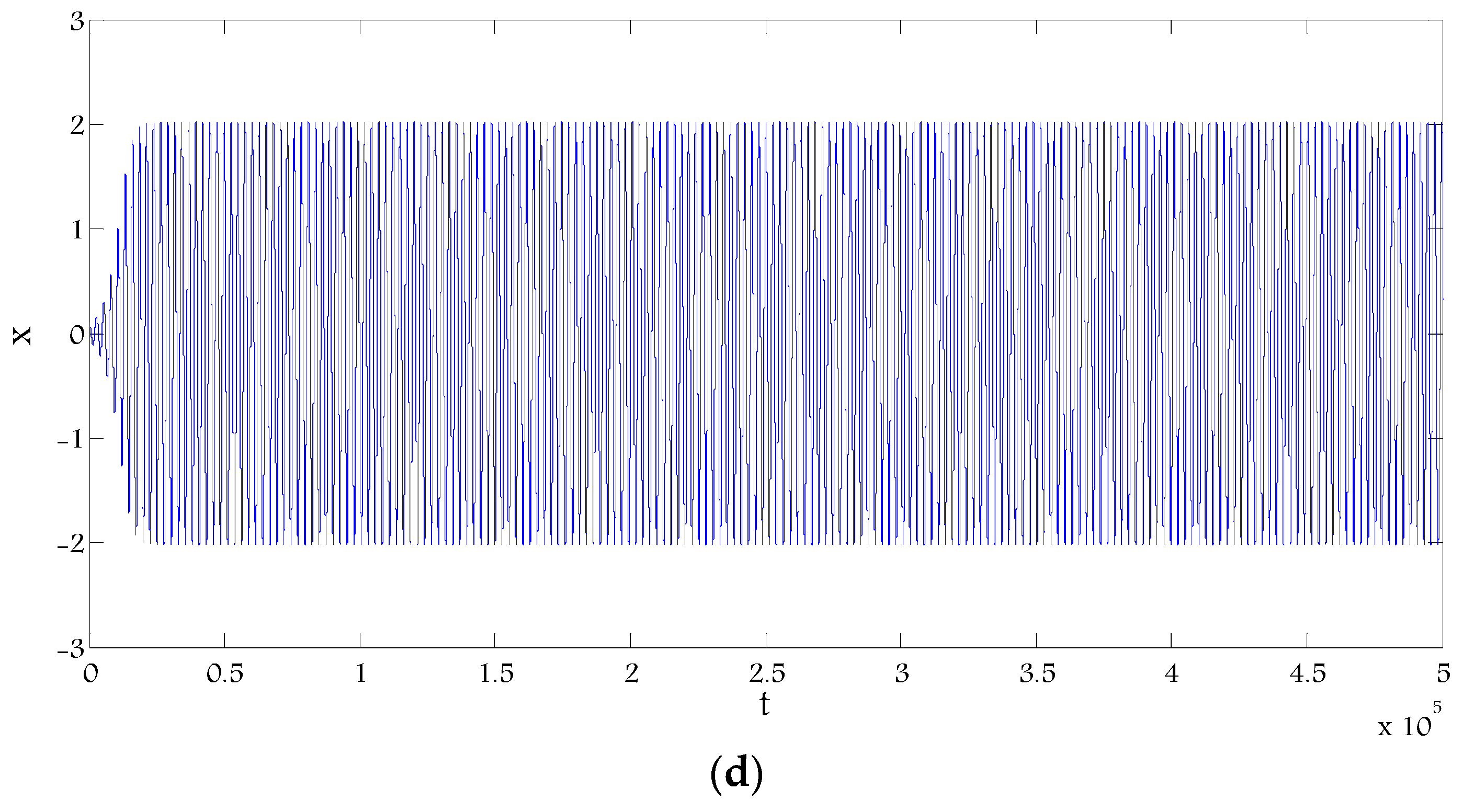
4.1. The Effect of Fractional-Order Time Delay
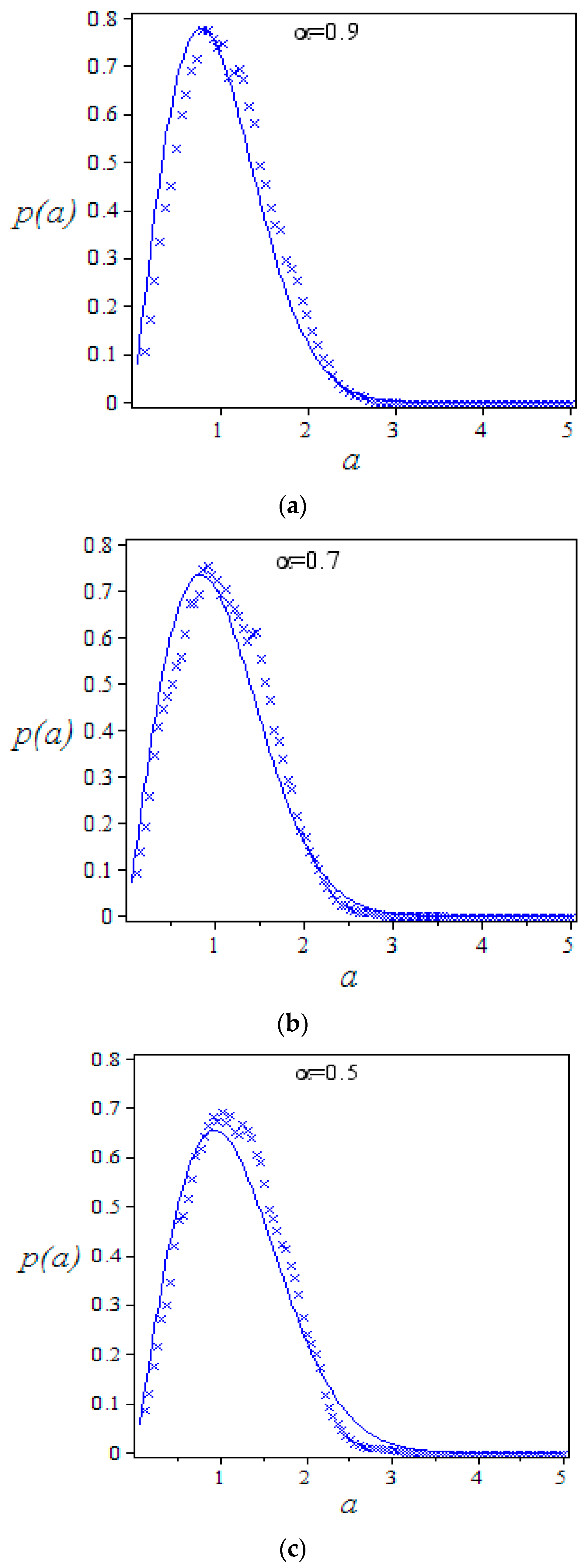
4.2. The Effect of the Fractional-Order
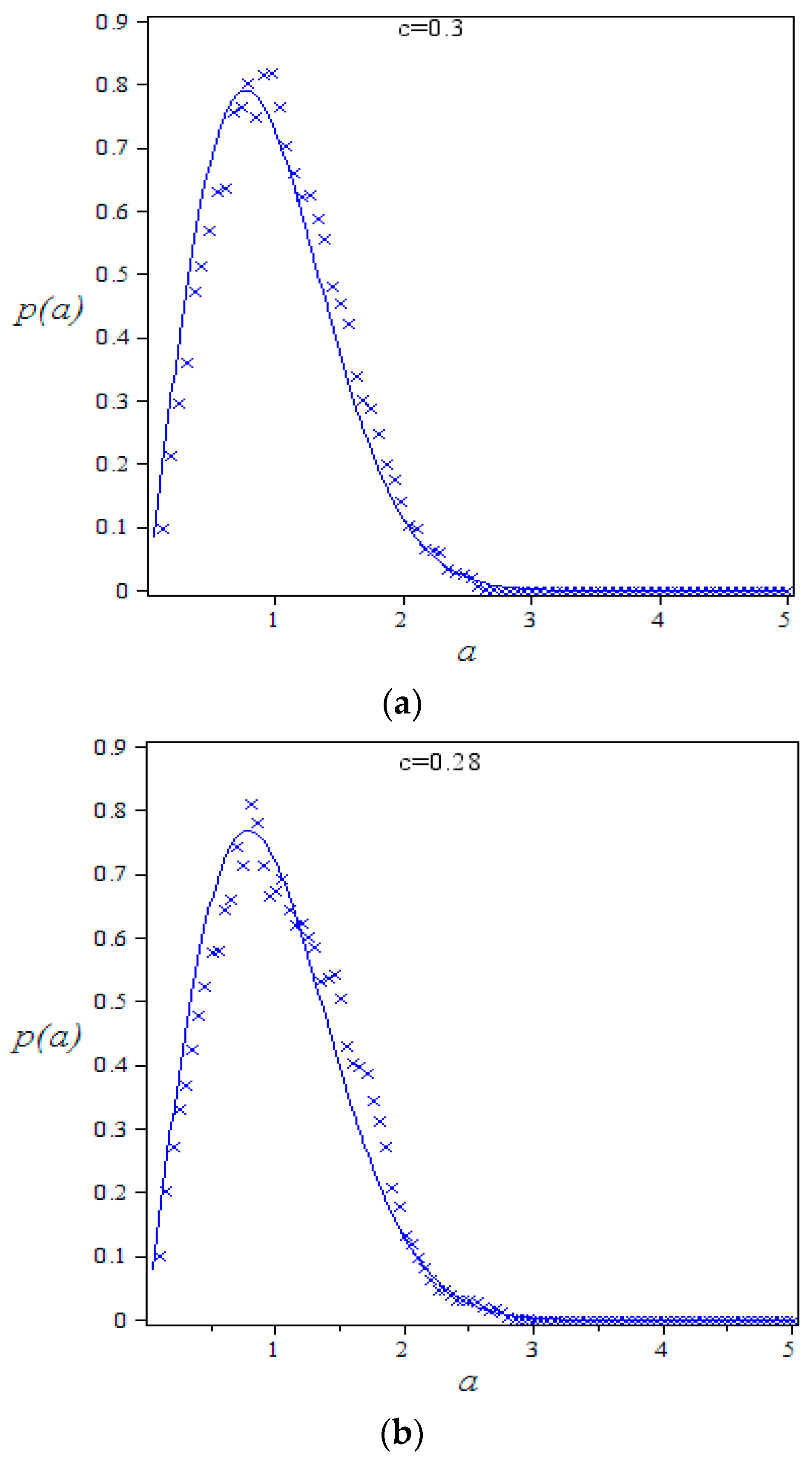
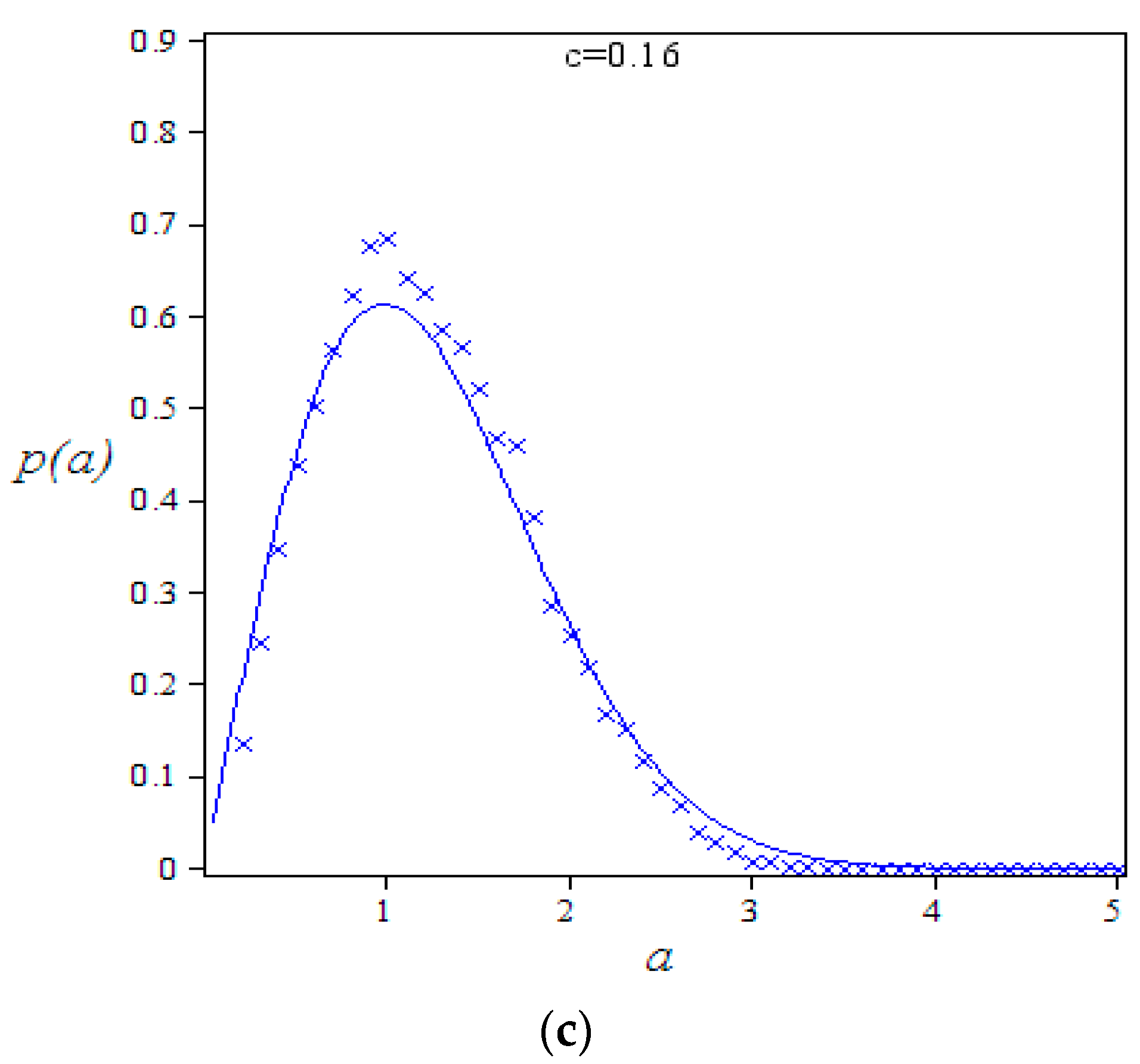
4.3. The Effect of Economic Control
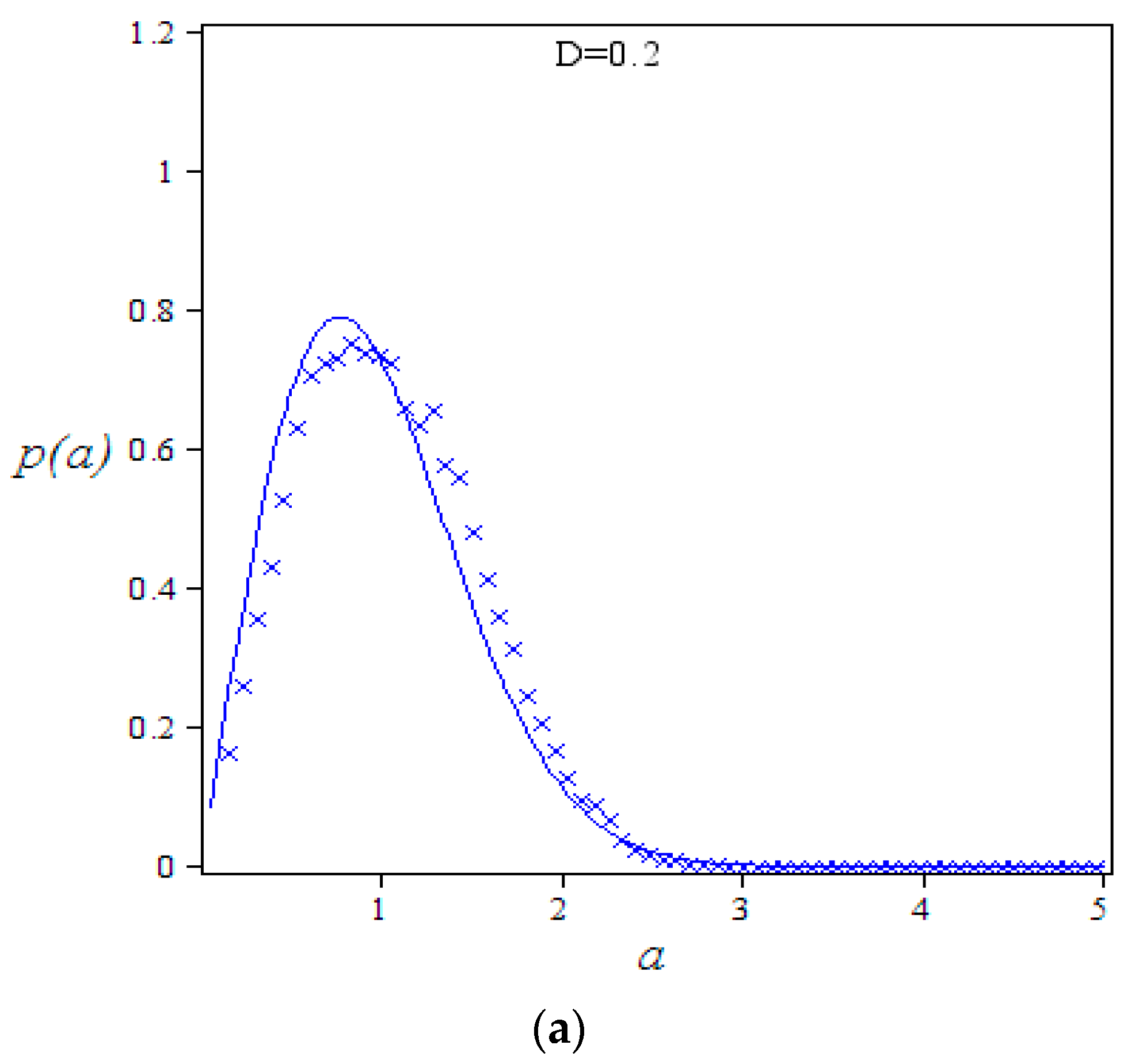
4.4. The Effect of Random Excitation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Goodwin, R.M. The nonlinear accelerator and the persistence of business cycles. Econom. J. Econom. Soc. 1951, 19, 1–17. [Google Scholar] [CrossRef]
- Li, S.; Li, Q.; Li, J.; Feng, J. Chaos prediction and control of Goodwin’s nonlinear accelerator model. Nonlinear Anal. Real World Appl. 2011, 12, 1950–1960. [Google Scholar] [CrossRef]
- Li, J.; Feng, C.S. First-passage failure of a business cycle model under time-delayed feedback control and wide-band random excitation. Phys. A Stat. Mech. Appl. 2010, 389, 5557–5562. [Google Scholar] [CrossRef]
- Yoshida, H.; Asada, T. Dynamic analysis of policy lag in a Keynes–Goodwin model: Stability, instability, cycles and chaos. J. Econ. Behav. Org. 2007, 62, 441–469. [Google Scholar] [CrossRef]
- Ma, J.; Gao, Q. Stability and Hopf bifurcations in a business cycle model with delay. Appl. Math. Comput. 2009, 215, 829–834. [Google Scholar] [CrossRef]
- Wu, X.P.; Wang, L. Multi-parameter bifurcations of the Kaldor–Kalecki model of business cycles with delay. Nonlinear Anal. Real World Appl. 2010, 11, 869–887. [Google Scholar] [CrossRef]
- Hattaf, K.; Riad, D.; Yousfi, N. A generalized business cycle model with delays in gross product and capital stock. Chaos Solitons Fractals 2017, 98, 31–37. [Google Scholar] [CrossRef]
- Riad, D.; Hattaf, K.; Yousfi, N. Dynamics of a delayed business cycle model with general investment function. Chaos Solitons Fractals 2016, 85, 110–119. [Google Scholar] [CrossRef]
- Liu, X.; Cai, W.; Lu, J.; Wang, Y. Stability and Hopf bifurcation for a business cycle model with expectation and delay. Commun. Nonlinear Sci. Numer. Simul. 2015, 25, 149–161. [Google Scholar] [CrossRef]
- Li, J.; Ren, Z.; Wang, Z. Response of nonlinear random business cycle model with time delay state feedback. Phys. A Stat. Mech. Appl. 2008, 387, 5844–5851. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, J. Fractional calculus—A different approach to the analysis of viscoelastically damped structures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 1985, 23, 918–925. [Google Scholar] [CrossRef]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Kelly, J.M.; Koh, C. Application of fractional derivatives to seismic analysis of base isolated models. Earthq. Eng. Struct. Dyn. 1990, 19, 229–241. [Google Scholar]
- Rossikhin, Y.A.; Shitikova, M.V. Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev. 1997, 50, 15–67. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional calculus for dynamic problems of solid mechanics: Novel trends and recent results. Appl. Mech. Rev. 2010, 63, 010801. [Google Scholar] [CrossRef]
- Gemant, A. XLV. On fractional differentials. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1938, 25, 540–549. [Google Scholar] [CrossRef]
- Pritz, T. Analysis of four-parameter fractional derivative model of real solid materials. J. Sound Vib. 1996, 195, 103–115. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Podlubny, I. Mathematics in Science and Engineering. In Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Shen, Y.; Yang, S.; Xing, H.; Gao, G. Primary resonance of Duffing oscillator with fractional-order derivative. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3092–3100. [Google Scholar] [CrossRef]
- Niu, J.; Shen, Y.; Yang, S.; Li, S. Analysis of Duffing oscillator with time-delayed fractional-order PID controller. Int. J. Non-Linear Mech. 2017, 92, 66–75. [Google Scholar] [CrossRef]
- Laskin, N. Fractional market dynamics. Phys. A Stat. Mech. Appl. 2000, 287, 482–492. [Google Scholar] [CrossRef]
- Yin, C.; Zhong, S.-M.; Chen, W.-F. Design of sliding mode controller for a class of fractional-order chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 356–366. [Google Scholar] [CrossRef]
- Chen, W.-C. Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fractals 2008, 36, 1305–1314. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, X.; Shi, G. Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Comput. Math. Appl. 2011, 62, 1531–1539. [Google Scholar] [CrossRef]
- Pan, I.; Das, S.; Das, S. Multi-objective active control policy design for commensurate and incommensurate fractional order chaotic financial systems. Appl. Math. Model. 2015, 39, 500–514. [Google Scholar] [CrossRef]
- Danca, M.-F.; Garrappa, R.; Tang, W.K.; Chen, G. Sustaining stable dynamics of a fractional-order chaotic financial system by parameter switching. Comput. Math. Appl. 2013, 66, 702–716. [Google Scholar] [CrossRef]
- Spanos, P.; Zeldin, B. Random vibration of systems with frequency-dependent parameters or fractional derivatives. J. Eng. Mech. 1997, 123, 290–292. [Google Scholar] [CrossRef]
- Chen, L.; Wang, W.; Li, Z.; Zhu, W. Stationary response of Duffing oscillator with hardening stiffness and fractional derivative. Int. J. Non-Linear Mech. 2013, 48, 44–50. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, W. Stochastic jump and bifurcation of Duffing oscillator with fractional derivative damping under combined harmonic and white noise excitations. Int. J. Non-Linear Mech. 2011, 46, 1324–1329. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, W.Q. Stochastic stability of Duffing oscillator with fractional derivative damping under combined harmonic and white noise parametric excitations. Acta Mech. 2009, 207, 109–120. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, W. First passage failure of SDOF nonlinear oscillator with lightly fractional derivative damping under real noise excitations. Probab. Eng. Mech. 2011, 26, 208–214. [Google Scholar] [CrossRef]
- Chen, L.; Li, Z.; Zhuang, Q.; Zhu, W. First-passage failure of single-degree-of-freedom nonlinear oscillators with fractional derivative. J. Vib. Control 2013, 19, 2154–2163. [Google Scholar] [CrossRef]
- Chen, L.; Hu, F.; Zhu, W. Stochastic dynamics and fractional optimal control of quasi integrable Hamiltonian systems with fractional derivative damping. Fract. Calc. Appl. Anal. 2013, 16, 189–225. [Google Scholar] [CrossRef]
- Huang, Z.L.; Jin, X.L. Response and stability of a SDOF strongly nonlinear stochastic system with light damping modeled by a fractional derivative. J. Sound Vib. 2009, 319, 1121–1135. [Google Scholar] [CrossRef]
- Hu, F.; Zhu, W.Q.; Chen, L.C. Stochastic fractional optimal control of quasi-integrable Hamiltonian system with fractional derivative damping. Nonlinear Dyn. 2012, 70, 1459–1472. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Liu, D. Response of Fractional Oscillators With Viscoelastic Term Under Random Excitation. J. Comput. Nonlinear Dyn. 2014, 9, 031015. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Liu, D. A method to stochastic dynamical systems with strong nonlinearity and fractional damping. Nonlinear Dyn. 2016, 83, 2311–2321. [Google Scholar] [CrossRef]
- Liu, D.; Li, J.; Xu, Y. Principal resonance responses of SDOF systems with small fractional derivative damping under narrow-band random parametric excitation. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3642–3652. [Google Scholar] [CrossRef]
- Lin, Z.; Li, J.; Li, S. On a business cycle model with fractional derivative under narrow-band random excitation. Chaos Solitons Fractals 2016, 87, 61–70. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Xu, W.; Li, J.; Jia, W.; Li, S. Study on the Business Cycle Model with Fractional-Order Time Delay under Random Excitation. Entropy 2017, 19, 354. https://doi.org/10.3390/e19070354
Lin Z, Xu W, Li J, Jia W, Li S. Study on the Business Cycle Model with Fractional-Order Time Delay under Random Excitation. Entropy. 2017; 19(7):354. https://doi.org/10.3390/e19070354
Chicago/Turabian StyleLin, Zifei, Wei Xu, Jiaorui Li, Wantao Jia, and Shuang Li. 2017. "Study on the Business Cycle Model with Fractional-Order Time Delay under Random Excitation" Entropy 19, no. 7: 354. https://doi.org/10.3390/e19070354
APA StyleLin, Z., Xu, W., Li, J., Jia, W., & Li, S. (2017). Study on the Business Cycle Model with Fractional-Order Time Delay under Random Excitation. Entropy, 19(7), 354. https://doi.org/10.3390/e19070354



