Some Remarks on Classical and Classical-Quantum Sphere Packing Bounds: Rényi vs. Kullback–Leibler ^†

Abstract

We review the use of binary hypothesis testing for the derivation of the sphere packing bound in channel coding, pointing out a key difference between the classical and the classical-quantum setting. In the first case, two ways of using the binary hypothesis testing are known, which lead to the same bound written in different analytical expressions. The first method historically compares output distributions induced by the codewords with an auxiliary fixed output distribution, and naturally leads to an expression using the Renyi divergence. The second method compares the given channel with an auxiliary one and leads to an expression using the Kullback–Leibler divergence. In the classical-quantum case, due to a fundamental difference in the quantum binary hypothesis testing, these two approaches lead to two different bounds, the first being the “right” one. We discuss the details of this phenomenon, which suggests the question of whether auxiliary channels are used in the optimal way in the second approach and whether recent results on the exact strong-converse exponent in classical-quantum channel coding might play a role in the considered problem.

1. Introduction

One of the central problems in coding theory deals with determining upper and lower bounds on the probability of error when communication over a given channel is attempted at some rate R. The capacity of the channel C is defined as the highest rate at which communication is possible with probability of error that vanishes as the blocklength of the code grows to infinity (see [1,2,3]). At rates $R<C$, it is known that the probability of error vanishes exponentially fast in the blocklength, and a classic problem in information theory is the determination of that exponential speed or, as is it customary to say, of the error exponent. This problem was dealt with in the classical setting back in the 1960s, when most of the still strongest results were obtained [4,5,6,7,8]. Instead, for classical-quantum channels, the topic is relatively more recent; first results were obtained around 1998 ([9,10]) and new ones are still in progress.

An important bound on error exponents is the so-called sphere packing bound, a fundamental lower bound on the probability of error of optimal codes and hence an upper bound on achievable error exponents. This particular result was first derived in different forms in the 1960s for classical channels (of different types) and more recently in [11,12,13] for classical-quantum channels. The aim of this paper is to present a detailed and self-contained discussion of the differences between the classical and classical-quantum settings, pointing out connections with an important open problem first suggested by Holevo in [10] and possibly with recent results derived by Mosonyi and Ogawa in [14].

2. The Problem

We consider a classical-quantum channel with finite input alphabet $\mathcal{X}$ and associated density operators $W_x$, $x\in \mathcal{X}$, in a finite dimensional Hilbert space $\mathcal{H}$. The n-fold product channel acts in the tensor product space $\mathcal{H}={\mathcal{H}}^{\otimes n}$ of n copies of $\mathcal{H}$. To a sequence $\mathit{x}=(x_1,x_2,\dots ,x_n)$, we associate the signal state ${\mathit{W}}_{\mathit{x}}=W_{x_1}\otimes W_{x_2},\dots ,\otimes W_{x_n}$. A block code with M codewords is a mapping from a set of M messages $\{1,\dots ,M\}$ into a set of M codewords $\{{\mathit{x}}_1,\dots ,{\mathit{x}}_M\}$, and the rate of the code is $R=\left(\log M\right)/n$. A quantum decision scheme for such a code, or Positive-Operator Valued Measure (POVM), is a collection of M positive operators $\{{\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2,\dots ,{\mathsf{\Pi }}_M\}$ such that $\sum {\mathsf{\Pi }}_m=I$, where I is the identity operator. The probability that message $m^{\prime }$ is decoded when message m is transmitted is ${\mathsf{P}}_{m^{\prime }|m}=\mathrm{Tr}{\mathsf{\Pi }}_{m^{\prime }}{\mathit{W}}_{{\mathit{x}}_m}$ and the probability of error after sending message m is

$${\mathsf{P}}_{\mathrm{e}|m}=1-\mathrm{Tr}\left({\mathsf{\Pi }}_m{\mathit{W}}_{{\mathit{x}}_m}\right).$$

The maximum error probability of the code is defined as the largest ${\mathsf{P}}_{\mathrm{e}|m}$; that is,

$${\mathsf{P}}_{\mathrm{e},\max }=\underset{m}{\max }{\mathsf{P}}_{\mathrm{e}|m}.$$

When all the operators $W_x$ commute, the channel is classical and we will use the classical notation $W_x\left(y\right)$ to indicate the eigenvalues of the operators, which are the transition probabilities from inputs x to outputs $y\in \mathcal{Y}$. Similarly, ${\mathit{W}}_{\mathit{x}}\left(\mathit{y}\right)$ will represent the transition probabilities from input sequences $\mathit{x}$ to output sequences $\mathit{y}\in {\mathcal{Y}}^n$. In the classical case, it can be proved that optimal decision schemes can always be assumed to have separable measurements which commute with the states. Hence, we will use the classical notation ${\mathit{W}}_{{\mathit{x}}_m}\left({\mathcal{Y}}_m\right)$ in place of $\mathrm{Tr}{\mathsf{\Pi }}_m{\mathit{W}}_{{\mathit{x}}_m}$, where ${\mathcal{Y}}_m\in {\mathcal{Y}}^n$ is the decoding region for message m.

Let ${\mathsf{P}}_{\mathrm{e},\max }^{\left(n\right)}\left(R\right)$ be the smallest maximum error probability among all codes of length n and rate at least R. We define the reliability function of the channel as

$$E\left(R\right)=\underset{n\to \infty }{\lim \sup }-\frac{1}{n}\log {\mathsf{P}}_{\mathrm{e},\max }^{\left(n\right)}\left(R\right).$$

(1)

In this paper, we focus on the so-called sphere packing upper bound on $E\left(R\right)$, which states that

$$E\left(R\right)\le E_{\mathrm{sp}}\left(R\right)$$

(2)

where

$$E_{\mathrm{sp}}\left(R\right)=\underset{P}{\max }{E}_{\mathrm{sp}}^{\mathrm{cc}}(R,P)$$

(3)

and

$$\begin{array}{cc}\hfill E_{\mathrm{sp}}^{\mathrm{cc}}(R,P)& =\underset{0<s<1}{\sup }\left[E_0^{\mathrm{cc}}(s,P)-\frac{s}{1-s}R\right],\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill E_0^{\mathrm{cc}}(s,P)& =\underset{Q}{\min }\left[\frac{1}{s-1}\sum _{x}P\left(x\right)\log \mathrm{Tr}\left(W_x^{1-s}{Q}^s\right)\right],\hfill \end{array}$$

(5)

the minimum being over density operators Q. Here $E_{\mathrm{sp}}^{\mathrm{cc}}(R,P)$ is an upper bound on the error exponent achievable by so-called constant composition codes; that is, such that in each codeword symbols appear with empirical frequency P. For classical channels, $E_0^{\mathrm{cc}}(s,P)$ is written in the standard notation as

$$E_0^{\mathrm{cc}}(s,P)=\underset{Q}{\min }\left[\frac{1}{s-1}\sum _{x}P\left(x\right)\log \sum _y{W}_x{\left(y\right)}^{1-s}Q{\left(y\right)}^s\right].$$

(6)

3. Binary Hypothesis Testing

3.1. Classical Case

We start by recalling that in classical binary hypothesis testing between two distributions $P_0$ and $P_1$ on some set $\mathcal{V}$, based on n independent extractions, the trade-off of the achievable exponents for the error probabilities of the first and second kind can be expressed parametrically, for $0<s<1$, as (e.g., [7])

$$\begin{array}{cc}\hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|0}& =-\mu \left(s\right)+s{\mu }^{\prime }\left(s\right)+o\left(1\right)\hfill \end{array}$$

(7)

$$\begin{array}{ccc}& \hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|1}& =-\mu \left(s\right)-(1-s){\mu }^{\prime }\left(s\right)+o\left(1\right)\hfill \end{array}$$

(8)

where

$$\mu \left(s\right)=\log \sum _{v\in \mathcal{V}}{P}_0{\left(v\right)}^{1-s}{P}_1{\left(v\right)}^s.$$

(9)

The quantity $\mu \left(s\right)$ defined above is actually a scaled version of the Rényi divergence, usually defined as

$$D_{\alpha }(P\parallel Q)=\frac{1}{\alpha -1}\log \sum _{v\in V}P{\left(v\right)}^{\alpha }Q{\left(v\right)}^{1-\alpha }.$$

(10)

We have in fact $\mu \left(s\right)=-s{D}_{1-s}(P_0\parallel P_1)$. A key role in the derivation of the above result is played by the tilted mixture $P_s$, defined as

$$P_s\left(v\right)=\frac{P_0{\left(v\right)}^{1-s}{P}_1{\left(v\right)}^s}{{\sum }_{v^{\prime }}{P}_0{\left(v^{\prime }\right)}^{1-s}{P}_1{\left(v^{\prime }\right)}^s}.$$

(11)

Roughly speaking, the probability of error for the optimal test is essentially due to the set of those sequences in ${\mathcal{V}}^n$ with empirical distribution close to $P_s$.

A graphical representation relating the above equations suggested in [7] is shown in Figure 1. Figure 2 shows an interpretation of the role of the Rényi divergence. Note that one has the well-known property

$$\begin{array}{cc}\hfill \underset{\alpha \to 1}{\lim }{D}_{\alpha }(P\parallel Q)& =\sum _{v\in \mathcal{V}}P\left(v\right)\log \frac{P\left(v\right)}{Q\left(v\right)}\hfill \end{array}$$

(12)

$$\begin{array}{cc}& =D_{\mathrm{KL}}(P\parallel Q),\hfill \end{array}$$

(13)

which explains the endpoints of the curve in Figure 2. In particular (though some technicalities would be needed for a rigorous derivation), the quantity $D_{\mathrm{KL}}(P\parallel Q)$ governs the “Stein regime”; if in the binary hypothesis test ${{\mathsf{P}}_{\mathrm{e}}}_{|0}$ is only required to be bounded away from 1 as $n\to \infty$, then $-\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|1}$ is asymptotically upper-bounded by $D_{\mathrm{KL}}(P_0\parallel P_1)$. This can be stated equivalently as saying that regions ${\mathcal{S}}_n\subseteq {\mathcal{V}}^n$ for which $P_0\left({\mathcal{S}}_n\right)>ϵ$ satisfy $P_1\left({\mathcal{S}}_n\right)>e^{-n{D}_{\mathrm{KL}}(P_0\parallel P_1)+o\left(n\right)}$.

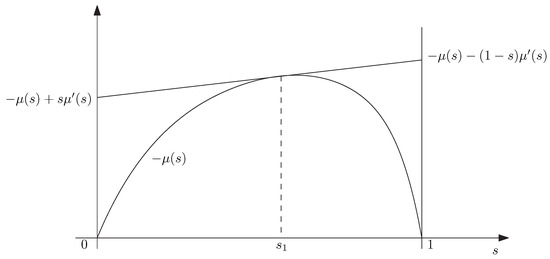
Figure 1. Interpretation of the error exponents in binary hypothesis testing from [7].

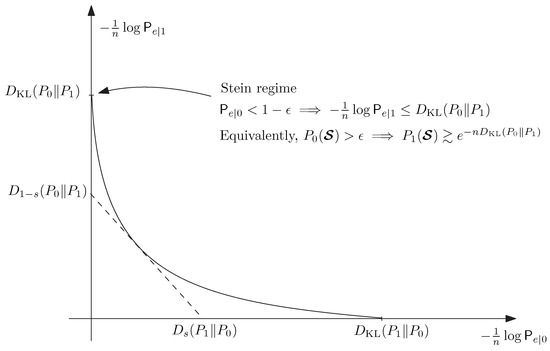
Figure 2. Error exponents in binary hypothesis testing.

An explicit computation of the derivatives ${\mu }^{\prime }\left(s\right)$, or just a different way of deriving the bound, shows that equivalent expressions for the error exponents are (see for example [2])

$$\begin{array}{cc}\hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|0}& =D_{\mathrm{KL}}(P_s\parallel P_0)+o\left(1\right)\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|1}& =D_{\mathrm{KL}}(P_s\parallel P_1)+o\left(1\right)\hfill \end{array}$$

(15)

where $P_s$ is the tilted mixture already defined in (11). This second representation gives another interpretation of the result. As said for the previous approach, the error events essentially occur in the set of sequences in ${\mathcal{V}}^n$ with empirical distribution close to $P_s$, whose total probabilities under $P_0$ and $P_1$ vanish, according to Stein’s lemma as mentioned above, with exponents given by $D_{\mathrm{KL}}(P_s\parallel P_0)$ and $D_{\mathrm{KL}}(P_s\parallel P_1)$, respectively. One can notice that the problem of determining the trade-off of the error exponents in the test between $P_0$ and $P_1$ is essentially reduced to the problem of testing $P_s$ against $P_i$, $i=0,1$ in the Stein regime where ${{\mathsf{P}}_{\mathrm{e}}}_{|s}$ is bounded away from 1.

3.2. Quantum Case

In a binary hypothesis testing between two density operators ${\sigma }_0$ and ${\sigma }_1$, based on n independent extractions (but with global measurement), the error exponents of the first and second kind can be expressed parametrically as (see [15]):

$$\begin{array}{cc}\hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\sigma }_0}& =-\mu \left(s\right)+s{\mu }^{\prime }\left(s\right)+o\left(1\right)\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\sigma }_1}& =-\mu \left(s\right)-(1-s){\mu }^{\prime }\left(s\right)+o\left(1\right)\hfill \end{array}$$

(17)

where, in complete analogy with the classical case,

$$\mu \left(s\right)=\log \mathrm{Tr}{\sigma }_0^{1-s}{\sigma }_1^s.$$

(18)

Upon differentiation, one finds for example for (16):

$$-\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\sigma }_0}=-\log \mathrm{Tr}\left({\sigma }_0^{1-s}{\sigma }_1^s\right)+\mathrm{Tr}\left[\frac{{\sigma }_0^{1-s}{\sigma }_1^s}{\mathrm{Tr}{\sigma }_0^{1-s}{\sigma }_1^s}\left(\log {\sigma }_1^s-\log {\sigma }_0^s\right)\right]+o\left(1\right).$$

When ${\sigma }_0$ and ${\sigma }_1$ commute (i.e., in the classical case), we can define the density operator

$${\sigma }_s=\frac{{\sigma }_0^{1-s}{\sigma }_1^s}{\mathrm{Tr}{\sigma }_0^{1-s}{\sigma }_1^s}$$

(19)

and use the property $\log {\sigma }_1^s-\log {\sigma }_0^s=\log {\sigma }_0^{1-s}{\sigma }_1^s-\log {\sigma }_0$ to obtain

$$\begin{array}{cc}\hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\sigma }_0}& =\mathrm{Tr}{\sigma }_s(\log {\sigma }_s-\log {\sigma }_0)+o\left(1\right)\hfill \end{array}$$

(20)

$$\begin{array}{cc}& =D_{\mathrm{KL}}({\sigma }_s\parallel {\sigma }_0)+o\left(1\right).\hfill \end{array}$$

(21)

In a similar way, we find

$$\begin{array}{cc}\hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\sigma }_1}& =D_{\mathrm{KL}}({\sigma }_s\left|\right|{\sigma }_1)+o\left(1\right).\hfill \end{array}$$

(22)

This is indeed the second form of the bound as already mentioned in Section 3.1. However, if ${\sigma }_0$ and ${\sigma }_1$ do not commute, the above simplification is not possible. Hence, the two error exponents cannot be expressed in terms of the Kullback–Leibler divergence. So, unlike in the classical binary hypothesis testing, the problem of determining the trade-off of the error exponents in the test between ${\sigma }_0$ and ${\sigma }_1$ cannot be reduced to the problem of testing some ${\sigma }_s$ against ${\sigma }_i$, $i=0,1$ in the Stein regime.

To verify that this is actually a property of the quantum binary hypothesis testing and not an artificial effect of the procedure used, it is useful to consider the case of pure states; that is, when operators ${\sigma }_0$ and ${\sigma }_1$ have rank 1, say ${\sigma }_0=|{\psi }_0⟩⟨{\psi }_0|$ and ${\sigma }_1=|{\psi }_1⟩⟨{\psi }_1|$, with non-orthogonal ${\psi }_0$ and ${\psi }_1$ . In this case, ${\sigma }_0^{1-s}={\sigma }_0$ and ${\sigma }_1^s={\sigma }_1$, so one simply has

$$\begin{array}{cc}\hfill \mu \left(s\right)& =\log \mathrm{Tr}{\sigma }_0{\sigma }_1\hfill \end{array}$$

(23)

$$\begin{array}{cc}& =\log |⟨{\psi }_0|{\psi }_1⟩{|}^2,\hfill \end{array}$$

(24)

and at least one of the two error exponents is not larger than $-\log |⟨{\psi }_0|{\psi }_1⟩{|}^2$. These quantities cannot be expressed as $D_{\mathrm{KL}}({\sigma }_s\parallel {\sigma }_i)$, $i=0,1$ for any ${\sigma }_s$, because

$$D_{\mathrm{KL}}(\rho \parallel {\sigma }_i)=\left\{\begin{array}{cc}0\hfill & \rho ={\sigma }_i\hfill \\ +\infty \hfill & \rho \ne {\sigma }_i\hfill \end{array}\right.,i=0,1,$$

(25)

since ${\sigma }_0$ and ${\sigma }_1$ are pure.

4. Classical Sphere-Packing Bound

Two proofs are known for the classical version of the bound, which naturally lead to two equivalent yet different analytical expressions for the function $E_{\mathrm{sp}}\left(R\right)$. The first was developed at the Massachusetts Institute of Technology (MIT) ([5,7]) while the other is due to Haroutunian [16,17]. A preliminary technical feature common to both procedures is that they both focus on some constant-composition sub-code which has virtually the same rate as the original code, but where all codewords have the same empirical composition P. In both cases, then, the key ingredient is binary hypothesis testing (BHT).

4.1. The MIT Proof

The first proof (see [5,7]) is based on a binary hypothesis test between the output distributions ${\mathit{W}}_{{\mathit{x}}_m}$ induced by the codewords ${\mathit{x}}_1,\dots ,{\mathit{x}}_M$ and an auxiliary output product distribution $\mathit{Q}=Q^{\otimes n}$ on ${\mathcal{Y}}^n$. Let ${\mathcal{Y}}_m\subseteq {\mathcal{Y}}^n$ be the decision region for message m. Since $\mathit{Q}$ is a distribution, for at least one m, we have

$$\begin{array}{cc}\hfill \mathit{Q}\left({\mathcal{Y}}_m\right)& \le 1/M\hfill \end{array}$$

(26)

$$\begin{array}{cc}& =e^{-nR}.\hfill \end{array}$$

(27)

Considering a binary hypothesis test between ${\mathit{W}}_{{\mathit{x}}_m}$ and $\mathit{Q}$, with ${\mathcal{Y}}_m$ as decision region for ${\mathit{W}}_{{\mathit{x}}_m}$, Equation (26) gives an exponential upper bound on the probability of error under hypothesis $\mathit{Q}$, which implies a lower bound on the probability of error under hypothesis ${\mathit{W}}_{{\mathit{x}}_m}$, which is ${\mathit{W}}_{{\mathit{x}}_m}\left(\overline{{\mathcal{Y}}_m}\right)$, the probability of error for message m. Here the BHT is considered in the regime where both probabilities decrease exponentially. The standard procedure uses the first form of the bound mentioned in the previous section based on the Rényi divergence. The bound can be extended to the case of testing products of non-identical distributions; for the pair of distributions ${\mathit{W}}_{{\mathit{x}}_m}=W_{x_{m,1}}\otimes ,\dots ,W_{x_{m,n}}$ and $\mathit{Q}=Q\otimes ,\dots ,\otimes Q$, it gives the performance of an optimal test in the form

$$\begin{array}{cc}\hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\mathit{W}}_{{\mathit{x}}_m}}& =-\mu \left(s\right)+s{\mu }^{\prime }\left(s\right)+o\left(1\right)\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill -\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|\mathit{Q}}& =-\mu \left(s\right)-(1-s){\mu }^{\prime }\left(s\right)+o\left(1\right)\hfill \end{array}$$

(29)

where now

$$\mu \left(s\right)=\sum _{x}P\left(x\right)\left[\log \sum _{y\in \mathcal{Y}}{W}_x{\left(y\right)}^{1-s}Q{\left(y\right)}^s\right].$$

(30)

At this point, the arguments in [5,7] diverge a bit; while the former is not rigorous, it has the advantage of giving the tight bound for the arbitrary codeword composition P. The latter is instead rigorous, but only gives the tight bound for the optimal composition P. In [13], we proposed a variation which we believe to be rigorous and that at the same time gives the tight bound for an arbitrary composition P. The need for this variation will be clear in the discussion of classical-quantum channels in the next section.

For the test based on the decoding region ${\mathcal{Y}}_{\mathit{m}}$, the left hand side of (29) is lower-bounded by R due to (26). So, if we choose s and Q in such a way that the right hand side of (29) is roughly $R-ϵ$, then $-(1/n)\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\mathit{W}}_{{\mathit{x}}_m}}$ must be smaller than the right hand side of (28) computed for those same s and Q (for otherwise the decision region ${\mathcal{Y}}_{\mathit{m}}$ would give a test strictly better than the optimal one). This is obtained by choosing Q, as a function of s, as the minimizer of $-\mu \left(s\right)$ and then selecting s which makes the right hand side of (29) equal to $R-ϵ$ (whenever possible). Extracting ${\mu }^{\prime }\left(s\right)$ from (29) in terms of $\mu \left(s\right)$ and R and using it in (28), the probability of error for message m is bounded in terms of R. After some tedious technicalities, cf. [13] (Appendix A), we get

$$-\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\mathit{W}}_{{\mathit{x}}_m}}\le \underset{0<s<1}{\sup }\left[E_0^{\mathrm{cc}}(s,P)-\frac{s}{1-s}(R-ϵ)\right]+o\left(1\right)$$

(31)

where

$$\begin{array}{cc}\hfill E_0^{\mathrm{cc}}(s,P)& =\underset{Q}{\min }\left[\frac{1}{s-1}\sum _{x}P\left(x\right)\log \sum _y{W}_x{\left(y\right)}^{1-s}Q{\left(y\right)}^s\right]\hfill \end{array}$$

(32)

$$\begin{array}{cc}& =\underset{Q}{\min }\left[\frac{s}{1-s}\sum _{x}P\left(x\right)D_{1-s}(W_x\parallel Q)\right]\hfill \end{array}$$

(33)

$$\begin{array}{cc}& =\frac{s}{1-s}{I}_{1-s}(P,W),\hfill \end{array}$$

(34)

the minimum being over distributions Q and $I_{\alpha }(P,W)$ being the $\alpha$-mutual information as defined by Csiszár [18]. We thus find the bound, valid for codes with constant composition P

$$-\frac{1}{n}\log {\mathsf{P}}_{\mathrm{e},\max }\le \underset{0<s<1}{\sup }\frac{s}{1-s}\left[I_{1-s}(P,W)-R+ϵ\right]+o\left(1\right).$$

(35)

It is worth pointing out that the chosen Q, which achieves the minimum in the definition of $E_0(s,P)$, satisfies the constraint (cf. [5] (Equations (9.23), (9.24), and (9.50)), [19] (Corollary 3))

$$Q\left(y\right)=\sum _{x}P\left(x\right)V_x\left(y\right),\forall y\in \mathcal{Y},$$

(36)

where we define $V_x\left(y\right)$ as

$$V_x\left(y\right)=\frac{W_x^{1-s}\left(y\right)Q^s\left(y\right)}{{\sum }_{y^{\prime }}{W}_x^{1-s}\left(y^{\prime }\right)Q^s\left(y^{\prime }\right)}$$

(37)

note the analogy with the definition of $P_s$ in (11). So, the chosen Q is such that its tilted mixtures with the distributions $W_x$ induce Q itself on the output set $\mathcal{Y}$. Using the second representation of the error exponents in binary hypothesis testing mentioned in Section 3.1 (extended for independent extractions from non-identical distributions), we observe thus that the chosen Q induces the construction of an auxiliary channel V such that the induced mutual information with input distribution P, say $I(P,V)$, equals $D_{\mathrm{KL}}(V\parallel Q|P)={\sum }_{x}P\left(x\right)D_{\mathrm{KL}}(V_x\parallel Q)=R-ϵ$. The second proof of the sphere packing bound, which is summarized in the next section, takes this line of reasoning as a starting point.

4.2. Haroutunian’s Proof

In the second proof (see [16,17]), one considers the performance of the given coding scheme for channel W when used for an auxiliary channel V with same input and output sets such that $I(P,V)<R$. The converse to the coding theorem implies that the probability of error for channel V is bounded away from zero at rate R, which means that there exists a fixed $ϵ>0$ such that for any blocklength n, ${\mathit{V}}_{{\mathit{x}}_m}\left(\overline{{\mathcal{Y}}_m}\right)>ϵ$ for at least one m. Using the Stein lemma mentioned before, we deduce that

$$-\frac{1}{n}\log {\mathit{W}}_{{\mathit{x}}_m}\left(\overline{{\mathcal{Y}}_m}\right)\le n{D}_{\mathrm{KL}}(V\parallel W|P)+o\left(1\right)$$

(38)

where now

$$D_{\mathrm{KL}}(V\parallel W|P)=\sum _{x}P\left(x\right)\sum _{y}V\left(y\right)\log \frac{V\left(y\right)}{W\left(y\right)}.$$

(39)

After optimization over V, we deduce that the error exponent for channel W is bounded as

$$-\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\mathit{W}}_{{\mathit{x}}_m}}\le \underset{V:I(P,V)\le R}{\min }{D}_{\mathrm{KL}}(V\parallel W|P)+o\left(1\right).$$

(40)

We observe that a slightly different presentation (e.g., [17]) avoids the use of the Stein lemma by resorting to the strong converse rather than a weak converse. Indeed, for channel V, the coding scheme will actually incur an error probability $1-o\left(1\right)$, which means that for at least one codeword m we must have ${\mathit{V}}_{{\mathit{x}}_m}\left(\overline{{\mathcal{Y}}_m}\right)=1-o\left(1\right)$. Applying the data processing inequality for the Kullback–Leibler divergence, one thus finds that

$${\mathit{V}}_{{\mathit{x}}_m}\left(\overline{{\mathcal{Y}}_m}\right)\log \frac{{\mathit{V}}_{{\mathit{x}}_m}\left(\overline{{\mathcal{Y}}_m}\right)}{{\mathit{W}}_{{\mathit{x}}_m}\left(\overline{{\mathcal{Y}}_m}\right)}+{\mathit{V}}_{{\mathit{x}}_m}\left({\mathcal{Y}}_m\right)\log \frac{{\mathit{V}}_{{\mathit{x}}_m}\left({\mathcal{Y}}_m\right)}{{\mathit{W}}_{{\mathit{x}}_m}\left({\mathcal{Y}}_m\right)}\le n{D}_{\mathrm{KL}}(V\parallel W|P)$$

(41)

from which

$$\log {\mathit{W}}_{{\mathit{x}}_m}\left(\overline{{\mathcal{Y}}_m}\right)\ge -\frac{n{D}_{\mathrm{KL}}(V\parallel W|P)+1}{1+o\left(1\right)}.$$

(42)

So, strong converse can be traded for Stein’s lemma, and this fact (which appears as a detail here) will be seen to be related to a less trivial question.

The bound derived is precisely the same as in the previous section, and for the optimal choice of the channel V, if we define the output distribution $Q=PV$ as in (36), then (37) is satisfied for some s (see Equation (19) in [16]). So, we notice that the two proofs actually rely on a comparison between the original channel and equivalent auxiliary channels/distributions. In the first procedure, we start with an auxiliary distribution Q, but we find that the optimal choice of Q is such that the tilted mixtures with the $W_x$ distributions are the $V_x$ which give $PV=Q$. In the second procedure, we start with the auxiliary channel V, but we find that the optimal V induces an output distribution Q whose tilted mixtures with the $W_x$ are the $V_x$ themselves. It is worth noting that in this second procedure we use a converse for channel V; hidden in this step we are using the output distribution Q induced by V, which we directly use for W in the MIT approach.

These observations point out that while the MIT proof follows the first formulation of the binary hypothesis testing bound in terms of Rényi divergences, Haroutunian’s proof exploits the second formulation based on Kullback–Leiblrer divergences, but the compared quantities are equivalent. There seems to be no reason to prefer the first procedure given the simplicity of the second one.

5. Classical-Quantum Sphere-Packing Bound

The different behavior of binary hypothesis testing in the quantum case with respect to the classical has a direct impact on the sphere packing bound for classical-quantum channels. Both the MIT and Haroutunian’s approaches can be extended to this setting, but the resulting bounds are different. In particular, since the binary hypothesis testing is correctly handled with the Rényi divergence formulation, the MIT form of the bound extends to what one expects as the right generalization (in particular, it matches known achievability bounds for pure-state channels), while Haroutunian’s form extends to a weaker bound. It was already observed in [20] that the latter gives a trivial bound for all pure state channels, which is a direct consequence of what has already been shown for the simple binary hypothesis testing in the previous section.

It is useful to investigate this weakness at a deeper level in order to clearly see where the problem truly is. Let now $W_x$, $x\in \mathcal{X}$ be general non-commuting density operators, the states of the channel to be studied. Consider then an auxiliary classical-quantum channel with states $V_x$ and with capacity $C<R$. Again, the converse to the channel coding theorem holds for channel V, which implies that for any decoding rule, for at least one message the probability of error is larger than some fixed positive constant $ϵ$. In particular for the given POVM, for at least one m,

$$\mathrm{Tr}(I-{\mathsf{\Pi }}_m){\mathit{V}}_{{\mathit{x}}_m}>ϵ.$$

(43)

Using the quantum Stein lemma, we deduce

$$-\frac{1}{n}\log \mathrm{Tr}(I-{\mathsf{\Pi }}_m){\mathit{W}}_{{\mathit{x}}_m}>D_{\mathrm{KL}}(V\parallel W|P)+o\left(1\right).$$

(44)

and hence, again as in the classical case,

$$-\frac{1}{n}\log {{\mathsf{P}}_{\mathrm{e}}}_{|{\mathit{W}}_{{\mathit{x}}_m}}\le \underset{V:I(P,V)\le R}{\min }{D}_{\mathrm{KL}}(V\parallel W|P)+o\left(1\right).$$

(45)

In this case as well, one can use a strong converse to replace the Stein lemma with a simpler data processing inequality.

The problem we encounter in this case is that if W is a pure state channel, at rates $R<C$, any auxiliary channel $V\ne W$ gives $D_{\mathrm{KL}}(V\parallel W|P)=\infty$, so that the bound is trivial for all pure state channels. It is important to observe that this is not due to a weakness in the use of the Stein lemma or of the data processing inequality. In a binary hypothesis test between the pure state ${\mathit{W}}_{{\mathit{x}}_m}$ and a state ${\mathit{V}}_{{\mathit{x}}_m}$ built from a different channel V, one can notice that the POVM $\{A,I-A\}$ with $A={\mathit{W}}_{{\mathit{x}}_m}$ satisfies

$$\mathrm{Tr}(I-A){\mathit{V}}_{{\mathit{x}}_m}=1+o\left(1\right),\mathrm{Tr}(I-A){\mathit{W}}_{{\mathit{x}}_m}=0.$$

(46)

So, it is actually impossible to deduce a positive lower bound for $\mathrm{Tr}(I-{\mathsf{\Pi }}_m){\mathit{W}}_{{\mathit{x}}_m}$ using only the fact that $\mathrm{Tr}(I-{\mathsf{\Pi }}_m){\mathit{V}}_{{\mathit{x}}_m}$ is bounded away from zero, or even approaches one.

It is also worth checking what happens with the MIT procedure. All the steps can be extended to the classical-quantum case (see [13] for details) leading to a bound which has the same form as (31) where $E_0^{\mathrm{cc}}(s,P)$ is defined in analogy with (32) as

$$\begin{array}{cc}\hfill E_0^{\mathrm{cc}}(s,P)& =\underset{Q}{\min }\left[\frac{1}{s-1}\sum _{x}P\left(x\right)\log \mathrm{Tr}{W}_x^{1-s}{Q}^s\right]\hfill \end{array}$$

(47)

$$\begin{array}{cc}& =\underset{Q}{\min }\left[\frac{s}{1-s}\sum _{x}P\left(x\right)D_{1-s}(W_x\parallel Q)\right],\hfill \end{array}$$

(48)

the minimum being over all density operators Q, and $D_{1-s}(·\parallel ·)$ being the quantum Rényi divergence. However, as far as we know there is no analog of Equations (36) and (37), and the optimizing Q does not induce an auxiliary V such that $I(P,V)=R-ϵ$.

6. Auxiliary Channels and Strong Converses

We have presented the two main approaches to sphere packing as different procedures which are equivalent in the classical case but not in the classical-quantum case. However, it is actually possible to consider the two approaches as particular instances of one general approach where the channel W is compared to an auxiliary channel V, since the auxiliary distribution/state Q can be considered as a channel with constant $V_x=Q$. This principle is very well described in [21], where it is shown that essentially all known converse bounds in channel coding can be cast in this framework.

According to this interpretation, the starting point in Haroutunian’s proof is general enough to include the MIT approach as a special case. So, the weakness of the method in the classical-quantum case must be hidden in one of the intermediate steps. It is not difficult to notice that the key point is how the (possibly strong) converse is used in Haroutunian’s proof. The general auxiliary channel V is only assumed to have capacity $C<R$, and the strongest possible converse for V which can used is of the simple form ${\mathsf{P}}_{\mathrm{e}}=1-o\left(1\right)$, which is good enough in the classical case. In the MIT proof, instead, the auxiliary channel is such that $C=0$, so that the strong converse takes another simple form, ${\mathsf{P}}_{\mathrm{e}}\ge 1-e^{-nR}$. The critical point is that in the classical-quantum setting a converse of the form ${\mathsf{P}}_{\mathrm{e}}=1-o\left(1\right)$ for V does not lead to a lower bound on ${\mathsf{P}}_{\mathrm{e}}$ for W in general. What is needed is a sufficiently fast exponential convergence to 1 of ${\mathsf{P}}_{\mathrm{e}}$ for channel V, which essentially suggests that V should be chosen with capacity not too close to R, and that the exact strong converse exponent for V should be used.

The natural question to ask at this point is what the optimal (here we mean optimal memoryless channel for bounding the error exponent in the asymptotic regime) auxiliary channel is when the exact exponent of the strong converse is used. At high rates, the question is not really meaningful for all those cases where the known versions of the sphere packing bound coincide with achievability results; that is, for classical channels and for pure state channels [9]. However, in the remaining cases (i.e., in the low rate region for the mentioned channels or in the whole range of rates $0<R<C$ for general non-commuting mixed-state channels), the question is legitimate. In the classical case, since the choice of an (optimal) auxiliary channel with $C=0$ or $C=R^{-}$ leads to the same result, one might expect that any other intermediate choice would give the same result. This can be indeed be proved by noticing that any version of the sphere packing derived with the considered scheme, independently of the used auxiliary channel, will always hold also when list decoding is considered for any fixed list-size L (see [7] for details or notice that the converse to the coding theorem for V would also hold in this setting). Since the bound obtained with the mentioned choices of auxiliary Q and V is achievable at any rate R when list-size decoding is used with sufficiently large list-size L (see [3] (Prob. 5.20)), no other auxiliary channel can give a better bound.

For classical-quantum channels, instead, the question is perhaps not trivial; it is worth pointing out that even the exact strong converse exponent has been determined only very recently [14]. What is very interesting is that while in the classical case the strong converse exponent for $R>C$ is expressed in terms of Rényi divergence [22,23] ( similarly as error exponents for $R<C$), for classical-quantum channels, the strong converse exponents are expressed in terms of the so-called “sandwiched” Rényi divergence defined by

$${\tilde{D}}_{\alpha }(\rho ,\sigma )=\frac{1}{\alpha -1}\log \mathrm{Tr}{\left({\sigma }^{\frac{1-\alpha }{2\alpha }}\rho {\sigma }^{\frac{1-\alpha }{2\alpha }}\right)}^{\alpha }.$$

(49)

The problem to study would thus be more or less as follows: Consider an auxiliary channel V with capacity $C<R$ and evaluate its strong converse exponent in terms of sandwiched Rényi divergences. Fix this exponent as the probability of error under hypothesis ${\mathit{V}}_{{\mathit{x}}_m}$ in a test between ${\mathit{W}}_{{\mathit{x}}_m}$ and ${\mathit{V}}_{{\mathit{x}}_m}$, where ${\mathsf{\Pi }}_m$ is the operator in favor of ${\mathit{W}}_{{\mathit{x}}_m}$ and $I-{\mathsf{\Pi }}_m$ is the one in favor of ${\mathit{V}}_{{\mathit{x}}_m}$. Then, deduce a lower bound for the probability of error under hypothesis ${\mathit{W}}_{{\mathit{x}}_m}$ using the standard binary hypothesis testing bound in terms of Rényi divergences. It is not entirely clear to this author that the optimal auxiliary channel should necessarily always be one such that $C=0$, as used up to now. Since for non-commuting mixed-state channels the current known form of sphere packing bound is not yet matched by any achievability result, one cannot exclude the possibility that it is not the tightest possible form.