An Entropic Approach for Pair Trading
Abstract
:1. Introduction
2. Model
3. Main Results
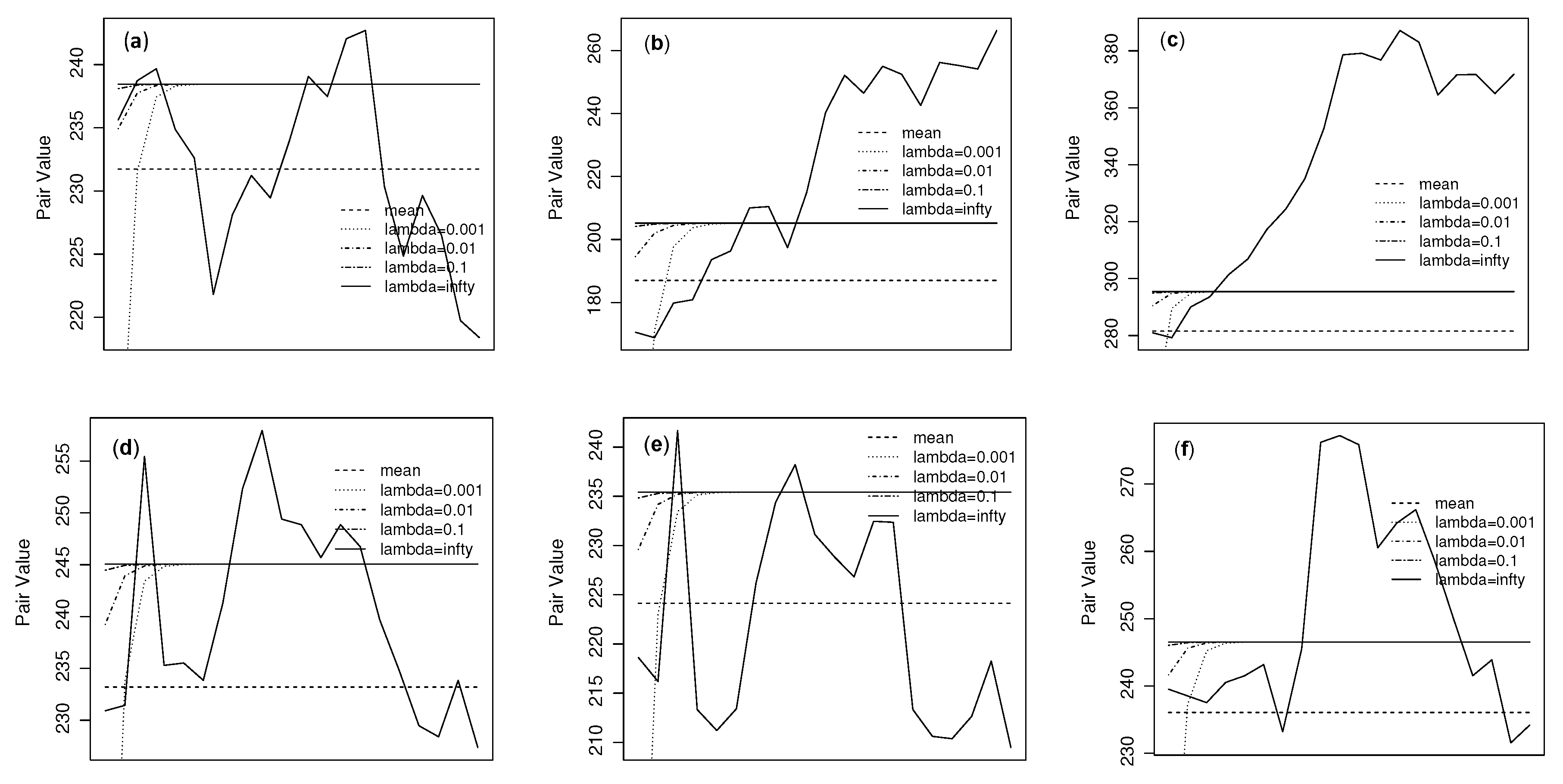
Numerical Example
4. Proof of Theorem 1
5. Concluding Remarks
Acknowledgments
Conflicts of Interest
References
- Elliott, R.; Van Der Hoek, J.; Malcolm, W. Pairs trading. Quant. Financ. 2005, 5, 271–276. [Google Scholar] [CrossRef]
- Gatev, E.; Goetzman, W.; Rouwenhorst, K. Pairs trading: Performance of a relative-value arbitrage rule. Rev. Financ. Stud. 2006, 19, 787–827. [Google Scholar] [CrossRef]
- Avellaneda, M.; Lee, J. Statistical arbitrage in the US equities market. Quant. Financ. 2010, 10, 761–782. [Google Scholar] [CrossRef]
- Kakushadze, Z. Mean-reversion and optimization. J. Asset Manag. 2015, 16, 14–40. [Google Scholar] [CrossRef]
- Caporale, G.; Gil-Alana, L.; Plastun, A. Searching for inefficiencies in exchange rate dynamics. Comput. Econ. 2017, 49, 405–432. [Google Scholar] [CrossRef]
- Chen, C.; Lin, T. Nonparametric tolerance limits for pair trading. Financ. Res. Lett. 2017, 21, 1–9. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Z.; Sriboonchitta, S.; Lee, S. Pair trading based on quantile forecasting of smooth transition GARCH models. N. Am. J. Econ. Financ. 2017, 39, 38–55. [Google Scholar] [CrossRef]
- Ekström, E.; Lindberg, C.; Tysk, J. Optimal liquidation of a pairs trade. In Advanced Mathematical Methods for Finance; Nunno, G., Øksendal, B., Eds.; Springer: Berlin, Germany, 2011. [Google Scholar]
- Riedel, F. Optimal stopping with multiple priors. Econometrica 2009, 77, 857–908. [Google Scholar]
- Krätschmer, V.; Schoenmakers, J. Representations for optimal stopping under dynamic monetary utility functionals. SIAM J. Financ. Math. 2010, 1, 811–832. [Google Scholar] [CrossRef]
- Krätschmer, V.; Ladkau, M.; Laeven, R.; Schoenmakers, J.; Stadje, M. Robust Optimal Stopping. Available online: http://www.uni-ulm.de/fileadmin/websiteuniulm/mawi.inst.140/Team/MStadje/KLLSS-StoppingAmbiguity-041715-a.pdf (accessed on 30 June 2017).
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Serguieva, A.; Hunter, J. Fuzzy interval methods in investment risk appraisal. Fuzzy Sets Syst. 2004, 142, 443–466. [Google Scholar]
- Zhou, X.; Dong, M. Can fuzzy logic make technical analysis 20/20? Financ. Anal. J. 2004, 60, 54–75. [Google Scholar] [CrossRef]
- Gradojevic, N.; Gencay, R. Fuzzy logic, trading uncertainty and technical trading. J. Bank. Financ. 2013, 37, 578–586. [Google Scholar] [CrossRef]
- Bowden, R. Directional entropy and tail uncertainty, with applications to financial hazard. Quant. Financ. 2011, 11, 437–446. [Google Scholar] [CrossRef]
- Gradojevic, N.; Gencay, R. Overnight interest rates and aggregate market expectations. Econ. Lett. 2008, 100, 27–30. [Google Scholar] [CrossRef]
- Gencay, R.; Gradojevic, N. Crash of ’87—was it expected? Aggregate market fears and long range dependence. J. Empir. Financ. 2010, 17, 270–282. [Google Scholar] [CrossRef]
- Gradojevic, N.; Caric, M. Predicting systemic risk with entropic indicators. J. Forecast. 2017, 36, 16–25. [Google Scholar] [CrossRef]
- Yang, J.; Qiu, W. A measure of risk and a decision-making model based on expected utility and entropy. Eur. J. Oper. Res. 2005, 164, 792–799. [Google Scholar] [CrossRef]
- Stutzer, M.J. Simple entropic derivation of a generalized Black-Scholes option pricing model. Entropy 2000, 2, 70–77. [Google Scholar] [CrossRef]
- Kitamura, Y.; Stutzer, M.J. Connections between entropic and linear projections in asset pricing estimation. J. Econ. 2002, 107, 159–174. [Google Scholar] [CrossRef]
- Bekiros, S. Timescale analysis with an entropy-based shift-invariant discrete wavelet transform. Comput. Econ. 2014, 44, 231–251. [Google Scholar] [CrossRef]
- Peskir, G.; Shiryaev, A. Optimal Stopping and Free-Boundary Problems; Birkhäuser Verlag: Basel, Switzerland, 2006. [Google Scholar]
- Detlefsen, K.; Scandolo, G. Conditional and dynamic convex risk measures. Financ. Stoch. 2005, 9, 539–561. [Google Scholar] [CrossRef]
- Föllmer, H.; Penner, I. Convex risk measures and the dynamics of their penalty functions. Stat. Decis. 2006, 24, 61–96. [Google Scholar] [CrossRef]
| Pair 1 | 0.152 | 0.152 | 0.165 | 0.165 |
| Pair 2 | 0.321 | 0.170 | 0.170 | 0.170 |
| Pair 3 | 0.071 | 0.028 | 0.028 | 0.028 |
| Pair 4 | 0.189 | 0.076 | 0.076 | 0.076 |
| Pair 5 | 0.097 | 0.088 | 0.088 | 0.088 |
| Pair 6 | 0.093 | 0.133 | 0.133 | 0.133 |
| Names | Return |
|---|---|
| Fullcast Holdings Co., Ltd. (code: 4848) | 0.099 |
| Daiichi Commodities Co., Ltd. (8746) | −0.113 |
| Fuji Oil Co., Ltd. (5017) | −0.091 |
| FIDEA Holdings Co., Ltd. (8713) | −0.125 |
| Yoshicon Co., Ltd. (5280) | 0.016 |
| PADO Corporation (4833) | −0.157 |
| Sado Steam Ship Co., Ltd. (9176) | −0.016 |
| Joban Kaihatsu Co., Ltd. (1782) | −0.047 |
| Meiwa Estate Company Limited (8869) | −0.026 |
| Oi Electric Co., Ltd. (6822) | −0.059 |
| Takata Corporation (7312) | −0.034 |
| Toei Reefer Line Ltd. (9133) | −0.147 |
| Nihon House Holdings Co., Ltd. (1873) | −0.076 |
| Sanei Architecture Planning Co., Ltd. (3228) | 0.521 |
| Shinhoku Steel Corporation (5542) | −0.275 |
| Daiko Denshi Tsushin Ltd. (8023) | −0.226 |
| Shinnihon Corporation (1879) | 0.193 |
| Asahi Industries Co., Ltd. (5456) | −0.121 |
| Seiwa Electric MFG. Co., Ltd. (6748) | −0.050 |
| Daisue Construction Co., Ltd. (1814) | −0.129 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshikawa, D. An Entropic Approach for Pair Trading. Entropy 2017, 19, 320. https://doi.org/10.3390/e19070320
Yoshikawa D. An Entropic Approach for Pair Trading. Entropy. 2017; 19(7):320. https://doi.org/10.3390/e19070320
Chicago/Turabian StyleYoshikawa, Daisuke. 2017. "An Entropic Approach for Pair Trading" Entropy 19, no. 7: 320. https://doi.org/10.3390/e19070320
APA StyleYoshikawa, D. (2017). An Entropic Approach for Pair Trading. Entropy, 19(7), 320. https://doi.org/10.3390/e19070320





