Enthalpy of Mixing in Al–Tb Liquid
Abstract
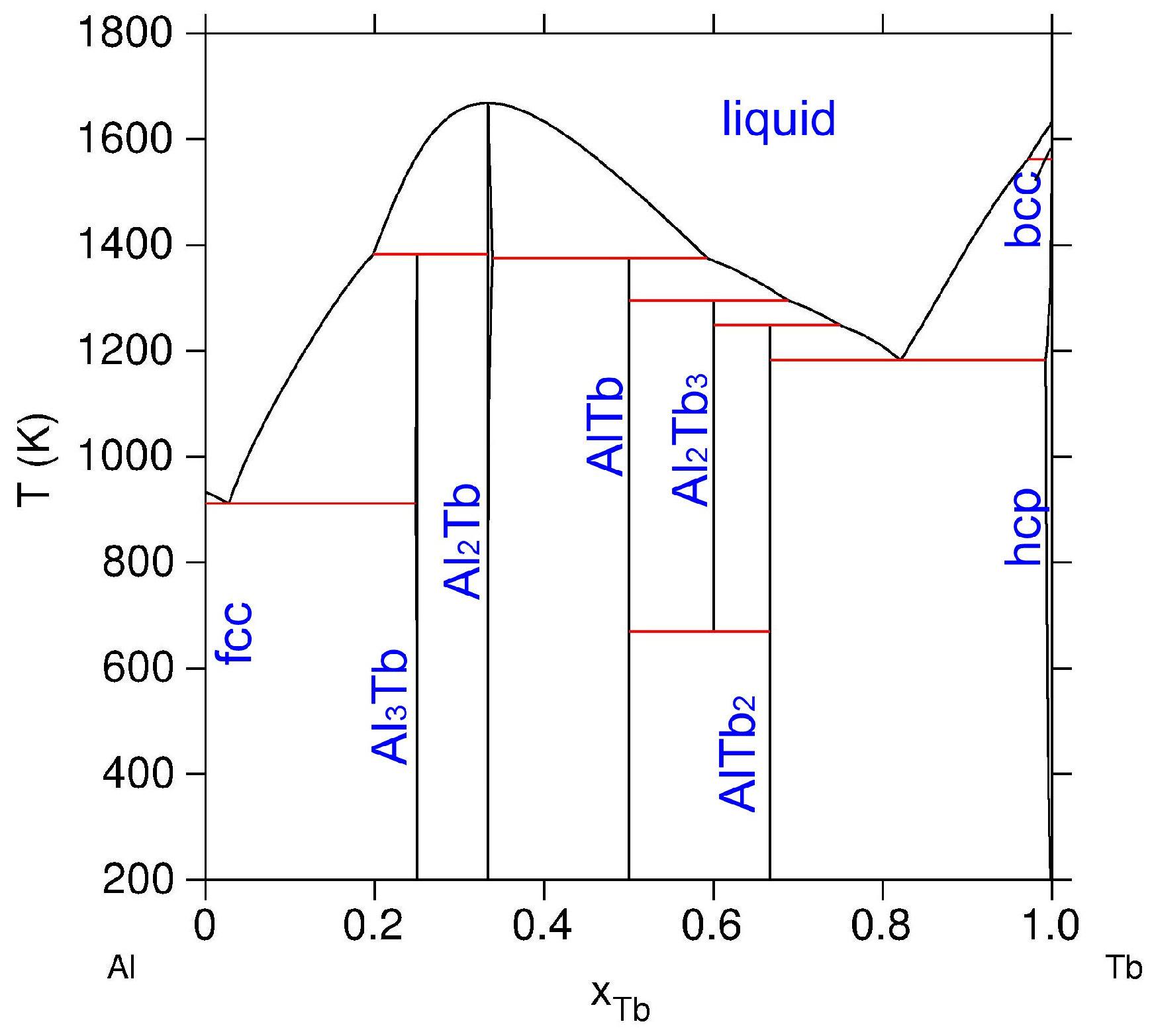
:1. Introduction
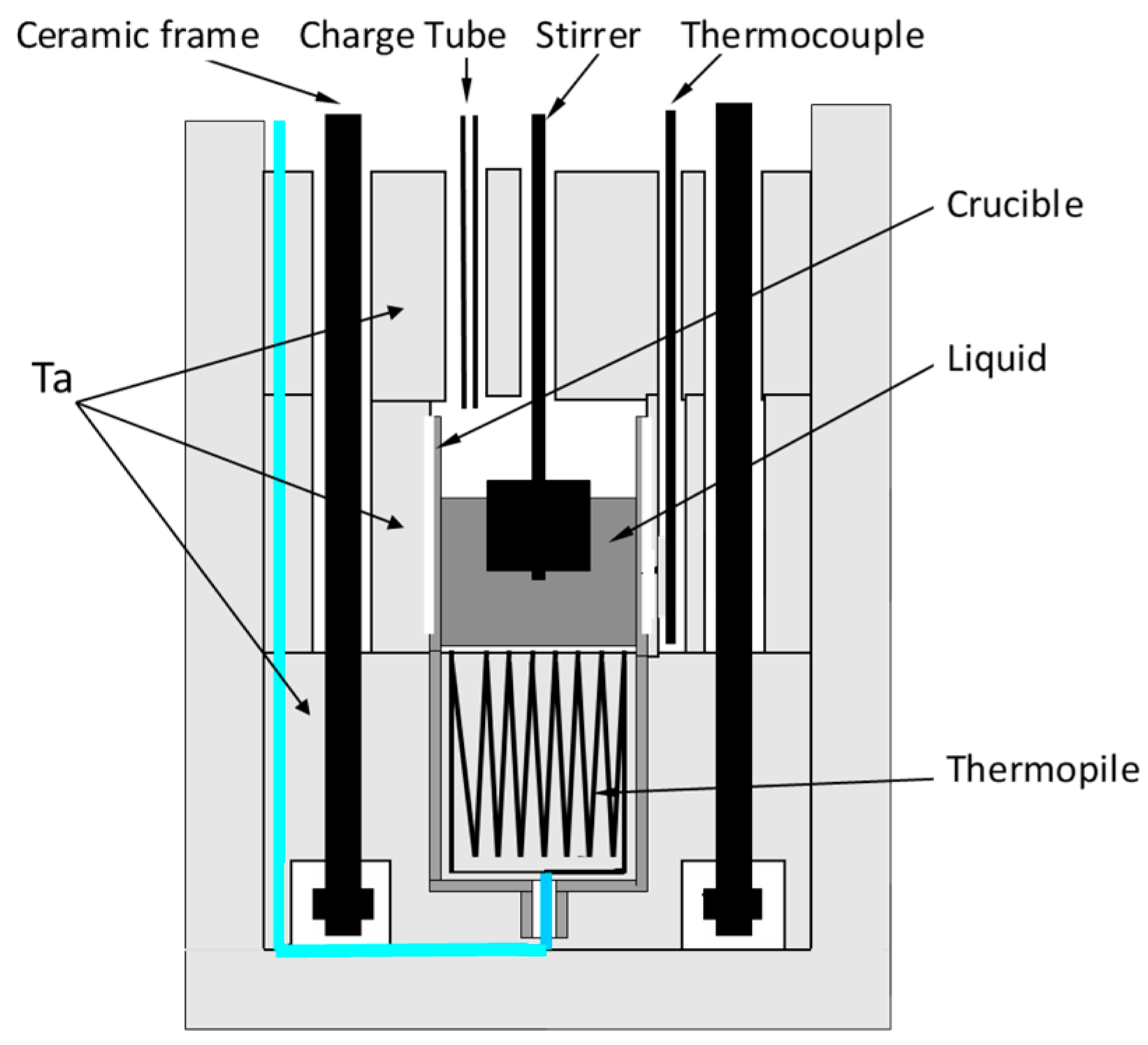
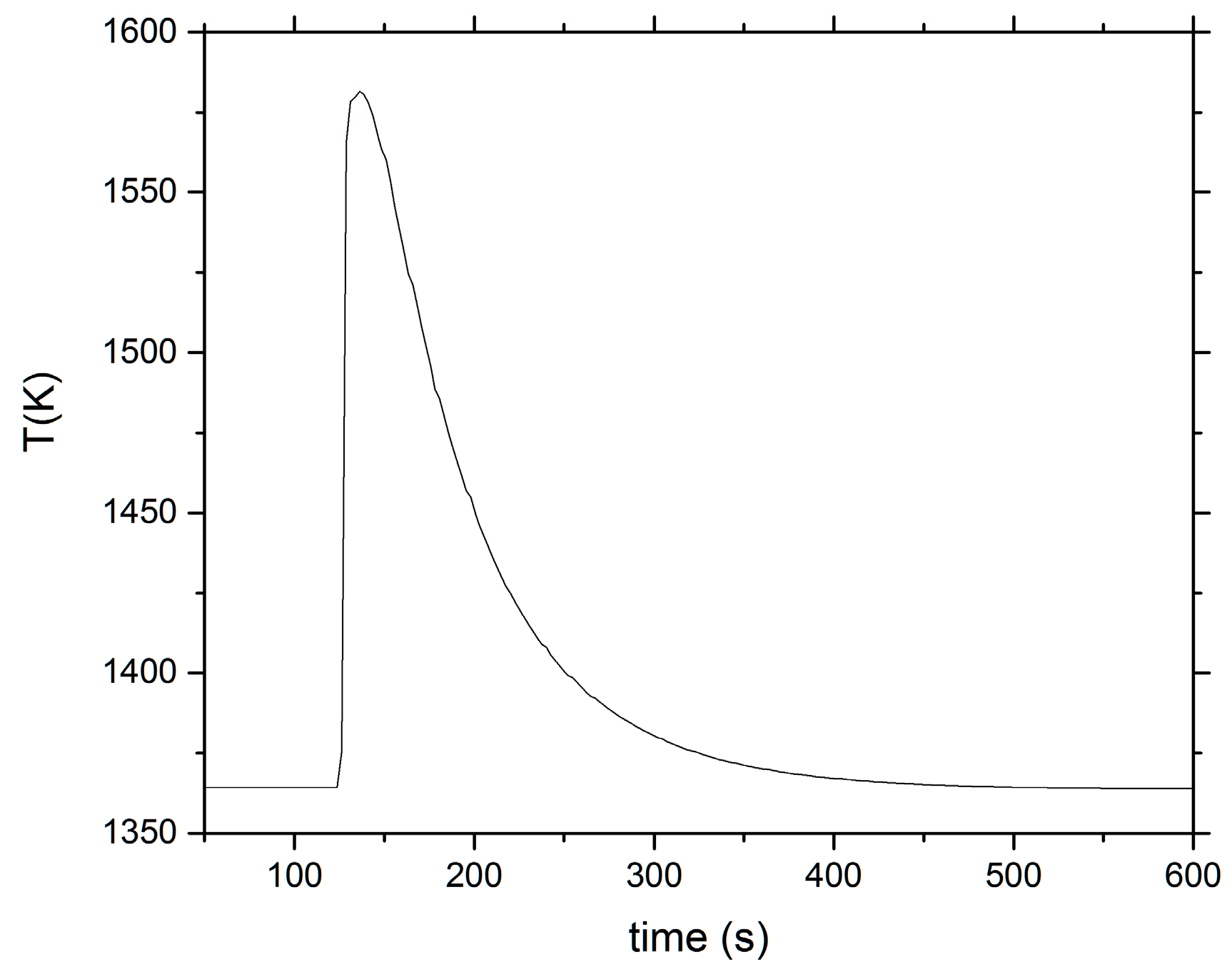
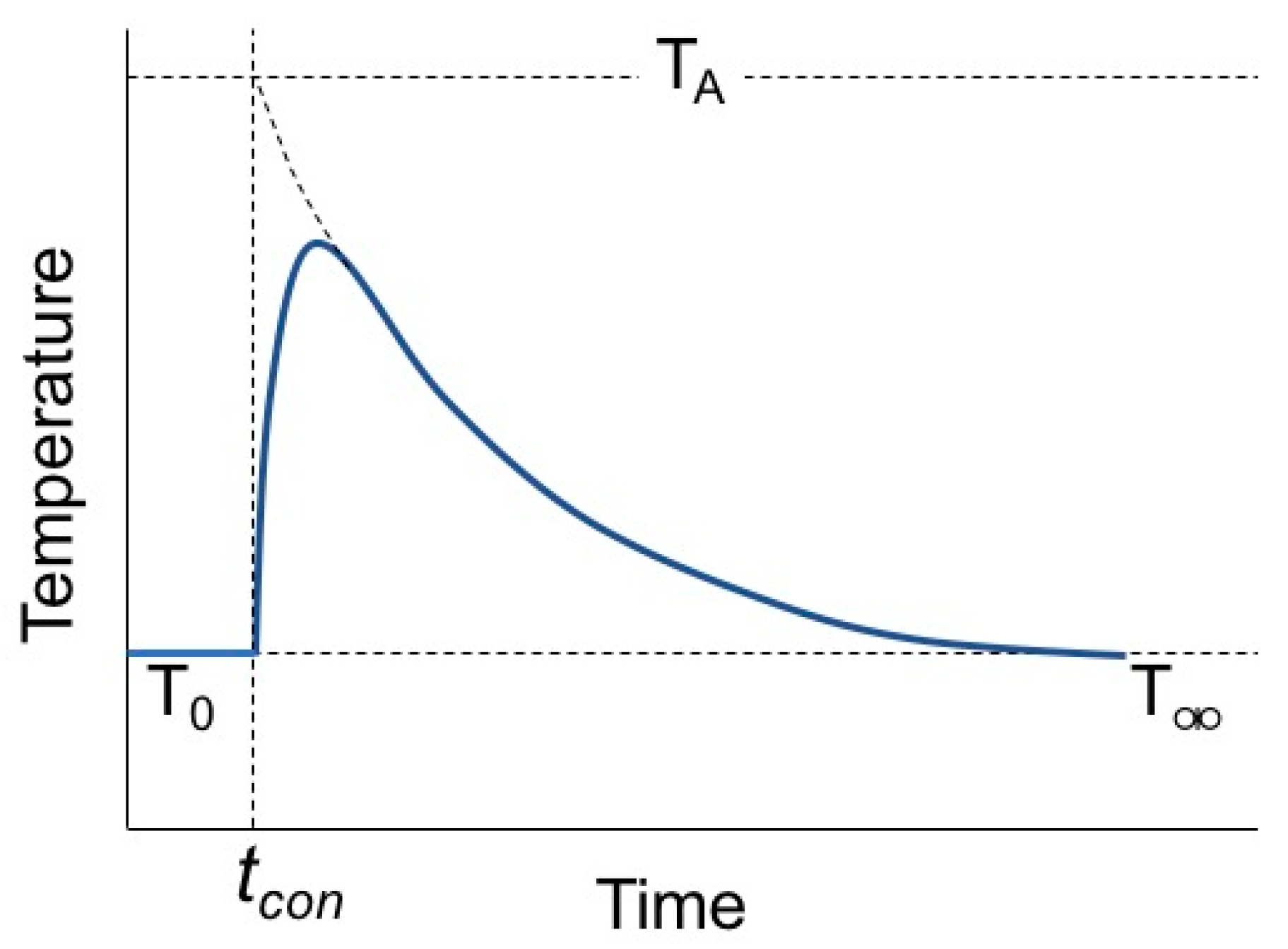
2. Calorimetry Experiments
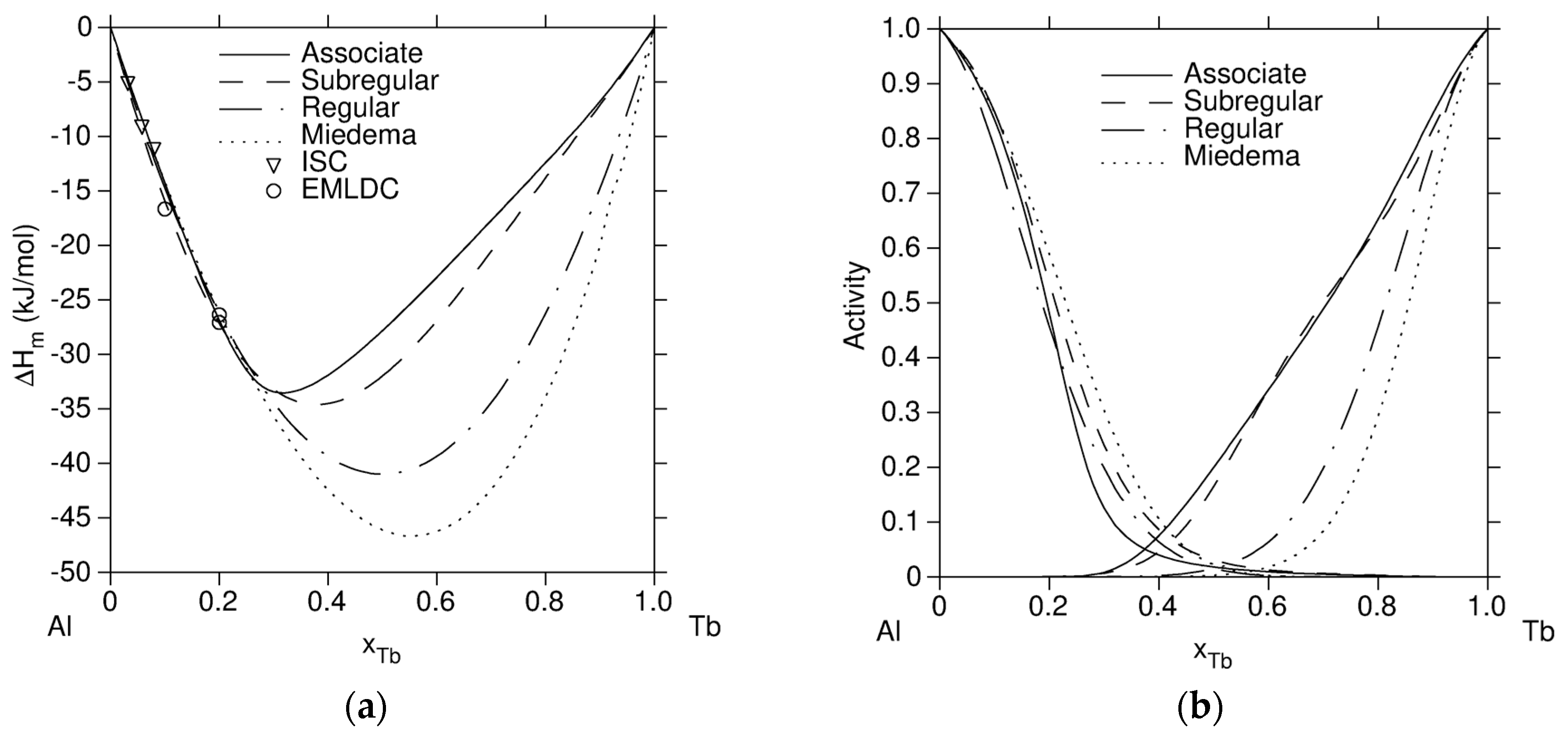
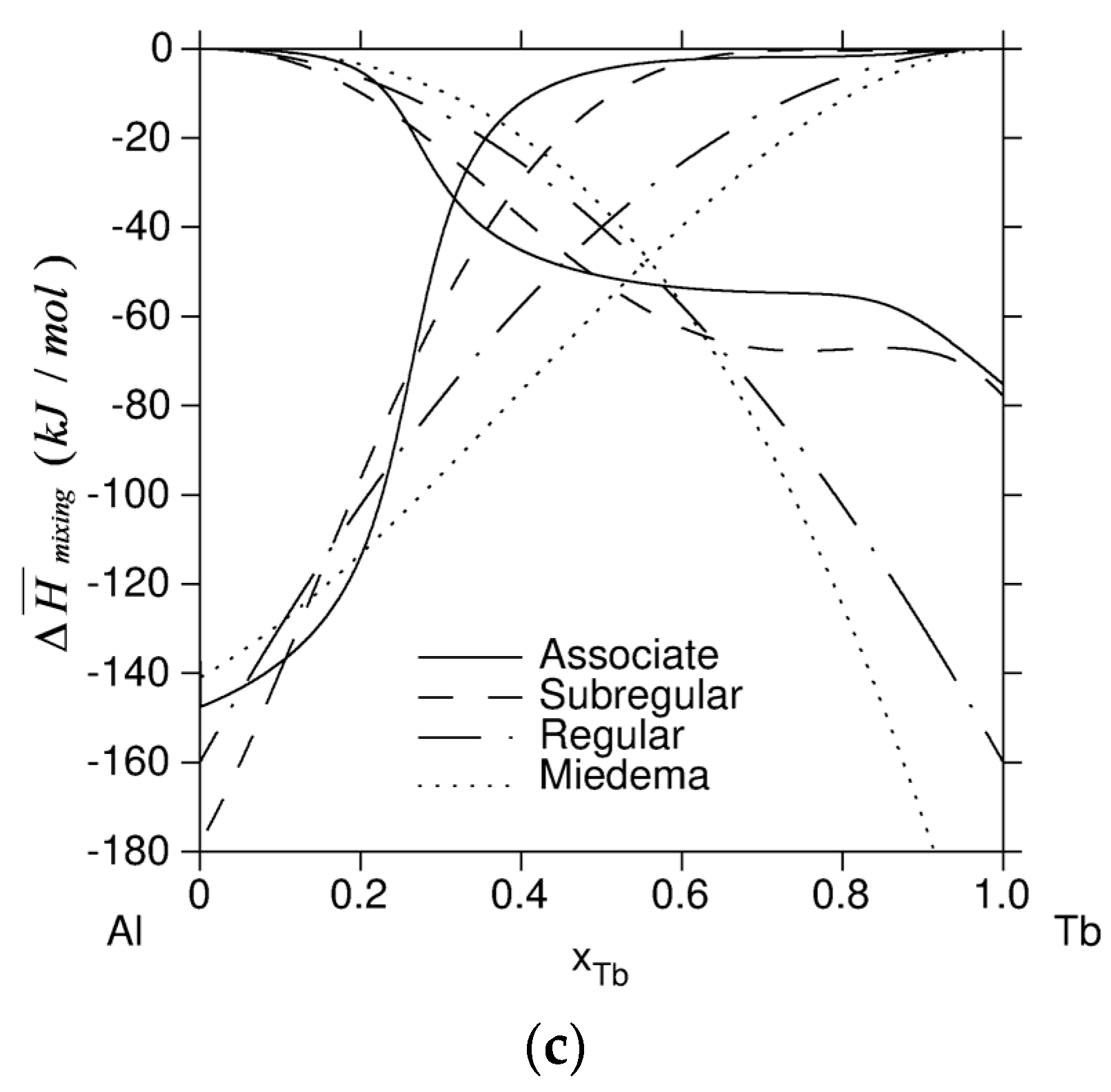
3. Analysis and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| ISC | EMLDC | |||
|---|---|---|---|---|
| Incremental Mass, Al (g) | Cumulative Mass, Al (g) | Calibration Const. (β) | Total Mass, Al (g) | Calibration Const. (φ) |
| - | 0.10152 | −0.33261 | 0.5206 | 2.692 |
| 0.06331 | 0.16483 | −0.32971 | 0.5159 | 2.710 |
| 0.04129 | 0.20612 | −0.31686 | 0.5190 | 2.657 |
| 0.04251 | 0.24863 | −0.30591 | 0.5133 | 2.693 |
| 0.06162 | 0.31025 | −0.32572 | 0.5173 | 2.717 |
| - | - | - | 0.5168 | 2.718 |
| Mean | - | −0.32216 | - | 2.698 |
| Standard Deviation (SD) | - | 0.01085 | - | 0.023 |
| SD (relative) | - | 3.4% | - | 0.85% |
| Relative Uncert. (1.5 SD) | - | 5.0% | - | 1.3% |
Appendix B
| Parameter | Description | Units |
|---|---|---|
| Stephan-Boltzmann constant (taken here as 5.67 × 10−8) | J/m2sK4 | |
| Total hemispherical emissivity (taken here as 0.084) | - | |
| Specimen heat capacity | J/mol | |
| Mass of specimen | g | |
| Specimen molar mass | g/mol | |
| Surface area of specimen | m2 | |
| Volume of specimen | m3 | |
| Fall duration | s | |
| Heat transfer coefficient | W/m2K | |
| Dynamic viscosity (gas) (taken here as 1.90 × 10−5) | Ns/m2 | |
| Thermal conductivity (gas) (taken here as 0.1513) | W/mK | |
| Specimen diameter | m | |
| Fluid velocity (taken as the average fall velocity) | m/s | |
| Specimen density | Kg/m3 |
Appendix C
References
- Xing, L.Q.; Hufnagel, T.C.; Eckert, J.; Loser, W.; Schultz, L. Relation between short-range order and crystallization behavior in Zr-based amorphous alloys. Appl. Phys. Lett. 2000, 77, 1970–1972. [Google Scholar] [CrossRef]
- Chen, G.L.; Hui, X.D.; He, G.; Bian, Z. Multicomponent chemical short range order, undercooling, and the formation of bulk metallic glasses. Mater. Trans. 2001, 42, 1095–1102. [Google Scholar] [CrossRef]
- Chen, G.L.; Hui, X.D.; Fan, S.W.; Kou, H.C.; Yao, K.F. Concept of chemical short range order domain and the glass forming ability in multicomponent liquid. Intermetallics 2002, 10, 1221–1232. [Google Scholar] [CrossRef]
- Jakse, N.; Pasturel, A. Glass forming ability and short-range order in a binary bulk metallic glass by ab initio molecular dynamics. Appl. Phys. Lett. 2008, 93, 113104. [Google Scholar] [CrossRef]
- Hao, S.G.; Kramer, M.J.; Wang, C.Z.; Ho, K.M.; Nandi, S.; Kreyssig, A.; Goldman, A.I.; Wessels, V.; Sahu, K.K.; Kelton, K.F.; et al. Experimental and Ab initio structural studies of liquid Zr2Ni. Phys. Rev. B 2009, 79, 104206. [Google Scholar] [CrossRef]
- Huang, L.; Wang, C.Z.; Hao, S.G.; Kramer, M.J.; Ho, K.M. Short-and medium-range order in amorphous Zr2Ni metallic alloy. Phys. Rev. B 2010, 81, 094118. [Google Scholar] [CrossRef]
- Fang, X.W.; Wang, C.Z.; Yao, Y.X.; Ding, Z.J.; Ho, K.M. Signature of Al11Sm3 fragments in undercooled Al90Sm10 liquid from ab initio molecular dynamics simulations. J. Phys. Condens. Matter 2011, 23, 235104. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.F.; Lin, D.Y.; Chen, X.H.; Liu, Z.K.; Hui, X.D. Sluggish mobility and strong icosahedral ordering in Mg–Zn–Ca liquid and glassy alloys. Acta Mater. 2014, 67, 266–277. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, Y.; Ye, Z.; Zhang, Y.; Wang, C.-Z.; Mendelev, M.I.; Ott, R.T.; Kramer, M.J.; Ding, Z.-J.; Ho, K.-M. Solute-solute correlations responsible for the prepeak in structure factors of undercooled Al-rich liquids: A molecular dynamics study. J. Phys. Condens. Matter 2015, 27, 205701. [Google Scholar] [CrossRef] [PubMed]
- Sterkhova, I.; Lad’yanov, V.; Kamaeva, L.; Umnova, N.; Umnov, P. On the tendency of the Co-, Ni-, and Fe-based melts to the bulk amorphization. Metall. Mater. Trans. A 2016, 47, 5487–5495. [Google Scholar] [CrossRef]
- Zhu, A.W.; Shiflet, G.J.; Miracle, D.B. Glass forming ranges of Al-rare earth metal alloys: Thermodynamic and kinetic analysis. Scr. Mater. 2004, 50, 987–991. [Google Scholar] [CrossRef]
- Iwamatsu, M.; Lai, S.K. Lowest-energy structures of 13-atom binary clusters: Do icosahedral clusters exist in binary liquid alloys? J. Non Cryst. Solids 2007, 353, 3698–3703. [Google Scholar] [CrossRef]
- Zhu, A.W.; Shiflet, G.J.; Poon, S.J. Atomic bond deficiency as a structural defect in amorphous metals: Relevance to glass transitions. Acta Mater. 2008, 56, 593–601. [Google Scholar] [CrossRef]
- Tian, H.; Zhang, C.; Wang, L.; Zhao, J.J.; Dong, C.; Wen, B.; Wang, Q. Ab initio molecular dynamics simulation of binary Cu64Zr36 bulk metallic glass: Validation of the cluster-plus-glue-atom model. J. Appl. Phys. 2011, 109, 123520. [Google Scholar] [CrossRef]
- Tian, H.; Liu, H.; Zhang, C.; Zhao, J.J.; Dong, C.; Wen, B. Ab initio molecular dynamics simulation of binary Ni62.5Nb37.5 bulk metallic glass: Validation of the cluster-plus-glue-atom model. J. Mater. Sci. 2012, 47, 7628–7634. [Google Scholar] [CrossRef]
- Hao, S.G.; Wang, C.Z.; Li, M.Z.; Napolitano, R.E.; Mendelev, M.I.; Ho, K.M. Prediction of cooling rate dependent ordering in metallic glass transition using a two-state model. Comput. Mater. Sci. 2010, 49, 615–618. [Google Scholar] [CrossRef]
- Hao, S.G.; Wang, C.Z.; Li, M.Z.; Napolitano, R.E.; Ho, K.M. Dynamic arrest and glass formation induced by self-aggregation of icosahedral clusters in Zr1−xCux alloys. Phys. Rev. B 2011, 84, 064203. [Google Scholar] [CrossRef]
- Guo, J.Q.; Ohtera, K.; Kita, K.; Nagahora, J.; Kazama, N.S. Crystallization behavior of Al100−xSmx (x = 8–14 at%) amorphous-alloys. Mater. Lett. 1995, 24, 133–138. [Google Scholar] [CrossRef]
- Inoue, A. Amorphous, nanoquasicrystalline and nanocrystalline alloys in Al-based systems. Prog. Mater. Sci. 1998, 43, 365–520. [Google Scholar] [CrossRef]
- Rizzi, P.; Antonione, C.; Baricco, M.; Battezzati, L.; Armelao, L.; Tondello, E.; Fabrizio, M.; Daolio, S. Crystals and nanocrystals in rapidly solidified Al–Sm alloys. Nanostruct. Mater. 1998, 10, 767–776. [Google Scholar] [CrossRef]
- Wilde, G.; Sieber, H.; Perepezko, J.H. Glass formation versus nanocrystallization in an Al92Sm8 alloy. Scr. Mater. 1999, 40, 779–783. [Google Scholar] [CrossRef]
- Wilde, G.; Sieber, H.; Perepezko, J.H. Glass formation in Al-rich Al–Sm alloys during solid state processing at ambient temperature. J. Non Cryst. Solids 1999, 252, 621–625. [Google Scholar] [CrossRef]
- Tjong, S.C.; Wang, J.Q. Microstructure and devitrification behavior of melt-spun Al-rich metallic glasses and nanostructured composites. Z. Metallkunde 2001, 92, 610–616. [Google Scholar]
- Perepezko, J.H.; Hebert, R.J.; Wu, R.I.; Wilde, G. Primary crystallization in amorphous Al-based alloys. J. Non Cryst. Solids 2003, 317, 52–61. [Google Scholar] [CrossRef]
- Kalay, Y.E.; Chumbley, L.S.; Kramer, M.J.; Anderson, I.E. Local structure in marginal glass forming Al–Sm alloy. Intermetallics 2010, 18, 1676–1682. [Google Scholar] [CrossRef]
- Kalay, Y.E.; Yeager, C.; Chumbley, L.S.; Kramer, M.J.; Anderson, I.E. Initial crystallization in a nanostructured Al–Sm rare earth alloy. J. Non Cryst. Solids 2010, 356, 1416–1424. [Google Scholar] [CrossRef]
- Zhang, F.; McBrearty, I.; Ott, R.T.; Park, E.; Mendelev, M.I.; Kramer, M.J.; Wang, C.Z.; Ho, K.M. Discovery of a meta-stable Al–Sm phase with unknown stoichiometry using a genetic algorithm. Scr. Mater. 2014, 81, 32–35. [Google Scholar] [CrossRef]
- Ye, Z.; Zhang, F.; Sun, Y.; Mendelev, M.I.; Ott, R.T.; Park, E.; Besser, M.F.; Kramer, M.J.; Ding, Z.; Wang, C.Z.; et al. Discovery of a metastable Al20Sm4 phase. Appl. Phys. Lett. 2015, 106, 101903. [Google Scholar] [CrossRef]
- Bokas, G.B.; Zhao, L.; Perepezko, J.H.; Szlufarska, I. On the role of Sm in solidification of Al–Sm metallic glasses. Scr. Mater. 2016, 124, 99–102. [Google Scholar] [CrossRef]
- Sanders, W.S.; Warner, J.S.; Miracle, D.B. Stability of Al-rich glasses in the Al–La–Ni system. Intermetallics 2006, 14, 348–351. [Google Scholar] [CrossRef]
- Hackenberg, R.E.; Gao, M.C.; Kaufman, L.; Shiflet, G.J. Thermodynamics and phase equilibria of the Al–Fe–Gd metallic glass-forming system. Acta Mater. 2004, 52, 3745. [Google Scholar] [CrossRef]
- Wang, W.; Tang, Z.L.; Zhan, C.Y.; Nie, Z.R. Calculations of formation enthalpies of Al–Re intermetallics. Rare Met. Mater. Eng. 2009, 38, 2100–2105. [Google Scholar]
- Wang, H.Y.; Gao, X.Y.; Zeng, J.M.; Ren, H.P.; Zhao, Y.J. First-principles of phase stability and solubility of Al–Re (La, Y) alloy. Rare Met. Mater. Eng. 2017, 46, 735–739. [Google Scholar]
- Wu, R.I.; Wilde, G.; Perepezko, J.H. Glass formation and primary nanocrystallization in Al-base metallic glasses. Mater. Sci. Eng. A 2001, 301, 12–17. [Google Scholar] [CrossRef]
- Sun, S.P.; Yi, D.Q.; Liu, H.Q.; Zang, B.; Jiang, Y. Calculation of glass forming ranges in Al–Ni–Re (Ce, La, Y) ternary alloys and their sub-binaries based on Miedema’s model. J. Alloys Compd. 2010, 506, 377–387. [Google Scholar] [CrossRef]
- Zhu, A.W.; Poon, S.J.; Shiflet, G.J. On glass formability of Al–Gd–Ni (Fe). Scr. Mater. 2004, 50, 1451–1455. [Google Scholar] [CrossRef]
- Csontos, A.A.; Shiflet, G.J. Formation and chemistry of nanocrystalline phases formed during deformation in aluminum-rich metallic glasses. Nanostruct. Mater. 1997, 9, 281–289. [Google Scholar] [CrossRef]
- Baricco, M.; Gaertner, F.; Cacciamani, G.; Rizzi, P.; Battezzati, L.; Greer, A.L. Thermodynamics of homogeneous crystal nucleation in Al–Re metallic glasses. Mater. Sci. Forum 1998, 269, 553–558. [Google Scholar] [CrossRef]
- Boucharat, N.; Rosner, H.; Perepezko, J.H.; Wilde, G. Devitrification of Al-based glass forming alloys. Mater. Sci. Eng. A 2004, 375, 713–717. [Google Scholar] [CrossRef]
- Jia, Y.B.; Song, H.F.; Chao, Q.; Wang, Q.; Dong, Y.D. Glass-forming ability and thermal stability of (Ce–La)–Ni–Al bulk amorphous alloys. Rare Metal Mater. Eng. 2010, 39, 997–1001. [Google Scholar]
- Antonowicz, J. Atomic packing and phase separation in Al-rare earth metallic glasses. J. Mater. Sci. 2010, 45, 5040–5044. [Google Scholar] [CrossRef]
- Li, R.; Stoica, M.; Wang, G.; Park, J.M.; Li, Y.; Zhang, T.; Eckert, J. Glass formation, thermal properties, and elastic constants of La–Al–Co alloys. J. Mater. Res. 2010, 25, 1398–1404. [Google Scholar] [CrossRef]
- Chen, Z.; Angell, C.A.; Richert, R. On the dynamics of liquids in their viscous regime approaching the glass transition. Eur. Phys. J. E 2012, 35, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Angell, C.A. The viscous-liquid-glassy-solid problem. Acs. Sym. Ser. 1997, 676, 14–26. [Google Scholar]
- Angell, C.A. Entropy and fragility in supercooling liquids. J. Res. Natl. Inst. Stand. Technol. 1997, 102, 171–185. [Google Scholar] [CrossRef] [PubMed]
- Gschneidner, K.A., Jr.; Calderwood, F.W. The Al–Re (aluminum-rare earth) systems. Bull. Alloy Phase Diagr. 1988, 9, 658–668. [Google Scholar] [CrossRef]
- Benigni, P.; Hassam, S.; Decreton, A.; Mikaelian, G.; Gajavalli, K.; Barrachin, M.; Fischer, E.; Rogez, J. Enthalpy of mixing in the Ag–Cd–In ternary liquid phase. J. Chem. Thermodyn. 2017, 107, 207–215. [Google Scholar] [CrossRef]
- Debski, A.; Gasior, W. Calorimetric measurements of the Li–Zn system. Direct reaction method and mixing enthalpy. J. Chem. Thermodyn. 2016, 98, 111–117. [Google Scholar] [CrossRef]
- Nusperling, E.M.; Thiedemann, U.; Schaefers, K.; Qin, J.; Rosner-Kuhn, M.; Frohberg, M.G. Mixing enthalpy measurements of liquid Fe–Nb–V alloys by levitation alloying calorimetry. Rev. Metall. 1997, 94, 219–226. [Google Scholar]
- Naguet, C.; Azzaoui, M.; Fionari, J.M.; Vassiliev, V.; Hertz, J.; Bourkba, A.; Bouirden, L. Semi-experimental mixing enthalpy of ternary liquid phases as a support of phase-diagrams calculation. J. Chim. Phys. 1997, 94, 1026–1035. [Google Scholar] [CrossRef]
- Zhou, S.; Napolitano, R.E. Phase equilibria and thermodynamic limits for partitionless crystallization in the Al–La binary system. Acta Mater. 2006, 54, 831–840. [Google Scholar] [CrossRef]
- Jin, L.L.; Kang, Y.B.; Chartrand, P.; Fuerst, C.D. Thermodynamic evaluation and optimization of Al–La, Al–Ce, Al–Pr, Al–Nd and Al–Sm systems using the modified quasichemical model for liquids. Calphad 2011, 35, 30–41. [Google Scholar] [CrossRef]
- Gao, M.C.; Rollett, A.D.; Widom, M. Lattice stability of aluminum-rare earth binary systems: A first-principles approach. Phys. Rev. B 2007, 75, 174120. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, X.; Bu, F.; Meng, F.; Zheng, T.; Zhang, D.; Meng, J. First-principles phase stability and elastic properties of Al–La binary system intermetallic compounds. Intermetallics 2015, 60, 92–97. [Google Scholar] [CrossRef]
- Esin, Y.O.; Kolesnikov, S.P.; Baev, V.M.; Petrushevskii, M.S.; Geld, P.V. Formation enthalpies of liquid binary-alloys of aluminum and tin with lanthanum. Zhurnal Fizicheskoi Khimii 1981, 55, 1587–1588. [Google Scholar]
- Sommer, F.; Keita, M.; Krull, H.G.; Predel, B.; Lee, J.J. Thermodynamic investigations of Al–La alloys. J. Less Common Met. 1988, 137, 267–275. [Google Scholar] [CrossRef]
- Borzone, G.; Cardinale, A.M.; Parodi, N.; Cacciamani, G. Aluminum compounds of the rare earths: Enthalpies of formation of Yb–Al and La–Al alloys. J. Alloys Compd. 1997, 247, 141–147. [Google Scholar] [CrossRef]
- Gao, M.C.; Unlu, N.; Shiflet, G.J.; Mihalkovic, M.; Widom, M. Reassessment of Al–Ce and Al–Nd binary systems supported by critical experiments and first-principles energy calculations. Met. Mater. Trans. A 2005, 36, 3269–3279. [Google Scholar] [CrossRef]
- Kang, Y.B.; Pelton, A.D.; Chartrand, P.; Fuerst, C.D. Critical evaluation and thermodynamic optimization of the Al–Ce, Al–Y, Al–Sc and Mg–Sc binary systems. Calphad 2008, 32, 413–422. [Google Scholar] [CrossRef]
- Ivanov, M.I.; Berezutskii, V.V.; Shevchenko, M.A.; Kudin, V.G.; Sudavtsova, V.S. Thermodynamic properties of binary Al–Ce and Ce–Fe alloys. Powder Metall. Met. Ceram. 2015, 54, 80–92. [Google Scholar] [CrossRef]
- Esin, Y.O.; Ryss, G.M.; Geld, P.V. Enthalpies of the formation of liquid alloys of cerium with aluminum. Zhurnal Fizicheskoi Khimii 1979, 53, 2380–2381. [Google Scholar]
- Kober, V.I.; Lebedev, V.A.; Nichkov, I.F.; Raspopin, S.P.; Yamshchi, L.F. Thermodynamic properties of aluminum-rich Ce–Al alloys. Russ. Metall. 1973, 2, 163–166. [Google Scholar]
- Shevchenko, M.O.; Berezutskii, V.V.; Ivanov, M.I.; Sudavtsova, V.S. Thermodynamic properties of binary Al–Pr alloys. Powder Metall. Met. Ceram. 2016, 55, 78–90. [Google Scholar] [CrossRef]
- Zviadadze, G.N.; Chkhikvadze, L.A.; Kereselidze, M.V. Thermodynamic properties of binary melts of some rare earth metals with aluminum. Soobshch. Akad. Nauk. Gruz. SSR 1976, 81, 149–152. [Google Scholar]
- Zhou, S.H.; Wang, Y.; Chen, L.Q.; Liu, Z.K.; Napolitano, R.E. Solution-based thermodynamic modeling of the Ni–Ta and Ni–Mo–Ta systems using first-principle calculations. Calphad 2009, 33, 631–641. [Google Scholar] [CrossRef]
- Zhou, S.H.; Napolitano, R.E. Modeling of thermodynamic properties and phase equilibria for the Al–Sm binary system. Met. Mater.Trans. A 2008, 39, 502–512. [Google Scholar] [CrossRef]
- Shevchenko, M.O.; Berezutski, V.V.; Ivanov, M.I.; Kudin, V.G.; Sudavtsova, V.S. Thermodynamic properties of alloys of the binary Al–Sm, Sm–Sn and ternary Al–Sm–Sn systems. J. Phase Equilib. Diffus. 2015, 36, 39–52. [Google Scholar] [CrossRef]
- Bo, H.; Liu, L.B.; Hu, J.L.; Zhang, X.D.; Jin, Z.P. Thermodynamic re-assessment of the Al–Gd and Gd–Zr systems. Thermochim. Acta 2014, 591, 51–56. [Google Scholar] [CrossRef]
- Jin, L.; Kang, Y.B.; Chartrand, P.; Fuerst, C.D. Thermodynamic evaluation and optimization of Al–Gd, Al–Tb, Al–Dy, Al–Ho and Al–Er systems using a modified quasichemical model for the liquid. Calphad 2010, 34, 456–466. [Google Scholar] [CrossRef]
- Grobner, J.; Kevorkov, D.; Schmid-Fetzer, R. Thermodynamic calculation of Al–Gd and Al–Gd–Mg phase equilibria checked by key experiments. Z. Metallkunde 2001, 92, 22–27. [Google Scholar]
- Kanibolotsky, D.S.; Golovataya, N.V.; Lisnyak, V.V. Calorimetric study of liquid gadolinium-based alloys. J. Therm. Anal. Calorim. 2004, 76, 323–327. [Google Scholar] [CrossRef]
- Kanibolotsky, D.S.; Golovataya, N.V.; Bieloborodova, O.A.; Lisnyak, V.V. Calorimetric investigation of liquid Al–Ga–Gd alloys. Thermochim. Acta 2004, 421, 111–115. [Google Scholar] [CrossRef]
- Bo, H.; Liu, L.B.; Xiong, X.; Jin, Z.P. Thermodynamic assessment of the Al–Dy, Dy–Zr and Al–Dy–Zr systems. Chin. Sci. Bull. 2014, 59, 1738–1746. [Google Scholar] [CrossRef]
- Meng, F.G.; Zhang, L.G.; Liu, H.S.; Liu, L.B.; Jin, Z.P. Thermodynamic optimization of the Al–Yb binary system. J. Alloys Compd. 2008, 452, 279–282. [Google Scholar] [CrossRef]
- Sommer, F. Association model for the description of thermodynamic functions of liquid alloys II.—Numerical treatment and results. Z. Metallkunde 1982, 73, 77–86. [Google Scholar]
- Miedema, A.R. A simple model for alloys: I. Rules for the alloying behaviour of transition metals. Philips Tech. Rev. 1973, 33, 149–160. [Google Scholar]
- Miedema, A.R. A simple model for alloys: II. The influence of ionicity on the stability and other physical properties of alloys. Philips Tech. Rev. 1973, 33, 196–202. [Google Scholar]
- Zhang, R.F.; Zhang, S.H.; He, Z.J.; Jing, J.; Sheng, S.H. Miedema calculator: A thermodynamic platform for predicting formation enthalpies of alloys within framework of Miedema’s theory. Comput. Phys. Commun. 2016, 209, 58–69. [Google Scholar] [CrossRef]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 4, 317–425. [Google Scholar] [CrossRef]
- Colinet, C.; Pastural, A.; Buschow, K.H.J. Molar enthalpies of formation of LnAl2 compounds. J. Chem. Thermodyn. 1985, 17, 1133–1139. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]


| System | CALPHAD Assessments | FP Calculations of Crystal Phase Energies | Experimental Measurement of Liquid Mixing Properties |
|---|---|---|---|
| Al–La | [51,52] | [53,54] | [55,56,57] |
| Al–Ce | [52,58,59] | [53] | [60,61,62] |
| Al–Pr | [52,63] | [53] | [63,64] |
| Al–Nd | [52,58] | [53] | [64] |
| Al–Pm | - | [53] | - |
| Al–Sm | [52,65] | [53,66] | [67] |
| Al–Eu | - | [53] | - |
| Al–Gd | [68,69,70] | [53] | [71,72] |
| Al–Tb | [69] | [53] | - |
| Al–Dy | [69,73] | [53] | - |
| Al–Ho | [69] | [53] | - |
| Al–Tm | - | [53] | - |
| Al–Yb | [74] | [53] | - |
| Al–Lu | - | [53] | - |
| Parameter | Value |
|---|---|
| Ta | 298 K |
| T0 | 1364 K |
| 9.4869 g | |
| mAl | 0.7009 g |
| MAl | 26.98 g/mol |
| MTb | 158.93 g/mol |
| 826.05 J | |
| 278.26 J | |
| −13,247.6 sK | |
| −0.08336 ± 5% J/sK |
| mAl (g) | δmTb (g) | mTb (g) | δqmix (J/mol) | ∆Hmix (J/mol) | |
|---|---|---|---|---|---|
| 10.1878 | 1.8528 | 1.8528 | 0.03 | −4955.05 | −4955.05 |
| - | 1.5676 | 3.4288 | 0.05 | −3994.04 | −8949.09 |
| - | 1.4322 | 4.8610 | 0.08 | −2044.05 | −10,993.1 |
| 10.85 | 6.4362 | 6.4362 | 0.09 | −1074.16 | - |
| - | 1.4510 | 7.8872 | 0.11 | −943.902 | - |
| # | Type | Mass (g) | Tdrop (K) | Tcon | T0 (K) | TA (K) | T∞ (K) | RMSE (K) | qcal (J/mol) | ∆Hmix (kJ/mol) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | cal | 0 | 0.5206 | 1245.0 | 1241.8 | 292.3 | 304.4 | 294.9 | 0.013 | 744.4 | 2.692 | - |
| 2 | cal | 0 | 0.5159 | 1161.8 | 1159.1 | 298.0 | 309.0 | 294.7 | 0.004 | 684.9 | 2.710 | - |
| 3 | cal | 0 | 0.5190 | 1176.3 | 1173.5 | 298.2 | 309.7 | 295.2 | 0.031 | 697.6 | 2.657 | - |
| 4 | cal | 0 | 0.5133 | 1078.9 | 1076.5 | 295.9 | 306.2 | 294.6 | 0.042 | 632.7 | 2.693 | - |
| 5 | cal | 0 | 0.5173 | 1303.7 | 1297.7 | 296.5 | 309.0 | 294.7 | 0.016 | 773.2 | 2.717 | - |
| 6 | cal | 0 | 0.5168 | 1258.9 | 1255.7 | 298.1 | 310.1 | 295.3 | 0.001 | 744.7 | 2.718 | - |
| 7 | meas | 0.1 | 0.4796 | 1292.0 | 1286.1 | 297.5 | 305.6 | 296.2 | 0.015 | 493.1 | 2.698 | −16.61 |
| 8 | cal | 0 | 0.2476 | 1080.3 | 1076.5 | 292.9 | 298.1 | 293.2 | 0.001 | 307.5 | 2.570 | - |
| 9 | cal | 0 | 0.2467 | 1245.6 | 1240.7 | 295.4 | 301.4 | 293.7 | 0.024 | 353.6 | 2.585 | - |
| 10 | meas | 0.2 | 0.3476 | 1406.5 | 1394.7 | 294.6 | 300.4 | 294.0 | 0.004 | 343.2 | 2.578 | −27.08 |
| 11 | meas | 0.2 | 0.3249 | 1439.5 | 1426.7 | 293.1 | 298.8 | 293.2 | 0.007 | 332.0 | 2.578 | −26.37 |
| Regular | Subregular | Associate | |||
|---|---|---|---|---|---|
| i | Al | Al | Al | Tb | Al2Tb |
| j | Tb | Tb | Tb | Al2Tb | Al |
| (J/mol) | −160,000 | −128,000 + 29.001T | −75,252 | −20,342 | −35,455 |
| (J/mol) | - | −80,455 + 30.998T | - | - | - |
| (J/mol) | - | 30,342 | - | - | - |
| (J/mol) | - | - | −113,233 + 18.904T | ||
| Notes | | computed from | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Tackes, C.; Napolitano, R. Enthalpy of Mixing in Al–Tb Liquid. Entropy 2017, 19, 290. https://doi.org/10.3390/e19060290
Zhou S, Tackes C, Napolitano R. Enthalpy of Mixing in Al–Tb Liquid. Entropy. 2017; 19(6):290. https://doi.org/10.3390/e19060290
Chicago/Turabian StyleZhou, Shihuai, Carl Tackes, and Ralph Napolitano. 2017. "Enthalpy of Mixing in Al–Tb Liquid" Entropy 19, no. 6: 290. https://doi.org/10.3390/e19060290
APA StyleZhou, S., Tackes, C., & Napolitano, R. (2017). Enthalpy of Mixing in Al–Tb Liquid. Entropy, 19(6), 290. https://doi.org/10.3390/e19060290




