Game-Theoretic Optimization of Bilateral Contract Transaction for Generation Companies and Large Consumers with Incomplete Information
Abstract
:1. Introduction
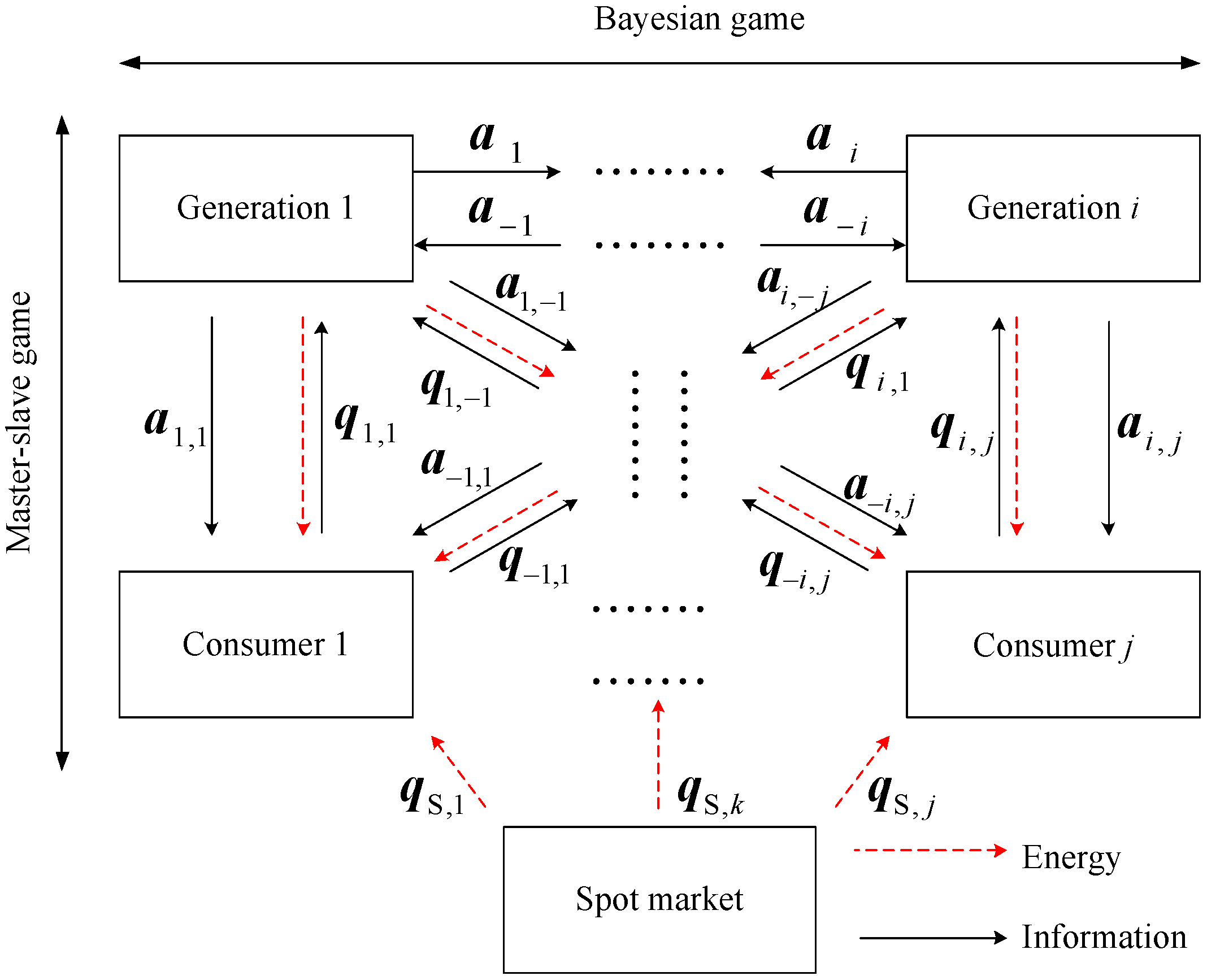
2. System Model
2.1. Purchase Cost Model of Large Consumers
2.2. Profit Model of Generation Companies
3. Bayesian Game for Generation Companies
3.1. Bayesian Game Formulation
3.2. Karush–Kuhn–Tucker (KKT) Conditions for Large Consumers
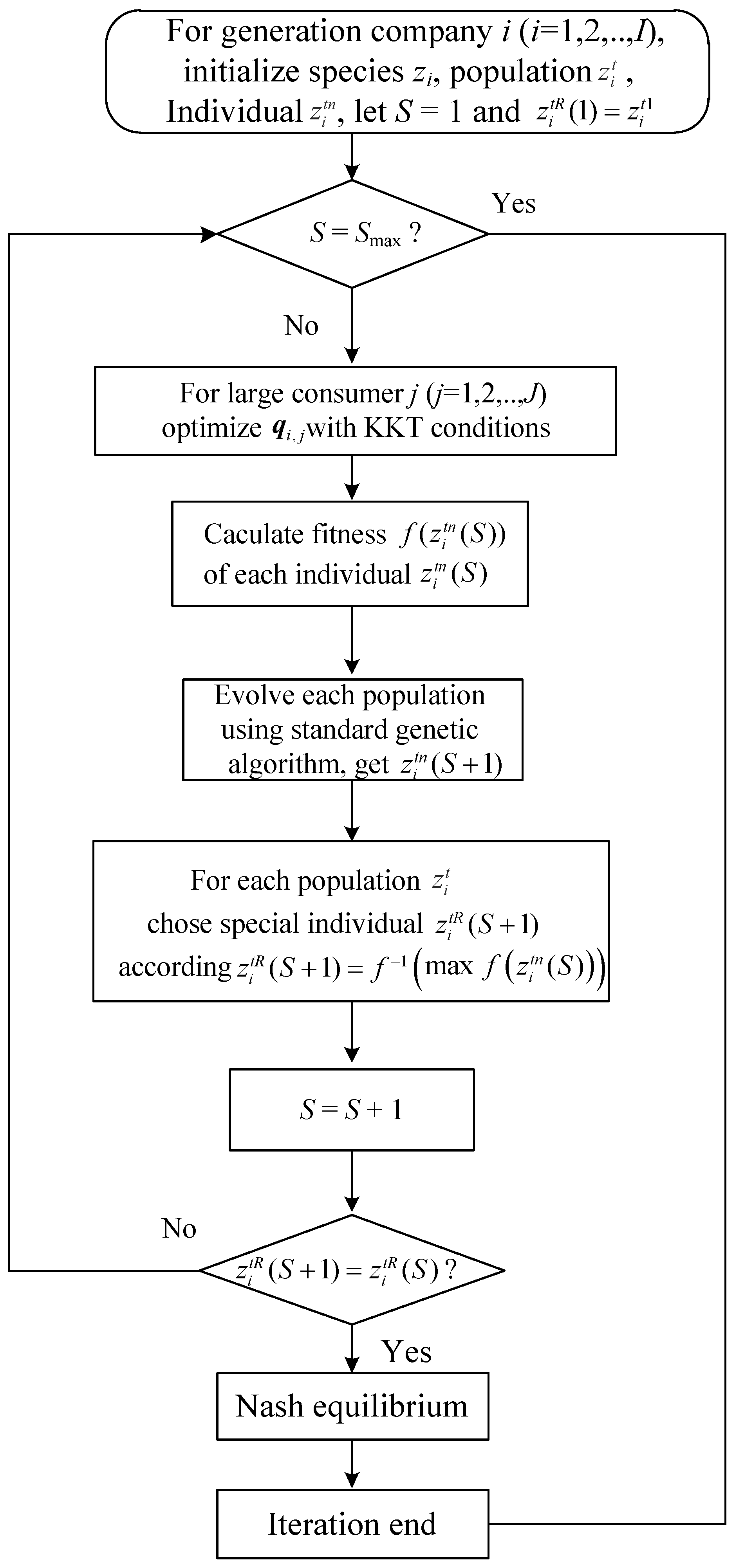
3.3. Co-Evolution Algorithm for Bayesian Nash Equilibrium
- (1)
- Establish species corresponding to each generation company, and then establish population according to each type of each company, where t represents type number of company i; assume that is a genetic individual in the population .
- (2)
- Since species and population only represent a part of the global solution, it is necessary to evaluate individual with information of other species . Accordingly, we choose a special individual to represent the information of species in the global solution. Suppose that the present number of evolution is S, then the fitness function of individual in species can be designed as
- (3)
- As for the selection method of individual , the mechanism of elite is adopted in the paper. That is, for species in the Sth evolution is the individual who has the highest fitness value in the th evolution:
- (4)
- Run step (2) and (3) and obtain fitness values of each individual for each species via standard genetic algorithm, and then determine .
- (5)
- Repeat steps (2)–(4) until the maximum number of evolution is reached or is unchanged.
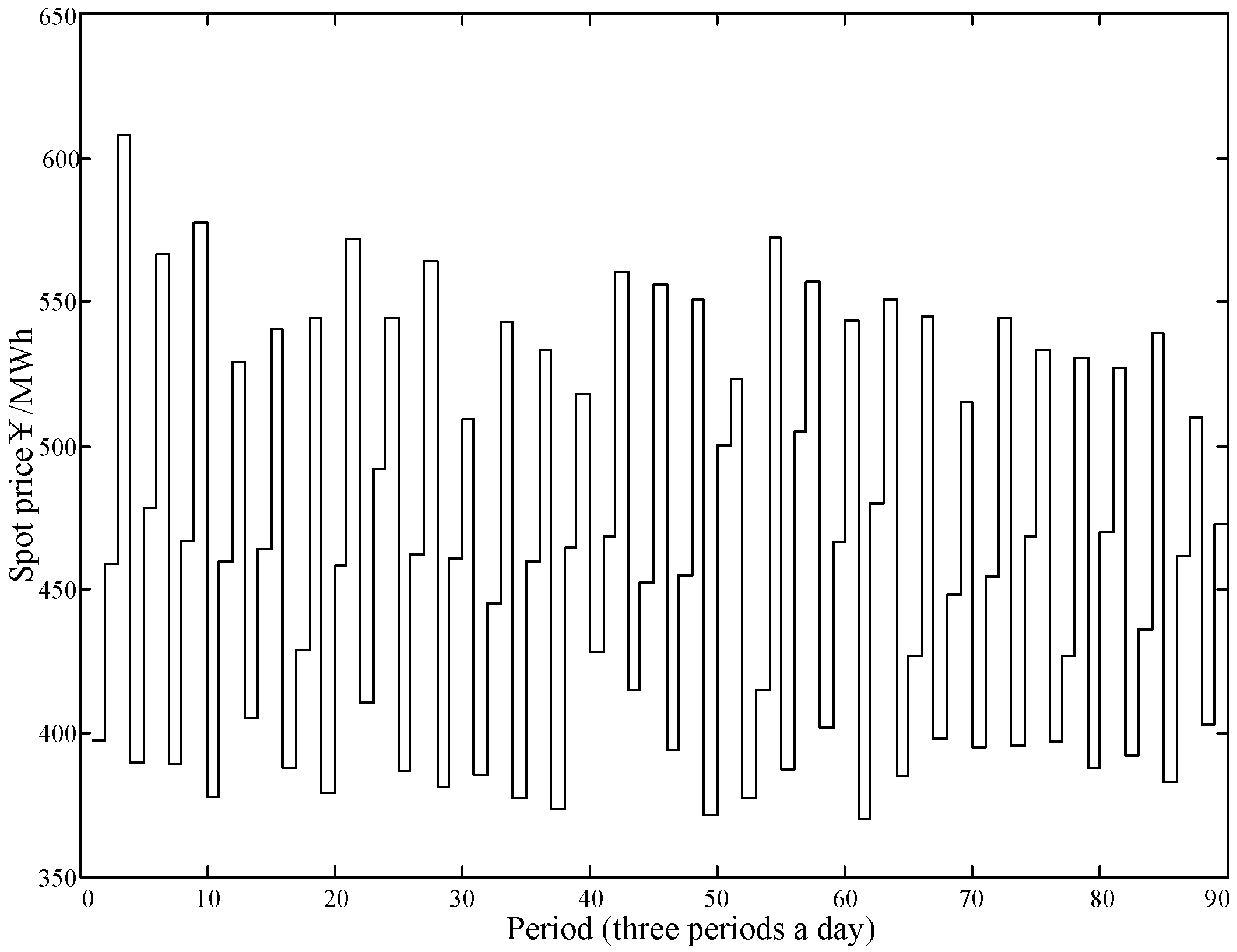
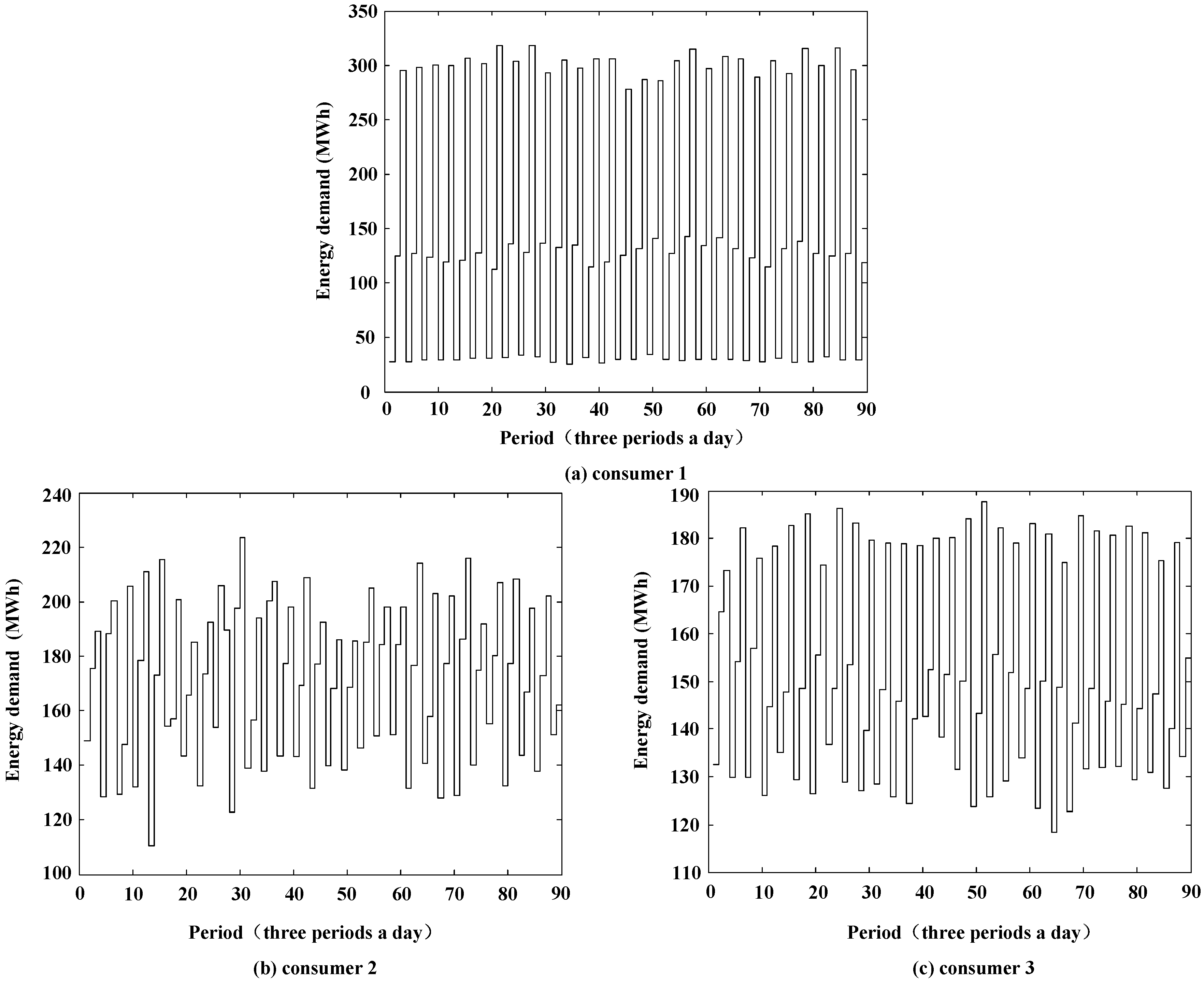
4. Simulation Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Results of Optimal Purchase Strategies for Three Large Consumers
| Type | Company | Consumers | Type | Company | Consumers | ||||
|---|---|---|---|---|---|---|---|---|---|
| Combination | 1 | 2 | 3 | Combination | 1 | 2 | 3 | ||
| a | 4854.09 | 4555.05 | 4168.93 | a | 4175.14 | 3842.23 | 3464.32 | ||
| (1,1,1) | b | 3760.87 | 3405.54 | 3061.54 | (2,2,3) | b | 2925.55 | 2377.20 | 2058.60 |
| c | 4783.59 | 4563.14 | 3981.81 | c | 5779.30 | 5372.17 | 4962.63 | ||
| a | 4994.53 | 4692.75 | 4383.03 | a | 3822.11 | 3389.97 | 2981.15 | ||
| (1,1,2) | b | 3873.22 | 3515.70 | 3232.82 | (2,3,1) | b | 4110.44 | 3984.17 | 3578.06 |
| c | 4415.49 | 3816.26 | 3181.75 | c | 4919.85 | 4479.31 | 3972.91 | ||
| a | 4716.82 | 4527.74 | 4111.67 | a | 3950.31 | 3524.35 | 3181.15 | ||
| (1,1,3) | b | 3651.06 | 3383.69 | 3015.73 | (2,3,2) | b | 4264.28 | 4145.42 | 3818.07 |
| c | 5142.51 | 4947.63 | 4407.83 | c | 4392.34 | 3688.84 | 3116.52 | ||
| a | 5124.98 | 4773.64 | 4442.60 | a | 3768.90 | 3361.37 | 2928.56 | ||
| (1,2,1) | b | 2809.03 | 2265.58 | 1921.25 | (2,3,3) | b | 4048.33 | 3949.85 | 3514.96 |
| c | 5144.77 | 4854.60 | 4346.71 | c | 5361.45 | 4877.56 | 4411.56 | ||
| a | 5262.37 | 4873.78 | 4616.48 | a | 3826.16 | 3383.29 | 3064.31 | ||
| (1,2,2) | b | 2906.61 | 2354.59 | 2075.82 | (3,1,1) | b | 4012.91 | 3643.84 | 3326.66 |
| c | 4711.05 | 4105.90 | 3555.28 | c | 5203.66 | 44960.30 | 4423.68 | ||
| a | 5015.67 | 4764.08 | 4405.43 | a | 3935.67 | 3461.92 | 3208.95 | ||
| (1,2,3) | b | 2783.09 | 2257.09 | 1888.22 | (3,1,2) | b | 4122.42 | 3722.47 | 3471.30 |
| c | 5484.05 | 5217.74 | 4743.57 | c | 4835.31 | 4229.80 | 3658.71 | ||
| a | 4761.07 | 4342.83 | 3981.75 | a | 3735.76 | 3380.35 | 3035.13 | ||
| (1,3,1) | b | 3872.83 | 3785.04 | 3337.39 | (3,1,3) | b | 3922.51 | 3640.90 | 3297.48 |
| c | 4659.57 | 4280.18 | 3732.25 | c | 5530.30 | 5315.08 | 4810.32 | ||
| a | 4912.06 | 4484.77 | 4181.25 | a | 4015.51 | 3532.74 | 3268.57 | ||
| (1,3,2) | b | 4051.47 | 3974.30 | 3603.38 | (3,2,1) | b | 3036.04 | 2502.11 | 2199.52 |
| c | 4159.13 | 3483.50 | 2858.90 | c | 5519.23 | 5209.39 | 4764.10 | ||
| a | 4638.49 | 4304.84 | 3922.47 | a | 4090.46 | 3588.79 | 3378.51 | ||
| (1,3,3) | b | 3816.23 | 3734.39 | 3258.35 | (3,2,2) | b | 3117.41 | 2564.38 | 2321.68 |
| c | 5052.99 | 4692.89 | 4191.61 | c | 5076.91 | 4483.53 | 3997.83 | ||
| a | 3977.67 | 3633.05 | 3213.26 | a | 3949.21 | 3541.30 | 3258.02 | ||
| (2,1,1) | b | 3954.63 | 3530.26 | 3223.33 | (3,2,3) | b | 3011.98 | 2511.62 | 2187.79 |
| c | 5106.52 | 4771.00 | 4251.45 | c | 5835.23 | 5545.00 | 5128.74 | ||
| a | 4122.99 | 3755.65 | 3418.30 | a | 3729.56 | 3181.95 | 2867.78 | ||
| (2,1,2) | b | 4059.26 | 3618.53 | 3370.95 | (3,3,1) | b | 4233.25 | 4129.60 | 3701.27 |
| c | 4658.31 | 4021.91 | 3458.01 | c | 5042.65 | 4624.73 | 4096.12 | ||
| a | 3898.76 | 3617.82 | 3167.32 | a | 3827.89 | 3276.63 | 3017.47 | ||
| (2,1,3) | b | 3888.97 | 3519.29 | 3190.25 | (3,3,2) | b | 4397.13 | 4287.41 | 3950.75 |
| c | 5482.39 | 5141.34 | 4657.14 | c | 4554.60 | 3859.22 | 3275.74 | ||
| a | 4217.57 | 3841.49 | 3487.04 | a | 3663.77 | 3165.33 | 2830.62 | ||
| (2,2,1) | b | 2950.90 | 2376.61 | 2076.77 | (3,3,3) | b | 4186.74 | 4101.91 | 3639.33 |
| c | 5394.40 | 5021.13 | 4579.98 | c | 5427.46 | 5007.91 | 4518.17 | ||
| a | 4313.62 | 3931.25 | 3647.20 | ||||||
| (2,2,2) | b | 3027.74 | 2448.41 | 2204.90 | |||||
| c | 4915.50 | 4274.78 | 3787.63 |
References
- Zhang, X.; Liu, F.; Peng, T.; Li, Z.; Pang, B.; Geng, J. A discussion on key issues for direct trading between power users and plants. Autom. Electr. Power Syst. 2014, 38, 33–37. [Google Scholar]
- Bharti, D.; De, M. A new graph theory based loss allocation framework for bilateral power market using diakoptics. Int. J. Electr. Power Energy Syst. 2016, 77, 395–403. [Google Scholar] [CrossRef]
- Algarvio, H.; Lopes, F.; Santana, J. Bilateral Contracting in Multi-agent Energy Markets: Forward Contracts and Risk Management. Int. J. Electr. Power Energy Syst. 2015, 524, 260–269. [Google Scholar]
- Mari, L.; Nabona, N.; Pages-Bernaus, A. Medium-term power planning in electricity markets with pool and bilateral contracts. Eur. J. Oper. Res. 2016, 260, 395–443. [Google Scholar] [CrossRef]
- Sivrikaya, B.T.; Cebi, F.; Turan, H.H.; Kasap, N.; Delen, D. A fuzzy long-term investment planning model for a GenCo in a hybrid electricity market considering climate change impacts. Eur. J. Oper. Res. 2016, 1–17. [Google Scholar] [CrossRef]
- Rahimiyan, M.; Baringo, L.; Conejo, A.J. Energy management of a cluster of interconnected price-responsive demands. IEEE Trans. Power Syst. 2014, 29, 645–655. [Google Scholar] [CrossRef]
- Karandikar, R.G.; Khaparde, S.A.; Kulkarni, S.V. Strategic evaluation of bilateral contract for electricity retailer in restructured power market. Int. J. Electr. Power Energy Syst. 2010, 32, 457–463. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Conejo, A.J.; Plazas, M.A. Optimal price and quantity determination for retail electric power contracts. IEEE Trans. Power Syst. 2006, 21, 180–187. [Google Scholar] [CrossRef]
- Zhang, F.; Wen, F.; Yan, H.; Yu, Z.; Zhong, Z.; Huang, J. A multi-round negotiation model for bilateral market environment. Autom. Electr. Power Syst. 2010, 34, 29–35. [Google Scholar]
- Kazempour, S.J.; Conejo, A.J.; Ruiz, C. Strategic bidding for a large consumer. IEEE Trans. Power Syst. 2015, 30, 848–856. [Google Scholar] [CrossRef]
- Fleten, S.E.; Pettersen, E.; Ruiz, C. Constructing bidding curves for a price-taking retailer in the Norwegian electricity market. IEEE Trans. Power Syst. 2005, 20, 701–708. [Google Scholar] [CrossRef]
- Liu, X.; Gao, B.; Wu, C.; Tang, Y. Bayesian game-theoretic energy management for residential users in smart grid. In Proceedings of the 2016 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems, Chengdu, China, 19–22 June 2016; pp. 67–71. [Google Scholar]
- Wang, C.; Tang, W.; Zhao, R. Static Bayesian games with finite fuzzy types and the existence of equilibrium. Inf. Sci. 2008, 178, 4688–4698. [Google Scholar] [CrossRef]
- Rabinovich, Z.; Naroditskiy, V.; Gerding, E.H. Computing pure Bayesian-Nash equilibria in games with finite actions and continuous types. Artif. Intell. 2013, 195, 106–139. [Google Scholar] [CrossRef]
- Palamarchuk, S. Bilateral contracts for electricity delivery: Scheduling and arrangement. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Russia, 1–5 July 2007; pp. 843–848. [Google Scholar]
- Wei, W.; Liu, F.; Mei, S. Energy Pricing and Dispatch for Smart Grid Retailers Under Demand Response and Market Price Uncertainty. IEEE Trans. Smart Grid 2015, 6, 1364–1374. [Google Scholar] [CrossRef]
- Oliveira, F.; Ruiz, C.; Conejo, A. Contract design and supply chain coordination in the electricity industry. Eur. J. Oper. Res. 2013, 227, 527–537. [Google Scholar] [CrossRef]
- Xia, W.; Lv, L.; Liu, P. Economic game theory research on bilateral electricity pricing in direct power purchase. Mod. Electr. Power 2015, 32, 71–75. [Google Scholar]
- Liu, Z.; Ren, Y.; Wang, E.; Tang, H. Swarm simulation on high low matching auction mechanism based on secondary trade of bilateral contract. Autom. Electr. Power Syst. 2007, 31, 26–29. [Google Scholar]
- Wu, C.; Gao, B.; Tang, Y.; Wang, Q. Master-slave Game based Bilateral Contracht Transaction Model for Generation Companies and Large Consumers. Autom. Electr. Power Syst. 2016, 40, 56–62. [Google Scholar]
- Bahmani-Firouzi, B.; Sharifinia, S.; Azizipanah-Abarghooee, R.; Niknam, T. Scenario-based optimal bidding strategies of GENCOs in the incomplete information electricity market using a new improved prey-predator optimization algorithm. IEEE Syst. J. 2015, 9, 1485–1495. [Google Scholar] [CrossRef]
- Soleymani, S. Bidding strategy of generation companies using PSO combined with SA method in the pay as bid markets. Int. J. Electr. Power Energy Syst. 2011, 33, 1272–1278. [Google Scholar] [CrossRef]
- Li, T.; Shahidehpour, M. Strategic bidding of transmission-constrained GENCOs with incomplete information. IEEE Trans. Power Syst. 2005, 20, 437–447. [Google Scholar] [CrossRef]
- Wang, J.; Shahidehpour, M.; Li, Z. Strategic generation capacity expansion planning with incomplete information. IEEE Trans. Power Syst. 2009, 24, 1002–1010. [Google Scholar] [CrossRef]
- Hu, X.; Ralph, D. Using EPECs to model bilevel games in restructured electricity markets with locational prices. Oper. Res. 2007, 55, 809–827. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Games with incomplete information played by Bayesian players, I-III: Part I. The basic model. Manag. Sci. 2004, 50, 1804–1817. [Google Scholar] [CrossRef]
- Roger, B.M. Game Theory: Analysis of Conflict; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Rosen, J.B. Existence and uniqueness of equilibrium points for concave n-person games. Econom. J. Econom. Soc. 1965, 33, 1804–1817. [Google Scholar]
- Munson, T.S.; Facchinei, F.; Ferris, M.C. The semismooth algorithm for large scale complementarity problems. Inf. J. Comput. 2001, 13, 294–311. [Google Scholar] [CrossRef]
- De Luca, T.; Facchinei, F.; Kanzow, C. A theoretical and numerical comparison of some semismooth algorithms for complementarity problems. Comput. Optim. Appl. 2000, 16, 173–205. [Google Scholar] [CrossRef]
- Chen, H.; Wong, K.; Nguyen, H.M. Analyzing oligopolistic electricity market using coevolutionary computation. IEEE Trans. Power Syst. 2006, 21, 143–152. [Google Scholar] [CrossRef]
- Chen, H.; Wong, K.; Chung, C.Y. A coevolutionary approach to analyzing supply function equilibrium model. IEEE Trans. Power Syst. 2006, 21, 1019–1028. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, H.; Zhang, Y. A coevolutionary approach to calculating equilibrium for oligopolistic electricity market. Autom. Electr. Power Syst. 2009, 33, 42–46. [Google Scholar]
- Zare, K.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K. Risk-based electricity procurement for large consumers. IEEE Trans. Power Syst. 2011, 26, 1826–1835. [Google Scholar] [CrossRef]
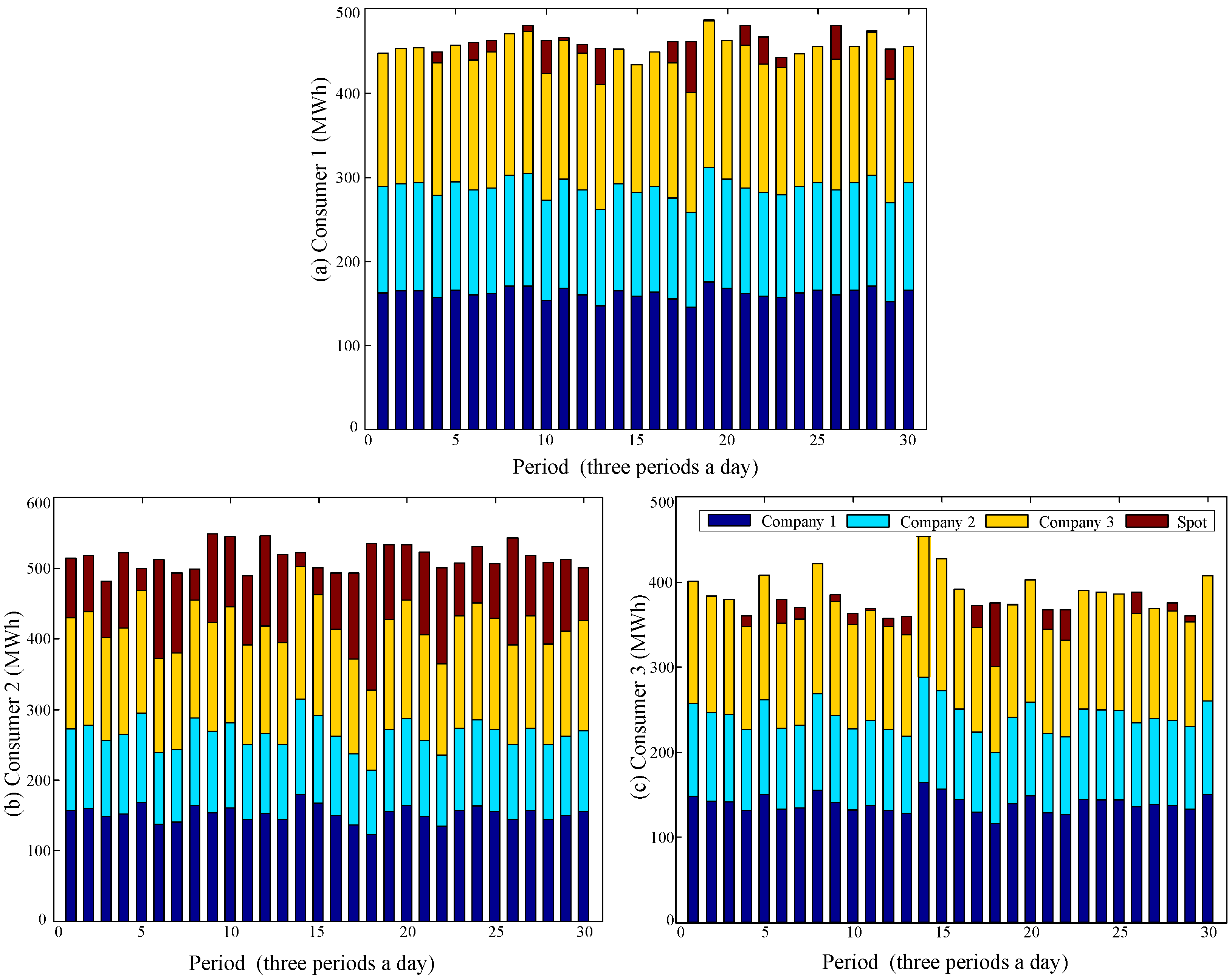
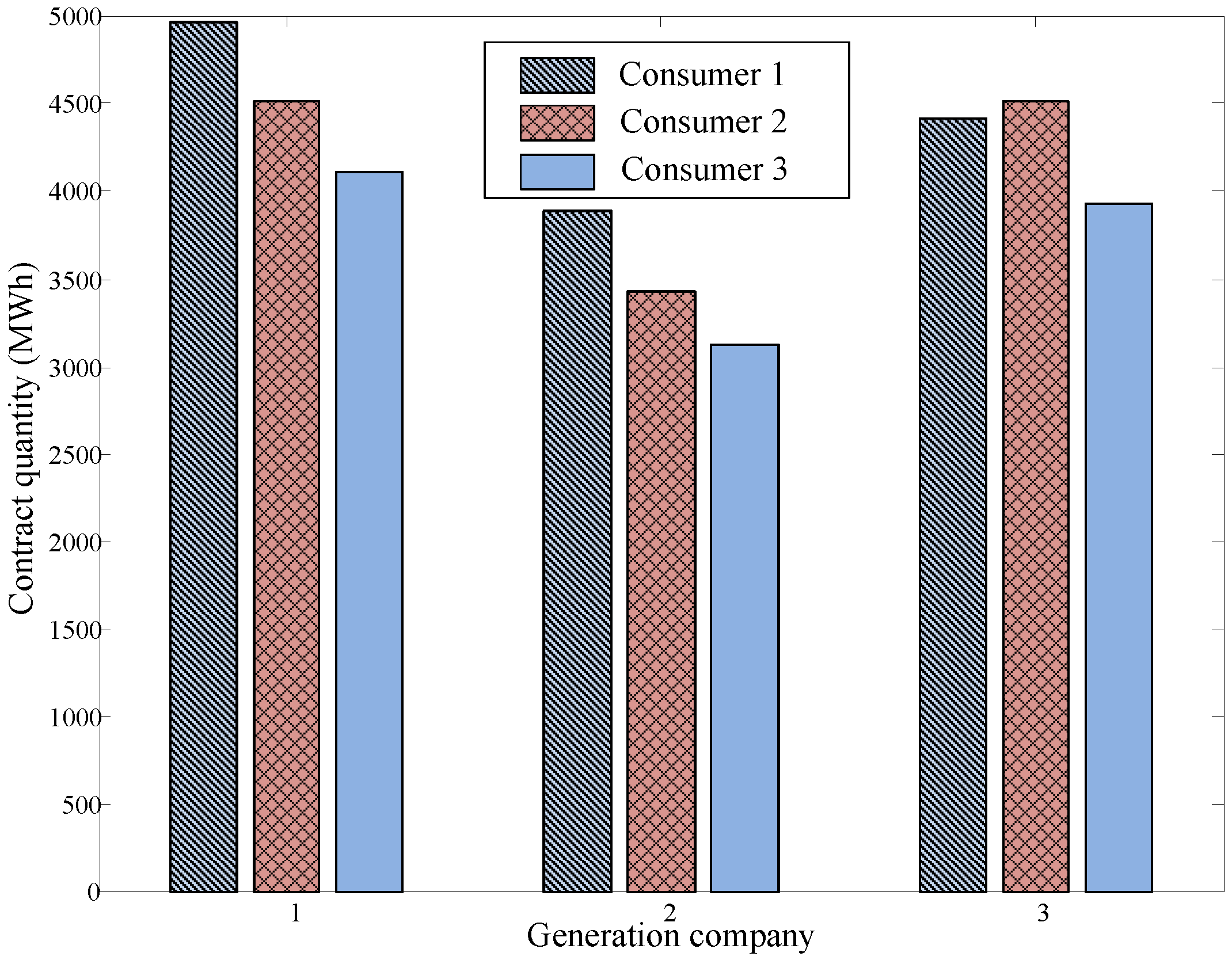
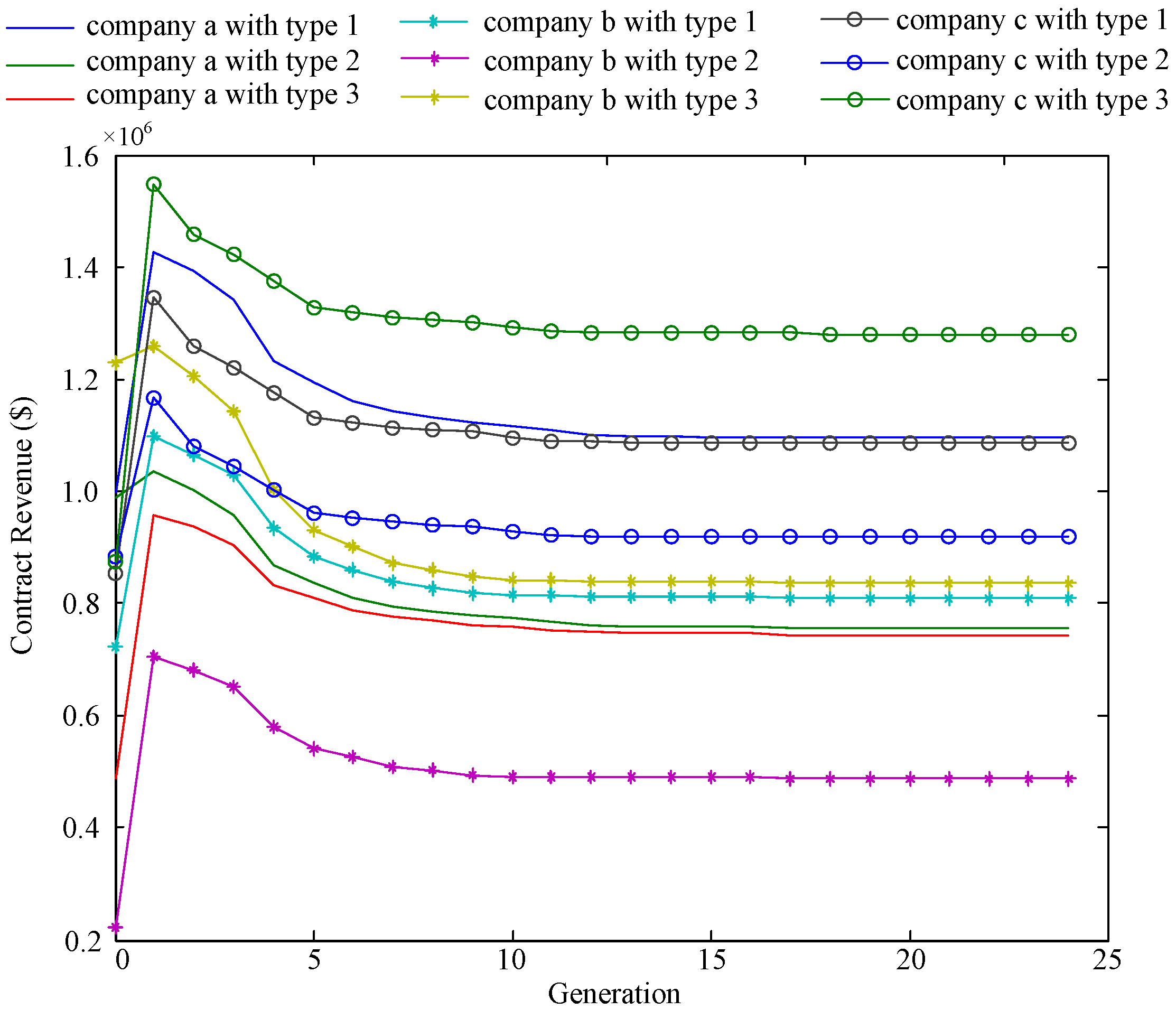
| Time Spans | Hours of the Day |
|---|---|
| Off-peak | 1, 2, 3, 4, 5, 6, 7, 8 |
| Mid-peak | 9, 10, 15, 16, 17, 18, 23, 24 |
| On-Peak | 11, 12, 13, 14, 19, 20, 21, 22 |
| Company | Type | A | B | b | p | ||
|---|---|---|---|---|---|---|---|
| (¥/MWh) | ((¥/MWh) | ((¥/MWh) | (/¥MWh) | (/¥MWh) | |||
| 1 | 320 | 0.4 | 0.8 | 350 | 500 | 0.3 | |
| a | 2 | 352 | 0.36 | 0.8 | 350 | 500 | 0.3 |
| 3 | 338 | 0.5 | 0.8 | 350 | 500 | 0.4 | |
| 1 | 330 | 0.5 | 1.0 | 350 | 500 | 0.3 | |
| b | 2 | 370 | 0.45 | 1.0 | 350 | 500 | 0.3 |
| 3 | 350 | 0.03 | 1.0 | 350 | 500 | 0.4 | |
| 1 | 340 | 0.3 | 0.6 | 350 | 500 | 0.3 | |
| c | 2 | 360 | 0.25 | 0.6 | 350 | 500 | 0.3 |
| 3 | 320 | 0.35 | 0.6 | 350 | 500 | 0.4 |
| Company | Type | Consumer 1 | Consumer 2 | Consumer 3 |
|---|---|---|---|---|
| 1 | 362.45 | 354.60 | 355.26 | |
| a | 2 | 391.19 | 380.65 | 382.11 |
| 3 | 369.32 | 365.69 | 367.17 | |
| 1 | 365.17 | 359.90 | 361.34 | |
| b | 2 | 402.24 | 397.19 | 399.43 |
| 3 | 399.35 | 381.87 | 382.10 | |
| 1 | 385.90 | 374.85 | 376.45 | |
| c | 2 | 410.67 | 399.17 | 402.18 |
| 3 | 366.31 | 358.13 | 359.79 |
| Company | Consumer 1 | Consumer 2 | Consumer 3 |
|---|---|---|---|
| a | 363.20 | 355.80 | 356.75 |
| b | 365.18 | 359.78 | 360.36 |
| c | 396.42 | 376.02 | 377.67 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Ling, J.; Wu, C.; Chen, N.; Liu, X.; Gao, B. Game-Theoretic Optimization of Bilateral Contract Transaction for Generation Companies and Large Consumers with Incomplete Information. Entropy 2017, 19, 272. https://doi.org/10.3390/e19060272
Tang Y, Ling J, Wu C, Chen N, Liu X, Gao B. Game-Theoretic Optimization of Bilateral Contract Transaction for Generation Companies and Large Consumers with Incomplete Information. Entropy. 2017; 19(6):272. https://doi.org/10.3390/e19060272
Chicago/Turabian StyleTang, Yi, Jing Ling, Cheng Wu, Ning Chen, Xiaofeng Liu, and Bingtuan Gao. 2017. "Game-Theoretic Optimization of Bilateral Contract Transaction for Generation Companies and Large Consumers with Incomplete Information" Entropy 19, no. 6: 272. https://doi.org/10.3390/e19060272
APA StyleTang, Y., Ling, J., Wu, C., Chen, N., Liu, X., & Gao, B. (2017). Game-Theoretic Optimization of Bilateral Contract Transaction for Generation Companies and Large Consumers with Incomplete Information. Entropy, 19(6), 272. https://doi.org/10.3390/e19060272





