Fractional Diffusion in a Solid with Mass Absorption
Abstract
:1. Introduction
2. Fundamental Solution to the Cauchy Problem
2.1. Standard Diffusion (, )
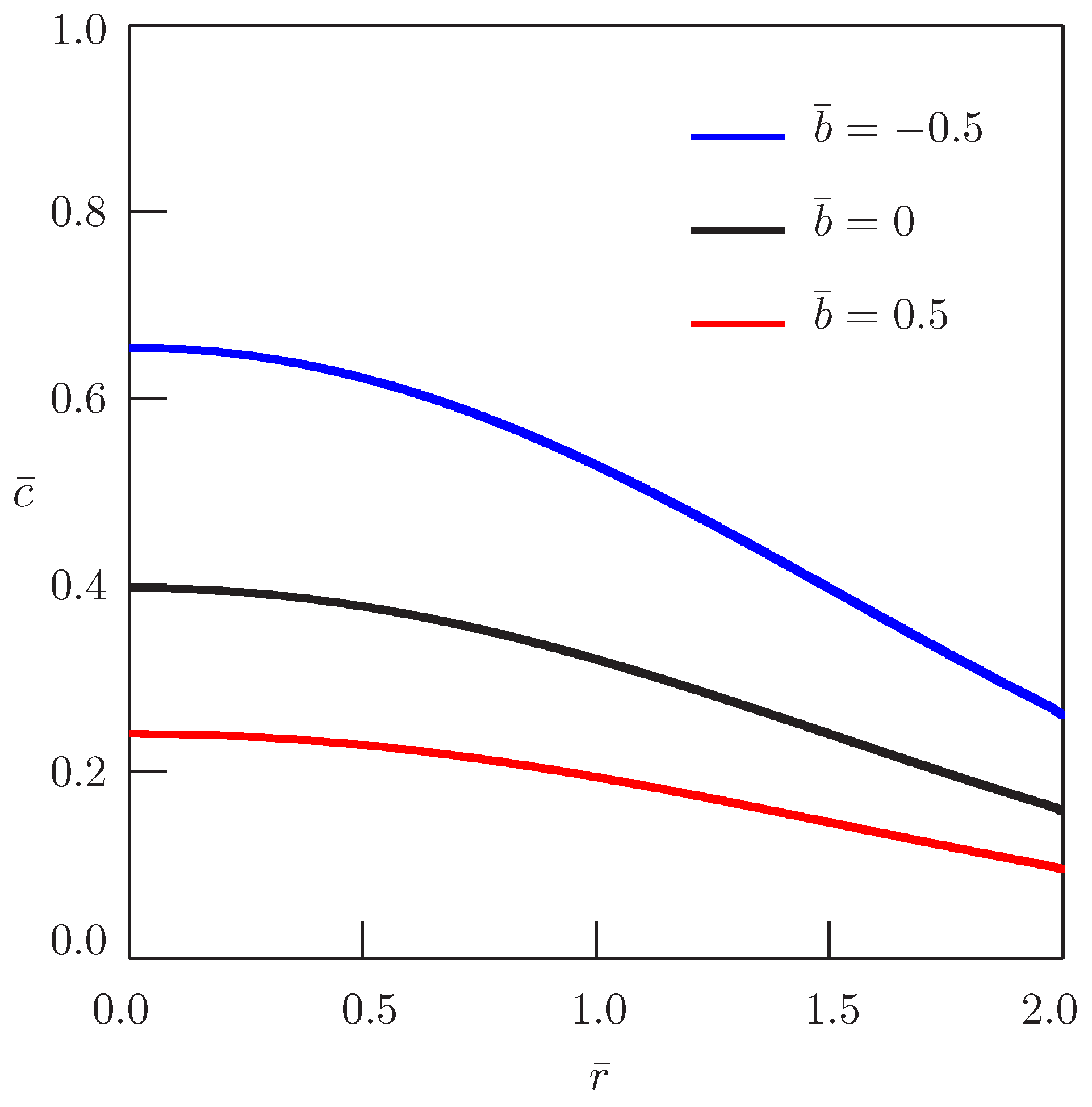
2.2. Localized Diffusion (, )
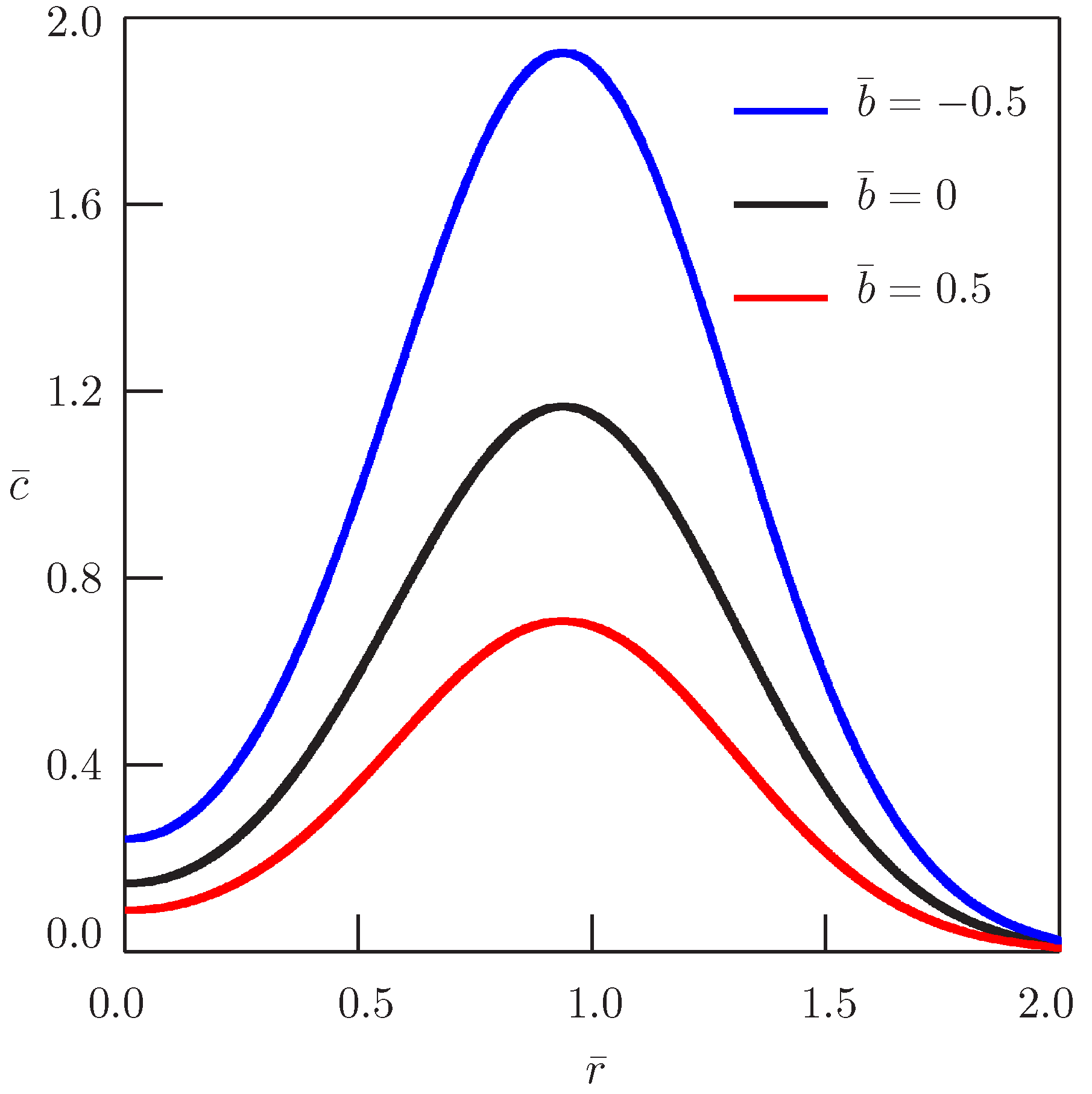
2.3. Subdiffusion with and
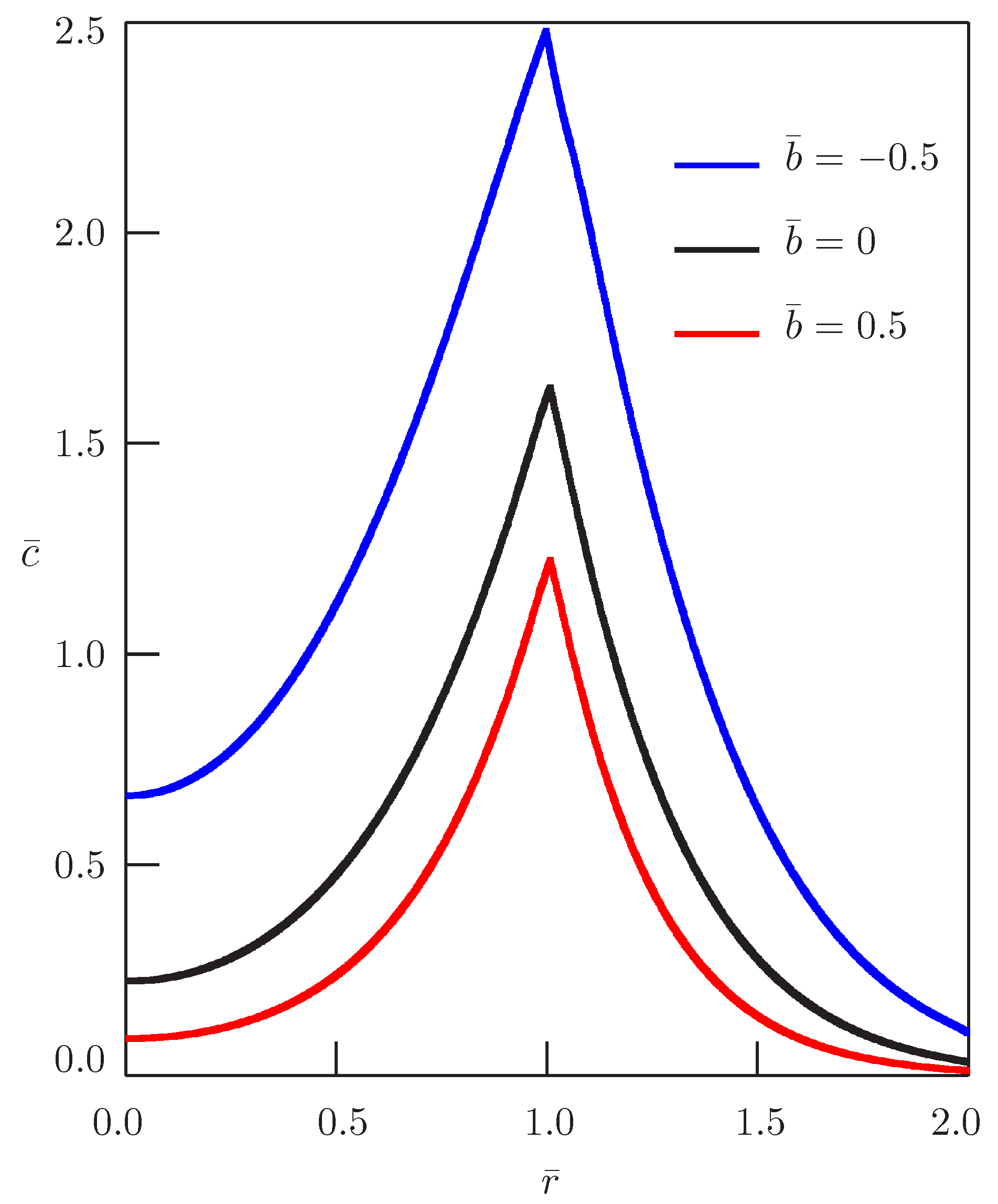
2.4. Cauchy Diffusion with ,
3. Fundamental Solution to the Source Problem
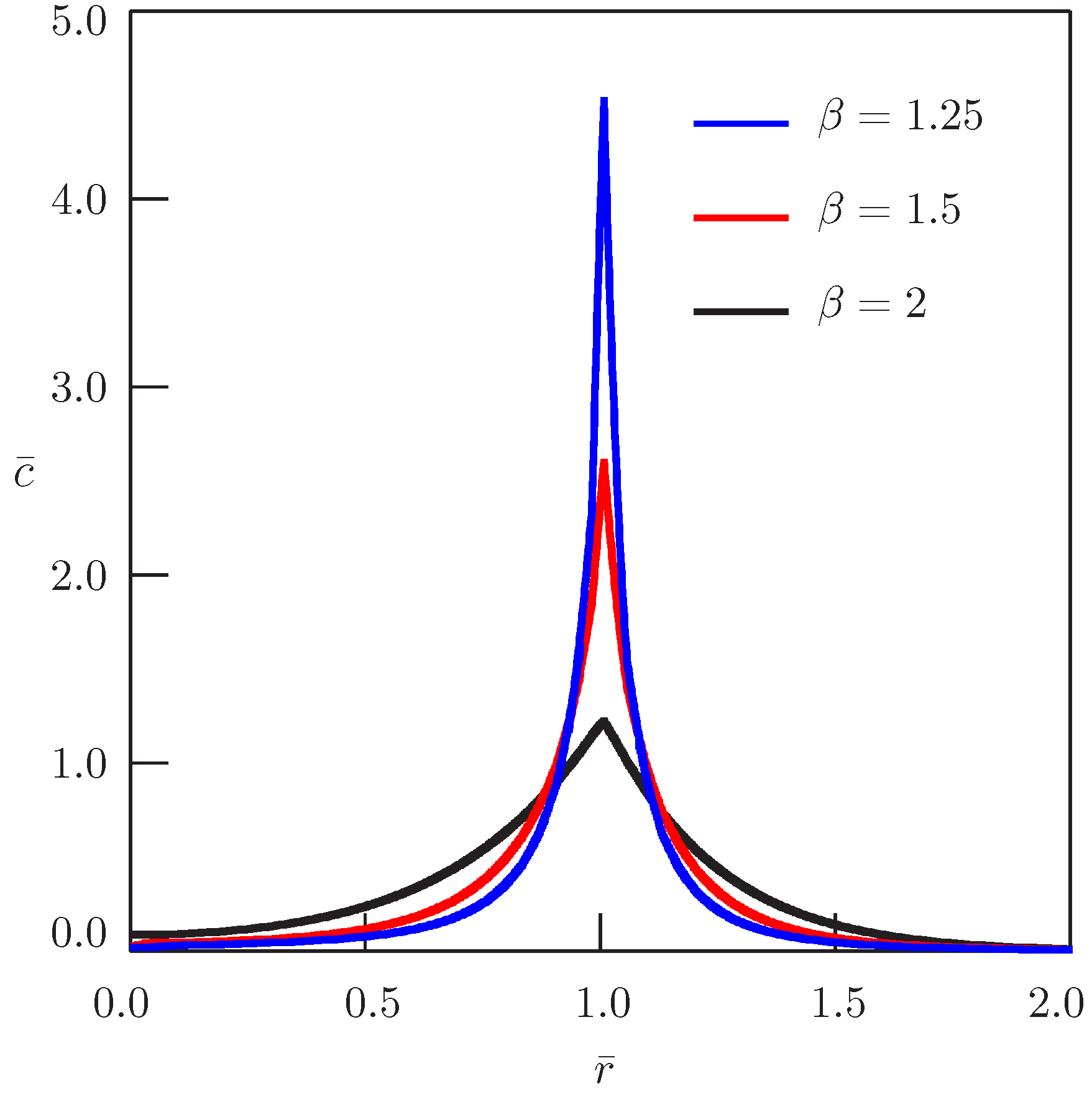
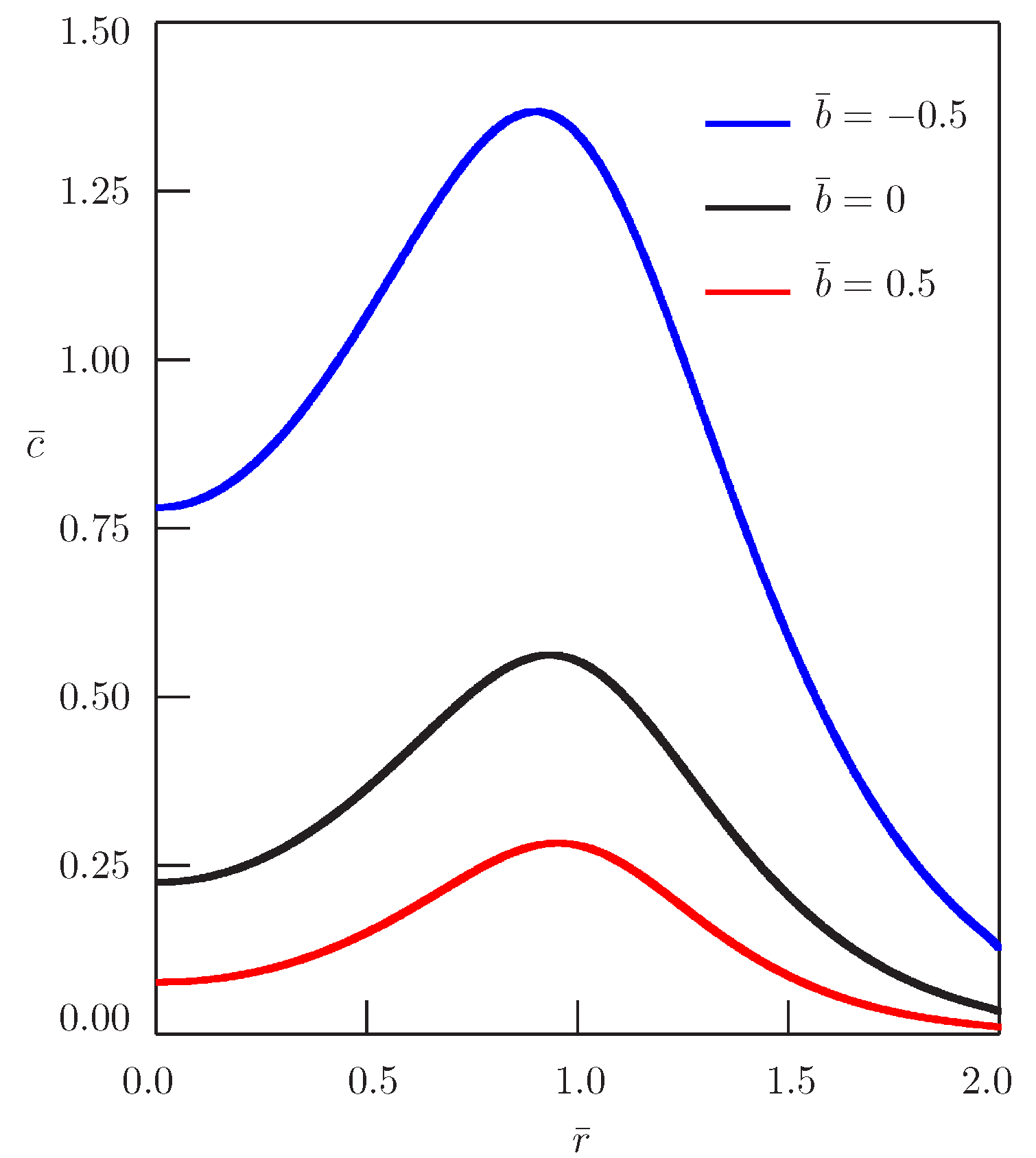
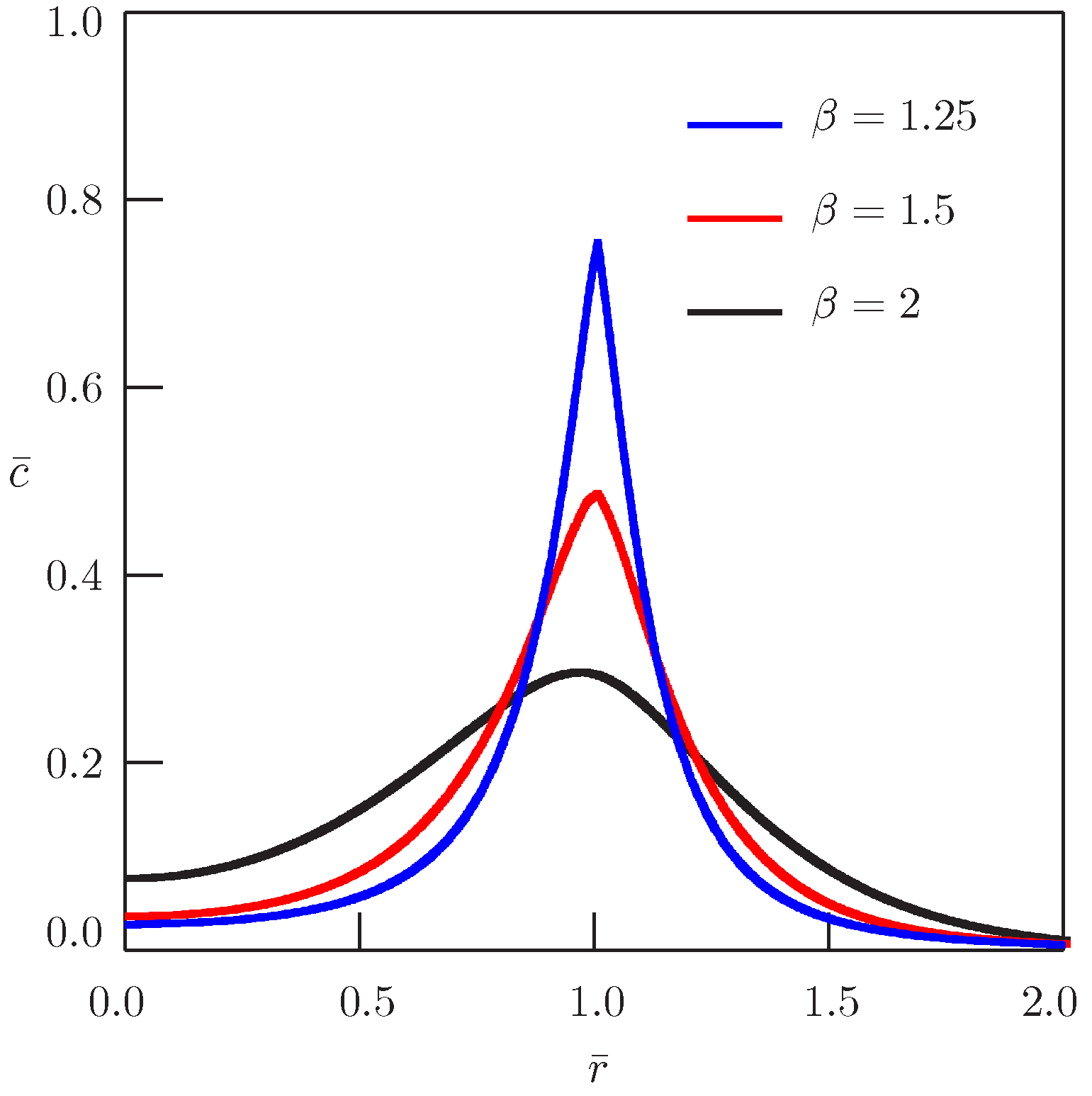
Subdiffusion with and
4. Discussion
Author Contributions
Conflicts of Interest
Appendix A. Integrals
References
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Polyanin, A.D. Handbook of Linear Partial Differential Equations for Engineers and Scientists; Chapman & Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [PubMed]
- Nyborg, W.L. Solutions of the bio-heat transfer equation. Phys. Med. Biol. 1988, 33, 785–792. [Google Scholar] [CrossRef] [PubMed]
- Lakhssassi, A.; Kengne, E.; Semmaoui, H. Investigation of nonlinear temperature distribution in biological tissues by using bioheat transfer equation of Pennes’ type. Nat. Sci. 2010, 2, 131–138. [Google Scholar] [CrossRef]
- Abad, E.; Yuste, S.B.; Lindenberg, K. Survival probability of an immobile target in a sea of evanescent diffusive or subdiffusive traps: A fractional equation approach. Phys. Rev. E 2012, 86, 061120. [Google Scholar] [CrossRef] [PubMed]
- Povstenko, Y. Fractional heat conduction equation and associated thermal stresses. J. Therm. Stresses 2005, 28, 83–102. [Google Scholar] [CrossRef]
- Povstenko, Y. Theory of thermoelasticity based on the space-time-fractional heat conduction equation. Phys. Scr. 2009, 136, 014017. [Google Scholar] [CrossRef]
- Povstenko, Y. Non-axisymmetric solutions to time-fractional diffusion-wave equation in an infinite cylinder. Fract. Calc. Appl. Anal. 2011, 14, 418–435. [Google Scholar] [CrossRef]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional calculus: Integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: Wien, Austria, 1997; pp. 223–276. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Random walk models for space-fractional diffusion processes. Fract. Calc. Appl. Anal. 1998, 1, 167–191. [Google Scholar]
- Hanyga, A. Multidimensional solutions of space-fractional diffusion equations. Proc. R. Soc. Lond. A 2001, 457, 2993–3005. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Saichev, A.I.; Zaslavsky, G.M. Fractional kinetic equations: Solutions and applications. Chaos 1997, 7, 753–764. [Google Scholar] [CrossRef] [PubMed]
- Gorenflo, R.; Mainardi, F.; Moretti, D.; Pagnini, G.; Paradisi, P. Discrete random walk models for space-time fractional diffusion. Chem. Phys. 2002, 284, 521–541. [Google Scholar] [CrossRef]
- Matignion, D. Diffusive representations for fractional Laplacian: System theory framework and numerical issues. Phys. Scr. T 2009, 136, 014009. [Google Scholar] [CrossRef]
- Sneddon, I.N. The Use of Integral Transforms; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2001, 4, 153–192. [Google Scholar]
- Hanyga, A. Multidimensional solutions of space-time-fractional diffusion equations. Proc. R. Soc. Lond. A 2002, 458, 429–450. [Google Scholar] [CrossRef]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Datsko, B.; Gafiychuk, V. Complex nonlinear dynamics in subdiffusive activator-inhibitor systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1673–1680. [Google Scholar] [CrossRef]
- Baleanu, D.; Tenreiro Machado, J.A.; Luo, A.C.J. (Eds.) Fractional Dynamics and Control; Springer: New York, NY, USA, 2012. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Higher Education Press: Bejing, China; Springer: Berlin, Germany, 2010. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013. [Google Scholar]
- Uchaikin, V.; Sibatov, R. Fractional Kinetics in Solids: Anomalous Charge Transport in Semiconductors, Dielectrics and Nanosystems; World Scientific: Hackensack, NJ, USA, 2013. [Google Scholar]
- Povstenko, Y. Thermoelasticity based on fractional heat conduction equation. In Proceedings of the 6th International Congress on Thermal Stresses, Vienna, Austria, 26–29 May 2005; Ziegler, F., Heuer, R., Adam, C., Eds.; Vienna University of Technology: Vienna, Austria, 2005; Volume 2, pp. 501–504. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity; Springer: New York, NY, USA, 2015. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers, Inc.: Redding, CA, USA, 2006. [Google Scholar]
- Nonnenmacher, T.F.; Metzler, R. Applications of fractional calculus techniques to problems in biophysics. In Applications of Fractional Calculus in Physics; Hilfer, R., Ed.; World Scientific: Singapore, 2000; pp. 377–428. [Google Scholar]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Petráš, I. Fractional Order Systems. Modeling and Control Applications; World Scientific: Hackensack, NJ, USA, 2010. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls. Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Valério, D.; Sá da Costa, J. An Introduction to Fractional Control; The Institution of Engineering and Technology: London, UK, 2013. [Google Scholar]
- Weeks, E.R.; Weitz, D.A. Subdiffusion and the cage effect studied near the colloidal glass transition. Chem. Phys. 2002, 284, 361–377. [Google Scholar] [CrossRef]
- Hilfer, R. Experimental evidence for fractional time evolution in glass forming materials. Chem. Phys. 2002, 284, 399–408. [Google Scholar] [CrossRef]
- Kimmich, R. Strange kinetics, porous media, and NMR. Chem. Phys. 2002, 284, 253–285. [Google Scholar] [CrossRef]
- Arkhincheev, V.E. Anomalous diffusion and charge relaxation on comb model: Exact solutions. Phys. A Stat. Mech. Appl. 2000, 280, 304–314. [Google Scholar] [CrossRef]
- Arkhincheev, V.E. Diffusion on random comb structure: Effective medium approximation. Phys. A Stat. Mech. Appl. 2002, 307, 131–141. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. To the theoretical explanation of the “universal response”. Phys. Status Solidi B 1984, 123, 739–745. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. On the theory of relaxation with remnant temperature. Phys. Status Solidi B 1984, 124, 389–393. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Schmidt, M.G.W.; Sagués, F. Reaction-subdiffusion equations. Phys. Rev. E 2006, 73, 031102. [Google Scholar] [CrossRef] [PubMed]
- Henry, B.I.; Langlands, T.A.M.; Wearne, S.L. Anomalous diffusion with linear reaction dynamics: From continuous time random walks to fractional reaction-diffusion equations. Phys. Rev. E 2006, 74, 031116. [Google Scholar] [CrossRef] [PubMed]
- Abad, E.; Yuste, S.B.; Lindenberg, K. Reaction-subdiffusion and reaction-superdiffusion equations for evanescent particles performing continuous-time random walks. Phys. Rev. E 2010, 81, 031115. [Google Scholar] [CrossRef] [PubMed]
- Méndez, V.; Fedotov, S.; Horsthemke, W. Reaction-Transport Systems: Mesoscopic Foundations, Fronts, and Spatial Instabilities; Springer: Berlin, Germany, 2010. [Google Scholar]
- Yuste, S.B.; Abad, E.; Lindenberg, K. Reactions in subdiffusive media and associated fractional equations. In Fractional Dynamics. Recent Advances; Klafter, J., Lim, S.C., Metzler, R., Eds.; World Scientific: Hackensack, NJ, USA, 2012; pp. 77–106. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin, Germany, 2014. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1955; Volume 3. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.-H. Anomalous diffusion and fractional transport equations. In Fractional Dynamics. Recent Advances; Klafter, J., Lim, S.C., Metzler, R., Eds.; World Scientific: Hackensack, NJ, USA, 2012; pp. 3–32. [Google Scholar]
- Gorenflo, R.; Loutchko, J.; Luchko, Y. Computation of the Mittag-Leffler function and its derivatives. Fract. Calc. Appl. Anal. 2002, 5, 491–518. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Volume 2: Special Functions; Gordon and Breach: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Eason, G.; Noble, B.; Sneddon, I.N. On certain integrals of Lipschitz-Hankel type involving products of Bessel functions. Philos. Trans. R. Soc. Lond. Ser. A 1955, 247, 529–551. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Povstenko, Y.; Kyrylych, T.; Rygał, G. Fractional Diffusion in a Solid with Mass Absorption. Entropy 2017, 19, 203. https://doi.org/10.3390/e19050203
Povstenko Y, Kyrylych T, Rygał G. Fractional Diffusion in a Solid with Mass Absorption. Entropy. 2017; 19(5):203. https://doi.org/10.3390/e19050203
Chicago/Turabian StylePovstenko, Yuriy, Tamara Kyrylych, and Grażyna Rygał. 2017. "Fractional Diffusion in a Solid with Mass Absorption" Entropy 19, no. 5: 203. https://doi.org/10.3390/e19050203
APA StylePovstenko, Y., Kyrylych, T., & Rygał, G. (2017). Fractional Diffusion in a Solid with Mass Absorption. Entropy, 19(5), 203. https://doi.org/10.3390/e19050203





