Carnot-Like Heat Engines Versus Low-Dissipation Models
Abstract
:1. Introduction
2. Correspondence between the HE’s Variables of Both Models
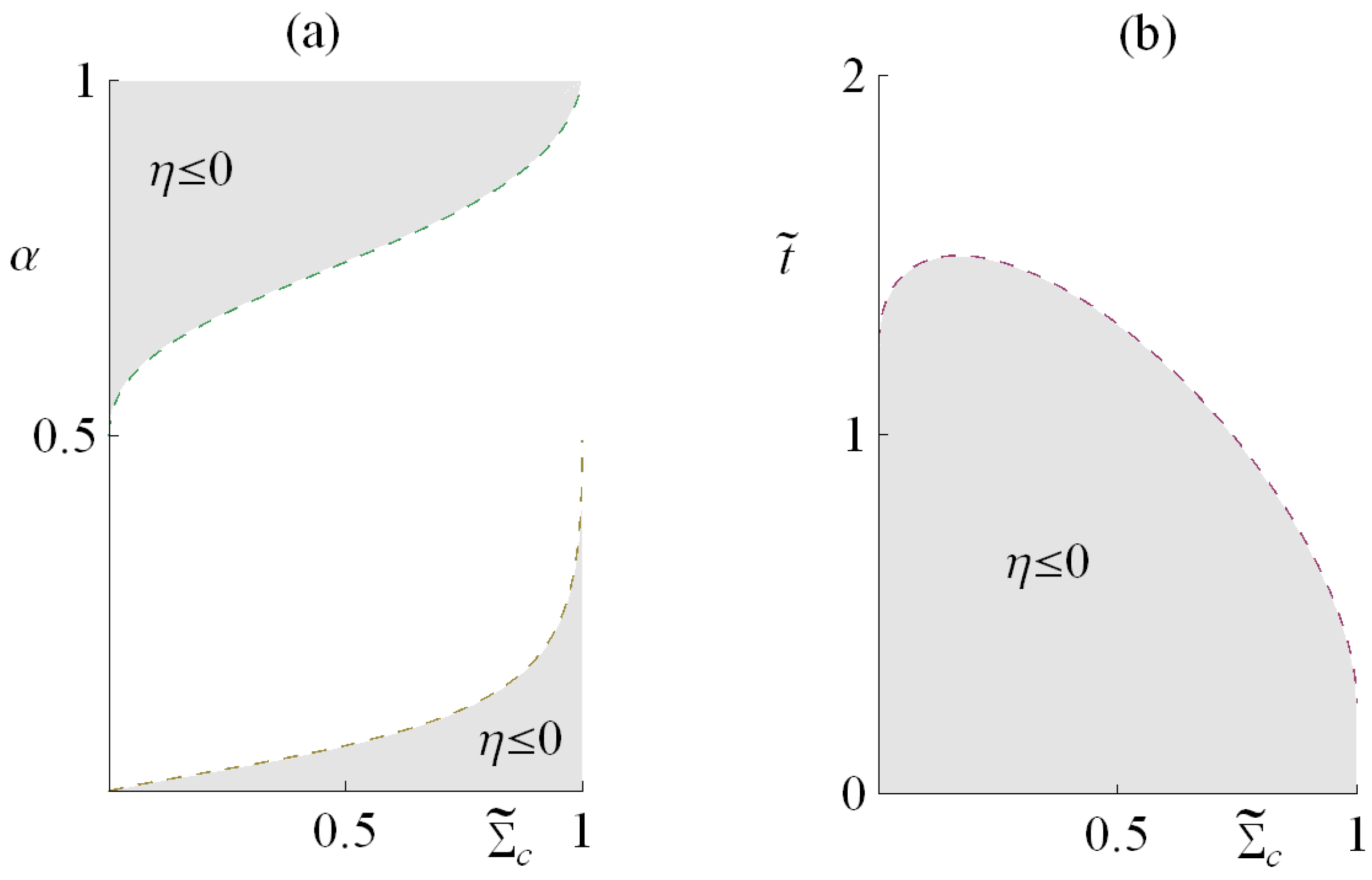
3. Physical Space of the HE Variables
4. Maximum-Power Regime
4.1. Low Dissipation Heat Engine
4.2. Carnot-Like Model without Heat Leak (Endoreversible Model)
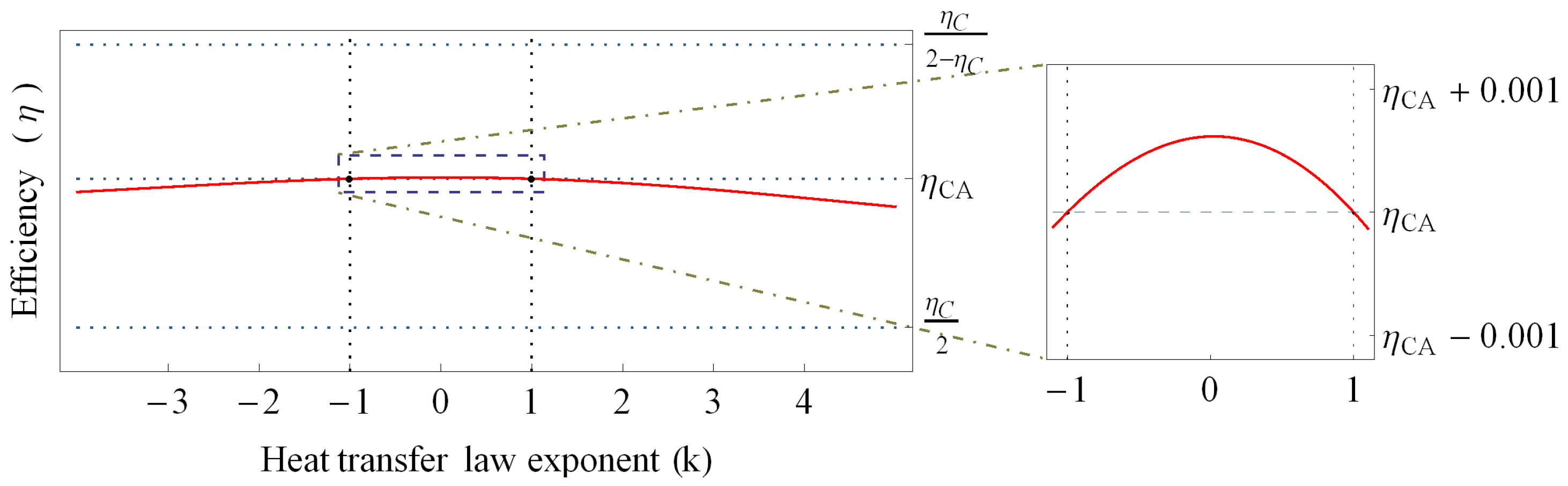
4.3. Carnot-Like Model with Heat Leak
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot Engine at Maximum Power Output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Vaudrey, A.; Lanzetta, F.; Feidt, M. H. B. Reitlinger and the origins of the Efficiency at Maximum Power formula for Heat Engines. J. Non-Equilib. Thermodyn. 2014, 39, 199–203. [Google Scholar] [CrossRef]
- Calvo Hernández, A.; Roco, J.M.M.; Medina, A.; Velasco, S.; Guzmán-Vargas, L. The maximum power efficiency 1-root tau: Research, education, and bibliometric relevance. Eur. Phys. J. Spec. Topics 2015, 224, 809–821. [Google Scholar] [CrossRef]
- Arias-Hernandez, L.A.; Angulo-Brown, F.; Paez-Hernandez, R.T. First-order irreversible thermodynamic approach to a simple energy converter. Phys. Rev. E 2008, 77, 011123. [Google Scholar] [CrossRef] [PubMed]
- Izumida, Y.; Okuda, K. Efficiency at maximum power of minimally nonlinear irreversible heat engines. Europhys. Lett. 2012, 97, 10004. [Google Scholar] [CrossRef]
- Apertet, Y.; Ouerdane, H.; Goupil, C.; Lecoeur, P. Irreversibilities and efficiency at maximum power of heat engines: The illustrative case of a thermoelectric generator. Phys. Rev. E 2012, 85, 031116. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Tu, Z.C. Efficiency at maximum power output of linear irreversible Carnot-like heat engines. Phys. Rev. E 2012, 85, 011127. [Google Scholar] [CrossRef] [PubMed]
- Apertet, Y.; Ouerdane, H.; Goupil, C.; Lecoeur, P. Efficiency at maximum power of thermally coupled heat engines. Phys. Rev. E 2012, 85, 041144. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Ayala, J.; Arias-Hernandez, L.A.; Angulo-Brown, F. Connection between maximum-work and maximum-power thermal cycles. Phys. Rev. E 2013, 88, 052142. [Google Scholar] [CrossRef] [PubMed]
- Sheng, S.; Tu, Z.C. Universality of energy conversion efficiency for optimal tight-coupling heat engines and refrigerators. J. Phys. A Math. Theor. 2013, 46, 402001. [Google Scholar] [CrossRef]
- Aneja, P.; Katyayan, H.; Johal, R.S. Optimal engine performance using inference for non-identical finite source and sink. Mod. Phys. Lett. B 2015, 29, 1550217. [Google Scholar] [CrossRef]
- Sheng, S.Q.; Tu, Z.C. Constitutive relation for nonlinear response and universality of efficiency at maximum power for tight-coupling heat engines. Phys. Rev. E 2015, 91, 022136. [Google Scholar] [CrossRef] [PubMed]
- Cleuren, B.; Rutten, B.; van den Broeck, C. Universality of efficiency at maximum power: Macroscopic manifestation of microscopic constraints. Eur. Phys. J. Spec. Topics 2015, 224, 879–889. [Google Scholar] [CrossRef]
- Izumida, Y.; Okuda, K. Linear irreversible heat engines based on the local equilibrium assumptions. New J. Phys. 2015, 17, 085011. [Google Scholar] [CrossRef]
- Long, R.; Liu, W. Efficiency and its bounds of minimally nonlinear irreversible heat engines at arbitrary power. Phys. Rev. E 2016, 94, 052114. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y. Optimizing work output for finite-sized heat reservoirs: Beyond linear response. Phys. Rev. E 2016, 93, 012120. [Google Scholar] [CrossRef] [PubMed]
- Schmiedl, T.; Seifert, U. Optimal Finite-Time Processes in Stochastic Thermodynamics. Phys. Rev. Lett. 2007, 98, 108301. [Google Scholar] [CrossRef] [PubMed]
- Tu, Z.C. Efficiency at maximum power of Feynman’s ratchet as a heat engine. J. Phys. A Math. Theor. 2008, 41, 312003. [Google Scholar] [CrossRef]
- Schmiedl, T.; Seifert, U. Efficiency at maximum power: An analytically solvable model for stochastic heat engines. Europhys. Lett. 2008, 81, 20003. [Google Scholar] [CrossRef]
- Schmiedl, T.; Seifert, U. Efficiency of molecular motors at maximum power. Europhys. Lett. 2008, 83, 30005. [Google Scholar] [CrossRef]
- Esposito, M.; Lindenberg, K.; van den Broeck, C. Universality of Efficiency at Maximum Power. Phys. Rev. Lett. 2009, 102, 130602. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Lindenberg, K.; van den Broeck, C. Thermoelectric efficiency at maximum power in a quantum dot. Europhys. Lett. 2009, 85, 60010. [Google Scholar] [CrossRef]
- Golubeva, N.; Imparato, A. Efficiency at Maximum Power of Interacting Molecular Machines. Phys. Rev. Lett. 2012, 109, 190602. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Wang, J.; He, J.; Ma, Y. Efficiency at maximum power of a heat engine working with a two-level atomic system. Phys. Rev. E 2013, 87, 042119. [Google Scholar] [CrossRef] [PubMed]
- Uzdin, R.; Kosloff, R. Universal features in the efficiency at maximum work of hot quantum Otto engines. Europhys. Lett. 2014, 108, 40001. [Google Scholar] [CrossRef]
- Curto-Risso, P.L.; Medina, A.; Calvo Hernández, A. Theoretical and simulated models for an irreversible Otto cycle. J. Appl. Phys. 2008, 104, 094911. [Google Scholar] [CrossRef]
- Curto-Risso, P.L.; Medina, A.; Calvo Hernández, A. Optimizing the operation of a spark ignition engine: Simulation and theoretical tools. J. Appl. Phys. 2009, 105, 094904. [Google Scholar] [CrossRef]
- Correa, L.A.; Palao, J.P.; Alonso, D. Internal dissipation and heat leaks in quantum thermodynamic cycles. Phys. Rev. E 2015, 92, 032136. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Salas, N.; López-Palacios, L.; Velasco, S.; Calvo Hernández, A. Optimization criteria, bounds, and efficiencies of heat engines. Phys. Rev. E 2010, 82, 051101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Huang, C.; Lin, G.; Chen, J. Universality of efficiency at unified trade-off optimization. Phys. Rev. E 2016, 93, 032152. [Google Scholar] [CrossRef] [PubMed]
- Iyyappan, I.; Ponmurugan, M. Thermoelectric energy converters under a trade-off figure of merit with broken time-reversal symmetry. arXiv 2016. [Google Scholar]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Arias-Hernández, L.A.; Angulo-Brown, F. A general property of endoreversible thermal engines. J. Appl. Phys. 1997, 81, 2973–2979. [Google Scholar] [CrossRef]
- Long, R.; Li, B.; Liu, Z.; Liu, W. Ecological analysis of a thermally regenerative electrochemical cycle. Energy 2016, 107, 95–102. [Google Scholar] [CrossRef]
- Esposito, M.; Kawai, R.; Lindenberg, K.; van den Broeck, C. Efficiency at Maximum Power of Low-Dissipation Carnot Engines. Phys. Rev. Lett. 2010, 105, 150603. [Google Scholar] [CrossRef] [PubMed]
- De Tomás, C.; Roco, J.M.M.; Calvo Hernández, A.; Wang, Y.; Tu, Z.C. Low-dissipation heat devices: Unified trade-off optimization and bounds. Phys. Rev. E 2013, 87, 012105. [Google Scholar] [CrossRef] [PubMed]
- Holubec, V.; Ryabov, A. Efficiency at and near maximum power of low-dissipation heat engines. Phys. Rev. E 2015, 92, 052125. [Google Scholar] [CrossRef] [PubMed]
- Holubec, V.; Ryabov, A. Erratum: Efficiency at and near maximum power of low-dissipation heat engines. Phys. Rev. E 2015, 93, 059904. [Google Scholar] [CrossRef] [PubMed]
- Holubec, V.; Ryabov, A. Maximum effciency of low-dissipation heat engines at arbitrary power. J. Stat. Mech. 2016, 2016, 073204. [Google Scholar] [CrossRef]
- Calvo Hernández, A.; Medina, A.; Roco, J.M.M. Time, entropy generation, and optimization in low-dissipation heat devices. New J. Phys. 2015, 17, 075011. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Calvo Hernández, A.; Roco, J.M.M. Irreversible and endoreversible behaviors of the LD-model for heat devices: The role of the time constraints and symmetries on the performance at maximum χ figure of merit. J. Stat. Mech. 2016, 2016, 073202. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Calvo Hernández, A.; Roco, J.M.M. From maximum power to a trade-off optimization of low-dissipation heat engines: Influence of control parameters and the role of entropy generation. Phys. Rev. E 2017, 95, 022131. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Wu, F.; Ma, Y.; He, J.; Wang, J.; Calvo Hernández, A.; Roco, J.M.M. Coefficient of performance for a low-dissipation Carnot-like refrigerator with nonadiabatic dissipation. Phys. Rev. E 2013, 88, 062115. [Google Scholar] [CrossRef] [PubMed]





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Ayala, J.; Roco, J.M.M.; Medina, A.; Calvo Hernández, A. Carnot-Like Heat Engines Versus Low-Dissipation Models. Entropy 2017, 19, 182. https://doi.org/10.3390/e19040182
Gonzalez-Ayala J, Roco JMM, Medina A, Calvo Hernández A. Carnot-Like Heat Engines Versus Low-Dissipation Models. Entropy. 2017; 19(4):182. https://doi.org/10.3390/e19040182
Chicago/Turabian StyleGonzalez-Ayala, Julian, José Miguel M. Roco, Alejandro Medina, and Antonio Calvo Hernández. 2017. "Carnot-Like Heat Engines Versus Low-Dissipation Models" Entropy 19, no. 4: 182. https://doi.org/10.3390/e19040182
APA StyleGonzalez-Ayala, J., Roco, J. M. M., Medina, A., & Calvo Hernández, A. (2017). Carnot-Like Heat Engines Versus Low-Dissipation Models. Entropy, 19(4), 182. https://doi.org/10.3390/e19040182








