Entropy in Natural Time and the Associated Complexity Measures
Abstract
:1. Introduction
2. Natural Time and Natural Time Entropy
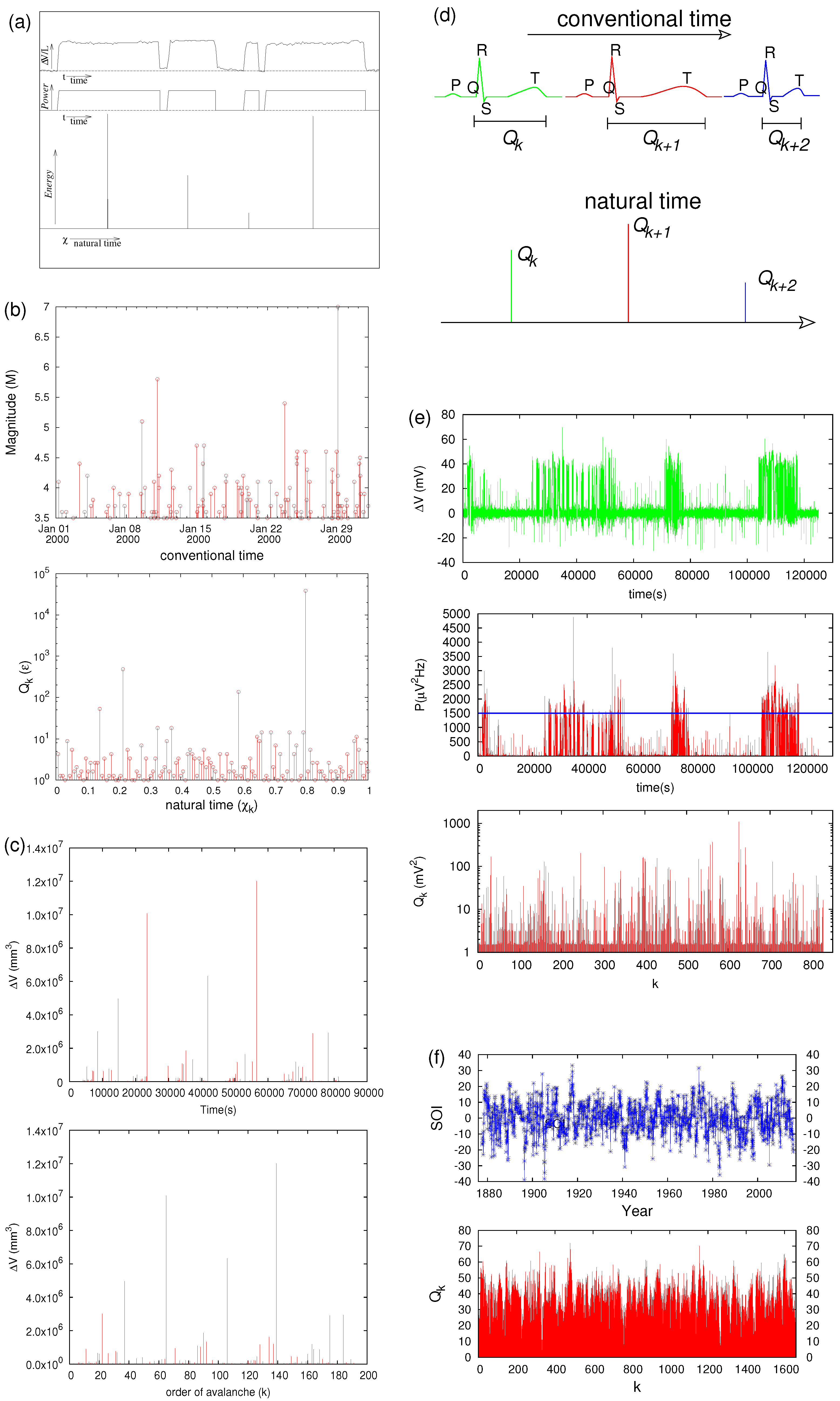
2.1. Analysis of Complex Time Series in Natural Time
2.2. Entropy in Natural Time
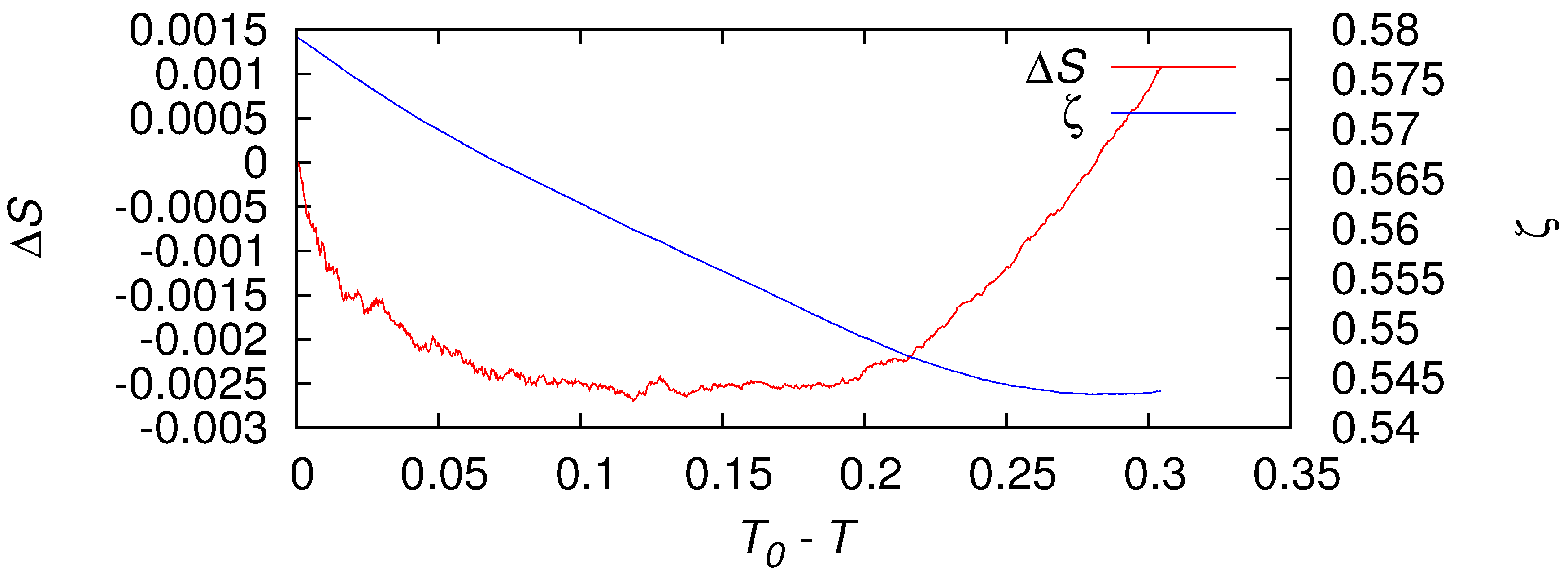
2.3. Complexity Measures Based on the Entropy in Natural Time
2.3.1. Complexity Measures Based on S
2.3.2. Complexity Measures Based on
3. Applications of the Natural Time Entropy in Various Complex Systems
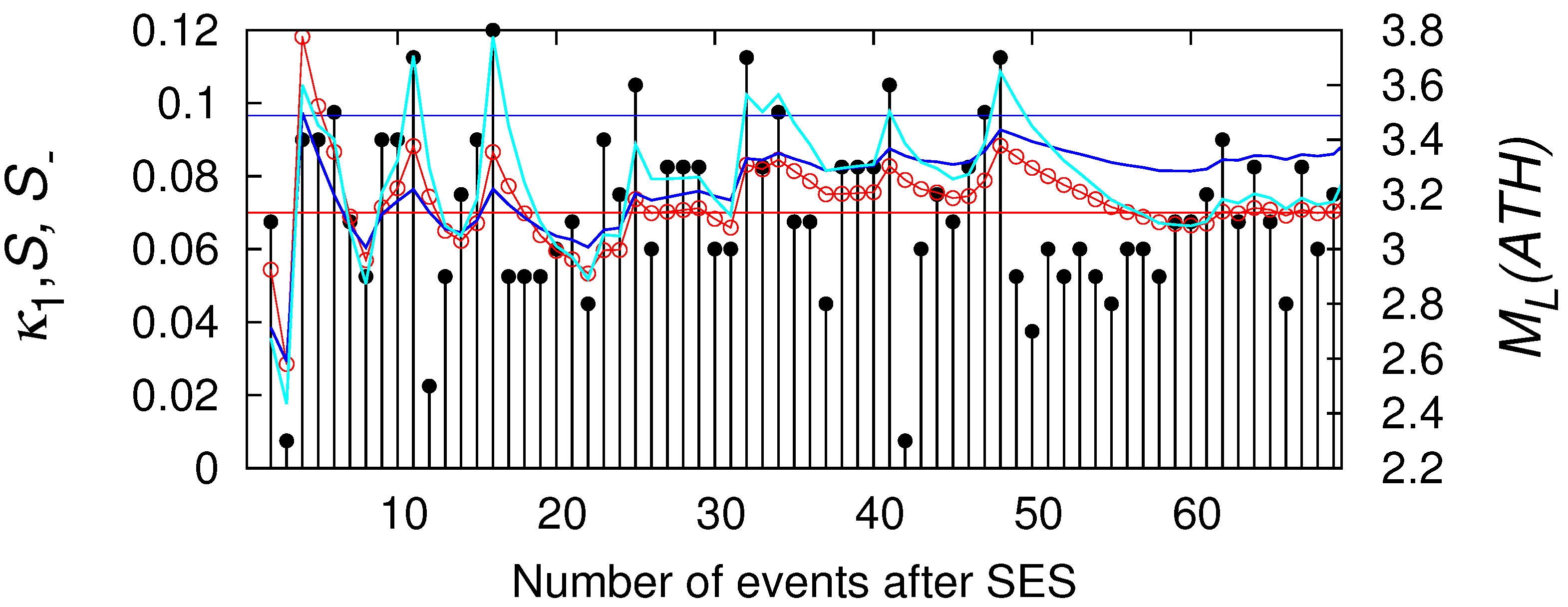
3.1. Results for the Electric and Magnetic Signals that Precede Rupture
3.2. Results for the Penetration of Magnetic Flux Avalanches in Type II Superconductors
3.3. Olami–Feder–Christensen Earthquake Model
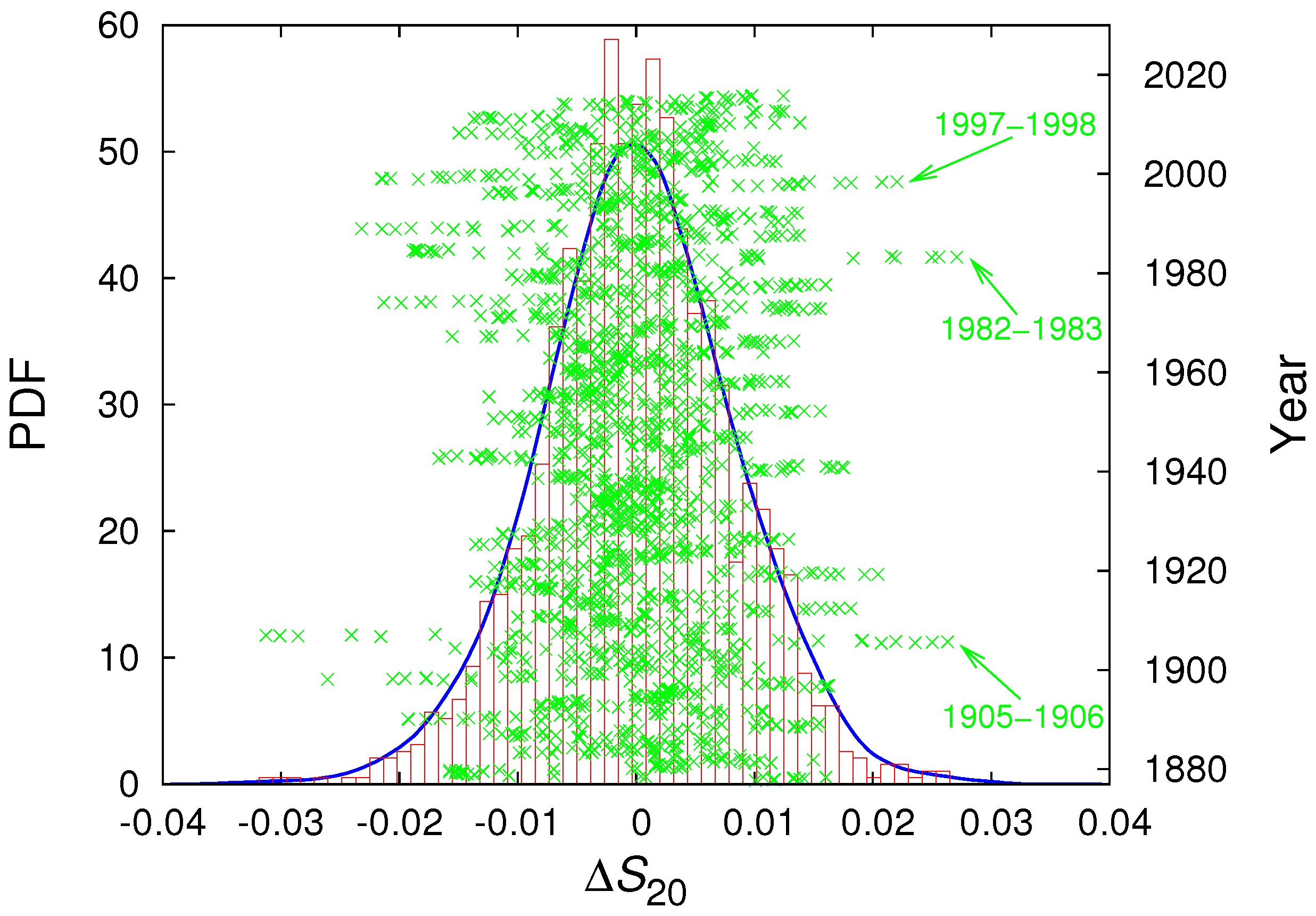
3.4. Earthquakes
3.5. Electrocardiograms
- When analyzing the RR and QRS intervals of the ECG in natural time, the subjects suffering from sudden cardiac death (SCD) violate [22] one or more of the four healthy limits related to , , and .
- When analyzing the QT intervals of the ECG in natural time for –8 heartbeats, the SCD subjects exhibit [26] almost one order of magnitude larger fluctuations than those of the healthy ones.
- When employing in the analysis of the RR and NN intervals of long duration ECG of SCD patients, the fluctuations of appear to maximize [27] during the last three hours before the ventricular fibrillation.
- When employing in the analysis of the RR and NN intervals of long-duration ECG, N, N together with (RR) and (NN) may allow the separation [27] of individuals into four classes: healthy, SCD, congestive heart failure (CHF) and atrial fibrillation (AF) individuals.
- The analysis suggested in the previous point is also valid [28] for models of healthy or patient heart dynamics.
- When analyzing the NN intervals of long-duration ECG recordings, the combination of with and enables (see Table 1 of [29]) the ternary distinction in healthy, SCD and CHF individuals.
3.6. Atmospheric Physics
3.6.1. Ozone Hole Dynamics over Antarctica
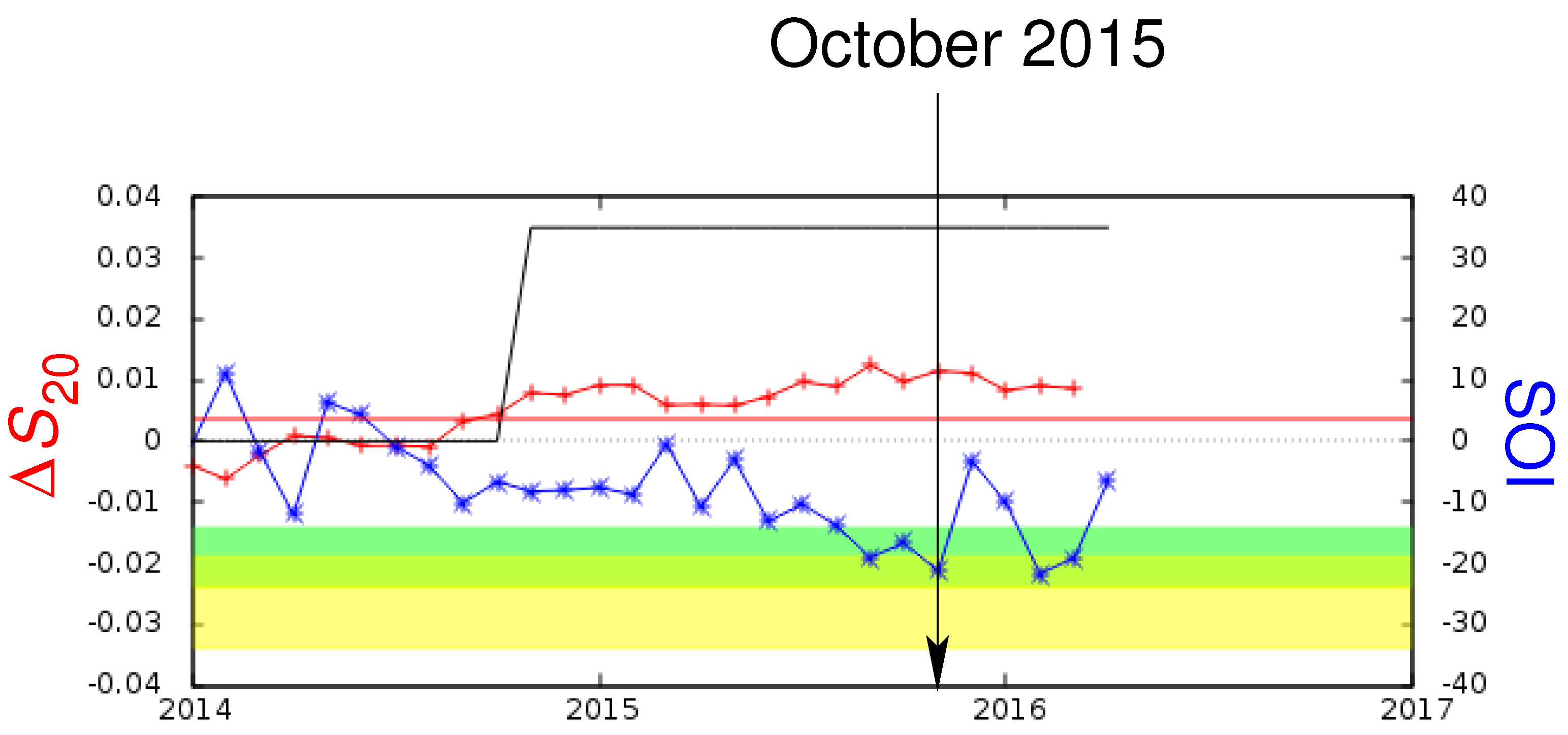
3.6.2. Forecasting the Intensity of El Niño/La Niña Southern Oscillation
4. Discussion and Perspectives
5. Materials and Methods
6. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | 3-dimensional |
| AF | Atrial fibrillation |
| CHF | Congestive heart failure |
| ECG | Electrocardiograms |
| EM | Electromagnetic |
| ENSO | El Niño/La Niña Southern Oscillation |
| EQ | Earthquake |
| GR | Gutenberg–Richter |
| OFC | Olami–Feder–Christensen |
| NTA | Natural time analysis |
| Probability density function | |
| SCD | Sudden cardiac death |
| SES | Seismic electric signals |
| SOC | Self-organized criticality |
| SOI | Southern Oscillation Index |
| ULF | Ultra-low frequency |
References
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef] [PubMed]
- Bak, P. How Nature Works: The Science of Self-Organized Criticality; Springer: New York, NY, USA, 1996. [Google Scholar]
- Jensen, H.J. Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Pruessner, G. Self-Organised Criticality Theory, Models and Characterisation; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Stanley, H.E. Scaling, universality, and renormalization: Three pillars of modern critical phenomena. Rev. Mod. Phys. 1999, 71, S358–S366. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Hausdorff, J.M.; Ivanov, P.C.; Peng, C.K.; Stanley, H.E. Fractal dynamics in physiology: Alterations with disease and aging. Proc. Natl. Acad. Sci. USA 2002, 99, 2466–2472. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Spatio-Temporal complexity aspects on the interrelation between Seismic Electric Signals and Seismicity. Practica of Athens Academy 2001, 76, 294–321. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Long-range correlations in the electric signals that precede rupture. Phys. Rev. E 2002, 66, 011902. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Seismic Electric Signals and Seismicity: On a tentative interrelation between their spectral content. Acta Geophys. Pol. 2002, 50, 337–354. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time. Precursory Seismic Electric Signals, Earthquakes and other Complex Time-Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Varotsos, P.; Alexopoulos, K. Thermodynamics of Point Defects and Their Relation with Bulk Properties; North Holland: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Attempt to distinguish electric signals of a dichotomous nature. Phys. Rev. E 2003, 68, 031106. [Google Scholar] [CrossRef] [PubMed]
- Olami, Z.; Feder, H.J.S.; Christensen, K. Self-organized criticality in a continuous, nonconservative cellular automaton modeling earthquakes. Phys. Rev. Lett. 1992, 68, 1244–1247. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.; Sarlis, N.; Skordas, E. On the Motivation and Foundation of Natural Time Analysis: Useful Remarks. Acta Geophys. 2016, 64, 841–852. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Long-range correlations in the electric signals the precede rupture: Further investigations. Phys. Rev. E 2003, 67, 021109. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.; Sarlis, N.V.; Skordas, E.S.; Uyeda, S.; Kamogawa, M. Natural time analysis of critical phenomena. Proc. Natl. Acad. Sci. USA 2011, 108, 11361–11364. [Google Scholar] [CrossRef] [PubMed]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Nagao, T.; Kamogawa, M.; Uyeda, S. Spatiotemporal variations of seismicity before major earthquakes in the Japanese area and their relation with the epicentral locations. Proc. Natl. Acad. Sci. USA 2015, 112, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Lőrincz, K.A.; Wijngaarden, R.J. Edge effect on the power law distribution of granular avalanches. Phys. Rev. E 2007, 76, 040301. [Google Scholar] [CrossRef] [PubMed]
- Lőrincz, K.A. Avalanche Dynamics in a Three-Dimensional Pile of Rice. Ph.D. Thesis, Vrije Universiteit, Amsterdam, The Netherlands, 2008. [Google Scholar]
- Troup, A.J. The ‘southern oscillation’. Q. J. R. Meteorol. Soc. 1965, 91, 490–506. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Entropy in the natural time domain. Phys. Rev. E 2004, 70, 011106. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Tanaka, H.K.; Skordas, E.S. Some properties of the entropy in the natural time. Phys. Rev. E 2005, 71, 032102. [Google Scholar] [CrossRef] [PubMed]
- Lesche, B. Instabilities of Renyi entropies. J. Stat. Phys. 1982, 27, 419–422. [Google Scholar] [CrossRef]
- Lesche, B. Renyi entropies and observables. Phys. Rev. E 2004, 70, 017102. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Natural entropy fluctuations discriminate similar-looking electric signals emitted from systems of different dynamics. Phys. Rev. E 2005, 71, 011110. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Identifying sudden cardiac death risk and specifying its occurrence time by analyzing electrocardiograms in natural time. Appl. Phys. Lett. 2007, 91, 064106. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Heart rate variability in natural time and 1/f “noise”. EPL 2009, 87, 18003. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Christopoulos, S.R.G.; Bemplidaki, M.M. Change ΔS of the entropy in natural time under time reversal: Complexity measures upon change of scale. EPL 2015, 109, 18002. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. Scale-specific order parameter fluctuations of seismicity in natural time before mainshocks. EPL 2011, 96, 59002. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. The use of the Entropy in the natural time-domain to distinguish electric signals. Practica of Athens Academy 2003, 78, 281–298. [Google Scholar]
- Varotsos, P.; Alexopoulos, K. Physical Properties of the variations of the electric field of the earth preceding earthquakes, I. Tectonophysics 1984, 110, 73–98. [Google Scholar] [CrossRef]
- Varotsos, P.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals. Tectonophysics 1991, 188, 321–347. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals, II. Tectonophysics 1993, 224, 1–37. [Google Scholar] [CrossRef]
- Varotsos, P. The Physics of Seismic Electric Signals; TERRAPUB: Tokyo, Japan, 2005. [Google Scholar]
- Varotsos, P.; Alexopoulos, K.; Lazaridou-Varotsou, M.; Nagao, T. Earthquake predictions issued in Greece by seismic electric signals since February 6, 1990. Tectonophysics 1993, 224, 269–288. [Google Scholar] [CrossRef]
- Varotsos, P.; Eftaxias, K.; Lazaridou, M.; Nomicos, K.; Sarlis, N.; Bogris, N.; Makris, J.; Antonopoulos, G.; Kopanas, J. Recent earthquake prediction results in Greece based on the observation of Seismic Electric Signals. Acta Geophys. Pol. 1996, 44, 301–327. [Google Scholar]
- Uyeda, S.; Kamogawa, M. The Prediction of Two Large Earthquakes in Greece. Eos Trans. Am. Geophys. Union 2008, 89, 362–363. [Google Scholar] [CrossRef]
- Uyeda, S.; Kamogawa, M. Comment on ‘The Prediction of Two Large Earthquakes in Greece’. Eos Trans. Am. Geophys. Union 2010, 91, 162–163. [Google Scholar] [CrossRef]
- Lazaridou-Varotsos, M.S. Earthquake Prediction by Seismic Electric Signals: The Success of the VAN Method Over Thirty Years; Springer Praxis Books: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Uyeda, S.; Nagao, T.; Orihara, Y.; Yamaguchi, T.; Takahashi, I. Geoelectric potential changes: Possible precursors to earthquakes in Japan. Proc. Natl. Acad. Sci. USA 2000, 97, 4561–4566. [Google Scholar] [CrossRef] [PubMed]
- Uyeda, S.; Hayakawa, M.; Nagao, T.; Molchanov, O.; Hattori, K.; Orihara, Y.; Gotoh, K.; Akinaga, Y.; Tanaka, H. Electric and magnetic phenomena observed before the volcano-seismic activity in 2000 in the Izu Island Region, Japan. Proc. Natl. Acad. Sci. USA 2002, 99, 7352–7355. [Google Scholar] [CrossRef] [PubMed]
- Orihara, Y.; Kamogawa, M.; Nagao, T.; Uyeda, S. Independent component analysis of geoelectric field data in the northern Nagano, Japan. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2009, 85, 435–442. [Google Scholar] [CrossRef] [PubMed]
- Uyeda, S.; Kamogawa, M.; Tanaka, H. Analysis of electrical activity and seismicity in the natural time domain for the volcanic-seismic swarm activity in 2000 in the Izu Island region, Japan. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Orihara, Y.; Kamogawa, M.; Nagao, T.; Uyeda, S. Preseismic anomalous telluric current signals observed in Kozu-shima Island, Japan. Proc. Natl. Acad. Sci. USA 2012, 109, 19125–19128. [Google Scholar] [CrossRef] [PubMed]
- Uyeda, S.; Al-Damegh, E.; Dologlou, E.; Nagao, T. Some relationship between VAN seismic electric signals (SES) and earthquake parameters. Tectonophysics 1999, 304, 41–55. [Google Scholar] [CrossRef]
- Sarlis, N.; Lazaridou, M.; Kapiris, P.; Varotsos, P. Numerical Model of the Selectivity Effect and ΔV/L criterion. Geophys. Res. Lett. 1999, 26, 3245–3248. [Google Scholar] [CrossRef]
- Kondo, S.; Uyeda, S.; Nagao, T. The selectivity of the Ioannina VAN station. J. Geodyn. 2002, 33, 433–461. [Google Scholar] [CrossRef]
- Orihara, Y.; Noda, Y.; Nagao, T.; Uyeda, S. A possible case of SES selectivity at Kozu-shima Island. J. Geodyn. 2002, 33, 425–432. [Google Scholar] [CrossRef]
- Huang, Q.; Lin, Y. Selectivity of seismic electric signal (SES) of the 2000 Izu earthquake swarm: A 3D FEM numerical simulation model. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2010, 86, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.; Alexopoulos, K.; Nomicos, K. Seismic Electric Currents. Practica of Athens Academy 1981, 56, 277–286. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Lazaridou, M.; Kapiris, P. Transmission of stress induced electric signals in dielectric media. J. Appl. Phys. 1998, 83, 60–70. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Lazaridou, M. Transmission of stress induced electric signals in dielectric media. Part II. Acta Geophys. Pol. 2000, 48, 141–177. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, E. Transmission of stress induced electric signals in dielectric media. Part III. Acta Geophys. Pol. 2000, 48, 263–297. [Google Scholar]
- Varotsos, P.V.; Sarlis, N.V.; Skordas, E.S. Electric Fields that “arrive” before the time derivative of the magnetic field prior to major earthquakes. Phys. Rev. Lett. 2003, 91, 148501. [Google Scholar] [CrossRef] [PubMed]
- Sarlis, N.; Varotsos, P. Magnetic field near the outcrop of an almost horizontal conductive sheet. J. Geodyn. 2002, 33, 463–476. [Google Scholar] [CrossRef]
- Skordas, E.; Sarlis, N. On the anomalous changes of seismicity and geomagnetic field prior to the 2011 9.0 Tohoku earthquake. J. Asian Earth Sci. 2014, 80, 161–164. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, S.; Lazaridou, M. Additional evidence on some relationship between Seismic Electric Signals(SES) and earthquake focal mechanism. Tectonophysics 2006, 412, 279–288. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Tanaka, H.K.; Lazaridou, M.S. Entropy of seismic electric signals: Analysis in the natural time under time reversal. Phys. Rev. E 2006, 73, 031114. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Detrended fluctuation analysis of the magnetic and electric field variations that precede rupture. Chaos 2009, 19, 023114. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Rojas, A.; Telesca, L.; Angulo-Brown, F. Entropy of geoelectrical time series in the natural time domain. Nat. Hazards Earth Syst. Sci. 2011, 11, 219–225. [Google Scholar] [CrossRef]
- Varotsos, P. A review and analysis of electromagnetic precursory phenomena. Acta Geophys. Pol. 2001, 49, 1–42. [Google Scholar]
- Xu, G.; Han, P.; Huang, Q.; Hattori, K.; Febriani, F.; Yamaguchi, H. Anomalous behaviors of geomagnetic diurnal variations prior to the 2011 off the Pacific coast of Tohoku earthquake (Mw9.0). J. Asian Earth Sci. 2013, 77, 59–65. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Xu, G.; Ashida, R.; Chen, C.H.; Febriani, F.; Yamaguchi, H. Further investigations of geomagnetic diurnal variations associated with the 2011 off the Pacific coast of Tohoku earthquake (Mw 9.0). J. Asian Earth Sci. 2015, 114, 321–326. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Huang, Q.; Hirooka, S.; Yoshino, C. Spatiotemporal characteristics of the geomagnetic diurnal variation anomalies prior to the 2011 Tohoku earthquake (Mw 9.0) and the possible coupling of multiple pre-earthquake phenomena. J. Asian Earth Sci. 2016, 129, 13–21. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Potirakis, S.; Eftaxias, K. Criticality features in ULF magnetic fields prior to the 2011 Tohoku earthquake. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2015, 91, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Potirakis, S.M.; Karadimitrakis, A.; Eftaxias, K. Natural time analysis of critical phenomena: The case of pre-fracture electromagnetic emissions. Chaos 2013, 23, 023117. [Google Scholar] [CrossRef] [PubMed]
- Potirakis, S.M.; Contoyiannis, Y.; Eftaxias, K.; Koulouras, G.; Nomicos, C. Recent Field Observations Indicating an Earth System in Critical Condition Before the Occurrence of a Significant Earthquake. IEEE Geosci. Remote Sens. Lett. 2015, 12, 631–635. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Contoyiannis, Y.; Melis, N.S.; Kopanas, J.; Antonopoulos, G.; Balasis, G.; Kontoes, C.; Nomicos, C.; Eftaxias, K. Recent seismic activity at Cephalonia (Greece): A study through candidate electromagnetic precursors in terms of non-linear dynamics. Nonlinear Process. Geophys. 2016, 23, 223–240. [Google Scholar] [CrossRef]
- Potirakis, S.; Eftaxias, K.; Schekotov, A.; Yamaguchi, H.; Hayakawa, M. Criticality features in ultra-low frequency magnetic fields prior to the 2013 M6.3 Kobe earthquake. Ann. Geophys. 2016, 59, S0317. [Google Scholar]
- De Gennes, P.G. Superconductivity of Metals and Alloys; Addison-Wesley: New York, NY, USA, 1966. [Google Scholar]
- Campbell, A.M.; Evetts, J.E. Flux vortices and transport currents in type II superconductors. Adv. Phys. 2001, 50, 1249. [Google Scholar] [CrossRef]
- Altshuler, E.; Johansen, T.H. Colloquium: Experiments in vortex avalanches. Rev. Mod. Phys. 2004, 76, 471. [Google Scholar] [CrossRef]
- Welling, M.S.; Aegerter, C.M.; Wijngaarden, R.J. Self-organized criticality induced by quenched disorder: Experiments on flux avalanches in NbHx films. Phys. Rev. B 2005, 71, 104515. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Varotsos, P.A.; Skordas, E.S. Flux avalanches in YBa2Cu3O7-x films and rice piles: Natural time domain analysis. Phys. Rev. B 2006, 73, 054504. [Google Scholar] [CrossRef]
- Sarlis, N.; Skordas, E.; Varotsos, P. Similarity of fluctuations in systems exhibiting Self-Organized Criticality. EPL 2011, 96, 28006. [Google Scholar] [CrossRef]
- Aegerter, C.M.; Welling, M.S.; Wijngaarden, R.J. Self-organized criticality in the Bean state in YBa2Cu3O7-x thin films. Europhys. Lett. 2004, 65, 753. [Google Scholar] [CrossRef]
- Aegerter, C.M.; Gunther, R.; Wijngaarden, R.J. Avalanche dynamics, surface roughening, and self-organized criticality: Experiments on a three-dimensional pile of rice. Phys. Rev. E 2003, 67, 051306. [Google Scholar] [CrossRef] [PubMed]
- Aegerter, C.M.; Lőrincz, K.A.; Welling, M.S.; Wijngaarden, R.J. Extremal dynamics and the approach to the critical state: Experiments on a three dimensional pile of rice. Phys. Rev. Lett. 2004, 92, 058702. [Google Scholar] [CrossRef] [PubMed]
- De Sousa Vieira, M. Simple deterministic self-organized critical system. Phys. Rev. E 2000, 61, R6056–R6059. [Google Scholar] [CrossRef]
- Davidsen, J.; Schuster, H.G. Simple model for 1/fα noise. Phys. Rev. E 2002, 65, 026120. [Google Scholar] [CrossRef] [PubMed]
- Ramos, O.; Altshuler, E.; Måløy, K.J. Quasiperiodic Events in an Earthquake Model. Phys. Rev. Lett. 2006, 96, 098501. [Google Scholar] [CrossRef] [PubMed]
- Burridge, R.; Knopoff, L. Model and theoretical seismicity. Bull. Seismol. Soc. Am. 1967, 57, 341–371. [Google Scholar]
- Braun, O.M.; Barel, I.; Urbakh, M. Dynamics of Transition from Static to Kinetic Friction. Phys. Rev. Lett. 2009, 103, 194301. [Google Scholar] [CrossRef] [PubMed]
- Ben-David, O.; Rubinstein, S.M.; Fineberg, J. Slip-stick and the evolution of frictional strength. Nature 2010, 463, 76–79. [Google Scholar] [CrossRef] [PubMed]
- Helmstetter, A.; Hergarten, S.; Sornette, D. Properties of foreshocks and aftershocks of the nonconservative self-organized critical Olami–Feder–Christensen model. Phys. Rev. E 2004, 70, 046120. [Google Scholar] [CrossRef] [PubMed]
- De Carvalho, J.X.; Prado, C.P.C. Self-Organized Criticality in the Olami–Feder–Christensen Model. Phys. Rev. Lett. 2000, 84, 4006–4009. [Google Scholar] [CrossRef] [PubMed]
- Miller, G.; Boulter, C.J. Measurements of criticality in the Olami–Feder–Christensen model. Phys. Rev. E 2002, 66, 016123. [Google Scholar] [CrossRef] [PubMed]
- Pérez, C.J.; Corral, A.; Díaz-Guilera, A.; Christensen, K.; Arenas, A. On Self-Organized Criticality and Synchronization in Lattice Models of Coupled Dynamical Systems. Int. J. Mod. Phys. B 1996, 10, 1111–1151. [Google Scholar] [CrossRef]
- Mousseau, N. Synchronization by Disorder in Coupled Systems. Phys. Rev. Lett. 1996, 77, 968–971. [Google Scholar] [CrossRef] [PubMed]
- Jánosia, I.M.; Kertész, J. Self-organized criticality with and without conservation. Physica A 1993, 200, 179–188. [Google Scholar] [CrossRef]
- Ceva, H. Influence of defects in a coupled map lattice modeling earthquakes. Phys. Rev. E 1995, 52, 154–158. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Current Methods of Lattice Defect Analysis Using Dilatometry and Self-Diffusion. Critical Review and Proposals. Physica Status Solidi (b) 1982, 110, 9–31. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Calculation of the migration volume of vacancies in ionic solids from macroscopic parameters. Physica Status Solidi (a) 1978, 47, 133–136. [Google Scholar] [CrossRef]
- Kostopoulos, D.; Varotsos, P.; Mourikis, S. The conductivity of crystalline NaI. Can. J. Phys. 1975, 53, 1318–1320. [Google Scholar] [CrossRef]
- Varotsos, P. Point defect parameters in β-PbF2 revisited. Solid State Ionics 2008, 179, 438–441. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K.; Nomicos, K. Comments on the pressure variation of the Gibbs energy for bound and unbound defects. Physica Status Solidi (b) 1982, 111, 581–590. [Google Scholar] [CrossRef]
- Peixoto, T.P.; Davidsen, J. Network of recurrent events for the Olami–Feder–Christensen model. Phys. Rev. E 2008, 77, 066107. [Google Scholar] [CrossRef] [PubMed]
- Pepke, S.L.; Carlson, J.M. Predictability of self-organizing systems. Phys. Rev. E 1994, 50, 236–242. [Google Scholar] [CrossRef]
- Hergarten, S.; Neugebauer, H.J. Foreshocks and Aftershocks in the Olami–Feder–Christensen Model. Phys. Rev. Lett. 2002, 88, 238501. [Google Scholar] [CrossRef] [PubMed]
- Wissel, F.; Drossel, B. Transient and stationary behavior of the Olami–Feder–Christensen model. Phys. Rev. E 2006, 74, 066109. [Google Scholar] [CrossRef] [PubMed]
- Lise, S.; Paczuski, M. Self-organized criticality and universality in a nonconservative earthquake model. Phys. Rev. E 2001, 63, 036111. [Google Scholar] [CrossRef] [PubMed]
- Gutenberg, B.; Richter, C.F. Magnitude and energy of earthquakes. Ann. Geophys. 1956, 9, 1–15. [Google Scholar]
- Rundle, J.B.; Turcotte, D.L.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 2003, 41, 1019. [Google Scholar] [CrossRef]
- Kanamori, H. Quantification of Earthquakes. Nature 1978, 271, 411–414. [Google Scholar] [CrossRef]
- Bach, M.; Wissel, F.; Drossel, B. Olami–Feder–Christensen model with quenched disorder. Phys. Rev. E 2008, 77, 067101. [Google Scholar] [CrossRef] [PubMed]
- Lippiello, E.; Godano, C.; de Arcangelis, L. Dynamical Scaling in Branching Models for Seismicity. Phys. Rev. Lett. 2007, 98, 098501. [Google Scholar] [CrossRef] [PubMed]
- Lippiello, E.; de Arcangelis, L.; Godano, C. Influence of Time and Space Correlations on Earthquake Magnitude. Phys. Rev. Lett. 2008, 100, 038501. [Google Scholar] [CrossRef] [PubMed]
- Bottiglieri, M.; de Arcangelis, L.; Godano, C.; Lippiello, E. Multiple-Time Scaling and Universal Behavior of the Earthquake Interevent Time Distribution. Phys. Rev. Lett. 2010, 104, 158501. [Google Scholar] [CrossRef] [PubMed]
- Lippiello, E.; Godano, C.; de Arcangelis, L. The earthquake magnitude is influenced by previous seismicity. Geophys. Res. Lett. 2012, 39, L05309. [Google Scholar] [CrossRef]
- Lennartz, S.; Bunde, A.; Turcotte, D.L. Modelling seismic catalogues by cascade models: Do we need long-term magnitude correlations? Geophys. J. Int. 2011, 184, 1214–1222. [Google Scholar] [CrossRef]
- Hergarten, S.; Krenn, R. Synchronization and desynchronization in the Olami–Feder–Christensen earthquake model and potential implications for real seismicity. Nonlinear Process. Geophys. 2011, 18, 635–642. [Google Scholar] [CrossRef]
- Bonachela, J.A.; Mũnoz, M.A. Self-organization without conservation: True or just apparent scale-invariance? J. Stat. Mech. Theory Exp. 2009, 2009, P09009. [Google Scholar] [CrossRef]
- Yang, X.; Du, S.; Ma, J. Do Earthquakes Exhibit Self-Organized Criticality? Phys. Rev. Lett. 2004, 92, 228501. [Google Scholar] [CrossRef] [PubMed]
- Sarlis, N.; Skordas, E.; Varotsos, P. The change of the entropy in natural time under time-reversal in the Olami–Feder–Christensen earthquake model. Tectonophysics 2011, 513, 49–53. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Tanaka, H.K.; Lazaridou, M.S. Attempt to distinguish long-range temporal correlations from the statistics of the increments by natural time analysis. Phys. Rev. E 2006, 74, 021123. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A. What happened before the last five strong earthquakes in Greece. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2006, 82, 86–91. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Fluctuations, under time reversal, of the natural time and the entropy distinguish similar looking electric signals of different dynamics. J. Appl. Phys. 2008, 103, 014906. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. Non-extensive and natural time analysis of seismicity before the Mw6.4, October 12, 2013 earthquake in the South West segment of the Hellenic Arc. Physica A 2014, 414, 163–173. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Hloupis, G. Multiresolution wavelets and natural time analysis before the January–February 2014 Cephalonia (Mw6.1 & 6.0) sequence of strong earthquake events. Phys. Chem. Earth Parts A/B/C 2015, 85–86, 201–209. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Seismic Electric Signals and 1/f noise in natural time. arXiv, 2007; arXiv:0711.3766v3. [Google Scholar]
- Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S.; Varotsos, P.A. Investigation of seismicity after the initiation of a Seismic Electric Signal activity until the main shock. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2008, 84, 331–343. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mictus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet—Components of a new research resource for complex physiologic signals. Circulation 2000, 101, E215. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, C.; Tzanis, C. A new tool for the study of the ozone hole dynamics over Antarctica. Atmos. Environ. 2012, 47, 428–434. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Tzanis, C.; Cracknell, A.P. Precursory signals of the major El Niño Southern Oscillation events. Theor. Appl. Climatol. 2016, 124, 903–912. [Google Scholar] [CrossRef]
- Varotsos, C.; Tzanis, C. A new El Niño-Southern Oscillation forecasting tool based on Southern Oscillation Index. Atmos. Chem. Phys. Discuss. 2012, 12, 17443–17463. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Tzanis, C.G.; Sarlis, N.V. On the progress of the 2015–2016 El Niño event. Atmos. Chem. Phys. 2016, 16, 2007–2011. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Tzanis, C.G.; Sarlis, N.V. On the progress of the 2015–2016 El Niño event. Atmos. Chem. Phys. Discuss. 2015, 15, 35787–35797. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Seismic Electric Signals: An additional fact showing their physical interconnection with seismicity. Tectonophysics 2013, 589, 116–125. [Google Scholar] [CrossRef]
- Tanaka, H.K.; Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. A plausible universal behaviour of earthquakes in the natural time-domain. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2004, 80, 283–289. [Google Scholar] [CrossRef]
- Papasimakis, N.; Pallikari, F. Correlated and uncorrelated heart rate fluctuations during relaxing visualization. EPL 2010, 90, 48003. [Google Scholar] [CrossRef]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarlis, N.V. Entropy in Natural Time and the Associated Complexity Measures. Entropy 2017, 19, 177. https://doi.org/10.3390/e19040177
Sarlis NV. Entropy in Natural Time and the Associated Complexity Measures. Entropy. 2017; 19(4):177. https://doi.org/10.3390/e19040177
Chicago/Turabian StyleSarlis, Nicholas V. 2017. "Entropy in Natural Time and the Associated Complexity Measures" Entropy 19, no. 4: 177. https://doi.org/10.3390/e19040177
APA StyleSarlis, N. V. (2017). Entropy in Natural Time and the Associated Complexity Measures. Entropy, 19(4), 177. https://doi.org/10.3390/e19040177





