Abstract
Numerical investigation of the effects of magnetic field strength, thermal radiation, Joule heating, and viscous heating on a forced convective flow of a non-Newtonian, incompressible power law fluid in an axisymmetric stretching sheet with variable temperature wall is accomplished. The power law shear thinning viscosity-shear rate model for the anisotropic solutions and the Rosseland approximation for the thermal radiation through a highly absorbing medium are considered. The temperature dependent heat sources, Joule heating, and viscous heating are considered as the source terms in the energy balance. The non-dimensional boundary layer equations are solved numerically in terms of similarity variable. A parameter study on the Nusselt number, viscous components of entropy generation, and thermal components of entropy generation in fluid is performed as a function of thermal radiation parameter (0 to 2), Brinkman number (0 to 10), Prandtl number (0 to 10), Hartmann number (0 to 1), power law index (0 to 1), and heat source coefficient (0 to 0.1).
1. Introduction
The study of the axisymmetric flow of a power-law fluid past a stretching sheet from the perspective of the thermodynamic and forced convective heat transfer aspects happens in many applications such as the polymer industry [1], metallic plate cooling [2], plastic sheet drawing [3], drawing of wire and fiber [4], hot rolling [5], paper fabrication [6], aerodynamics [7], etc. The heat transfer occurrence is an important criterion in such applications as the nature of the final product is dependent on the heat transfer rate [8,9,10]. There are some studies that consider the control of the temperature and velocity fields for the axisymmetric power-law fluid flow of a past a stretching sheet without allowing for the thermal radiation [11,12], whereas on the other hand, heat transfer by concurrent radiation and convection is significant in numerous circumstances [13,14].
Considering its scientific applications, Crane [15] initiated the study on boundary layer flow in cylindrical coordinates owing to a stretching cylinder. Crane’s work was advanced in heat transmission by Wang [16], viscid effects by Burde [17] and Ishak [18,19], stagnation point special effects by Mastroberardino [20] and Weidman and Ali [21], slip effects by Wang and Ng [22], oscillation by Munawar et al. [23], hydromagnetic effects and permeable wall by Vajravelu et al. [24], haemodynamic applications by Joodaki et al. [25] and Forman et al. [26,27], optimum length of artery rings [28], stretching wall in vascular development by Jones [29], wall-blood interactions by Das et al. [30], etc.
Entropy generation effects in polymer applications [31,32,33] due to flow and heat transfer over stretching flat plates in Cartesian coordinates have been investigated by numerous researchers [34,35,36,37,38,39,40,41]. On the other hand, a smaller number of investigations are considered in collected works concerning the study of entropy generation effects in flow over stretching surfaces in cylindrical coordinates [42,43] in comparison with Cartesian coordinate studies.
In the current paper, an optically thick (highly absorbing medium) incompressible power law fluid passes a radially stretching sheet. The radiative properties of various polymers are presented in [44]. The index of refraction as a function of wavelength for various polymers was decreased uniformly by increases of the wavelength and the index of refraction as a function of temperature for PMMA (λ = 589.3 nm) and a critical point was observed at 105 °C [44]. In addition, ultraviolet light transmission through PMMA increased with the increase in wavelength and the transmissivity of CAB, PC and glass as a function of wavelength is changed through all wavelength domains.
The mechanical and thermo-physical properties of polymer liquid crystals used in this manuscript were obtained from [45] with respect to the Rosseland approximation [46]. The numerical procedure from standard routines [47] is compared with previous works on MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat [48,49,50,51]. Various fluids such as Sisko Fluid [52] are investigated with various models such as the multiscale [53] and hybrid molecular continuum methods [54,55], in porous media [56] and parallel plate confining boundaries [57] and slip law effects [58] with nanoparticles [59]. The deriving forces of some flows come from propagation of viscous gravity flows [60,61] with the opposing force of a porous media matrix [60,62,63,64,65,66,67,68,69,70,71,72,73,74].
Considering all the above, the goal of the present article was to investigate entropy production in a steady state fully developed forced convection incompressible flow over an axisymmetric stretching sheet such that the stretching wall is subjected to different wall temperatures and the Rosseland approximation model. The effects of thermal radiation coefficient, Prantdl number, Hartmann number, and Brinkmann number on entropy generation are investigated numerically and the results are interpreted using graphs.
2. Governing Equations
Shrinkage is the contraction of a molded part as it cools after injection. Most of this is inherent shrinkage that occurs in the mold process while cooling and a small amount of shrinkage occurs after ejection as the part continues to cool, especially for Delrin (an acetal homopolymer with an excellent balance of properties that bridges the gap between metal and plastic). Stretching, as an opposite phenomena to control the shrinkage and cure the residual stress, is important in practice and applications such as injection and mold opening tolerance [44,45]. Typical shrink rates vary between 0.001/in/in and 0.020/in/in with the most common being around 0.006/in/in (ABS = 0.005–0.007, acetal = 0.018–0.025, acrylic = 0.002–0.008, nylon 6 = 0.006–0.014, nylon 66 = 0.012–0.018, polycarbonate = 0.005–0.007, PET = 0.005–0.012, polyethylene = 0.015–0.050, polypropylene = 0.010–0.025, PP (30% glass) = 0.004–0.0045, polystyrene = 0.002–0.006, PS (30% glass) = 0.0005–0.0010, PVC = 0.003–0.0008). In addition, an asymmetrical shrinkage resin is used for common tolerances ranges of isotropic plastics. For example polymers filled with long glass fibers which shrink more in the cross (transverse) direction than the longitudinal (flow) direction should not be used for round holes and core pins. To study the critical thermodynamics aspects of laminar power law flow over an infinitely radially stretching sheet, an axisymmetric 2-dimensional sketch as shown in Figure 1 is well considered. The fluid is considered non-Newtonian and incompressible. As exemplified, the fluid in contact with the surface of the non-permeable stretching sheet will travel along with the sheet without any slippage.
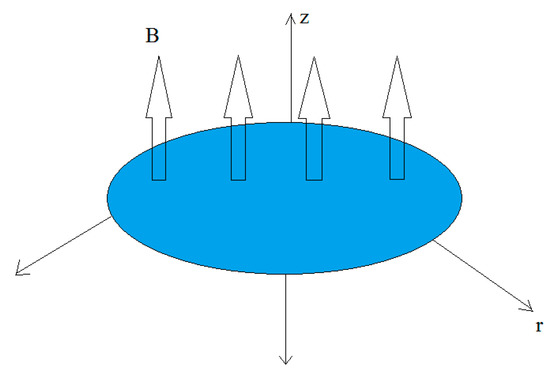
Figure 1.
Schematic representation of the considered problem.
Meanwhile some polymers have outstanding optical properties and are easy to mold and form into any shape; they are frequently used to substitute transparent materials, for instance inorganic glass. Polymers have been introduced into a diversity of applications, for instance automotive headlights, signal light covers, optical fibers, imitation jewelry, chandeliers, toys and home appliances.
Organic materials like polymers are also an excellent choice for high impact applications where inorganic materials such as glass would easily shatter. Conversely, as a result of the difficulties encountered in upholding dimensional stability, they are not apt for precision optical needs. Additional drawbacks include lower scratch resistance, when associated to inorganic glasses, making them impractical for certain applications, for instance automotive windshields. The r- and z-components of the velocity at any point are denoted by v and u; while the stretching sheet (z = 0) is maintained at the uniform temperatures Tw, respectively. The temperature difference between the medium temperature, T∞, and the stretching sheet, Tw, is also assumed to be high enough to induce heat transfer due to radiation. Since an infinitely large medium is assumed, the flow velocity at far distances from the plate is assumed to be zero. In cylindrical coordinates the continuity is (by the assumptions of vφ = 0 and vzz ≫ vrr):
where (u, v) are the velocity components in the (z, r) directions. The normal to the sheet magnetic field which is applied on the fluid is used for the control of velocity profile of the mold near the sheet. Magneto hydrodynamics (MHD) forces (or hydromagnetics) are a kind of Lorentz force created in electrically conducting fluids with magnetic properties. The external magnetic fields can produce currents in the moving conductive fluid near the sheet, which in turn polarizes the fluid but is not strong enough to affect the external magnetic field. The set of equations that describe MHD are a combination of the Navier-Stokes equations of fluid dynamics and Maxwell’s equations of electromagnetism. In cylindrical coordinates the momentum equations is (by the assumptions of vφ = 0 and vzz ≫ vrr):
where (u, v) are the velocity components in the (z, r) directions, ρ is the fluid density, ρ is the fluid electric conductivity, K is the flow consistency index and n is the power law index. The power law model is a simple model that accurately represents the shear thinning region in the viscosity versus strain rate curve, but neglects the Newtonian plateau present at small strain rates. For n = 1 the fluid is Newtonian, with a dynamic coefficient of viscosity k. For n > 1 the behavior of the fluid is dilatant or shear-thickening (rare in polymer cases) and for 0 < n < 1 the behavior is shear-thinning. The power law indexes for common thermoplastics at ordinary mold temperatures are: n = 0.41 for high density polyethylene, n = 0.39 for low density polyethylene, n = 0.66 for polyamide, n = 0.98 for polycarbonate, n = 0.38 for polypropylene, n = 0.28 for polystyrene, n = 0.26 for polyvinyl chloride.
The maximum temperatures reached at a specific pressure loss and flow rate are a design variable in mold extrusion processes to ensure an economically feasible system. Here the heat is considered to be produced by Joule heating, viscous heating, radiative heating, and temperature dependent sources. The applied external magnetic field which polarized the fluid causes the Joule heating in it. This heat source term, also known as Ohmic heating and resistive heating, is the process by which the passage of an electric current through a conductor releases heat. The amount of heat released is proportional to the square of the current. This relationship is known as Joule’s first law or the Joule–Lenz law. The viscous heating in polymers is also caused by dispersive and distributive mixing heads during extrusion.
The energy equation for thermal radiative absorbance of thermal radiation in a semi-transparent gray medium is assumed here to be reigned by the Rosseland approximation [46] for conductive radiative heat flux. The diffusion approximation is extremely convenient to use. The equation of energy is:
The last term in Equation (3) is a linearized internal heating source which can affect the injection molding process and the final product. This term is considered to be increased by any increase of temperature as the increase of temperature can increase the chemical reaction rates and physical collisions between polymer chains. Following the Rosseland approximation (for the case of an optically thin grey medium) with radiative heat flux qr in Equation (3) is modeled as:
where σ* and χ are the Stephan-Boltzman constant and the Rosseland-mean absorption coefficient (for absorption, scattering, and/or extinction) of the optically thick medium, respectively. As the differences within the flow are such that T4 can be expressed as a linear function of temperature, , expanding T4 in a Taylor series about T∞ and neglecting higher order terms thus:
One may define a radiative conductivity. This model is more valuable for the optically thick medium with optical thickness (χ × r) greater than 3 and the boundary layer equation that governs the heat transfer phenomenon is written as [38]:
where T is the medium temperature, k is the thermal conductivity of the fluid, μ is the viscosity of the fluid, σ is the Stefan-Boltzmann constant, and n is the refractive index. The associated boundary conditions at the solid walls and infinity are:
The system of Equations (1), (2) and (6)–(11) can be solved numerically or analytically. Similar equations are solved in other studies by numerical methods [47,48,49] or analytical series solution methods [45]. In thermodynamics, entropy is a measure of disorder and defined as a degree of the number of specific means where a thermodynamic system could be settled. The entropy is a state function and its alteration is associated to the initial and final state. In keeping with the Second Law of Thermodynamics, the entropy of an insulated system on no condition decreases; such a system will automatically change in the direction of thermodynamic equilibrium, the arrangement with maximum entropy. The present system which is not isolated and has irreversible processes that decrease in entropy provided they increase the entropy of its surroundings by at least that same quantity (increasing the combined entropy of the system and its environment).
The irreversibility in the boundary layer flow of a blood fluid has two components of energy and momentum. Consequently, local volumetric entropy production may occur as a result of fluid friction and heat transfer in the direction of finite temperature gradients. Following Jamalabadi [50], the volumetric rate of entropy generation is given by:
The first term in Equation (12) refers to the heat transfer irreversibility and the second term symbolizes the local entropy generation rate due to fluid friction, correspondingly. As well the third term is produced by magneto-hydrodynamic (MHD) effects while the forth term is the contribution of the internal heat source.
The equivalent stream formulations of momentum and energy equations are:
where ψ denotes the stream function and is defined as:
where θ denotes the dimensionless temperature and is defined as:
and NR is 16kR where kR is the radiation conductivity:
Since Equation (13) is a parabolic partial differential equation and since there is no geometric length scale in the problem, a similarity type of solution will be sought. The r component of velocity will have the following functional form:
where η is the similarity variable, f is the dimensionless stream function, and the prime denotes differentiation with respect to η, but when η is constant, v should be constant. By introducing the ansatz of:
and:
we find the radial velocity component from Equation (15) as:
comparing Equation (19) and Equation (22) results in:
or:
and:
respectively. Then Equation (21) can be rewritten as:
As well the other component of velocity from Equation (16) is:
then the components of Equation (2) are:
substituting the stream function from Equation (26) in Equation (13) results in:
or in a simpler form:
by equating the power of the r in viscous term similar to the inertia term in Equation (32) the following equality for “p” is derived:
that is:
as well by equating the order of the coefficient of the highest degree terms of ‘f’ in viscous term similar to the inertia term in Equation (32) the following equality for ‘α’ is derived:
Since the similarity variable is:
The resulted axial velocity component from Equations (28) and (34) is:
Although the similarity parameter η, is independent of the radial coordinate when it describes the motion of a Newtonian fluid (in the case n = 1), the velocity is linearly dependent on the radial coordinates as stated by Equation (19). To explore the physical meaning of the results of the similarity solution in a Newtonian case with variable viscosity see Makinde et al. [48].
As well, for values of n < 1, the similarity variable is an increasing function of both variables “r” and “z”. This fact seems to be in contrast to the similarity variable in Cartesian coordinate which is a ratio between the variables “y” and “x” (Blasius boundary layer). Again, those figures with n < 1 are physically inadmissible. This difference between the cylindrical coordinates and Cartesian coordinates is not essential as in a similarity solution we look for a solution in which at least one coordinate lacks a distinguished origin; more physically, it describes a flow which “looks the same” either at all times, or at all length scales.
In addition, based on the Equation (32) the magnetic field distribution should be in the form of:
to have a similarity solution for the problem.
According to the similarity variable found in Equation (35), by substituting the stream function from Equation (21) in left hand side of Equation (14) results in:
According to the similarity variable found in Equation (35), by substituting the stream function from Equation (21) in left hand side of Equation (14) results in:
In addition, based on Equation (39) the heat source coefficient distribution should be in the form of:
and the temperature distribution as:
to have a similarity solution for the problem.
In order to elucidate the physical principle, in this paper the non-dimensionalized variables are presented. The non-dimensional parameters which arise are:
Dimensionless heat source number:
Prandtl group is used for thermal boundary layer thickness (the ratio of momentum diffusivity to thermal diffusivity):
for contribution of the convective heat transfer the Peclet number is used (the ratio of the thermal energy convected to the fluid to the thermal energy conducted within the fluid):
The effect of the applied magnetic field can measured by the Hartman number (the ratio of electromagnetic force to the viscous force):
The Brinkman number is used to determine the relative importance between dissipation effects and fluid conduction effects (the ratio between heat produced by viscous dissipation and heat transported by molecular conduction. i.e., the ratio of viscous heat generation to external heating):
The Bejan number proposed to measure the ratio of heat transfer irreversibility divided by total irreversibility due to heat transfer and fluid friction for the power-law non-Newtonian boundary layer flow. The Bejan number is given by:
and finally, the entropy generation number:
In general, the entropy generation number proposed by Bejan and the entropy generation per unit amount of heat transferred are not same. The entropy generation number is to evaluate the irreversibility of heat process and is proposed which is in consistent with the entropy generation per unit amount of heat transferred in entropy generation analysis.
Substituting various derivatives that appear in the boundary-layer Equations (9) and (10), and considering dimensionless parameters in Equations (13), (14) and (21)–(24), the non-dimensional momentum and energy equations as a system of ordinary coupled differential equations can be rewritten as:
In addition, the non-dimensional form of the boundary conditions in the equations from Equation (3) to Equation (6) can be rewritten as:
The minimization of entropy generation in boundary layers with heat transfer attracts substantial interest from engineers studying heat transfer amplification methods. In such practices the key objective is to increase the solid–fluid heat transfer constant compared with the coefficient of the unaugmented (untouched) surface. On the other hand, a parallel objective is to register this enhancement without causing a destructive increase in the stretching sheet power required by the forced-convection arrangement. These two objectives reveal the conflict that goes along with putting into practice any intensification procedure: a design alteration that improves the thermal contact can be expected to augment the mechanical stretching power requirement. In dimensionless forms, local components of entropy generation can be expressed as follows:
The contribution due to viscous loss:
the contribution made by heat transfer:
the contribution due to MHD forces (Ohmic dissipation):
the contribution made by heat source:
the contribution due to fluid friction is the summation of viscous heating and MHD heating:
The Bejan number:
and entropy generation number:
3. Results and Discussion
This paper presents the results of a detailed theoretical investigation on the viscous propagation of non-Newtonian stretching sheet-motivated currents. Regarding the Navier-Stokes theory, a self-similarity solution for viscous propagation of power-law currents that has not been experimentally evaluated was used. Solving Equations (49) and (50) with the boundary conditions of Equations (51)–(55) is presented in this section. That system of ordinary differential equations are the governing equations of steady state power law forced convection flow in thermal radiative absorbing medium with viscous effects over an axisymmetric stretching sheet under no-slip conditions. After solving that problem the entropy generation in the power law flow is discussed.
This has the advantage that the integration region is then finite. The non-dimensional first order differential governing Equation (48) is solved numerically by using the Runge-Kutta-Fehlberg method with shooting technique [51] for various finite boundary layer lengths. The grid size of 0.01 is chosen were the maximum change in final value is less than 10−4. The results are compared with the solution of Crocco-transformed Equation and plotted in Figure 2. The deduction of the boundary layer equations, by use of the order of magnitude analysis on governing Navier-Stokes equations of viscous fluid flow leads to a parabolic partial differential equations, rather than the elliptical form of the full Navier-Stokes equations. As the second order method for parabolic partial differential equations with 100 points is used, the order of magnitude of the error of the converged solution is less than 10−4. Other than this, the Table 1 presents a comparison of the f″ between the present results and those obtained previously [52] for special case of, Ha = 0, n = 0, and nonlinear stretching (m = −1/3).
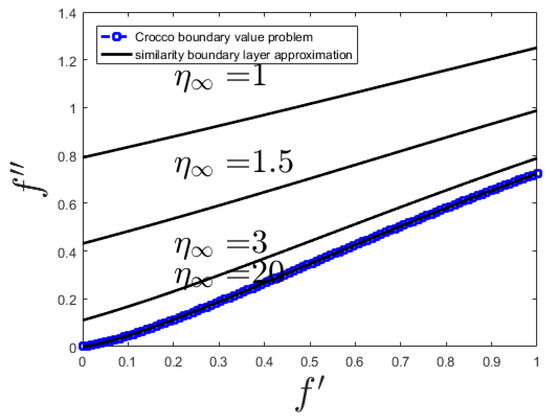
Figure 2.
Prantdl boundary layer equation for various boundary layer thicknesses versus the Crocco solution [51].

Table 1.
Comparison of the f″ between the present results and those obtained previously [52] for special case of, Ha = 0, n = 0, and nonlinear stretching (m = −1/3).
The derivative of the dimensionless temperature which is a measure of the Nusselt number for the power-law indexes of 0.01, 0.1, 0.708 and 1 is illustrated in Figure 3 for Pr = 1. For all curves the η∞ is considered as 20 and by increasing the power-law index the thermal boundary layer thickness is smaller and the effect of the moving surface just sensed at near distances. The finite value of similarity variable at the right boundary represents the infinity condition to a value far from the initial point for numerical calculation. Without the magnetic field the temperature decreases as the distance from the wall increases while the existence of a magnetic field causes an upsurge of temperature at the η∞ equal to 5 and decreases after this peak As shown, by increasing the power-law index the thinner thermal boundary layer leads to a higher rate of heat exchange. The maximum Nusselt number occurs at the n = 0.1. In Figure 4 the dimensionless thermal entropy generated versus similarity variable for various power-law indexes is presented. As shown most of the thermal entropy generation occurs near the stretching wall and it increases with the increase of the power law index.
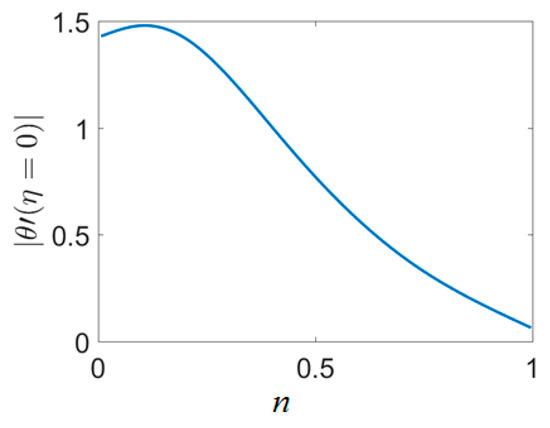
Figure 3.
First derivative of dimensionless temperature versus power-law index for Ha = 1, NR = 0, Br = 0.
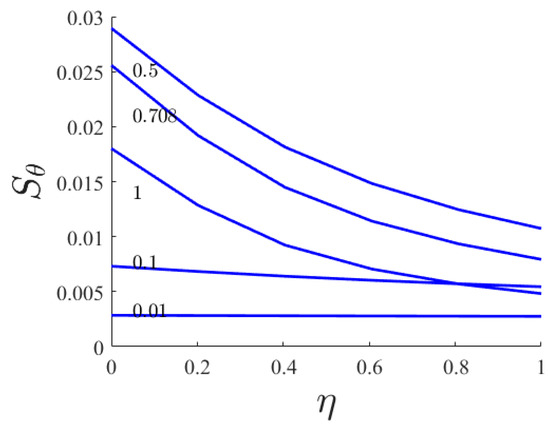
Figure 4.
Dimensionless thermal entropy generated versus similarity variable for various power-law indexes (Ha = 1; Pr = 1; NR = 0; Br = 0).
The derivative of dimensionless temperature which is a measure of the Nusselt number for Prantdl numbers in the range of 0.01 through 7 for polystyrene (n = 0.28) at various Prantdl numbers for Hartmann numbers equal to unity, is exemplified in Figure 5. As demonstrated, generally by increasing the Prantdl number the thermal boundary layer depth is reduced and the effect of the stretching sheet surface is felt in the fluid near it. As revealed by the growth of the Prantdl number the skinny thermal boundary layer causes a greater heat transfer rate up until Pr = 3.5. After the maximum Nusselt number any increase of the Prantdl number causes a decrease of the first derivative of the dimensionless temperature. In Figure 6 the dimensionless thermal entropy generated versus similarity variable for various Prantdl numbers is presented. As shown most of the thermal entropy generation occurs near the stretching wall and it decreases rapidly as the Prantdl number increases within the range from η∞ to less than unity.
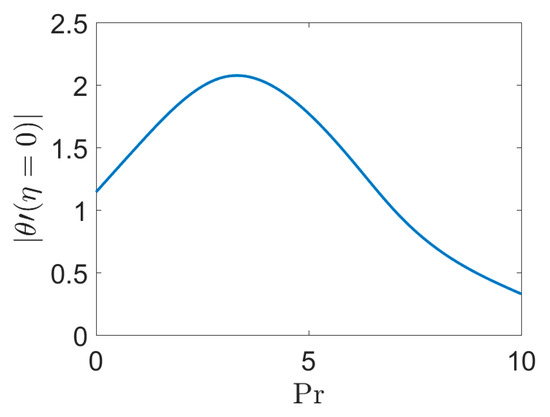
Figure 5.
First derivative of the dimensionless temperature versus Prantdl number for Ha = 1, NR = 0, Br = 0, n = 0.28.
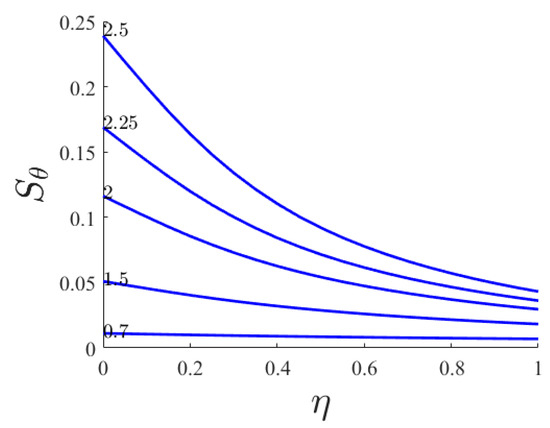
Figure 6.
Dimensionless thermal entropy generated versus similarity variable for various Prantdl numbers (Ha = 1; n = 0.28; NR = 0; Br = 0).
In Figure 7 and Figure 8 the effects of the thermal radiation parameter on various thermal and entropy generation aspects of the system for the high density polyethylene (n = 0.41) are illustrated. The thermal boundary layer depth is increased by increasing the thermal radiation parameter (in η∞ < 1) and the effect of a stretching sheet surface affects the temperature in the adjacent fluid. The matching derivative of the dimensionless temperature is proportional to the Nusselt number for the thermal radiation parameters in range of 0.01 through 10 on a logarithmic scale, as exemplified in Figure 7. As discovered by intensification of the thermal radiation parameter the lean thermal boundary layer causes a better convective heat transfer. The constant rate of decrease of Nusselt number based on the thermal radiation parameter is maintained through the whole domain of NR < 2.
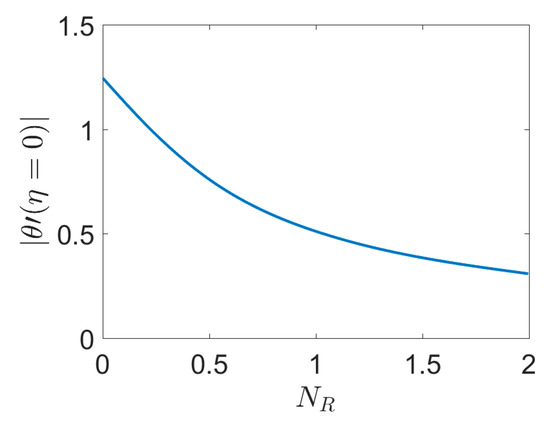
Figure 7.
First derivative of dimensionless temperature versus thermal radiation parameters Br = 0, Pr = 1, n = 0.41.
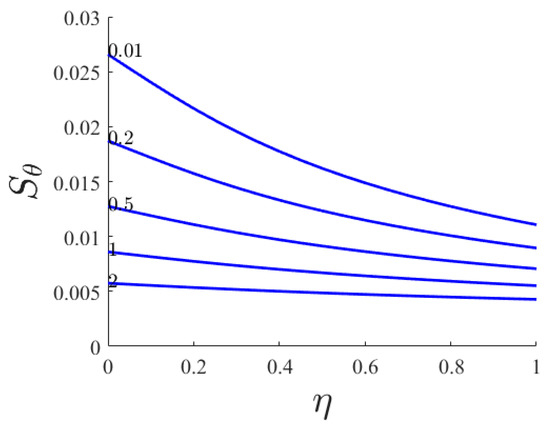
Figure 8.
Dimensionless thermal entropy generated versus similarity variable for various thermal radiation parameters (n = 0.66; Pr = 1; Br = 0).
In Figure 8 the dimensionless thermal entropy produced versus similarity variable for numerous thermal radiation parameters is revealed. As shown most of the thermal entropy generation occurs near the stretching sheet and it decreases quickly as the thermal radiation parameter increases.
The effect of the Brinkman parameter as a measure of viscous dissipation is demonstrated in Figure 9 for low density polyethylene. As shown the θ″ value at the wall is increased linearly by increasing Br, even while at low Br it changes smoothly as presented in the figure. Figure 10 exemplifies the effect of the Brinkman number on the dimensionless temperature component of the entropy profiles. As seen by increasing Br the temperature component of the entropy increases, especially near the wall. The maximum again appears at the walls. By increasing of distance from the stretching wall, the dimensionless temperature profile decreases and this loss is more for lower Brinkman numbers.
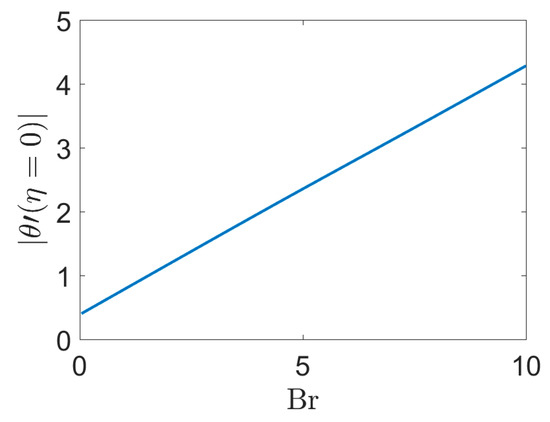
Figure 9.
First derivative of dimensionless temperature versus Brinkman number. Ha = 1, Pr = 1, n = 0.39, NR = 0.
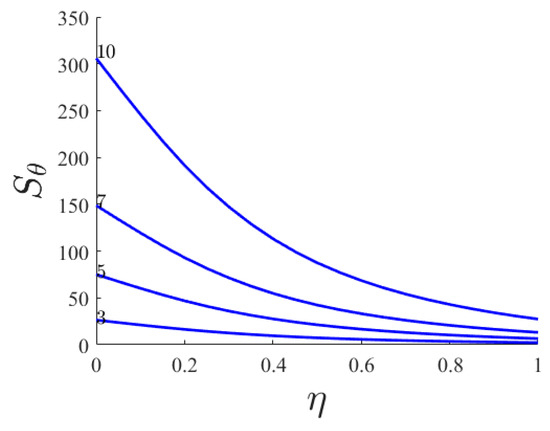
Figure 10.
Dimensionless thermal entropy generated versus similarity variable for various Brinkman numbers (Ha = 1; n = 0.66; Pr = 1; NR = 0).
As illustrated in Figure 11 the Br has less effect on total Su than Sθ, but similarly it is increased by increases of Br. The Su values maintain near the wall values as far distances from the wall than Sθ.
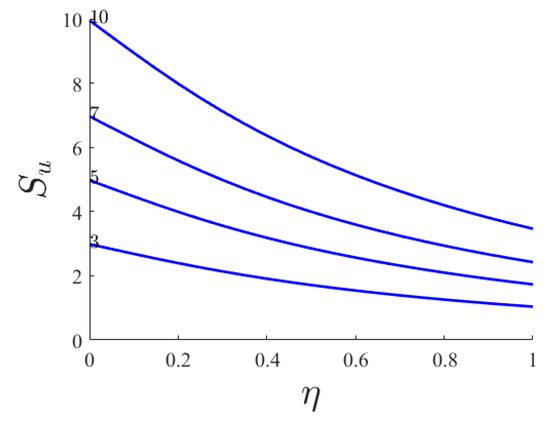
Figure 11.
Dimensionless viscous entropy generated versus similarity variable for various Brinkman numbers (Ha = 1; n = 0.66; Pr = 1; NR = 0).
There is a significant body of research on multi-scale modelling in simulations of flow and heat transfer problems [54], hybrid molecular continuum method using point wise coupling [55], and coupling strategies for hybrid molecular-continuum simulation methods. This method is a physics-based model; it uses generalized hydrodynamic equations and can be interpreted as a regularization of the Navier-Stokes equations. As the onset of turbulence has not yet been calculated for the axisymmetric stretching wall, a multiscale computational fluid dynamics method is a good approach to solve viscous flow problems in a thin boundary layer and capture the small flow scales of turbulence.
The critical value of the Hartmann number shows its effect on the Nusselt number at the wall in Figure 12. The first derivative of dimensionless temperature versus Hartmann number decreased for Ha < 0.8 and increased for Ha > 0.8 based on the Hartmann number for polypropylene at Pr = 5. The minimum Nusselt number occurs at a Hartmann number equal to 0.8. At this moment the wall cannot deliver its heat to the fluid based on its overheating. Figure 13 illustrates the dimensionless thermal entropy generated versus similarity variable for various Hartmann numbers. As plotted, with the increase of Hartmann number and distance from the wall the thermal entropy generation is decreased. A similar behavior can be observed in Figure 14 for the dimensionless viscous entropy generated versus similarity variable for various Hartmann numbers.
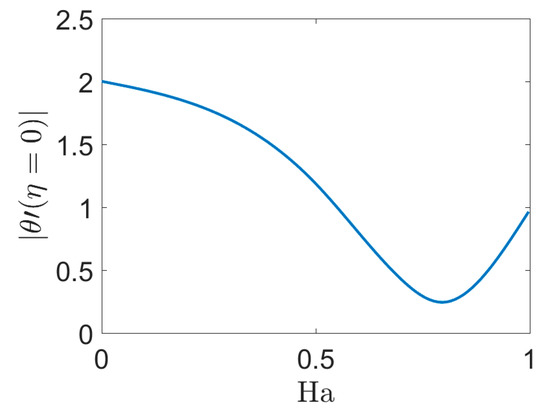
Figure 12.
First derivative of dimensionless temperature versus Hartmann number. Br = 1, Pr = 5, n = 0.38, NR = 0.
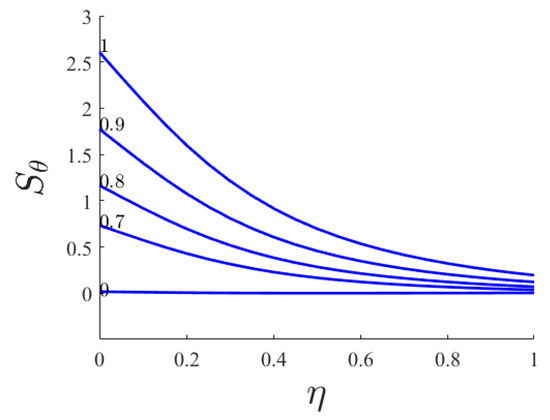
Figure 13.
Dimensionless thermal entropy generated versus similarity variable for various Hartmann numbers (Br = 1; n = 0.66; Pr = 1; NR = 0).
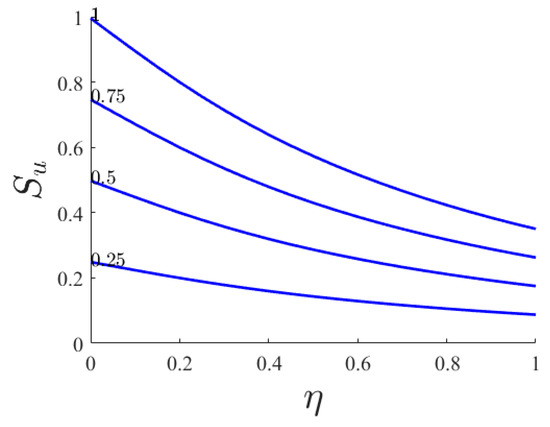
Figure 14.
Dimensionless viscous entropy generated versus similarity variable for various Hartmann numbers (Br = 1; n = 0.66; Pr = 1; NR = 0).
The critical value of the heat source number for polyamide at Pr = 1 displays its consequence on the Nusselt number at the wall in Figure 15. As shown the first derivative of the dimensionless temperature versus heat source number decreased for Q < 0.006 and increased for Q > 0.006 based on the heat source number. The minimum Nusselt number occurs at a Hartmann number equal to 0.8. At this value the wall cannot deliver its heat to the fluid based on its overheating. Figure 16 illustrates the dimensionless thermal entropy generated versus similarity variable for various heat source numbers. As plotted, with the increase of heat source number and distance from the wall the thermal entropy generation is decreased. Table 2 summarizes all the important results, by different parameter.
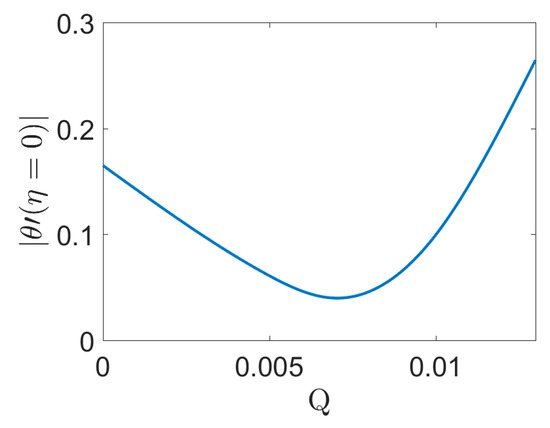
Figure 15.
First derivative of dimensionless temperature versus heat source number. Br = 0, Ha = 0, Pr = 1, n = 0.66, NR = 0.
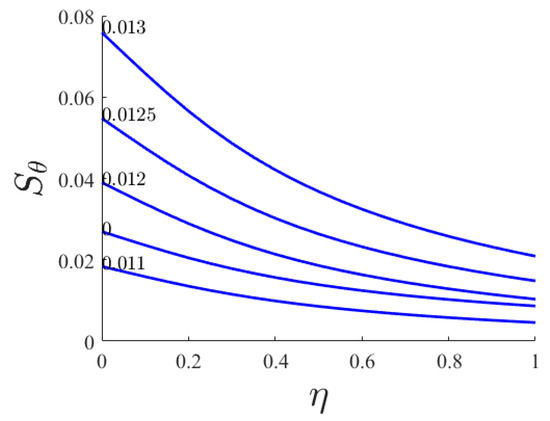
Figure 16.
Dimensionless thermal entropy generated versus similarity variable for various heat source numbers.

Table 2.
Parameters effects on heat transfer and entropy characteristics.
To present the result of boundary layer analysis in an application a uniform grid of 0.5 m × 0.3 m with 0.01 grid size is used for the case of K = 0.35 Pa0.26, c = 0.001 m2/3·s−1, n = 0.26. The stream lines is plotted to show the flow direction towards the stretching sheet in Figure 17. The velocity vector components are found from the Equations (19) and (36). As shown the maximum velocity is increased near the axis of symmetry and when the fluid approaches the stretching surface.
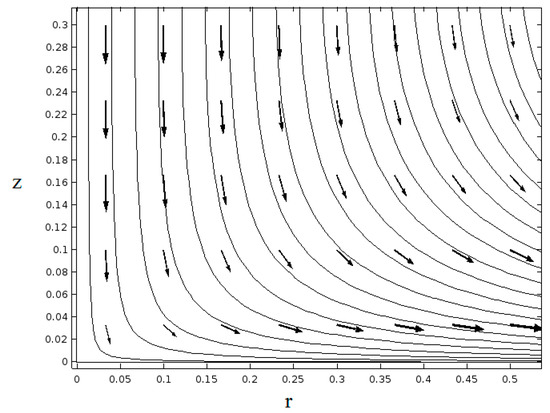
Figure 17.
The stream lines over the stretching sheet.
After finding the effects of the involved parameters of the problem on flow and heat transfer, the entropy generation numbers, as well as the Bejan number, for various values of Hartmann numbers are evaluated. The generation of entropy at the local differential level could be presented by the entropy and Bejan numbers. Figure 18 and Figure 19 illustrate the effect of the Hartmann number on Bejan number and entropy number, respectively. Both numbers versus similarity variable for various Hartmann numbers are decreasing as radial distance goes on. As well, the increase of magnetic field causes an increase in both numbers.
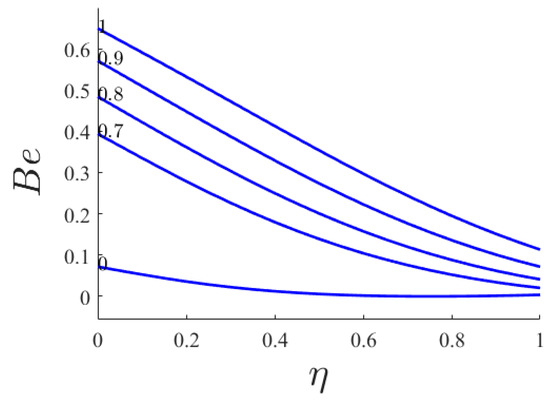
Figure 18.
Bejan number versus similarity variable for various Hartmann numbers.
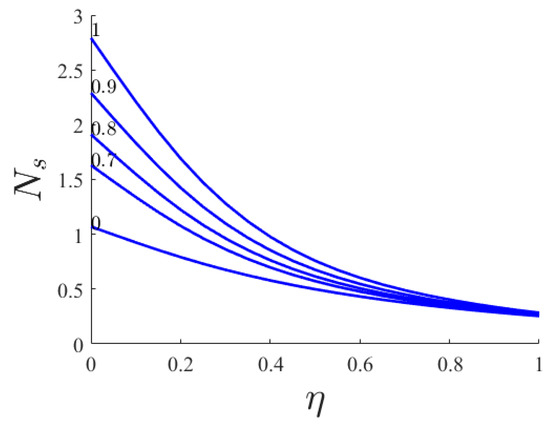
Figure 19.
Entropy number versus similarity variable for various Hartmann numbers.
4. Conclusions
In this study, a thorough investigation of the steady state flow near an axisymmetric stretching sheet with thermal radiation, Joule heating, temperature dependent heat sources and viscous heating has been performed. In order to get the similarity solution, the magnetic field, the heat source and the temperature of the plate must have specific distributions. This limitation should be considered in the practical applications of the method and results of this paper. The results can be summarized as follows:
- (1)
- The coupled model is able to simulate the flow of a shear thinning fluid. By increasing n, the boundary layer of heat transfer is decreased and the heat transfer on the stretching sheet is increased. The justification and the reason behind the trends depicted have been explained in detail.
- (2)
- By increasing Pr, the boundary layer of heat transfer is decreased and the heat transfer rate on the stretching sheet is increased. Such a development of the heat flux over the heat source prevents the cooling of the fluid on the bottom wall. An increment in Prandtl number shows a marked reduction in the temperature profile.
- (3)
- By increasing NR, the boundary layer of heat transfer is increased and the convective heat transfer rate on the stretching sheet is decreased. A reduction of Nu can be explained by an attenuation of the convective flow and also by narrowing of the boundary layer.
- (4)
- In two-dimensional (2D) non-Newtonian flow, by increasing Br, the boundary layer of heat transfer and the convective heat transfer rate on the stretching sheet are increased.
- (5)
- By increasing Ha, the boundary layer of heat transfer and the convective heat transfer rate on the stretching sheet have a minimum at Ha = 0.8. An increase in the Ha leads to an attenuation of convective flow and less intensive cooling of the bottom part of the cavity. Average Nusselt and Bejan numbers and average total entropy generation are increasing functions of Ha.
- (6)
- By increasing Q, the boundary layer of heat transfer and the convective heat transfer rate on the stretching sheet has minimum on Q = 0.006.
- (7)
- By increasing n, Pr the heat transfer part of the entropy increases dramatically while the viscous part of the entropy is not changed.
Author Contributions
Conceptualization, supervision, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing the original draft, review and editing is done by MYAJ. Project administration and Resources are provided by Payam Hooshmand, Hamed Rajabzadeh Gatabi, Navid Bagheri, Ashkan Hesabi, Isma’il Pirzadeh, and Majid Oveisi. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Be | local Bejan number | |
| Br | Brinkmann number | |
| Cp | specific heat at constant pressure | J/kg·K |
| Ha | Harttmann number | |
| k | thermal conductivity of the fluid | W/mK |
| K | flow consistency index | |
| n | power law index | |
| n* | refractive index | |
| NR | Radiative number | |
| Q | Heat source coefficient | |
| r | Coordinate component | m |
| Pr | Prantdl number | |
| S‴ | dimensionless average entropy generation | J/Ksm3 |
| Su | dimensionless local entropy generation due to fluid friction | J/Ksm3 |
| St | dimensionless local entropy generation due to the heat transfer | J/Ksm3 |
| T | medium temperature | K |
| u | velocity component in the zrdirection | m/s |
| v | velocity component in the r direction | m/s |
| z | Coordinate component | m |
Greek Symbol
| α | thermal diffusivity | m2/s |
| θ | dimensionless temperature | |
| σ | fluid electric conductivity | S/m |
| ρ | fluid density | kg/m3 |
| σ* | Stephan-Boltzman constant | kg·s−3·K−4 |
| χ | Rosseland-mean absorption coefficient | |
| μ | viscosity of the fluid | Pa·s |
| ρCp | heat capacitance | J/m3·K |
References
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Grubka, J.; Bobba, K.M. Heat transfer characteristics of a continuous stretching surface with variable temperature. J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- Ali, M.E. On thermal boundary layer on a power law stretched surface with suction or injection. Int. J. Heat Fluid Flow 1995, 16, 280–290. [Google Scholar] [CrossRef]
- Chen, C.H. Laminar mixed convection adjacent to vertical, continuously stretching sheets. Heat Mass Transf. 1998, 33, 471–476. [Google Scholar] [CrossRef]
- Datta, B.K.; Roy, P.; Gupta, A.S. Temperature field in a flow over a stretching that within uniform heat flux. Int. Commun. Heat Transf. 1985, 12, 89–94. [Google Scholar] [CrossRef]
- Chen, C.K.; Char, M.I. Heat transfer on a continuous stretching surface with suction or blowing. J. Math. Anal. Appl. 1988, 135, 568–580. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A. Heat transfer over a stretching surface with variable heat flux. J. Phys. D Appl. Phys. 1998, 31. [Google Scholar] [CrossRef]
- Makhmalbaf, M.H.M. Experimental study on convective heat transfer coefficient around a vertical hexagonal rod bundle. Heat Mass Transf. 2012, 48, 1023–1029. [Google Scholar] [CrossRef]
- Makhmalbaf, H.; Liu, T.; Merati, P. Experimental Simulation of Buoyancy-Driven Vortical Flow in Jupiter Great Red Spot. In Proceedings of the 68th Annual Meeting of the APS Division of Fluid Dynamics, Boston, MA, USA, 22–24 November 2015.
- Cortell, R. Flow and heat transfer of a fluid through a porous medium over a stretching surface with internal heat generation/absorption and suction/blowing. Fluid Dyn. Res. 2005, 37, 231–245. [Google Scholar] [CrossRef]
- Liao, S.J. An analytic solution of unsteady boundary-layer flows caused by an impulsively stretching plate. Commun. Nonlinear Sci. Numer. Simul. 2006, 11, 326–339. [Google Scholar] [CrossRef]
- Mehmood, A.; Ali, A. Analytic homotopy solution of generalized three dimensional channel flow due to uniform stretching of the plate. Acta Mech. Sin. 2007, 23, 502–510. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet. Heat Mass Transf. 2008, 44, 921–927. [Google Scholar] [CrossRef]
- Crane, L.J. Boundary layer flow due to stretching cylinder. Z. Angew. Math. Phys. 1975, 25, 619–622. [Google Scholar] [CrossRef]
- Wang, C.Y. Fluid flow due to stretching cylinder. Phys. Fluids 1988, 31, 466–468. [Google Scholar] [CrossRef]
- Burde, H.I. On the motion of fluid near a stretching circular cylinder. J. Appl. Math. Mech. 1988, 53, 271–273. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R. Laminar boundary layer flow along a stretching cylinder. Eur. J. Sci. Res. 2009, 36, 22–29. [Google Scholar]
- Ishak, A.; Nazar, R.; Pop, I. Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Energy Convers. Manag. 2008, 49, 3265–3269. [Google Scholar] [CrossRef]
- Mastroberardino, A.; Paullet, J.E. Existence and priori bounds for steady stagnation flow toward a stretching cylinder. J. Math. Anal. Appl. 2010, 365, 701–710. [Google Scholar] [CrossRef]
- Weidman, P.D.; Ali, M.E. Aligned and nonaligned radial stagnation flow on a stretching cylinder. Eur. J. Mech. B Fluids 2011, 30, 120–128. [Google Scholar] [CrossRef]
- Wang, C.Y.; Ng, C.O. Slip flow due to a stretching cylinder. Int. J. Nonlinear Mech. 2011, 45, 1191–1194. [Google Scholar] [CrossRef]
- Munawar, S.; Mehmood, A.; Ali, A. Unsteady flow of viscous fluid over the vacillate stretching cylinder. Int. J. Numer. Methods Fluids 2011, 70, 671–681. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.V.; Santhi, S.R. Axisymmetric magneto-hydrodynamic (MHD) flow and heat transfer at a non-isothermal stretching cylinder. Appl. Math. Comput. 2012, 219, 3993–4005. [Google Scholar] [CrossRef]
- Joodaki, H.; Forman, J.; Forghani, A.; Overby, B.; Kent, R.; Crandall, J.; Beahlen, B.; Beebe, M.; Bostrom, O. Comparison of kinematic behaviour of a first generation obese dummy and obese PMHS in frontal sled tests. In Proceedings of the 2015 IRCOBI Conference, Lyon, France, 9–11 September 2015; pp. 9–11.
- Forman, J.L.; Joodaki, H.; Forghani, A.; Riley, P.O.; Bollapragada, V.; Lessley, D.J.; Overby, B.; Heltzel, S.; Kerrigan, J.R.; Crandall, J.R.; Yarboro, S. Whole-body Response for Pedestrian Impact with a Generic Sedan Buck. Stapp Car Crash J. 2015, 59, 401–444. [Google Scholar]
- Forman, J.L.; Joodaki, H.; Forghani, A.; Riley, P.; Bollapragada, V.; Lessley, D.; Overby, B.; Heltzel, S.; Crandall, J. Biofidelity Corridors for Whole-Body Pedestrian Impact with a Generic Buck. In Proceedings of the 2015 IRCOBI Conference, Lyon, France, 9–11 September 2015.
- Chen, X.; Pavlish, K.; Benoit, J.N. Myosin phosphorylation triggers actin polymerization in vascular smooth muscle. Am. J. Physiol. Heart Circ. Physiol. 2008, 295, H2172–H2177. [Google Scholar] [CrossRef] [PubMed]
- Jones, E.A.V. The initiation of blood flow and flow induced events in early vascular development. Semin. Cell Dev. Biol. 2011, 22, 1028–1035. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Paul, A.; Taylor, M.D.; Banerjee, R.K. Pulsatile arterial wall-blood flow interaction with wall pre-stress computed using an inverse algorithm. Biomed. Eng. Online 2015, 14, S1–S18. [Google Scholar] [CrossRef] [PubMed]
- Blachon, A.; Marque, S.R.A.; Roubaud, V.; Siri, D. Diasteromeric Effect on the Homolysis of the C–ON Bond in Alkoxyamines: A DFT Investigation of 1,3-Diphenylbutyl-TEMPO. Polymers 2010, 2, 353–363. [Google Scholar] [CrossRef]
- Yu, J.; Liu, F.; Tang, P.; Qiu, F.; Zhang, H.; Yang, Y. Effect of Geometrical Asymmetry on the Phase Behavior of Rod-Coil Diblock Copolymers. Polymers 2016, 8, 184. [Google Scholar] [CrossRef]
- Kogej, K. Thermodynamic Analysis of the Conformational Transition in Aqueous Solutions of Isotactic and Atactic Poly(Methacrylic Acid) and the Hydrophobic Effect. Polymers 2016, 8, 168. [Google Scholar] [CrossRef]
- Munawar, S.; Mehmood, A.; Ali, A. Time-dependent flow and heat transfer over a stretching cylinder. Chin. J. Phys. 2012, 50, 828–848. [Google Scholar]
- Mukhopadhyay, S.; Ishak, A. Mixed convection flow along a stretching cylinder in a thermally stratified medium. J. Appl. Math. 2012, 8. [Google Scholar] [CrossRef]
- Shateyi, S.; Marewo, G.T. A new numerical approach for the laminar boundary layer flow and heat transfer along a stretching cylinder embedded in a porous medium with variable thermal conductivity. J. Appl. Math. 2013, 7. [Google Scholar] [CrossRef]
- Si, X.; Li, L.; Zheng, L.; Zhang, X.; Liu, B. The exterior unsteady viscous flow and heat transfer due to a porous expanding stretching cylinder. Comput. Fluids 2014, 105, 280–284. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.V.; Santhi, S.R.; Umesh, V. Fluid flow and heat transfer over a permeable stretching cylinder. J. Appl. Fluids Mech. 2014, 7, 111–120. [Google Scholar]
- Odat, M.Q.A.; Damseh, R.A.; Nimr, M.A.A. Effect of magnetic field on entropy generation due to laminar forced convection past a horizontal flat plate. Entropy 2004, 4, 293–303. [Google Scholar] [CrossRef]
- Makinde, O.D.; Osalusi, E. Entropy generation in a liquid film falling along an inclined porous heated plate. Mech. Res. Commun. 2006, 33, 692–698. [Google Scholar] [CrossRef]
- Makinde, O.D. Irreversibility analysis for a gravity driven non-Newtonian liquid film along an inclined isothermal plate. Phys. Scr. 2006, 74, 642–645. [Google Scholar] [CrossRef]
- Munawar, S.; Ali, A.; Mehmood, A. Thermal analysis of the flow over an oscillatory stretching cylinder. Phys. Scr. 2012, 86. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy analysis of magnetohydrodynamic flow and heat transfer due to a stretching cylinder. J. Taiwan Inst. Chem. Eng. 2014, 45, 780–786. [Google Scholar] [CrossRef]
- Osswald, T.; Baur, E.; Brinkmann, S.; Oberbach, K.; Schmachtenberg, E. International Plastics Handbook 4E: The Resource for Plastics Engineers, 4th ed.; Hanser Publications: Munich, Germany, 2006. [Google Scholar]
- Brostow, W. Mechanical and Thermophysical Properties of Polymer Liquid Crystals; Chapman & Hall: New York, NY, USA, 1998; Volume 3. [Google Scholar]
- Rosseland, S. Theoretical Astrophysics: Atomic Theory and the Analysis of Stellar Atmospheres and Envelopes; Clarendon Press: Oxford, UK, 1936. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Makinde, O.D.; Mabood, F.; Khanc, W.A.; Tshehla, M.S. MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. J. Mol. Liq. 2016, 219, 624–630. [Google Scholar] [CrossRef]
- Motsa, S.S.; Sibanda, P. On the solution of MHD flow over a nonlinear stretching sheet by an efficient semi-analytical technique. Int. J. Numer. Methods Fluids 2012, 68, 1524–1537. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y. Entropy generation in boundary layer flow of a micro polar fluid over a stretching sheet embedded in a highly absorbing medium. Front. Heat Mass Transf. 2015, 6, 1–13. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y.; Hooshmand, P.; Bagheri, N.; KhakRah, H.; Dousti, M. Numerical Simulation of Williamson Combined Natural and Forced Convective Fluid Flow between Parallel Vertical Walls with Slip Effects and Radiative Heat Transfer in a Porous Medium. Entropy 2016, 18, 147. [Google Scholar] [CrossRef]
- Khan, M.; Munir, A.; Shahzad, A. Convective Heat Transfer to Sisko Fluid over a Nonlinear Radially Stretching Sheet. In Heat Transfer Studies and Applications; Kazi, S.N., Ed.; Intech: Rijeka, Croatia, 2015; pp. 341–361. [Google Scholar]
- Drikakis, D.; Asproulis, N. Multiscale Computational Modelling of Flow and Heat Transfer. Int. J. Numer. Method Heat Fluid Flow 2010, 20, 517–528. [Google Scholar] [CrossRef]
- Asproulis, N.; Kalweit, M.; Drikakis, D. A hybrid molecular continuum method using point wise coupling. Adv. Eng. Softw. 2012, 46, 85–92. [Google Scholar] [CrossRef]
- Kalweit, M.; Drikakis, D. Coupling strategies for hybrid molecular—Continuum simulation methods. Proc. IMechE Part C 2008, 222, 797–806. [Google Scholar] [CrossRef]
- Di Federico, V.; Archetti, R.; Longo, S. Spreading of axisymmetric non-Newtonian power-law gravity currents in porous media. J. Non-Newton. Fluid Mech. 2012, 189–190, 31–39. [Google Scholar] [CrossRef]
- De Haro, M.L.; Cuevas, S.; Beltrán, A. Heat transfer and entropy generation in the parallel plate flow of a power-law fluid with asymmetric convective cooling. Energy 2014, 66, 750–756. [Google Scholar] [CrossRef]
- Anand, V. Slip law effects on heat transfer and entropy generation of pressure driven flow of a power law fluid in a microchannel under uniform heat flux boundary condition. Energy 2014, 76, 716–732. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and Das’ model. Entropy 2016, 18, 9. [Google Scholar] [CrossRef]
- Pascal, J.P.; Pascal, H. Similarity solutions to gravity flows of non-Newtonian fluids through porous media. Int. J. Non-Linear Mech. 1993, 28, 157–167. [Google Scholar] [CrossRef]
- Chowdhury, M.R.; Testik, F.Y. Viscous propagation of two-dimensional non-Newtonian gravity currents. Fluid Dyn. Res. 2012, 44, 4. [Google Scholar] [CrossRef]
- Tosco, T.; Sethi, R. Transport of Non-Newtonian Suspensions of Highly Concentrated Micro- and Nanoscale Iron Particles in Porous Media: A Modeling Approach. Environ. Sci. Technol. 2010, 44, 9062–9068. [Google Scholar] [CrossRef] [PubMed]
- Ciriello, V.; Longo, S.; Di Federico, V. On shear thinning fluid flow induced by continuous mass injection in porous media with variable conductivity. Mech. Res. Commun. 2013, 52, 101–107. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V.; Chiapponi, L.; Archetti, R. Experimental verification of power-law non-Newtonian axisymmetric porous gravity currents. J. Fluid Mech. 2013, 731. [Google Scholar] [CrossRef]
- Longo, S.; di Federico, V.; Archetti, R.; Chiapponi, L.; Ciriello, V.; Ungarish, M. On the axisymmetric spreading of non-Newtonian power-law gravity currents of time-dependent volume: An experimental and theoretical investigation focused on the inference of rheological parameters. J. Non-Newton. Fluid Mech. 2013, 201, 69–79. [Google Scholar] [CrossRef]
- Di Federico, V.; Longo, S.; Chiapponi, L.; Archetti, R.; Ciriello, V. Radial gravity currents in vertically graded porous media: Theory and experiments for Newtonian and power-law fluids. Adv. Water Resour. 2014, 70, 65–76. [Google Scholar] [CrossRef]
- Longo, S.; Di Federic, V.; Chiapponi, L. Non-Newtonian power-law gravity currents propagating in confining boundaries. Environ. Fluid Mech. 2015, 15, 515–535. [Google Scholar] [CrossRef]
- Longo, S.; Ciriello, V.; Chiapponi, L.; Di Federico, V. Combined effect of rheology and confining boundaries on spreading of gravity currents in porous media. Adv. Water Resour. 2015, 79, 140–152. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V.; Chiapponi, L. Propagation of viscous gravity currents inside confining boundaries: The effects of fluid rheology and channel geometry. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V. Stability Analysis of Gravity Currents of a Power-Law Fluid in a Porous Medium. Math. Probl. Eng. 2015, 2015, 286487. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V.; Chiapponi, L. A dipole solution for power-law gravity currents in porous formations. J. Fluid Mech. 2015, 778, 534–551. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V. Unsteady Flow of Shear-Thinning Fluids in Porous Media with Pressure-Dependent Properties. Transp. Porous Med. 2015, 110, 429–447. [Google Scholar] [CrossRef]
- Ciriello, V.; Longo, S.; Chiapponi, L.; Di Federico, V. Porous gravity currents: A survey to determine the joint influence of fluid rheology and variations of medium properties. Adv. Water Resour. 2016, 92, 105–115. [Google Scholar] [CrossRef]
- Longo, S.; Chiapponi, L.; di Federico, V. On the propagation of viscous gravity currents of non-Newtonian fluids in channels with varying cross section and inclination. J. Non-Newton. Fluid Mech. 2016, 235, 95–108. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).