Distance-Based Lempel–Ziv Complexity for the Analysis of Electroencephalograms in Patients with Alzheimer’s Disease
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects and EEG Recording
2.2. Synthetic Data
2.3. Distance-Based Lempel–Ziv Complexity
- Non-negative, i.e., D(x, y) ≥ 0;
- Symmetric, i.e., D(x, y) = D(y, x);
- Satisfy the triangle inequality, i.e., D(x, y) ≤ D(x, z) + D(z, y )
2.4. Statistical Analysis
3. Results
3.1. dLZC of Synthetic Data
3.2. dLZC of EEG Data
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bird, T.D. Alzheimer’s disease and other primary dementias. In Harrison’s Principles of Internal Medicine, 15th ed.; Braunwald, E., Fauci, A.S., Kasper, D.L., Hauser, S.L., Longo, D.L., Jameson, J.L., Eds.; McGraw-Hill: New York, NY, USA, 2001; pp. 2391–2399. [Google Scholar]
- Kalaria, R.N.; Maestre, G.E.; Arizaga, R.; Friedland, R.P.; Galasko, D.; Hall, K.; Luchsinger, J.A.; Ogunniyi, A.; Perry, E.K.; Potocnik, F.; et al. Alzheimer’s disease and vascular dementia in developing countries: Prevalence, management, and risk factors. Lancet Neurol. 2008, 7, 812–826. [Google Scholar] [CrossRef]
- Blennow, K.; de Leon, M.J.; Zetterberg, H. Alzheimer’s disease. Lancet 2006, 368, 387–403. [Google Scholar] [CrossRef]
- Minati, L.; Edginton, T.; Bruzzone, M.G.; Giaccone, G. Current Concepts in Alzheimer’s Disease: A Multidisciplinary Review. Am. J. Alzheimers Dis. Other Dement. 2009, 24, 95–121. [Google Scholar] [CrossRef] [PubMed]
- Hardy, J.; Selkoe, D. The amyloid hypothesis of Alzheimer’s disease: Progress and problems on the road to therapeutics. Science 2002, 297, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Delbeuck, X.; van der Linden, M.; Collette, F. Alzheimer’s disease as a disconnection syndrome? Neuropsychol. Rev. 2003, 13, 79–92. [Google Scholar] [CrossRef] [PubMed]
- Morrison, J.H.; Scherr, S.; Lewis, D.A.; Campbell, M.J.; Bloom, F.E.; Rogers, L.; Benoit, R. The laminar and regional distribution of neocortical somatostatin and neuritic plaques: Implications for Alzheimer’s disease as a global neocortical disconnection syndrome. In The Biological Substrates of Alzheimer’s Disease; Scheibel, A.B., Wechsler, A.F., Eds.; Academic Press: Orlando, FL, USA, 1986; pp. 115–131. [Google Scholar]
- Jeong, J. EEG dynamics in patients with Alzheimer’s disease. Clin. Neurophysiol. 2004, 115, 1490–1505. [Google Scholar] [CrossRef] [PubMed]
- Prince, M.; Bryce, R.; Ferri, C. World Alzheimer Report 2011: The Benefits of Early Diagnosis and Intervention. Available online: https://www.alz.co.uk/research/world-report-2011 (accessed on 13 January 2017).
- Reiman, E.M.; Quiroz, Y.T.; Fleisher, A.S.; Chen, K.; Velez-Pardo, C.; Jimenez-Del-Rio, M.; Fagan, A.M.; Shah, A.R.; Alvarez, S.; Arbelaez, A.; et al. Brain imaging and fluid biomarker analysis in young adults at genetic risk for autosomal dominant Alzheimer’s disease in the presenilin 1 E280A kindred: A case-control study. Lancet Neurol. 2012, 11, 1048–1056. [Google Scholar] [CrossRef]
- Knopman, D.S.; Boeve, B.F.; Petersen, R.C. Essentials of the proper diagnoses of mild cognitive impairment, dementia, and major subtypes of dementia. Mayo Clin. Proc. 2003, 78, 1290–1308. [Google Scholar] [CrossRef] [PubMed]
- McKhann, G.; Drachman, D.; Folstein, M.; Katzman, R.; Price, D.; Stadlan, E.M. Clinical-diagnosis of Alzheimer’s disease: Report of the NINCDS-ADRDA Work Group under the auspices of Department of Health and Human Services Task Force on Alzheimer’s Disease. Neurology 1984, 34, 939–944. [Google Scholar] [CrossRef] [PubMed]
- Rossor, M. Alzheimer’s disease. In Brain Diseases of the Nervous System; Donaghy, M., Ed.; Oxford University Press: Oxford, UK, 2001; pp. 750–754. [Google Scholar]
- McKhann, G.M.; Knopman, D.S.; Chertkow, H.; Hyman, B.T.; Jack, C.R., Jr.; Kawas, C.H.; Klunk, W.E.; Koroshetz, W.J.; Manly, J.J.; Mayeux, R.; et al. The diagnosis of dementia due to Alzheimer’s disease: Recommendations from the National Institute on Aging-Alzheimer’s Association workgroups on diagnostic guidelines for Alzheimer’s disease. Alzheimers Dement. 2011, 7, 263–269. [Google Scholar] [CrossRef] [PubMed]
- Dauwels, J.; Vialatte, F.; Cichocki, A. Diagnosis of Alzheimer’s disease from EEG signals: Where are we standing? Curr. Alzheimer Res. 2010, 7, 487–505. [Google Scholar] [CrossRef] [PubMed]
- Stam, C. Chaos, continuous EEG, and cognitive mechanisms: A future for clinical neurophysiology. Am. J. Electroneurod. Technol. 2003, 43, 211–227. [Google Scholar]
- Stam, C. Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field. Clin. Neurophysiol. 2005, 116, 2266–2301. [Google Scholar] [CrossRef] [PubMed]
- Dauwels, J.; Vialatte, F.; Musha, T.; Cichocki, A. A comparative study of synchrony measures for the early diagnosis of Alzheimer’s disease based on EEG. NeuroImage 2010, 49, 668–693. [Google Scholar] [CrossRef] [PubMed]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Abásolo, D.; Hornero, R.; Gómez, C.; García, M.; López, M. Analysis of EEG background activity in Alzheimer’s disease patients with Lempel–Ziv complexity and Central Tendency Measure. Med. Eng. Phys. 2006, 28, 315–322. [Google Scholar] [CrossRef] [PubMed]
- Dauwels, J.; Srinivasan, K.; Ramasubba Reddy, M.; Musha, T.; Vialatte, F.B.; Latchoumane, C.; Jeong, J.; Cichocki, A. Slowing and loss of complexity in Alzheimer’s EEG: Two sides of the same coin? Int. J. Alzheimers Dis. 2011, 2011, 539621. [Google Scholar] [CrossRef] [PubMed]
- Labate, D.; la Foresta, F.; Morabito, G.; Palamara, I.; Morabito, F.C. Entropic measures of EEG complexity in Alzheimer’s disease through a multivariate multiscale approach. IEEE Sens. J. 2013, 13, 3284–3292. [Google Scholar] [CrossRef]
- Wen, J.; Li, C. Similarity analysis of DNA sequences based on the LZ complexity. Internet Electron. J. Mol. Des. 2007, 6, 1–12. [Google Scholar]
- Zhang, X.S.; Zhu, Y.S.; Thakor, N.V.; Wang, Z.Z. Detecting ventricular tachycardia and fibrillation by complexity measure. IEEE Trans. Biomed. Eng. 1999, 46, 548–555. [Google Scholar] [CrossRef] [PubMed]
- Christen, M.; Kohn, A.; Ott, T.; Stoop, R. Measuring spike pattern reliability with the Lempel–Ziv-distance. J. Neurosci. Methods 2006, 156, 342–350. [Google Scholar] [CrossRef] [PubMed]
- Otu, H.H.; Sayood, K. A new sequence distance measure for phylogenetic tree construction. Bioinformatics 2003, 19, 2122–2130. [Google Scholar] [CrossRef] [PubMed]
- Zozor, S.; Ravier, P.; Buttelli, O. On Lempel–Ziv complexity for multidimensional data analysis. Physica A 2005, 345, 285–302. [Google Scholar] [CrossRef]
- Wendling, F.; Bellanger, J.J.; Bartolomei, F.; Chauvel, P. Relevance of nonlinear lumped-parameter models in the analysis of depth-EEG epileptic signals. Biol. Cibern. 2000, 83, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Quiroga, R.Q.; Arnhold, J.; Grassberger, P. Learning driver-response relationships from synchronization patterns. Phys. Rev. E 2000, 61, 5142–5148. [Google Scholar] [CrossRef]
- Niso, G.; Bruña, R.; Pereda, E.; Gutiérrez, R.; Bajo, R.; Maestú, F.; del Pozo, F. HERMES: Towards an Integrated Toolbox to Characterize Functional and Effective Brain Connectivity. Neuroinformatics 2013, 11, 405–434. [Google Scholar] [CrossRef] [PubMed]
- Simons, S.; Abásolo, D. Can Distance Measures Based on Lempel–Ziv Complexity Help in the Detection of Alzheimer’s Disease from Electroencephalograms? In Proceedings of the IFMBE Proceedings 41—XIII Mediterranean Conference on Medical and Biological Engineering and Computing 2013, Seville, Spain, 25–28 September 2013; pp. 698–701.
- Zhang, X.S.; Roy, R.J.; Jensen, E.W. EEG complexity as a measure of depth of anesthesia for patients. IEEE Trans. Biomed. Eng. 2001, 48, 1424–1433. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Jeong, J.; Gore, J.; Peterson, B. Mutual information analysis of the EEG in patients with Alzheimer’s disease. Clin. Neurophysiol. 2001, 112, 827–835. [Google Scholar] [CrossRef]
- Johnson, V.E. Revised standards for statistical evidence. Proc. Natl Acad. Sci. USA 2013, 110, 19313–19317. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Abásolo, D.; Escudero, J.; Hornero, R.; Gómez, C.; Espino, P. Approximate entropy and auto mutual information analysis of the electroencephalogram in Alzheimer’s disease patients. Med. Biol. Eng. Comput. 2008, 46, 1019–1028. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Escudero, J.; Abásolo, D.; Hornero, R.; Espino, P.; López, M. Analysis of electroencephalograms in Alzheimer’s disease patients with multiscale entropy. Physiol. Meas. 2006, 27, 1091–1106. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Abásolo, D.; Simons, S.; Escudero, J. Univariate and Multivariate Generalized Multiscale Entropy to Characterise EEG Signals in Alzheimer’s disease. Entropy 2017, 19, 31. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Peng, C.-K.; Lipsitz, L.A. What is physiologic complexity and how does it change with aging and disease? Neurobiol. Aging 2002, 23, 23–26. [Google Scholar] [CrossRef]
- Abásolo, D.; Hornero, R.; Espino, P.; Álvarez, D.; Poza, J. Entropy analysis of the EEG background activity in Alzheimer’s disease patients. Physiol. Meas. 2006, 27, 241–253. [Google Scholar] [CrossRef] [PubMed]
- Abásolo, D.; Hornero, R.; Escudero, J.; Espino, P. A study on the possible usefulness of detrended fluctuation analysis of the electroencephalogram background activity in Alzheimer’s disease. IEEE Trans. Biomed. Eng. 2008, 55, 2171–2179. [Google Scholar] [CrossRef] [PubMed]
- McBride, J.; Zhao, X.; Munro, N.; Smith, C.; Jicha, G.; Jiang, Y. Resting EEG Discrimination of Early Stage Alzheimer’s Disease from Normal Aging Using Inter-Channel Coherence Network Graphs. Ann. Biomed. Eng. 2013, 41, 1233–1242. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Wang, J.; Li, S.; Yu, H.; Deng, B.; Wei, X. Multiple feature extraction and classification of electroencephalograph signal for Alzheimers’ with spectrum and bispectrum. Chaos 2015, 25, 013110. [Google Scholar] [CrossRef] [PubMed]
- Sankari, Z.; Adeli, H.; Adeli, A. Intrahemispheric, interhemispheric, and distal EEG coherence in Alzheimer’s disease. Clin. Neurophysiol. 2011, 122, 897–906. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.J.; Nolte, G.; Daffertshofer, A. Phase lag index: Assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Hum. Brain Mapp. 2007, 28, 1178–1193. [Google Scholar] [CrossRef] [PubMed]
- Wan, B.; Ming, D.; Qi, H.; Xue, Z.; Yin, Y.; Zhou, Z.; Cheng, L. Linear and nonlinear quantitative EEG analysis. IEEE Eng. Med. Biol. Mag. 2008, 27, 58–63. [Google Scholar] [PubMed]
- McBride, J.; Zhao, X.; Munro, N.; Jicha, G.; Smith, C.; Jiang, Y. Discrimination of mild cognitive impairment and Alzheimer’s disease using transfer entropy measures of scalp EEG. J. Healthc. Eng. 2015, 6, 55–70. [Google Scholar] [CrossRef] [PubMed]
- McBride, J.C.; Zhao, X.; Munro, N.B.; Jicha, G.A.; Schmitt, F.A.; Kryscio, R.J.; Smith, C.D.; Jiang, Y. Sugihara causality analysis of scalp EEG for detection of early Alzheimer’s disease. Neuroimage Clin. 2014, 7, 258–265. [Google Scholar] [CrossRef] [PubMed]
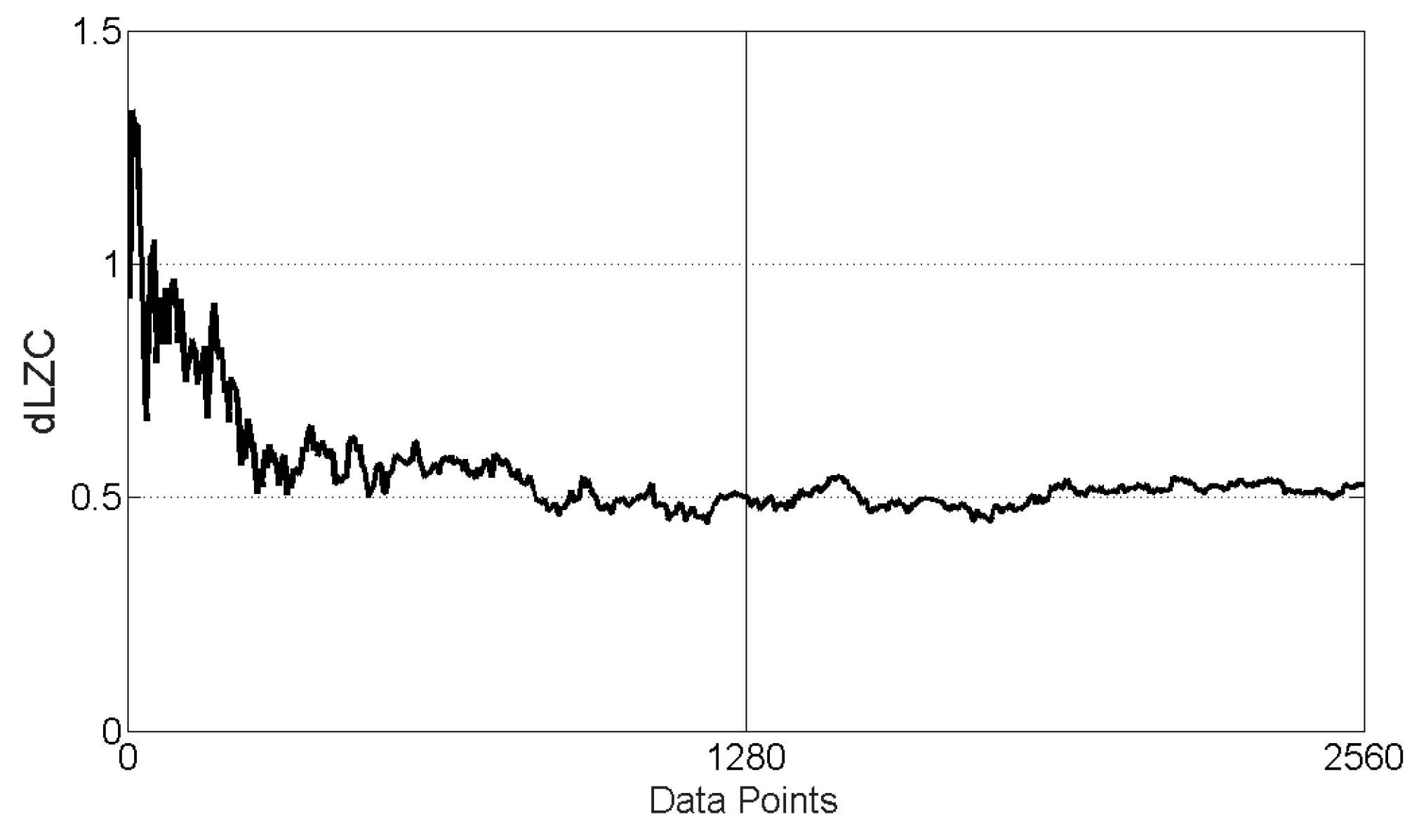
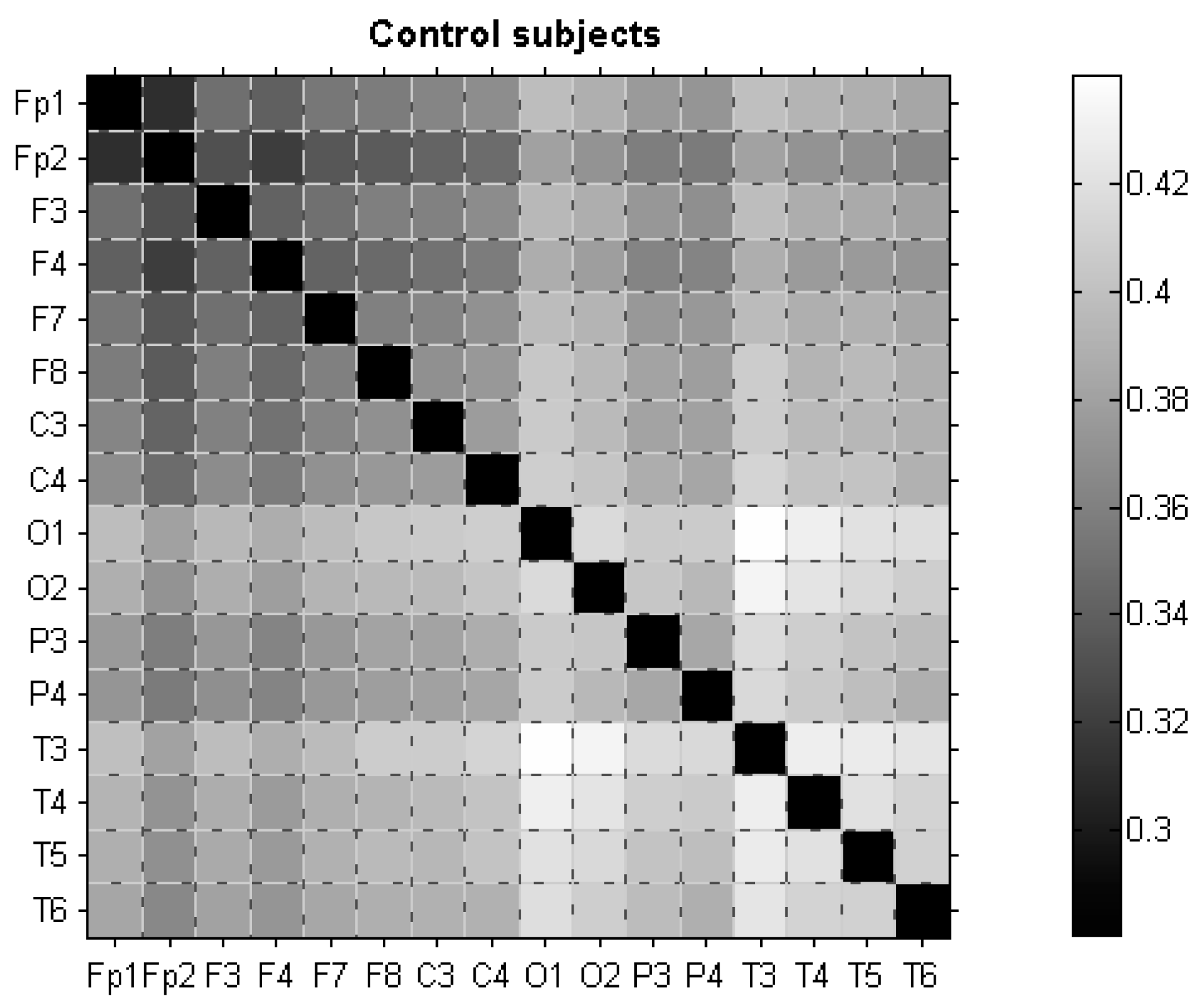
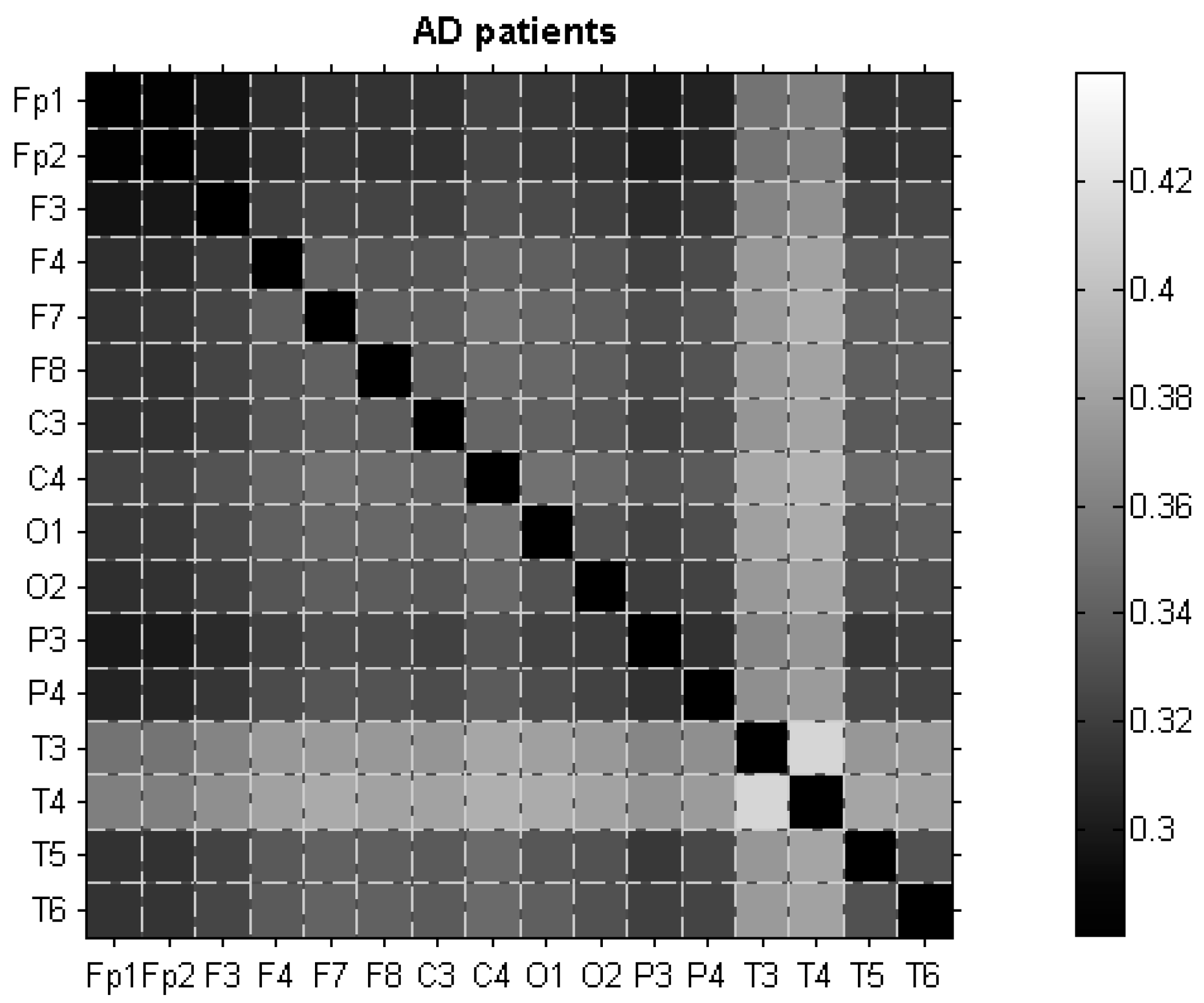
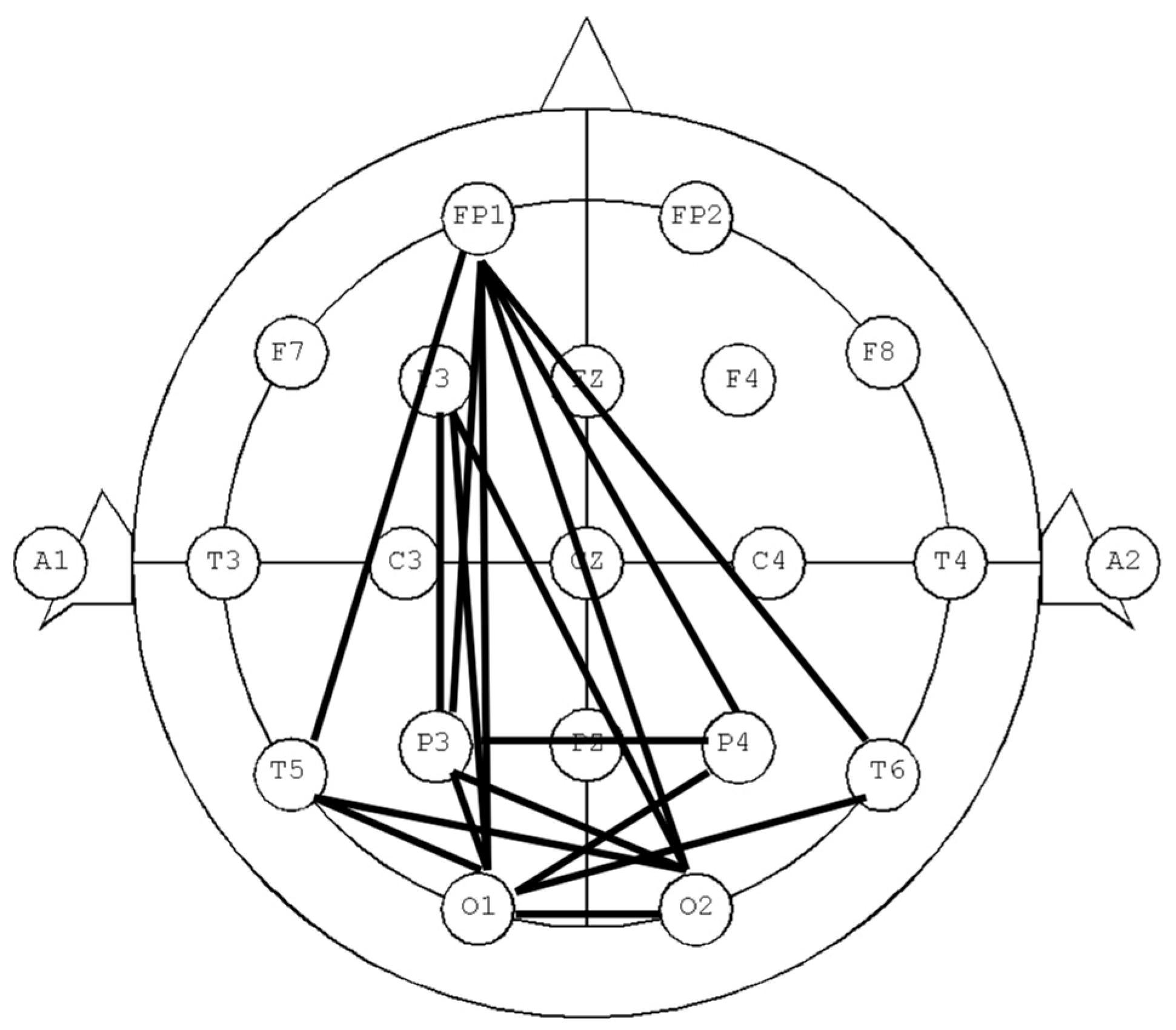
| Coupling | Rössler–Rössler | Rössler–Lorenz |
|---|---|---|
| 0.0 | 0.2609 | 0.2786 |
| 0.05 | 0.2388 | 0.2698 |
| 0.1 | 0.2123 | 0.3450 |
| 0.15 | 0.2211 | 0.3317 |
| 0.2 | 0.2167 | 0.3892 |
| 0.25 | 0.2433 | 0.3715 |
| 0.3 | 0.1592 | 0.4157 |
| 0.35 | 0.2344 | 0.3406 |
| 0.4 | 0.2477 | 0.3848 |
| 0.45 | 0.2654 | 0.4467 |
| 0.5 | 0.2521 | 0.3715 |
| 0.55 | 0.2433 | 0.4069 |
| 0.6 | 0.2433 | 0.3317 |
| 0.65 | 0.2344 | 0.4202 |
| 0.7 | 0.2521 | 0.4334 |
| 0.75 | 0.2433 | 0.3450 |
| 0.8 | 0.2211 | 0.4025 |
| 0.85 | 0.2433 | 0.3804 |
| 0.9 | 0.2388 | 0.3052 |
| 0.95 | 0.2433 | 0.3582 |
| 1.0 | 0.2521 | 0.2698 |
| Region | Electrode Pair | Subject-Based | Epoch-Based | ||||
|---|---|---|---|---|---|---|---|
| Sensitivity | Specificity | Accuracy | Sensitivity | Specificity | Accuracy | ||
| DL | Fp1-O1 | 63.64 | 81.82 | 72.73 | 69.97 | 66.92 | 68.67 |
| Fp1-P3 | 63.64 | 72.73 | 68.18 | 62.89 | 69.58 | 65.75 | |
| Fp1-T5 | 72.73 | 63.64 | 68.18 | 68.84 | 67.68 | 68.34 | |
| F3-O1 | 81.82 | 72.73 | 77.27 | 73.94 | 63.88 | 69.64 | |
| F3-P3 | 72.73 | 72.73 | 72.73 | 61.19 | 72.24 | 65.91 | |
| LPL | O1-P3 | 72.73 | 81.82 | 77.27 | 75.35 | 72.24 | 74.03 |
| O1-T5 | 72.73 | 81.82 | 77.27 | 81.02 | 68.82 | 75.81 | |
| I | Fp1-O2 | 72.73 | 81.82 | 77.27 | 77.05 | 65.40 | 72.08 |
| Fp1-P4 | 63.64 | 81.82 | 72.73 | 62.04 | 63.12 | 62.50 | |
| Fp1-T6 | 63.64 | 90.91 | 77.27 | 63.17 | 68.44 | 65.42 | |
| F3-O2 | 72.73 | 63.64 | 68.18 | 83.85 | 59.32 | 73.38 | |
| O1-O2 | 72.73 | 63.64 | 68.18 | 83.57 | 71.10 | 78.25 | |
| O1-P4 | 72.73 | 81.82 | 77.27 | 78.75 | 69.20 | 74.68 | |
| O1-T6 | 63.64 | 90.91 | 77.27 | 78.47 | 70.72 | 75.16 | |
| O2-P3 | 81.82 | 54.55 | 68.18 | 78.19 | 69.96 | 74.68 | |
| O2-T5 | 81.82 | 63.64 | 72.73 | 75.35 | 71.10 | 73.54 | |
| P3-P4 | 54.55 | 63.64 | 59.09 | 67.14 | 67.30 | 67.21 | |
| Mean ± SD | LAR | LAL | LPR | LPL * | DR | DL * | I |
|---|---|---|---|---|---|---|---|
| Controls | 0.35 ± 0.05 | 0.36 ± 0.04 | 0.40 ± 0.05 | 0.40 ± 0.04 | 0.37 ± 0.03 | 0.39 ± 0.04 | 0.38 ± 0.04 |
| AD patients | 0.33 ± 0.05 | 0.32 ± 0.05 | 0.34 ± 0.06 | 0.33 ± 0.07 | 0.33 ± 0.05 | 0.32 ± 0.05 | 0.34 ± 0.05 |
| Region | Subject-Based | Epoch-Based | ||||
|---|---|---|---|---|---|---|
| Sensitivity | Specificity | Accuracy | Sensitivity | Specificity | Accuracy | |
| LPL | 54.55 | 63.64 | 59.09 | 74.22 | 69.96 | 72.40 |
| DL | 72.73 | 63.64 | 68.18 | 67.42 | 66.54 | 67.05 |
| Method | Electrode | Subject-Based | Epoch-Based | ||||
|---|---|---|---|---|---|---|---|
| Sensitivity | Specificity | Accuracy | Sensitivity | Specificity | Accuracy | ||
| Sample Entropy (SampEn) (m = 1, r = 0.25) [42] | P3 | 72.73 | 81.82 | 77.27 | NR | NR | NR |
| P4 | 63.64 | 90.91 | 77.27 | NR | NR | NR | |
| O1 | 81.82 | 72.73 | 77.27 | NR | NR | NR | |
| O2 | 90.91 | 63.64 | 77.27 | NR | NR | NR | |
| Lempel-Ziv Complexity (LZC) (3 symbol conversion) [20] | T5 | 72.73 | 72.73 | 72.73 | NR | NR | NR |
| P3 | 81.82 | 81.82 | 81.82 | NR | NR | NR | |
| P4 | 72.73 | 90.91 | 81.82 | NR | NR | NR | |
| O1 | 90.91 | 72.73 | 81.82 | NR | NR | NR | |
| Slope of Multiscale Entropy (MSE) (m = 1, r = 0.25, 12 scales) for large time scales [39] | F3 | 81.82 | 81.82 | 81.82 | NR | NR | NR |
| F7 | 81.82 | 72.73 | 77.27 | NR | NR | NR | |
| Fp1 | 90.91 | 90.91 | 90.91 | NR | NR | NR | |
| Fp2 | 100 | 72.73 | 86.36 | NR | NR | NR | |
| T5 | 90.91 | 81.82 | 86.36 | NR | NR | NR | |
| T6 | 81.82 | 81.82 | 81.82 | NR | NR | NR | |
| P3 | 81.82 | 90.91 | 86.36 | NR | NR | NR | |
| P4 | 72.73 | 90.91 | 81.82 | NR | NR | NR | |
| O1 | 81.82 | 90.91 | 86.36 | NR | NR | NR | |
| O2 | 81.82 | 81.82 | 81.82 | NR | NR | NR | |
| Approximate Entropy (ApEn) (m = 1, r = 0.25) [37] | P3 | 72.73 | 81.82 | 77.27 | NR | NR | NR |
| P4 | 63.64 | 81.82 | 72.73 | NR | NR | NR | |
| O1 | 81.82 | 72.73 | 77.27 | NR | NR | NR | |
| O2 | 90.91 | 63.64 | 77.27 | NR | NR | NR | |
| Auto-Mutual Information (AMI) rate of decrease [37] | T5 | 90.91 | 72.73 | 81.82 | NR | NR | NR |
| T6 | 81.82 | 81.82 | 81.82 | NR | NR | NR | |
| P3 | 100.00 | 81.82 | 90.91 | NR | NR | NR | |
| P4 | 81.82 | 81.82 | 81.82 | NR | NR | NR | |
| O1 | 81.82 | 81.82 | 81.82 | NR | NR | NR | |
| O2 | 81.82 | 81.82 | 81.82 | NR | NR | NR | |
| * Detrended Fluctuation Analysis (DFA) (α2) [43] | T5 | 54.55 | 81.82 | 68.18 | 54.05 | 85.19 | 69.10 |
| T6 | 72.73 | 72.73 | 72.73 | 60.98 | 79.50 | 69.91 | |
| O1 | 54.55 | 72.73 | 63.64 | 60.98 | 81.71 | 71.07 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simons, S.; Abásolo, D. Distance-Based Lempel–Ziv Complexity for the Analysis of Electroencephalograms in Patients with Alzheimer’s Disease. Entropy 2017, 19, 129. https://doi.org/10.3390/e19030129
Simons S, Abásolo D. Distance-Based Lempel–Ziv Complexity for the Analysis of Electroencephalograms in Patients with Alzheimer’s Disease. Entropy. 2017; 19(3):129. https://doi.org/10.3390/e19030129
Chicago/Turabian StyleSimons, Samantha, and Daniel Abásolo. 2017. "Distance-Based Lempel–Ziv Complexity for the Analysis of Electroencephalograms in Patients with Alzheimer’s Disease" Entropy 19, no. 3: 129. https://doi.org/10.3390/e19030129
APA StyleSimons, S., & Abásolo, D. (2017). Distance-Based Lempel–Ziv Complexity for the Analysis of Electroencephalograms in Patients with Alzheimer’s Disease. Entropy, 19(3), 129. https://doi.org/10.3390/e19030129







