Entropy Generation Analysis and Performance Evaluation of Turbulent Forced Convective Heat Transfer to Nanofluids
Abstract
:1. Introduction
2. Problem Description
3. Numerical Approach
3.1. Properties of Nanofluids
3.2. Governing Equations of CFD Calculation
- Continuity equation:
- Momentum equation:
- Energy equation:where the variables with bar represent mean parameters, i.e., mean velocity and mean temperature. The μt and αt are the turbulent viscosity and turbulent thermal diffusivity separately, which should be determined using the turbulence model, i.e., standard k–ω model in this work. The model has incorporated modifications for low-Reynolds number effects and shear flow spreading. The transport equations of turbulence kinetic energy k and the specific dissipation rate ω yield as [48]:in which, Gk represents the production term of turbulence kinetic energy due to mean velocity gradients, while Yk represents the dissipation term of turbulence kinetic energy due to turbulence, analogously in the equation of specific dissipation rate ω. Besides, Γk and Γω are the diffusivity of k and ω respectively. The detailed introduction of these term can be obtained in [48]. Through the values of k and ω, the turbulent viscosity and thermal diffusivity are computed as:where Prt is the turbulent Prandtl number and the coefficient is a damping function of turbulent viscosity accounting for low-Reynolds number correction, and it is given by [48]:in which, = = 1 for high-Reynolds number flow, and the variables or parameters are calculated as [48]:
3.3. Entropy Generation
- By assuming the local equilibrium of turbulent kinetic energy, the exact dissipation approximately equals to the production of density and the turbulent dissipation rate; the turbulent dissipation rate is directly proportional to the production of turbulence kinetic energy and specific turbulent dissipation rate; therefore, the equation can be rewritten as:in which, the coefficient Cμ is set as a constant, 0.09.
- By using the Boussinesq approach and a constant turbulent Prandtl number, the entropy generation because of fluctuating temperature gradients is replaced by:
3.4. Boundary Conditions
3.5. Solution Method
4. Results and Discussion
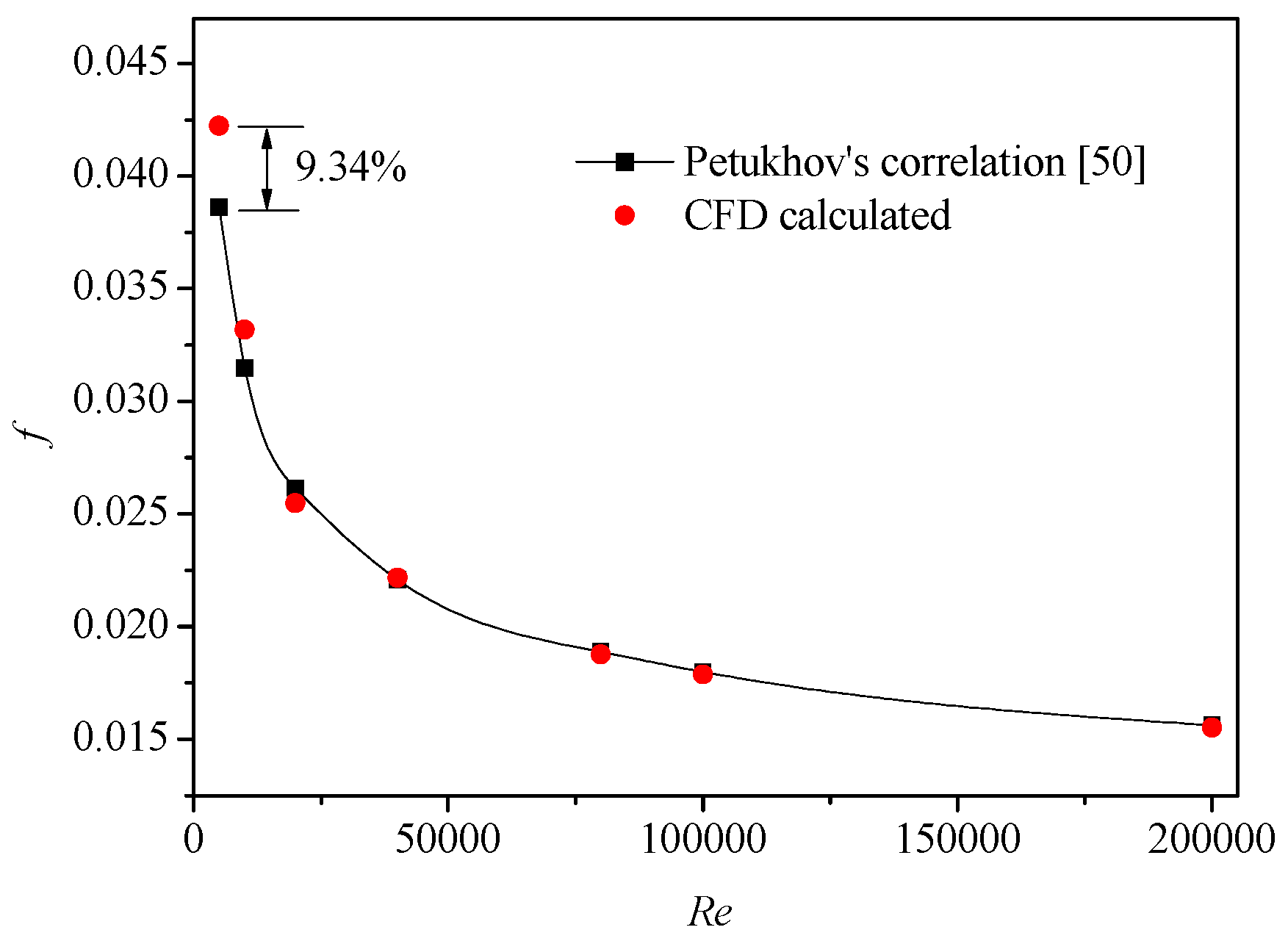
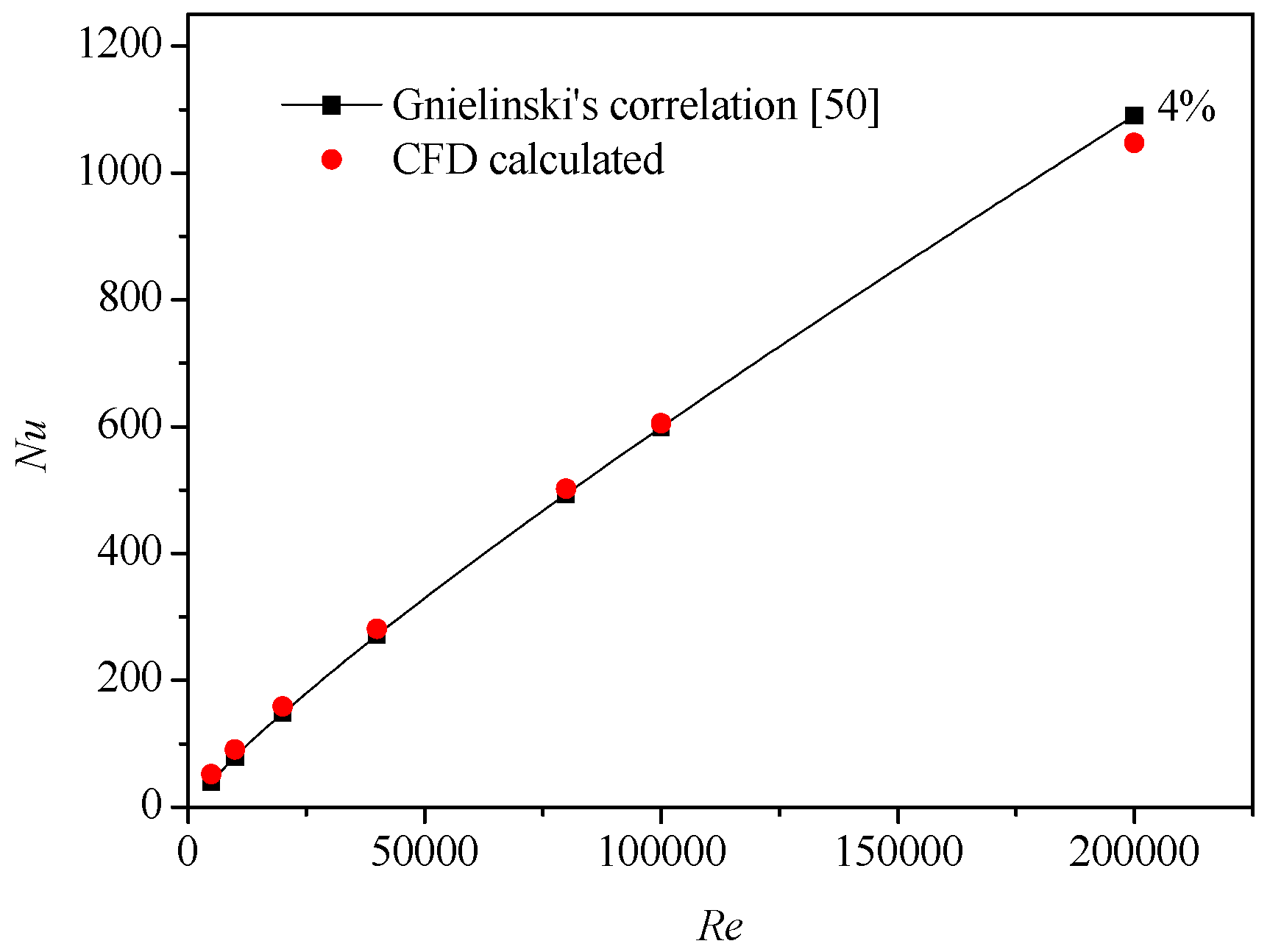
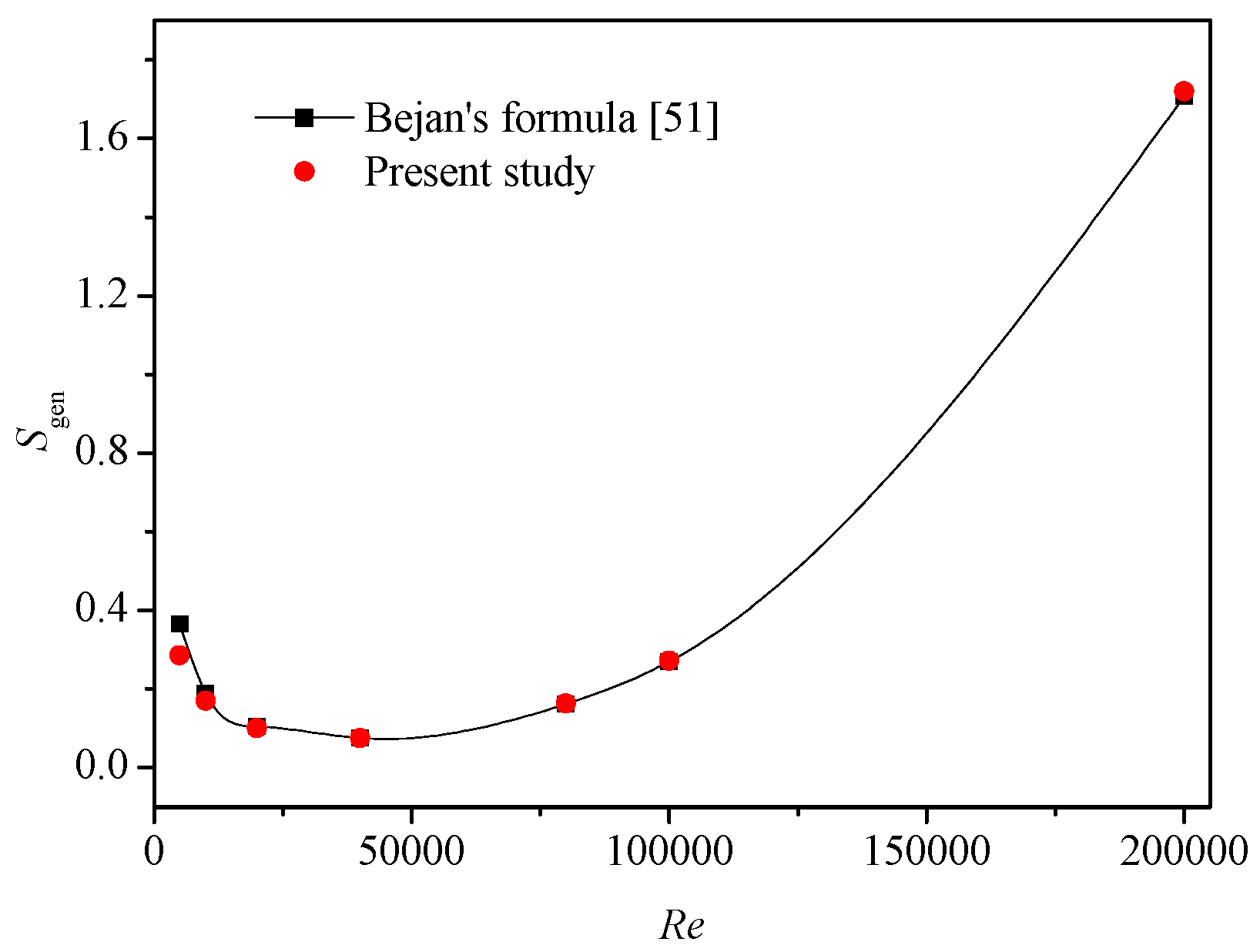
4.1. Verification and Validation
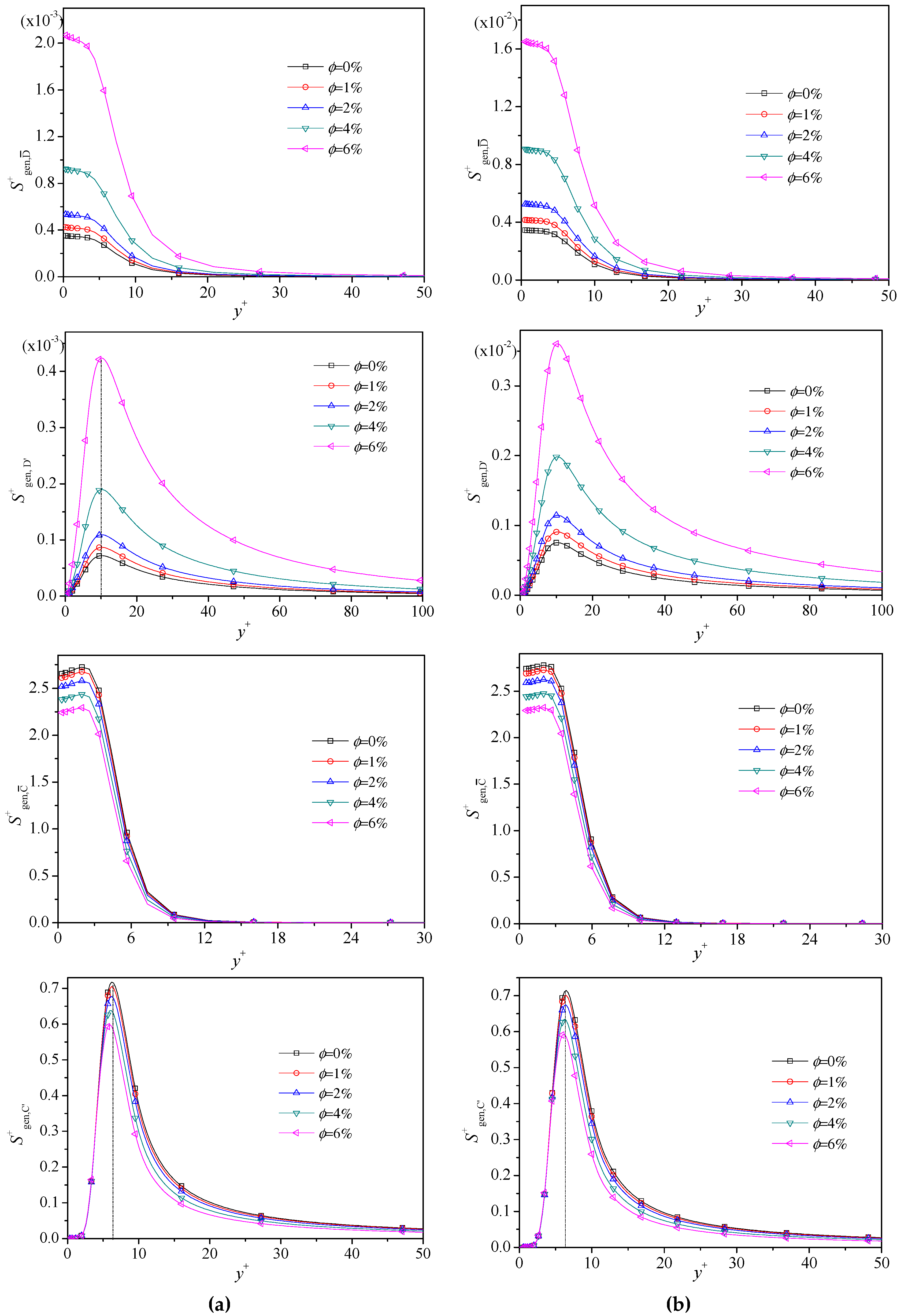
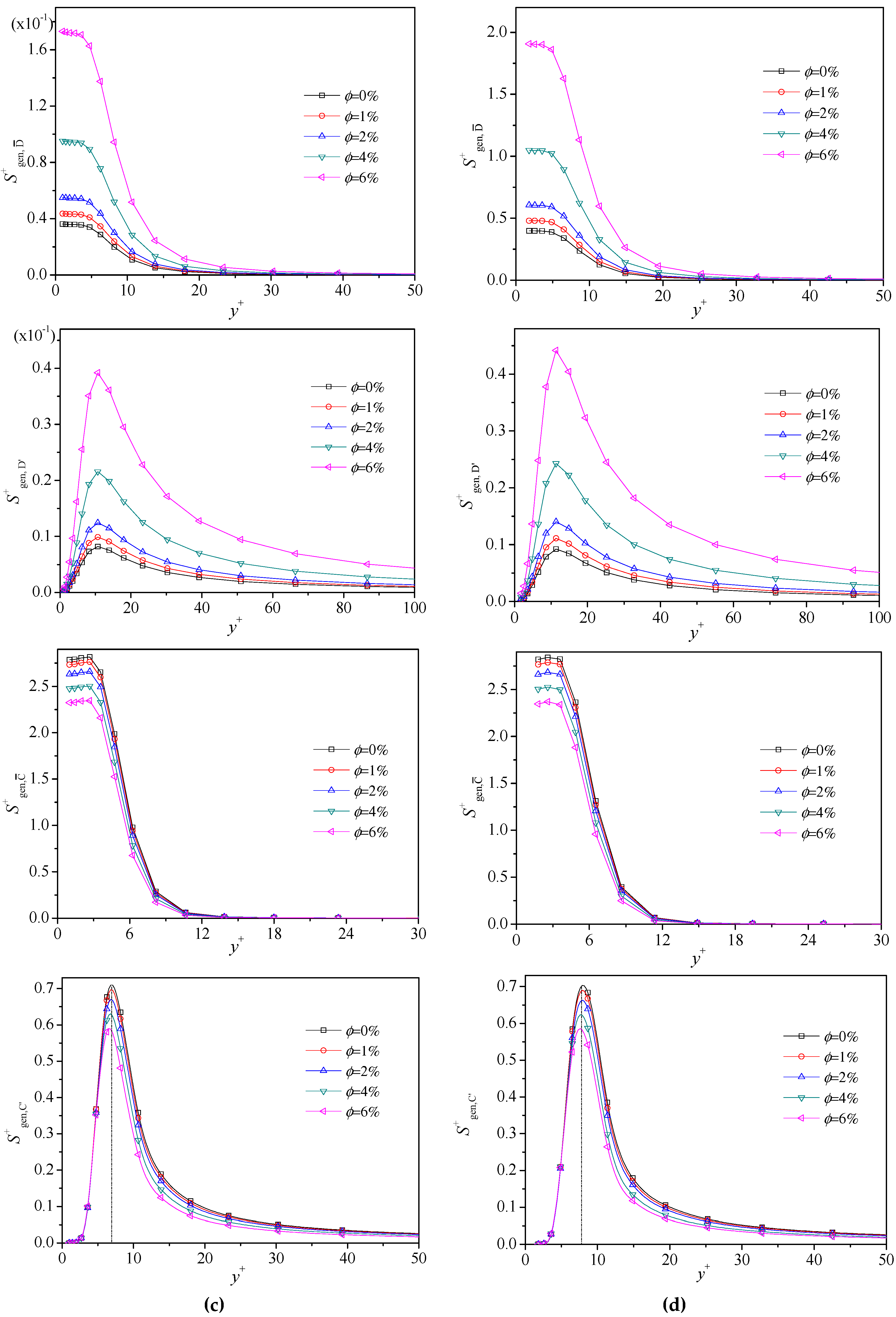
4.2. Local Entropy Generation Profile
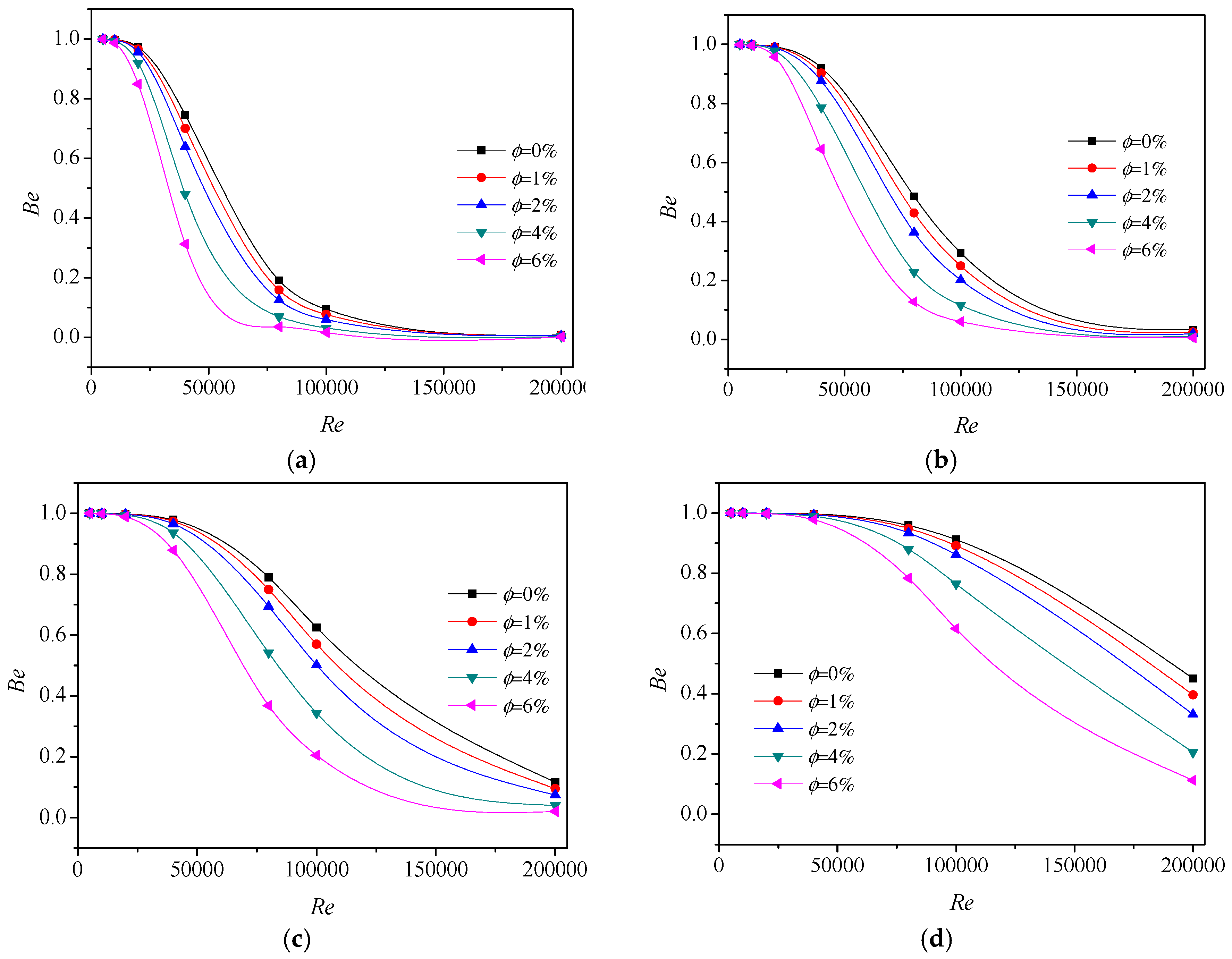
4.3. Thermodynamic Irreversilities
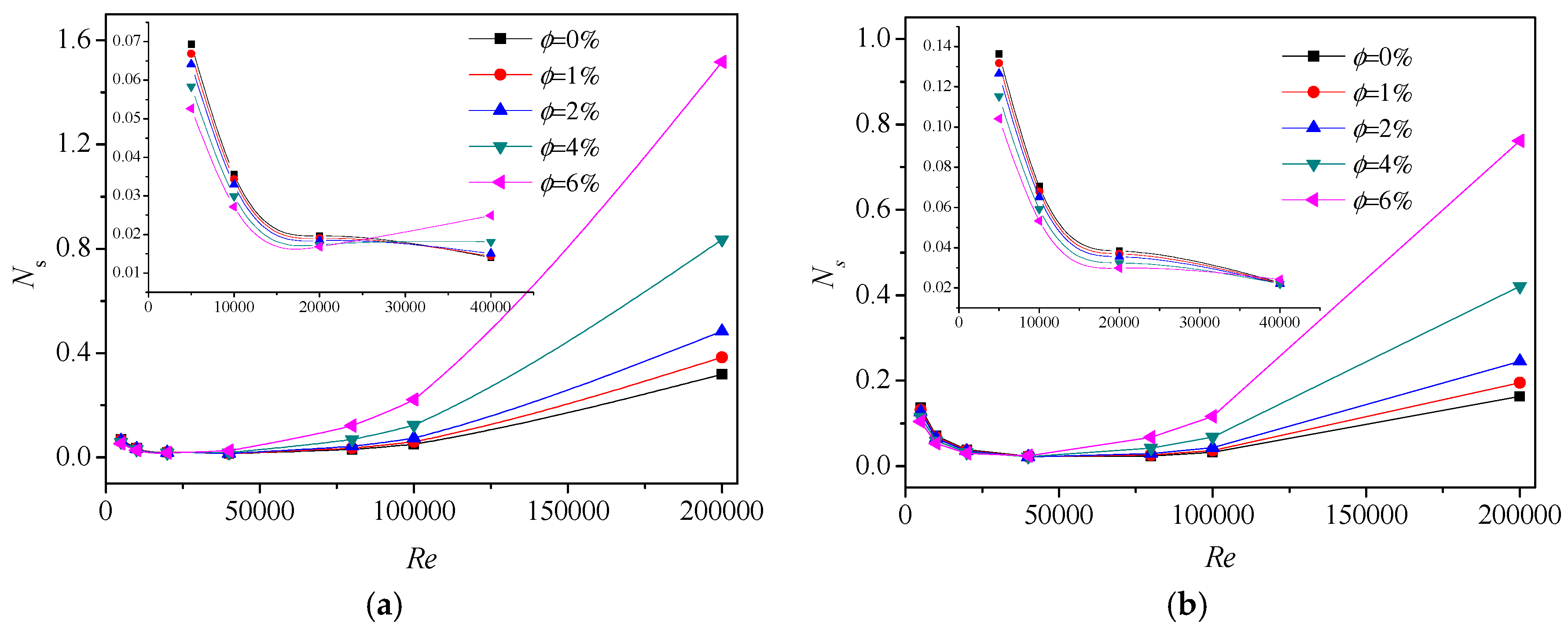
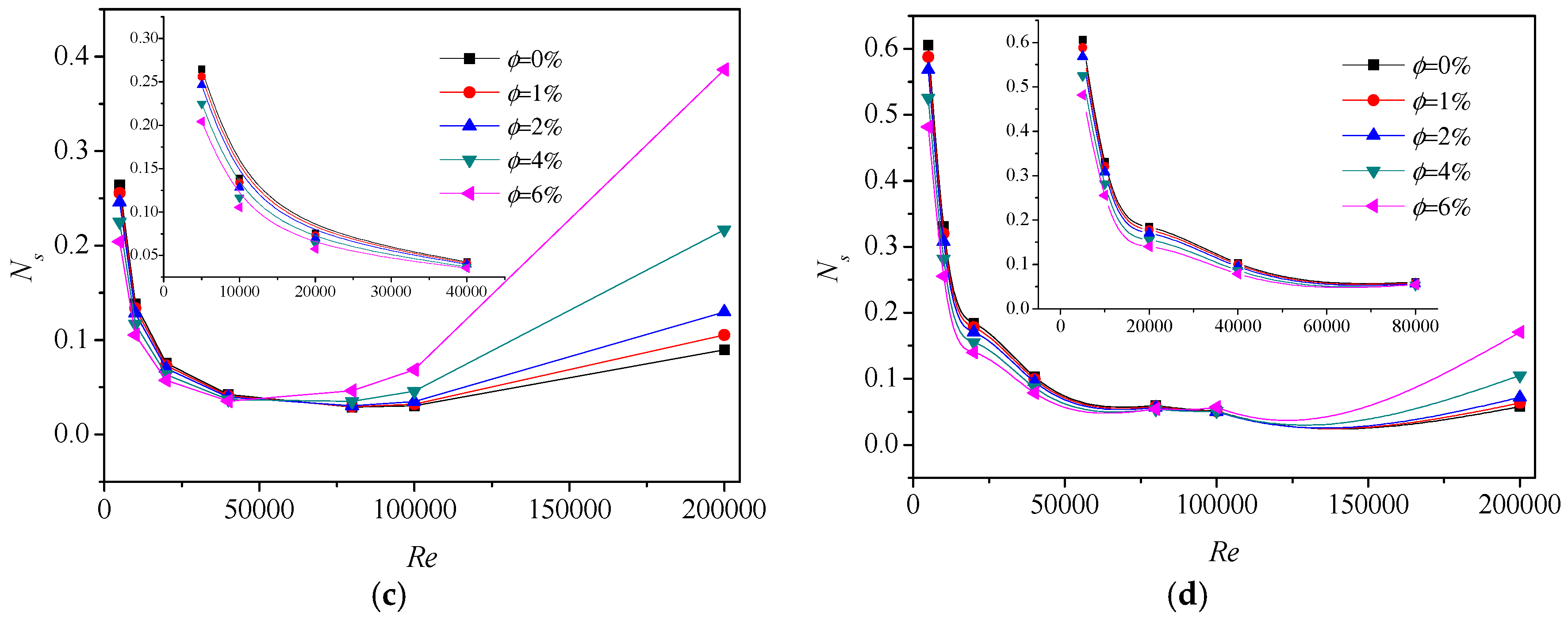
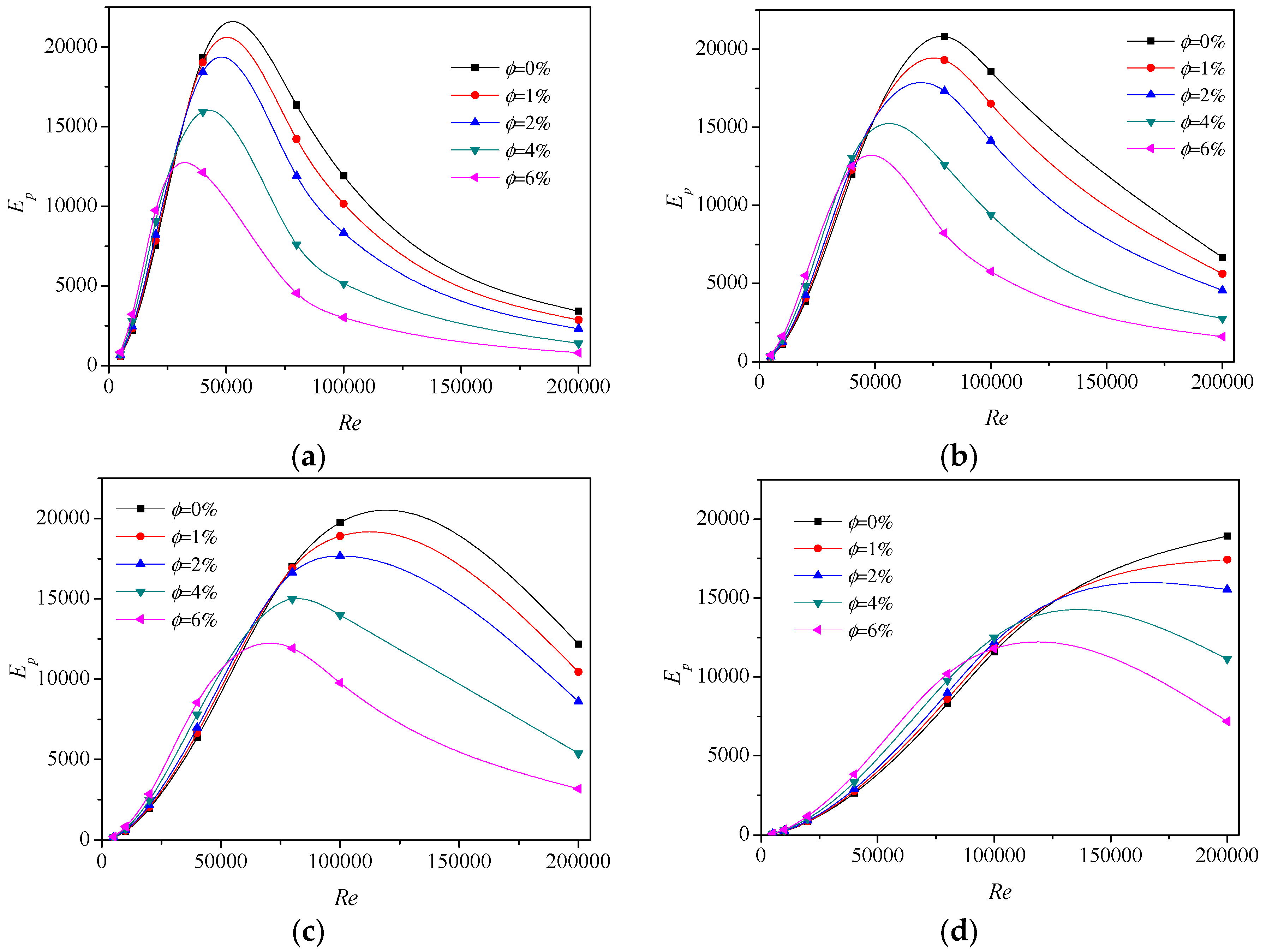
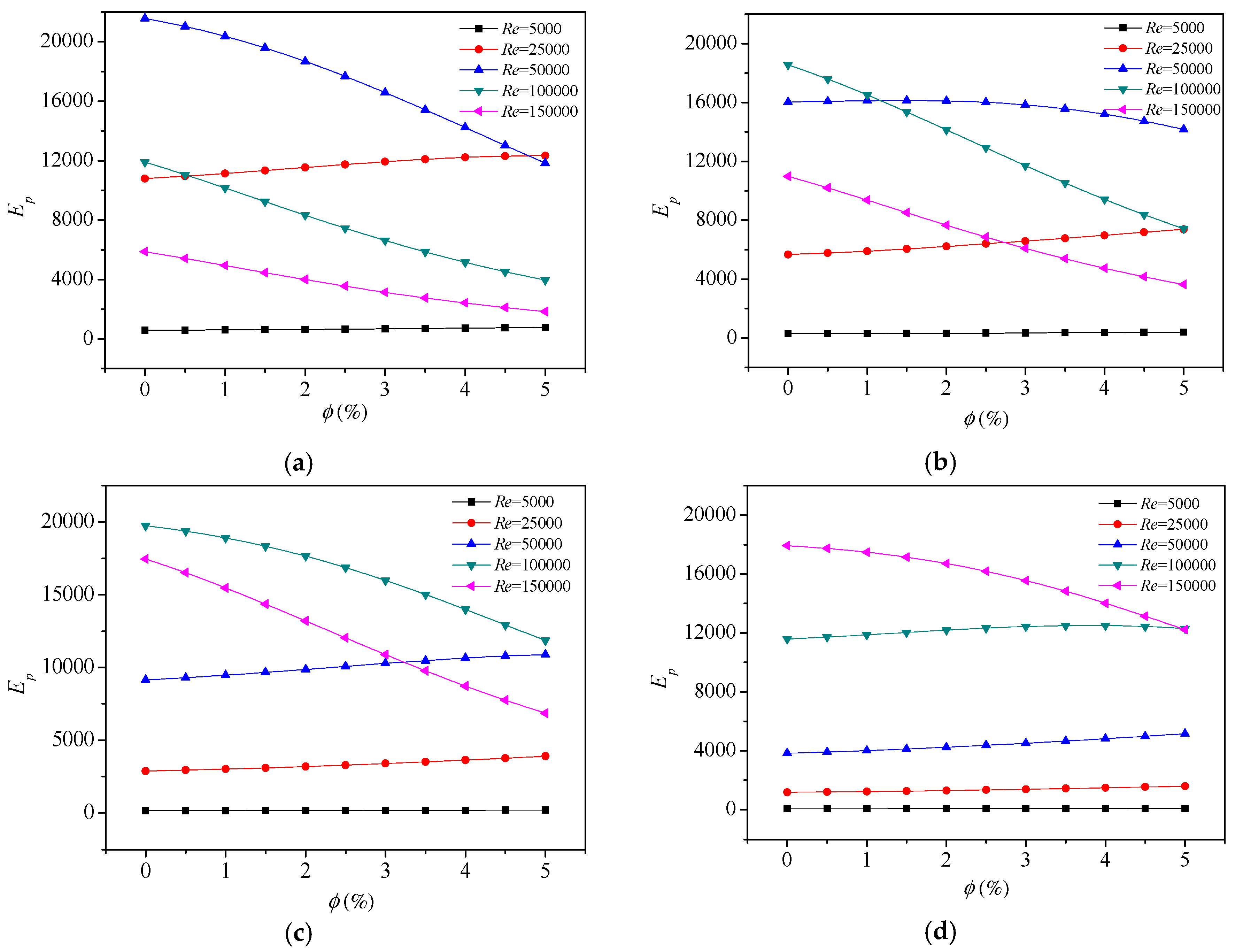
4.4. Performance Evaluation
5. Conclusions
- (1)
- Peak values of local entropy generation due to the mean parameters exist in the viscous sublayer (y+ ~ 5), while those due to fluctuating parameters lie in the buffer layer (y+ > 10) for all nanofluids at different Reynolds number.
- (2)
- Intersection points of total entropy generations for water and other nanofluids have been observed, where the total irreversibilities are equal. The entropy generations decrease before the intersection while increase after the intersection as particle concentration increases, when the heat transfer enhancement through nanofluids is an inadvisable approach from an EGM viewpoint.
- (3)
- The Bejan number, which determines whether the irreversibilities due to heat transfer are dominant, is shown to decrease as the Re increases, particle concentration increases and heat flux reduces.
- (4)
- By definition of the evaluation parameter of Ep, the optimal Reynolds number Reop and the advisable Reynolds number Read can be determined. The decrease of particle concentration and increase of heat flux lead to the growth of Reop. Besides, if Re < Read, the further addition of nanoparticles improves the performance of heat transfer, but if Re > Read, the penalty of Ep occurs.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Be | Bejan number |
| cp | specific heat capacity at constant pressure, J/kg·K |
| Cμ | parameter in the turbulent model |
| Ep | evaluation of performance |
| k | turbulent kinetic energy, m2/s2 |
| Ns | dimensionless entropy generation rate |
| Nu | Nusselts number |
| P | mean pressure, Pa |
| Prt | turbulent Prandtl number |
| q | heat flux, W/m2 |
| Re | Reynolds number |
| S | entropy generation rate, W/m·K |
| T | temperature, K |
| u | velocity, m/s |
| V | volume of fluid domain, m3 |
Greek Letters
| coefficient in the turbulence model | |
| αt | turbulent thermal diffusivity, m2/s |
| Δ | medium variable calculating thermodynamic of nanofluids, W2/m2·K2 |
| ε | turbulent energy dissipated per unit mass, m2/s3 |
| λ | thermal conductivity, W/m·K |
| μ | viscosity, kg/m·s |
| ρ | density, kg/m3 |
| particle concentration | |
| ω | specific dissipation rate, 1/s |
Subscripts and Superscripts
| bf | base fluid |
| C | heat conduction process |
| D | dissipation process |
| gen | generation |
| k | turbulent kinetic |
| nf | nanofluids |
| p | particle |
| ω | specific dissipation rate |
| fluctuating variables | |
| volumetric parameters | |
| mean variables |
Abbreviations
| CFD | computational fluid dynamics |
| EGM | entropy generation minimization |
| EGR | entropy generation rate |
| RANS | Reynolds Averaged Navier–Stokes Equations |
| SIMPLEC | Semi-Implicit Method for Pressure-Linked Equations-Consistent |
References
- Choi, S.U.S. Enhancing Thermal Conductivity of fluids with Nanoparticles. Dev. Appl. Non-Newton. Flows FED/MD 1995, 231, 99–105. [Google Scholar]
- Kakac, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- He, Y.R.; Jin, Y.; Chen, H.S.; Ding, Y.L.; Cang, D.Q.; Lu, H.L. Heat transfer and flow behavior of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. Int. J. Heat Mass Transf. 2007, 50, 2272–2281. [Google Scholar] [CrossRef]
- Xuan, Y.M.; Li, Q. Investigation on convective heat transfer and flow features of nanofluids. J. Heat Transf. 2003, 125, 151–155. [Google Scholar] [CrossRef]
- Li, Q.; Xuan, Y.M. Convective heat transfer and flow characteristic of Cu-water nanofluid. Sci. China Ser. E 2002, 45, 408–416. [Google Scholar]
- Xuan, Y.M.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Rea, U.; Mckrell, T.; Hu, L.W.; Buongiorno, J. Laminar convective heat transfer and viscous pressure loss of alumina-water and zirconia-water nanofluids. Int. J. Heat Mass Transf. 2009, 52, 2042–2048. [Google Scholar] [CrossRef]
- Maiga, S.E.B.; Palm, S.J.; Nguyen, C.T.; Roy, G.; Galanis, N. Heat transfer enhancement by using nanofluids in forced convection flows. Int. J. Heat Fluid Flow 2005, 26, 530–546. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Numerical investigation on nanofluids turbulent convection heat transfer inside a circular tube. Int. J. Therm. Sci. 2011, 50, 341–349. [Google Scholar] [CrossRef]
- Pantzali, M.N.; Kanaris, A.G.; Antoniadis, K.D.; Mouza, A.A.; Paras, S.V. Effect of nanofluids on the performance of miniature plate heat exchanger with modulated surface. Int. J. Heat Fluid Flow 2009, 30, 691–699. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Roy, G.; Gauthier, C.; Galanis, N. Heat transfer enhancement using Al2O3-water nanofluid for an electronic liquid cooling system. Appl. Therm. Eng. 2007, 27, 1501–1506. [Google Scholar] [CrossRef]
- Tsai, T.H.; Chein, R.Y. Performance analysis of nanofluid-cooled micro channel heat sinks. Int. J. Heat Fluid Flow 2007, 28, 1013–1026. [Google Scholar] [CrossRef]
- Li, P.; Xie, Y.; Zhang, D.; Xie, G.N. Heat transfer enhancement and entropy generation of nanofluids laminar convection in microchannels with flow control devices. Entropy 2016, 18, 134. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Second law analysis of Al2O3-water nanofluid turbulent forced convection in a circular cross section tube with constant wall temperature. Adv. Mech. Eng. 2013. [Google Scholar] [CrossRef]
- Chon, C.H.; Kihm, K.D. Thermal conductivity enhancement of nanofluids by Brownian motion. J. Heat Transf. 2005, 127, 810. [Google Scholar] [CrossRef]
- Yu, C.J.; Richter, A.G.; Datta, A.; Durbin, M.K.; Dutta, P. Observation of molecular layering in thin liquid films using X-ray reflectivity. Phys. Rev. Lett. 1999, 82, 2326–2329. [Google Scholar] [CrossRef]
- Keblinski, P.; Phillpot, S.R.; Choi, S.U.S.; Eastman, J.A. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int. J. Heat Mass Transf. 2002, 45, 855–863. [Google Scholar] [CrossRef]
- Yu, W.; Choi, S.U.S. The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A renovated Maxwell model. J. Nanopart. Res. 2003, 5, 167–171. [Google Scholar] [CrossRef]
- Ding, Y.L.; Wen, D.S. Particle migration in a flow of nanoparticle suspensions. Powder Technol. 2005, 149, 84–92. [Google Scholar] [CrossRef]
- Mwesigye, A.; Huan, Z.J. Thermodynamics analysis and optimization of fully developed turbulent forced convection in a circular tube with water-Al2O3 nanofluid. Int. J. Heat Mass Transf. 2015, 89, 694–706. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, H.C.; Tong, J.F.; Wang, X.W.; Wang, H.; Zhang, Y.N. Entropy assessment on direct contact condensation of subsonic steam jets in a water tank through numerical investigation. Entropy 2016, 18, 21. [Google Scholar] [CrossRef]
- Herwig, H.; Wenterodt, T. Second Law Analysis of Momentum and Heat Transfer in Unit Operations. Int. J. Heat Mass Transf. 2011, 54, 1323–1330. [Google Scholar] [CrossRef]
- Schmandt, B.; Herwig, H. Loss Coefficients in Laminar Flows: Essential for the Design of Micro Flow Systems. PAMM 2011, 11, 27–30. [Google Scholar] [CrossRef]
- Jin, Y.; Herwig, H. Turbulent flow and heat transfer in channels with shark skin surfaces: Entropy generation and its physical significance. Int. J. Heat Mass Transf. 2014, 70, 10–22. [Google Scholar] [CrossRef]
- Goudarzi, N.; Talebi, S. Improving performance of two-phase natural circulation loops by reducing of entropy generation. Energy 2015, 93, 882–899. [Google Scholar] [CrossRef]
- Khalkhali, H.; Faghri, A.; Zuo, Z.J. Entropy generation in a heat pipe system. Appl. Therm. Eng. 1999, 19, 1027–1043. [Google Scholar] [CrossRef]
- Myat, A.; Thu, K.; Kim, Y.D.; Chakraborty, A.; Chun, W.G.; Ng, K.C. A second law analysis and entropy generation minimization of an absorption chiller. Appl. Therm. Eng. 2011, 31, 2405–2413. [Google Scholar] [CrossRef]
- Singh, P.K.; Anoop, T.; Sundararajan, T.; Das, S.K. Entropy generation due to flow and heat transfer in nanofluids. Int. J. Heat Mass Transf. 2010, 53, 4757–4767. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Entropy generation analysis of turbulent convection flow of Al2O3 nanofluid in a circular tube subjected to constant wall heat flux. Energy Convers. Manag. 2014, 77, 306–314. [Google Scholar] [CrossRef]
- Siavashi, M.; Jamali, M. Heat transfer and entropy generation analysis of turbulent flow of TiO2-water nanofluid inside annuli with different radius ratios using two-phase mixture model. Appl. Therm. Eng. 2016, 100, 1149–1160. [Google Scholar] [CrossRef]
- Kuppusamy, N.R.; Mohammed, H.A.; Lim, C.W. Numerical investigation of trapezoidal grooved microchannel heat sink using nanofluids. Thermochim. Acta 2013, 573, 39–56. [Google Scholar] [CrossRef]
- Roy, G.; Nguyen, C.T.; Lajoie, P.R. Numerical investigation of laminar flow and heat transfer in a radial flow cooling system with the use of nanofluids. Superlattices Microstruct. 2004, 35, 497–511. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. An experimental study on the heat transfer performance and pressure drop of TiO2-water nanofluids flowing under a turbulent flow regime. Int. J. Heat Mass Transf. 2010, 53, 334–344. [Google Scholar]
- Akbari, M.; Galanis, N.; Behzadmehr, A. Comparative assessment of single and two-phase models for numerical studies of nanofluid turbulent forced convection. Int. J. Heat Fluid Flow 2012, 37, 136–146. [Google Scholar] [CrossRef]
- Li, P.; Zhang, D.; Xie, Y.H. Heat transfer and flow analysis of Al2O3-water nanofluids in microchannel with dimple and protrusion. Int. J. Heat Mass Transf. 2014, 73, 456–467. [Google Scholar] [CrossRef]
- Pinto, R.V.; Fiorelli, F.A.S. Review of the mechanisms responsible for heat transfer enhancement using nanofluids. Appl. Therm. Eng. 2016, 108, 720–739. [Google Scholar] [CrossRef]
- Rabiee, A.; Atf, A. A computational fluid dynamics investigation of various nanofluids in a boiling flow field. Prog. Nucl. Energy 2017, 95, 61–69. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.S.; Choi, S.U. Thermal conductivity of nanoparticle-fluid mixture. J. Thermophys. Heat Transf. 1999, 13, 474–480. [Google Scholar] [CrossRef]
- Brinkman, H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571–581. [Google Scholar] [CrossRef]
- Batchelor, G.K. The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 1977, 83, 97–117. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. Int. J. Heat Mass Transf. 2011, 54, 4410–4428. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Vajjha, R.S.; Das, D.K. Experimental determination of thermal conductivity of three nanofluids and development of new correlations. Int. J. Heat Mass Transf. 2009, 52, 4675–4682. [Google Scholar] [CrossRef]
- Buongiorno, J.; Venerus, D.C.; Prabhat, N.; McKrell, T.; Townsend, J.; Christianson, R.; Tolmachev, Y.V.; Keblinski, P.; Hu, L.; Alvarado, J.L.; et al. A benchmark study on the thermal conductivity of nanofluids. J. Appl. Phys. 2009, 106, 094312. [Google Scholar] [CrossRef]
- Wang, X.Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kleinstreuer, C.; Al-Nimr, M.A.; Pop, I.; Sahin, A.Z.; Wongwises, S. A review of entropy generation in nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar] [CrossRef]
- Fluent Inc. Fluent 14.0 Theory Guide; Fluent Inc.: Pittsburgh, PA, USA, 2012. [Google Scholar]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Ghajar, A.J.; Ma, H. Heat and Mass Transfer: Fundamentals & Applications, 4th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]

| Substances | ρ (kg/m3) | cp (J/kg·K) | μ (Pa·s) | λ (W/m·K) |
|---|---|---|---|---|
| Water | 998.2 | 4182.0 | 0.001003 | 0.6 |
| Al2O3 | 3970 | 765 | - | 40 |
| Nodes | f | Difference (%) | Nu | Difference (%) | Ns * | Difference (%) | |
|---|---|---|---|---|---|---|---|
| 1 | 157,628 | 0.0249 | 8.52 | 306.2722 | 5.65 | 0.01756 | 16.8 |
| 2 | 268,068 | 0.0229 | 3.00 | 289.8880 | 3.23 | 0.01503 | 7.72 |
| 3 | 462,844 | 0.0223 | 1.08 | 281.1345 | 0.42 | 0.01396 | 0.12 |
| 4 | 923,844 | 0.0220 | - | 279.6317 | - | 0.01393 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Zhang, H.-C.; Yang, X.; Shi, L. Entropy Generation Analysis and Performance Evaluation of Turbulent Forced Convective Heat Transfer to Nanofluids. Entropy 2017, 19, 108. https://doi.org/10.3390/e19030108
Ji Y, Zhang H-C, Yang X, Shi L. Entropy Generation Analysis and Performance Evaluation of Turbulent Forced Convective Heat Transfer to Nanofluids. Entropy. 2017; 19(3):108. https://doi.org/10.3390/e19030108
Chicago/Turabian StyleJi, Yu, Hao-Chun Zhang, Xie Yang, and Lei Shi. 2017. "Entropy Generation Analysis and Performance Evaluation of Turbulent Forced Convective Heat Transfer to Nanofluids" Entropy 19, no. 3: 108. https://doi.org/10.3390/e19030108
APA StyleJi, Y., Zhang, H.-C., Yang, X., & Shi, L. (2017). Entropy Generation Analysis and Performance Evaluation of Turbulent Forced Convective Heat Transfer to Nanofluids. Entropy, 19(3), 108. https://doi.org/10.3390/e19030108







