“Over-Learning” Phenomenon of Wavelet Neural Networks in Remote Sensing Image Classifications with Different Entropy Error Functions
Abstract
:1. Introduction
2. Method of Study
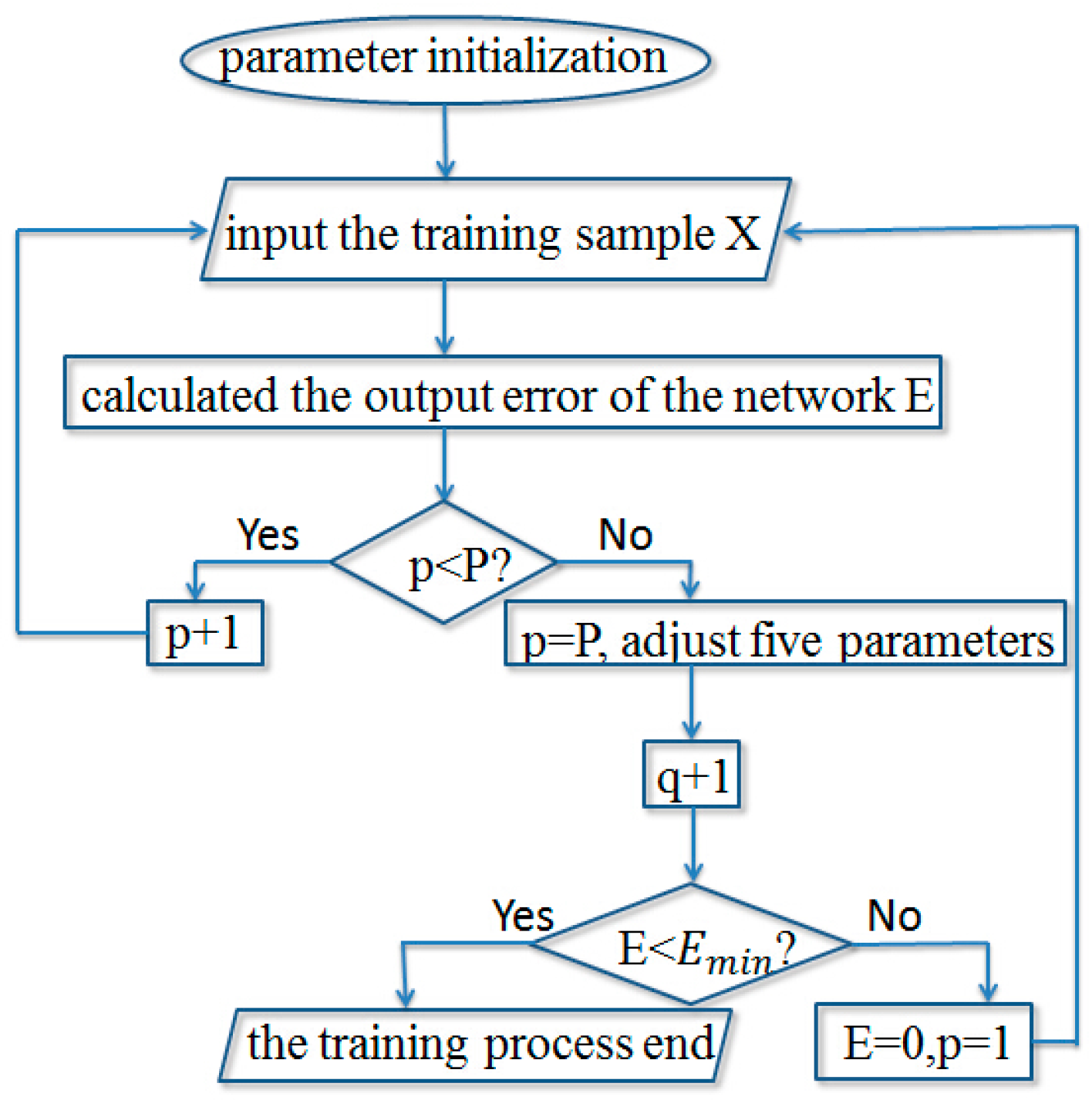
2.1. Structure and Training Process of the Wavelet Neural Network
- (a)
- The preprocessing of the original image is implemented, the features are extracted, and the expert interpretation chart is determined.
- (b)
- The region of interest is selected.
- (c)
- The wavelet neural network model is built, and the number of nodes in each layer is determined (numbers of the input layer nodes equal to numbers of features; numbers of the hidden layer nodes is determined by the testing; numbers of the output layer nodes equal to numbers of classified types), as shown in Figure 1.
- (d)
- The characteristic value of the pixels in the region of interest is used as the input, in order to conduct the training of the wavelet neural network. Setting the number of times of iterations is 100. Setting the output minimum error Emin of the neural is 1 × 10−5. If the output error E < Emin, then end the training. If the E > Emin, then repeat training the network.
- (e)
- The classification result is simulated in order to obtain the classification results of the diagram, and make an accuracy assessment of classification.
- (f)
- The number of nodes of the hidden layer and the number of iterations are adjusted. Trainings are conducted and classification results of the networks with different entropy error function are compared.
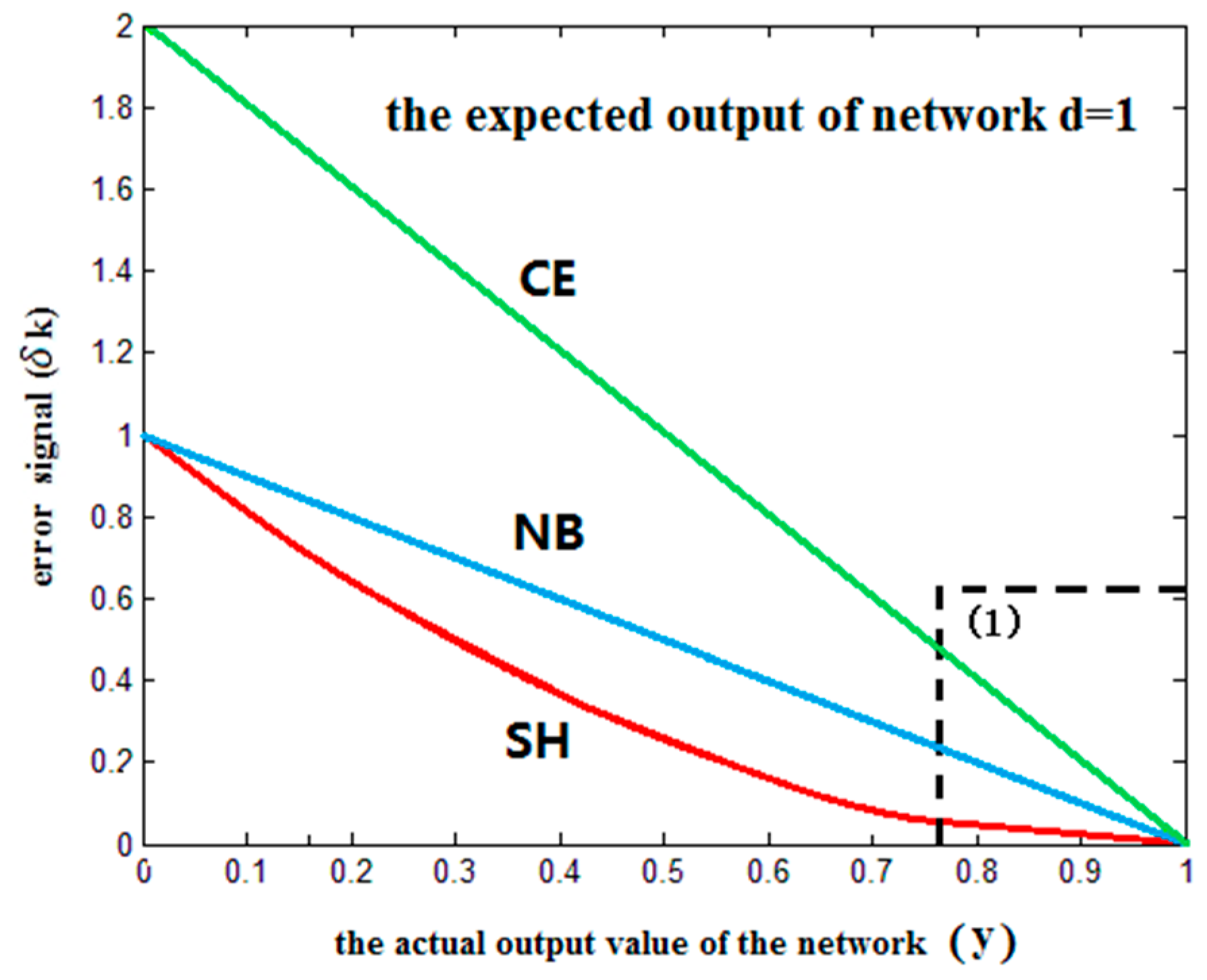
2.2. Entropy Error Function
2.2.1. NB Entropy Error Function
2.2.2. CE Entropy Error Function
2.2.3. SH Entropy Error Function
2.3. “Over-Learning” Phenomenon and Method of Study
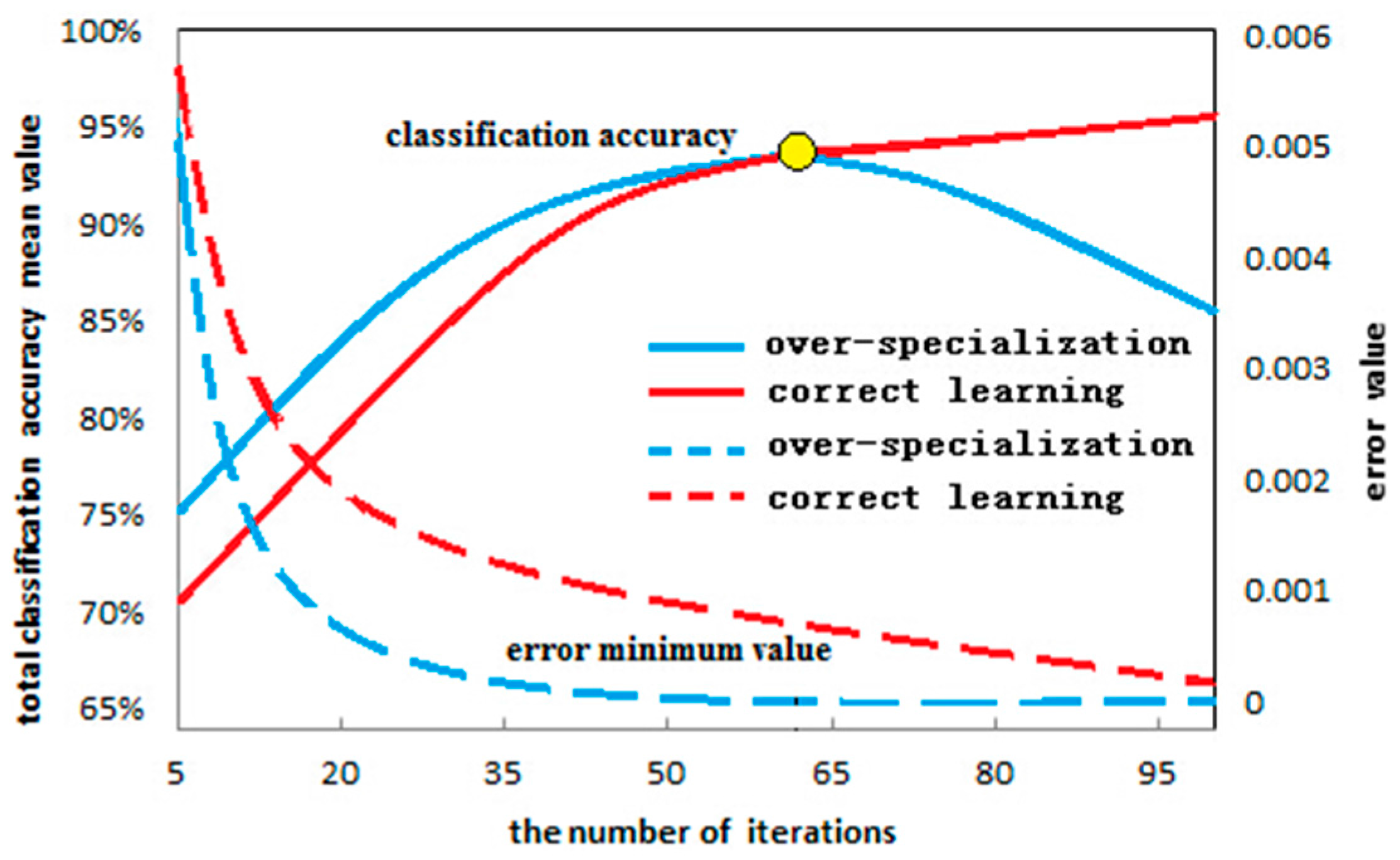
2.3.1. “Over-Learning” Phenomenon
2.3.2. Study Method for the “Over-Learning” Phenomenon
Remote Sensing Image Characteristics and the “Over-Learning” Phenomenon
Number of Hidden Nodes and “Over-Learning” Phenomenon in the Neural Network
Investigation of “Over-Learning” Phenomenon through the Training Process of the Neural Network
3. Experiment and Analysis
3.1. Experiment Images
3.1.1. Data of Experiment 1
3.1.2. Data of Experiment 2
3.1.3. Data of Experiment 3
3.1.4. Data of Experiment 4
3.1.5. Data of Experiment 5
3.1.6. Data of Experiment 6
3.2. Result Analysis of “Over-Learning” Phenomenon
3.2.1. Investigation of “Over-Learning” Phenomenon through the Training Process of Neural Network
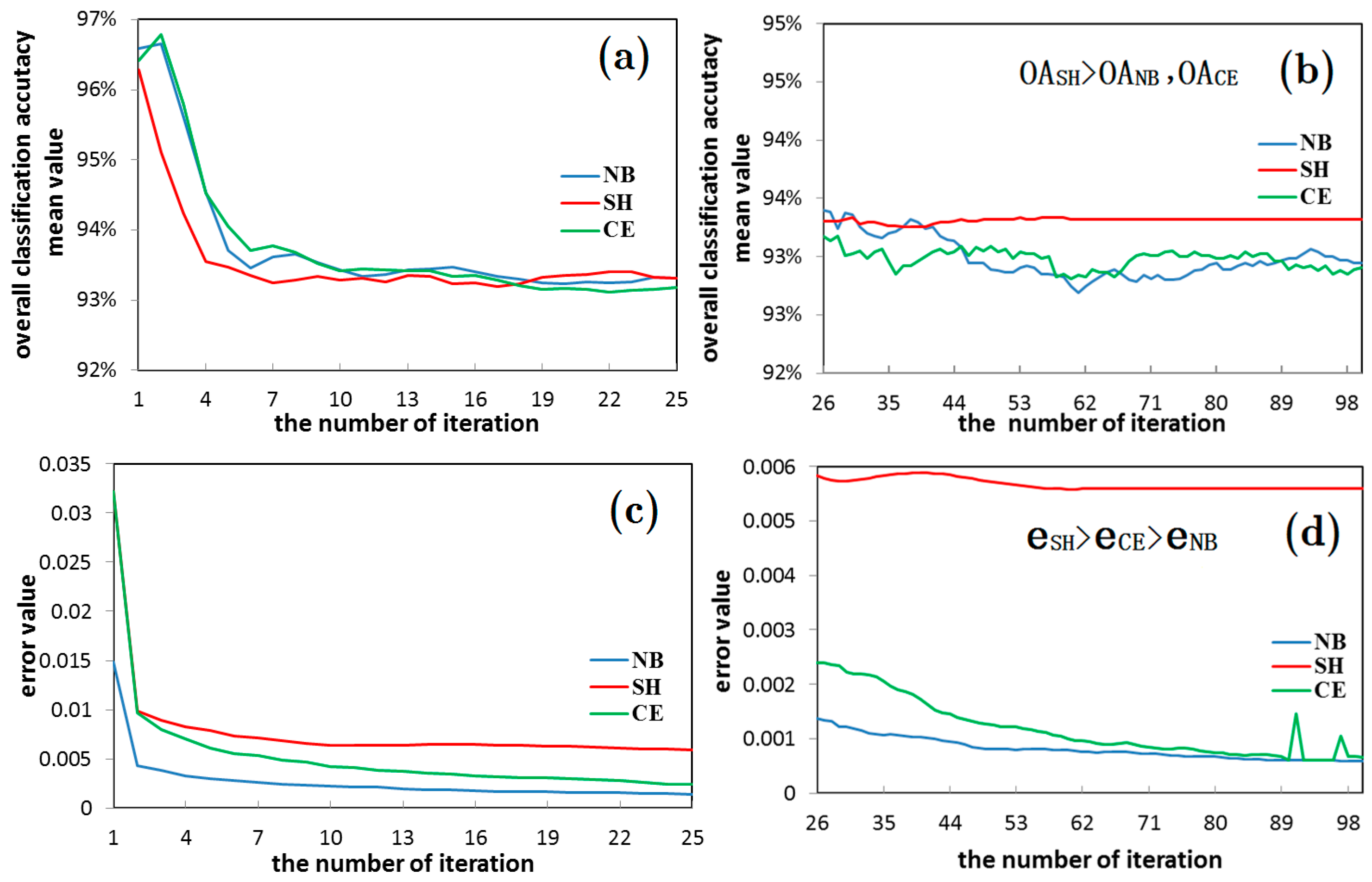
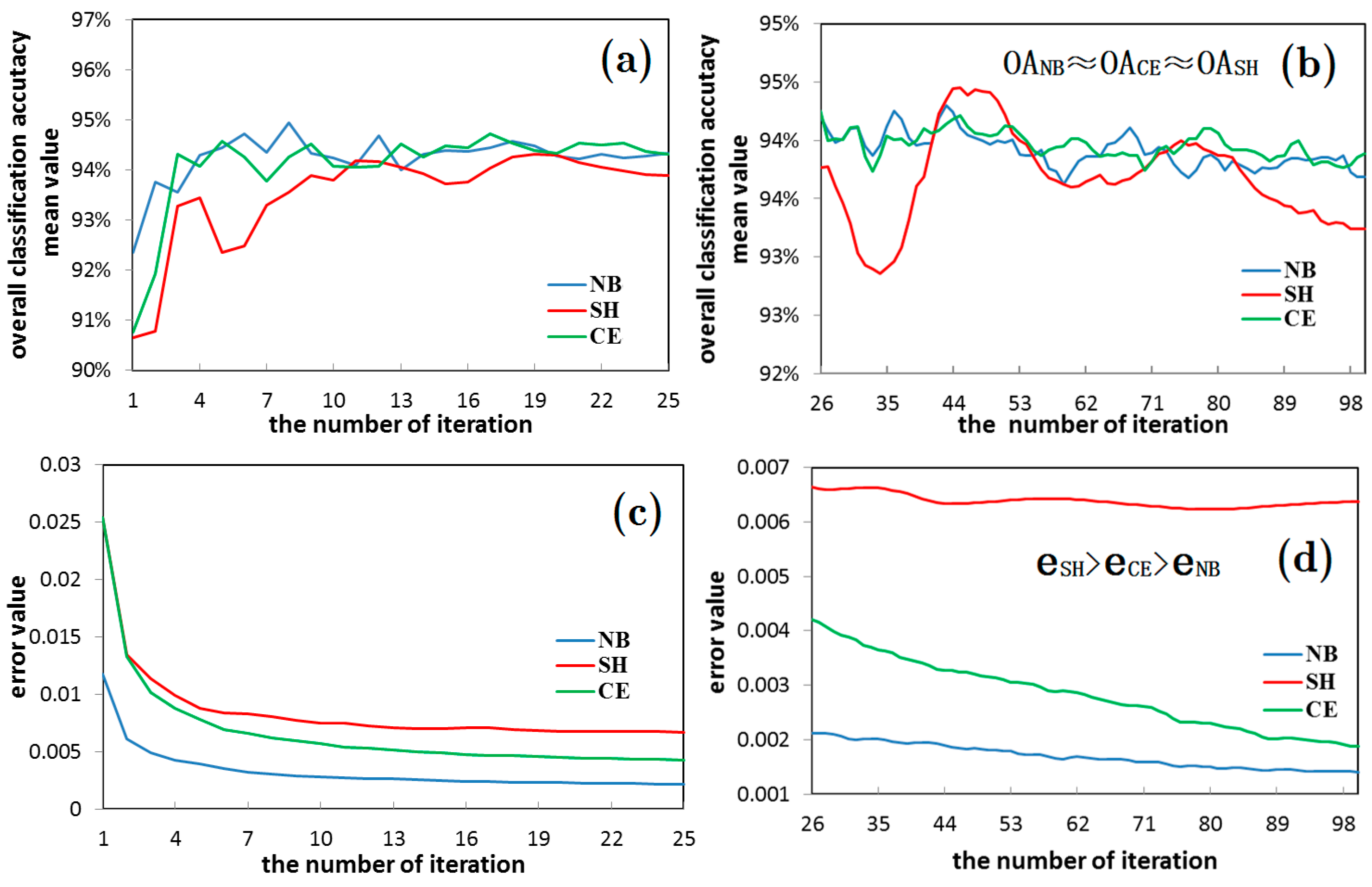
- A network will exhibit an over-learning phenomenon only for a very small size of images with a very low complexity degree. The lager the image size, the larger the AI index of an image, the more complex an image. In the case of that, the “over-learning” phenomenon will not be frequent. During the experiment, the “over-learning” phenomenon is obvious only in the 50 × 50 high-resolution image of houses, and hyper-spectral image of Heihe, which has the smallest AI index. At that time, the minimum error value of the SH entropy error function neural network is larger than that of NB and CE. However, the classification accuracy of the SH entropy error network is higher than that of the NB and CE. Therefore, the SH entropy error network shows a good “over-learning” resistance ability, while the NB and SH entropy error function networks exhibits the “over-learning” phenomenon.
- In most experiments (SAR, multi-spectral, and hyper-spectral image), the classification accuracy of the SH entropy error is lower than that of the NB and CE, and the classification accuracy of the SH entropy error will be higher than NB and CE only when the image complexity degree is very low. These results in fact show that the wavelet neural network for the remote sensing image will not easily cause an “over-learning” phenomenon. Also, the NB and CE networks will exhibit an “over-learning” phenomenon only when the image is small, such as merely containing 50 × 50 pixels (however, this is rare).
3.2.2. Remote Sensing Image Characteristics and “Over-Learning” Phenomenon
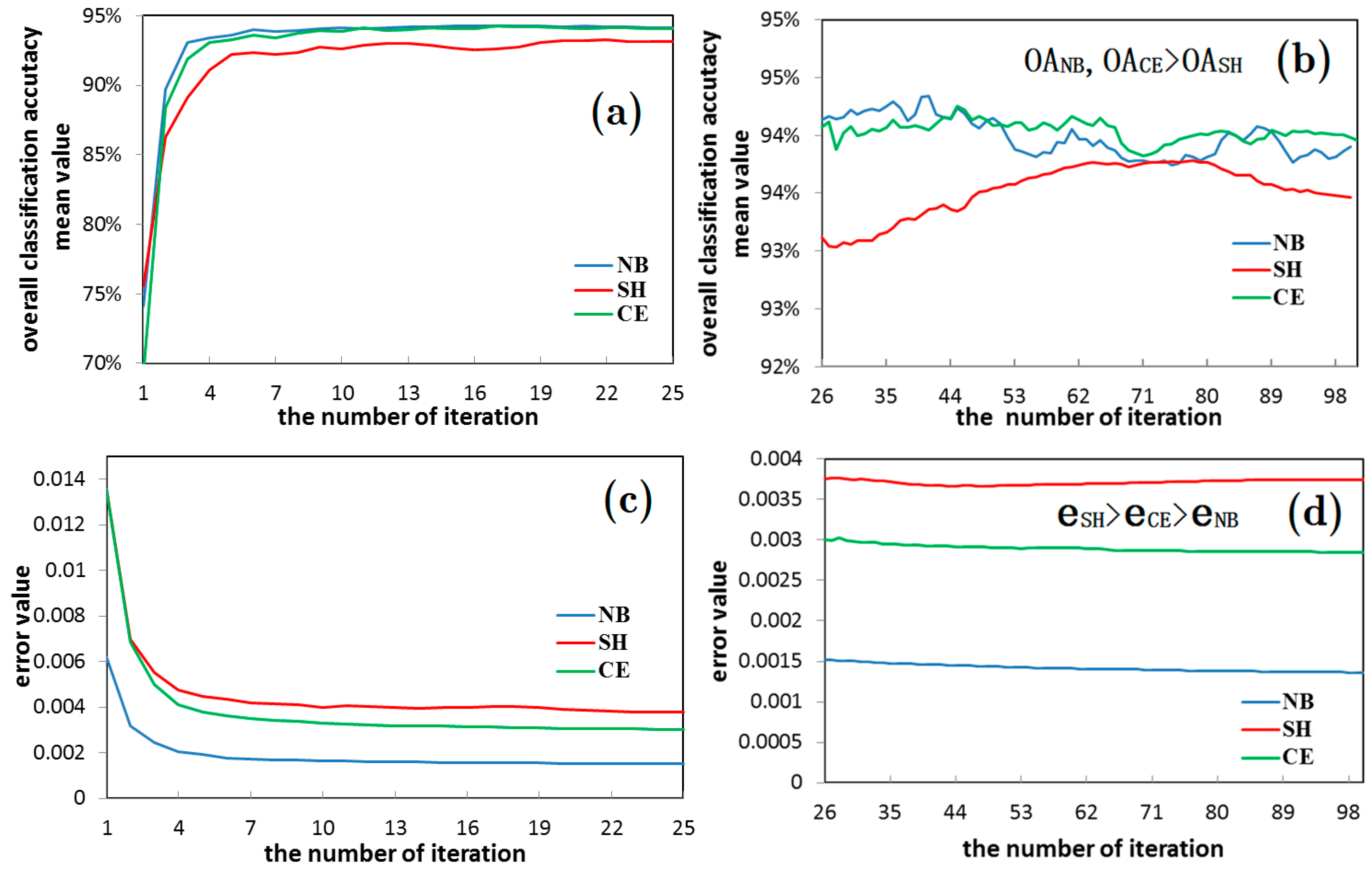
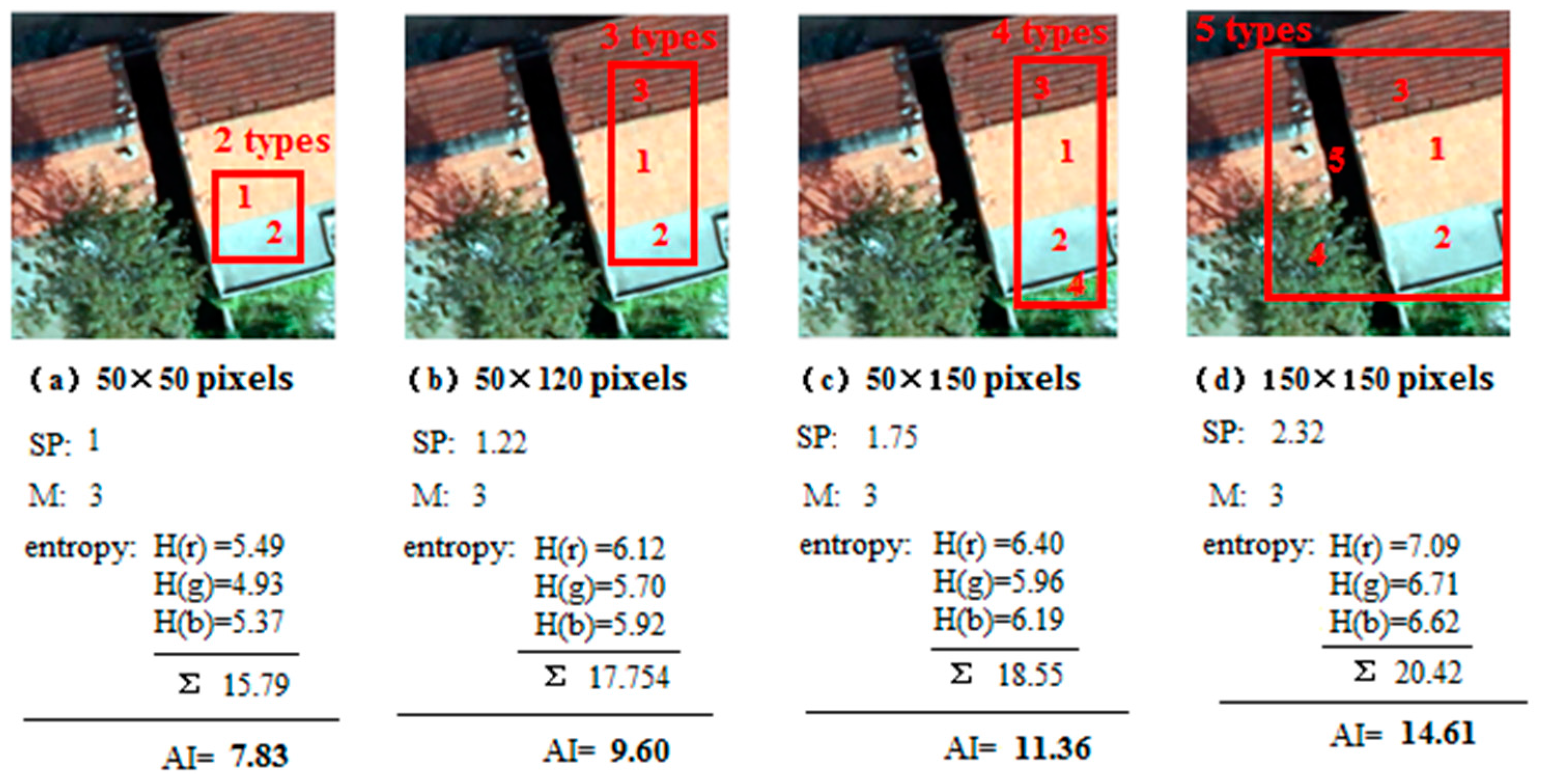
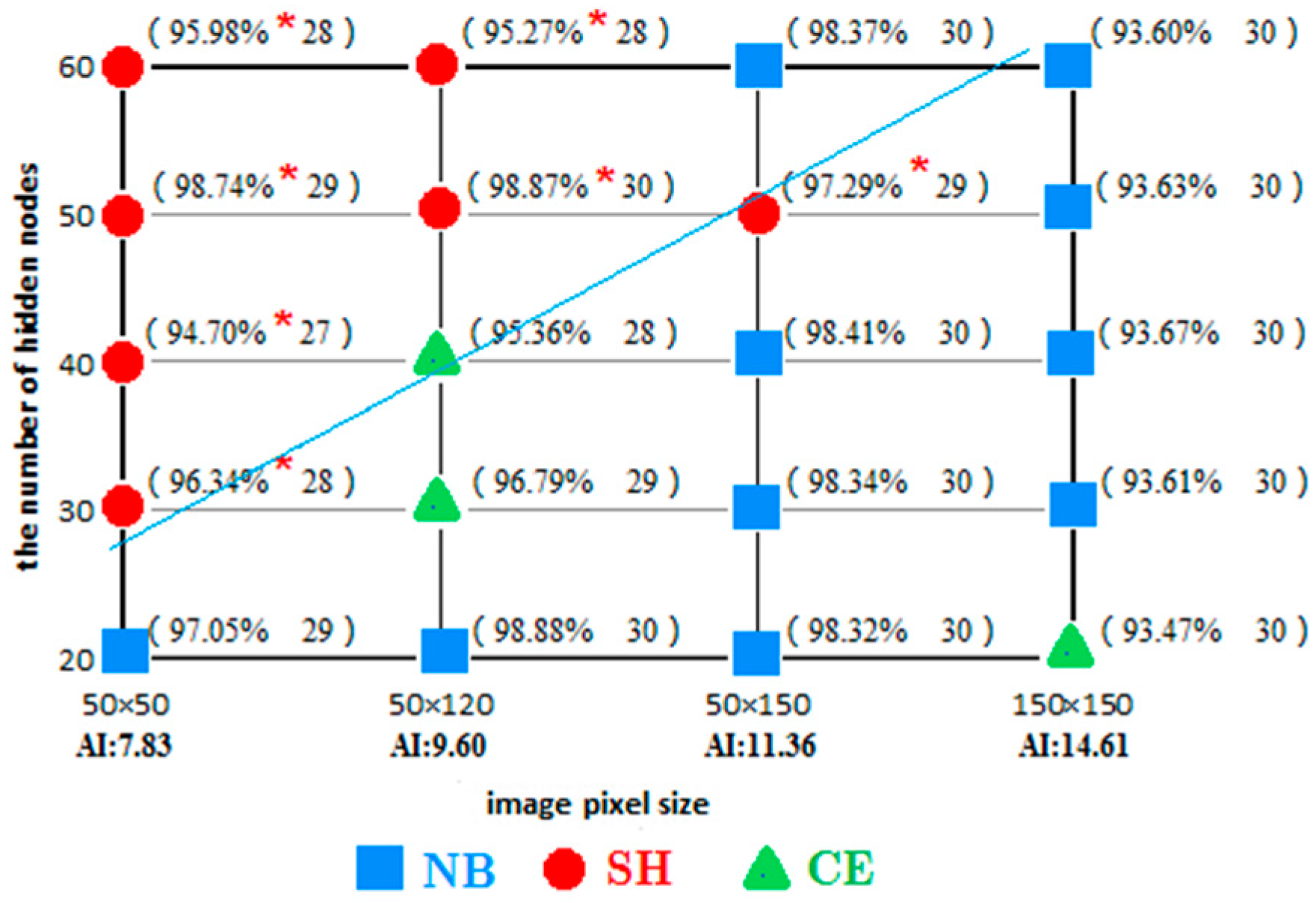
- It is found in the classification experiment of high-resolution image of houses (as shown in the Figure 14 and Figure 16) that the SH entropy function network has a higher overall classification accuracy than the NB and CE under the small pixel image (50 × 50 pixels), or when the image characteristic is simple. This is more obvious when the number of hidden layer nodes is increased. For example, in the 50 × 50 pixels image classification (AI index was 7.82), the classification accuracy of the SH entropy error network with four hidden layer nodes (30, 40, 50, and 60) is higher than the NB or CE. This indicates that the NB and CE entropy error function network has a surplus learning ability, and experienced an “over-learning” phenomenon, while the SH network has a moderate learning ability, and an “over-learning” resistance ability. Therefore, the SH error function is the recommended selection.
- In the large-pixel images, the classification accuracy of the NB and CE entropy error function network is found to be higher than the SH, with the increase of the complexity degree of the ground features. For example, in the 150 × 150 pixel image classification (AI index was 14.61, and the complexity degree of image obviously rises compared with the 50 × 50 pixel), for the five hidden layer nodes, the classification accuracy of the NB and CE entropy error function network is higher than the SH. These results indicate that the network learning ability is not in surplus and an “over-learning” phenomenon does not exist. Therefore in this study, the NB or CE entropy error functions are commended to be selected in order to guarantee the classification accuracy of the network.
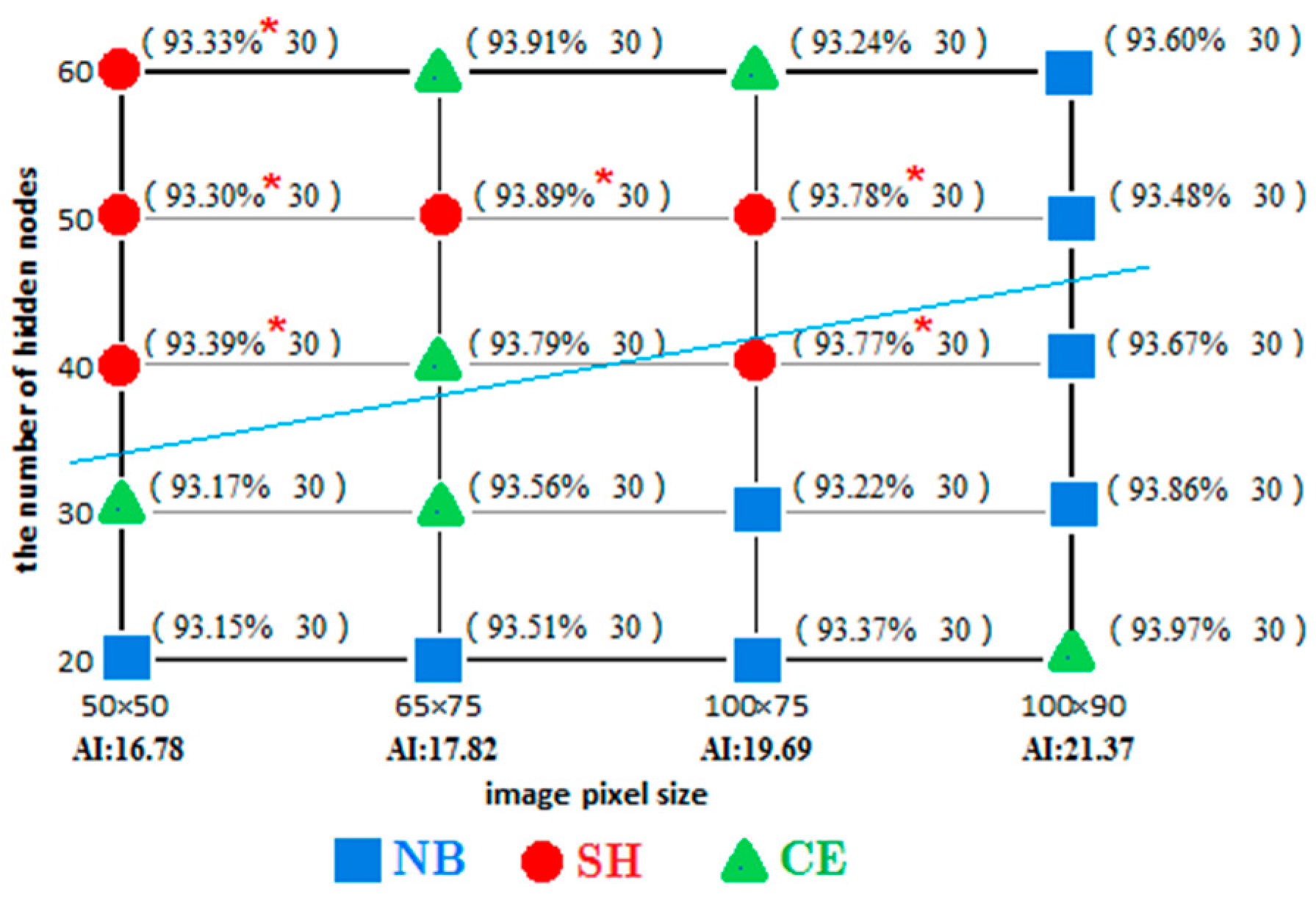
- There was also a similar law in the hyper-spectral image of the Heihe River. For example, the network easily has an “over-learning” phenomenon when the image complexity degree is low with the small image condition. Meanwhile, with the large image condition, the network does not easily have an “over-learning” phenomenon when the image complexity degree is high (as shown in Figure 15 and Figure 17).
3.2.3. Different Hidden Layer Nodes and “Over-Learning” Phenomenon in the Neural Network
- The possibility of “over-learning” increases with the increase in the number of hidden layer nodes. This is due to the fact that the increase in the hidden layer nodes of the neural network is helpful in improving the network learning ability. Not only does the classification of the 50 × 50 small image exhibit an “over-learning” phenomenon, namely the classification accuracy of the SH was higher than NB and CE (as shown in Figure 16 and Figure 17), but also the larger 50 × 120 image also exhibits an “over-learning” phenomenon when the number of hidden layer nodes is up to 50 (as shown in Table 3).
- Therefore, the suitable number of hidden layer nodes should be set during the neural network training, provided that the accuracy requirement is satisfied, in order to prevent an “over-learning” phenomenon. In addition, the overall classification accuracy of the wavelet neural network in the SH entropy error function shows an increasing trend with the increase in the number of hidden layer nodes. This is due to the fact that the occurrence possibility of an “over-learning” phenomenon rises. However, the classification accuracy of the SH entropy error in most of the experiments is lower than the NB and CE, which makes clear that the wavelet neural network of the NB and CE entropy error function was very robust (as shown in Table 3).
4. Conclusions
- As far as the remote sensing images are concerned, the wavelet neural network will not easily cause an “over-learning” phenomenon, and the NB and CE networks will experience “over-learning” phenomenon only when the image is very small (however, this is rare). It will be more difficult to exhibit an “over-learning” phenomenon when the image complexity degree become higher.
- The number of hidden layer nodes is also one of the factors influencing the “over-learning” phenomenon. With the increase in the number of hidden layer nodes, the simple and small images with a low complexity degree will have a higher possibility of causing an “over-learning” phenomenon. However, most of remote sensing images are complex, and have only a small possibility of causing an “over-learning” phenomenon.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Singha, S.; Bellerby, T.J.; Trieschmann, O. Detection and classification of oil spill and look-alike spots from SAR imagery using an artificial neural network. Int. Geosci. Remote Sens. Symp. 2012, 53, 5630–5633. [Google Scholar]
- Collingwood, A.; Treitz, P.; Charbonneau, F.; Atkinson, D. Artificial neural network modeling of high arctic phytomass using synthetic aperture radar and multispectral data. Remote Sens. 2014, 6, 2134–2153. [Google Scholar] [CrossRef]
- Taravat, A.; Proud, S.; Peronaci, S.; Del-Frate, F.; Oppelt, N. Multilayer Perceptron Neural Networks Model for Meteosat Second Generation SEVIRI Daytime Cloud Masking. Remote Sens. 2015, 7, 1529–1539. [Google Scholar] [CrossRef]
- Tang, J.; Deng, C.; Huang, G.B.; Zhao, B. Compressed-domain ship detection on spaceborne optical image using deep neural network and extreme learning machine. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1174–1185. [Google Scholar] [CrossRef]
- Ghamisi, P.; Chen, Y.; Zhu, X.X. A Self-Improving Convolution Neural Network for the Classification of Hyperspectral Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1537–1541. [Google Scholar] [CrossRef]
- Li, J.; Du, Q.; Li, Y. An efficient radial basis function neural network for hyperspectral remote sensing image classification. Soft Comput. 2016, 20, 4753–4759. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional Neural Networks for Large-Scale Remote-Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 55, 645–657. [Google Scholar] [CrossRef]
- Li, Y.; Xie, W.; Li, H. Hyperspectral image reconstruction by deep convolutional neural network for classification. Pattern Recognit. 2017, 63, 371–383. [Google Scholar] [CrossRef]
- Nogueira, K.; Penatti, O.A.B.; dos Santos, J.A. Towards better exploiting convolutional neural networks for remote sensing scene classification. Pattern Recognit. 2017, 61, 539–556. [Google Scholar] [CrossRef]
- Zhong, Y.; Fei, F.; Liu, Y.; Zhao, B.; Jiao, H.; Zhang, L. SatCNN: Satellite image dataset classification using agile convolutional neural networks. Remote Sens. Lett. 2017, 8, 136–145. [Google Scholar] [CrossRef]
- Heermann, P.D.; Khazenie, N. Classification of multispectral remote sensing data using a back-propagation neural network. IEEE Trans. Geosci. Remote Sens. 1992, 30, 81–88. [Google Scholar] [CrossRef]
- Li, Z.Y. Supervised classification of multispectral remote sensing image using a BP neural network. J. Infrared Millim. Waves 1998, 17, 153–156. [Google Scholar]
- Burks, T.F.; Shearer, S.A.; Gates, R.S.; Donohue, K.D. Backpropagation neural network design and evaluation for classifying weed species using color image texture. Trans. ASAE 2000, 43, 1029–1037. [Google Scholar] [CrossRef]
- Song, K.; Li, L.; Li, S.; Tedesco, L.; Duan, H.; Li, Z.; Shi, K.; Du, J.; Zhao, Y.; Shao, T. Using partial least squares-artificial neural network for inversion of inland water Chlorophyll-a. IEEE Trans. Geosci Remote Sens. 2014, 52, 1502–1517. [Google Scholar] [CrossRef]
- Rumerhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagation errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Zhang, Q.; Benveniste, A. Wavelet networks. IEEE Trans. Neural Netw. 1992, 3, 889–898. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Chen, S.; Ma, Y.; Shen, C.; Zhang, Y. Impact of different saturation encoding modes on object classification using a BP wavelet neural network. Int. J. Remote Sens. 2014, 35, 7878–7897. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, G.; Liu, H. Fault Diagnosis of Analog Circuit Based on BP Wavelet Neural Network. Meas. Control Technol. 2007, 26, 64–69. [Google Scholar]
- Hsu, P.H.; Yang, H.H. Hyperspectral image classification using wavelet networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2007, Barcelona, Spain, 23–28 July 2007.
- Jin, C. Structure Modality of the Error Function for Feedforward Neural Networks. J. Comput. Res. Dev. 2003, 40, 913–917. [Google Scholar]
- Ampazis, N.; Perantonis, S.J. Two highly efficient second-order algorithms for training feedforward networks. IEEE Trans. Neural Netw. 2002, 13, 1064–1074. [Google Scholar] [CrossRef] [PubMed]
- Benediktsson, J.A.; Swain, P.H.; Ersoy, O.K. Conjugate-gradient neural networks in classification of multisource and very-high-dimensional remote sensing data. Int. J. Remote Sens. 1993, 14, 2883–2903. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory. IEEE Trans. Neural Netw. 1995, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.B.; Venetsanopoulos, A.N. Fast learning algorithms for neural networks. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1992, 39, 453–474. [Google Scholar] [CrossRef]
- Van, O.A.; Nienhuis, B. Improving the Convergence of the Back-Propagation Algorithm. Neural Netw. 1992, 5, 465–471. [Google Scholar] [CrossRef]
- Oh, S.H.; Lee, Y. A modified error function to improve the error back-propagation algorithm for multi-layer perceptrons. ETRI J. 1995, 17, 11–22. [Google Scholar] [CrossRef]
- Oh, S.H. Improving the Error Back Propagation Algorithm with a Modified Error Function. IEEE Trans. Neural Netw. 1997, 8, 799–803. [Google Scholar] [PubMed]
- Li, Y.; Qin, G.; Wen, X.; Hu, N. Neural Network Learning Algorithm of Over-learning and Solving Method. J. Vib. Meas. Diagn. 2002, 22, 260–264. [Google Scholar]
- Sun, J. Principles and Applications of Remote Sensing; Wuhan University Press: Wuhan, China, 2009. [Google Scholar]
- Blamire, P.A. The influence of relative sample size in training artificial neural networks. Int. J. Remote Sens. 1996, 17, 223–230. [Google Scholar] [CrossRef]
- Foody, G.M.; Mcculloch, M.B.; Yates, W.B. Classification of remotely sensed data by an artificial neural network: Issues related to training data characteristics. Photogramm. Eng. Remote Sens. 1995, 61, 391–401. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell. Syst. Tech. J. 1948, 27, 623–659. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.R.; Zhao, L.Y. Modified Linear-Prediction Based Band Selection for Hyperspectral Image. Acta Opt. Sin. 2013, 33, 256–263. [Google Scholar]
- Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (Hiwater): Scientific Objectives and Experimental Design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
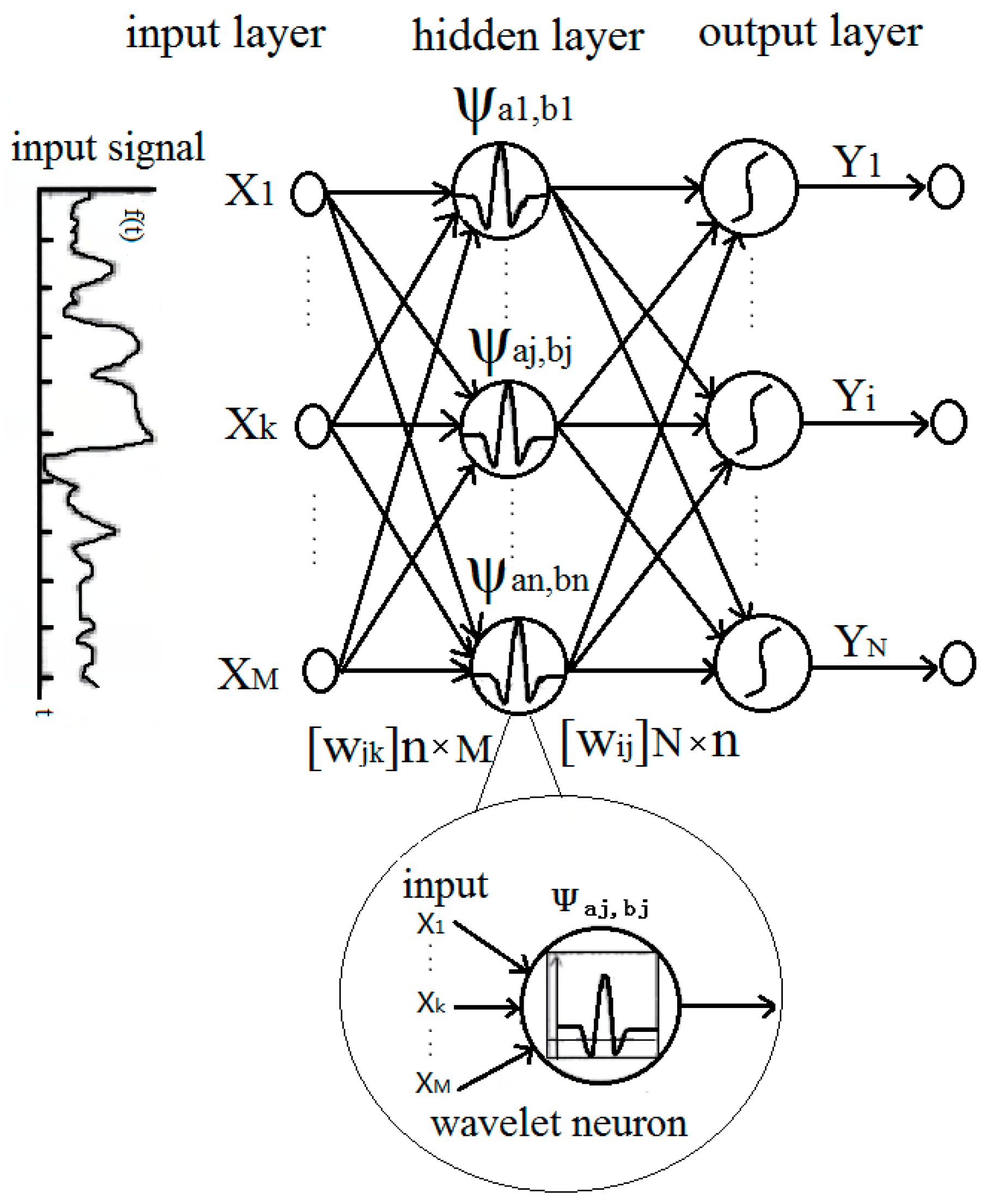







| Parameter | Explanation |
|---|---|
| p (p = 1, 2, …, P) | number of input samples |
| k (k = 1, 2, …, M) | number of nodes in the input layer |
| j (j = 1, 2, …, n) | number of nodes in the hidden layer |
| i (i = 1, 2, …, N) | number of nodes in the output layer |
| weight matrix n × M from the input layer to the hidden layer, with as the weight connecting node j of hidden layer with the node k of the input layer); (the initial value is a random value of [−1, 1]) | |
| weight matrix N × n from the hidden layer to the output layer, with as the weight connecting the node i of the output layer and node j of the hidden layer; (the initial value is a random value of [−1, 1]) | |
| the kth input of the pth sample in the input layer | |
| input of the jth node in the hidden layer of the pth sample | |
| input of the ith node in the output layer of the pth sample | |
| aj and bj | scaling parameter and translation parameter of the jth node of the hidden layer, respectively |
| output of the jth node of the hidden layer of the pth sample | |
| threshold value at the ith node of the output layer, (the initial value is a random value of [−1, 1]) | |
| the ith actual output in the output layer of the pth sample |
| Gradient | NB Error Function | CE Error Function | SH Error Function |
|---|---|---|---|
| Iteration 100 | Hidden Nodes 30 | Hidden Nodes 40 | Hidden Nodes 50 | ||||
|---|---|---|---|---|---|---|---|
| Sorting of Overall | Sorting of Error | Sorting of Overall | Sorting of Error | Sorting of Overall | Sorting of Error | ||
| Classification Accutacy | Minimum Value | Classification Accutacy | Minimum Value | Classification Accutacy | Minimum Value | ||
| test data 1 | Sea ice 93 × 2545 (SIR-C) | NB > CE > SH | SH > CE > NB | NB > CE > SH | SH > CE > NB | NB > CE > SH | SH > CE > NB |
| test data 2 | Indian pines 145 × 145 (HSI) | NB > CE > SH | SH > CE > NB | NB > SH > CE | SH > CE > NB | NB > SH > CE | SH > CE > NB |
| test data 3 | Snow mountain 300 × 300 (HRG) | NB > CE > SH | SH > CE > NB | NB > CE > SH | SH > CE > NB | NB > CE > SH | SH > CE > NB |
| test data 4 | Nanjing 400 × 400 (TM) | NB > CE > SH | SH > CE > NB | NB = CE > SH | SH > CE > NB | NB > CE > SH | SH > CE > NB |
| test data 5 | Building 50 × 50 (HRG) | SH > NB > CE | SH > CE = NB | SH > CE > NB | SH > CE = NB | SH > NB > CE | SH > CE = NB |
| test data 6 | Building 50 × 120 (HRG) | CE > NB > SH | SH > CE = NB | CE > NB > SH | SH > CE = NB | SH > CE > NB | SH > NB > CE |
| test data 7 | Heihe river 50 × 50 (HSI) | CE > NB > SH | SH > CE > NB | SH > NB > CE | SH > CE > NB | SH > NB > CE | SH > NB > CE |
| test data 8 | Heihe river 100 × 90 (HSI) | NB > CE > SH | SH > CE > NB | NB > CE > SH | SH > CE > NB | NB > CE > SH | SH > CE > NB |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, D.; Zhang, Y.; Shan, X.; Cui, J.; Wu, H. “Over-Learning” Phenomenon of Wavelet Neural Networks in Remote Sensing Image Classifications with Different Entropy Error Functions. Entropy 2017, 19, 101. https://doi.org/10.3390/e19030101
Song D, Zhang Y, Shan X, Cui J, Wu H. “Over-Learning” Phenomenon of Wavelet Neural Networks in Remote Sensing Image Classifications with Different Entropy Error Functions. Entropy. 2017; 19(3):101. https://doi.org/10.3390/e19030101
Chicago/Turabian StyleSong, Dongmei, Yajie Zhang, Xinjian Shan, Jianyong Cui, and Huisheng Wu. 2017. "“Over-Learning” Phenomenon of Wavelet Neural Networks in Remote Sensing Image Classifications with Different Entropy Error Functions" Entropy 19, no. 3: 101. https://doi.org/10.3390/e19030101
APA StyleSong, D., Zhang, Y., Shan, X., Cui, J., & Wu, H. (2017). “Over-Learning” Phenomenon of Wavelet Neural Networks in Remote Sensing Image Classifications with Different Entropy Error Functions. Entropy, 19(3), 101. https://doi.org/10.3390/e19030101





