Permutation Entropy: Too Complex a Measure for EEG Time Series?
Abstract
:1. Introduction
2. An Overview of Permutation Entropy
2.1. Sequences of Ordinal Patterns
2.2. Estimating the Permutation Entropy of EEG
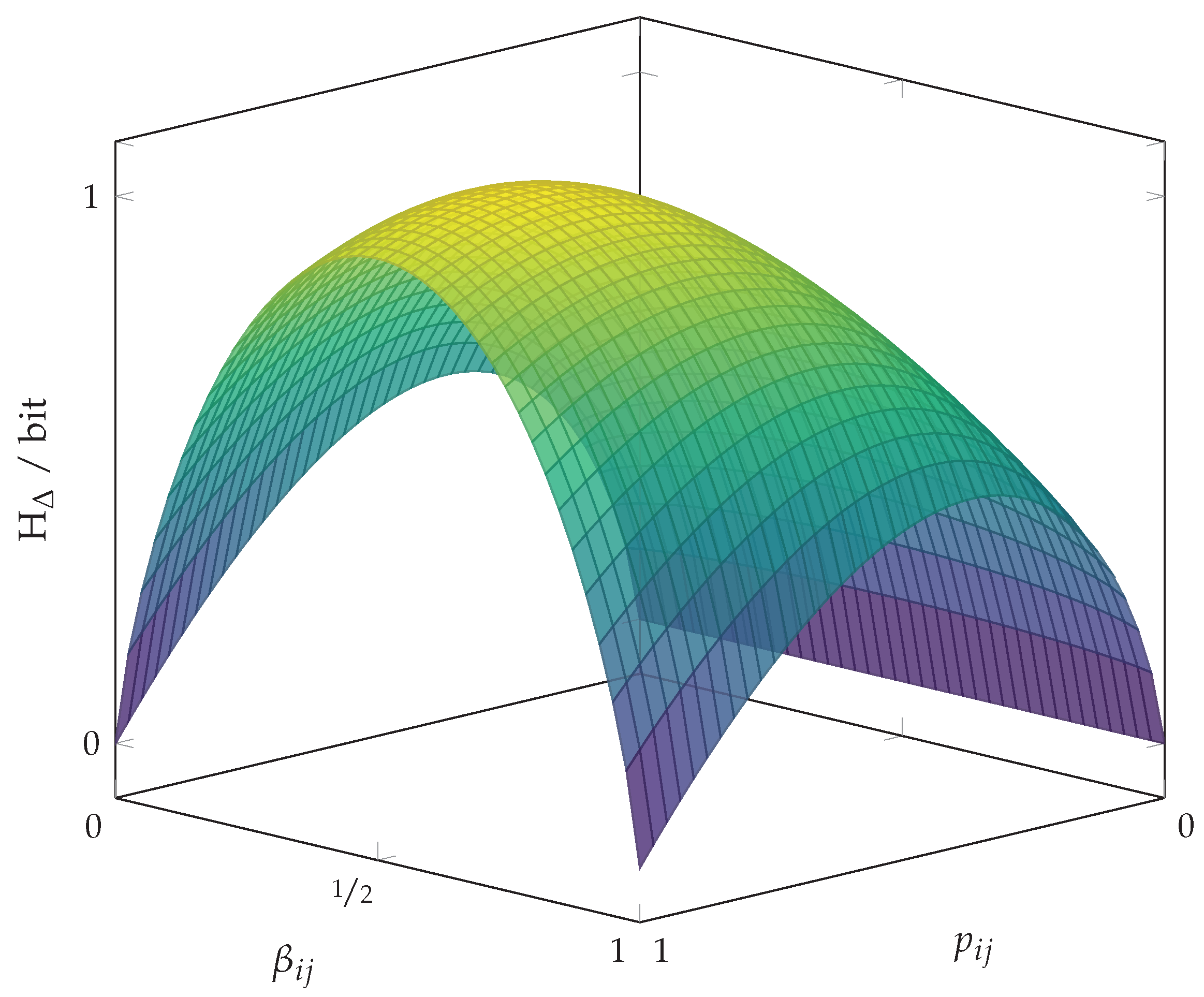
3. Shannon Entropy and Pairwise Probability Balances
Pairwise Probability Balances
4. Complexity and Pseudo-Complexity
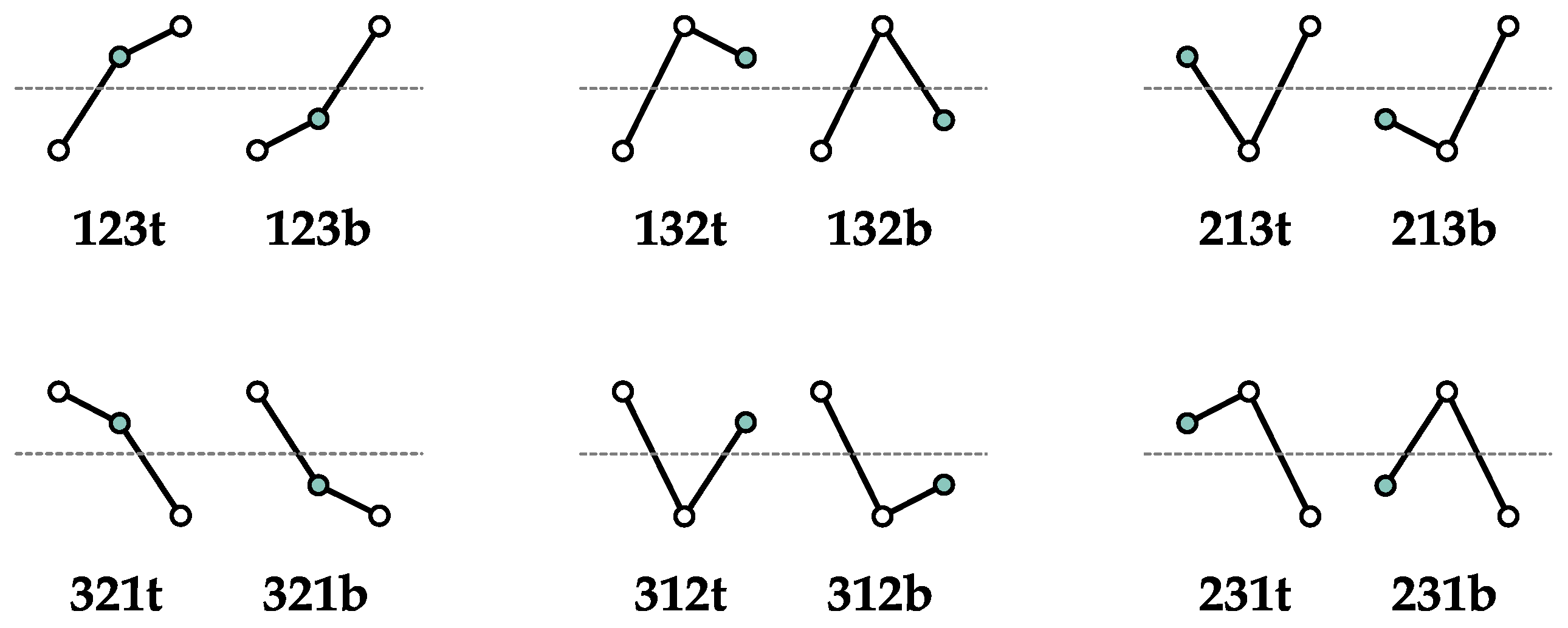
4.1. A New Class of Ordinal Patterns?
4.2. Pseudo-Complexity in Ordinal Pattern Analysis
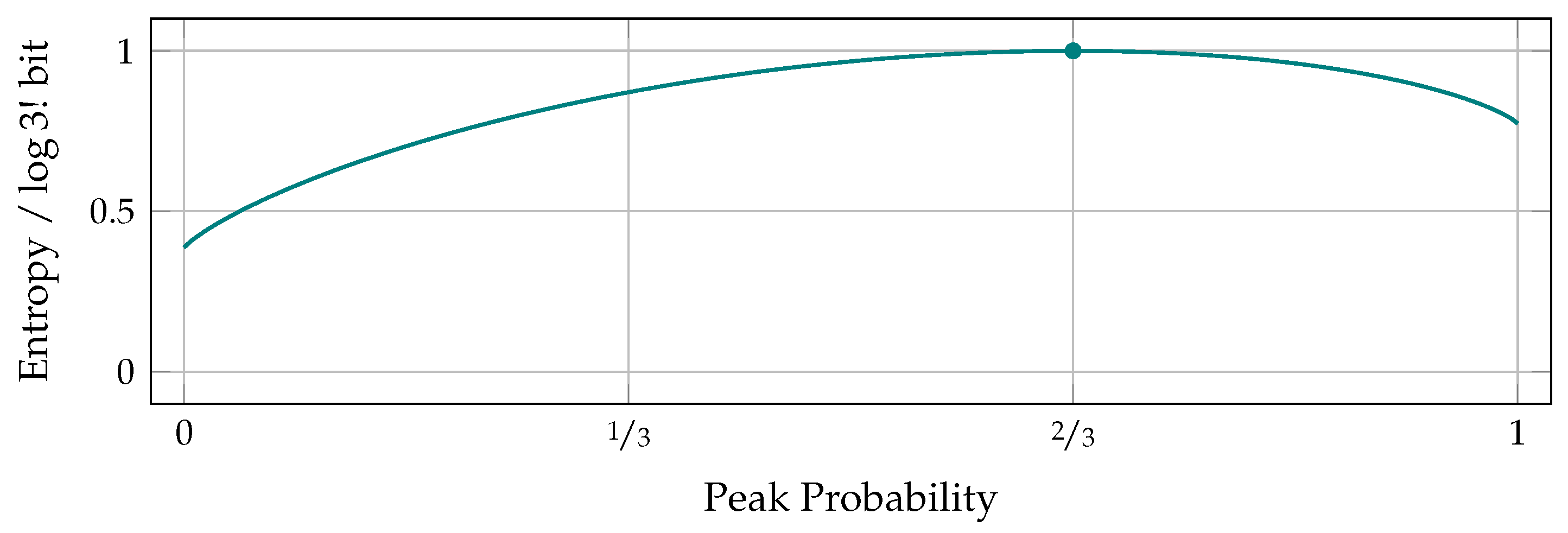
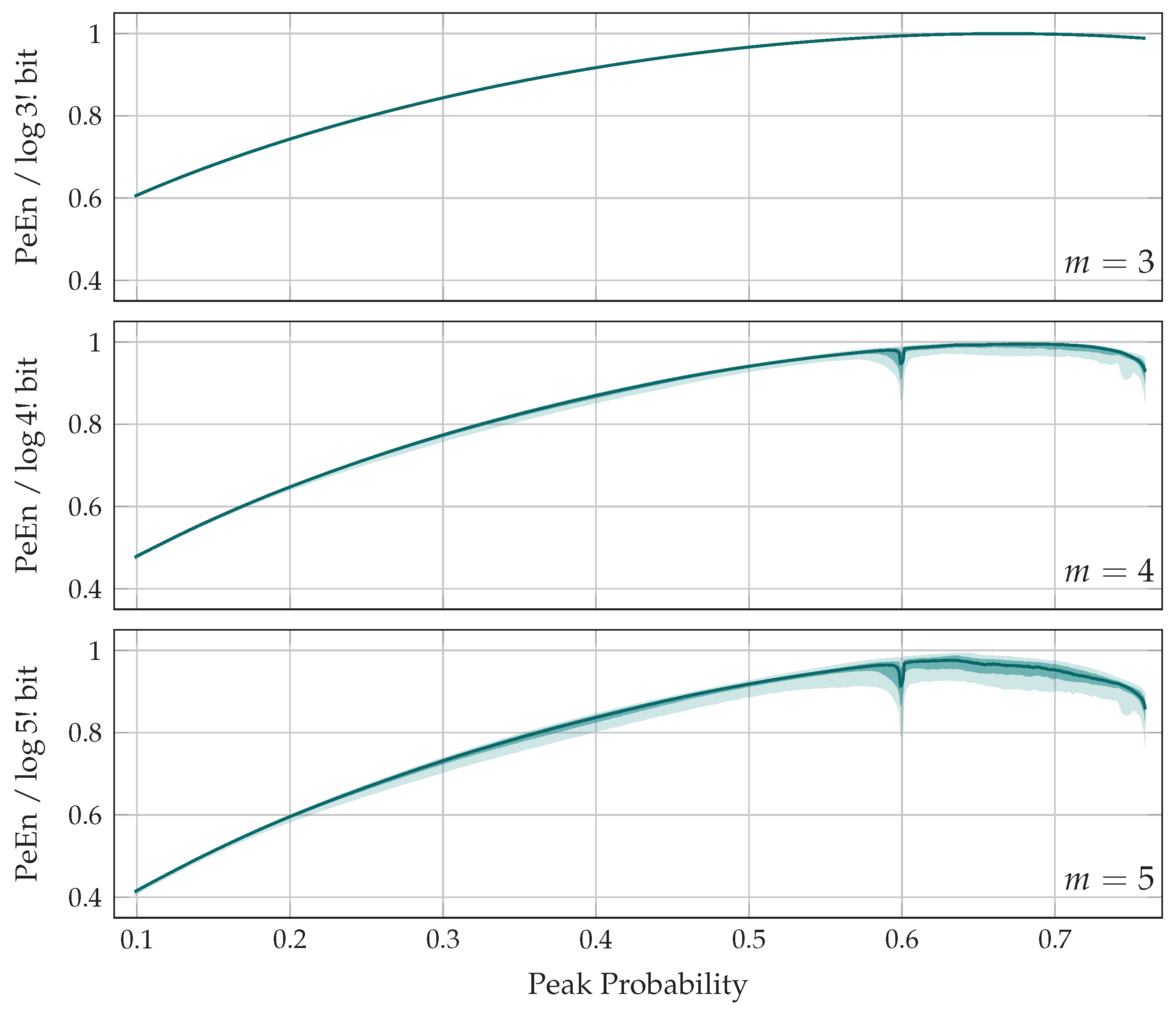
5. The Entropy of Peaks
5.1. An Open-Source, Open-Data Approach
5.2. EEG Segmentation and Processing
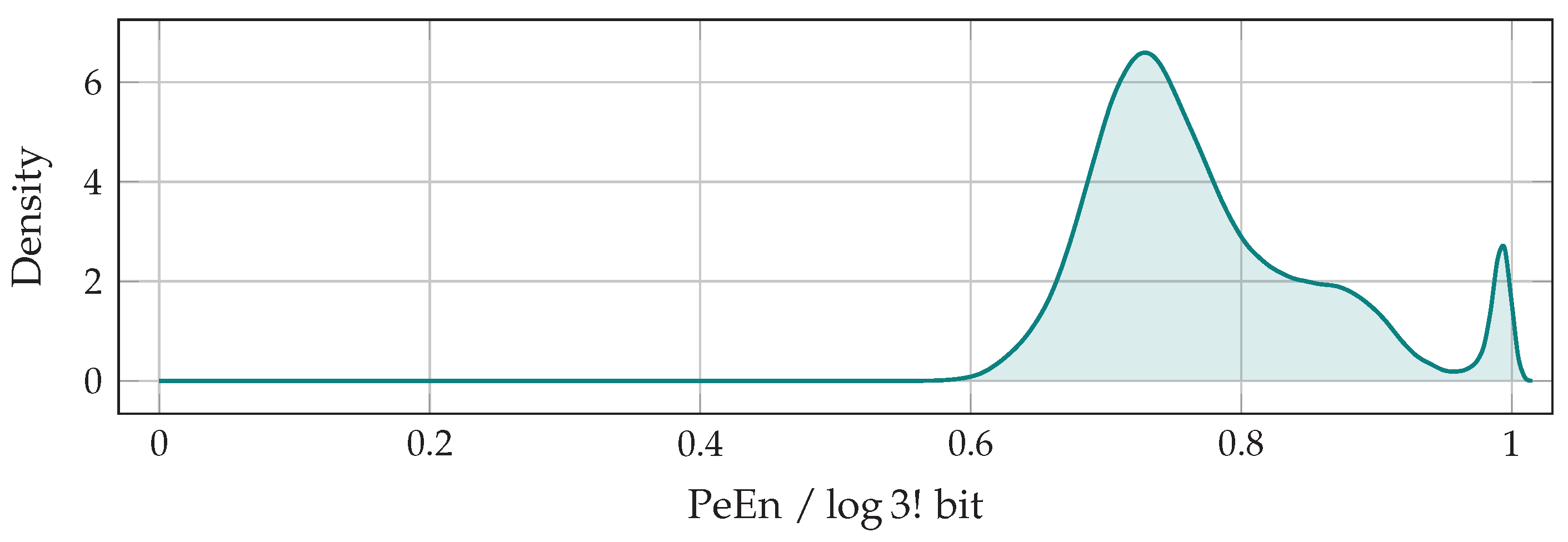
5.3. The Principle Components of Probability Balances
5.4. Eliminating Pseudo-Complexity
6. Linearising Permutation Entropy
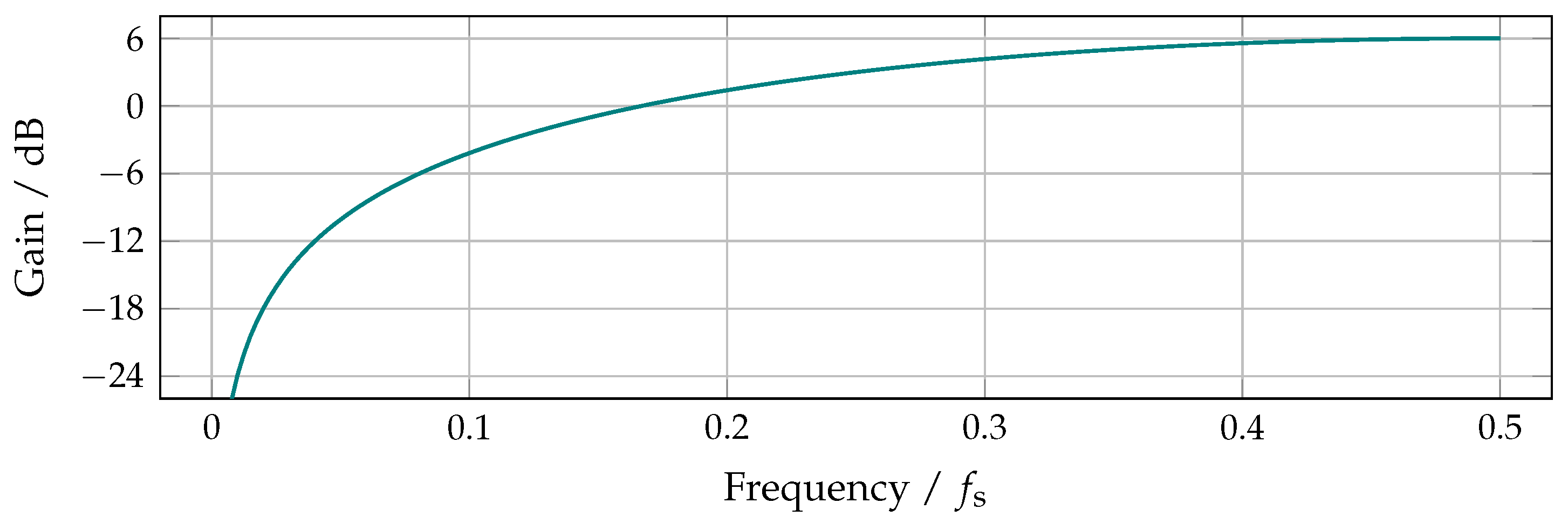
6.1. Signal Peaks and Spectral Bandwidth
6.2. Counting the Zigzags of EEG
7. Permutation Entropy as a Spectral Estimator
7.1. Zero Crossings and the Dominant Frequency Principle
7.2. Kedem’s Higher Order Crossings
7.3. The Spectral Estimation Hypothesis
8. Higher Pattern Orders and Time Delays
8.1. Prospects for Patterns of Higher Order
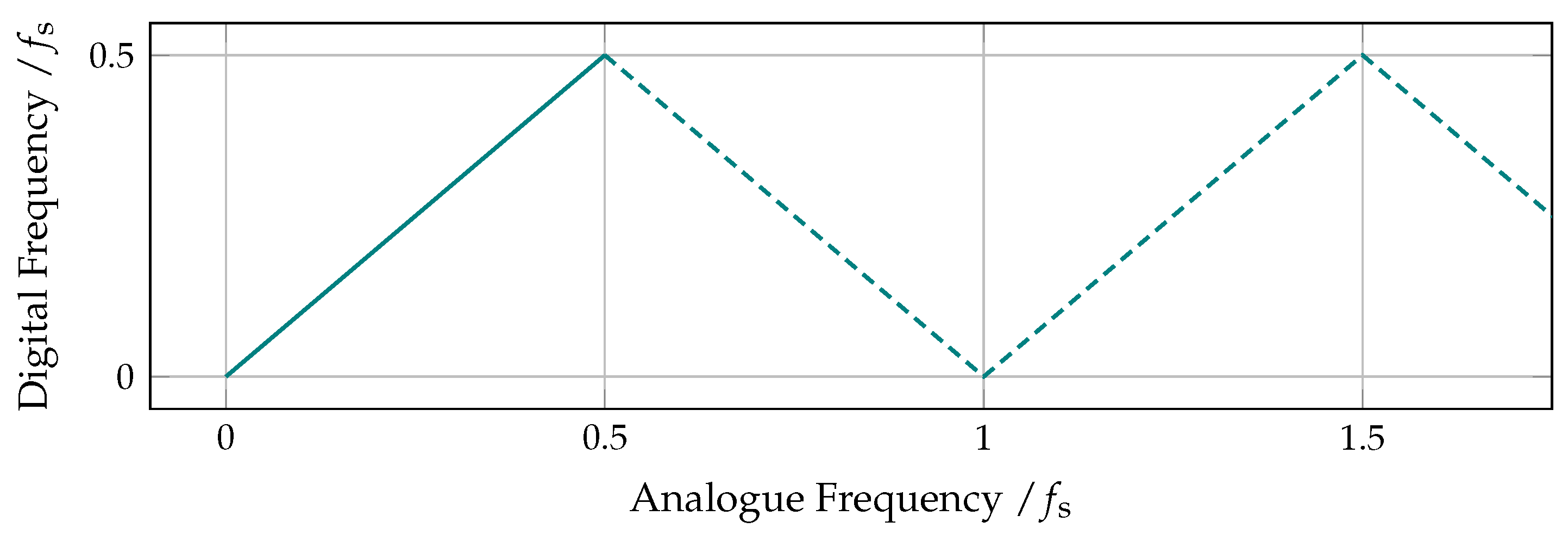
8.2. Sampling, Resampling and Aliasing
8.3. The Time Delay as a Downsampling Factor
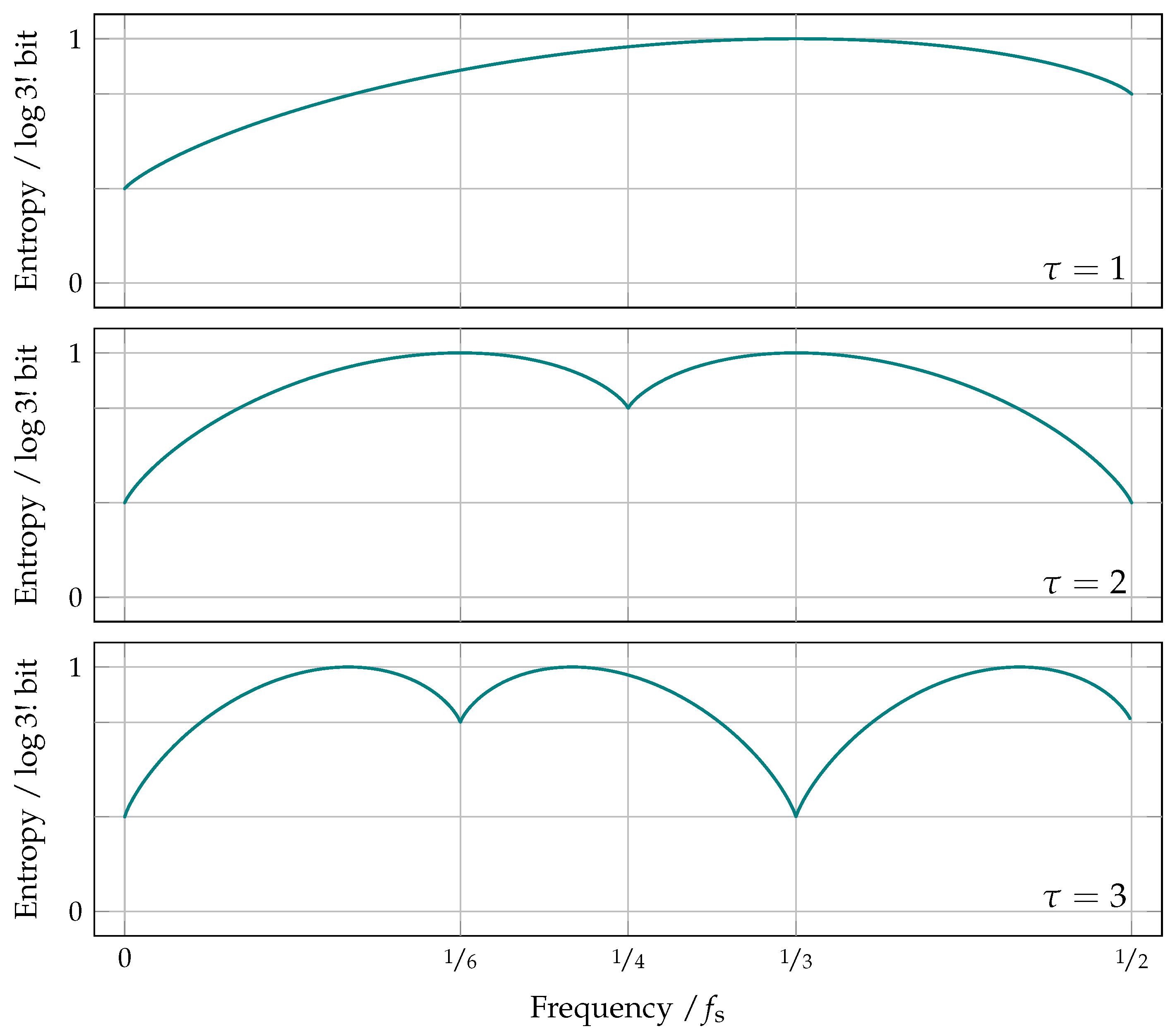
8.4. Frequency Aliasing in Permutation Entropy
8.5. Anti-Aliased Permutation Entropy
9. Conclusions
9.1. There Are Only So Many Signal Characteristics
9.2. Next Steps in Ordinal Pattern-Based EEG Analysis
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Amigó, J.M.; Keller, K.; Unakafova, V.A. Ordinal symbolic analysis and its application to biomedical recordings. Phil. Trans. R. Soc. A 2014, 373, 20140091. [Google Scholar] [CrossRef] [PubMed]
- Fadlallah, B.; Chen, B.; Keil, A.; Príncipe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, X.; Liang, Z.; Voss, L.J.; Sleigh, J.W. Multiscale permutation entropy analysis of EEG recordings during sevoflurane anesthesia. J. Neural Eng. 2010, 7, 046010. [Google Scholar] [CrossRef] [PubMed]
- Morabito, F.C.; Labate, D.; La Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate Multi-Scale Permutation Entropy for Complexity Analysis of Alzheimer’s Disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude-aware Permutation Entropy: Illustration in Spike Detection and Signal Segmentation. Comput. Methods Progr. Biomed. 2016, 128, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C. A New Kind of Permutation Entropy Used to Classify Sleep Stages from Invisible EEG Microstructure. Entropy 2017, 19, 197. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Iverson, K.E. A Programming Language. In Proceedings of the Spring Joint Computer Conference, AIEE-IRE ’62 (Spring), San Francisco, CA, USA, 1–3 May 1962; ACM: New York, NY, USA, 1962; pp. 345–351. [Google Scholar]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Terzano, M.G.; Parrino, L.; Sherieri, A.; Chervin, R.; Chokroverty, S.; Guilleminault, C.; Hirshkowitz, M.; Mahowald, M.; Moldofsky, H.; Rosa, A.; et al. Atlas, rules, and recording techniques for the scoring of cyclic alternating pattern (CAP) in human sleep. Sleep Med. 2001, 2, 537–553. [Google Scholar] [CrossRef]
- Nicolaou, N.; Georgiou, J. The Use of Permutation Entropy to Characterize Sleep Electroencephalograms. Clin. EEG Neurosci. 2011, 42, 24–28. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Eaton, J.W. GNU Octave and reproducible research. J. Process Control 2012, 22, 1433–1438. [Google Scholar] [CrossRef]
- Kemp, B.; Värri, A.; Rosa, A.C.; Nielsen, K.D.; Gade, J. A simple format for exchange of digitized polygraphic recordings. Electroenceph. Clin. Neurophysiol. 1992, 82, 391–393. [Google Scholar] [CrossRef]
- Requicha, A.A.G. The Zeros of Entire Functions: Theory and Engineering Applications. Proc. IEEE 1980, 68, 308–328. [Google Scholar] [CrossRef]
- Shoeb, A.H. Application of Machine Learning to Epileptic Seizure Onset Detection and Treatment. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Kedem, B. Spectral Analysis and Discrimination by Zero-Crossings. Proc. IEEE 1986, 74, 1477–1493. [Google Scholar] [CrossRef]
- Rice, S.O. Statistical Properties of a Sine Wave Plus Random Noise. Bell Syst. Tech. J. 1948, 27, 109–157. [Google Scholar] [CrossRef]
- Shannon, C. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Olofsen, E.; Sleigh, J.W.; Dahan, A. Permutation entropy of the electroencephalogram: A measure of anaesthetic drug effect. Br. J. Anaesth. 2008, 101, 810–821. [Google Scholar] [CrossRef] [PubMed]
- Burch, N.R.; Nettleton, W.J.; Sweeney, J.; Edwards, R.J. Period analysis of the electroencephalogram on a general-purpose digital computer. Ann. N. Y. Acad. Sci. 1964, 115, 827–843. [Google Scholar] [CrossRef] [PubMed]
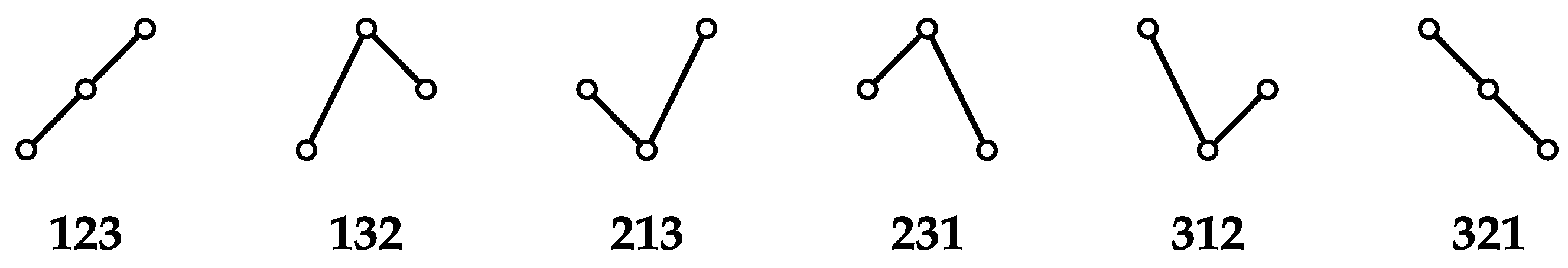
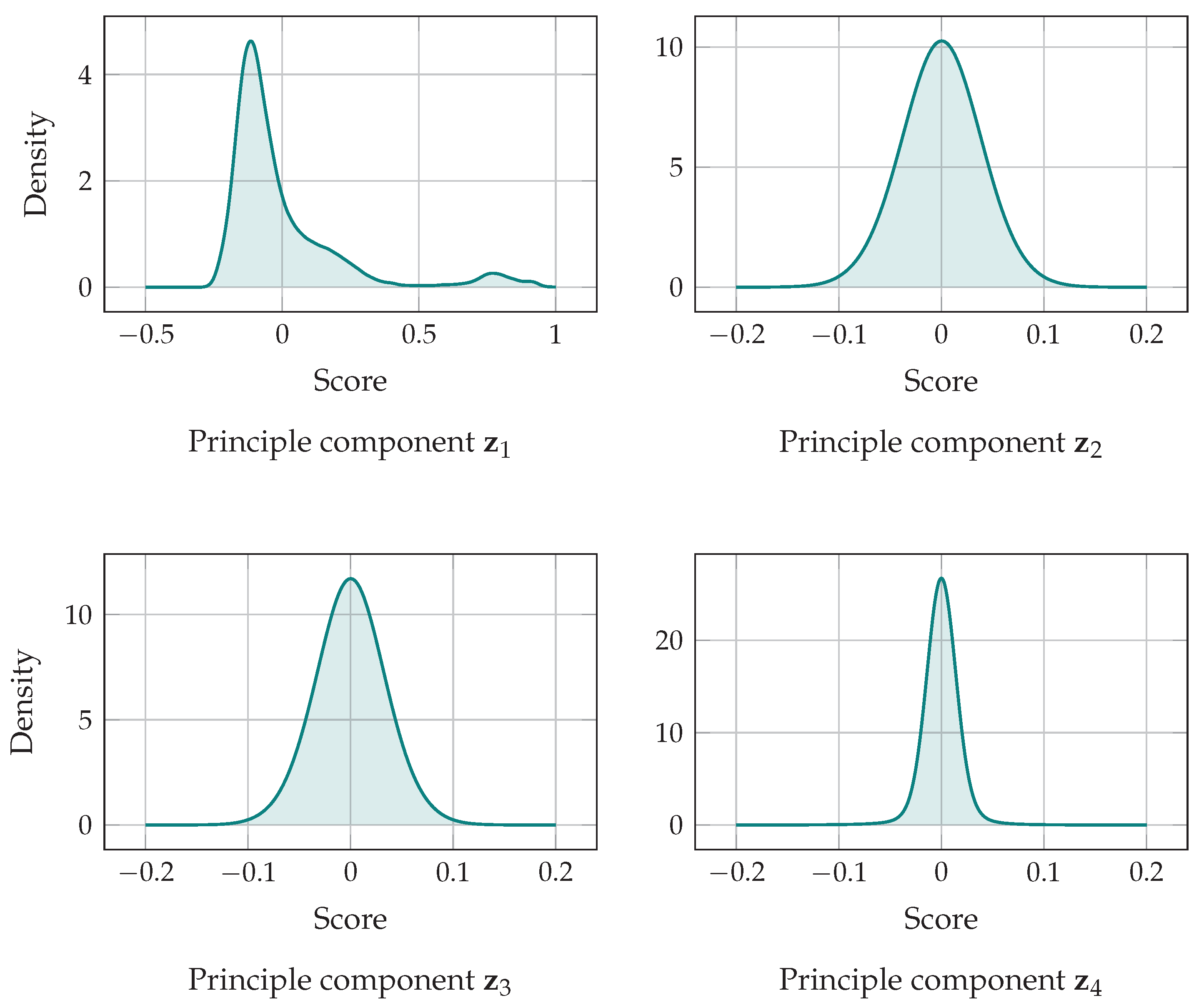
| Component | Eigenvalue | Explained Variation | Spearman Correlation |
|---|---|---|---|
| × 10 | |||
| × 10 | |||
| × 10 | |||
| × 10 |
| Index | Balance | Weight | Mean | Media | Mode | |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 9 | ||||||
| 12 | ||||||
| 14 | ||||||
| 15 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 10 | ||||||
| 11 | ||||||
| 13 | ||||||
| Database | Number of Epochs | Spearman Correlation | ||||
|---|---|---|---|---|---|---|
| CAP | ||||||
| CHB-MIT | ||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berger, S.; Schneider, G.; Kochs, E.F.; Jordan, D. Permutation Entropy: Too Complex a Measure for EEG Time Series? Entropy 2017, 19, 692. https://doi.org/10.3390/e19120692
Berger S, Schneider G, Kochs EF, Jordan D. Permutation Entropy: Too Complex a Measure for EEG Time Series? Entropy. 2017; 19(12):692. https://doi.org/10.3390/e19120692
Chicago/Turabian StyleBerger, Sebastian, Gerhard Schneider, Eberhard F. Kochs, and Denis Jordan. 2017. "Permutation Entropy: Too Complex a Measure for EEG Time Series?" Entropy 19, no. 12: 692. https://doi.org/10.3390/e19120692
APA StyleBerger, S., Schneider, G., Kochs, E. F., & Jordan, D. (2017). Permutation Entropy: Too Complex a Measure for EEG Time Series? Entropy, 19(12), 692. https://doi.org/10.3390/e19120692




