Tsallis Entropy Theory for Modeling in Water Engineering: A Review
Abstract
1. Introduction
2. Tsallis Entropy Theory
2.1. Definition of Entropy
2.2. Properties of Tsallis Entropy
2.3. Principle of Maximum Entropy
2.3.1. Specification of Constraints
2.3.2. Entropy Maximizing Using Lagrange Multipliers
2.3.3. Determination of Probability Distribution
2.3.4. Determination of the Lagrange Multipliers
2.3.5. Determination of Maximum Entropy
3. Applications in Water Engineering: Overview
4. Problems Requiring Entropy Maximization
4.1. Frequency Distributions
4.2. Network Evaluation and Design
4.3. Directional Information Transfer Index
4.4. Reliability of Water Distribution Networks
5. Problems Requiring Coupling with another Theory
5.1. Hydraulic Geometry
5.2. Evaporation
6. Problems Involving Physical Relations
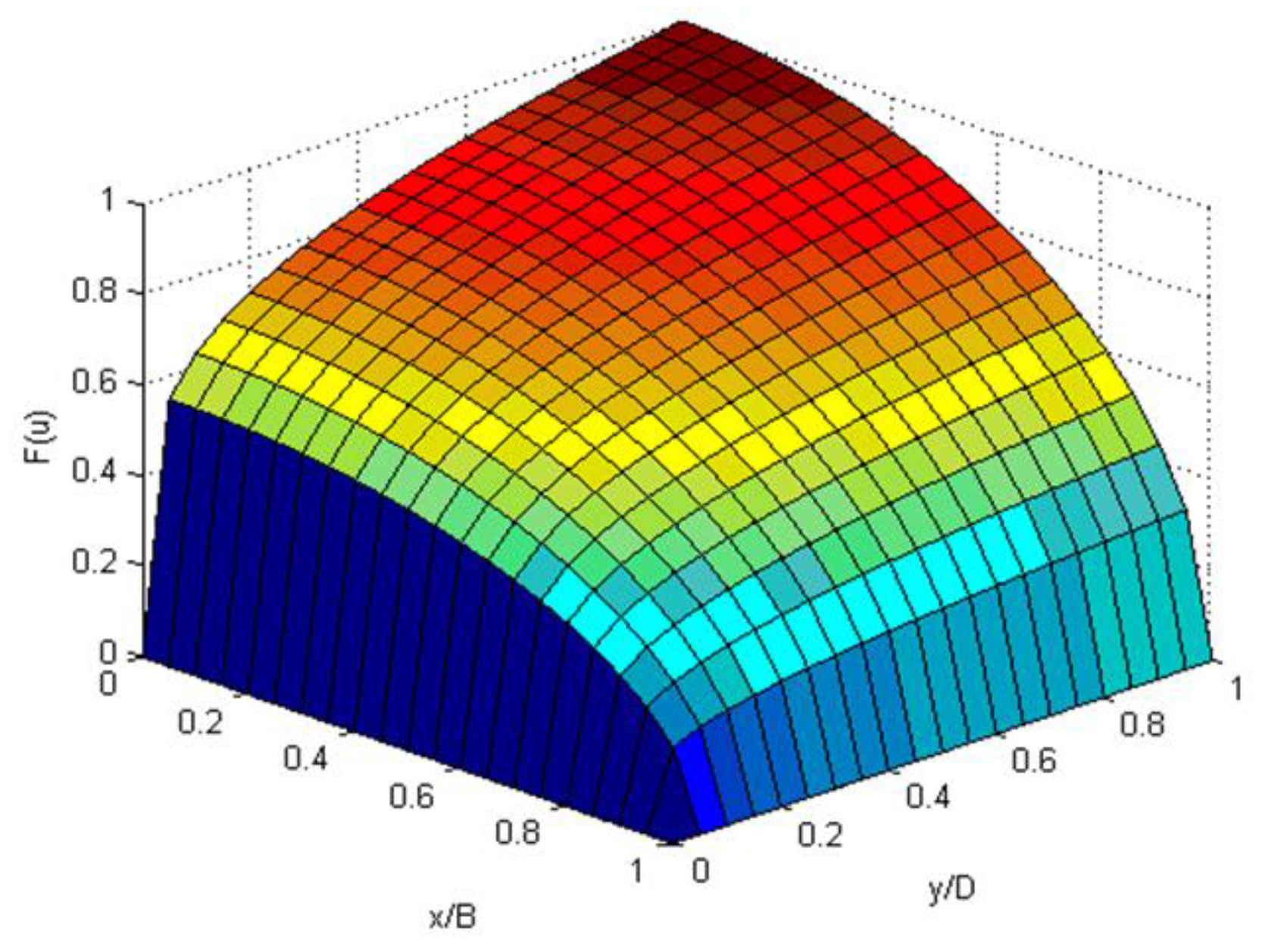
6.1. Hypotheses on Cumulative Probability Distribution Function
6.2. One-Dimensional Velocity Distribution
6.3. Two-Dimensional Velocity Distribution
6.4. Suspended Sediment Concentration
6.5. Sediment Discharge
6.6. Flow-Duration Curve
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Notation
| B | channel width |
| c | sediment concentration |
| Cr | constraint |
| D | water depth |
| E | evaporation |
| f(x) | probability density function |
| G | ground heat flux |
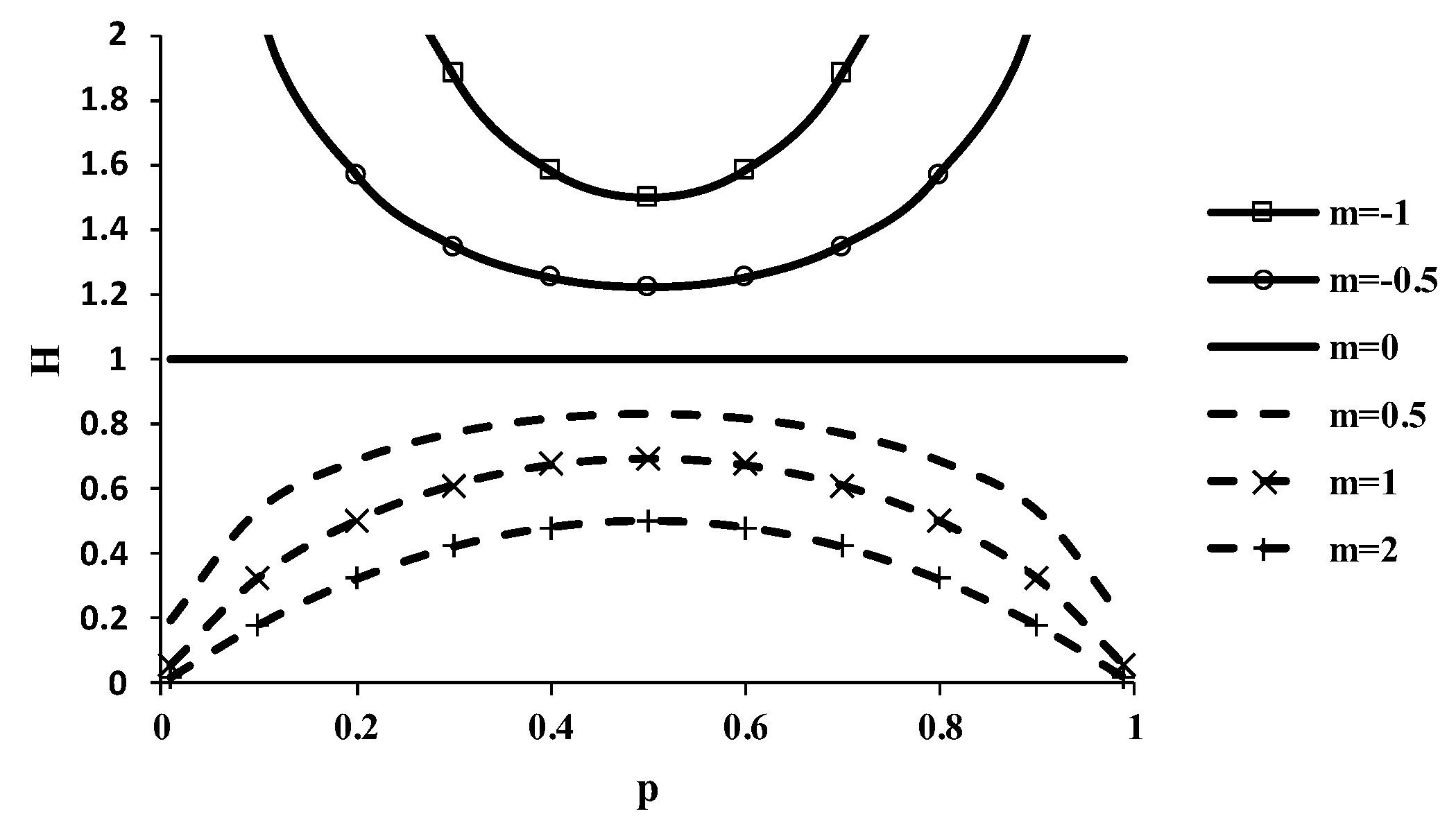
| H | entropy |
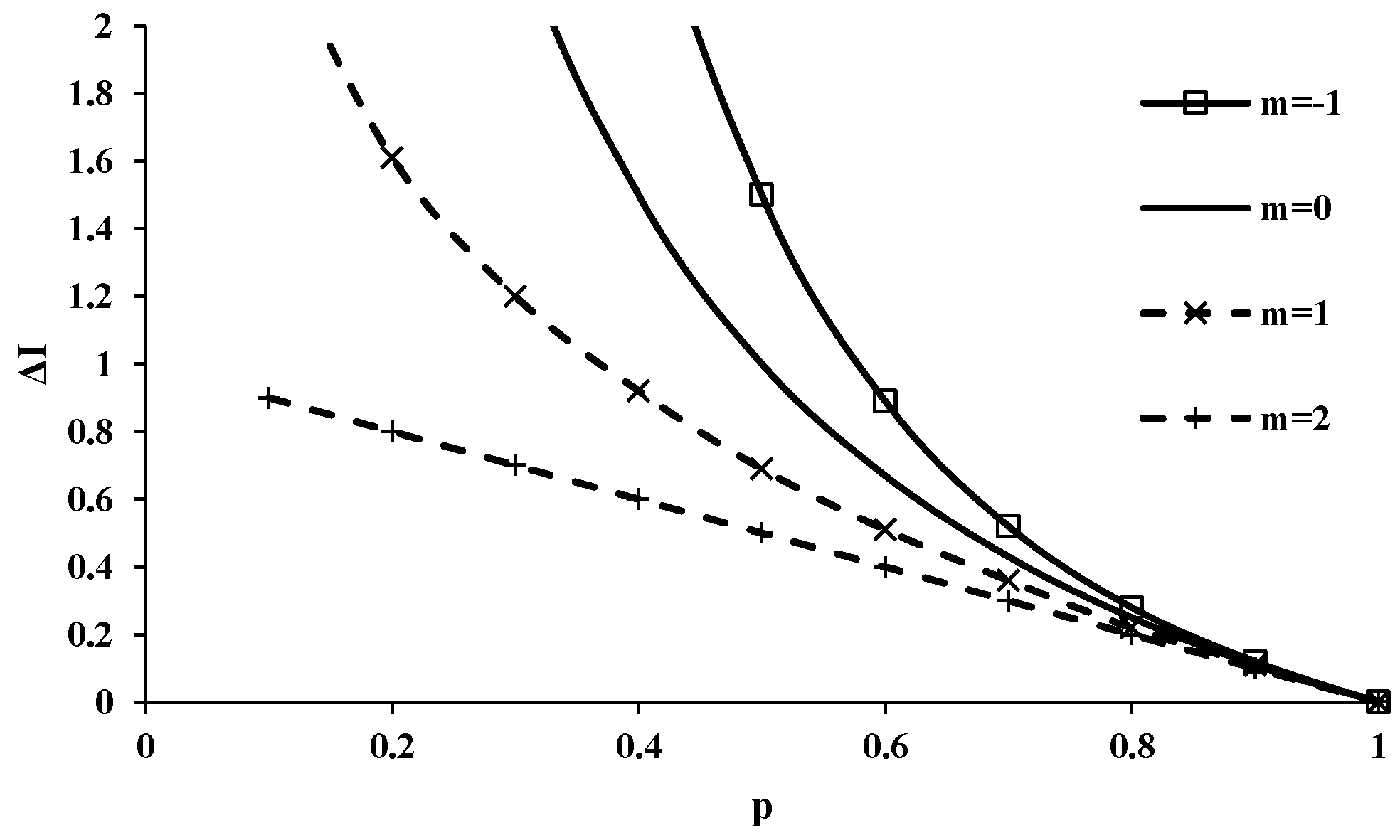
| ΔI(xi) | gain in information |
| k = (1 − m)/m | |
| m | Tsallis entropy index |
| n | Manning’s n |
| N | natural number representative |
| pi | probability |
| Q | flow |
| qs | sediment discharge |
| R | net radiative |
| Sj | entropic measure of redundancy |
| u | velocity |
| x | transverse direction |
| y | vertical dimension |
| σ2 | variance |
| λi | Langrange multiplier |
| μ1 | first moment |
| μ2 | second moment |
| w | surface soil moisture |
References
- Singh, V.P. Hydrologic Systems: Vol. 1. Rainfall-Runoff Modeling; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Singh, V.P. Hydrologic Systems: Vol. 2. Watershed Modeling; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Singh, V.P. (Ed.) Computer Models of Watershed Hydrology; Water Resources Publications: Highland Ranch, CO, USA, 1995. [Google Scholar]
- Salas, J.D.; Delleur, J.W.; Yevjevich, V.; Lane, W.L. Applied Modeling of Hydrologic Time Series; Water Resources Publications: Littleton, CO, USA, 1995. [Google Scholar]
- Beven, K.J. Rainfall-Runff Modelling: The Primer; Wiley: Chichester, UK, 2001. [Google Scholar]
- Sivakumar, B.; Berndtsson, R. Advances in Data-Based Approaches for Hydrologic Modeling and Forecasting; World Scientific Publishing Company: Singapore, 2010. [Google Scholar]
- Singh, V.P. Handbook of Applied Hydrology, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Singh, V.P. Kinematic Wave Modeling in Water Resources: Surface Water Hydrology; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Singh, V.P. Kinematic Wave Modeling in Water Resources: Environmental Hydrology; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Harmancioglu, N.B.; Fistikoglu, O.; Ozkul, S.D.; Singh, V.P.; Alpaslan, M.N. Water Quality Monitoring Network Design; Kluwer Academic Publishers: Boston, MA, USA, 1999; p. 299. [Google Scholar]
- Singh, V.P.; Luo, H. Entropy theory for distribution of one-dimensional velocity in open channels. J. Hydrol. Eng. 2011, 16, 725–735. [Google Scholar] [CrossRef]
- Luo, H.; Singh, V.P. Entropy theory for two-dimensional velocity distribution. J. Hydrol. Eng. 2011, 16, 303–315. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Two-dimensional velocity distribution in open channels using the Tsallis entropy. J. Hydrol. Eng. 2013, 18, 331–339. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. One-dimensional velocity distribution in open channels using Tsallis entropy. J. Hydrol. Eng. 2014, 19, 290–298. [Google Scholar] [CrossRef]
- Simons, D.B.; Senturk, F. Sediment Transport Technology; Water Resources Publications: Highland Ranch, CO, USA, 1976. [Google Scholar]
- Cui, H.; Singh, V.P. Suspended sediment concentration in open channels using Tsallis entropy. J. Hydrol. Eng. 2014, 19, 966–977. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Computation of suspended sediment discharge in open channels by combining Tsallis entropy-based methods and empirical formulas. J. Hydrol. Eng. 2014, 19, 18–25. [Google Scholar] [CrossRef]
- Singh, V.P. On the theories of hydraulic geometry. Int. J. Sediment Res. 2003, 18, 196–218. [Google Scholar]
- Singh, V.P.; Yang, C.T.; Deng, Z.Q. Downstream hydraulic geometry relations: 1. Theoretical development. Water Resour. Res. 2003, 39, 1337. [Google Scholar] [CrossRef]
- Singh, V.P.; Yang, C.T.; Deng, Z.Q. Downstream hydraulic geometry relations: 2. Calibration and testing. Water Resour. Res. 2003, 39, 1338. [Google Scholar] [CrossRef]
- Singh, V.P.; Zhang, L. At-a-station hydraulic geometry: I. Theoretical development. Hydrol. Process. 2008, 22, 189–215. [Google Scholar] [CrossRef]
- Singh, V.P.; Zhang, L. At-a-station hydraulic geometry: II. Calibration and testing. Hydrol. Process. 2008, 22, 216–228. [Google Scholar] [CrossRef]
- Singh, V.P.; Oh, J. A Tsallis entropy-based redundancy measure for water distribution network. Physica A 2014, 421, 360–376. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy Theory and Its Application in Environmental and Water Engineering; John Wiley & Sons: Sussex, UK, 2013. [Google Scholar]
- Singh, V.P. Entropy Theory in Hydraulic Engineering: An Introduction; ASCE Press: Reston, VA, USA, 2014. [Google Scholar]
- Singh, V.P. Entropy Theory in Hydrologic Science and Engineering; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Koutsoyiannis, D. Physics of uncertainty, the Gibbs paradox and indistinguishable particles. Stud. Hist. Philos. Mod. Phys. 2013, 44, 480–489. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour. 2012, 45, 51–57. [Google Scholar] [CrossRef]
- Shannon, C.E. The mathematical theory of communications, I and II. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Singh, V.P. The use of entropy in hydrology and water resources. Hydrol. Process. 1997, 11, 587–626. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic synthesis using entropy theory: Review. J. Hydrol. Eng. 2011, 16, 421–433. [Google Scholar] [CrossRef]
- Singh, V.P. Introduction to Tsallis Entropy Theory in Water Engineering; CRC Press/Taylor and Francis: Boca Raton, FL, USA, 2016. [Google Scholar]
- Tsallis, C. Entropic nonextensivity: A possible measure of complexity. Chaos Solitons Fractals 2002, 12, 371–391. [Google Scholar] [CrossRef]
- Tsallis, C. On the fractal dimension of orbits compatible with Tsallis statistics. Phys. Rev. E 1998, 58, 1442–1445. [Google Scholar] [CrossRef]
- Niven, R.K. The constrained entropy and cross-entropy functions. Physica A 2004, 334, 444–458. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Uncertainty, entropy, scaling and hydrological stochastics. 1. Marginal distributional properties of hydrological processes and state scaling. Hydrol. Sci. J. 2005, 50, 381–404. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Uncertainty, entropy, scaling and hydrological stochastics. 2. Time dependence of hydrological processes and time scaling. Hydrol. Sci. J. 2005, 50, 405–426. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. A toy model of climatic variability with scaling behavior. J. Hydrol. 2005, 322, 25–48. [Google Scholar] [CrossRef]
- Tsallis, C. Nonextensive statistical mechanics: Construction and physical interpretation. In Nonextensive Entropy-Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: New York, NY, USA, 2004; pp. 1–52. [Google Scholar]
- Tsallis, C. Nonextensive statistical mechanics and thermodynamics: Historical background and present status. In Nonextensive Statistical Mechanics and Its Applications; Abe, S., Okamoto, Y., Eds.; Series Lecture Notes in Physics; Springer: Berlin, Germany, 2001. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics, I. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics, II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Lombardo, F.; Volpi, E.; Koutsoyiannis, D.; Papalexiou, S.M. Just two moments! A cautionary note against use of high-order moments in multifractal models in hydrology. Hydrol. Earth Syst. Sci. 2014, 18, 243–255. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. A univariate model for longterm streamflow forecasting: I. Development. Stoch. Hydrol. Hydraul. 1991, 5, 173–188. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. A univariate model for longterm streamflow forecasting: II. Application. Stoch. Hydrol. Hydraul. 1991, 5, 189–205. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. A real-time flood forecasting model based on maximum entropy spectral analysis: I. Development. Water Resour. Manag. 1993, 7, 109–129. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. A real-time flood forecasting model based on maximum entropy spectral analysis: II. Application. Water Resour. Manag. 1993, 7, 131–151. [Google Scholar] [CrossRef]
- Krasovskaia, I. Entropy-based grouping of river flow regimes. J. Hydrol. 1997, 202, 173–191. [Google Scholar] [CrossRef]
- Krasovskaia, I.; Gottschalk, L. Stability of river flow regimes. Nordic Hydrol. 1992, 23, 137–154. [Google Scholar]
- Singh, V.P. Entropy-Based Parameter Estimation in Hydrology; Kluwer Academic Publishers: Boston, MA, USA, 1998; p. 365. [Google Scholar]
- Wang, J.; Bras, R.L. A model of evapotranspiration based on the theory of maximum entropy production. Water Resour. Res. 2011, 47, W03521. [Google Scholar] [CrossRef]
- Yang, C.T. Unit stream power and sediment transport. J. Hydraul. Div. ASCE 1972, 98, 1805–1826. [Google Scholar]
- Fiorentino, M.; Claps, P.; Singh, V.P. An entropy-based morphological analysis of river-basin networks. Water Resour. Res. 1993, 29, 1215–1224. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and 2-D velocity distribution in open channels. J. Hydraul. Eng. ASCE 1988, 114, 738–756. [Google Scholar] [CrossRef]
- Cao, S.; Knight, D.W. Design of threshold channels. Hydra 2000. In Proceedings of the 26th IAHR Congress, London, UK, 11–15 September 1995. [Google Scholar]
- Cao, S.; Knight, D.W. New Concept of hydraulic geometry of threshold channels. In Proceedings of the 2nd Symposium on the Basic Theory of Sedimentation, Beijing, China, 30 October–2 November 1995. [Google Scholar]
- Cao, S.; Knight, D.W. Entropy-based approach of threshold alluvial channels. J. Hydraul. Res. 1997, 35, 505–524. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy theory for movement of moisture in soils. Water Resour. Res. 2010, 46, 1–12. [Google Scholar] [CrossRef]
- Singh, V.P. Tsallis entropy theory for derivation of infiltration equations. Trans. ASABE 2010, 53, 447–463. [Google Scholar] [CrossRef]
- Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Krstanovic, P.F.; Singh, V.P. Evaluation of rainfall networks using entropy: 1. Theoretical development. Water Resour. Manag. 1992, 6, 279–293. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. Evaluation of rainfall networks using entropy: 2. Application. Water Resour. Manag. 1992, 6, 295–314. [Google Scholar] [CrossRef]
- Yang, Y.; Burn, D.H. An entropy approach to data collection network design. J. Hydrol. 1994, 157, 307–324. [Google Scholar] [CrossRef]
- Mogheir, Y.; Singh, V.P. Application of information theory to groundwater quality monitoring networks. Water Resour. Manag. 2002, 16, 37–49. [Google Scholar] [CrossRef]
- Perelman, L.; Ostfeld, A.; Salomons, E. Cross entropy multiobjective optimization for water distribution systems design. Water Resour. Res. 2008, 44, W09413. [Google Scholar] [CrossRef]
- Goulter, I.C. Current and future use of systems analysis in water distribution network design. Civ. Eng. Syst. 1987, 4, 175–184. [Google Scholar] [CrossRef]
- Goulter, I.C. Assessing the reliability of water distribution networks using entropy based measures of network redundancy. In Entropy and Energy Dissipation in Water Resources; Singh, V.P., Fiorentino, M., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992; pp. 217–238. [Google Scholar]
- Walters, G. Optimal design of pipe networks: A review. In Proceedings of the 1st International Conference Computational Water Resources, Rabat, Morocco, 14–18 March 1988; Computational Mechanics Publications: Southampton, UK, 1988; pp. 21–31. [Google Scholar]
- Leopold, L.B.; Maddock, T.J. Hydraulic Geometry of Stream Channels and Some Physiographic Implications; US Government Printing Office: Washington, DC, USA, 1953; p. 55.
- Langbein, W.B. Geometry of river channels. J. Hydraul. Div. ASCE 1964, 90, 301–311. [Google Scholar]
- Yang, C.T.; Song, C.C.S.; Woldenberg, M.J. Hydraulic geometry and minimum rate of energy dissipation. Water Resour. Res. 1981, 17, 1014–1018. [Google Scholar] [CrossRef]
- Wolman, M.G. The Natural Channel of Brandywine Creek, Pennsylvania; US Government Printing Office: Washington, DC, USA, 1955.
- Williams, G.P. Hydraulic Geometry of River Cross-Sections-Theory of Minimum Variance; US Government Printing Office: Washington, DC, USA, 1978.
- Wang, J.; Salvucci, G.D.; Bras, R.L. A extremum principle of evaporation. Water Resour. Res. 2004, 40, W09303. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. ON the cumulative distribution function for entropy-based hydrologic modeling. Trans. ASABE 2012, 55, 429–438. [Google Scholar] [CrossRef]
- Singh, V.P.; Luo, H. Derivation of velocity distribution using entropy. In Proceedings of the IAHR Congress, Vancouver, BC, Canada, 9–14 August 2009; pp. 31–38. [Google Scholar]
- Singh, V.P.; Byrd, A.; Cui, H. Flow duration curve using entropy theory. J. Hydrol. Eng. 2014, 19, 1340–1348. [Google Scholar] [CrossRef]
- Weijs, S.V.; van de Giesen, N.; Parlange, M.B. HydroZIP: How hydrological knowledge can be used to improve compression of hydrological data. Entropy 2013, 15, 1289–1310. [Google Scholar] [CrossRef]
- Chen, J.; Li, G. Tsallis wavelet entropy and its application in power signal analysis. Entropy 2014, 16, 3009–3025. [Google Scholar] [CrossRef]
- Furuichi, S.; Mitroi-Symeonidis, F.-C.; Symeonidis, E. On some properties of Tsallis hypoentropies and hypodivergences. Entropy 2014, 16, 5377–5399. [Google Scholar] [CrossRef]
- Lenzi, E.K.; da Silva, L.R.; Lenzi, M.K.; dos Santos, M.A.F.; Ribeiro, H.V.; Evangelista, L.R. Intermittent motion, nonlinear diffusion equation and Tsallis formalism. Entropy 2017, 19, 42. [Google Scholar] [CrossRef]
- Evren, A.; Ustaoğlu, E. Measures of qualitative variation in the case of maximum entropy. Entropy 2017, 19, 204. [Google Scholar] [CrossRef]
- Kalogeropoulos, N. The Legendre transform in non-additive thermodynamics and complexity. Entropy 2017, 19, 298. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, V.P.; Sivakumar, B.; Cui, H. Tsallis Entropy Theory for Modeling in Water Engineering: A Review. Entropy 2017, 19, 641. https://doi.org/10.3390/e19120641
Singh VP, Sivakumar B, Cui H. Tsallis Entropy Theory for Modeling in Water Engineering: A Review. Entropy. 2017; 19(12):641. https://doi.org/10.3390/e19120641
Chicago/Turabian StyleSingh, Vijay P., Bellie Sivakumar, and Huijuan Cui. 2017. "Tsallis Entropy Theory for Modeling in Water Engineering: A Review" Entropy 19, no. 12: 641. https://doi.org/10.3390/e19120641
APA StyleSingh, V. P., Sivakumar, B., & Cui, H. (2017). Tsallis Entropy Theory for Modeling in Water Engineering: A Review. Entropy, 19(12), 641. https://doi.org/10.3390/e19120641





