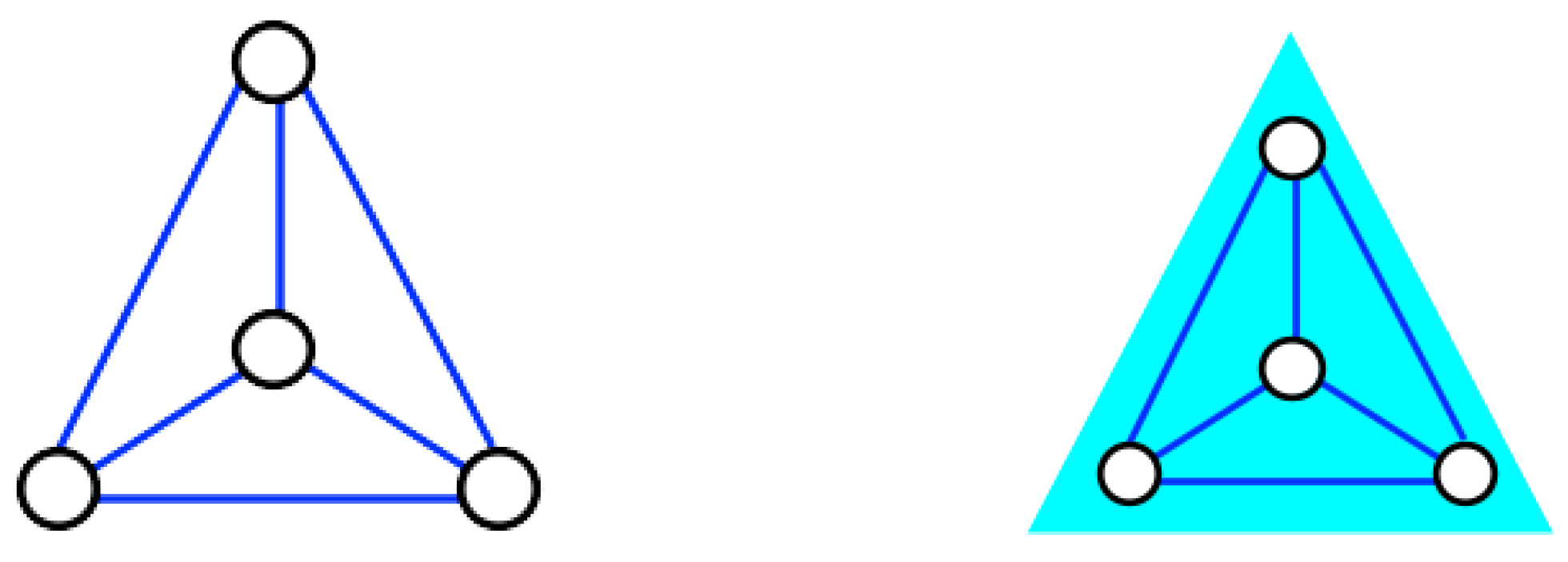1. Introduction
Statistical mechanics stems from classical (or quantum) mechanics. The latter prescribes which are the relevant quantities (i.e., the conserved ones). The former brings this further, and it predicts that the probability to observe a system in a microscopic state
, in thermal equilibrium, is given by:
where
is the energy of configuration
. The inverse temperature
is the only relevant parameter that needs to be adjusted, so that the ensemble average
matches the observed energy
U. It has been argued [
1] that the recipe that leads from
to the distribution
is maximum entropy: among all distributions that satisfy
, the one maximizing the entropy
should be chosen. Information theory clarifies that the distribution Equation (
1) is the one that assumes nothing else but
, or equivalently, that all other observables can be predicted from the knowledge of
.
This idea carries through more generally to inference problems: given a dataset of
N observations
of a system, one may invoke maximum entropy to infer the underlying distribution
that reproduces the empirical averages of a set
of observables
(
). This leads to Equation (
1) with:
where the parameters
should be fixed by solving the convex optimization problems:
that result from entropy maximization and are also known to coincide with maximum likelihood estimation (see [
2,
3,
4]).
For example, in the case of spin variables
, the distribution that reproduces empirical averages
and correlations
is the pairwise model:
which in the case
and
is the celebrated Ising model. The literature on inference of Ising models, stemming from the original paper on Boltzmann learning [
5] to early applications to neural data [
6] has grown considerably (see [
7] for a recent review), to the point that some suggested [
8] that a purely data-based statistical mechanics is possible.
Research has mostly focused on the estimate of the parameters
, which itself is a computationally challenging issue when
[
7], or in recovering sparse models, distinguishing true interactions (
) from spurious ones (
; see, e.g., [
9]). Little has been done to go beyond pairwise interactions (yet, see [
10,
11,
12,
13]). This is partly because pairwise interactions offer a convenient graphical representation of statistical dependences; partly because
ℓ-th order interactions require ∼n
parameters and the available data hardly ever allow one to go beyond
[
14]. Yet, strictly speaking, there may be no reason to believe that interactions among variables are only pairwise. The choice of form (
4) for the Hamiltonian represents an assumption on the intrinsic laws of motion, which reflects an a priori belief of the observer on the system. Conversely, one would like to have inference schemes that certify that pairwise interactions are really the relevant ones, i.e., those that need to be included in
H in order to reproduce correlations
of arbitrary order
ℓ [
15].
We contrast a view of inference as parameter estimation of a preassigned (pairwise) model, where maximum entropy serves merely an ancillary purpose, with the one where the ultimate goal of statistical inference is precisely to identify the minimal set of sufficient statistics that, for a given dataset , accurately reproduces all empirical averages. In this latter perspective, maximum entropy plays a key role in that it affords a sharp distinction between relevant variables (, ) (which are the sufficient statistics) and irrelevant ones, i.e., all other operators that are not a linear combination of the relevant ones, but whose values can be predicted through theirs. To some extent, understanding amounts precisely to distinguishing the relevant variables from the “dependent” ones: those whose values can be predicted.
Bayesian model selection provides a general recipe for identifying the best model
; yet, as we shall see, the procedure is computationally unfeasible for spin models with interactions of arbitrary order, even for moderate dimensions (
). Our strategy will then be to perform model selection within the class of mixture models, where it is straightforward [
16], and then, to project the result on spin models. The most likely models in this setting are those that enforce a symmetry among configurations that occur with the same frequency in the dataset. These symmetries entail a decomposition of the log-likelihood with a flavor that is similar to principal component analysis (yet of a different kind than that described in [
17]). This directly predicts the sufficient statistics
that need to be considered in maximum entropy inference. Interestingly, we find that the number of sufficient statistics depends on the frequency distribution of observations in the data. This implies that the dimensionality of the inference problem is not determined by the number of parameters in the model, but rather by the richness of the data.
The resulting model features interactions of arbitrary order, in general, but is able to recover sparse models in simple cases. An application to real data shows that the proposed approach is able to spot the prevalence of two-body interactions, while suggesting that some specific higher order terms may also be important.
3. Mapping Mixture Models into Spin Models
Model
allows for a representation in terms of the variables
, thanks to the relation:
which is of the same nature of the one discussed in [
11] and whose proof is deferred to
Appendix A. The index in
indicates that the coupling refers to model
and merely corresponds to a change of variables
; we shall drop it in what follows, if it causes no confusion.
In Bayesian inference,
should be considered as a random variable, whose posterior distribution for a given dataset
can be derived (see [
16] and
Appendix B). Then, Equation (
8) implies that also
is a random variable, whose distribution can also be derived from that of
.
Notice, however, that Equation (
8) spans only a
-dimensional manifold in the
-dimensional space
, because there are only
independent variables
. This fact is made more evident by the following argument: Let
be a
component vector such that:
In other words, the linear combination of the random variables
with coefficients
that satisfy Equation (
9) is not random at all. There are (generically)
vectors
that satisfy Equation (
9) each of which imposes a linear constraint of the form of Equation (
10) on the possible values of
.
In addition, there are
q orthogonal directions
that can be derived from the singular value decomposition of
:
This in turn implies that model
can be written in the exponential form (see
Appendix D for details):
where:
The exponential form of Equation (
12) identifies the variables
with the sufficient statistics of the model. The maximum likelihood parameters
can be determined using the knowledge of empirical averages of
alone, solving the equations
for all
. The resulting distribution is the maximum entropy distribution that reproduces the empirical averages of
. In this precise sense,
are the relevant variables. Notice that, the variables
are themselves an orthonormal set:
In particular, if we focus on the
partition of the set of states, the one assigning the same probability
to all states
that are observed
k times, we find that
exactly reproduces the empirical distribution. This is a consequence of the fact that the variables
that maximize the likelihood must correspond to the maximum likelihood estimates
, via Equation (
8). This implies that the maximum entropy distribution Equation (
12) reproduces not only the empirical averages
, but also that of the operators
for all
. A direct application of Equation (
8) shows that the maximum entropy parameters are given by the formula:
Similarly, the maximum likelihood parameters
are given by:
Notice that, when the set of states that are not observed is not empty, all couplings with diverge. Similarly, all with also diverge. We shall discuss later how to regularize these divergences that are expected to occur in the under-sampling regime (i.e., when ).
It has to be noted that, of the
q parameters
, only
are independent. Indeed, we find that one of the
q singular values
in Equation (
11) is practically zero. It is interesting to inspect the covariance matrix
of the deviations
from the expected values computed on the posterior distribution. We find (see
Appendix C and
Appendix D) that
has eigenvalues
along the eigenvectors
and zero eigenvalues along the directions
. The components
with the largest singular value
are those with the largest statistical error, so one would be tempted to consider them as “sloppy” directions, as in [
19]. Yet, by Equation (
17), the value of
itself is proportional to
, so the relative fluctuations are independent of
. Indeed “sloppy” modes appear in models that overfit the data, whereas in our case, model selection on mixtures ensures that the model
does not overfit. This is why relative errors on the parameters
are of comparable magnitude. Actually, variables
that correspond to the largest eigenvalues
are the most relevant ones, since they identify the directions along which the maximum likelihood distribution Equation (
12) tilts most away from the unconstrained maximal entropy distribution
. A further hint in this direction is that Equation (
17) implies that variables
with the largest
are those whose variation across states
typically correlates mostly with the variation of
in the sample.
Notice that the procedure outlined above produces a model that is sparse in the variables, i.e., it depends only on parameters, where q is, in the case of the partition, the number of different values that takes in the sample. Yet, it is not sparse in the variables. Many of the results that we have derived carry through with obvious modifications if the sums over are restricted to a subset of putatively relevant interactions. Alternatively, the results discussed above can be the starting point for the approximate scheme to find sparse models in the spin representation.
4. Illustrative Examples
In the following, we present simple examples clarifying the effects of the procedure outlined above.
4.1. Recovering the Generating Hamiltonian from Symmetries: Two and Four Spins
As a simple example, consider a system of two spins. The most general Hamiltonian that should be considered in the inference procedure is:
Imagine the data are generated from the Hamiltonian:
and let us assume that the number of samples is large enough, so that the optimal partition
groups configurations of aligned spins
distinguishing them from the configuration of unaligned ones
.
Following the strategy explained in
Section 2.1, we observe that
for both
and 2. Therefore, Equation (
8) implies
. Therefore, the
model only allows for
to be nonzero. In this simple case, symmetries induced by the
model (i.e.,
) directly produce a sparse model where all interactions that are not consistent with them are set to zero.
Consider now a four-spin system. Suppose that the generating Hamiltonian is that of a pairwise fully-connected model as in
Figure 1 (left), with the same couplings
. With enough data, we can expect that the optimal model is based on the partition
that distinguishes three sets of configurations:
depending on the absolute value of the total magnetization. The
model assigns the same probability
to configurations
in the same set
. Along similar lines to those in the previous example, it can be shown that any interaction of order one is put to zero (
), as well as any interaction of order three (
), because the corresponding interactions are not invariant under the symmetry
that leaves
invariant. The interactions of order two will on the other hand correctly be nonzero and take on the same value
. The value of the four-body interaction is:
This, in general, is different from zero. Indeed, a model with two- and four-body interactions shares the same partition
in Equation (
20). Therefore, unlike the example of two spins, symmetries of the
model do not allow one to recover uniquely the generative model (
Figure 1, left). Rather, the inferred model has a fourth order interaction (
Figure 1, right) that cannot be excluded on the basis of symmetries alone. Note that there are
= 32,768 possible models of four spins. In this case, symmetries allow us to reduce the set of possible models to just two.
4.2. Exchangeable Spin Models
Consider models where
is invariant under any permutation
of the spins, i.e.,
. For these models,
only depends on the total magnetization
. For example, the fully-connected Ising model:
belongs to this class. It is natural to consider the partition where
contain all configurations with
q spins
and
spins
(
). Therefore, when computing
, one has to consider
configurations. If
involves
m spins, then
of them will involve
j spins
, and the operator
takes the value
on these configurations. Therefore,
only depends on the number
of spins involved and:
This implies that the coefficients
of terms that involve
m spins must all be equal. Indeed, for any two operators
with
:
Therefore, the proposed scheme is able, in this case, to reduce the dimensionality of the inference problem dramatically, to models where interactions only depend on the number of spins involved in .
Note also that any non-null vector
such that
and
if
satisfies:
The vectors
corresponding to the non-zero singular values of
need to be orthogonal to each of these vectors, so they need to be constant for all
that involve the same number of spins. In other words,
only depend on the number
of spins involved. A suitable choice of a set of
n independent eigenvectors in this space is given by
that correspond to vectors that are constant within the sectors of
with
and are zero outside. In such a case, the sufficient statistics for models of this type are:
as it should indeed be. We note in passing that terms of this form have been used in [
20].
Inference can also be carried out directly. We first observe that the
are defined up to a constant. This allows us to fix one of them arbitrarily, so we will take
. If
is the number of observed configurations with
spins
, then the equation
(for
) reads:
so that, after some algebra,
From this, one can go back to the couplings of operators
using:
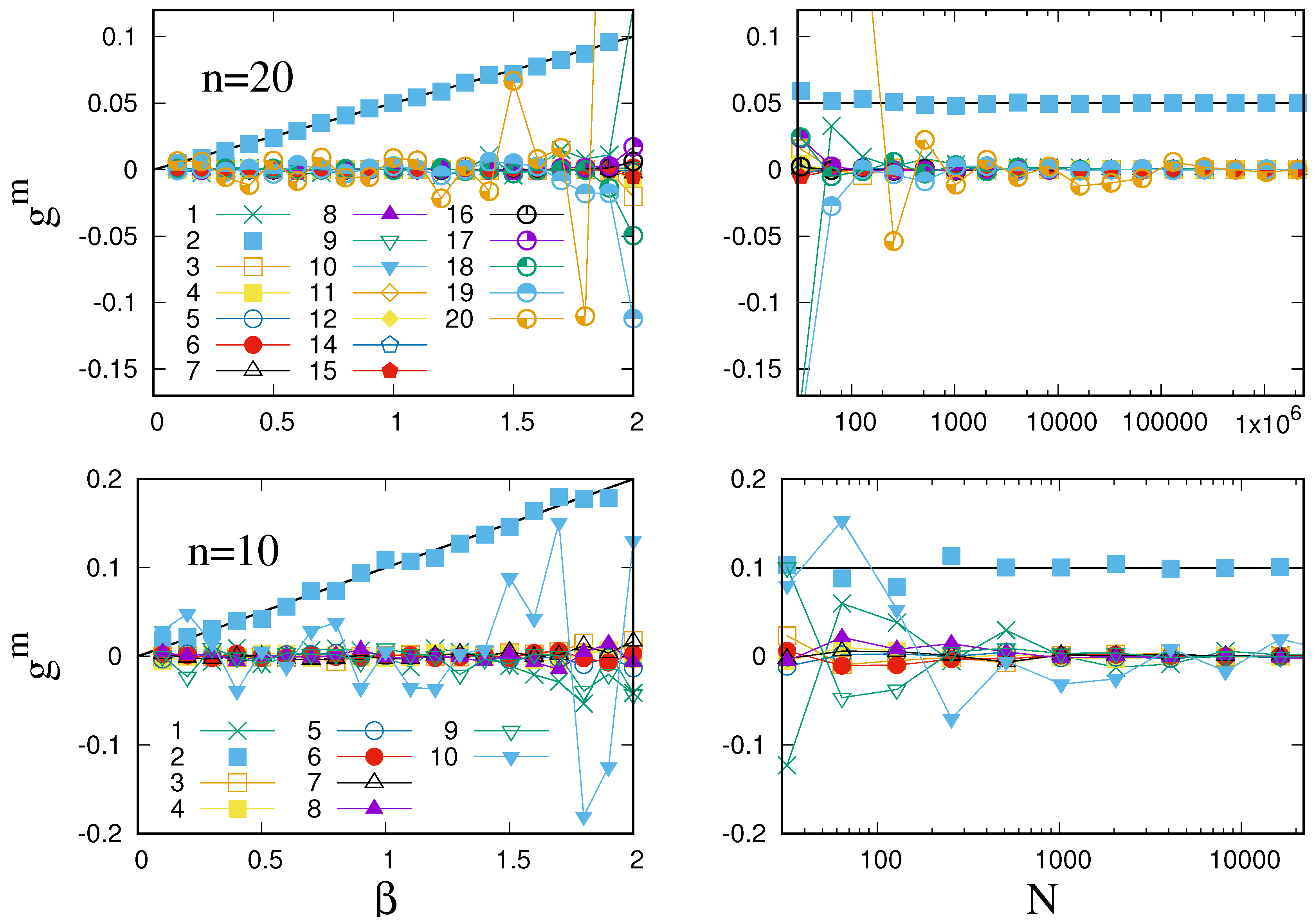
Figure 2 illustrates this procedure for the case of the mean field (pairwise) Ising model Equation (
22). As this shows, the procedure outlined above identifies the right model when the number of samples is large enough. If
N is not large enough, large deviations from theoretical results start arising in couplings of highest order, especially if
is large.
4.3. The Deep Under-Sampling Limit
The case where the number N of sampled configurations is so small that some of the configurations are never observed deserves some comments. As we have seen, taking the frequency partition , where , if , then divergences can manifest in those couplings where .
It is instructive to consider the deep under-sampling regime where the number
N of visited configurations is so small that configurations are observed at most once in the sample. This occurs when
. In this case, the most likely partitions are (i) the one where all states have the same probability
and (ii) the one where states observed once have probability
and states not yet observed have probability
, i.e.,
with
,
. Following [
16], it is easy to see that that generically, the probability of model
overweights the one of model
, because
. Under
, it is easy to see that
for all
. This, in turn, implies that
exactly for all
. We reach the conclusion that no interaction can be inferred in this case [
21].
Taking instead the partition
, a straightforward calculation shows that Equation (
8) leads to
. Here,
a should be fixed in order to solve Equation (
3). It is not hard to see that this leads to
. This is necessary in order to recover empirical averages, which are computed assuming that unobserved states
have zero probability.
This example suggests that the divergences that occur when assuming the partition, because of unobserved states () can be removed by considering partitions where unobserved states are clamped together with states that are observed once.
These singularities arise because, when all the singular values are considered, the maximum entropy distribution exactly reproduces the empirical distribution. This suggests that a further method to remove these singularities is to consider only the first
ℓ singular values (those with largest
) and to neglect the others, i.e., to set
for all other
’s. It is easy to see that this solves the problem in the case of the deep under-sampling regime considered above. There, only one singular value exists, and when this is neglected, one derives the result
,
again. In order to illustrate this procedure in a more general setting, we turn to the specific case of the U.S. Supreme Court data [
8].
4.4. A Real-World Example
We have applied the inference scheme to the data of [
8] that refer to the decisions of the U.S. Supreme Court on 895 cases. The U.S. Supreme Court is composed of nine judges, each of whom casts a vote against (
) or in favor (
) of a given case. Therefore, this is a
spin system for which we have
observations. The work in [
8] has fitted this dataset with a fully-connected pairwise spin model. We refer to [
8] for details on the dataset and on the analysis. The question we wish to address here is whether the statistical dependence between judges of the U.S. Supreme Court can really be described as a pairwise interaction, which hints at the direct influence of one judge on another one, or whether higher order interactions are also present.
In order to address this issue, we also studied a dataset
spins generated form a pairwise interacting model, Equation (
22), from which we generated
independent samples. The value of
was chosen so as to match the average value of two-body interactions fitted in the true dataset. This allows us to test the ability of our method to recover the correct model when no assumption on the model is made.
As discussed above, the procedure discussed in the previous section yields estimates that allow us to recover empirical averages of all the operators. These, for a finite sample size N, are likely to be affected by considerable noise that is expected to render the estimated extremely unstable. In particular, since the sample contains unobserved states, i.e., states with , we expect some of the parameters to diverge or, with a finite numerical precision, to attain large values.
Therefore, we also performed inference considering only the components with largest
in the singular value decomposition.
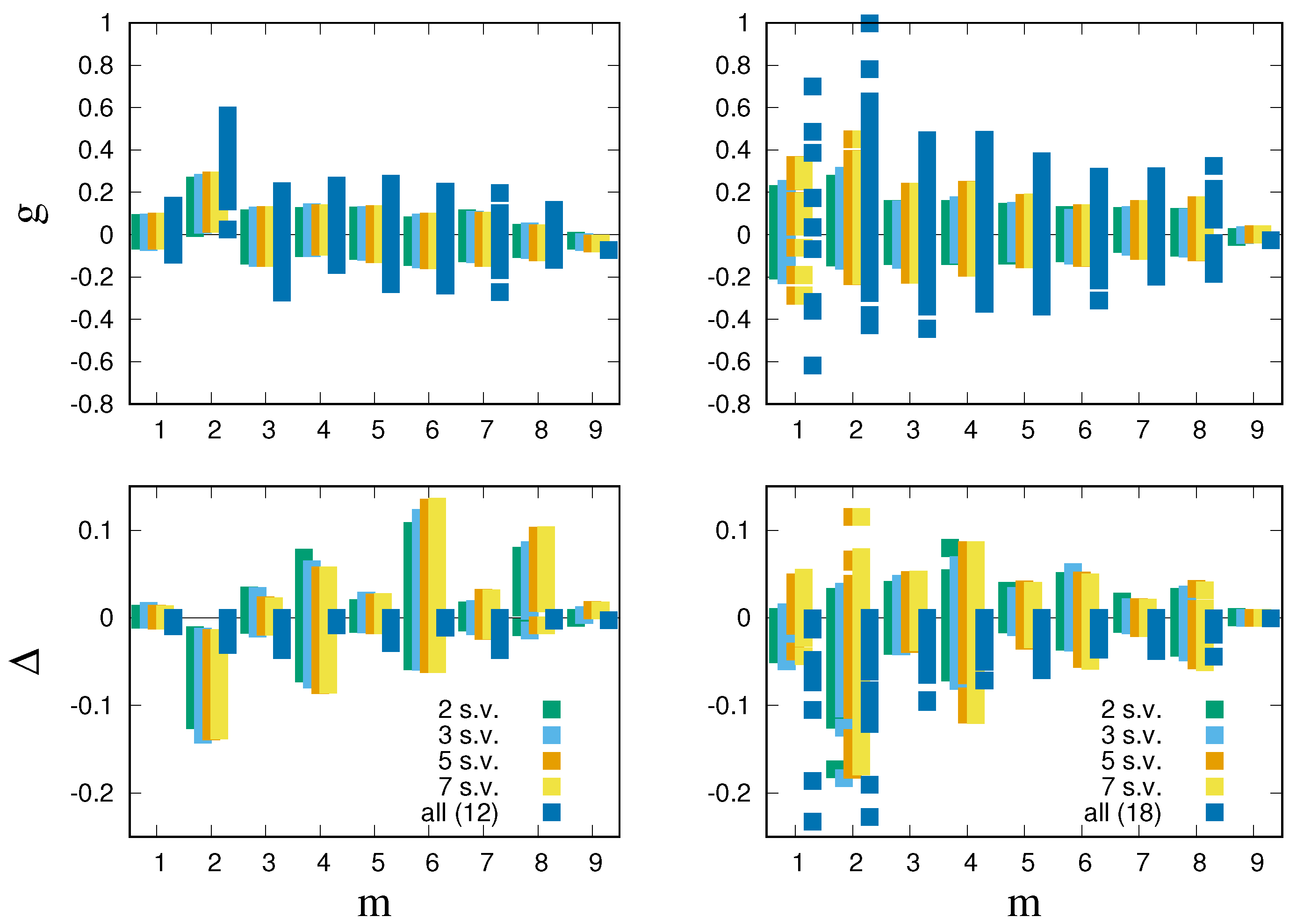
Table 1 reports the values of the estimated parameters
obtained for the U.S. Supreme Court considering only the top
to 7 singular values, and it compares them to those obtained when all singular values are considered. We observe that when enough singular values are considered, the estimated couplings converge to stable values, which are very different from those obtained when all 18 singular values are considered. This signals that the instability due to unobserved states can be cured by neglecting small singular values
.
This is confirmed by
Figure 3, which shows that estimates of
are much more stable when few singular values are considered (top right panel). The top left panel, which refer to synthetic data generated from Equation (
22), confirms this conclusion. The estimates
are significantly larger for a two-body interaction than for higher order and one-body interactions, as expected. Yet, when all singular values are considered, the estimated values of a two-body interaction fluctuate around values that are much larger than the theoretical one (
) and the ones estimated from fewer singular values.
In order to test the performance of the inferred couplings, we measure for each operator
the change:
in log-likelihood when
is set to zero. If
is positive or is small and negative, the coupling
can be set to zero without affecting much the ability of the model to describe the data. A large and negative
instead signals a relevant interaction
.
Clearly, for all when is computed using all the q components. This is because in that case, the log-likelihood reaches the maximal value it can possibly achieve. When not all singular values are used, can also attain positive values.
Figure 3 confirms our conclusions that inference using all the components is unstable. Indeed for the synthetic data, the loss in likelihood is spread out on operators of all orders, when all singular values are considered. When few singular values are considered, instead, the loss in likelihood is heavily concentrated on two body terms (
Figure 3, bottom left). Pairwise interactions stick out prominently because
for all two-body operators
. Still, we see that some of the higher order interactions, with even order, also generate significant likelihood losses.
With this insight, we can now turn to the U.S. Supreme Court data, focusing on inference with few singular values. Pairwise interactions stick out as having both sizable
(
Figure 3, top right) and significant likelihood loss (
Figure 3, bottom right). Indeed, the top interactions (those with minimal
) are prevalently pairwise ones.
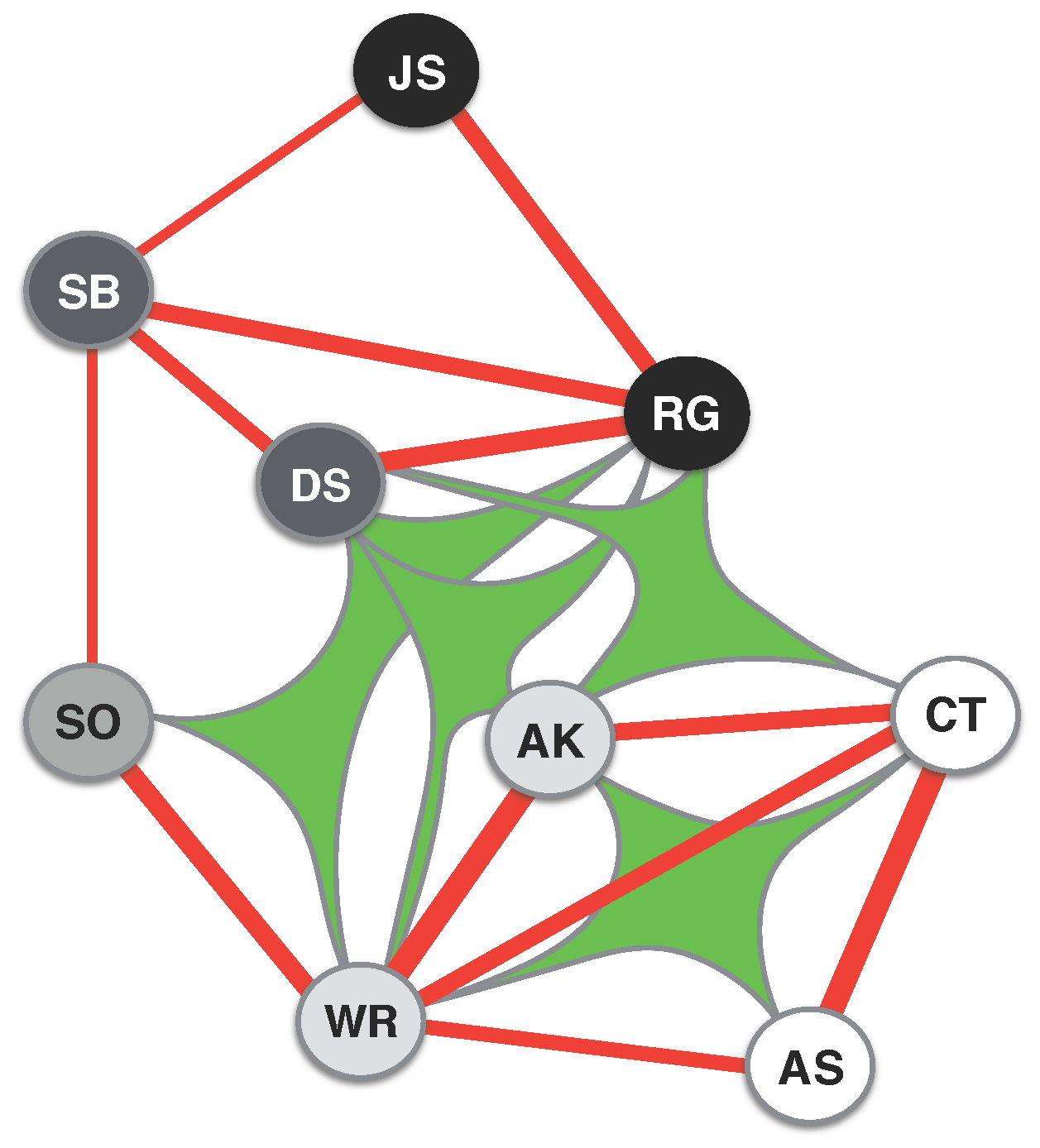
Figure 4 shows the hypergraph obtained by considering the top 15 interactions [
22], which are two- or four-body terms (see the caption for details). Comparing this with synthetic data, where we find that the top 19 interactions are all pairwise, we conjecture that four-body interactions may not be spurious. The resulting network clearly reflects the orientation of individual judges across an ideological spectrum going from liberal to conservative positions (as defined in [
8]). Interestingly, while two-body interactions describe a network polarized across this spectrum with two clear groups, four-body terms appear to mediate the interactions between the two groups. The prevalence of two-body interactions suggests that direct interaction between the judges is clearly important, yet higher order interactions seem to play a relevant role in shaping their collective behavior.
As in the analysis in [
8], single-body terms, representing a priori biases of individual judges, are not very relevant [
23].
5. Conclusions
The present work represents a first step towards a Bayesian model selection procedure for spin models with interactions of arbitrary order. Rather than tackling the problem directly, which would imply comparing an astronomical number of models even for moderate n, we show that model selection can be performed first on mixture models, and then, the result can be projected in the space of spin models. This approach spots symmetries between states that occur with a similar frequency, which impose constraints between the parameters . As we have seen, in simple cases, these symmetries are enough to recover the correct sparse model, imposing that for all those interactions that are not consistent with the symmetries. These symmetries allow us to derive a set of sufficient statistics (the relevant variables) whose empirical values allow one to derive the maximum likelihood parameters . The number q of sufficient statistics is given by the number of sets in the optimal partition of states. Therefore, the dimensionality of the inference problem is not related to the number of different interaction terms (or equivalently, of parameters ), but it is rather controlled by the number of different frequencies that are observed in the data. As the number N of samples increases, q increases and so does the dimensionality of the inference problem, until one reaches the well-sampled regime () when all states are well resolved in frequency.
It has been observed [
11] that the family of probability distributions of the form (
5) is endowed with a hierarchical structure that implies that high-order and low-order interactions are entangled in a nontrivial way. For example, we observe a non-trivial dependence between two- and four-body interactions. On the other hand, Ref. [
18] shows that the structure of interdependence between operators in a model is not simply related to the order of the interactions and is invariant with respect to gauge transformations that do not conserve the order of operators. This, combined with the fact that our approach does not introduce any explicit bias to favor an interaction of any particular order, suggests that the approach generates a genuine prediction on the relevance of interactions of a particular order (e.g., pairwise). Yet, it would be interesting to explore these issues further, combining the quasi-orthogonal decomposition introduced in [
11] with our approach.
It is interesting to contrast our approach with the growing literature on sloppy models (see, e.g., [
19]). Transtrum et al. [
19] have observed that inference of a given model is often plagued by overfitting that causes large errors in particular combinations of the estimated parameters.
Our approach is markedly different in that we stem right from the beginning from Bayesian model selection, and hence, we rule out overfitting from the outset. Our decomposition in singular values identifies those directions in the space of parameters that allow one to match the empirical distribution while preserving the symmetries between configurations observed with a similar frequency.
The approach discussed in this paper is only feasible when the number of variables n is small. Yet, the generalization to a case where the set of interactions is only a subset of the possible interactions is straightforward. This entails setting to zero all couplings relative to interactions . Devising decimation schemes for doing this in a systematic manner, as well as combining our approach with regularization schemes (e.g., LASSO) to recover sparse models comprise a promising avenue of research for exploring the space of models.