Group Sparsity and Graph Regularized Semi-Nonnegative Matrix Factorization with Discriminability for Data Representation

Abstract

Semi-Nonnegative Matrix Factorization (Semi-NMF), as a variant of NMF, inherits the merit of parts-based representation of NMF and possesses the ability to process mixed sign data, which has attracted extensive attention. However, standard Semi-NMF still suffers from the following limitations. First of all, Semi-NMF fits data in a Euclidean space, which ignores the geometrical structure in the data. What’s more, Semi-NMF does not incorporate the discriminative information in the learned subspace. Last but not least, the learned basis in Semi-NMF is unnecessarily part based because there are no explicit constraints to ensure that the representation is part based. To settle these issues, in this paper, we propose a novel Semi-NMF algorithm, called Group sparsity and Graph regularized Semi-Nonnegative Matrix Factorization with Discriminability (GGSemi-NMFD) to overcome the aforementioned problems. GGSemi-NMFD adds the graph regularization term in Semi-NMF, which can well preserve the local geometrical information of the data space. To obtain the discriminative information, approximation orthogonal constraints are added in the learned subspace. In addition, ${\ell }_{21}$ norm constraints are adopted for the basis matrix, which can encourage the basis matrix to be row sparse. Experimental results in six datasets demonstrate the effectiveness of the proposed algorithms.

1. Introduction

Nonnegative Matrix Factorization (NMF) [1] is a useful data representation technique for finding compact and low dimensional representations of data. NMF decomposes the nonnegative data matrix $\mathbf{X}$ into a basis matrix $\mathbf{U}$ and an encoding matrix $\mathbf{V}$ whose product can approximate the original data matrix $\mathbf{X}$. Due to the nonnegative constraint, NMF only allows additive combination, which leads to the parts-based representation. The parts-based representation is consistent with the psychological intuition of combining parts to form a whole, so NMF has been widely used in data mining and pattern-recognition problems. The nonnegative constraints distinguish NMF from many other traditional matrix factorization algorithms, such as Principal Component Analysis (PCA) [2], independent component analysis [3] and Singular Value Decomposition (SVD). However, the major limitation of NMF is that it cannot deal with mixed sign data.

To address the limitation of NMF while inheriting all its merits, Ding et al. [4] proposed Semi-Nonnegative Matrix Factorization (Semi-NMF), which can handle mixed sign items in data matrix $\mathbf{X}$. Specifically, Semi-NMF only imposes non-negative constraints on encoding matrix $\mathbf{V}$ and allows mixed signs in both the data matrix $\mathbf{X}$ and the basis matrix $\mathbf{U}$. This allows Semi-NMF to learn a new representation from any signed data and extends the range of application of NMF ideas.

Numerous studies [5,6,7] have demonstrated that data are usually drawn from sampling a probability distribution that has support on or near a submanifold of the ambient space. Some manifold learning algorithms such as ISOMAP[5], Locally Linear Embedding (LLE) [6], Laplacian Eigenmap [7], etc, have been proposed to detect the hidden manifold structure. All these algorithms use the locally invariant idea [8], i.e., the nearby points are very likely to have similar embeddings. If the geometrical structure is utilized, the learning performance will be evidently enhanced.

On the other hand, the discriminative information of data is very important in computer vision and pattern recognition. Usually, exploiting label information in the framework of NMF can allow obtaining discriminative information. For example, Liu et al. [9] proposed Constrained Nonnegative Matrix Factorization (CNMF), which imposes the label information for the objective function as hard constraints. Li et al. [10] developed a semi-supervised robust structured NMF, which exploited the block-diagonal structure in the framework of NMF. Unfortunately, under the unsupervised scenario, we cannot have any label information. However, through reformulation of the scaled indicator matrix, we find that there is an approximation orthogonal discriminability in the learned subspace. Adding approximation orthogonal constraints to the new representation, we could acquire some discriminative information in the learned subspace.

Donoho and Stodden [11] theoretically proved that NMF cannot guarantee decomposing an object into parts. In other words, NMF may be unable to result in the parts-based representation for some datasets. To ensure the parts-based representation, sparse constraints have been introduced to NMF. Hoyer [12] proposed sparse constrained NMF, which added the ${\ell }_1$ norm penalty on the basis and encoding matrix and obtained more sparse representation than standard NMF. However, the ${\ell }_1$ norm regularization cannot guarantee that all the data vectors are sparse in the same features [13], so it is not suitable for feature selection. To settle this issue, Nie [14] proposed a robust feature selection method emphasizing joint ${\ell }_{2,1}$-norm minimization on both the loss function and regularization. Yang et al. [15], Hou et al. [16] and Gu et al. [17] used the ${\ell }_{2,1}$-norm regularization in discriminant feature selection, sparse regression and subspace learning, respectively. The ${\ell }_{2,1}$-norm regularization is regarded as a powerful model for sparse feature selection and has attracted increasing attention [14,15,18].

The goal of this paper is to preserve the local geometrical structure of the mixed sign data and characterize the discriminative information in the learned subspace under the framework of Semi-NMF. In addition, we encourage the basis matrix to be group sparse, which is suitable to reserve the important basis vectors and remove the irrelevant ones. We propose a novel algorithm, called Group sparsity and Graph regularized Semi-Nonnegative Matrix Factorization with Discriminability (GGSemi-NMFD), for data representation. Graph regularization [19] has been introduced to encode the local structure of non-negative data in the framework of NMF. We apply it to preserve the intrinsic geometric structure of mixed sign data in the framework of Semi-NMF. In addition, discriminative information is also very important in pattern recognition. To incorporate the discriminative information of the data, we add approximate orthogonal constraints in the learned latent subspace, and thus improve the performance of Semi-NMF in clustering tasks. We further constrain the learned basis matrix to be row sparse. This is inspired by the intuition that different dimensions of basis vectors have different importance. For model optimization, we develop an effective iterative updating scheme for GGSemi-NMFD. Experimental results on six real-world datasets demonstrate the effectiveness of our approach.

To summarize, it is worthwhile to highlight three aspects of the proposed method here:

1. While the standard Semi-NMF models the data in the Euclidean space, GGSemi-NMFD exploits the intrinsic geometrical information of the data distribution and adds it as a regularization term. Hence, when the data are sampled from a high dimensional space’s submanifold, our algorithm is especially applicable.

2. To incorporate the discriminative information of the data, we add approximate orthogonal constraints in the learned space. By adding the approximate orthogonal constraints, our algorithm can have more discriminative power than the standard Semi-NMF.

3. Our algorithm adds ${\ell }_{2,1}$-norm constraints in the basis matrix, which can shrink some rows of basis matrix $\mathbf{U}$ to zero, making basis matrix $\mathbf{U}$ suitable for feature selection. By preserving the group sparse structure in the basis matrix, our algorithm can acquire more flexible and meaningful semantics.

The remainder of this paper is organized as follows: Section 2 presents a brief overview of related works. Section 3 introduces our GGSemi-NMFD algorithm and the optimization scheme. Experimental results on six real-world datasets are presented in Section 4. Finally, we draw the conclusion in Section 5.

2. Related Work

In this section, we briefly review some related works that are closely related to our work.

2.1. NMF

Given a non-negative data matrix $\mathbf{X}\in {\mathbf{R}}^{M\times N}$, the goal of NMF is to find a non-negative basis matrix $\mathbf{U}\in {\mathbf{R}}^{M\times K}$ and a non-negative encoding matrix $\mathbf{V}\in {\mathbf{R}}^{K\times N}$, where their product can well approximate the non-negative data matrix $\mathbf{X}$. Here, K denotes the desired reduced dimension.

The least square objective function of NMF is formulated as follows:

$$\begin{array}{c}\underset{\mathbf{U},\mathbf{V}}{min}{\parallel \mathbf{X}-\mathbf{U}\mathbf{V}\parallel }_F^2.\hfill \\ \mathrm{s}.\mathrm{t}.\mathbf{U}\ge 0,\mathbf{V}\ge 0.\hfill \end{array}$$

(1)

It is clear that Equation (1) is not convex when both $\mathbf{U}$ and $\mathbf{V}$ are taken as variables. However, it is convex in $\mathbf{U}$ when $\mathbf{V}$ is fixed and vice versa. Lee and Seung [20] presented an iterative multiplicative updating rules as follows:

$$\begin{array}{cc}\hfill U_{ik}=& U_{ik}\frac{{(\mathbf{X}{\mathbf{V}}^T)}_{ik}}{{(\mathbf{U}\mathbf{V}{\mathbf{V}}^T)}_{ik}}\hfill \\ \hfill V_{kj}=& V_{kj}\frac{{({\mathbf{U}}^T\mathbf{X})}_{kj}}{{({\mathbf{U}}^T\mathbf{U}\mathbf{V})}_{kj}}.\hfill \end{array}$$

(2)

Using the above updating rules, we could find the local optimal solution of Equation (1).

2.2. Semi-NMF

One limitation of NMF is that it cannot handle the mix signed data. To settle this issue, Ding et al. [4] proposed Semi-Nonnegative Matrix Factorization (Semi-NMF). Specifically, Semi-NMF relaxes the non-negative constraints to data matrix $\mathbf{X}$ and basis matrix $\mathbf{U}$ and only adds non-negative constraints in encoding matrix $\mathbf{V}$. In this way, Semi-NMF can process mix signed matrix and inherit all the merit of NMF. The objective function of Semi-NMF is written as follows:

$$\begin{array}{cc}\hfill \underset{\mathbf{U},\mathbf{V}}{min}\parallel \mathbf{X}& {-\mathbf{U}\mathbf{V}\parallel }_F^2.\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathbf{V}\ge 0.\hfill \end{array}$$

(3)

To solve Equation (3), Ding et al. [4] proposed the updating rule as follows:

$$\begin{array}{cc}\hfill \mathbf{U}=& \mathbf{X}\mathbf{V}{({\mathbf{V}}^T\mathbf{V})}^{-1}\hfill \\ \hfill V_{ik}=& V_{ik}\sqrt{\frac{{({\mathbf{X}}^T\mathbf{U})}_{ik}^{+}+{\left[\mathbf{V}{({\mathbf{U}}^T\mathbf{U})}^{-}\right]}_{ik}}{{({\mathbf{X}}^T\mathbf{U})}_{ik}^{-}+{\left[\mathbf{V}{({\mathbf{U}}^T\mathbf{U})}^{+}\right]}_{ik}}}.\hfill \end{array}$$

(4)

where we separate the positive and negative parts of a matrix $\mathbf{A}$ as:

$$A_{ik}^{+}=\frac{|A_{ik}|+A_{ik}}{2},A_{ik}^{-}=\frac{|A_{ik}|-A_{ik}}{2}$$

(5)

3. Model

In this section, we propose a novel algorithm, called Group sparsity and Graph regularized Semi-Nonnegative Matrix Factorization with Discriminability (GGSemi-NMFD), which considers the group sparsity of the basis matrix and better preserves the locally geometric structure of the data, as well as incorporates the discriminative information in the learned subspace.

3.1. Graph Regularized Semi-NMF

Spectral graph theory [21] and manifold learning theory [7] have demonstrated that the local geometrical structure can be effectively fitted through a nearest neighbor graph on a scatter of data points. For each data point ${\mathbf{x}}_{i.}\in \mathbf{X}$, we could find its k nearest neighbors ${\mathcal{N}}_i$ and put an edge between ${\mathbf{x}}_{i.}$ and its neighbors in the adjacent matrix $\mathbf{W}$. Thus, we could use the graph regularization term to measure the smoothness of the low-dimensional representation:

$$\begin{array}{cc}\hfill {\mathcal{R}}_1& =\frac{1}{2}\sum _{j,l=1}^N{\parallel {\mathbf{v}}_i-{\mathbf{v}}_j\parallel }^2\mathbf{W}\hfill \\ & =Tr(\mathbf{V}\mathbf{D}{\mathbf{V}}^T)-Tr(\mathbf{V}\mathbf{W}{\mathbf{V}}^T)\hfill \\ & =Tr(\mathbf{V}\mathbf{L}{\mathbf{V}}^T)\hfill \end{array}$$

(6)

where $\mathbf{D}$ is a diagonal matrix whose entries are column sums of $\mathbf{W}$, ${\mathbf{D}}_{ii}={\sum }_l{\mathbf{W}}_{jl}$. $\mathbf{L}=\mathbf{D}-\mathbf{W}$ is the graph Laplacian.

There are many ways to define adjacent weight matrix $\mathbf{W}$; here, we use the 0–1 weighting, since it is simple and effective. It is defined as:

$${\mathbf{W}}_{ij}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{\mathbf{x}}_i\in {\mathcal{N}}_j\mathrm{or}{\mathbf{x}}_j\in {\mathcal{N}}_i\hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right.$$

where ${\mathcal{N}}_i$ denotes the set of k nearest neighbors of data point ${\mathbf{x}}_i$. Combing the graph regularization term with the standard Semi-NMF objective function, we could obtain the graph regularized Semi-NMF; it can be written as follows:

$$\begin{array}{c}\underset{\mathbf{U},\mathbf{V}}{min}\parallel \mathbf{X}-{\mathbf{U}}^T{\mathbf{V}\parallel }_F^2+\alpha Tr(\mathbf{V}\mathbf{L}{\mathbf{V}}^T).\hfill \\ \hspace{1em}\hspace{1em}\mathrm{s}.\mathrm{t}.\mathbf{V}\ge 0.\hfill \end{array}$$

(7)

where the regularization parameter $\alpha \ge 0$ controls the smoothness of the new representation.

In [19], Cai et al. proposed Graph regularized Non-negative Matrix Factorization (GNMF), which considers the local invariance in the framework of NMF. However, the major difference between GGSemi-NMF and GNMF is that GGSemi-NMF constructs the data graph for any signed data, but GNMF constructs the data graph only for non-negative data. What is more, GNMF ignores the discriminative information and cannot guarantee the parts-based representations. Therefore, GGSemi-NMF extends GNMF and has some novel properties, which will be represented in detail as follows.

3.2. Discriminative Constraints

If we could obtain the discriminative information hidden in the data, it will be a benefit for learning a better representation. To address this issue, we follow the works in [22,23], where the indicated matrix is given. At first, we introduce the indicator matrix $\mathbf{Y}={\{0,1\}}^{N\times K}$, where $Y_{ij}=1$ if the i-th data point belongs to the j-th group. Then, the scaled indicator matrix can be defined as follows:

$$\mathbf{F}=\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}$$

(8)

where each column in $\mathbf{F}$ is:

$${\mathbf{F}}_j={[0,\dots ,0,\underset{n_j}{\underbrace{1,\dots ,1}},0,\dots ,0]}^T/\sqrt{n_j}$$

where $n_j$ is the number of samples in the j-th group. If the new representation $\mathbf{V}$ can obtain the discriminative information, it will be discriminative. Unfortunately, under the unsupervised scenario, we cannot have the label information in advance. However, we find that the scaled indicator matrix is strictly orthogonal:

$${\mathbf{F}}^T\mathbf{F}={({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{Y}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}={\mathbf{I}}_k$$

(9)

where ${\mathbf{I}}_k$ is a $K\times K$ identity matrix. Hence, ${\mathbf{V}}^T$ should also be orthogonal. However, the orthogonal constraint is too strict. Therefore, we relax it and let $\mathbf{V}$ be approximal orthogonal, i.e.,

$$\parallel {\mathbf{V}}^T\mathbf{V}-{\mathbf{I}}_k{\parallel }_F^2.$$

(10)

3.3. Group Sparse Constraints

Usually, basis matrix $\mathbf{U}$ has redundant and irrelevant basis vectors. Removing the non-significant basis vectors and keeping the important one will lead to learning a better representation. To achieve this aim, we choose the third regularization term to distinguish the importance of different dimensions of basis vectors. Specifically, we encourage the significant dimensions of basis vectors to be non-zero values and the non-significant ones to be zero. Motivated by [14,15], we add the ${\ell }_{2,1}$-norm constraint on the basis matrix $\mathbf{U}$, which propels some rows in $\mathbf{U}$ towards zero. Thus, we can reserve the important dimensions of basis vectors (i.e., items with non-zero values) and remove the unimportant ones (i.e., items with zero values). The ${\ell }_{2,1}$-norm is defined as follows:

$${\parallel \mathbf{U}\parallel }_{2,1}=\sum _{j=1}^K\parallel {\mathbf{u}}_{j.}\parallel .$$

(11)

where ${\mathbf{u}}_{j.}$ represents the j-th row of $\mathbf{U}$, which reveals the importance of the j-th basis vector.

3.4. Objective Function

By integrating Equations (7), (10) and (11), the overall loss function of GGSemi-NMFD is defined as:

$$\begin{array}{c}\underset{\mathbf{U},\mathbf{V}}{min}\parallel \mathbf{X}-{\mathbf{U}}^T{\mathbf{V}\parallel }_F^2+\alpha tr(\mathbf{V}\mathbf{L}{\mathbf{V}}^T)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}+\beta \parallel {\mathbf{V}}^T\mathbf{V}-{\mathbf{I}}_k{\parallel }_F^2+\lambda {\parallel \mathbf{U}\parallel }_{2,1},\hfill \\ \hspace{1em}\hspace{1em}\hspace{0.5em}\mathrm{s}.\mathrm{t}.\mathbf{V}\ge 0.\hfill \end{array}$$

(12)

where $\alpha$, $\beta$ and $\lambda$ are regularization parameters. Parameter $\alpha$ measures the smoothness of the learned representation; parameter $\beta$ controls the orthogonality of $\mathbf{V}$; and parameter $\lambda$ controls the degree of sparsity in basis matrix $\mathbf{U}$.

3.5. Optimization

In this section, we will give the solution to Equation (12). As we see, objective function Equation (12) is nonconvex in both $\mathbf{U}$ and $\mathbf{V}$ together, so we cannot have a closed-form solution. We will give an alternating scheme to optimize the objective function, which can achieve the local optimal solution in the following. For the ease of representation, we define:

$$\begin{array}{c}\mathcal{O}(\mathbf{U},\mathbf{V})=\parallel \mathbf{X}-{\mathbf{U}}^T{\mathbf{V}\parallel }_F^2+\alpha tr(\mathbf{V}\mathbf{L}{\mathbf{V}}^T)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\beta \parallel {\mathbf{V}}^T\mathbf{V}-{\mathbf{I}}_k{\parallel }_F^2+\lambda {\parallel \mathbf{U}\parallel }_{2,1}\hfill \end{array}$$

(13)

3.5.1. Updating Rule for $\mathbf{U}$

Optimizing Equation (12) with respect to $\mathbf{U}$ is equivalent to optimizing:

$$\underset{\mathbf{U}}{min}\parallel \mathbf{X}-{\mathbf{U}}^T{\mathbf{V}\parallel }_F^2+\lambda {\parallel \mathbf{U}\parallel }_{2,1}$$

(14)

Inspired by [14], the derivative of the objective function with respect to $\mathbf{U}$ is as follows:

$$\frac{\partial \mathcal{O}}{\partial \mathbf{U}}=2(\mathbf{V}{({\mathbf{U}}^T\mathbf{V}-\mathbf{X})}^T+\lambda \mathbf{E}\mathbf{U})$$

(15)

where $\mathbf{E}$ is a diagonal matrix with $e_{kk}=\frac{1}{2}{\parallel {\mathbf{w}}_{k.}\parallel }^2$. Letting $\frac{\partial \mathcal{O}}{\partial \mathbf{U}}=0$, we get the following updating rule for $\mathbf{U}$:

$$\mathbf{U}={(\mathbf{V}{\mathbf{V}}^T+\lambda \mathbf{E})}^{-1}\mathbf{V}{\mathbf{X}}^T.$$

(16)

3.5.2. Updating Rule for $\mathbf{V}$

Let $\mathsf{\Phi }$ be the Lagrange multiplier for constraint $\mathbf{V}\ge 0$. Keeping the part of $\mathcal{O}$ that is related to $\mathbf{V}$, the Lagrange function $\mathcal{L}(\mathbf{V})$ is defined as:

$$\begin{array}{c}\mathcal{L}(\mathbf{V})=\parallel \mathbf{X}-{\mathbf{U}}^T{\mathbf{V}\parallel }_F^2+\alpha tr(\mathbf{V}\mathbf{L}{\mathbf{V}}^T)\hfill \\ +\beta \parallel {\mathbf{V}}^T\mathbf{V}-{\mathbf{I}}_k{\parallel }_F^2+Tr(\mathsf{\Phi }{\mathbf{V}}^T)\hfill \\ =Tr(\mathbf{X}{\mathbf{X}}^T)-2Tr(\mathbf{X}{\mathbf{V}}^T\mathbf{U})+Tr({\mathbf{U}}^T\mathbf{V}{\mathbf{V}}^T\mathbf{U}+\alpha tr(\mathbf{V}\mathbf{L}{\mathbf{V}}^T)\hfill \\ +\beta Tr({\mathbf{V}}^T\mathbf{V}{\mathbf{V}}^T\mathbf{V}-2{\mathbf{V}}^T\mathbf{V}+\mathbf{I})+Tr(\mathsf{\Phi }{\mathbf{V}}^T)\hfill \end{array}$$

(17)

The partial derivative of $\mathcal{L}(\mathbf{V})$ with respect to $\mathbf{V}$ is as:

$$\begin{array}{c}\frac{\partial \mathcal{L}(\mathbf{V})}{\partial \mathbf{V}}=-2\mathbf{U}\mathbf{X}+2{\mathbf{V}}^T\mathbf{U}+2\mathbf{U}{\mathbf{U}}^T\mathbf{X}\hfill \\ +2\alpha \mathbf{V}\mathbf{L}+4\beta \mathbf{V}{\mathbf{V}}^T\mathbf{V}-4\beta \mathbf{V}+\mathsf{\Phi }\hfill \end{array}$$

(18)

By using the Karush–Kuhn–Tucker condition, i.e., ${\mathsf{\Phi }}_{jl}{V}_{jl}=0$, we get the following equations,

$$\begin{array}{c}{({(\mathbf{U}\mathbf{X})}^{+}+{(\mathbf{U}{\mathbf{U}}^T)}^{-}\mathbf{V}+\alpha \mathbf{V}{\mathbf{L}}^{-}+2\beta \mathbf{V})}_{jl}{V}_{jl}\hfill \\ ={({(\mathbf{U}\mathbf{X})}^{-}+{(\mathbf{U}{\mathbf{U}}^T)}^{+}\mathbf{V}+\alpha \mathbf{V}{\mathbf{L}}^{+}+2\beta \mathbf{V}{\mathbf{V}}^T\mathbf{V})}_{jl}{V}_{jl}\hfill \end{array}$$

(19)

where we separate the positive and negative parts of matrix $\mathbf{A}$ as:

$$A_{ik}^{+}=\frac{|A_{ik}|+A_{ik}}{2},A_{ik}^{-}=\frac{|A_{ik}|-A_{ik}}{2}$$

(20)

Then, we obtain the following multiplicative updating rule:

$$V_{jl}=V_{jl}\sqrt{\frac{{({(\mathbf{U}\mathbf{X})}^{+}+{(\mathbf{U}{\mathbf{U}}^T)}^{-}\mathbf{V}+\alpha \mathbf{V}{\mathbf{L}}^{-}+2\beta \mathbf{V})}_{jl}}{{({(\mathbf{U}\mathbf{X})}^{-}+{(\mathbf{U}{\mathbf{U}}^T)}^{+}\mathbf{V}+\alpha \mathbf{V}{\mathbf{L}}^{+}+2\beta \mathbf{V}{\mathbf{V}}^T\mathbf{V})}_{jl}}}$$

(21)

4. Experimental Section

To demonstrate the effectiveness of GGSemi-NMFD, we carried out extensive experiments on six public datasets: ORL, YALE, UMIST, Ionosphere, USPST and Waveform. All statistical significance tests were performed using Student’s t-tests with a significance level of 0.05. All the NMF-based methods are random initializations.

4.1. Datasets and Metrics

In our experiment, we use 6 datasets that are widely used as benchmark datasets in the clustering literature. The statistics of these datasets are summarized in Table 1.

Table 1. Statistics of the datasets.

Dataset	Example	Feature	Classes	Data Sign
ORL	400	1024	40	+
YALE	165	1024	15	+
UMIST	575	644	20	+
Ionosphere	351	34	2	±
USPST	2007	256	10	±
Waveform	2746	21	3	±

ORL: The ORL face dataset contains face images of 40 distinct persons. Each person has ten different images, taken at different times, totaling 400. All images are cropped to $32\times 32$ pixel grayscale images, and we reshape them into a 1024-dimensional vector.

YALE: The YALE face database contains 165 grayscale images in GIF format of 15 individuals. There are 11 images per subject, one per different facial expression or configuration. All images are cropped to $32\times 32$ pixel grayscale images, and we reshape them into a 1024-dimensional vector.

UMIST: The UMIST face databases contains 575 images from 20 individuals. All images are cropped to $23\times 28$ pixel grayscale images, and we reshape them into a 644-dimensional vector.

Ionosphere: Ionosphere is from the UCI repository. Ionosphere was collected by a radar system and consists of a phased array of 16 high-frequency antennas with a total transmitted power of the order of 6.4 kilowatts. The dataset consists of 351 instances with 34 numeric attributes.

USPST: The USPST dataset comes from the USPS system, and each image in USPST is presented at the resolution of $16\times 16$ pixels. It is the test split of the USPS.

Waveform: Waveform is obtainable at the UCI repository. It has three categories with 21 numerical attributes and 2746 instances.

We utilize clustering performance to evaluate the effectiveness of data representation. Clustering Accuracy (ACC) and Normalized Mutual Information (NMI) are two widely-used metrics for clustering performance, whose definitions are as follows:

$$\mathrm{ACC}=\frac{{\sum }_{i=1}^n\delta (s_i,map(r_i))}{n},$$

(22)

$$\mathrm{NMI}(C,C^{†})=\frac{MI(C,C^{†})}{max(H(C),H(C^{†}))},$$

(23)

where $r_i$ and $s_i$ are cluster labels of item i in clustering results and in the ground truth, respectively; $\delta (x,y)$ equals 1 if $x=y$ and equals 0 otherwise; and $map(r_i)$ is the permutation mapping function that maps $r_i$ to the equivalent cluster label in the ground truth. $H(C)$ denotes the entropy of cluster set C. $MI(C,C^{†})$ is the mutual information between C and $C^{†}$:

$$MI(C,C^{†})=\sum _{c_i\in C,c_j^{†}\in C^{†}}p(c_i,c_j^{†}){log}_2\frac{p(c_i,c_j^{†})}{p(c_i)p(c_j^{†})}.$$

(24)

$p(c_i)$ is the probability that a randomly-selected item from all testing items belongs to cluster $c_i$, and $p(c_i,c_j^{†})$ is the joint probability that a randomly-selected item is in $c_i$ and $c_j^{†}$ simultaneously. If C and $C^{†}$ are identical, $\mathrm{NMI}(C,C^{†})=1$. $\mathrm{NMI}(C,C^{†})=0$ when the two cluster sets are completely independent.

4.2. Compared Algorithms

To demonstrate how the clustering performance can be improved by our method, we compare the following popular clustering algorithms:

• Traditional K-means clustering algorithm (Kmeans).
• Kmeans clustering in Principal Component Analysis (PCA) [3].
• Nonnegative Matrix Factorization (NMF) [1].
• Semi-Nonnegative Matrix Factorization (Semi-NMF) [4].
• Graph regularized Non-negative Matrix Factorization (GNMF) [19].
• Our proposed Group sparsity and Graph regularized Semi-Nonnegative Matrix Factorization with Discriminability (GGSemi-NMFD).

4.3. Parameter Settings

Baseline methods have several parameters to be tuned. To compare these methods fairly, we perform grid search in the parameter space for each method and recode the best average results.

For datasets ORL, YALE and UMIST, we set K, the dimension of latent space, to the number of true classes of the dataset [19], for all NMF-based methods. For the dataset Ionosphere, since its class number is too small (only 2 classes), we set $K=20$ for NMF-based methods. We applied the compared methods to learn a new representation, and then, Kmeans was adapted for data clustering on the new data representation. For a given cluster number, 10 test runs were conducted on different classes of data randomly chosen from the dataset.

For GNMF, the number of nearest neighbors for constructing the data graph is set by searching the grid $\{1,2,\dots ,9\}$ according to [24], and the graph regularization parameter is chosen from $\{0.1,1,10,100,1000\}$.

For GGSemiNMFD, the number of the neighborhood size k is selected from $\{1,2,\dots ,9\}$. We also set $\alpha$, $\beta$ and $\lambda$ by searching the grid $\{{10}^{-4},{10}^{-3},\dots ,{10}^4\}$. If we adopt better parameter tuning, better clustering performance will be achieved.

Note that there is no parameter selection for Kmeans, PCA, NMF and Semi-NMF, given the number of clusters.

In the coming section, we repeat clustering 10 times, and the mean and the standard error are computed. Additionally, we report the best average result for each method.

4.4. Performance Comparison

Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7 show the clustering results on the ORL, YALE, UMIST, Ionosphere, USPST and Waveform datasets, respectively.

Table 2. Clustering performance on ORL.

Cluster No.	ACC (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
30	46.17 ± 2.51	45.70 ± 1.06	49.73 ± 2.93	50.15 ± 1.06	53.43 ± 1.53	54.40 ± 3.42
40	52.40 ± 2.53	50.35 ± 3.19	55.42 ± 2.59	54.68 ± 1.92	56.47 ± 2.72	60.25 ± 2.19
50	53.20 ± 2.67	53.77 ± 1.29	56.37 ± 2.96	55.84 ± 0.98	59.82 ± 2.45	61.18 ± 0.95
Cluster No.	NMI (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
30	64.49 ± 1.48	64.02 ± 1.72	67.50 ± 1.07	66.41 ± 0.72	69.67 ± 1.15	70.62 ± 2.40
40	70.78 ± 1.77	69.95 ± 1.83	73.93 ± 1.18	73.58 ± 1.23	74.96 ± 1.35	75.46 ± 0.98
50	75.46 ± 1.37	75.42 ± 0.79	76.87 ± 1.01	76.07 ± 2.71	78.11 ± 1.16	78.60 ± 0.61

Table 3. Clustering performance on YALE.

Cluster No.	ACC (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
10	33.88 ± 2.07	33.70 ± 2.06	34.39 ± 2.73	34.09 ± 3.18	35.48 ± 2.76	36.48 ± 1.56
15	38.12 ± 3.04	38.82 ± 2.90	40.48 ± 3.30	39.55 ± 1.52	41.09 ± 2.52	44.24 ± 2.98
20	40.52 ± 3.71	39.94 ± 2.17	41.58 ± 2.61	40.78 ± 0.98	42.45 ± 2.68	44.55 ± 3.25
Cluster No.	NMI (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
10	35.51 ± 1.68	35.26 ± 2.67	36.50 ± 1.87	35.86 ± 2.52	36.75 ± 2.59	39.48 ± 1.14
15	43.14 ± 2.31	44.65 ± 2.50	45.73 ± 2.85	45.29 ± 1.75	46.29 ± 1.35	49.33 ± 2.38
20	49.04 ± 3.51	48.38 ± 2.22	49.75 ± 1.84	49.38 ± 1.38	51.10 ± 1.86	52.90 ± 1.95

Table 4. Clustering performance on UMIST.

Cluster No.	ACC (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
15	39.55 ± 2.30	39.23 ± 1.24	40.54 ± 1.65	39.90 ± 1.81	51.10 ± 2.89	58.39 ± 5.49
20	39.91 ± 1.64	39.88 ± 2.06	42.98 ± 1.79	41.93 ± 1.83	54.37 ± 3.35	59.39 ± 4.21
25	39.51 ± 1.84	39.47 ± 2.13	42.44 ± 2.39	42.16 ± 1.77	54.30 ± 3.26	56.77 ± 1.82
Cluster No.	NMI (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
15	35.51 ± 1.68	35.26 ± 2.67	36.50 ± 1.87	35.86 ± 2.52	36.75 ± 2.59	39.48 ± 1.14
20	59.16 ± 2.10	59.71 ± 1.42	60.32 ± 0.95	60.16 ± 1.48	72.21 ± 1.50	75.21 ± 2.02
25	59.17 ± 3.51	59.71 ± 1.42	60.33 ± 0.95	60.16 ± 1.48	71.94 ± 1.11	75.07 ± 1.14

Table 5. Clustering performance on Ionosphere.

Cluster No.	ACC (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
2	70.88 ± 0.12	70.85 ± 0.14	-	71.70 ± 0.00	-	73.16 ± 0.66
4	67.95 ± 0.24	67.98 ± 0.20	-	69.03 ± 0.53	-	71.59 ± 1.31
6	57.83 ± 0.48	57.46 ± 0.89	-	58.42 ± 0.57	-	61.08 ± 2.60
Cluster No.	NMI (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
2	12.16 ± 0.22	12.14 ± 0.23	-	12.98 ± 0.00	-	15.98 ± 0.99
4	27.35 ± 0.19	27.32 ± 0.49	-	29.17 ± 0.32	-	33.83 ± 2.05
6	19.88 ± 0.77	19.83 ± 0.58	-	21.94 ± 1.86	-	24.03 ± 1.88

Table 6. Clustering performance on USPST.

Cluster No.	ACC (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
3	36.98 ± 0.18	37.03 ± 0.02	-	38.35 ± 0.03	-	39.56 ± 0.00
5	50.88 ± 0.02	50.87 ± 0.05	-	51.31 ± 0.04	-	54.61 ± 0.03
10	67.71 ± 0.51	67.80 ± 0.47	-	68.98 ± 0.19	-	74.22 ± 0.31
Cluster No.	NMI (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
3	23.97 ± 0.30	24.03 ± 0.04	-	28.92 ± 0.11	-	35.10 ± 0.00
5	45.83 ± 0.10	45.76 ± 0.12	-	46.56 ± 0.13	-	55.69 ± 0.05
10	61.90 ± 0.48	61.98 ± 0.46	-	63.15 ± 0.12	-	73.50 ± 0.41

Table 7. Clustering performance on Waveform.

Cluster No.	ACC (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
3	50.73 ± 0.00	50.71 ± 0.02	-	51.14 ± 0.02	-	57.78 ± 2.68
6	39.15 ± 0.18	39.10 ± 0.18	-	40.08 ± 0.07	-	54.33 ± 0.00
9	29.88 ± 0.51	30.40 ± 0.39	-	31.46 ± 0.54	-	33.14 ± 0.31
Cluster No.	NMI (%)
	Kmeans	PCA	NMF	Semi-NMF	GNMF	GGSemi-NMFD
3	35.74 ± 0.00	35.74 ± 0.00	-	36.70 ± 0.00	-	39.54 ± 2.83
6	36.55 ± 0.11	36.54 ± 0.09	-	37.67 ± 0.05	-	38.71 ± 0.04
9	32.90 ± 0.25	32.85 ± 0.28	-	33.43 ± 0.04	-	35.07 ± 0.38

The experiments reveal some important points.

• The NMF-based methods, including NMF, Semi-NMF, GNMF and GGSemi-NMFD, outperform the PCA and Kmeans methods, which demonstrates the merit of the parts-based representation in discovering the hidden factors.
• On nonnegative datasets, NMF demonstrates somewhat superior performance over Semi-NMF.
• For nonnegative datasets, methods considering the local geometrical structure of data, such as GNMF and GGSemi-NMFD, significantly outperform NMF and Semi-NMF, which suggests the importance of exploiting the intrinsic geometric structure of data.
• When dataset has mixed signs, NMF and GNMF cannot work. Semi-NMF tends to outperform Kmeans and PCA, which indicates the advantage of the parts-based representation in finding the hidden matrix factors even in the mixed sign data.
• Regardless of the datasets, our GGSemi-NMF always represents the best performance. This shows that by leveraging the power of parts-based representation, graph Laplacian regularization, group sparse constraints and discriminative information simultaneously, GGSemi-NMFD can learn a better compact and meaningful representation.

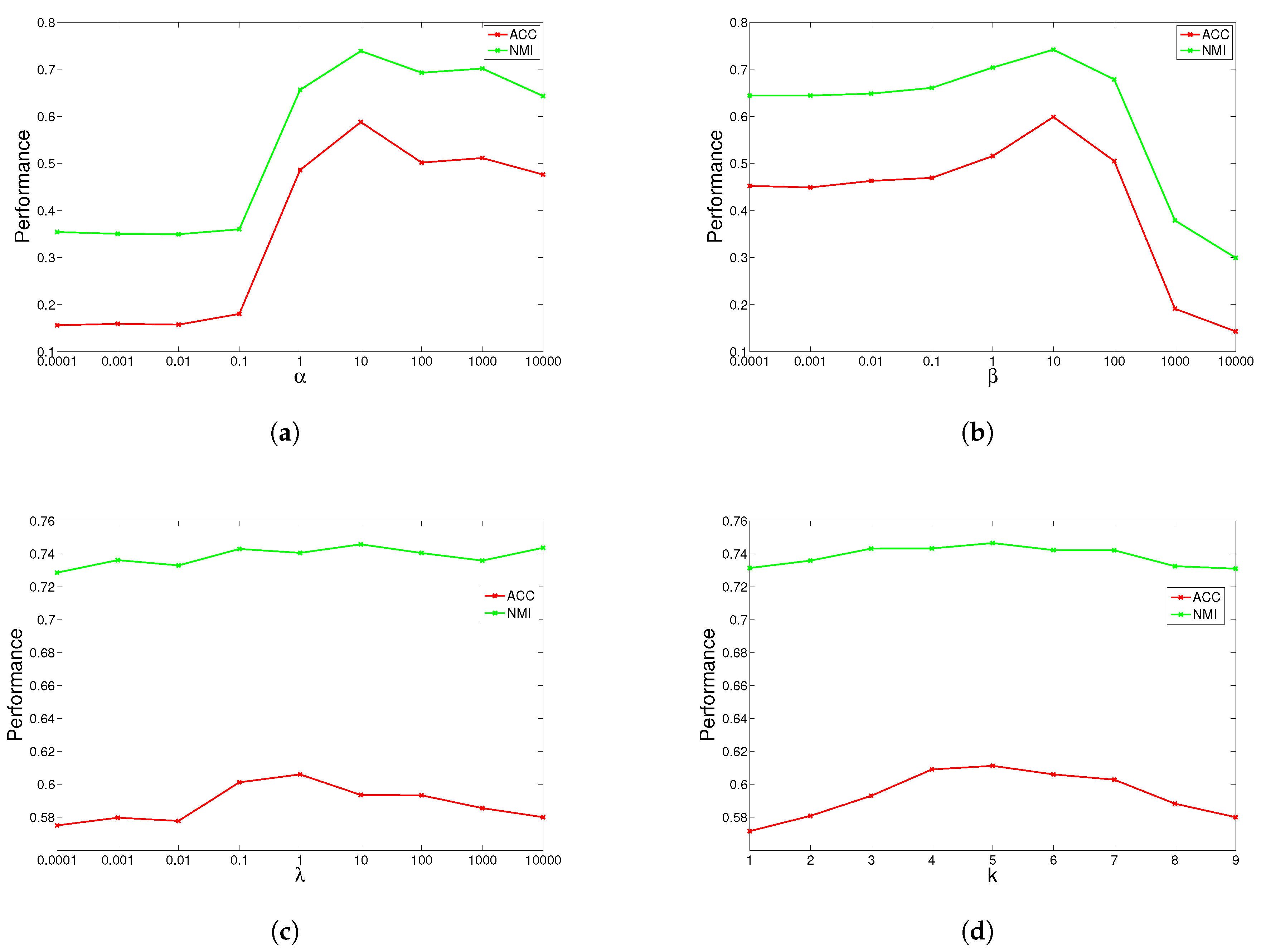
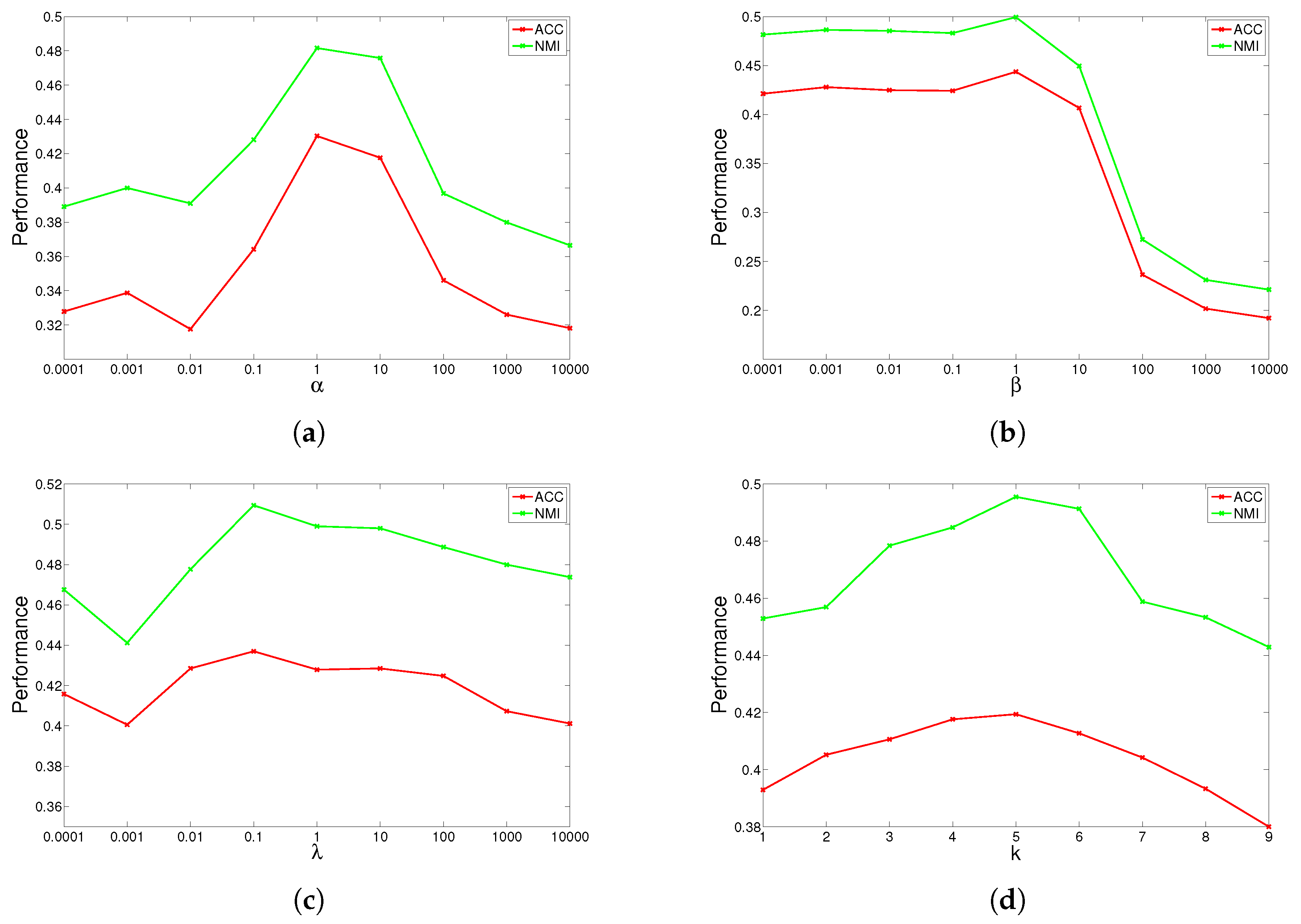
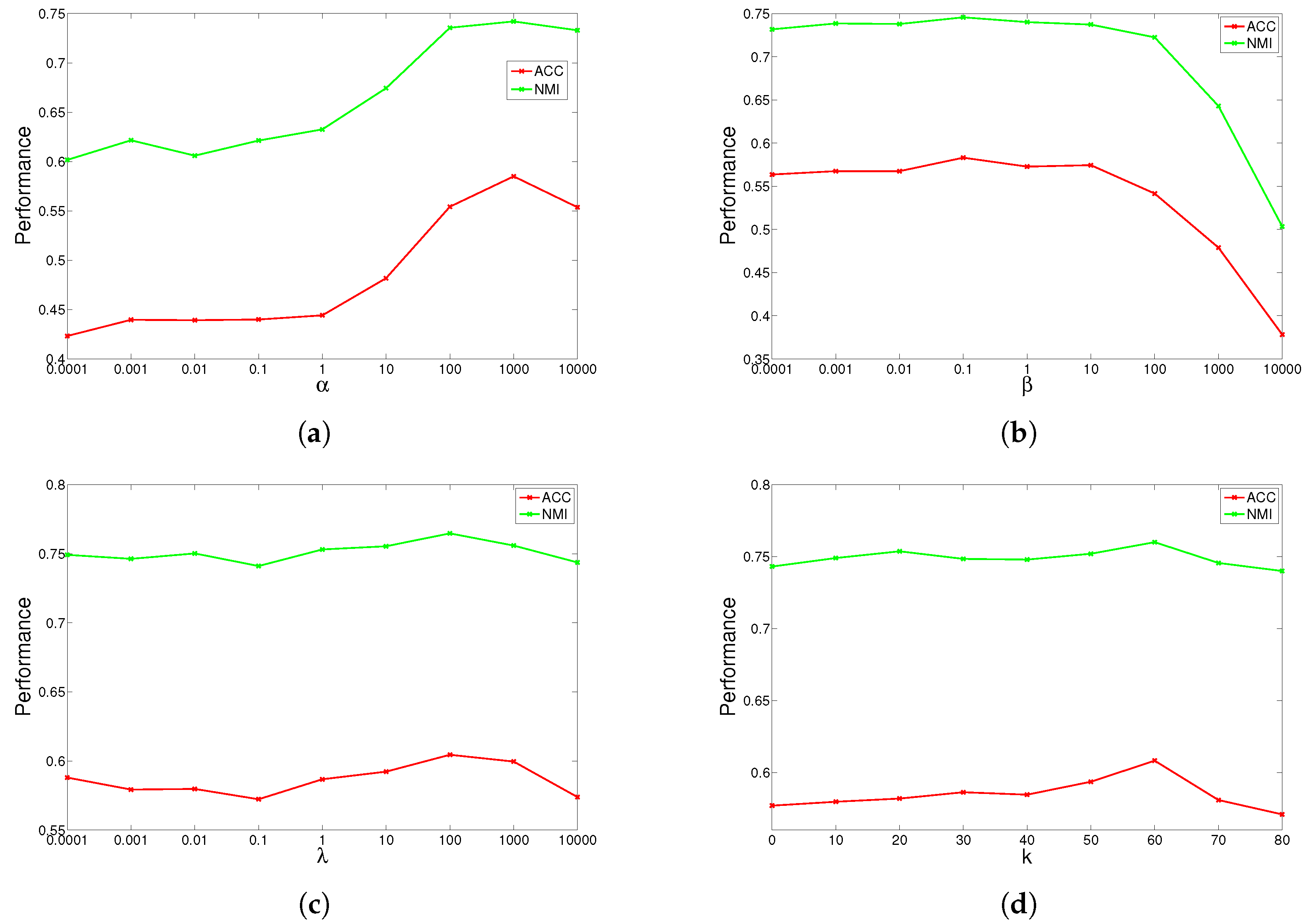
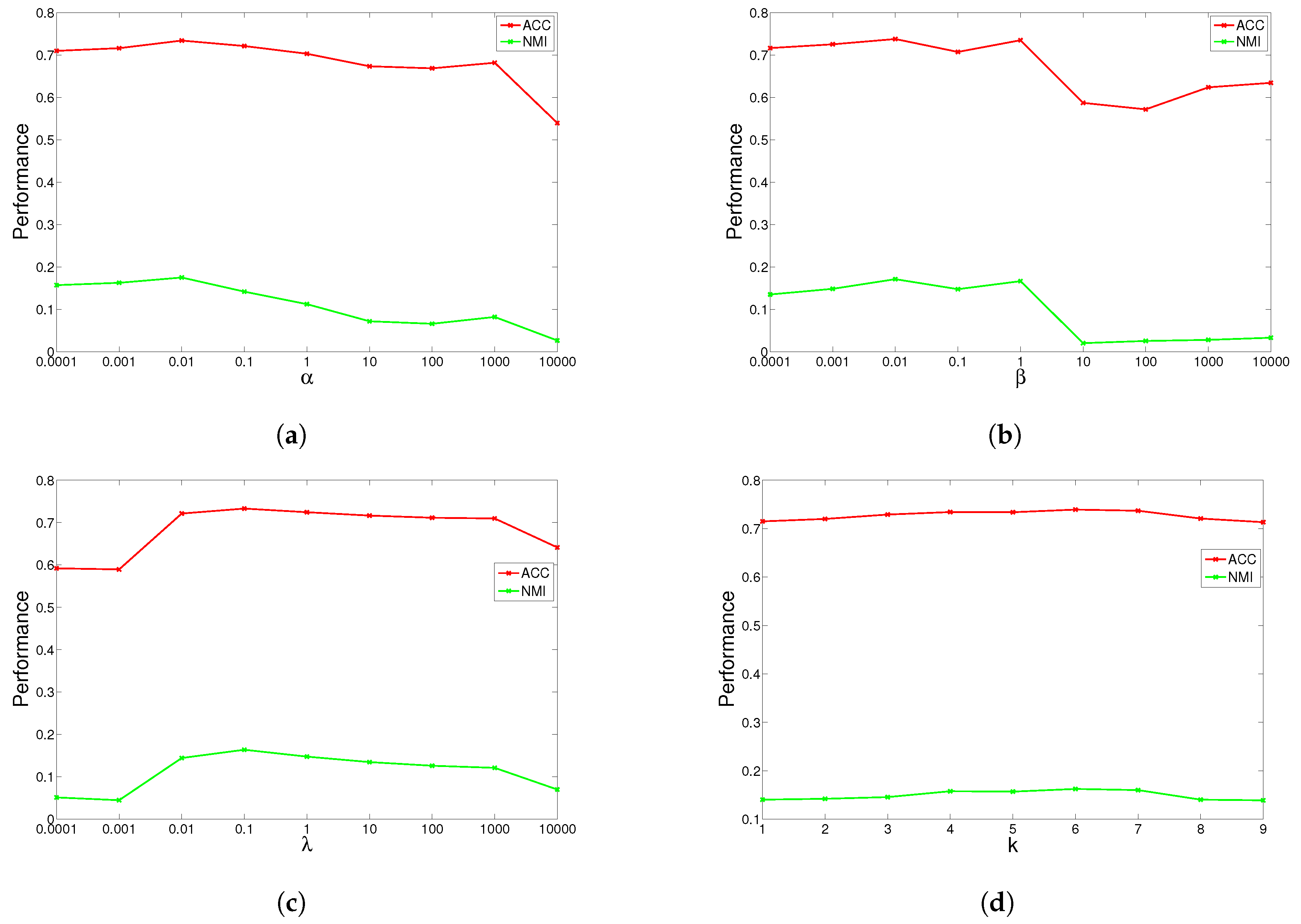
4.5. Parameter Study

GGSemi-NMFD has four parameters, $\alpha$, $\beta$, $\lambda$ and the number of nearest neighbors k. Parameter $\alpha$ measures the weight of the graph Laplacian; parameter $\beta$ controls the orthogonality of the learned representation; parameter $\lambda$ controls the sparse degree of the basis matrix; and k controls the complexity of the graph. We investigated their influence on GGSemi-NMFD’s performance by varying one parameter at a time while fixing the others. For each specific setting, we run GGSemi-NMFD 10 times, and the average performance was recorded.

The results are shown in Figure 1, Figure 2, Figure 3 and Figure 4 for ORL, YALE, UMIST and Ionosphere respectively (results for USPST and Waveform were similar to Ionosphere). We found that the four parameters have the same behavior: when increasing the parameter from a very tiny value, the performance curves first rose and then descended. This denotes that when assigned proper values, the graph Laplacian, approximation orthogonal and sparseness constraints, as well as the number of nearest neighbors are surely helpful to learn a better representation. For dataset ORL, we set $\alpha =\beta =10$, $\lambda =1$. For dataset YALE, we set $\alpha =\beta =1$. $\lambda =0.1$. For dataset UMIST, we set $\alpha =1000$, $\beta =0.1$ and $\lambda =100$. For dataset Ionosphere, we set $\alpha =\beta =0.01$, $\lambda =0.1$. For nearest neighbors k, we can observe from the result that GGSemi-NMF consistently outperforms the best baseline algorithms on four datasets when $k\in [3,7]$.

Figure 1. Influence of different parameter settings on the performance of GGSemi-NMFD in the ORL dataset: (a) varying $\alpha$ while setting $\beta =10$, $\lambda =1$ and $k=5$; (b) varying $\beta$ while setting $\alpha =10$, $\lambda =1$ and $k=5$; (c) varying $\lambda$ while setting $\alpha =10$, $\beta =10$ and $k=5$; (d) varying k while setting $\alpha =10$, $\lambda =10$ and $\lambda =1$.

Figure 2. Influence of different parameter settings on the performance of GGSemi-NMFD in the YALE dataset: (a) varying $\alpha$ while setting $\beta =1$, $\lambda =0.1$ and $k=5$; (b) varying $\beta$ while setting $\alpha =1$, $\lambda =0.1$ and $k=5$; (c) varying $\lambda$ while setting $\alpha =1$, $\beta =1$ and $k=5$; (d) varying k while setting $\alpha =1$, $\lambda =1$ and $\lambda =0.1$.

Figure 3. Influence of different parameter settings on the performance of GGSemi-NMFD in the UMIST dataset: (a) varying $\alpha$ while setting $\beta =0.1$, $\lambda =100$ and $k=5$; (b) varying $\beta$ while setting $\alpha =1000$, $\lambda =100$ and $k=5$; (c) varying $\lambda$ while setting $\alpha =1000$, $\beta =0.1$ and $k=5$; (d) varying k while setting $\alpha =1000$, $\lambda =0.1$ and $\lambda =100$.

Figure 4. Influence of different parameter settings on the performance of GGSemi-NMFD in the Ionosphere dataset: (a) varying $\alpha$ while setting $\beta =0.01$, $\lambda =0.1$ and $k=5$; (b) varying $\beta$ while setting $\alpha =0.01$, $\lambda =0.1$ and $k=5$; (c) varying $\lambda$ while setting $\alpha =0.01$, $\beta =0.01$ and $k=5$; (d) varying k while setting $\alpha =1000$, $\lambda =0.1$ and $\lambda =100$.

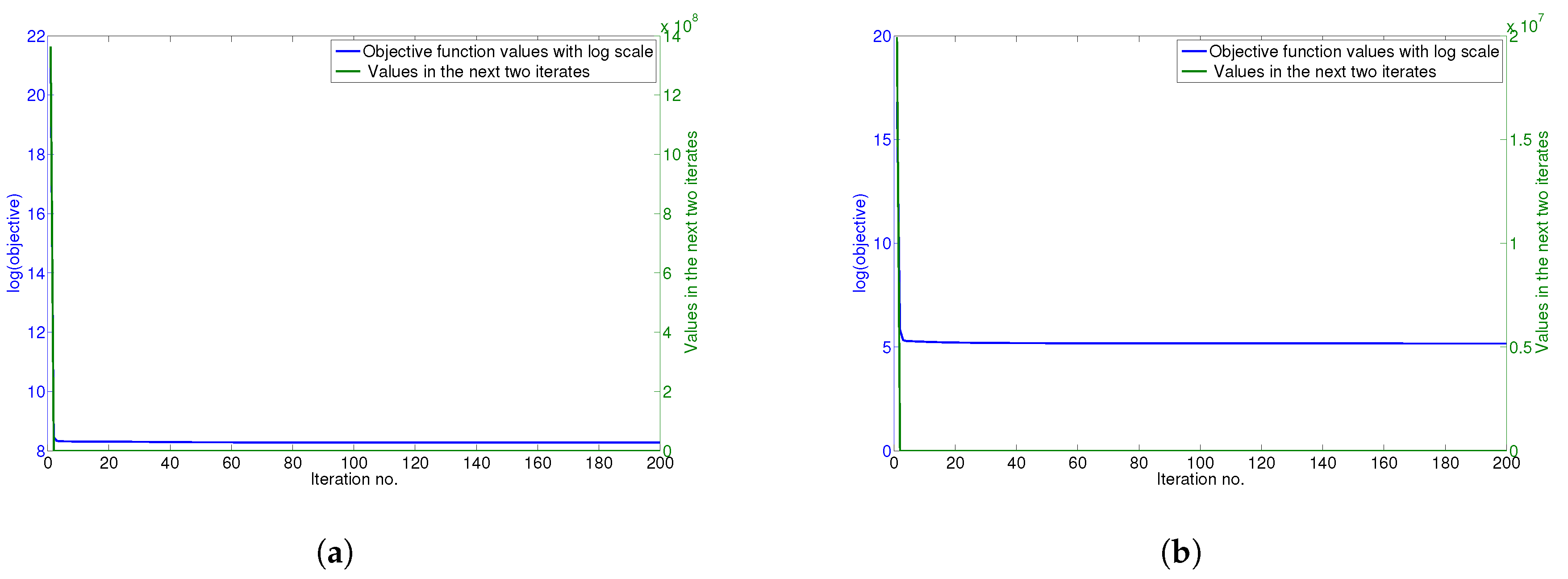
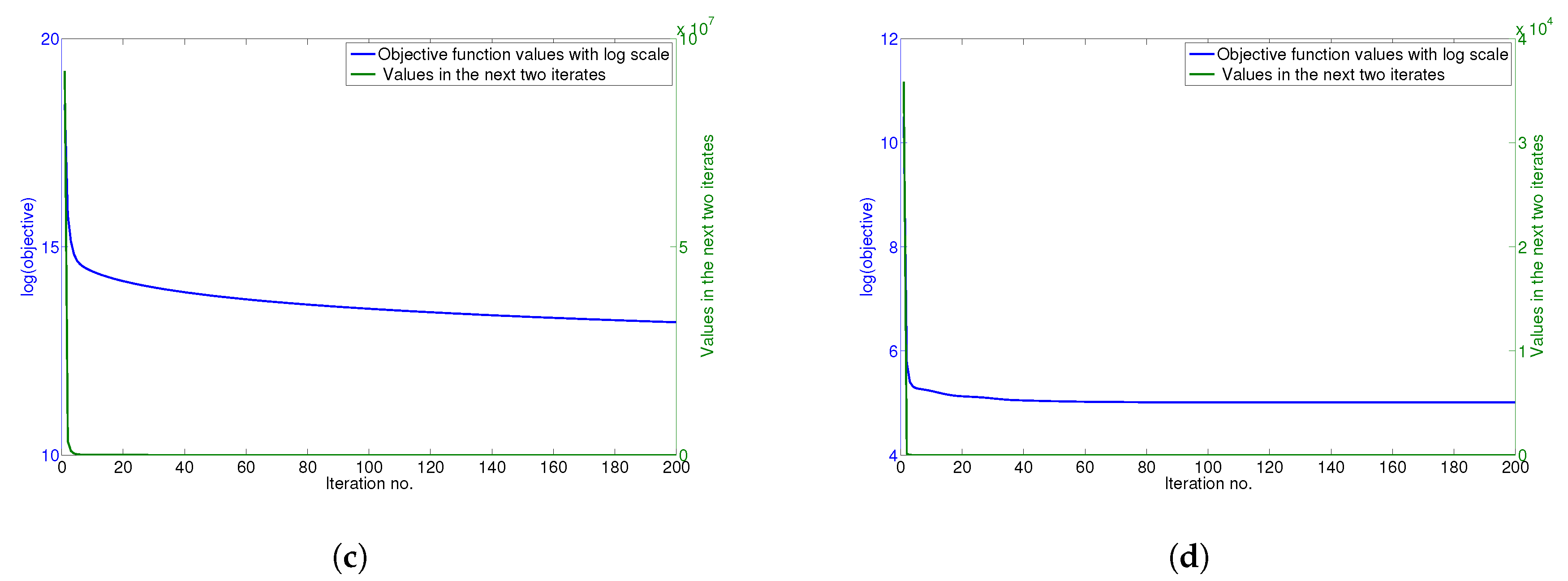
4.6. Convergence Analysis

The updating rules for minimizing the objective function of GGSemi-NMFD in Equation (12) are essentially iterative, and it can be proven that these rules are convergent. Figure 5a–d show the convergence curve of GGSemi-NMFD on datasets ORL, YALE, UMIST and Ionosphere, respectively. For each figure, we use the objective function values with log scale (blue line) and the values of the objective function in the next two iterates (green line) to measure the convergence of GGSemi-NMFD. As can be seen, usually within dozens of iterations, the multiplicative update rules for GGSemi-NMFD converge very fast.

Figure 5. Convergence analysis of GGSemi-NMFD on: (a) ORL; (b) YALE; (c) UMIST; and (d) Ionosphere. The y-axes for objective function values are in the log scale.

5. Conclusions

In this work, we proposed Group sparsity and Graph regularized Semi-Nonnegative Matrix Factorization with Discriminability (GGSemi-NMFD), a novel latent representation learning algorithm for representation learning from any signed data. GGSemi-NMFD tried to learn a semantic latent subspace of items by exploiting the graph Laplacian, discriminative information and sparse constraints, simultaneously. The graph Laplacian term encouraged items of the same category to be near each other. Approximation orthogonal constraints were introduced to incorporate some discriminative information in the learned subspace. Another novel property of GGSemi-NMFD was that it allowed each dimension of the basis matrix to be related or unrelated with new representation by imposing the ${\ell }_{2,1}$-norm penalty on basis matrix $\mathbf{U}$. Therefore, GGSemi-NMFD is able to learn a more plentiful and flexible semantic latent subspace. We proposed an efficient optimization method for GGSemi-NMFD and demonstrated its validity by six real-world data sets. Experimental results on six real-world data sets indicate that GGSemi-NMFD is effective and outperforms the baselines significantly. In our future work, we will investigate multi-view case [25], which can learn a more accurate representation from multi-view data.