Magnetic Engine for the Single-Particle Landau Problem
Abstract
1. Introduction
2. Partition Function for the Single-Particle Landau Problem
3. Thermodynamics and Magnetic Engine
3.1. The First Law of Thermodynamics: A Microscopic Approach
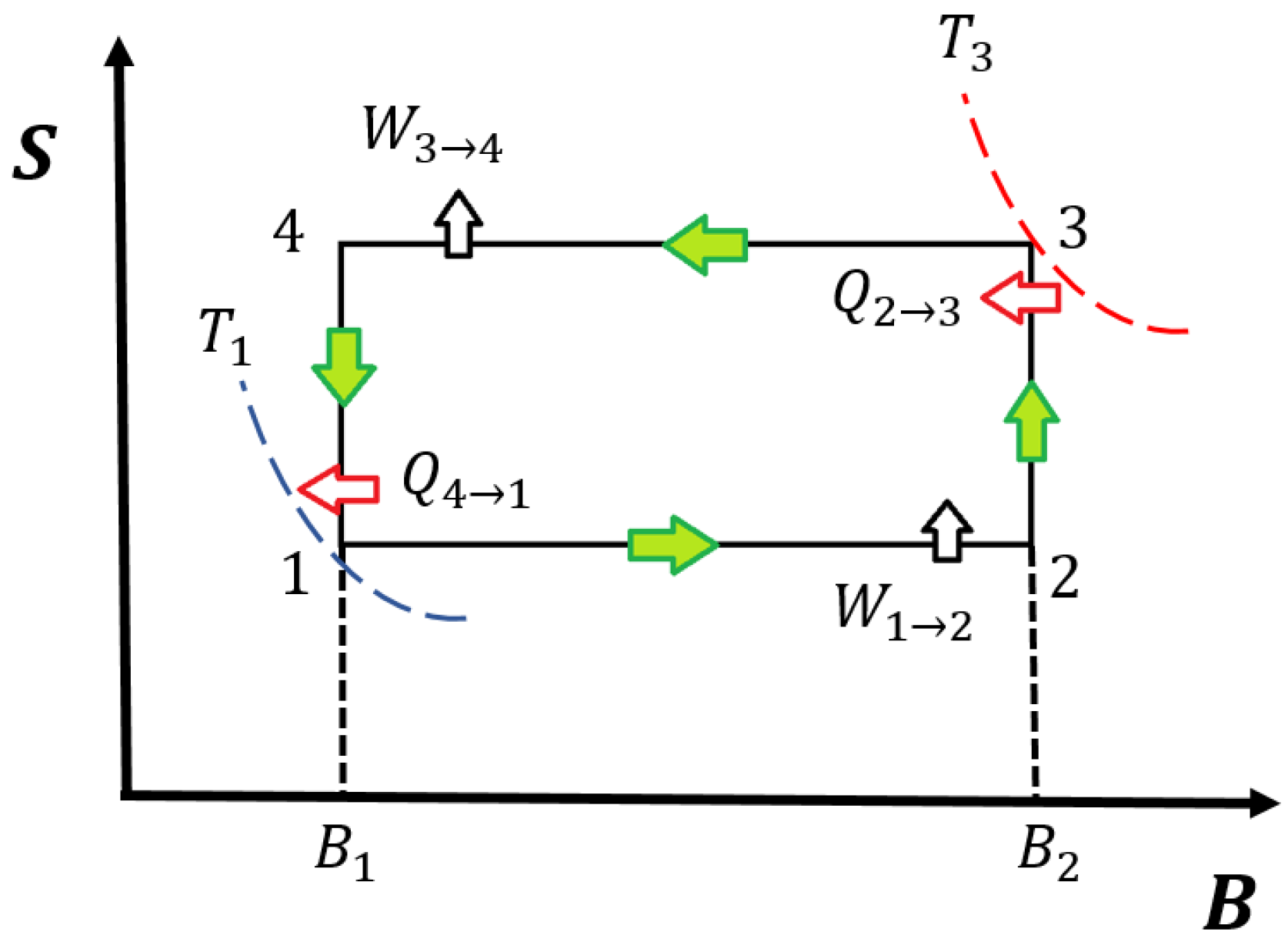
3.2. Magnetic Engine
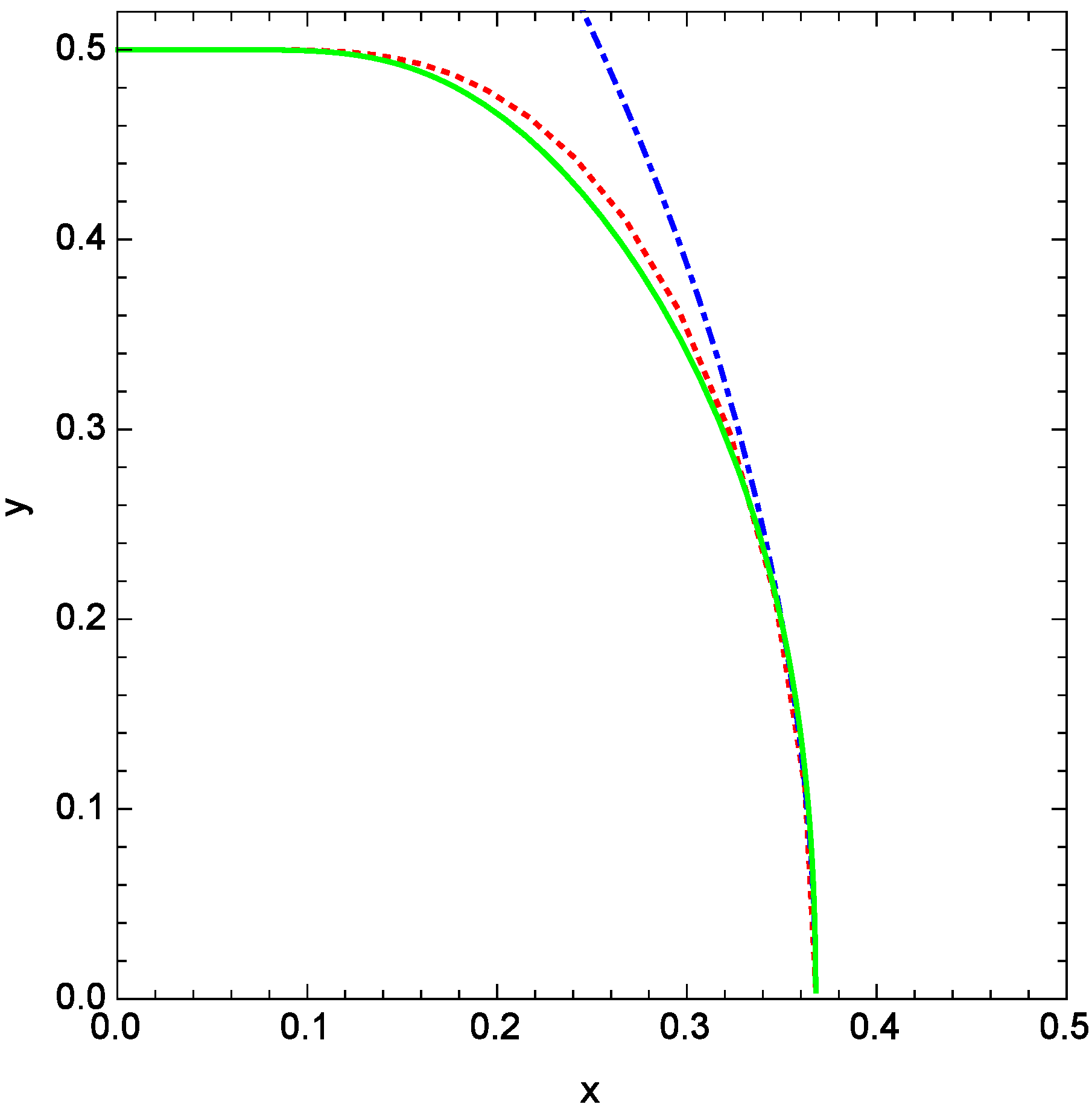
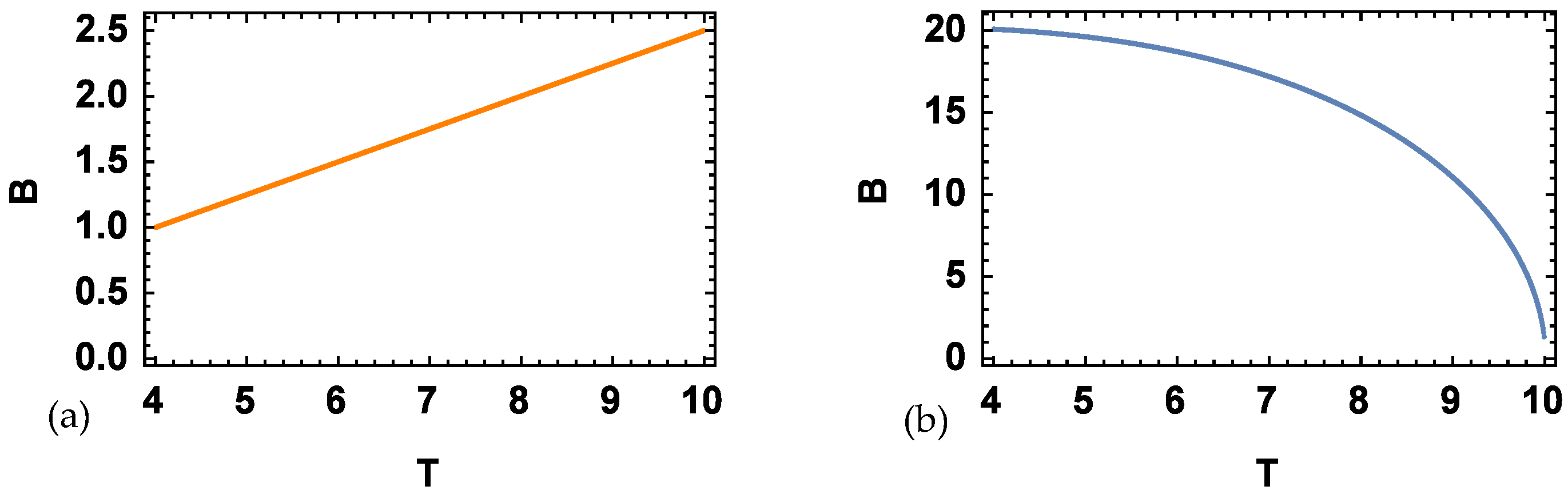
- Deducting the relation between the magnetic field and the temperature along an isoentropic trajectory solving the differential equation of first order given bywhich can be written aswhere is the specific heat at constant magnetic field.
- The other possibility is connecting the value for the entropy in two isoentropic trajectories in the formfinding the function for the magnetic field in terms of the temperature through numerical calculation. Finally, we parametrize this dependency in the efficiency by defining the ratiowhich represents the analogy of the compression ratio for the classical case. It is important to remember that the Landau radius is inversely proportional to the magnitude of the magnetic field. Therefore, for a major (minor) magnitude of the field, the Landau radius is smaller (bigger), and the r parameter is well defined.
Magnetic Engine for the Landau Problem
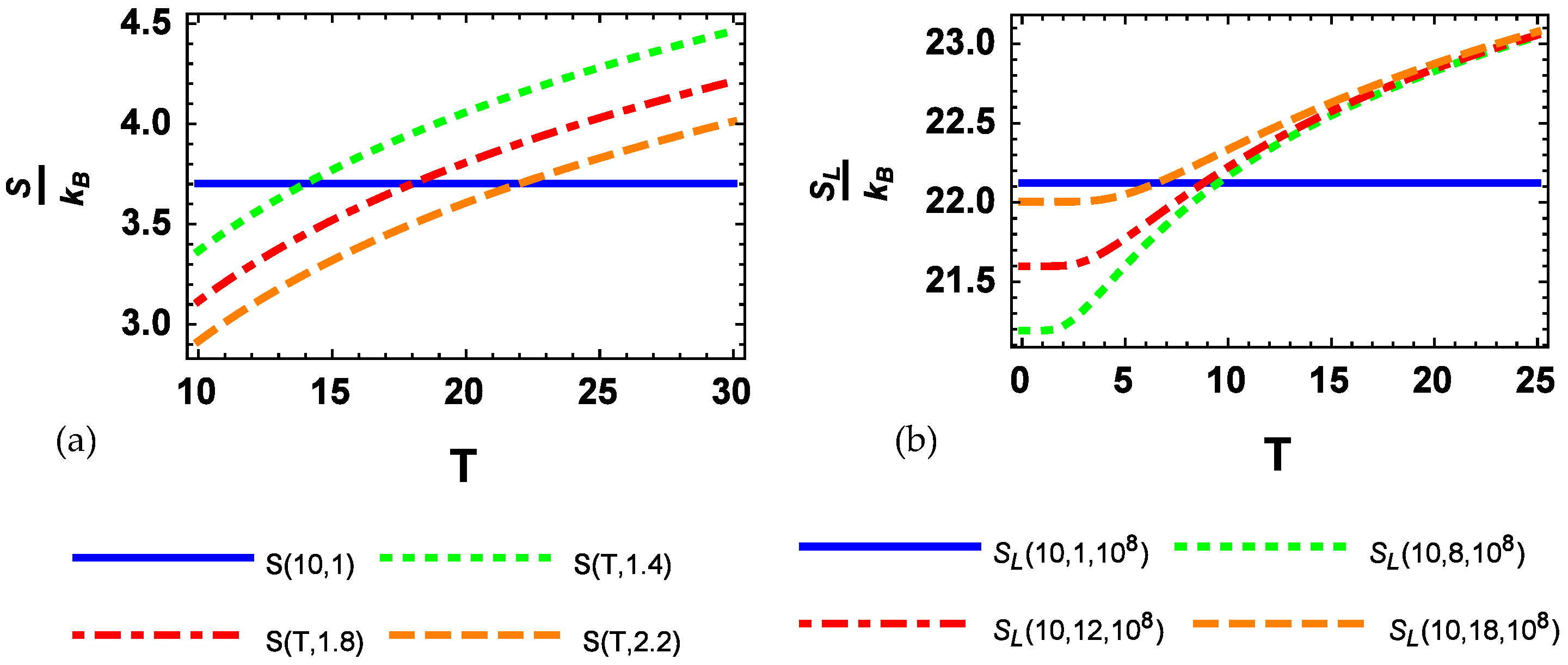
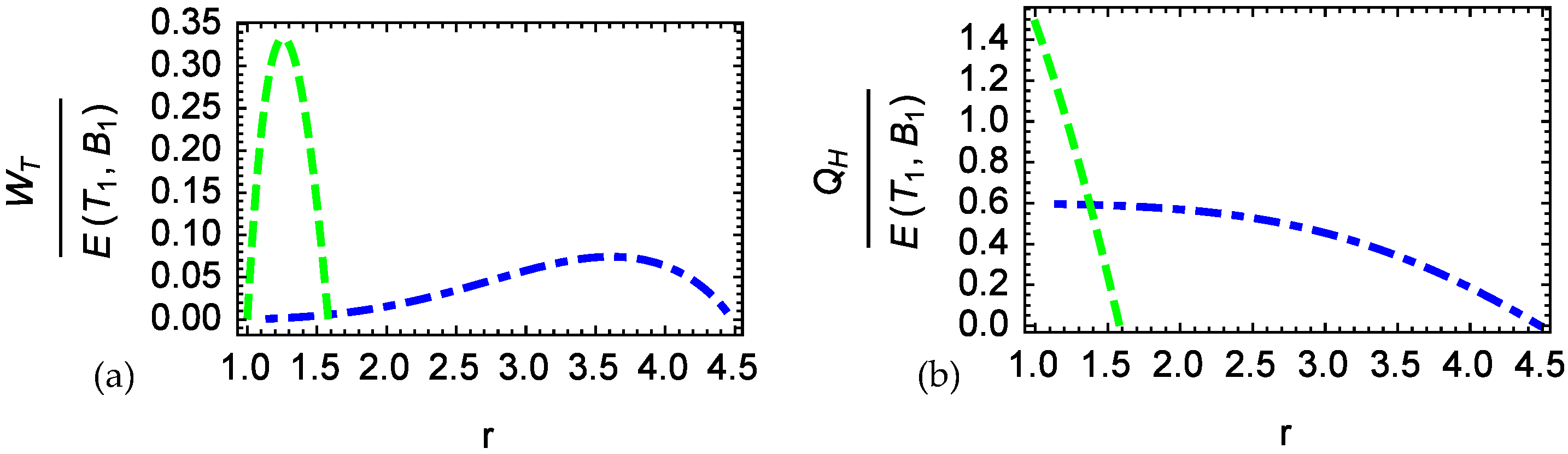
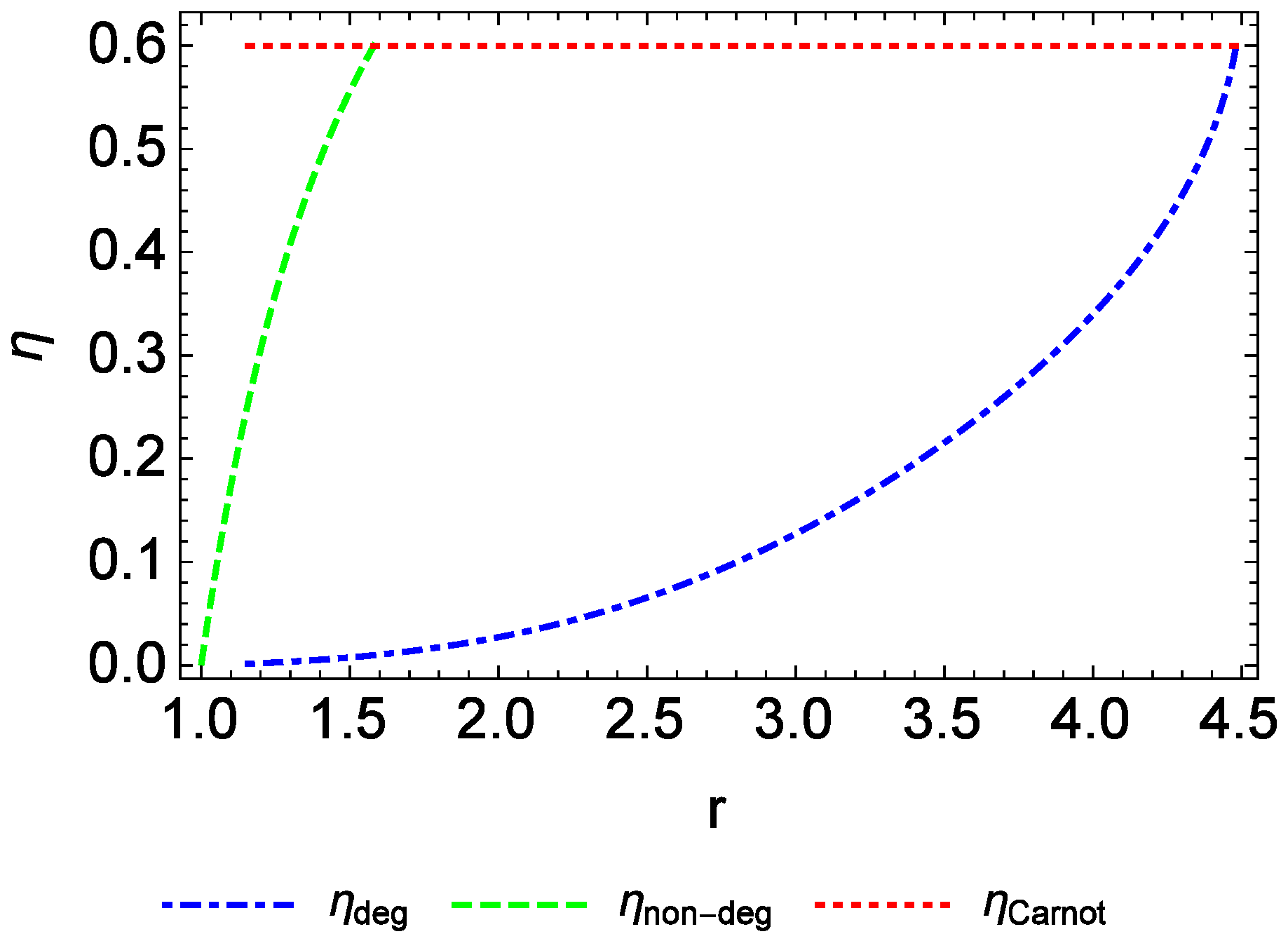
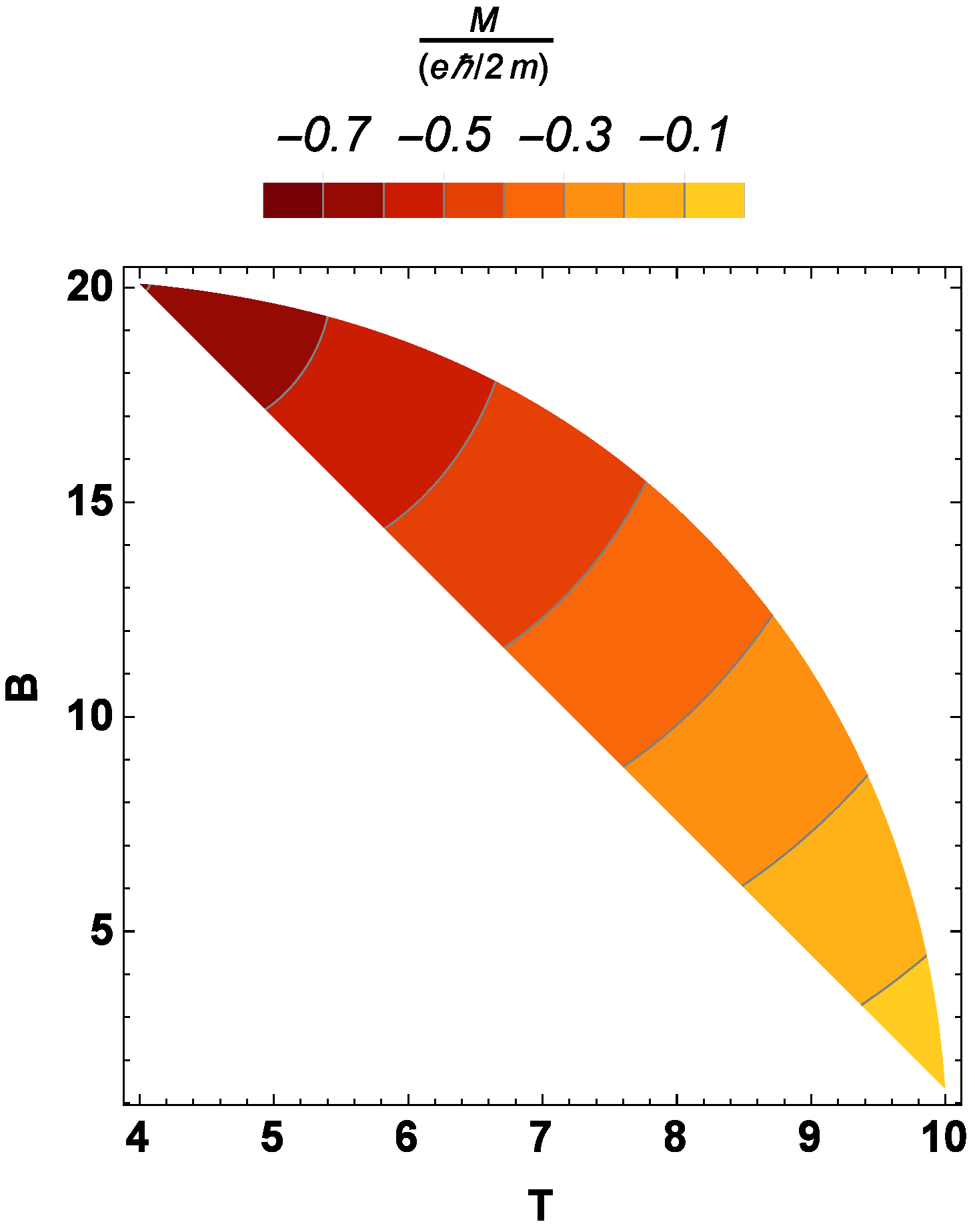
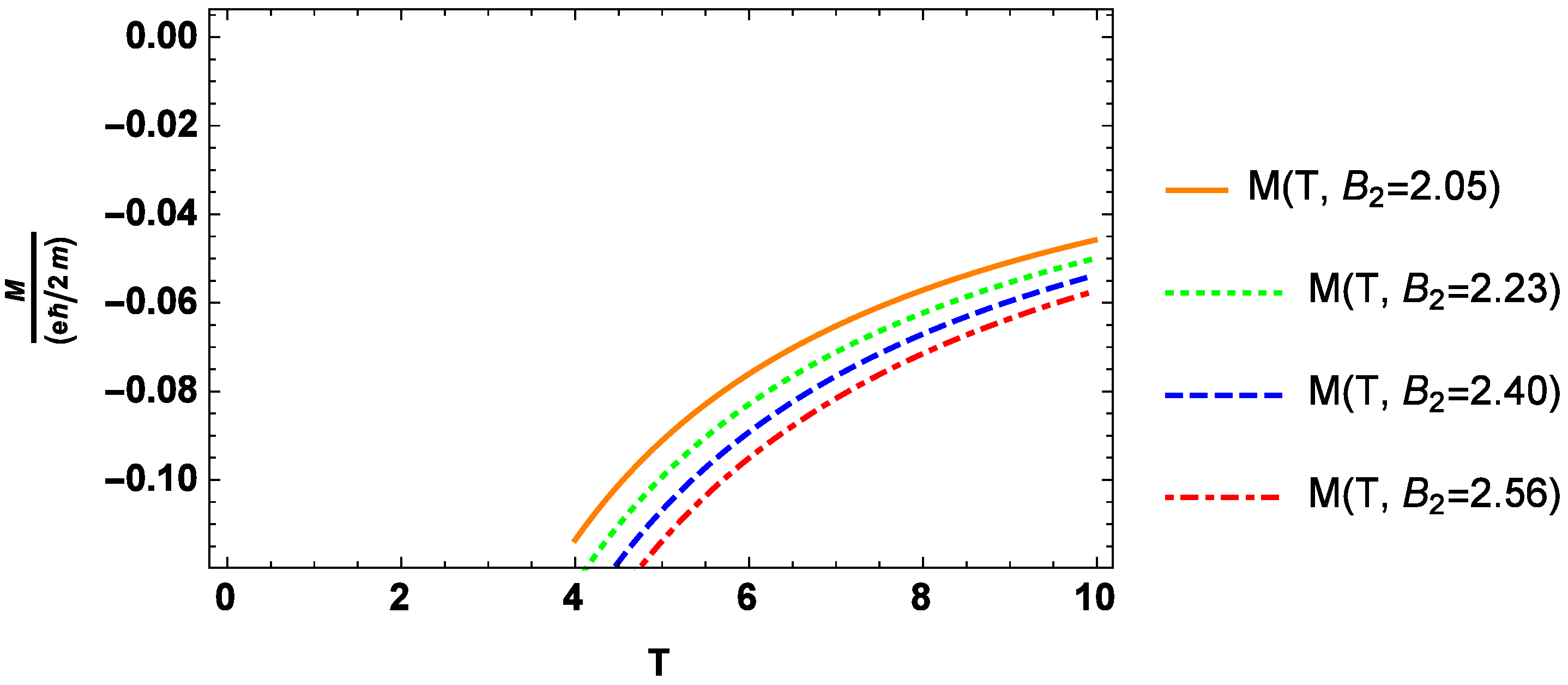
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Scovil, H.E.D.; Schulz-DuBois, D.O. Three-Level masers as a heat engines. Phys. Rev. Lett. 1959, 2, 262–263. [Google Scholar] [CrossRef]
- Huang, X.L.; Niu, X.Y.; Xiu, X.M.; Yi, X.X. Quantum Stirling heat engine and refrigerator with single and coupled spin systems. Eur. Phys. J. D 2014, 68. [Google Scholar] [CrossRef]
- Su, S.H.; Luo, X.Q.; Chen, J.C.; Sun, C.P. Angle-dependent quantum Otto heat engine based on coherent dipole-dipole coupling. EPL 2016, 115, 30002. [Google Scholar] [CrossRef]
- Liu, S.; Ou, C. Maximum Power Output of Quantum Heat Engine with Energy Bath. Entropy 2016, 18, 205. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting work from a single heath bath via vanishing quantum coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Zubairy, M.S.; Dorfmann, K.E.; Kim, M.B.; Svidzinsky, A. Quantum heat engine power can be increased by noise-induced coherence. Proc. Natl. Acad. Sci. USA 2011, 108, 15097–15100. [Google Scholar] [CrossRef] [PubMed]
- Bender, C.M.; Brody, D.C.; Meister, B.K. Quantum mechanical Carnot engine. J. Phys. A Math. Gen. 2000, 33, 4427–4436. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Meister, B.K. Entropy and temperature of quantum Carnot engine. Proc. R. Soc. Lond. A 2002, 458, 1519–1526. [Google Scholar] [CrossRef]
- Wang, J.H.; Wu, Z.Q.; He, J. Quantum Otto engine of a two-level atom with single-mode fields. Phys. Rev. E 2012, 85, 041148. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.L.; Xu, H.; Niu, X.Y.; Fu, Y.D. A special entangled quantum heat engine based on the two-qubit Heisenberg XX model. Phys. Scr. 2013, 88, 065008. [Google Scholar] [CrossRef]
- Muñoz, E.; Peña, F.J. Quantum heat engine in the relativistic limit: The case of Dirac particle. Phys. Rev. E 2012, 86, 061108. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, E.; Peña, F.J. Magnetically driven quantum heat engine. Phys. Rev. E 2014, 89, 052107. [Google Scholar] [CrossRef] [PubMed]
- Peña, F.J.; Muñoz, E. Magnetostrain-driven quantum heat engine on a graphene flake. Phys. Rev. E 2015, 91, 052152. [Google Scholar] [CrossRef] [PubMed]
- Peña, F.J.; Ferré, M.; Orellana, P.A.; Rojas, R.G.; Vargas, P. Optimization of a relativistic quantum mechanical engine. Phys. Rev. E 2016, 94, 022109. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; He, J.; He, X. Performance analysis of a two-state quantum heat engine working with a single-mode radiation field in a cavity. Phys. Rev. E 2011, 84, 041127. [Google Scholar] [CrossRef] [PubMed]
- Abe, S. Maximum-power quantum-mechanical Carnot engine. Phys. Rev. E 2011, 83, 041117. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.H.; He, J.Z. Optimization on a three-level heat engine working with two noninteracting fermions in a one-dimensional box trap. J. App. Phys. 2012, 111, 043505. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J.; He, J.; Ma, Y. Performance of a multilevel quantum heat engine of an ideal N-particle Fermi system. Phys. Rev. E 2012, 86, 021133. [Google Scholar] [CrossRef] [PubMed]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistic; Jhon Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- Tolman, R.C. The Principles of Statistical Mechanics; Oxford University Press: Oxford, UK, 1938. [Google Scholar]
- Chotorlishvili, L.; Azimi, M.; Stagraczyński, S.; Toklikishvili, Z.; Schüler, M.; Berakdar, J. Superadiabatic quantum heat engine with a multiferroic working medium. Phys. Rev. E 2016, 94, 032116. [Google Scholar] [CrossRef] [PubMed]
- Azimi, M.; Chorotorlisvili, L.; Mishra, S.K.; Vekua, T.; Hübner, W.; Berakdar, J. Quantum Otto heat engine based on a multiferroic chain working substance. New J. Phys. 2014, 16, 063018. [Google Scholar] [CrossRef]
- Jaramillo, J.; Beau, M.; del Campo, A. Quantum supremacy of many-particle thermal machines. New J. Phys. 2016, 18, 075019. [Google Scholar] [CrossRef]
- Del Campo, A.; Goold, J.; Paternostro, M. More bang for your buck: Super-adiabatic quantum engines. Sci. Rep. 2017, 4. [Google Scholar] [CrossRef]
- Kosloff, R.; Rezek, Y. The Quantum Harmonic Otto Cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef]
- Roßnagel, J.; Dawkins, T.K.; Tolazzi, N.K.; Abah, O.; Lutz, E.; Kaler-Schmidt, F.; Singer, K. A single-atom heat engine. Science 2016, 352, 325–329. [Google Scholar] [CrossRef] [PubMed]
- Kumar, J.; Sreeram, P.A.; Dattagupta, S. Low-temperature thermodynamics in the context of dissipative diamagnetism. Phys. Rev. E 2009, 79, 021130. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.D.; Lefkidis, G.; Hübner, W. Quantum Isobaric Process in Ni2. J. Supercond. Nov. Magn. 2013, 26, 1589–1594. [Google Scholar] [CrossRef]
- Dong, C.D.; Lefkidis, G.; Hübner, W. Quantum Magnetic quantum diesel in Ni2. Phys. Rev. B 2013, 88, 214421. [Google Scholar] [CrossRef]
- Hübner, W.; Lefkidis, G.; Dong, C.D.; Chaudhuri, D. Spin-dependent Otto quantum heat engine based on a molecular substance. Phys. Rev. B 2014, 90, 024401. [Google Scholar]
- Mehta, V.; Johal, R.S. Quantum Otto engine with exchange coupling in the presence of level degeneracy. Phys. Rev. E 2017, 96, 032110. [Google Scholar] [CrossRef]
- Mani, R.G.; Smet, J.H.; von Klitzing, K.; Narayanamurti, V.; Johnson, W.B.; Umansky, V. Zero-resistance states induced by electromagnetic-wave excitation in GaAs/AlGaAs heterostructures. Nature 2002, 420, 646–650. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T.; Zhang, P.; Sun, C.P. Quantum heat engine with multilevel quantum systems. Phys. Rev. E 2005, 72, 056110. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, E.; Peña, F.J.; González, A. Magnetically-Driven Quantum Heat Engines: The Quasi-Static Limit of Their Efficiency. Entropy 2016, 18, 173. [Google Scholar] [CrossRef]
- Quan, H.T. Quantum thermodynamic cycles and quantum heat engines (II). Phys. Rev. E 2009, 79, 041129. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Polleti, D. Work and efficiency of quantum Otto cycles in power-law trapping potentials. Phys. Rev. E 2014, 90, 012145. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.Y.; Chem, X.; Muga, J.G. Transient Particle Energies in Shortcuts to Adiabatic Expansions of Harmonic Traps. J. Phys. Chem. A 2016, 120, 2962–2969. [Google Scholar] [CrossRef] [PubMed]
- Beau, M.; Jaramillo, J.; del Campo, A. Scaling-up Quantum Heat Engines Efficiently via Shortcuts to Adiabaticity. Entropy 2016, 18, 168. [Google Scholar] [CrossRef]
- Deng, J.; Wang, Q.; Liu, Z.; Hänggi, P.; Gong, J. Boosting work characteristics and overall heat-engine performance via shortcuts to adibaticity: Quantum and classical systems. Phys. Rev. E 2013, 88, 062122. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peña, F.J.; González, A.; Nunez, A.S.; Orellana, P.A.; Rojas, R.G.; Vargas, P. Magnetic Engine for the Single-Particle Landau Problem. Entropy 2017, 19, 639. https://doi.org/10.3390/e19120639
Peña FJ, González A, Nunez AS, Orellana PA, Rojas RG, Vargas P. Magnetic Engine for the Single-Particle Landau Problem. Entropy. 2017; 19(12):639. https://doi.org/10.3390/e19120639
Chicago/Turabian StylePeña, Francisco J., Alejandro González, Alvaro S. Nunez, Pedro A. Orellana, René G. Rojas, and Patricio Vargas. 2017. "Magnetic Engine for the Single-Particle Landau Problem" Entropy 19, no. 12: 639. https://doi.org/10.3390/e19120639
APA StylePeña, F. J., González, A., Nunez, A. S., Orellana, P. A., Rojas, R. G., & Vargas, P. (2017). Magnetic Engine for the Single-Particle Landau Problem. Entropy, 19(12), 639. https://doi.org/10.3390/e19120639





