1. Introduction
Nonnegative Matrix Factorization (NMF) [
1] is a useful data representation technique for finding compact and low dimensional representations of data. NMF decomposes the nonnegative data matrix
into a basis matrix
and an encoding matrix
whose product can approximate the original data matrix
. Due to the nonnegative constraint, NMF only allows additive combination, which leads to the parts-based representation. The parts-based representation is consistent with the psychological intuition of combining parts to form a whole, so NMF has been widely used in data mining and pattern-recognition problems. The nonnegative constraints distinguish NMF from many other traditional matrix factorization algorithms, such as Principal Component Analysis (PCA) [
2], independent component analysis [
3] and Singular Value Decomposition (SVD). However, the major limitation of NMF is that it cannot deal with mixed sign data.
To address the limitation of NMF while inheriting all its merits, Ding et al. [
4] proposed Semi-Nonnegative Matrix Factorization (Semi-NMF), which can handle mixed sign items in data matrix
. Specifically, Semi-NMF only imposes non-negative constraints on encoding matrix
and allows mixed signs in both the data matrix
and the basis matrix
. This allows Semi-NMF to learn a new representation from any signed data and extends the range of application of NMF ideas.
Numerous studies [
5,
6,
7] have demonstrated that data are usually drawn from sampling a probability distribution that has support on or near a submanifold of the ambient space. Some manifold learning algorithms such as ISOMAP[
5], Locally Linear Embedding (LLE) [
6], Laplacian Eigenmap [
7], etc, have been proposed to detect the hidden manifold structure. All these algorithms use the locally invariant idea [
8], i.e., the nearby points are very likely to have similar embeddings. If the geometrical structure is utilized, the learning performance will be evidently enhanced.
On the other hand, the discriminative information of data is very important in computer vision and pattern recognition. Usually, exploiting label information in the framework of NMF can allow obtaining discriminative information. For example, Liu et al. [
9] proposed Constrained Nonnegative Matrix Factorization (CNMF), which imposes the label information for the objective function as hard constraints. Li et al. [
10] developed a semi-supervised robust structured NMF, which exploited the block-diagonal structure in the framework of NMF. Unfortunately, under the unsupervised scenario, we cannot have any label information. However, through reformulation of the scaled indicator matrix, we find that there is an approximation orthogonal discriminability in the learned subspace. Adding approximation orthogonal constraints to the new representation, we could acquire some discriminative information in the learned subspace.
Donoho and Stodden [
11] theoretically proved that NMF cannot guarantee decomposing an object into parts. In other words, NMF may be unable to result in the parts-based representation for some datasets. To ensure the parts-based representation, sparse constraints have been introduced to NMF. Hoyer [
12] proposed sparse constrained NMF, which added the
norm penalty on the basis and encoding matrix and obtained more sparse representation than standard NMF. However, the
norm regularization cannot guarantee that all the data vectors are sparse in the same features [
13], so it is not suitable for feature selection. To settle this issue, Nie [
14] proposed a robust feature selection method emphasizing joint
-norm minimization on both the loss function and regularization. Yang et al. [
15], Hou et al. [
16] and Gu et al. [
17] used the
-norm regularization in discriminant feature selection, sparse regression and subspace learning, respectively. The
-norm regularization is regarded as a powerful model for sparse feature selection and has attracted increasing attention [
14,
15,
18].
The goal of this paper is to preserve the local geometrical structure of the mixed sign data and characterize the discriminative information in the learned subspace under the framework of Semi-NMF. In addition, we encourage the basis matrix to be group sparse, which is suitable to reserve the important basis vectors and remove the irrelevant ones. We propose a novel algorithm, called Group sparsity and Graph regularized Semi-Nonnegative Matrix Factorization with Discriminability (GGSemi-NMFD), for data representation. Graph regularization [
19] has been introduced to encode the local structure of non-negative data in the framework of NMF. We apply it to preserve the intrinsic geometric structure of mixed sign data in the framework of Semi-NMF. In addition, discriminative information is also very important in pattern recognition. To incorporate the discriminative information of the data, we add approximate orthogonal constraints in the learned latent subspace, and thus improve the performance of Semi-NMF in clustering tasks. We further constrain the learned basis matrix to be row sparse. This is inspired by the intuition that different dimensions of basis vectors have different importance. For model optimization, we develop an effective iterative updating scheme for GGSemi-NMFD. Experimental results on six real-world datasets demonstrate the effectiveness of our approach.
To summarize, it is worthwhile to highlight three aspects of the proposed method here:
1. While the standard Semi-NMF models the data in the Euclidean space, GGSemi-NMFD exploits the intrinsic geometrical information of the data distribution and adds it as a regularization term. Hence, when the data are sampled from a high dimensional space’s submanifold, our algorithm is especially applicable.
2. To incorporate the discriminative information of the data, we add approximate orthogonal constraints in the learned space. By adding the approximate orthogonal constraints, our algorithm can have more discriminative power than the standard Semi-NMF.
3. Our algorithm adds -norm constraints in the basis matrix, which can shrink some rows of basis matrix to zero, making basis matrix suitable for feature selection. By preserving the group sparse structure in the basis matrix, our algorithm can acquire more flexible and meaningful semantics.
The remainder of this paper is organized as follows:
Section 2 presents a brief overview of related works.
Section 3 introduces our GGSemi-NMFD algorithm and the optimization scheme. Experimental results on six real-world datasets are presented in
Section 4. Finally, we draw the conclusion in
Section 5.
4. Experimental Section
To demonstrate the effectiveness of GGSemi-NMFD, we carried out extensive experiments on six public datasets: ORL, YALE, UMIST, Ionosphere, USPST and Waveform. All statistical significance tests were performed using Student’s t-tests with a significance level of 0.05. All the NMF-based methods are random initializations.
4.1. Datasets and Metrics
In our experiment, we use 6 datasets that are widely used as benchmark datasets in the clustering literature. The statistics of these datasets are summarized in
Table 1.
ORL: The ORL face dataset contains face images of 40 distinct persons. Each person has ten different images, taken at different times, totaling 400. All images are cropped to pixel grayscale images, and we reshape them into a 1024-dimensional vector.
YALE: The YALE face database contains 165 grayscale images in GIF format of 15 individuals. There are 11 images per subject, one per different facial expression or configuration. All images are cropped to pixel grayscale images, and we reshape them into a 1024-dimensional vector.
UMIST: The UMIST face databases contains 575 images from 20 individuals. All images are cropped to pixel grayscale images, and we reshape them into a 644-dimensional vector.
Ionosphere: Ionosphere is from the UCI repository. Ionosphere was collected by a radar system and consists of a phased array of 16 high-frequency antennas with a total transmitted power of the order of 6.4 kilowatts. The dataset consists of 351 instances with 34 numeric attributes.
USPST: The USPST dataset comes from the USPS system, and each image in USPST is presented at the resolution of pixels. It is the test split of the USPS.
Waveform: Waveform is obtainable at the UCI repository. It has three categories with 21 numerical attributes and 2746 instances.
We utilize clustering performance to evaluate the effectiveness of data representation. Clustering Accuracy (ACC) and Normalized Mutual Information (NMI) are two widely-used metrics for clustering performance, whose definitions are as follows:
where
and
are cluster labels of item
i in clustering results and in the ground truth, respectively;
equals 1 if
and equals 0 otherwise; and
is the permutation mapping function that maps
to the equivalent cluster label in the ground truth.
denotes the entropy of cluster set
C.
is the mutual information between
C and
:
is the probability that a randomly-selected item from all testing items belongs to cluster
, and
is the joint probability that a randomly-selected item is in
and
simultaneously. If
C and
are identical,
.
when the two cluster sets are completely independent.
4.2. Compared Algorithms
To demonstrate how the clustering performance can be improved by our method, we compare the following popular clustering algorithms:
4.3. Parameter Settings
Baseline methods have several parameters to be tuned. To compare these methods fairly, we perform grid search in the parameter space for each method and recode the best average results.
For datasets ORL, YALE and UMIST, we set
K, the dimension of latent space, to the number of true classes of the dataset [
19], for all NMF-based methods. For the dataset Ionosphere, since its class number is too small (only 2 classes), we set
for NMF-based methods. We applied the compared methods to learn a new representation, and then, Kmeans was adapted for data clustering on the new data representation. For a given cluster number, 10 test runs were conducted on different classes of data randomly chosen from the dataset.
For GNMF, the number of nearest neighbors for constructing the data graph is set by searching the grid
according to [
24], and the graph regularization parameter is chosen from
.
For GGSemiNMFD, the number of the neighborhood size k is selected from . We also set , and by searching the grid . If we adopt better parameter tuning, better clustering performance will be achieved.
Note that there is no parameter selection for Kmeans, PCA, NMF and Semi-NMF, given the number of clusters.
In the coming section, we repeat clustering 10 times, and the mean and the standard error are computed. Additionally, we report the best average result for each method.
4.4. Performance Comparison
The experiments reveal some important points.
The NMF-based methods, including NMF, Semi-NMF, GNMF and GGSemi-NMFD, outperform the PCA and Kmeans methods, which demonstrates the merit of the parts-based representation in discovering the hidden factors.
On nonnegative datasets, NMF demonstrates somewhat superior performance over Semi-NMF.
For nonnegative datasets, methods considering the local geometrical structure of data, such as GNMF and GGSemi-NMFD, significantly outperform NMF and Semi-NMF, which suggests the importance of exploiting the intrinsic geometric structure of data.
When dataset has mixed signs, NMF and GNMF cannot work. Semi-NMF tends to outperform Kmeans and PCA, which indicates the advantage of the parts-based representation in finding the hidden matrix factors even in the mixed sign data.
Regardless of the datasets, our GGSemi-NMF always represents the best performance. This shows that by leveraging the power of parts-based representation, graph Laplacian regularization, group sparse constraints and discriminative information simultaneously, GGSemi-NMFD can learn a better compact and meaningful representation.
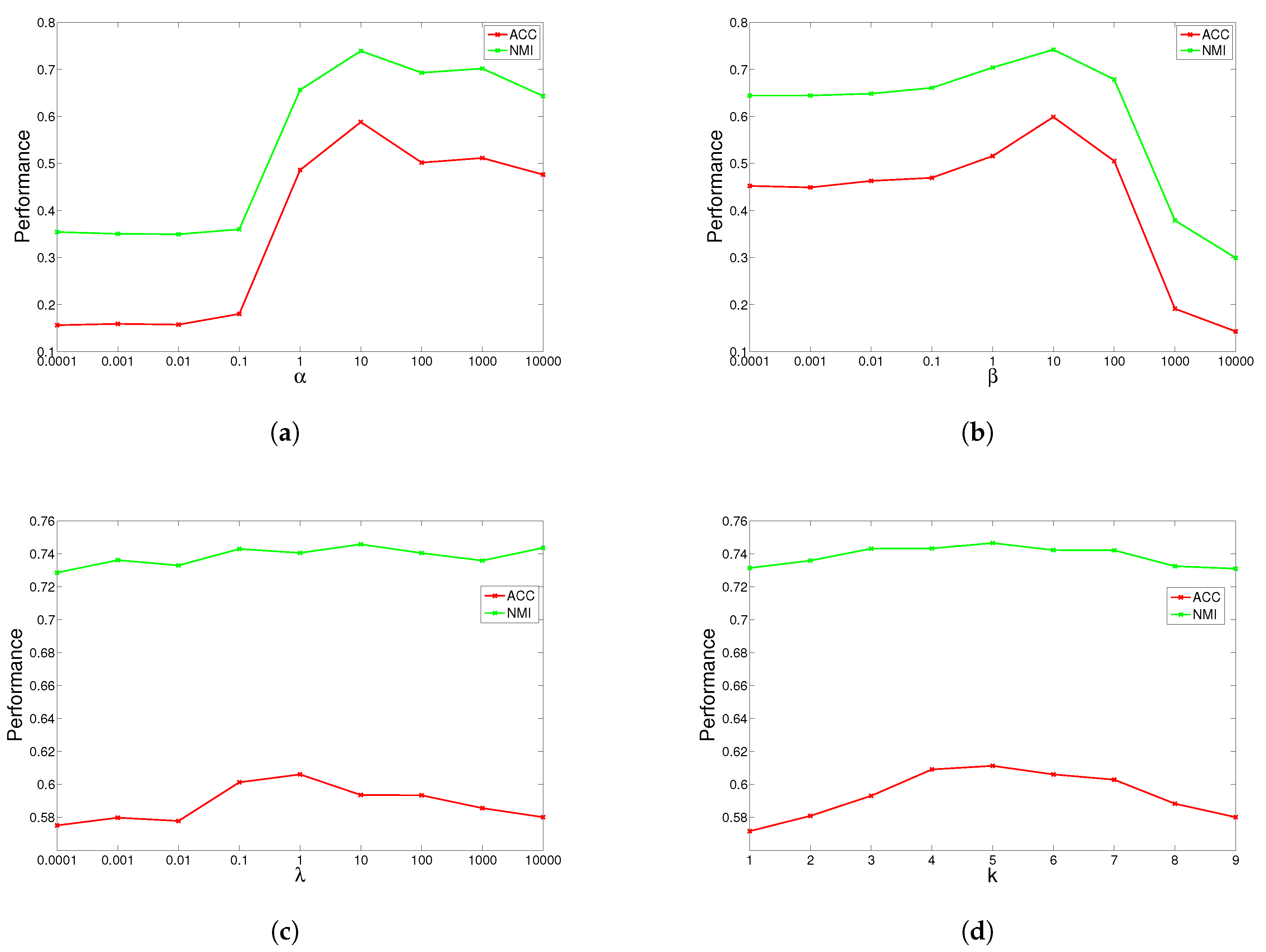
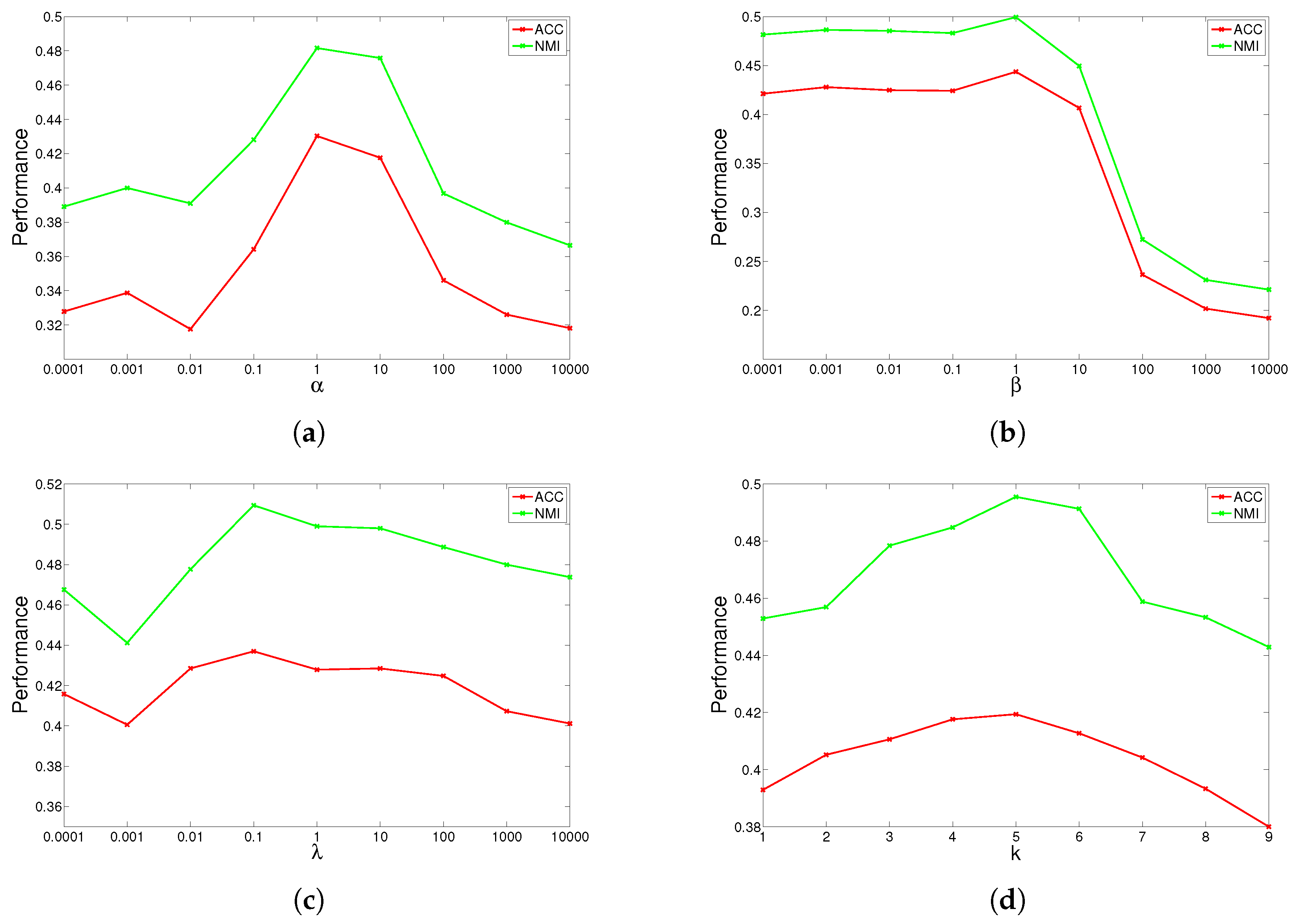
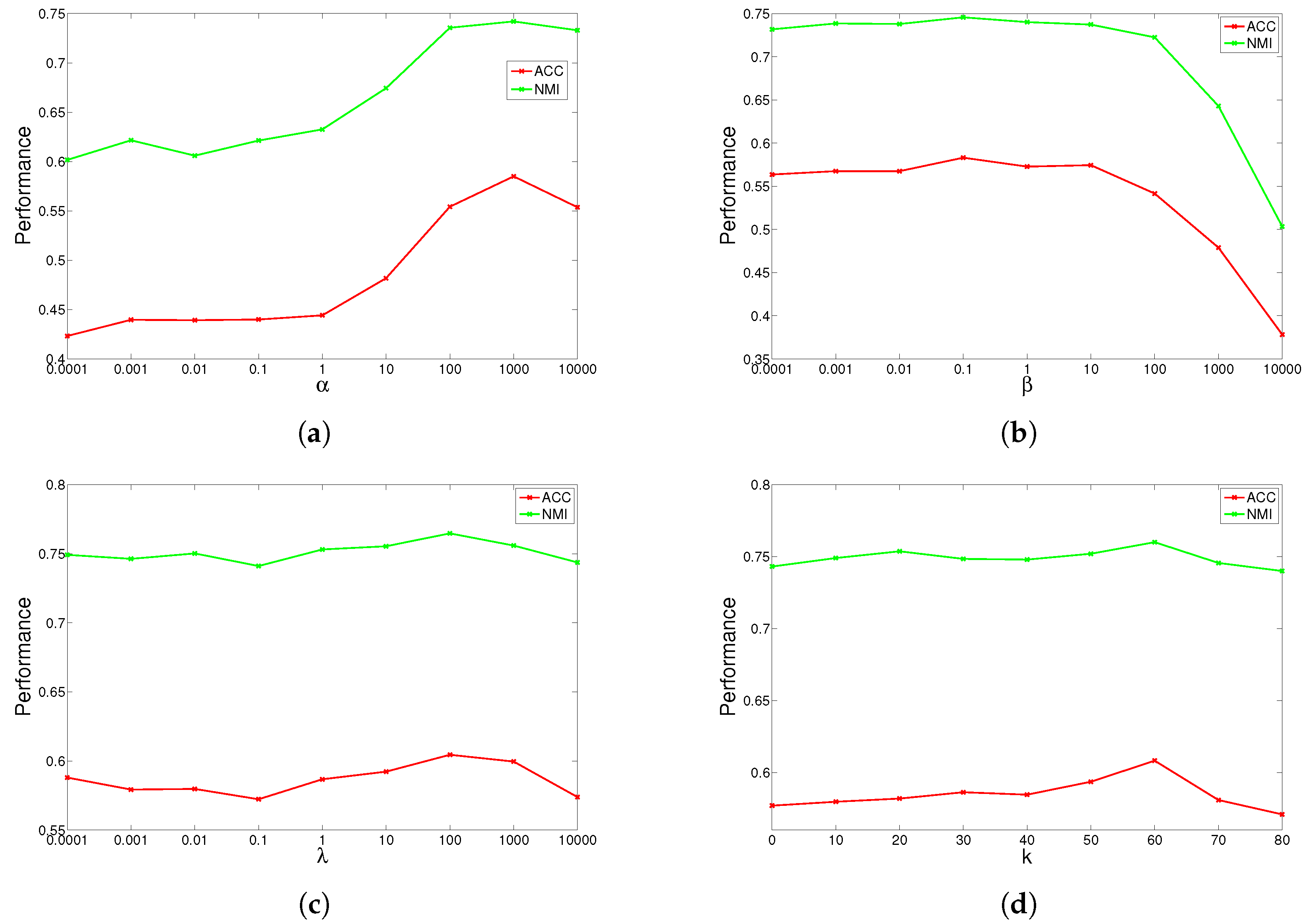
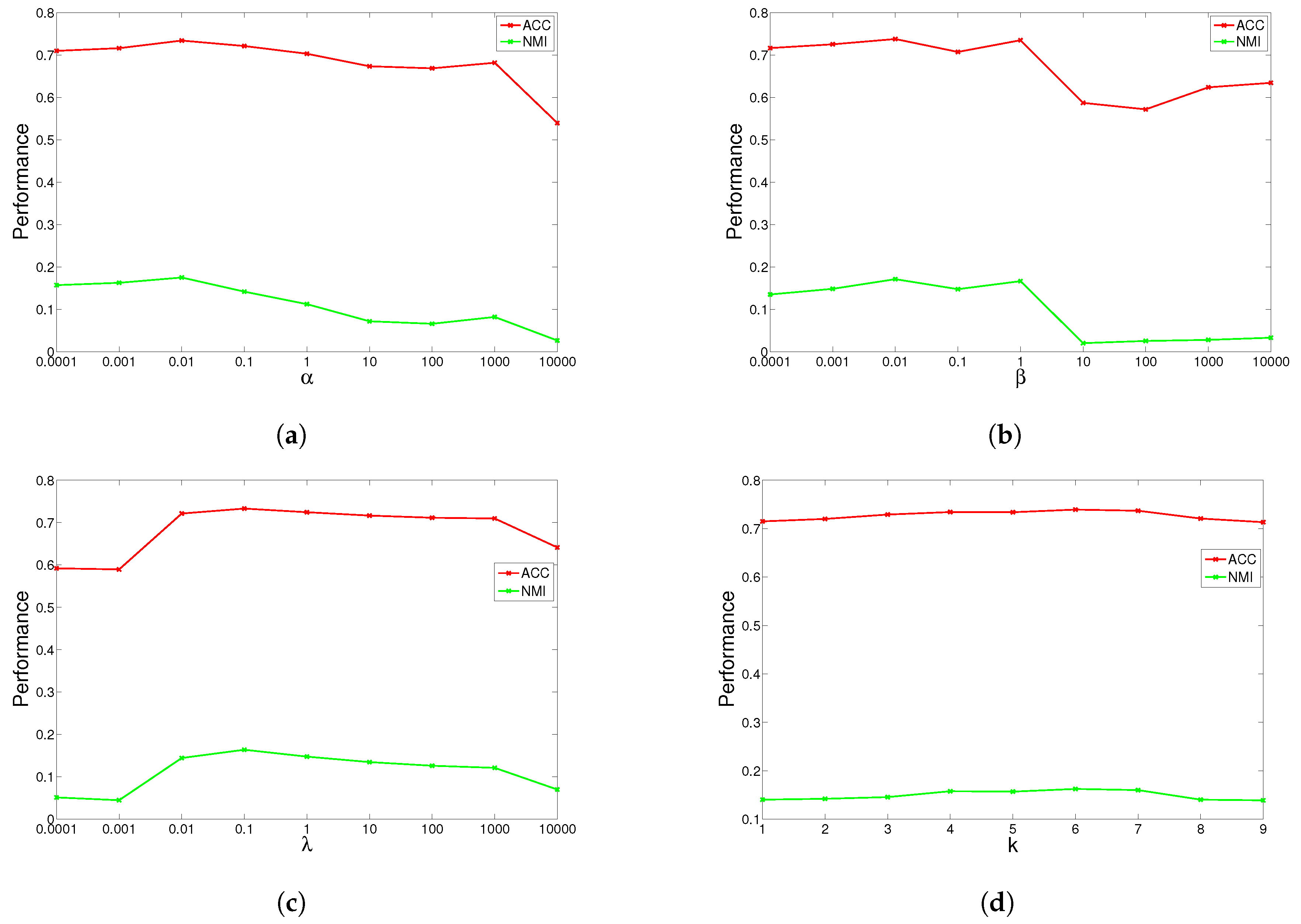
4.5. Parameter Study
GGSemi-NMFD has four parameters, , , and the number of nearest neighbors k. Parameter measures the weight of the graph Laplacian; parameter controls the orthogonality of the learned representation; parameter controls the sparse degree of the basis matrix; and k controls the complexity of the graph. We investigated their influence on GGSemi-NMFD’s performance by varying one parameter at a time while fixing the others. For each specific setting, we run GGSemi-NMFD 10 times, and the average performance was recorded.
The results are shown in
Figure 1,
Figure 2,
Figure 3 and
Figure 4 for ORL, YALE, UMIST and Ionosphere respectively (results for USPST and Waveform were similar to Ionosphere). We found that the four parameters have the same behavior: when increasing the parameter from a very tiny value, the performance curves first rose and then descended. This denotes that when assigned proper values, the graph Laplacian, approximation orthogonal and sparseness constraints, as well as the number of nearest neighbors are surely helpful to learn a better representation. For dataset ORL, we set
,
. For dataset YALE, we set
.
. For dataset UMIST, we set
,
and
. For dataset Ionosphere, we set
,
. For nearest neighbors
k, we can observe from the result that GGSemi-NMF consistently outperforms the best baseline algorithms on four datasets when
.
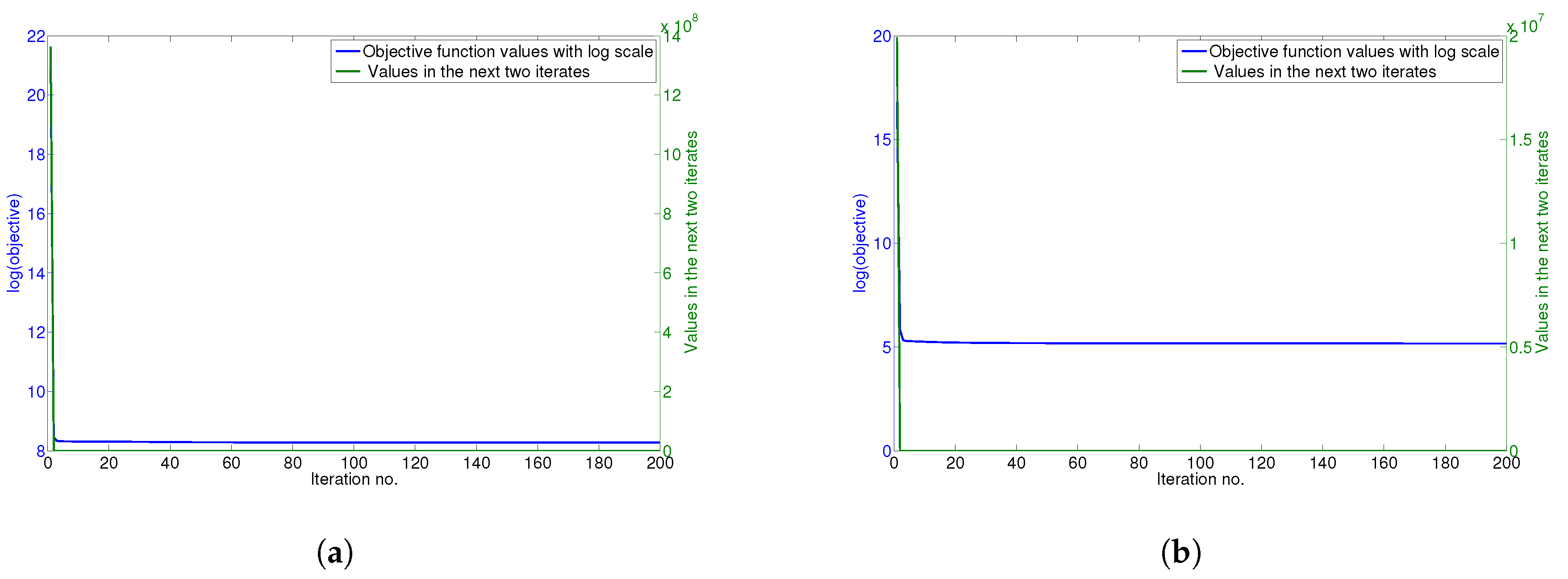
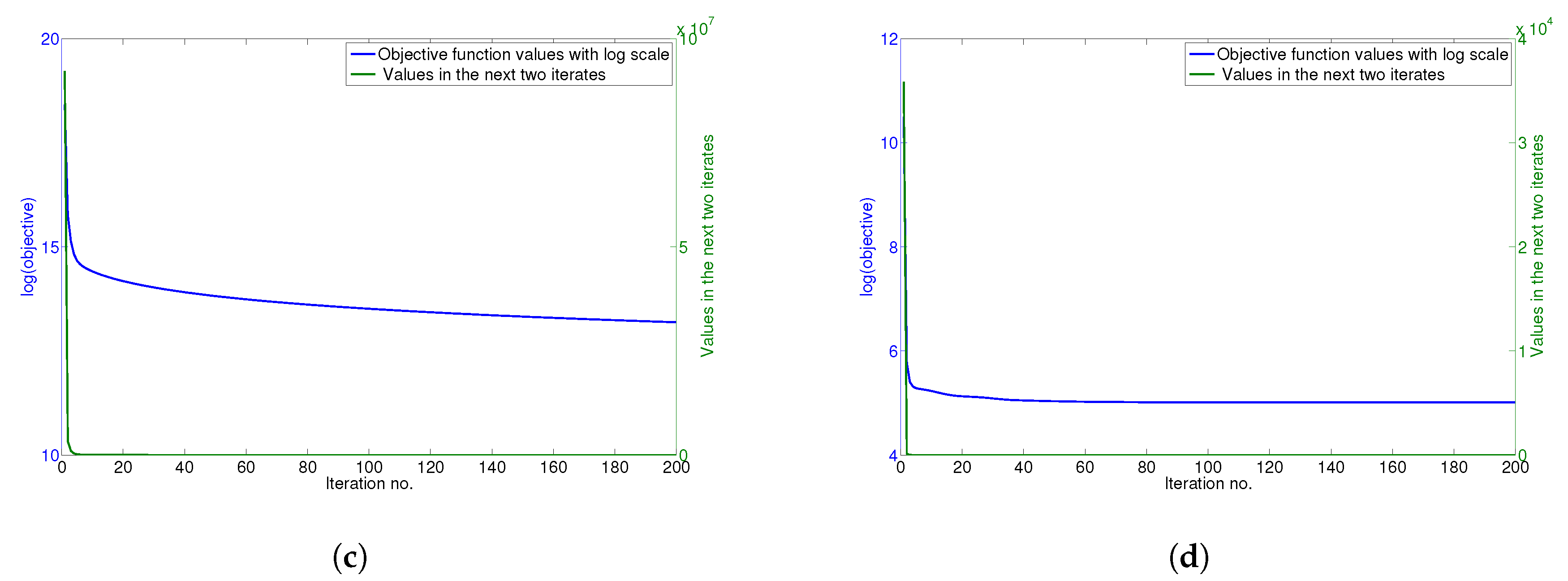
4.6. Convergence Analysis
The updating rules for minimizing the objective function of GGSemi-NMFD in Equation (
12) are essentially iterative, and it can be proven that these rules are convergent.
Figure 5a–d show the convergence curve of GGSemi-NMFD on datasets ORL, YALE, UMIST and Ionosphere, respectively. For each figure, we use the objective function values with log scale (blue line) and the values of the objective function in the next two iterates (green line) to measure the convergence of GGSemi-NMFD. As can be seen, usually within dozens of iterations, the multiplicative update rules for GGSemi-NMFD converge very fast.