3.1. Flow Structure and Temperature Distribution
The temperature distribution with limiting streamlines on the wall, and temperature distribution with streamlines on the span-wise middle section are used to analyze the detailed flow structures and heat transfer performance in this study.
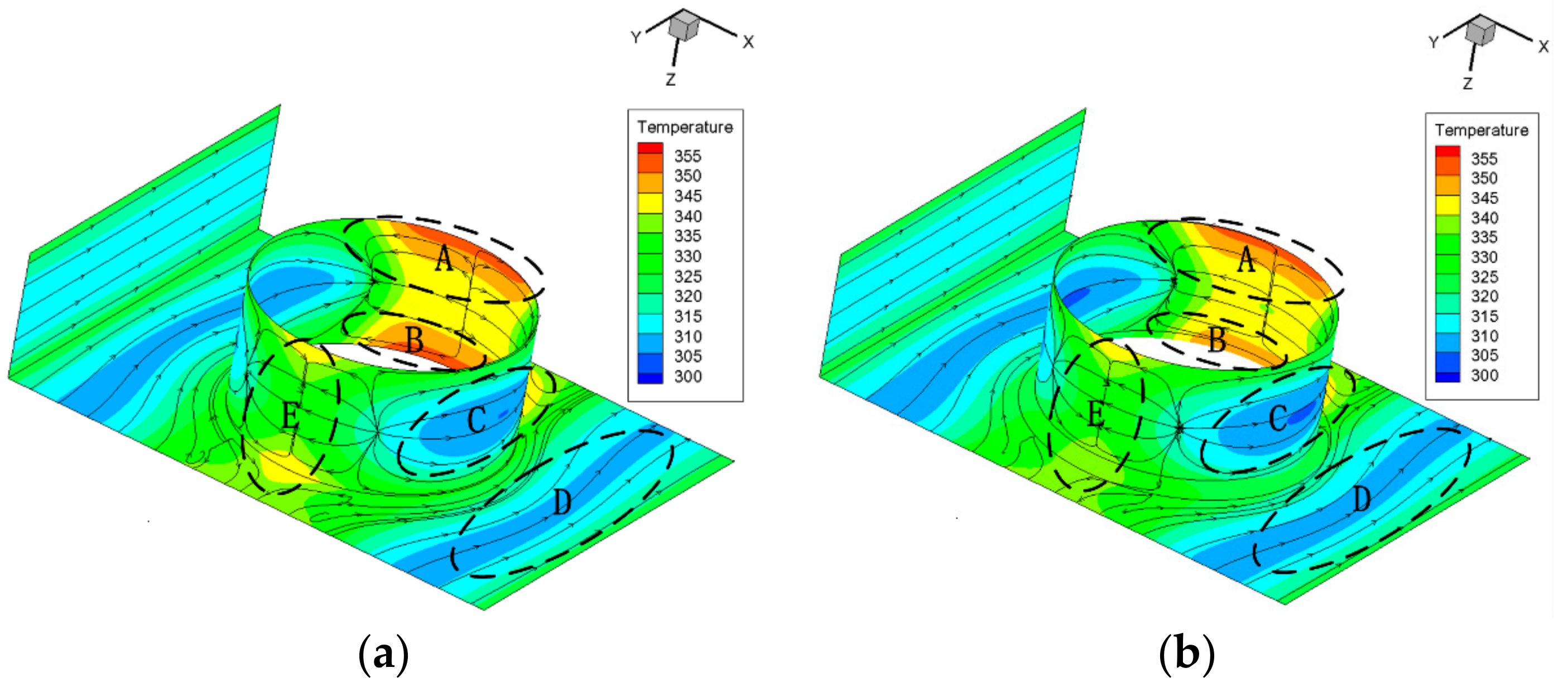
Figure 2 shows the temperature distribution with limiting streamlines on the pin-fin with fillet and bulb, and surrounding walls when the Reynolds number is 50, and the radius of fillet and bulb ranges from 0 μm to 15 μm. When
Re = 50, as the radius increases, the high temperature region A in the rear side of smooth pin-fin decreases gradually, and the temperature also goes down. When
r = 15 μm, the temperature in region A is slightly above the average temperature of the rear side, and the high temperature area disappears. It is obvious that the fillet and bulb weaken the symmetry of the flow field along the normal-wise direction, and the fluid from the rear side has the trend to flow upward, so the flow structure in region A has been improved. As the radius increases, the fillet and bulb influence the flow field even more, thus the high temperature region A decreases gradually. The temperature change trend of region B in rear side with proposed flow structures is the same with that of region A, but because of the direct effect of the fillet and bulb, the effects in region B are more obvious, and the high temperature area already disappears when
r = 10 μm. The flow in this area cools the wall surface more intensely, which significantly improves the heat and mass transfer in region B and thus greatly improves the local temperature uniformity. For region C in the side surface of the pin-fin, the temperature decreases with the increase of the radius, which means both the fillet and bulb strengthen the heat transfer process near the surface of the pin-fin at a low Reynolds number. Especially, the bulb makes the low temperature area move from the side surface of the pin-fin to the bulb when the radius is larger than 10 μm. For the fillet and bulb, the changes of temperature distribution in the bottom wall region D which is in contact with the fillet and bulb differ from each other as the radius increases. For the pin-fin with fillet, the temperature gradient decreases gradually, and the low temperature region gradually increases as the radius increases. When
r = 15 μm, the low temperature area occupies almost the whole mainstream area, and the overall thermal uniformity of the bottom wall is improved. For the pin-fin with bulb, the increase of the radius leads to the temperature decreases at all bottom walls, but it also results in the increase of temperature gradient gradually. For the leading edge of the pin-fin region E, its temperature decreases and approaches to the low temperature zone on both sides of the pin-fin with the increase of the radius. The triangle-shape high temperature area in this region decreases with the radius increasing, and it is more pronounced on the bottom side.
From the above analysis, the proposed structures significantly lower the temperature of the rear side surface, leading edge and side surface of the pin-fin and shrink the high temperature area, and its effect increases as the radius increases. The proposed flow structures improve the temperature uniformity of the microchannel, which can be useful for the laminar heat transfer enhancement researches employing triangular, square and circular pin-fins [
25,
26,
27,
28].
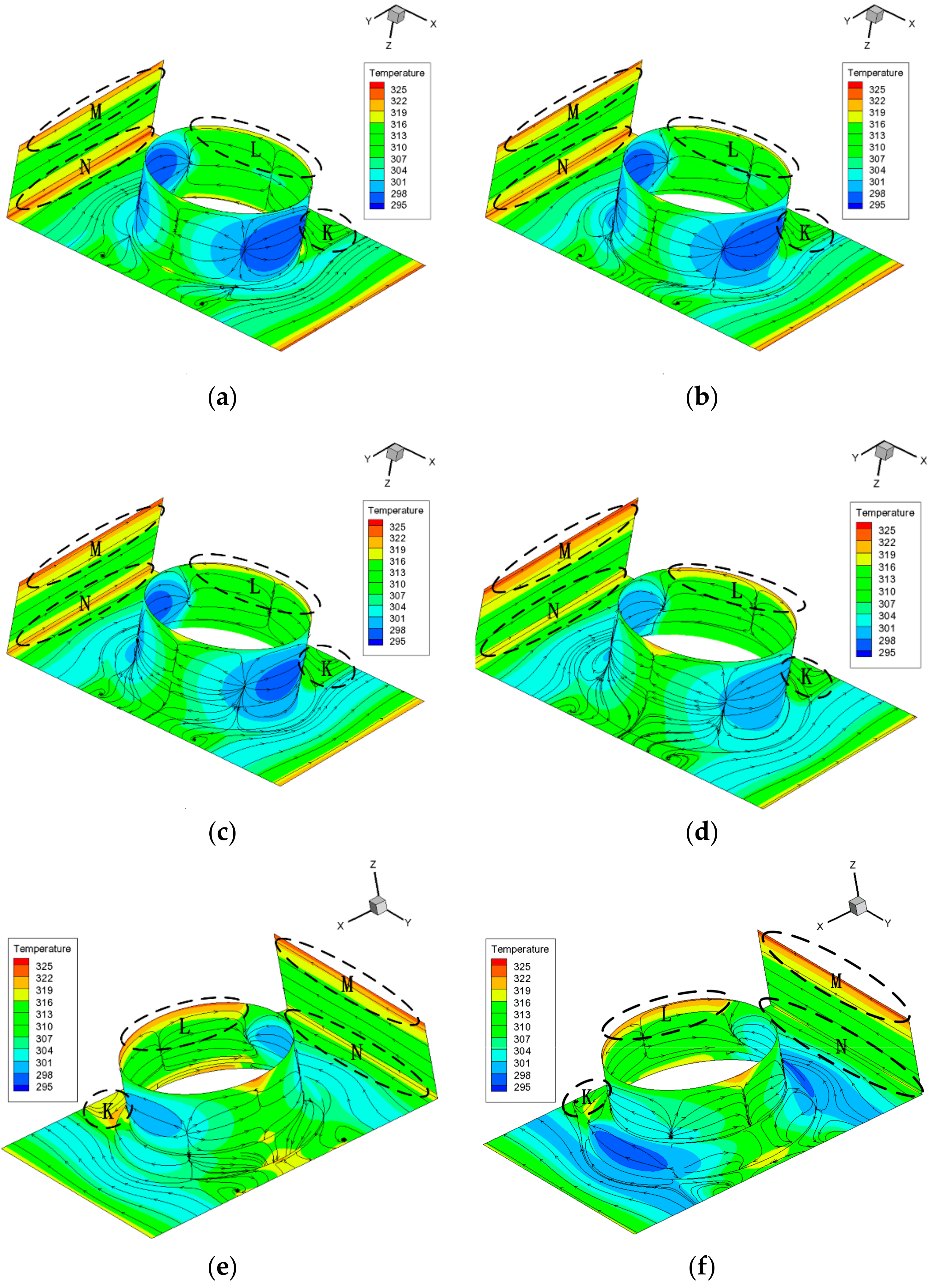
As shown in
Figure 3, when
Re = 200, compared to
Figure 2, the highest temperature region of pin-fin with both fillet and bulb has changed from the rear of the cylinder to the vortex region near the corner when
Re changes from 50 to 200. The high temperature region N is shrinking and cooling with the increment of the radius, which indicates that the local flow and heat transfer is refined. This is because the fillet and bulb enhance the mass transfer and admixture between the main flow and near-surface flow, decrease the average temperature of the bottom surface and the temperature gradient and intensify the heat and mass transfer near the vortex region. The same trend appears in the region near the side surface, which is highly expected and reasonable because with the increase of the velocity of the fluid, the fluid will wash the wall surface more violently which thus improves the heat transfer there. However, region M is expanding and heating with the increment of the radius, which indicates that flow and heat transfer deteriorates. The same trend appears on the top surface near the rear of the cylinder. This is because, at a high Reynolds number, the vortex in the corner and in wake of the rear of the cylinder is stronger, which suppresses the influence of the fillet and bulb on the flow on the top surface and region M, constrains the effect of the proposed structure to the lower half in the microchannel, limits it to develop in the span-wise direction and makes the low temperature flow away from the top surface. Besides, in the side surface of the cylinder, the temperature increases as the radius increases. With the increase of the radius, the geometrical structure in
z direction becomes more asymmetrical, which induces an asymmetrical flow field, with more violent flow washing the bottom. Thus, the asymmetrical flow field causes differences of heat transfer between region M and region N. The asymmetrical field makes it more difficult to evaluate the whole heat transfer performance. Therefore, more analysis is needed to find out whether the whole heat transfer performance is improved considering that different regions have different trends. Different structures also make a difference. For the result of pin-fin with bulb, compared to the result of pin-fin with fillet structure, a relatively higher temperature area appears in region L. Additionally, in region K it is interesting to note that the back flow in the rear in those with bulb shifts ahead compared to that with fillet. This phenomenon can explain the flow pattern differences in region L between two structures: The back flow with bulb causes more flow separation in the rear of the cylinder surface. This leads to the deterioration of heat transfer and thus the expansion of region L in the cases with bulb. Besides, the distribution of temperature field when
Re is 200 is similar to that of a
Re of 50 around the bottom area except that those with bulb have an undesirable greater temperature gradient.
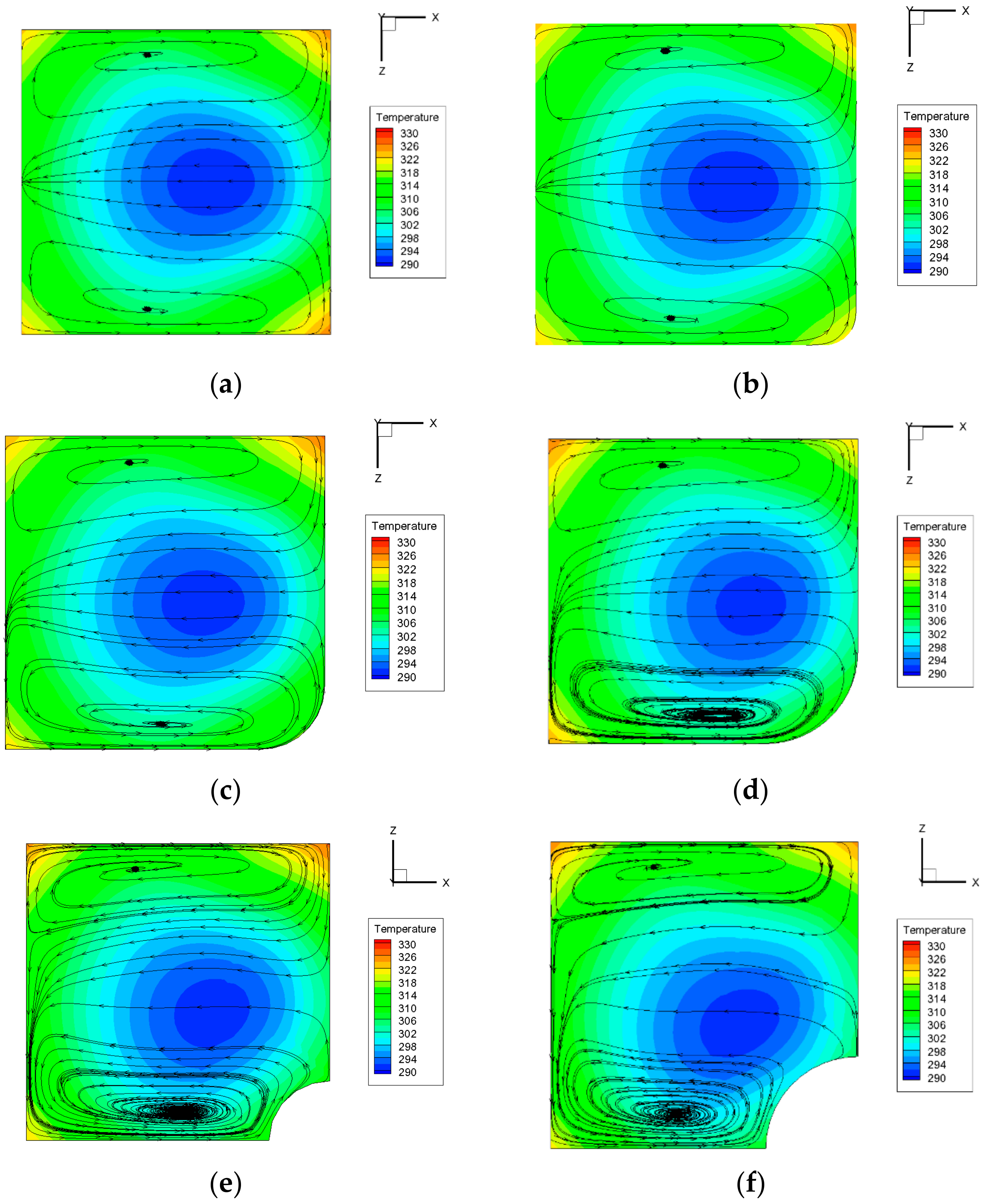
The distribution of temperature field and streamlines in the stream-wise mid-session surface with the radius of the fillet and bulb ranging from 2 μm to 15 μm are shown in
Figure 4. Only half of the area is given because the structure is symmetrical.
As shown in
Figure 4, the channel is full of strong secondary flow. When
Re is 50, in smooth microchannel, the secondary flow is symmetrical in the normal-wise direction. As for the case with a 15 μm fillet, due to the asymmetrical geometry structure, the secondary flow is no longer symmetrical, with a stronger secondary flow at the bottom and a weakened one at the top. It is worth noting that with the increment of the radius the secondary flow at the bottom expands upwards and gradually secondary flow in these two areas merges together into one. A similar trend is observed in the microchannel with bulbed pin-fin. The main low temperature region of those in smooth channel is symmetrical, circular and in the central of the channel while the region of those with fillet and bulb is asymmetrical and moves downwards, getting closer to the fillet and bulb. The maximum temperature is lower in those with fillet and bulb than that of smooth channel, especially in the regions near the fillet and bulb. The decrease of maximum temperature contributes to the decrease of the temperature gradient. It can be explained by the fact that after adding the fillet and bulb, the secondary flow, developing from two separate ones into one, has enhanced the heat transfer near the vortex region and thus the uniformity of the temperature field is strengthened. We can also find that in the microchannel with bulb, the secondary flow in the bottom is more violent than that in the channel with the fillet while the interaction between two secondary flows in different regions is weaker than that in the channel with fillet. It can be explained by the fact that in the channel with bulbed pin-fin, two enormous changes in geometrical structure, one of which is in the edge of the bulb and the bottom wall and the other one is in the edge of the bulb and the pin-fin surface. The first geometrical change has contributed to enhance the secondary flow at the bottom while the latter one hinders the development of the secondary flow upwards and thus weakens the interaction between the two areas.
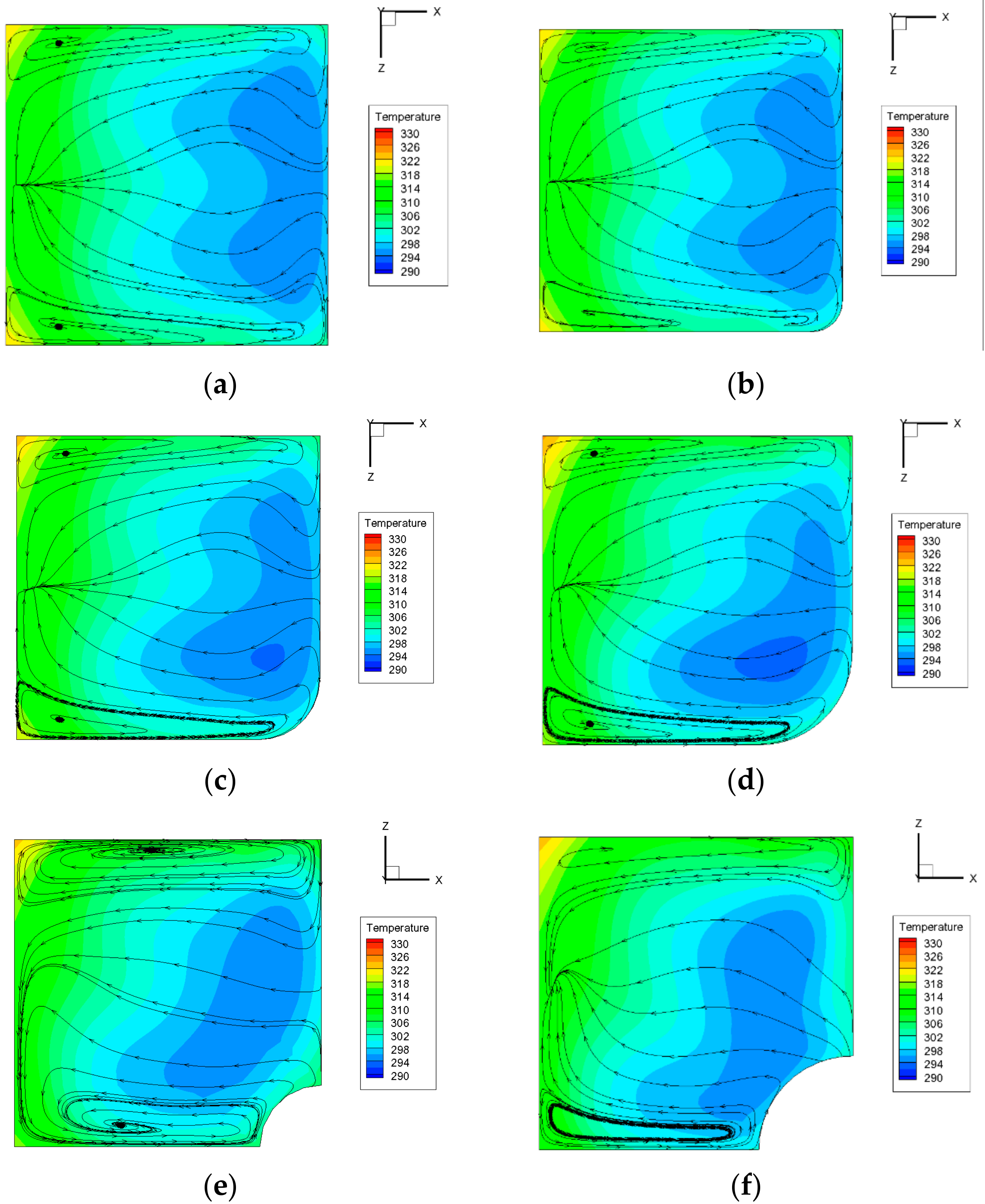
Figure 5 shows that when
Re = 200, the span-wise secondary flow both at the bottom and top is confined to the corner, its intensity is relatively less than that in the case of
Re = 50. The influences of fillet and bulb on the flow structure decreases, and the interaction of the upper and lower secondary flow is no longer obvious. However, the fillet and bulb have a great influence on the temperature distribution. As the radius increases, the mainstream low temperature core region is obvious asymmetry, and it moves downwards gradually. The lower secondary flow is more violent than that in the smooth structure, and thus enhances the heat transfer performance of the bottom wall. Besides, the increase of secondary flow constrains the high temperature area to the corner, reduces the average temperature and enhances the heat transfer performance. However, because of the movement of the mainstream low temperature core region, the temperature of the upper fluid rises, leading to the heat transfer deterioration of the top wall which is consistent with the result of
Figure 3. All the effects mentioned above are strongest when radius is 15 μm.