Thermodynamic Analysis for Buoyancy-Induced Couple Stress Nanofluid Flow with Constant Heat Flux
Abstract
:1. Introduction
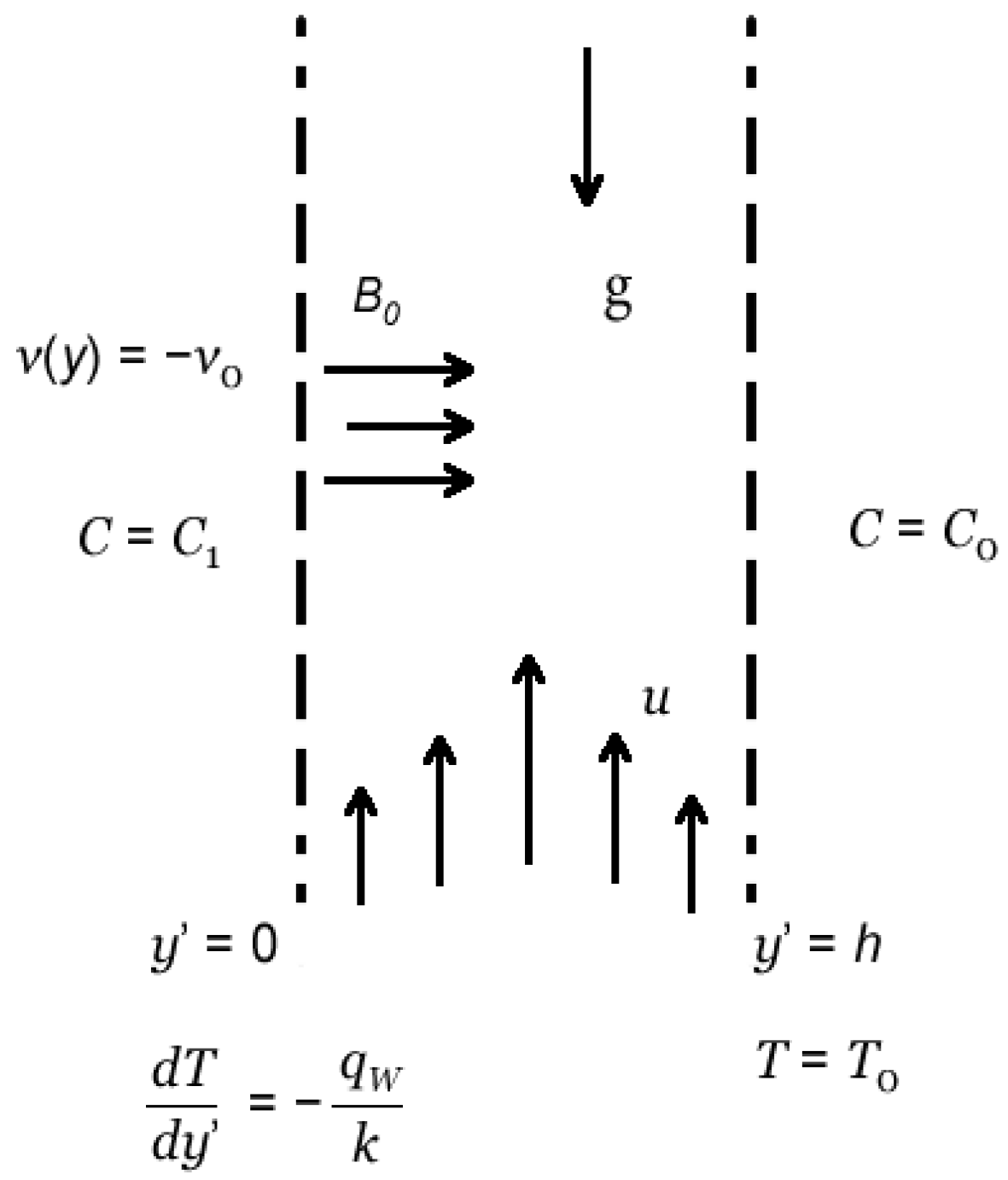
2. Mathematical Analysis
3. Entropy Analysis
4. Methodology of Solution
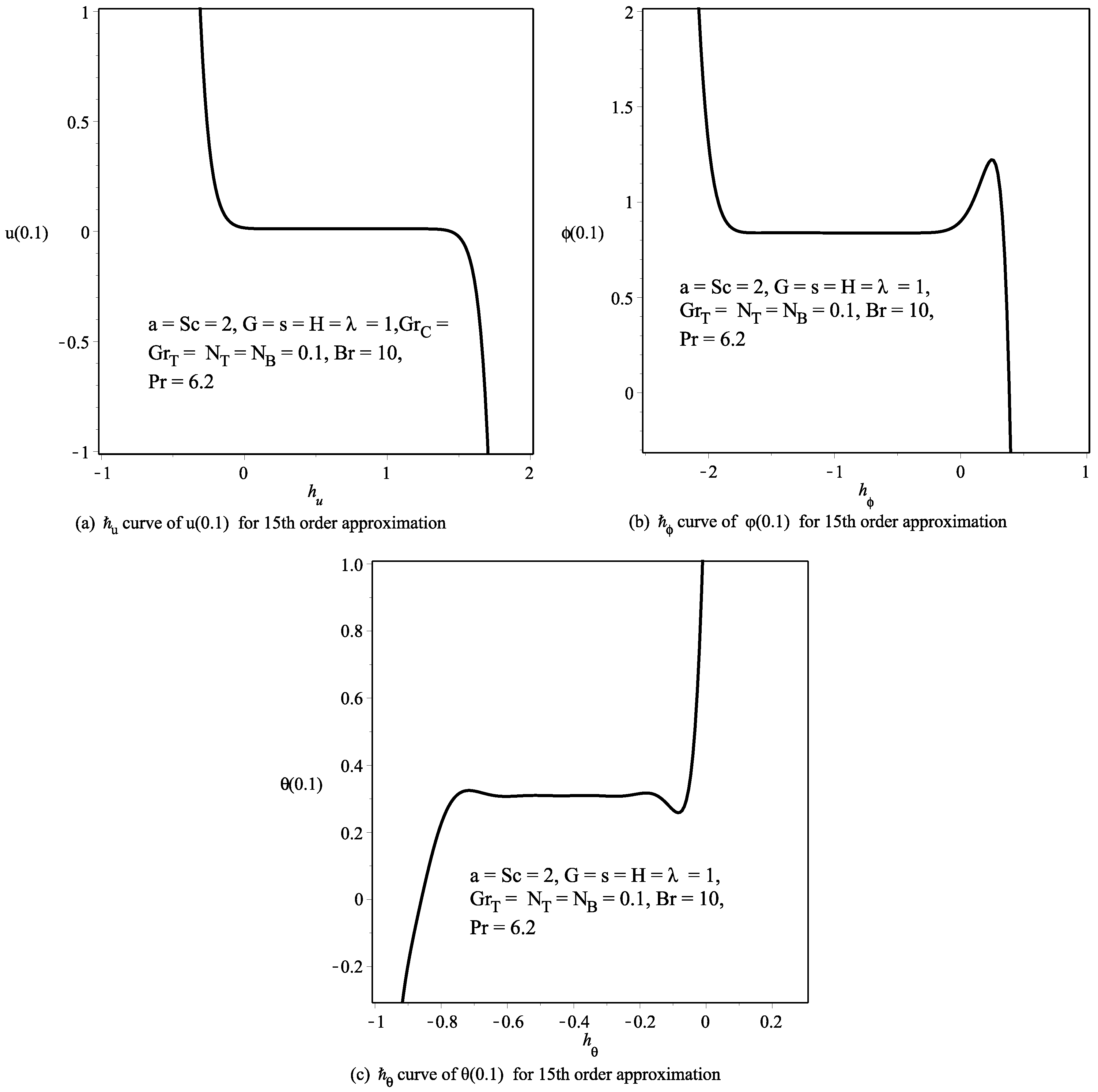
5. Convergence of the HAM Solution
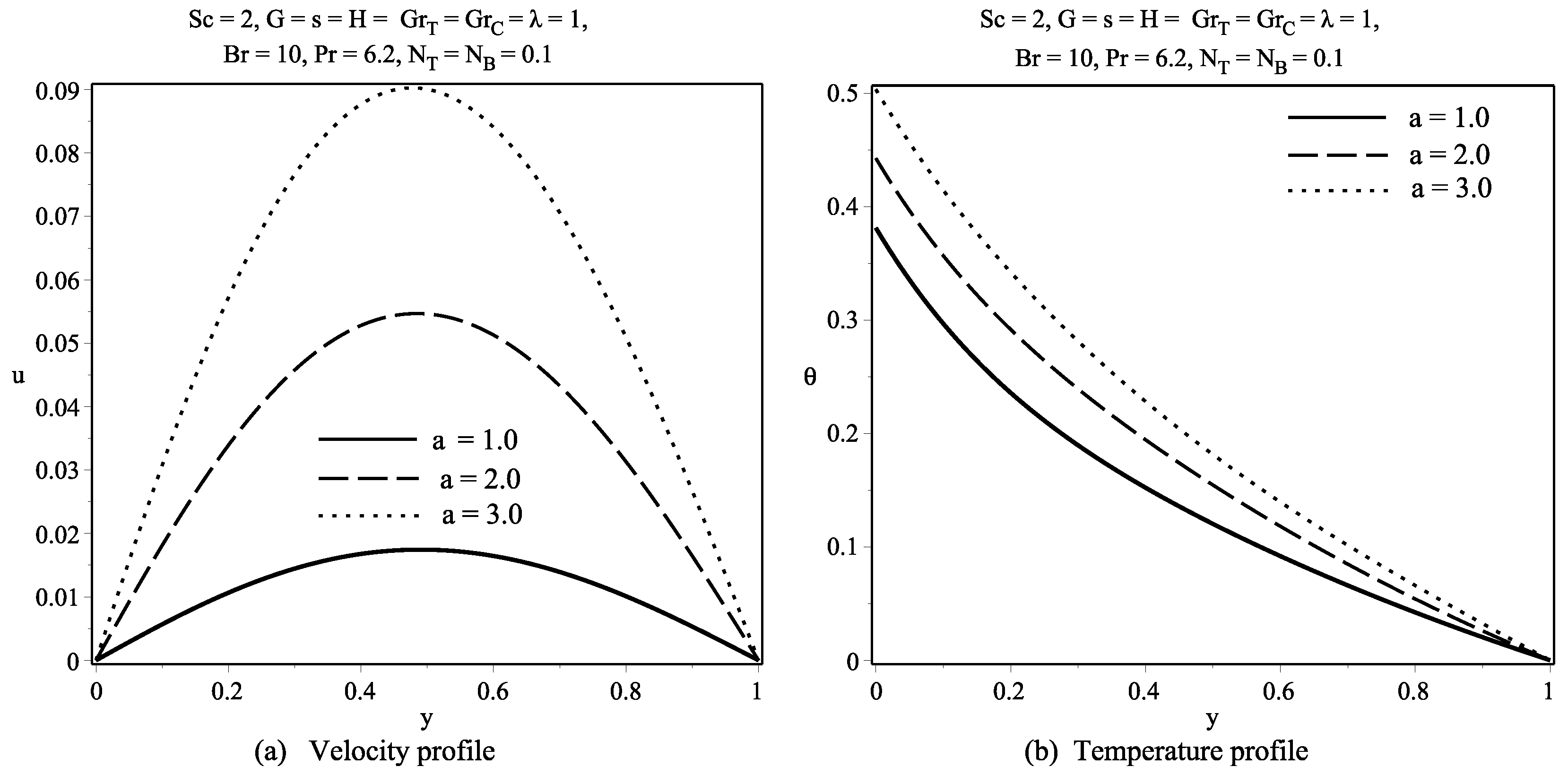
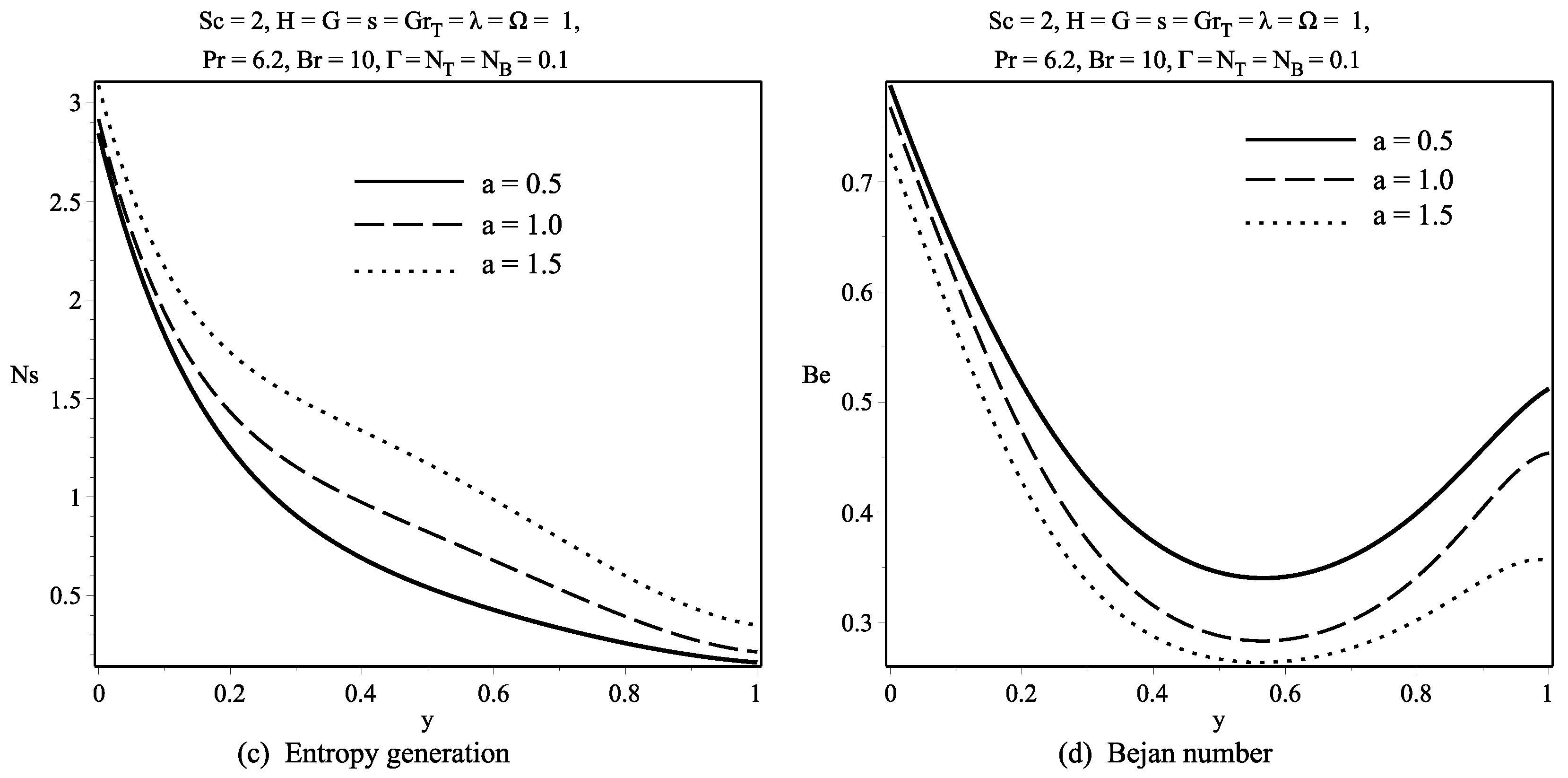
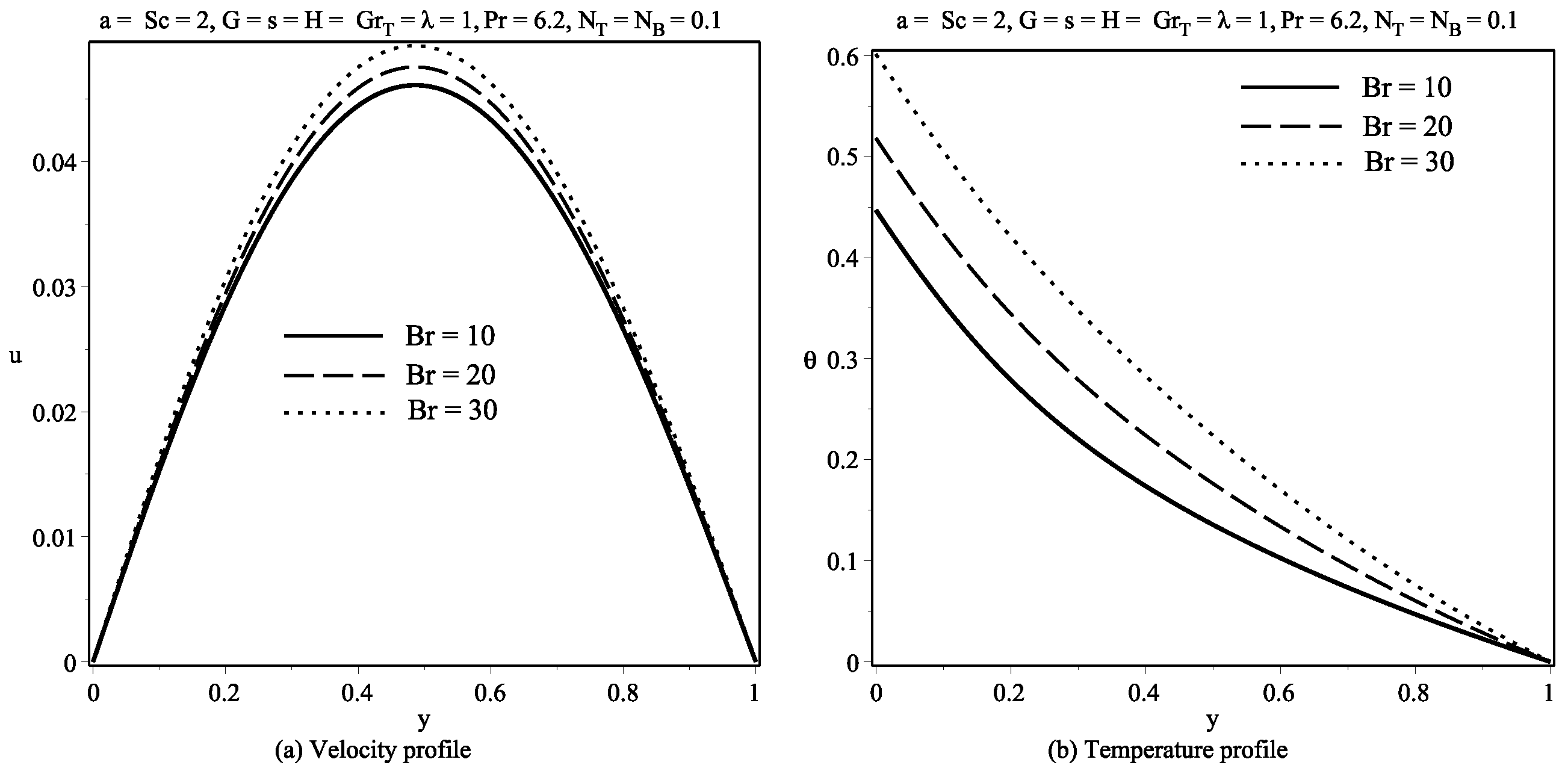
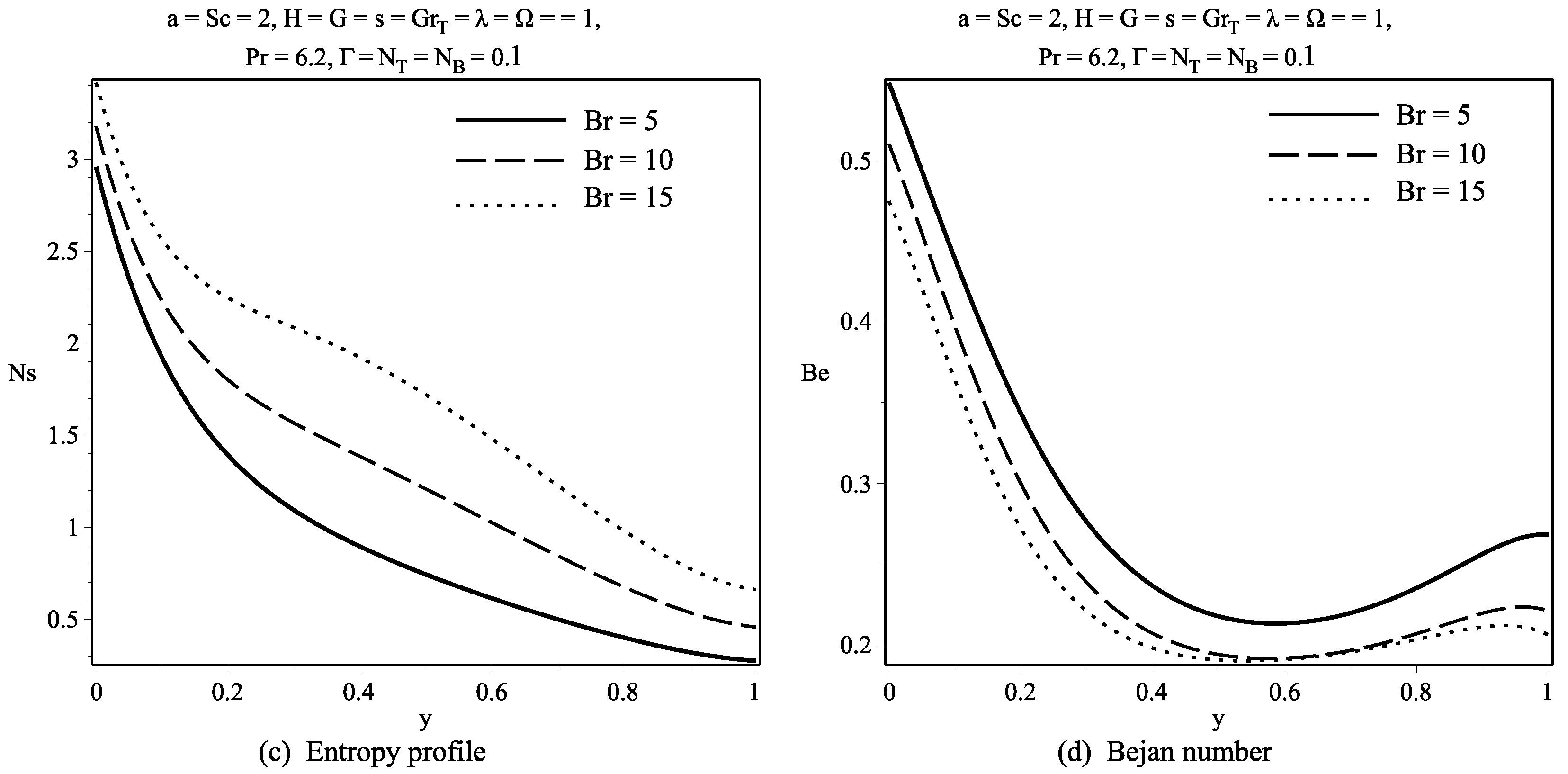
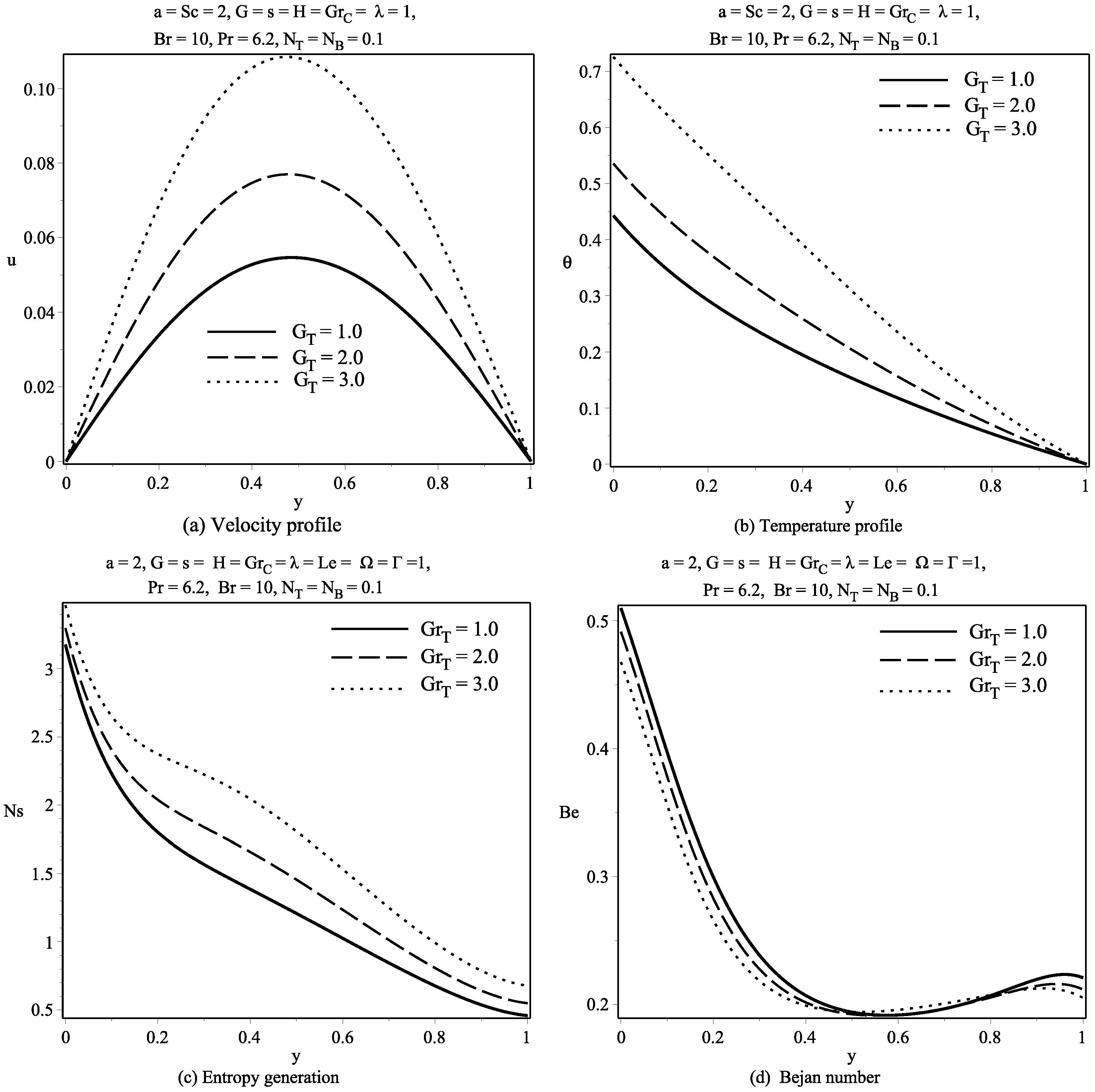
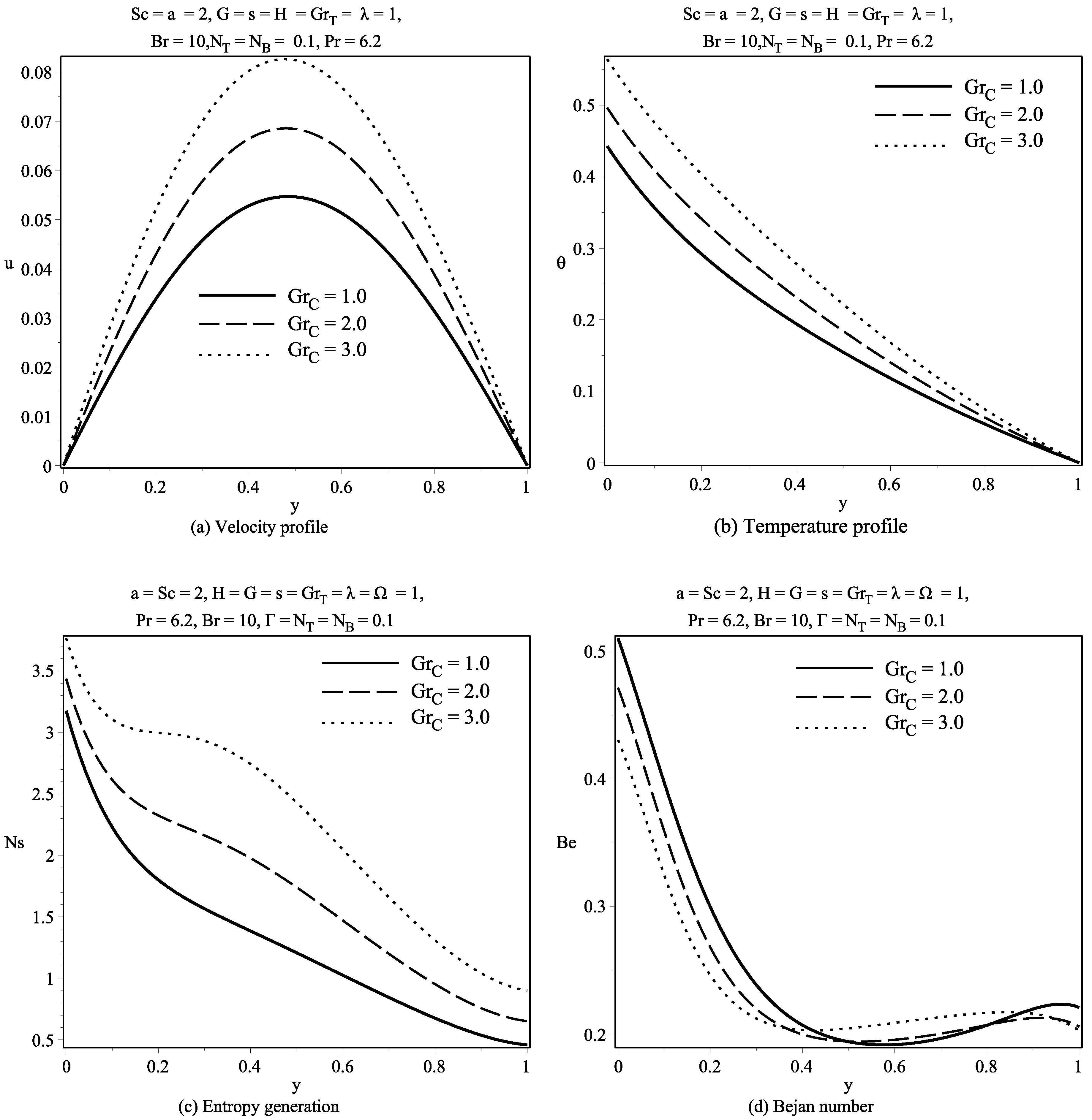
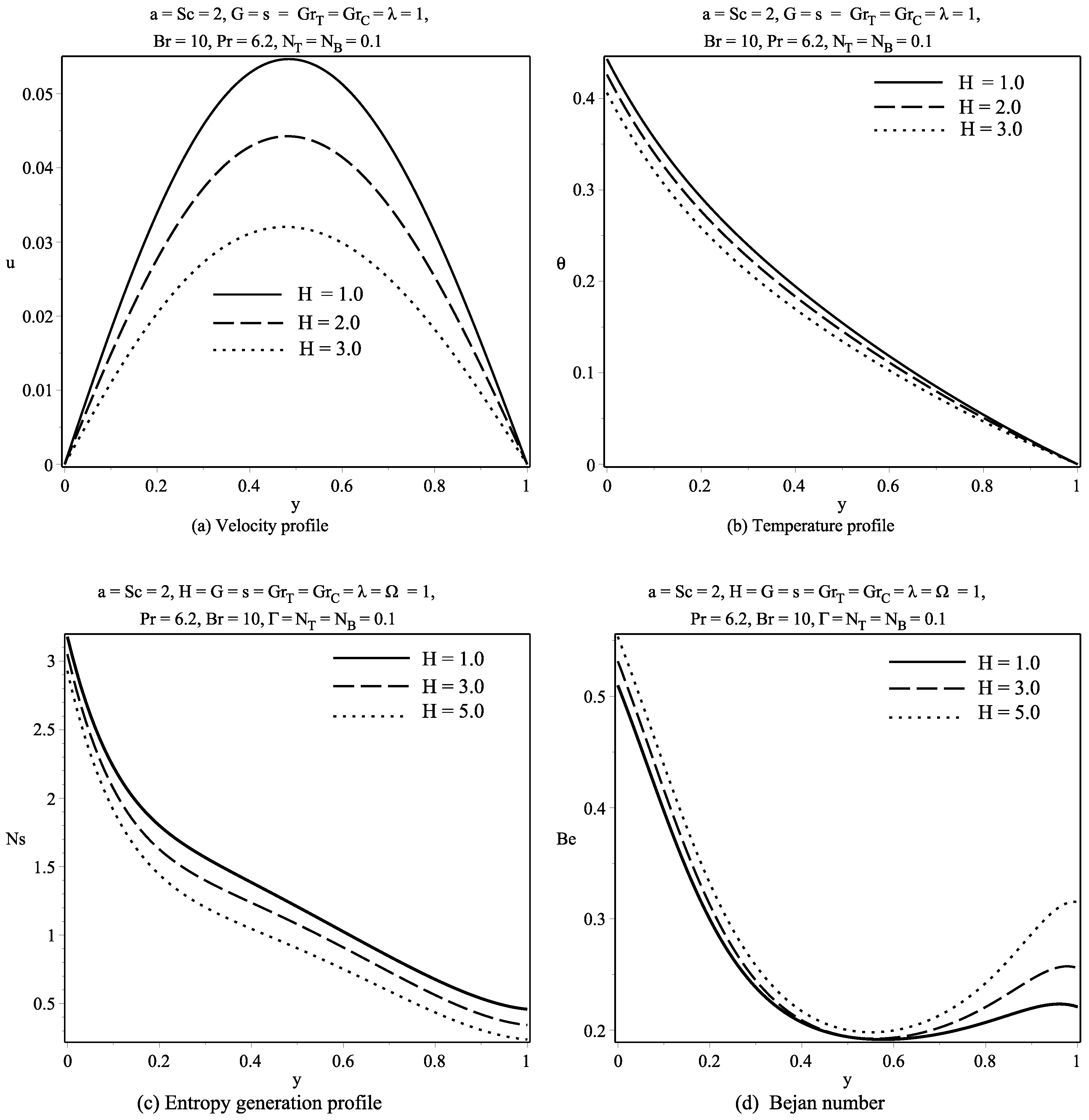
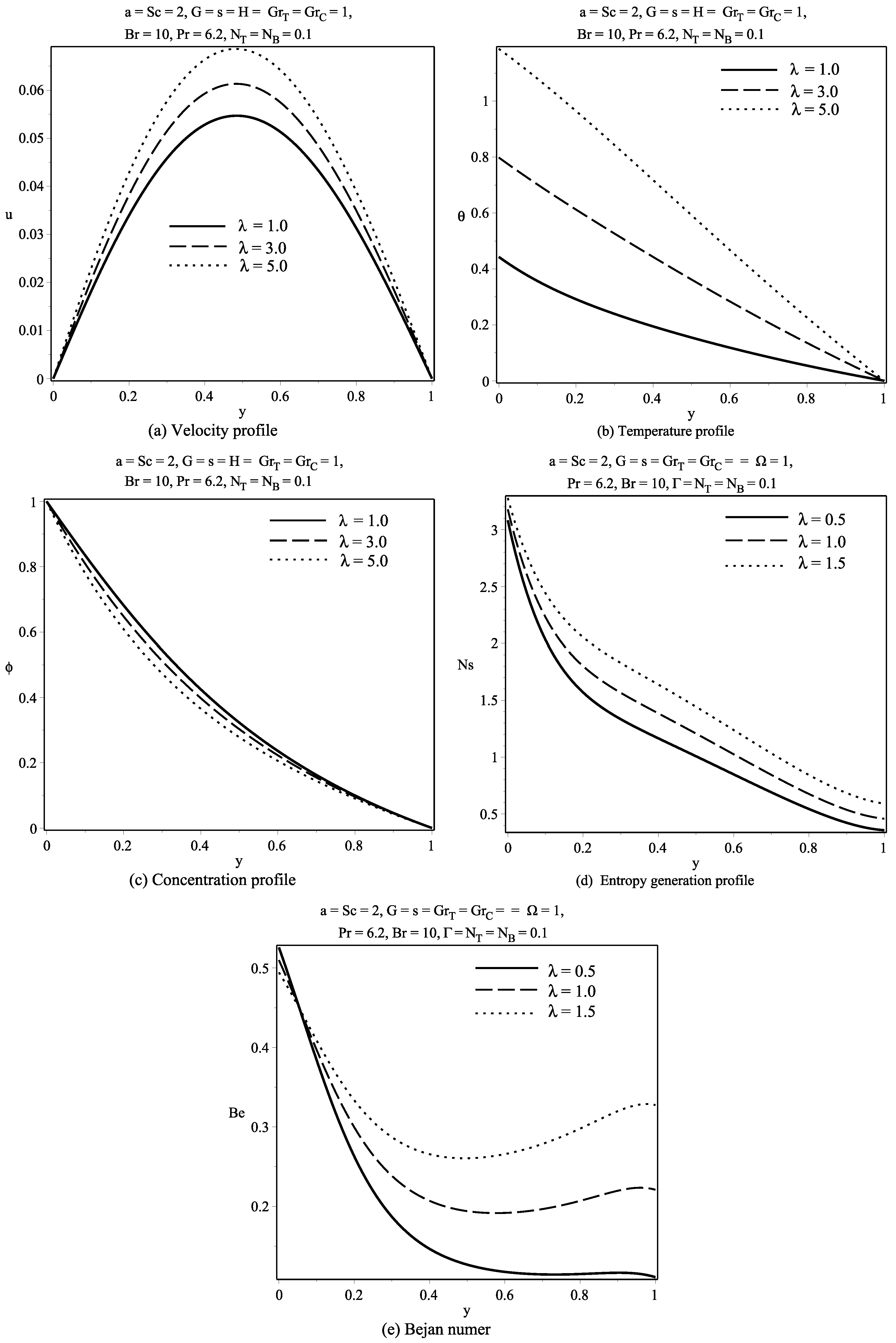
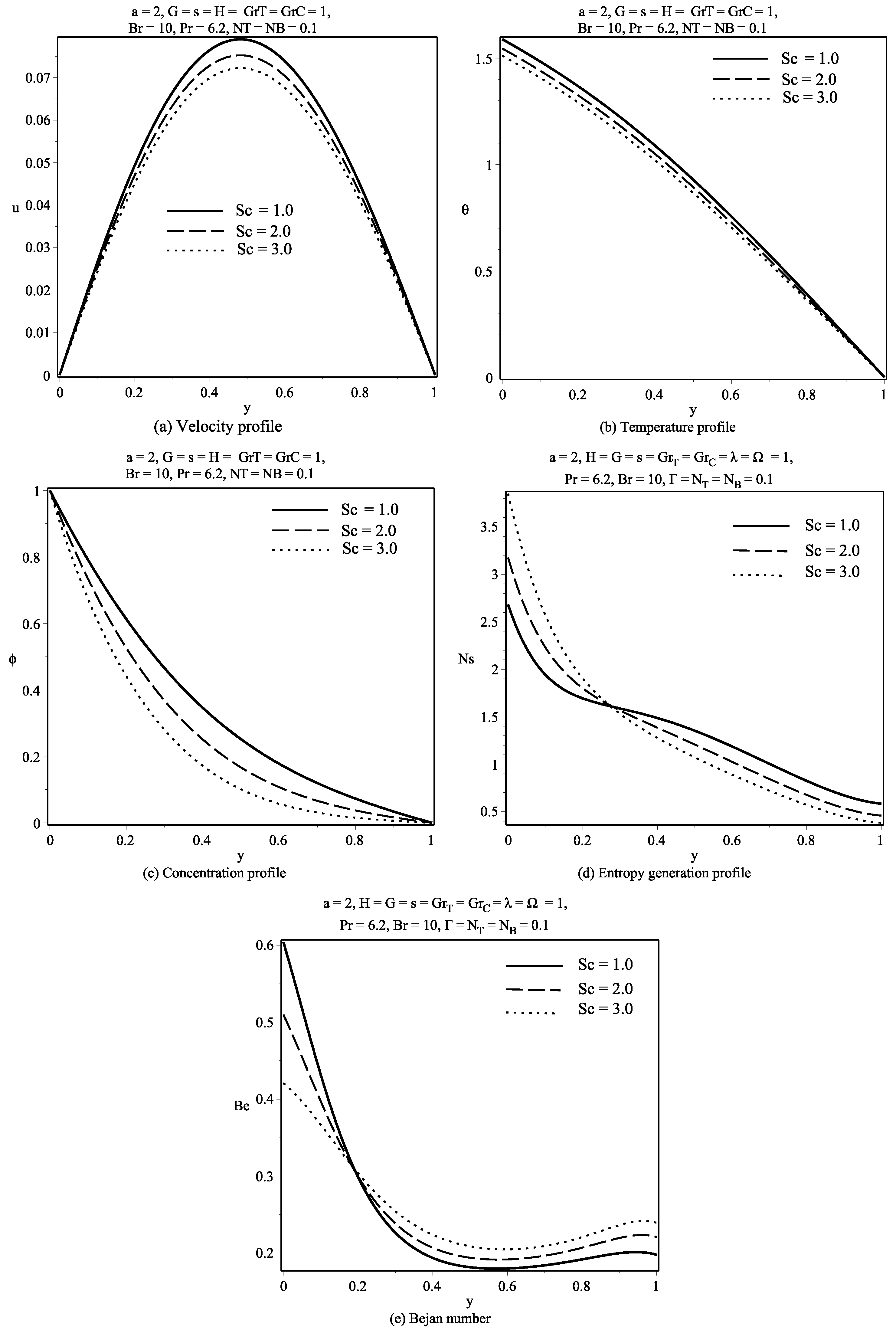
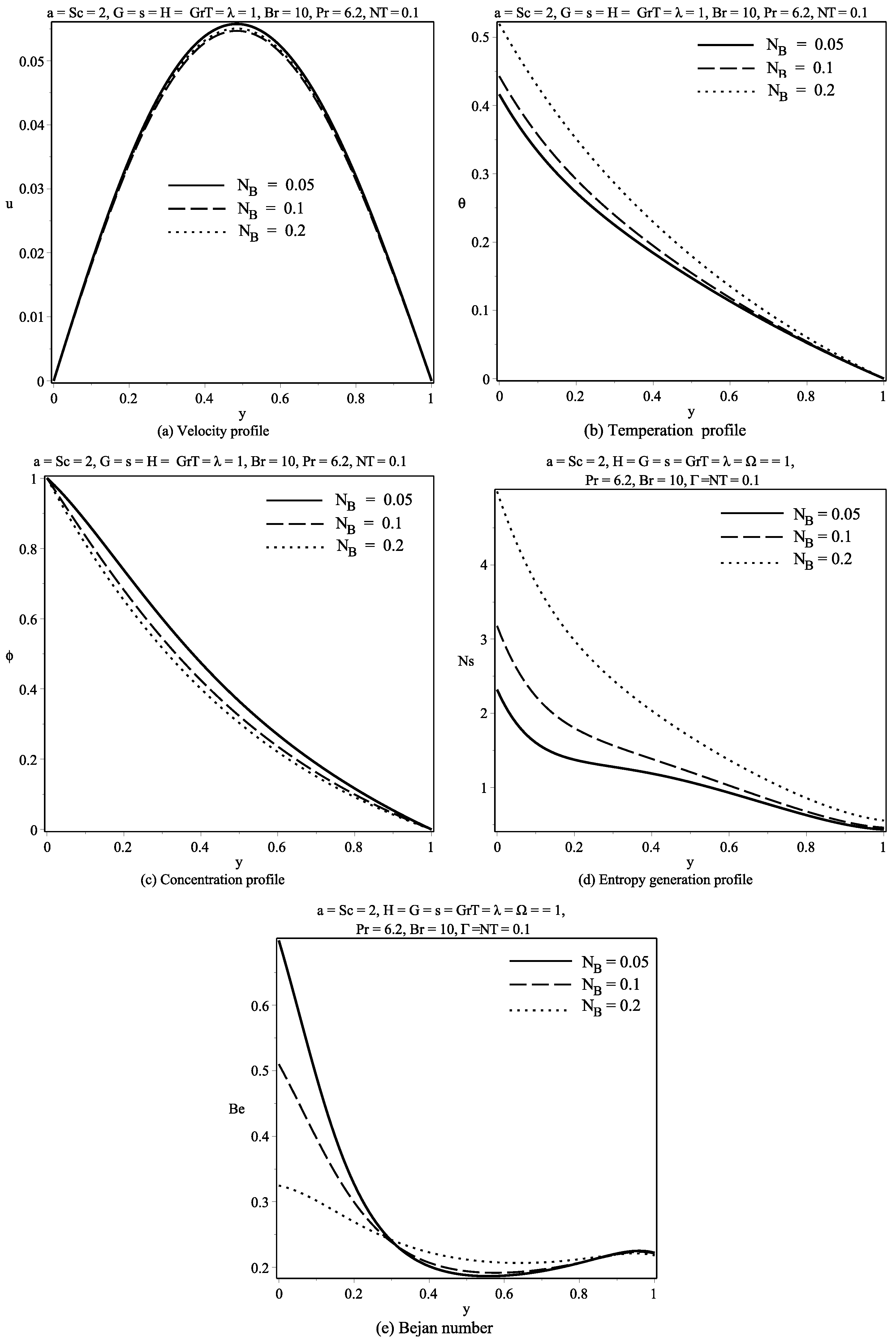
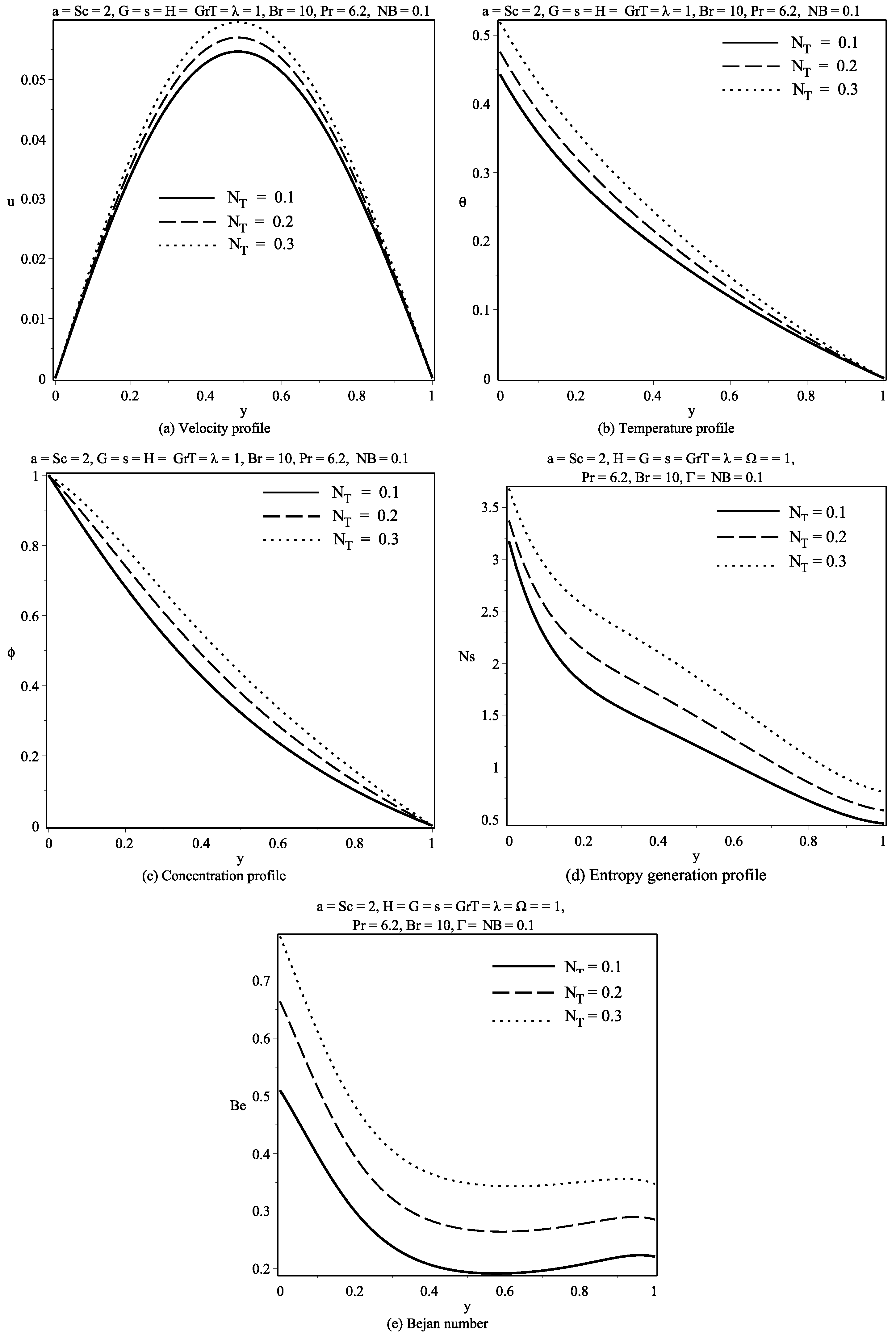
6. Discussion of Results
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Choi, S. Enhancing Thermal Conductivity of Fluids With Nanoparticles in Developments and Applications of Non-Newtonian Flows. ASME 1995, 66, 99–105. [Google Scholar]
- Sheikholeslami, M.; Ashorynejad, H.R.; Domairry, G.; Hashim, I. Flow and Heat Transfer of Cu-Water Nanofluid between a Stretching Sheet and a Porous Surface in a Rotating System. J. Appl. Math. 2012, 18. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji Bandpy, M.; Ellahi, R.; Hassan, M.; Soleimani, S. Effects of MHD on Cu-water nanofluid flow and heat transfer by means of CVFEM. J. Magn. Magn. Mater. 2014, 349, 188–200. [Google Scholar] [CrossRef]
- Das, K. Cu-water nanofluid flow and heat transfer over a shrinking sheet. J. Mech. Sci. Technol. 2014, 28, 5089–5094. [Google Scholar] [CrossRef]
- Heris, S.Z.; Etemad, S.G.; Esfahany, M.N. Convective Heat Transfer of a Cu/Water Nanofluid Flowing Through a Circular Tube. Exp. Heat Transf. 2009, 22, 217–227. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Heat transfer of Cu-water nanofluid flow between parallel plates. Powder Technol. 2013, 235, 873–879. [Google Scholar] [CrossRef]
- Domairry, G.; Hatami, M. Squeezing Cu-water nanofluid flow analysis between parallel plates by DTM-Pad Method. J. Mol. Liq. 2014, 193, 37–44. [Google Scholar] [CrossRef]
- Das, K.; Duari, P.R.; Kumar, P.K. Solar Radiation Effects on Cu-Water Nanofluid Flow over a Stretching Sheet with Surface Slip and Temperature Jump. Arab. J. Sci. Eng. 2014, 39, 9015–9023. [Google Scholar] [CrossRef]
- Hayat, T.; Rashid, M.; Imtiaz, M.; Alsaedi, A. Magnetohydrodynamic (MHD) flow of Cu-water nanofluid due to a rotating disk with partial slip. AIP Adv. 2015. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S. Intestinal Flow of a Couple Stress Nanofluid in Arteries. IEEE Trans. NanoBiosci. 2013, 12, 332–339. [Google Scholar] [CrossRef] [PubMed]
- Rehman, A.; Nadeem, S.; Malik, M.Y. Stagnation flow of couple stress nanofluid over an exponentially stretching sheet through a porous medium. J. Power Technol. 2013, 93, 122–132. [Google Scholar]
- Awais, M.; Saleem, S.; Hayat, T.; Irum, S. Hydromagnetic couple-stress nanofluid flow over a moving convective wall: OHAM analysis. Acta Astronaut. 2016, 129, 271–276. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Alsaedi, A.; Alhuthali, M.S. Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. J. Magn. Magn. Mater. 2015, 385, 222–229. [Google Scholar] [CrossRef]
- Hayat, T.; Sajjad, R.; Alsaedi, A.; Muhammad, T.; Ellahi, R. On squeezed flow of couple stress nanofluid between two parallel plates. Res. Phys. 2017, 7, 553–561. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite size devices and finite time processes. J. Appl. Phys. 1996, 79. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Ibáñez, G.; López, A.; Pantoja, J.; Moreira, J. Entropy generation analysis of a nanofluid flow in MHD porous microchannel with hydrodynamic slip and thermal radiation. Int. J. Heat Mass Transf. 2016, 100, 89–97. [Google Scholar] [CrossRef]
- Hussain, S.; Mehmood, K.; Sagheer, M. MHD mixed convection and entropy generation of water–alumina nanofluid flow in a double lid driven cavity with discrete heating. J. Magn. Magn. Mater. 2016, 419, 140–155. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Hakan, F.; Chamkha, A.J. MHD mixed convection and entropy generation of nanofluid filled lid driven cavity under the influence of inclined magnetic fields imposed to its upper and lower diagonal triangular domains. J. Magn. Magn. Mater. 2016, 406, 266–281. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Simulation of heat transfer and entropy generation of MHD natural convection of non-Newtonian nanofluid in an enclosure. Int. J. Heat Mass Transf. 2016, 92, 1066–1089. [Google Scholar] [CrossRef]
- Fersadou, I.; Kahalerras, H.; El Ganaoui, M. MHD mixed convection and entropy generation of a nanofluid in a vertical porous channel. Compt. Fld. 2015, 121, 164–179. [Google Scholar] [CrossRef]
- Abolbashari, A.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nanofluid. Powder Technol. 2014, 267, 256–267. [Google Scholar] [CrossRef]
- Cho, C.-C. Influence of magnetic field on natural convection and entropy generation in Cu–waternanofluid-filled cavity with wavy surfaces. Int. J. Heat Mass Transf. 2016, 101, 637–647. [Google Scholar] [CrossRef]
- Chen, C.; Chen, B.; Liu, C. Entropy generation in mixed convection magnetohydrodynamic nanofluid flow in vertical channel. Int. J. Heat Mass Transf. 2015, 91, 1026–1033. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Nanofluid hydrothermal behavior in existence of Lorentz forces considering Joule heating effect. J. Mol. Liq. 2016, 224, 526–537. [Google Scholar] [CrossRef]
- Mehrez, Z.; El Cafsi, A.; Belghith, A.; Patrick, L. MHD effects on heat transfer and entropy generation of nanofluid flow in an open cavity. J. Magn. Magn. Mater. 2015, 374, 214–224. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Freidooni, N. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Hajialigol, N.; Fattahi, A.; Ahmadi, M.H.; Qomi, M.E.; Kakoli, E. MHD mixed convection and entropy generation in a 3-D microchannel using Al2O3–water, nanofluid. J. Taiwan Inst. Chem. Eng. 2015, 46, 30–42. [Google Scholar] [CrossRef]
- Mahmoudi, A.H.; Pop, I.; Shahi, M.; Talebi, F. MHD natural convection and entropy generation in a trapezoidal enclosure using Cu–water nanofluid. Comput. Fluds 2013, 72, 46–62. [Google Scholar] [CrossRef]
- Uddin, M.J.; Anwar Bég, O.; Amin, N.S. Hydromagnetic transport phenomena from a stretching or shrinking nonlinear nanomaterial sheet with Navier slip and convective heating: A model for bio-nano-materials processing. J. Magn. Magn. Mater. 2014, 368, 252–261. [Google Scholar] [CrossRef]
- Khalili, S.; Tamim, H.; Khalili, A.; Rashidi, M.M. Unsteady convective heat and mass transfer in pseudoplastic nanofluid over a stretching wall. Adv. Powder Technol. 2015, 26, 1319–1326. [Google Scholar] [CrossRef]
- Mabood, F.; Shateyi, S.; Momoniat, E.; Freidoonimehr, N. MHD stagnation point flow heat and mass transfer of nanofluids in porous medium with radiation, viscous dissipation and chemical reaction. Adv. Powder Technol. 2016, 27, 724–749. [Google Scholar] [CrossRef]
- Khan, S.T.; Al-Khedhairy, A.A. ZnO and TiO2 nanoparticles as novel antimicrobial agents for oral hygiene: A review. J. Nanopart. Res. 2015, 17, 276. [Google Scholar] [CrossRef]
- Kherbeet, A.S.; Mohammed, H.A.; Salman, B.H.; Ahmed, H.E.; Alawi, O.A.; Rashidi, M.M. Experimental Study of Nanofluid Flow and Heat Transfer over Microscale Backward and Forward Facing Steps. Exp. Therm. Fluid Sci. 2015. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method; CRC Press: Boca Raton, FL, USA; Chapman and Hall: London, UK, 2003. [Google Scholar]
- Liao, S.J. Homotopy Analysis Method in Nonlinear Differential Equations; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
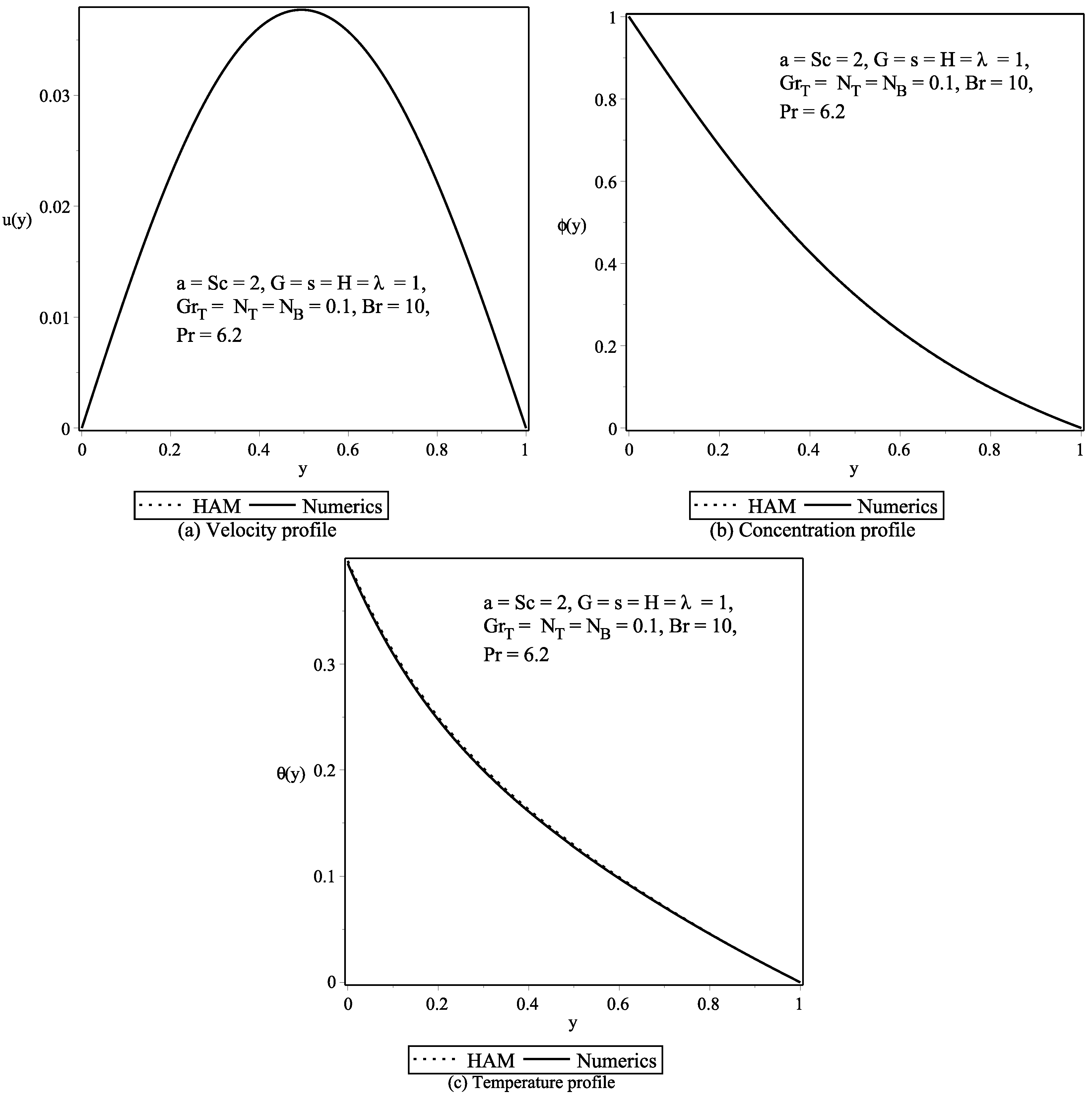
| y | u HAM | u RK4 | Abs. Error | HAM | RK4 | Abs. Error |
|---|---|---|---|---|---|---|
| 0 | 0.00000 | 0.00000 | 0.000 | 0.39475 | 0.39473 | 1.6129 × |
| 0.1 | 0.01212 | 0.01212 | 3.952 × | 0.30974 | 0.30972 | 2.0124 × |
| 0.2 | 0.02282 | 0.02282 | 7.308 × | 0.24748 | 0.24746 | 2.1147 × |
| 0.3 | 0.03104 | 0.03104 | 9.892 × | 0.19967 | 0.19965 | 2.8675 × |
| 0.4 | 0.03612 | 0.03612 | 1.155 × | 0.16087 | 0.16082 | 4.7640 × |
| 0.5 | 0.03772 | 0.03772 | 1.236 × | 0.12763 | 0.12758 | 3.2397 × |
| 0.6 | 0.03575 | 0.03575 | 1.246 × | 0.09787 | 0.09795 | 7.9192 × |
| 0.7 | 0.03042 | 0.03042 | 1.222 × | 0.07056 | 0.07083 | 2.7514 × |
| 0.8 | 0.02218 | 0.02218 | 1.174 × | 0.04524 | 0.04565 | 4.1654 × |
| 0.9 | 0.01171 | 0.01171 | 1.092 × | 0.02180 | 0.02212 | 3.2119 × |
| 1.0 | 0.00000 | 0.00000 | 9.20 × | 0.00000 | 0.00000 | 2.0000 × |
| y | HAM | RK4 | Abs. Error |
|---|---|---|---|
| 0 | 1.0000000 | 1.0000000 | 0.0000000 |
| 0.1 | 0.8387730 | 0. 8387837 | 1.07275 × |
| 0.2 | 0.6862309 | 0.6863211 | 9.01931 × |
| 0.3 | 0.5483278 | 0.5484970 | 1.6923 × |
| 0.4 | 0.4273287 | 0.4275787 | 2.5002 × |
| 0.5 | 0.3231850 | 0.3235501 | 3.65135 × |
| 0.6 | 0.2346430 | 0.2351325 | 4.84783 × |
| 0.7 | 0.1599510 | 0.16044790 | 5.280647 × |
| 0.8 | 0.0972060 | 0.0976057 | 3.99661 × |
| 0.9 | 0.0444898 | 0.0446433 | 1.534344 × |
| 1.0 | 0.0000000 | 0.000000 | 0.00000000 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adesanya, S.O.; Ogunseye, H.A.; Falade, J.A.; Lebelo, R.S. Thermodynamic Analysis for Buoyancy-Induced Couple Stress Nanofluid Flow with Constant Heat Flux. Entropy 2017, 19, 580. https://doi.org/10.3390/e19110580
Adesanya SO, Ogunseye HA, Falade JA, Lebelo RS. Thermodynamic Analysis for Buoyancy-Induced Couple Stress Nanofluid Flow with Constant Heat Flux. Entropy. 2017; 19(11):580. https://doi.org/10.3390/e19110580
Chicago/Turabian StyleAdesanya, Samuel O., Hammed A. Ogunseye, J. A. Falade, and R.S. Lebelo. 2017. "Thermodynamic Analysis for Buoyancy-Induced Couple Stress Nanofluid Flow with Constant Heat Flux" Entropy 19, no. 11: 580. https://doi.org/10.3390/e19110580
APA StyleAdesanya, S. O., Ogunseye, H. A., Falade, J. A., & Lebelo, R. S. (2017). Thermodynamic Analysis for Buoyancy-Induced Couple Stress Nanofluid Flow with Constant Heat Flux. Entropy, 19(11), 580. https://doi.org/10.3390/e19110580






