Abstract
In the present work, entropy generation in the flow and heat transfer of couple stress fluid through an infinite inclined channel embedded in a saturated porous medium is presented. Due to the channel geometry, the asymmetrical slip conditions are imposed on the channel walls. The upper wall of the channel is subjected to a constant heat flux while the lower wall is insulated. The equations governing the fluid flow are formulated, non-dimensionalized and solved by using the Adomian decomposition method. The Adomian series solutions for the velocity and temperature fields are then used to compute the entropy generation rate and inherent heat irreversibility in the flow domain. The effects of various fluid parameters are presented graphically and discussed extensively.
1. Introduction
Flow and heat transfer with constant heat flux through a porous medium has been a major challenge in several geological, medical, thermal problems and engineering applications. For instance, in the adsorption/water treatment processes, ground water flows, breathing filters, oil recovery, constructions of roads and buildings, as dryers and many more metallurgical and geothermal utilizations. Given the broad applications, several works have been reported in this active area of research. For example, Cimpean et al. [1] reported the convective fluid flow down an inclined plane subjected to constant heat flux. Hajipour and Dehkordi [2] examined the nanofluid channel flow that is partially filled with porous material. Mahmoudi [3] analyzed the forced convective flow subjected to constant heat flux and flowing through a nanochannel that is immersed in a porous medium with velocity slip and temperature jump conditions. In the work of Mahdavi et al. [4], the entropy generation in pipe flow with partial porous materials exposed to constant heat flux was investigated. Cimpean and Pop [5] discussed the steady flow of nanofluid in an inclined channel with a porous material and exposed to constant heat flux. Torabi et al. [6] presented a robust analysis of bifurcation problem associated with entropy minimization in a two-phase channel flow with partial porous medium and constant heat flux. For more results of flows in porous media, kindly see the following books [7,8,9,10,11].
From a practical applications point of view, fluid viscosity is highly sensitive to changes in temperature, especially when subjected to uniform heat flux. As reported by Sahin [12], by increasing the temperature of engine oil from 20 °C to 80 °C, its viscosity decreases by 24 times; water viscosity drops by 2.7 times while that of air reduces by 1.4 times. Therefore, for optimal performance in a thermo-fluid setup, there is need to introduce size-dependent polymer additives of mechanical significance that could sustain the rheological properties of these fluids needed at extremely high temperature. The classical Navier–Stokes theory does not support the inclusion of the microstructures or additives. However, following Stokes [13] couple stress theory, he elaborated the presence of body couples, couple stresses and non-symmetric stress tensor in a moving base fluid. Common examples of couple stress fluid are blood, lubricants, pharmaceutical mixtures, paints, synovial fluids and many more applications that contain tiny microstructures. By using the couple stress model, Srinivasacharya and Kaladhar [14] explained the hydromagnetic couple stress fluid flow through parallel disk taking the Hall and ion-slip effects into consideration. Ahmed et al. [15] applied the couple stress model to explain the magnetohydrodynamics (MHD) oscillatory flow in a rotating inclined channel. Akhtar and Shah [16] obtained an exact solution for unsteady flow of couple stress fluid in a channel. Recently, Aksoy [17] examined the couple stress fluid through a channel subjected to constant heat flux. More related studies on the theory and wide range of applications on the couple stress fluid model are documented in studies by Srinivasacharya and his collaborators in [15,16,17,18,19,20,21,22], Bég and his cohorts [23,24], and Hayat et al. [25,26] and references therein.
From an energy management perspective, it is well known that the performance of any thermo-fluid engineering set-up depends on the design and the operating temperature of the working fluid since heat transfer is an irreversible process. Therefore, for optimal performance, it is imperative to monitor the entropy generation in the flow channel. Recent findings have shown that the second law analysis approach is a reliable and efficient method for minimising entropy generation in a moving fluid. For instance, Ting et al. [27] utilized this method to describe the inherent irreversibility in Al2O3 nanofluid flow through heated leaky micro-channel. Anand [28] discussed the entropy production nanofluids through a heated tube. In [29], Chen et al. monitored the entropy generation rate in a buoyancy-induced nano fluid flow with frictional effects. López et al. [30] studied the entropy generation in radiative MHD nanofluid in a leaky vertical microchannel. In [31], Havzali et al. investigated the inherent irreversibility in a Newtonian gravity-driven flow through an inclined channel. Other related works on the second law analysis approach for minimizing entropy generation includes [32,33,34,35,36]. Interestingly, there is a thin line between the second law analysis approach and that described by the material cost flow accounting perspective [37,38,39] regarding waste management and achieving a cleaner production. Motivated by Hayat et al. [31,40,41,42,43,44,45,46], the present study addresses the second law analysis for a shear-induced asymmetrical slip couple stress fluid flow through saturated porous medium subjected to constant heat flux studied. To the best of our author’s knowledge, the thermal analysis reported here has not been investigated despite the enormity of the work done in this area of study. In the following section, the problem will be formulated and nondimensionalized. In Section 3, solutions of the dimensionless boundary-valued-problems will be obtained by using the rapidly convergent computational Adomian decomposition method [47,48,49] implemented in Mathematica 10.0. In Section 4, results are presented and discussed extensively, and the contributions to knowledge are presented in Section 5.
2. Model Formulation
Consider the steady flow of couple stress fluid through a parallel inclined channel of distance 2h apart as shown in Figure 1 below. The channel is further assumed to be filled up with porous materials of constant porous permeability.
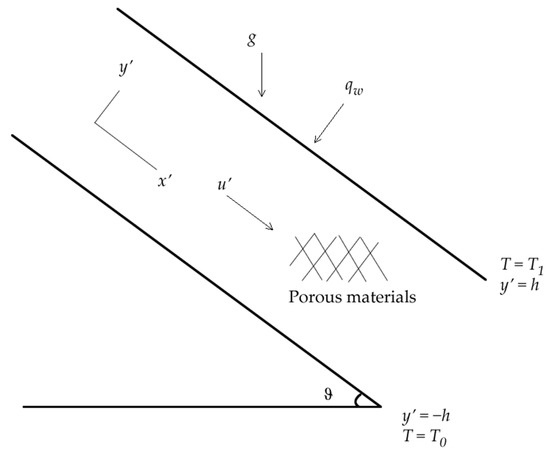
Figure 1.
Flow geometry.
The upper wall of the channel is subjected to constant heat flux while the lower wall is insulated. Therefore, the equation governing the gravity-driven steady fully developed couple stress fluid flow can be written as [17]:
where , and the additional term in (1) is due to the inclusion of porous materials that tend to restrict the flow. The slip boundary conditions along the channel walls are given by Devakar et al. [46] as:
For the thermal analysis, the lower wall of the channel is taken to be insulated while the upper plate is subjected to constant heat flux . Following Aksoy [17], the energy conservation equation for the chemically-inert porous medium can then be written as:
Together with the constant heat flux condition and the insulated wall condition:
respectively. In the fully developed flow situation, the momentum equation is independent of x′ as a result, constant. Thus, there is need to evaluate the mass flow rate by integrating (3) along the y-direction in the form:
By using (4), Equation (5) becomes
With (6) in (3), we get an energy equation for the couple stress fluid flow as follows:
together with the non-uniform boundary conditions
Introducing the following dimensionless variables and parameters
we get the following dimensionless equations:
subject to shear-induced and non-uniform wall boundary conditions
3. Adomian Method of Solution
To obtain the solution of the dimensionless Equations (10)–(12), we first write the differential equations in the integral forms as follows:
Observe that, to arrive at the integral equations in (13) and (14) above, the following boundary conditions have been used; and we now form an infinite series of the form:
Evidently, by substituting (15) in (13) and (14), we get the following recurrence relations:
Obtaining a few terms in (16), the partial sum
provides the approximate solution and is used to obtain expressions for the undetermined constants regarding the other boundary conditions remaining in (5). The expressions for the constants above are obtained by using the following boundary conditions:
while the condition was used to derive the unknown constant in (14). The convergent series solution is then used to determine the solution of (14) together with the thermal boundary conditions. Next, we code the scheme in a computer algebra package known as Mathematica 10.0 for easy iteration of the successive approximant (16) and (17), and the graphical results are presented as Figure 2, Figure 3, Figure 4 and Figure 5.
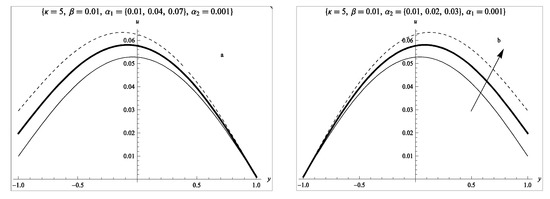
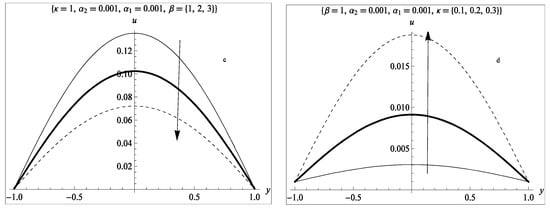
Figure 2.
Velocity profile: (a) effect of lower slip parameter; (b) effect of upper slip parameter; (c) effect of porous permeability parameter; (d) effect of the couple stress inverse parameter.
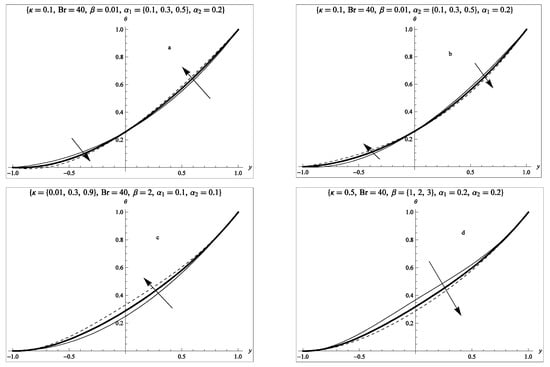
Figure 3.
Temperature profile (a) effect of lower slip parameter; (b) effect of upper slip parameter; (c) effect of couple stress inverse parameter; (d) effect of porous permeability parameter.
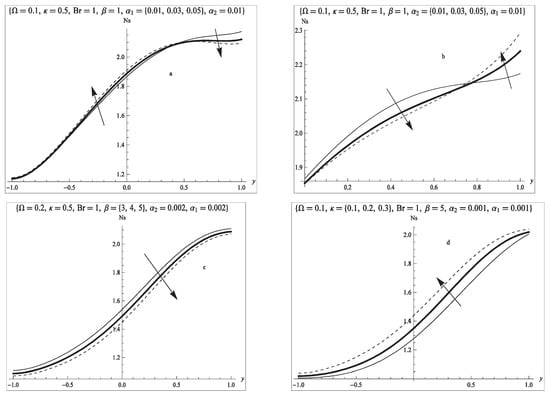
Figure 4.
Entropy generation (a) effect of lower slip parameter; (b) effect of upper slip parameter; (c) effect of porous permeability parameter; (d) effect of couple stress inverse parameter.
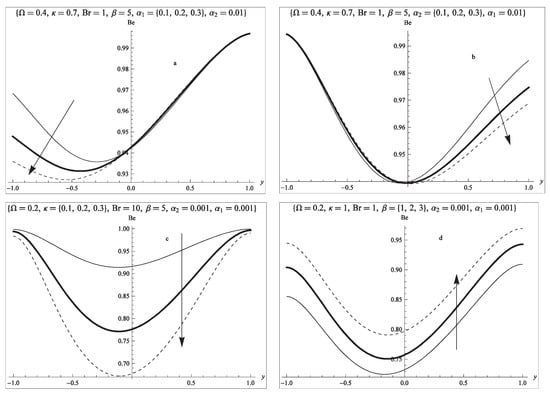
Figure 5.
Bejan number (a) effect of lower slip parameter; (b) effect of upper slip parameter; (c) effect of couple stress inverse parameter; (d) effect of porous permeability parameter.
The skin friction and the heat transfer rate are determined by
4. Entropy Generation Analysis
Due to the heat irreversibility in the flow channel, the expression for the entropy generation rate due to heat transfer and particles frictional interactions in the inclined channel can be written as:
In dimensionless form, we get
The first term of Equation (21) represents the heat irreversibility due to heat transfer while other terms described the thermal inefficiency are due to fluid friction irreversibility. In other words, let
Then, Bejan number is defined as the ratio of irreversibility due to heat transfer and the total entropy generated within the flow channel, i.e.,
Observe that Bejan number is bounded between zero and unity. In an exceptional case, when both heat transfer and frictional irreversibilities have equal contributions, Be attains 0.5.
5. Discussion
In this section, graphical results are plotted and discussed based on the fluid physics for dimensionless velocity, temperature distribution, entropy generation and heat irreversibility. Table 1 attests to the rapid convergence of the series solutions. In achieving this, the boundary conditions are used to evaluate the undetermined coefficient , and it is observed that convergence is reached with just a few terms of the series. Another significant result from the table is the convergence of the Nusselt number and Skin friction. Table 2 shows the comparison of the present results with previously obtained results in a particular case when , and the result shows a perfect agreement in the absence of the porous permeability parameter.

Table 1.
Rapid convergence of the series solution (17) at .

Table 2.
Validation of with [46] when .
Figure 2a shows the effect of variation in the lower wall slip parameter. It is observed that an increase in the slip parameter enhances the fluid flow at the lower wall of the channel while an increase in the upper wall slip is seen to elevate the flow velocity at the upper wall of the channel as presented in Figure 2b. In Figure 2c, an increase in the porous permeability parameter is observed to reduce the fluid flow velocity; this is physically true since an increase in the porous permeability parameter implies a reduction in the porous permeability of the medium. Figure 2d depicts the influence of the couple stress parameter on the fluid flow: it is observed that an increase in the parameter represents a decrease in the fluid viscosity, hence, as the fluid viscosity increases, the fluid flow velocity decreases.
Figure 3 shows the effect of variation of parameters on the temperature distribution in the flow channel. In Figure 3a, the effect of the rise in the lower slip parameter is presented. As observed from the figure, an increase in the lower slip is seen to decrease the fluid temperature in the region closer to the insulated plate, while it enhances the temperature of the fluid particles closer to the upper wall exposed to constant heat flux. The reverse phenomenon is experienced in Figure 3b as the parameter of higher slip increases. One observes an asymmetrical thermal structure in the two cases. The effect of the couple stress inverse parameter is shown in Figure 3c. From the plot, it is noticed that an increase in the couple stress inverse parameter enhances the fluid temperature due to a reduction in the dynamic viscosity of the fluid. Finally, as the porous permeability parameter increases, a decrease in the fluid temperature is observed. This is due to an increase in the permeability of the porous bed.
Figure 4 described the influence of fluid parameters on the entropy generation in the flow channel. As observed in Figure 2a and Figure 3a, the lower slip parameter at the insulated wall enhances the velocity profile, and this increase resulted in a decreased fluid temperature in Figure 3a. The net effect of the increased lower slip parameter on flow and heat transfer is seen on the entropy generation rate that is presented as Figure 4a. As observed, entropy generation is slightly higher in the entire flow region except at the upper region with constant heat flux where it falls. The reverse phenomenon is seen as the upper slip parameter is varied.
Figure 5a,b represent the effect of the slip parameter on the heat irreversibility ratio. In Figure 5a, as the lower slip parameter increases, there is a rise in heat generated by fluid friction, hence fluid friction irreversibility dominates over heat transfer irreversibility as the lower slip parameter increases. A similar explanation holds for the results presented in Figure 5b. In Figure 5c, we observed that, as the couple stress inverse increases, the fluid viscosity decreases, and both fluid friction and heat transfer contribute to the heat irreversibility. However, as the fluid viscosity increases, fluid friction decreases and heat transfer irreversibility dominates over irreversibility due to fluid friction. Finally, as the porous permeability parameter increases, the fluid velocity and frictional interaction decreases; therefore, heat transfer irreversibility dominates over fictional irreversibility, as seen in Figure 5d.
6. Conclusions
Entropy generation in the slip flow and heat transfer in the couple stress fluid through a parallel plate subjected to constant heat flux and saturated with porous materials are investigated. A rapidly convergent Adomian decomposition method is applied to obtain the approximate solution of the coupled problem. The influence of lower and upper slip parameters, couple stress inverse parameter and porous permeability parameter on the velocity, temperature, entropy generation production and the Bejan number are examined and discussed physically. The results show the influence of the couple stresses and porous permeability in minimizing entropy within the flow channel. It is important to note that the present analysis is limited to micro-scale thermal analysis, and subsequent analysis will incorporate a macroscale thermal description as presented in [50].
Acknowledgments
Samuel Olumide Adesanya wants to thank the management of Redeemer’s University for the approval of research visit to the University of Limpopo, South Africa. Michael Bamidele Fakoya wishes to express his gratitude to the Africa Centre for Sustainability Accounting and Management (ACSAM), School of Accountancy, University of Limpopo for making funds available to cover the publication costs to publish our paper in open access.
Author Contributions
Both authors have contributed substantially to the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| dimensionless lower and upper slip coefficients | |
| dimensional lower and upper slip parameters | |
| couple stress inverse parameter | |
| dimensionless fluid temperature | |
| fluid density | |
| dynamic viscosity | |
| porous permeability parameter | |
| couple stress coefficient | |
| dimensional and dimensionless fluid velocity | |
| modified Brinkman number | |
| maximum velocity | |
| Cartesian coordinates | |
| dimensionless pressure gradient | |
| characteristic velocity | |
| channel width | |
| fluid pressure | |
| specific heat capacity | |
| dimensional and referenced fluid temperatures | |
| constant heat flux | |
| porous permeability |
References
- Cimpean, D.; Pop, I.; Ingham, D.B.; Merkin, J.H. Fully Developed Mixed Convection Flow between Inclined Parallel Plates Filled with a Porous Medium. Transp. Porous Med. 2009, 77, 87–102. [Google Scholar] [CrossRef]
- Hajipour, M.; Dehkordi, A.M. Analysis of nanofluid heat transfer in parallel-plate vertical channels partially filled with porous medium. Int. J. Therm. Sci. 2012, 55, 103–113. [Google Scholar] [CrossRef]
- Mahmoudi, Y. Constant wall heat flux boundary condition in microchannels filled with a porous medium with internal heat generation under local thermal non-equilibrium condition. Int. J. Heat Mass Transf. 2015, 85, 524–542. [Google Scholar] [CrossRef]
- Mahdavi, M.; Saffar-Avval, M.; Tiari, S.; Mansoori, Z. Entropy generation and heat transfer numerical analysis in pipes partially filled with porous medium. Int. J. Heat Mass Transf. 2014, 79, 496–506. [Google Scholar] [CrossRef]
- Cimpean, D.S.; Pop, I. Fully developed mixed convection flow of a nanofluid through an inclined channel filled with a porous medium. Int. J. Heat Mass Transf. 2012, 55, 907–914. [Google Scholar] [CrossRef]
- Torabi, M.; Zhang, K.; Yang, G.; Wang, J.; Wu, P. Heat transfer and entropy generation analyses in a channel partially filled with porous media using local thermal nonequilibrium model. Energy 2015, 82, 922–938. [Google Scholar] [CrossRef]
- Neild, D.A.; Bejan, A. Convection in Porous Media, 4th ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Bagchi, A.; Kulacki, F.A. Natural Convection in Superposed Fluid-Porous Layers; Springer: New York, NY, USA, 2014. [Google Scholar]
- Pop, I.; Ingham, D.B. Convective Heat Transfer: Mathematical and Computational Modelling of Viscous Fluids and Porous Media; Pergamon Press: Oxford, UK, 2001. [Google Scholar]
- Vadasz, P. Emerging Topics in Heat and Mass Transfer in Porous Media; Springer: Berlin, Germany, 2008; Volume 22. [Google Scholar]
- Vafai, K. Porous Media: Applications in Biological Systems and Biotechnology; CRC Press: Tokyo, Japan, 2010. [Google Scholar]
- Sahin, A.Z. Entropy generation and pumping power in a turbulent fluid flow through a smooth pipe subjected to constant heat flux. Exergy Int. J. 2002, 2, 314–321. [Google Scholar] [CrossRef]
- Stokes, V.K. Couple stresses in fluid. Phys. Fluids 1966, 9, 1709–1715. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Kaladhar, K. Analytical solution for Hall and Ion-slip effects on mixed convection flow of couple stress fluid between parallel disks. Math. Comput. Model. 2013, 57, 2494–2509. [Google Scholar]
- Ahmed, S.; Bég, O.A.; Ghosh, S.K. A couple stress fluid modelling on free convection oscillatory hydromagnetic flow in an inclined rotating channel. Ain Shams Eng. J. 2014, 5, 1249–1265. [Google Scholar] [CrossRef]
- Akhtar, S.; Shah, N.A. Exact solutions for some unsteady flows of a couple stress fluid between parallel plates. Ain Shams Eng. J. 2016. [Google Scholar] [CrossRef]
- Aksoy, Y. Effects of couple stresses on the heat transfer and entropy generation rates for a flow between parallel plates with constant heat flux. Int. J. Therm. Sci. 2016, 107, 1–12. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; RamReddy, C. Soret and Dufour effects on mixed convection in a non-Darcy porous medium saturated with micropolar fluid. Nonlinear Anal. Model. Control 2011, 16, 100–115. [Google Scholar]
- Srinivasacharya, D.; Kaladhar, K. Mixed convection flow of couple stress fluid between parallel vertical plates with Hall and Ion-slip effects. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2447–2462. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Rao, G.M. Computational analysis of magnetic effects on pulsatile flow of couple stress fluid through a bifurcated artery. Comput. Methods Programs Biomed. 2016, 137, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Srinivasacharya, D.; Srinivasacharyulu, N.; Odelu, O. Flow and heat transfer of couple stress fluid in a porous channel with expanding and contracting walls. Int. Commun. Heat Mass Transf. 2009, 36, 180–185. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Srikanth, D. Effect of couple stresses on the pulsatile flow through a constricted annulus. C. R. Mec. 2008, 336, 820–827. [Google Scholar] [CrossRef]
- Bég, O.A.; Ghosh, S.K.; Ahmed, S.; Bég, T. Mathematical modelling of oscillatory magneto-convection of a couple-stress biofluid in an inclined rotating channel. J. Mech. Med. Biol. 2012, 12, 1250050. [Google Scholar] [CrossRef]
- Zueco, J.; Bég, O.A. Network numerical simulation applied to pulsatile non-Newtonian flow through a channel with couple stress and wall mass flux effects. Int. J. Appl. Math. Mech. 2009, 5, 1–16. [Google Scholar]
- Hayat, T.; Awais, M.; Safdar, A.; Hendi, A.A. Unsteady three-dimensional flow of couple stress fluid over a stretching surface with chemical reaction. Nonlinear Anal. Model. Control. 2012, 17, 47–59. [Google Scholar]
- Hina, S.; Mustafa, M.; Hayat, T. On the exact solution for peristaltic flow of couple-stress fluid with wall properties. Bulg. Chem. Commun. 2015, 47, 30–37. [Google Scholar]
- Ting, T.W.; Hung, Y.M.; Guo, N. Entropy generation of viscous dissipative nanofluid convection in asymmetrically heated porous micro channels with solid-phase heat generation. Energy Convers. Manag. 2015, 105, 731–745. [Google Scholar] [CrossRef]
- Anand, V. Entropy generation analysis of laminar flow of a nanofluid in a circular tube immersed in an isothermal external fluid. Energy 2015, 93, 154–164. [Google Scholar] [CrossRef]
- Chen, B.S.; Liu, C.C. Entropy generation in mixed convection magnetohydrodynamic nanofluid flow in vertical channel. Int. J. Heat Mass Transf. 2015, 91, 1026–1033. [Google Scholar] [CrossRef]
- López, A.; Ibáñez, G.; Pantoja, J.; Moreira, J.; Lastres, O. Entropy generation analysis of MHD nanofluid flow in a porous vertical microchannel with nonlinear thermal radiation, slip flow and convective-radiative boundary conditions. Int. J. Heat Mass Transf. 2017, 107, 982–994. [Google Scholar] [CrossRef]
- Havzali, M.; Arikoglu, A.; Komurgoz, G.; Keser, H.I.; Ozkol, I. Analytical–Numerical analysis of entropy generation for gravity-driven inclined channel flow with initial transition and entrance effects. Phys. Scr. 2008, 78, 045401. [Google Scholar] [CrossRef]
- Das, S.; Jana, R.N. Entropy generation due to MHD flow in a porous channel with Navier slip. Ain Shams Eng. J. 2014, 5, 575–584. [Google Scholar] [CrossRef]
- Adesanya, S.O. Second Law Analysis for Third-Grade Fluid with Variable Properties. J. Thermodyn. 2014, 2014, 452168. [Google Scholar] [CrossRef]
- Adesanya, S.O.; Kareem, S.O.; Falade, A.J.; Arekete, S.A. Entropy generation analysis for a reactive couple stress fluid flow through a channel saturated with porous material. Energy 2015, 93, 1239–1245. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and Das’ model. Entropy 2016, 18, 9. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Entropy generation due to natural convection of a nanofluid in a partially open triangular cavity. Adv. Powder Technol. 2017, 28, 244–255. [Google Scholar] [CrossRef]
- Fakoya, M.B.; van der Poll, H.M. Integrating ERP and MFCA systems for improved waste-reduction decisions in a brewery in South Africa. J. Clean. Prod. 2013, 40, 136–140. [Google Scholar] [CrossRef]
- Fakoya, M.B.; van der Poll, B. The feasibility of applying material flow cost accounting as an integrative approach to brewery waste-reduction decisions. Afr. J. Bus. Manag. 2012, 6, 9783. [Google Scholar]
- Fakoya, M.B. Adopting material flow cost accounting model for improved waste-reduction decisions in a micro-brewery. Environ. Dev. Sustain. 2015, 17, 1017–1030. [Google Scholar] [CrossRef]
- Hayat, T.; Hina, S.; Ali, N. Simultaneous effects of slip and heat transfer on the peristaltic flow. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1526–1537. [Google Scholar] [CrossRef]
- Hayat, T.; Farooq, M.A.; Javed, T.; Sajid, M. Partial slip effects on the flow and heat transfer characteristics in a third-grade fluid. Nonlinear Anal. Real World Appl. 2009, 10, 745–755. [Google Scholar] [CrossRef]
- Hayat, T.; Javed, M.; Asghar, S. Slip effects in peristalsis. Numer. Methods Partial Differ. Equ. 2011, 27, 1003–1015. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Q.; Ali, N. Influence of partial slip on the peristaltic flow in a porous medium. Phys. Lett. A 2008, 387, 3399–3409. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Q.; Qureshi, M.U.; Ali, N.; Hendi, A.A. Influence of slip condition on the peristaltic transport in an asymmetric channel with heat transfer: An exact solution. Int. J. Numer. Methods Fluids 2011, 67, 1944–1959. [Google Scholar] [CrossRef]
- Ellahi, R.; Hayat, T.; Mahomed, F.M.; Asghar, S. Effects of slip on the nonlinear flow of a third-grade fluid. Nonlinear Anal. Real World Appl. 2010, 11, 139–146. [Google Scholar] [CrossRef]
- Devakar, M.; Sreenivasu, D.; Shankar, B. Analytical solutions of couple stress fluid flows with slip boundary conditions. Alex. Eng. J. 2014, 53, 723–730. [Google Scholar]
- Siddiqui, A.M.; Hameed, M.; Siddiqui, B.M.; Ghori, Q.K. Use of Adomian decomposition method in the study of parallel plate flow of a third-grade fluid. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2388–2399. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Ashorynejad, H.R. Investigation of squeezing unsteady nanofluid flow using ADM. Powder Technol. 2013, 239, 259–265. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Ashorynejad, H.R.; Rokni, H.B. Analytical investigation of Jeffery-Hamel flow with high magnetic field and nano particle by Adomian decomposition method. Appl. Math. Mech. 2012, 33, 1553–1564. [Google Scholar] [CrossRef]
- Gray, W.G.; Miller, C.T. Thermodynamically constrained averaging theory approach for heat transport in single-fluid-Phase porous medium systems. J. Heat Transf. 2009, 131, 101002. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
