1. Introduction
The electron and other charged leptons are considered fundamental particles in the present Standard Model of particle physics. According to the overwhelming majority of data on (high-energy) electron-electron/electron-positron collisions and atomic physics such a classification rests on the fact that no structural charge-density and spin distributions are revealed by typical scattering processes and spectroscopic experiments. Moreover, in many condensed-matter systems the notion of the Quantum Mechanics (QM) of a point-like, spinning particle together with the exclusion principle do describe the collective behavior of electrons in a highly satisfactory and realistic way [
1]. However, the quantitative description of strongly correlated two-dimensional electrons associated, e.g., with high-temperature superconductivitiy, seems to demand a deviating treatment. Here a spatial separation between charge and spin is a serious option favored by the data [
2].
To describe the spatial probability density for the presence of a point-like electron in terms of the square of a wave function based on de Broglie’s particle-wave duality [
3], whose time evolution is governed by the Hamiltonian of the isolated system, is an extremely successful and useful concept: About a century ago, it started to revolutionize our understanding of atomic stability and of the discreteness of the spectra of light emitted by excited atoms [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17], the chemical bond [
18], and the role of and interplay between electrons in condensed matter and hot plasmas thanks to the development of efficient calculational procedures for (extended) multi-electron systems. Moreover, new computational and conceptual horizons, enabled by quantum field theoretical (QFT) second quantization in the framework of Quantum Electrodynamics (QED) [
19,
20,
21] and its electroweak generalization [
22,
23,
24,
25], have yielded accurate predictions of radiative corrections to atomic energy levels, to the electron’s magnetic moment, and in electroweak scattering cross sections.
Why then is there a need for a deeper understanding of the nature of the free electron and its properties as revealed by the application of external forces, the implied (classical) radiation reaction, and tree-level as well as radiative quantum behavior playing out in scattering processes? The answer to this question touches a number of basic problems.
First, already on the classical level Maxwell’s equation and the Lorentz force equation do not describe the phenomenon of radiation reaction: This local field theory ignores the back-reaction onto an electron induced by the radiation emitted by this particle when under acceleration in an external field. Various proposals on how to modify the force equation were made in the literature, see, e.g., [
26,
27], but a basic theory yielding an effective, unique correction is not available. As was shown in [
26], the effects of radiation reaction can dominate the dynamics of the electron for strong accelerations posited by high-power laser pulses.
Second, even though QM and QFT provide an efficient and reliable computational framework there are conceptual questions. Why does the electron as a particle have a modest rest mass of
if probing its structure by high-energetic scattering experiments at four-momentum transfers
Q up to several hundreds of GeV/
c does not indicate any deviation from structurelessness or point-particle behavior? Classically speaking, such a point-likeness would imply the spatial integral of its Coulombic electric field energy density and hence its rest mass
to be of order
Q. Namely, in natural units
one has
which contradicts the value in Equation (
1). Notice that radiative corrections to
, computable in QED in terms of powers of a small coupling constant
, must, by the very definition of a renormalized perturbation series, be much smaller than
. Concerning another aspect of the electron’s potential structure, one may ask how a finite magnetic moment can possibly be related to the spin of a point particle? Yet, although (or possibly because) it ignores this basic question, representation theory in QM is immensely successful in classifying the effect of coupled angular momentum on energy levels and on the overall dynamics of composite systems.
Third, Louis de Broglie’s deep ideas, underlying the proposal of wave-particle duality for the electron [
3], in their original form imply that the electron is anything but a particle of vanishing spatial extent. Strictly speaking, this contradicts Born’s intepretation of the square of the wave function describing the probability density for the spatial occurrence of a point particle. De Broglie argues [
28] by considering respective changes, under a Lorentz boost at velocity
v, of the electron’s rest mass
, associated with the frequency
of an internal “clock” oscillation via Planck’s quantum of action
h as
and viewed as the zero component of the electron’s four-momentum. Subsequently, he contrasts this with the disparate changes of the same
internal frequency as implied by time dilatation. As a consequence, the increase of particle energy from
to
can be decomposed into a reduction of internal heat from
to
plus an increase of (quasi-)translational energy from zero to
:
where
, the relativistic spatial momentum is given as
, and
c denotes the speed of light in vacuum. Notice that
refers to Planck’s formulation of relativistic thermodynamics which, in a straight forward way and without directly addressing dissipative processes, assures proper Lorentz-transformation behavior of an exhaustive set of thermodynamical quantities. This may be contrasted with Ott’s formulation [
29,
30] whose justification appears to be rather mysterious to the present author. Notice also that the second term on the right-hand side of Equation (
4)—the (quasi-)translational energy—reduces to nonrelativistic kinetic energy
only modulo a factor of two for
. This is an unexplained point which eventually needs to be clarified. It is absurd, however, to assign an internal heat
Q to a point particle. The present work proposes that the thermodynamics of an isolated electron at rest and the existence of a preferred internal frequency
are consequences of the existence of a compact, spatial region containing an electric, BPS-like monopole (after an electric-magnetically dual interpretation [
31,
32]), which accommodates the electron’s charge and mass, representing a blob of deconfining phase of SU(2) Quantum Yang-Mills theory immersed into a confining-phase environment. Macroscopically seen, this blob represents the self-intersection of an SU(2) center vortex loop, that is, (again, after an electric-magnetically dual interpretation [
31,
32]) a figure-eight shaped, one-fold knotted loop of electric center flux inducing a magnetic moment twice as large as the fundamental unit provided by a single center-vortex loop, see
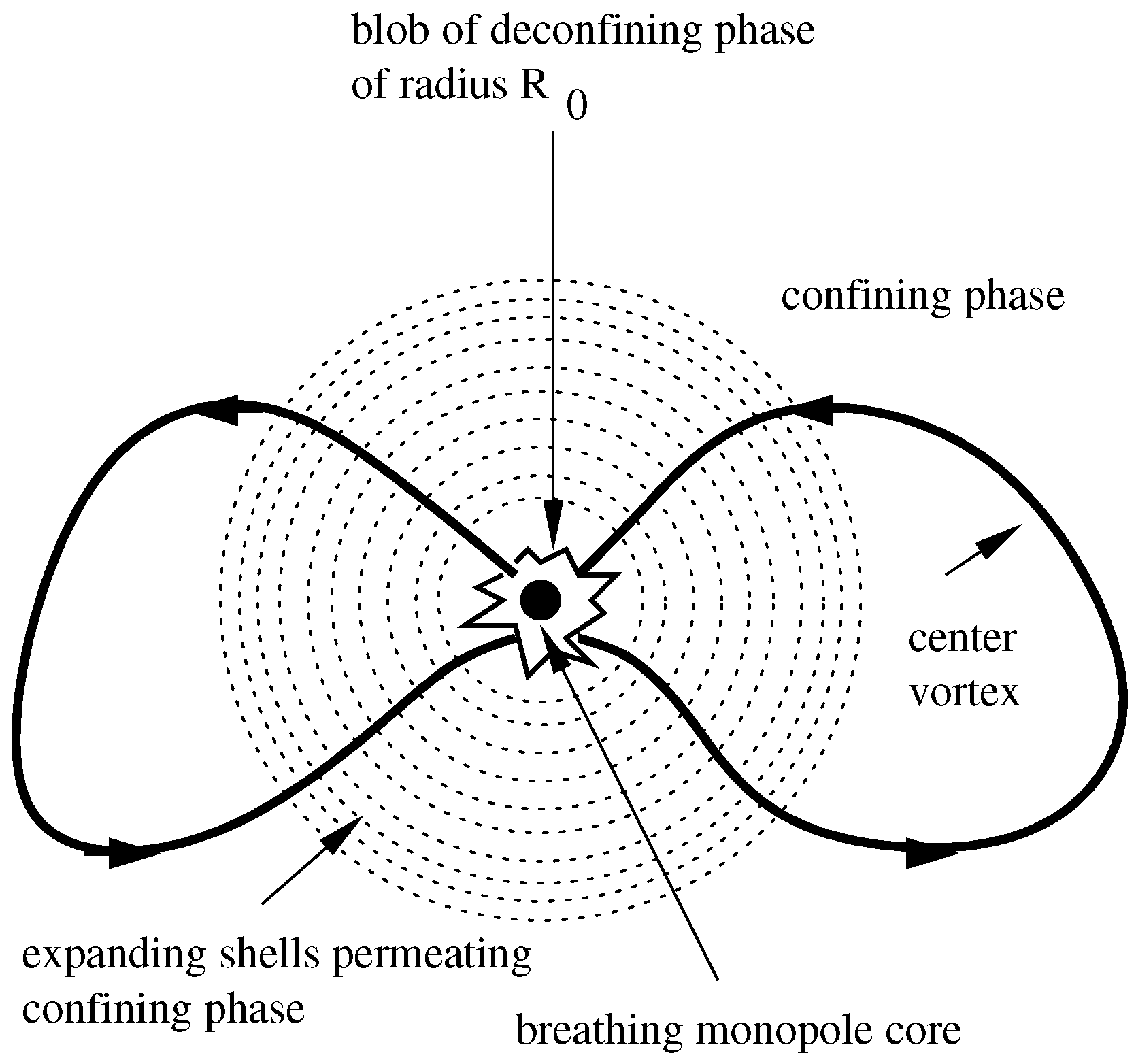
Figure 1.
Finally, deeper insight into the functioning of the electron as a quantum particle is destined to shed light on the “sweet mysteries” of Quantum Mechanics (e.g., instantaneous state reduction by measurement) and the renormalization problem in perturbative Quantum Field Theory.
The present work offers a conceptual scheme for the description of the unaccelerated electron which supports de Broglie’s ideas. This scheme draws on the following developments: (i) Phase structure of SU(2) Yang-Mills thermodynamics [
31,
32], composition and wave/particle like excitability of the deconfining thermal ground state [
33,
34], and principle nature of solitonic excitations in the confining phase [
35,
36]; (ii) Recent results on the classical dynamics of the strongly (and isotropically) perturbed BPS monopole [
37]. Pairing with the work in [
37], there are insightful and supporting treatments of linear perturbations of the BPS monopole (spectrum of quasi-normal modes in [
38]).
As a consequence of (i) and (ii) the quantum thermodynamics within the self-intersection region of a center-vortex loop manifests itself as follows (in natural units): Created by the dissociation of a large-holonomy caloron, a BPS monopole, with the asymptotic value of its Higgs field modulus at temperature
given as
due to maximum (anti)caloron holonomy (Temperature
of the intersection region is slightly higher than the critical temperature
of the deconfining-preconfining phase transition:
, see
Section 3) [
39,
40,
41,
42,
43,
44,
45,
46] and the value of the coupling constant
e in the adjoint Higgs model roughly determined by the plateau value
[
31,
32] is immersed into deconfining SU(2) Yang-Mills thermodynamics. At
, see
Section 2, the pressure of deconfining SU(2) Yang-Mills thermodynamics vanishes. The contribution to the total pressure from a static (noninteracting) BPS monopole [
47,
48] is also nil. In the absence of interactions between such an explicit monopole and deconfining SU(2) Yang-Mills thermodynamics the intersection region would thus be static at temperature
, that is, non-expanding and non-contracting.
The unperturbed monopole’s rest mass is given as [
47,
48]
where
denotes its asymptotic adjoint Higgs field, and the energy density
of deconfining SU(2) Yang-Mills thermodynamics at
reads
see
Section 2, where
denotes the energy density of the thermal ground state, and
is the Yang-Mills scale, related to
as
The fact that the explicit monopole is subject to perturbations, issued by quantum kicks due to caloron/anticaloron centers [
33], leads to a fluctuating re-distribution of stress-energy within the self-intersection region. This situation is characterized, e.g., by the existence of a breathing mode of the monopole core whose (circular) frequency
essentially represents
[
28] and is given by the mass
of the vector modes [
37].
The remainder of this paper is intended to corroborate and explain the above-sketched model of the electron in more quantitative terms, thereby considering a few (rather small) corrections to the results obtained in the simplified treatment of [
49] where complete ground-state dominance of the deconfining thermodynamics within the intersection region was assumed. Since our derivations heavily rest on a grasp of the phase structure of an SU(2) Yang-Mills theory we will briefly review it in
Section 2.
Section 3 discusses the deconfining pressure
P and derives the ratio
and the value of the coupling
e (slightly higher than
) at the zero
of
P. The mass of the noninteracting BPS monopole, given by the first of Equation (
6), thus is slightly decreased compared to the value given by the expression to the far right, and the mass
of the vector modes is mildly increased. The results obtained in [
37] on the dynamics of the spherically perturbed monopole are reviewed in
Section 4. Finally, in
Section 5 we combine the results of
Section 2,
Section 3 and
Section 4 to propose a model for the electron as a genuine quantum particle of finite extent in
Section 5.
Section 6 summarizes this work and gives an outlook to future activity.
2. Review on Phase Structure of SU(2) Yang-Mills Thermodynamics
SU(2) Yang-Mills thermodynamics occurs in three distinct phases [
50]. The high-temperature, deconfining phase is characterized by a thermal ground state, composed of overlapping, topological-charge-modulus unity calorons and anticalorons. At a given temperature
, the spatial extent of their densely packed centers is determined by a radius
which also sets the preferred (anti)caloron scale parameter for the spatial coarse-graining process involving a homogeneously and adjointly transforming two-point function of the fundamental Yang-Mills field-strength tensor
evaluated on a Harrington-Shepard (HS) (that is, trivial-holonomy) caloron and its anticaloron [
51,
52]. Here
denotes the modulus of the emergent, adjoint, and inert scalar field representing coarse-grained (anti)caloron centers,
T refers to temperature as defined by the inverse temporal period of the HS-(anti)caloron, and
is the Yang-Mills scale. The latter emerges as an integration constant when solving a first-order, ordinary differential equation for
’s potential. This first-order equation expresses the intactness of (Euclidean) BPS saturation within (anti)caloron centers. A departure from (anti)selfduality in the field configuration, reflecting the overlap of (anti)caloron peripheries, is manifested by a finite ground-state pressure
and energy density
. The associated, effective gauge-field configuration
is obtained as a zero-curvature solution to the effective Yang-Mills equation
where
denotes the effective Yang-Mills field-strength tensor.
Excitations of the deconfining thermal ground state are partially massive (mass
) by virtue of the adjoint Higgs mechanisam invoked by the field
. These massive excitations never propagate in a wavelike way: their high would-be frequencies probe the interior of (anti)caloron centers to provoke an indeterministic, quantum-like response. On the level of free thermal quasi-particles (that is, not taking into account feeble radiative effects [
31,
32,
53]) the massive sector thus merely represents uncorrelated, Bose-Einstein distributed energy and momentum fluctuations. The
massless sector, on the other hand, may propagate in a wavelike fashion if a constraint on intensity and frequency is satisfied [
33], governed by the Yang-Mills scale
of the theory.
The thermal ground state of the deconfining phase rearranges itself into a different structure at the critical temperature
where screened BPS monopoles and antimonopoles, released by rarely occurring large-holonomy calorons and anticalorons, become massless, therefore abundant, and, as a consequence, form a condensate. This marks the onset of the preconfining phase. Energetically, the condensate of monopoles and antimonopoles together with its massive gauge-mode excitations (Meissner-Ochsenfeld effect or Abelian Higgs mechanism [
54]) is not stable immediately at
since the energy density of the deconfining phase is lower within the following temperature range [
31,
32]:
Shortly below
the entropy density of the system approaches zero, and the thermal ground state of the preconfining phase decays into (spatial)
n-fold self-intersecting center-vortex loops (
). Since their masses scale as
but their multiplicities (number of distinct topologies at given
n) scale more than factorially in
n [
55,
56] the very concept of a partition function is inapplicable. This is the characteristics of a highly nonthermal Hagedorn transition: the homogeneity of pressure, energy density, and other “would-be” thermodynamical quantities is strongly violated, and the SU(2) Yang-Mills plasma exhibits a highly turbulent behavior.
5. Size Estimates
Based on [
49] we would now like to perform an improved estimate of the radius
associated with the region of self-intersection. The idea is to prescribe at
, where deconfining SU(2) thermodynamics does not exert any pressure, that the rest mass of the quantum particle electron,
see Equations (
15) and (
16), decomposes into that of a static monopole
compare with Equations (
6) and (
15), and the energy
of deconfining SU(2) thermodynamics contained in the volume
:
In writing Equation (
19), Equation (
9) of [
49] and Equations (
13) and (
14) were used. Interactions between the monopole and deconfining SU(2) thermodynamics (caloron and anticaloron centers [
33] invoking energy transfer from quasi-particle excitations to the monopole which partially radiates this energy back into the Yang-Mills plasma) will effectively introduce spatial fluctuations of temperature
T about the equilibrium value
, but they won’t change the energy content of the overall system. Solving Equation (
19) for
, we obtain the mean radial extent of the system as
To ensure that the use of infinite-volume thermodynamics, which has led to Equation (
20), is consistent we need to compare
to the correlation length
of the thermal ground state [
31,
32]. Appealing to Equations (
5) and (
24) below, one easily derives
Thus
which justifies the use of infinite-volume thermodynamics in deriving Equation (
20).
Comparing
to the Compton wave length
m, we have
Thus,
is 2.43 times larger than the Bohr radius
which, in turn, is
times larger than the monopole core radius
m
. It is remarkable that according to Equation (
16) the relation between electron mass
(that is, monopole-core breathing frequency
[
37]) and
, is in agreement with
(or
). Therefore, the electron is
not a point particle in the present model: Its charge is distributed over a spatial region whose radius matches the Compton wave length
but (quantum) moves within a much larger volume of radius
m of deconfining phase. Scattering experiments do not reveal an inner structure because
quantum thermodynamics within radius
—the state of maximum entropy—is structureless. Moreover, the Yang-Mills scale
, which is determined from
(monopole originated by dissociation of maximally non-trivial holonomy caloron) and Equation (
19), reads
Therefore,
keV. For a comparison, the demonstrator tokamak ITER is envisaged to operate at an average electron temperature of 8.8 keV!
The important work [
37] points out that high-frequency oscillations in the profile function
w of the off-Cartan gauge fields, belonging to the perturbed monopole, develop expanding shells. If these shells are considered to penetrate the confining phase (
) such that the static Coulomb field of the monopole, arising from a temporal average over many cycles of the monopole core-vibration, can actually permeate this phase, then we may estimate the Coulomb-field correction
to the “thermodynamical” mass
as
This is only a ∼1.9% correction to
. Notice the strong conceptual difference to the model of the classical electron whose radius defines the entire rest mass
via Coulomb self-energy.
Finally, we would like to mention that, in assigning half a Bohr magneton to the magnetic moment carried by a single center-vortex loop, a
g-factor of two naturally arises by the electron being composed of two such center-vortex loops by virtue of the region of self-intersection, see
Figure 1.