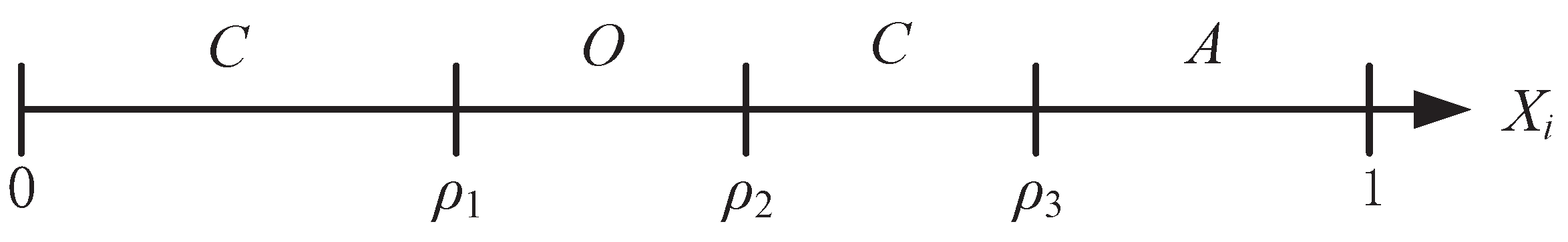1. Introduction
With the development of deep-space exploration missions and Space Information Network (SIN) applications, the Ka-band and higher Q/V band channels are viewed as a primary solution to improve communication capacity [
1]. Compared to commonly used X-band, Ka-band can offer 50 times higher bandwidth [
2,
3]. The Mars Reconnaissance Orbiter (MRO) mission demonstrated the availability and feasibility of the Ka-band for the future exploration missions [
4,
5].
However, the Ka-band channel is much more sensitive to the weather conditions surrounding the terrestrial stations, such as rainfall, which can significantly degrade the quality of service [
6,
7]. Furthermore, the space nodes in SIN only have limited communication resource, thus the optimal transmission policy should consider the trade-off between complexity and transmission performance [
8,
9]. Considering the huge distance and long propagation delay in SINs, the handshake process of conventional Transmission Control Protocol/Internet Protocol (TCP/IP) is not suitable for space communication scenarios [
10,
11]. Generally, the delay tolerant network protocols that Consultative Committee for Space Data Systems File Delivery Protocol (CFDP) and Licklider Transmission Protocol (LTP) are widely used in SIN communication scenarios [
12,
13,
14], where the transmitter can obtain the delayed Channel State Information (CSI) from Negative Acknowledgment (NACK) feedback [
15,
16].
In previous studies [
17,
18,
19], the time-varying rain attenuation at the Ka-band channel is used to model to a two-state Gilbert–Elliot (GE) channel, and several works have focused on the optimal data transmission policy. In [
20], three data transmission actions were proposed to be chosen at the beginning of each time slot to maximize the expected long-term throughput.
For the Mars-to-Earth communications over deep space time-varying channels, an optimal data transmission policy has been developed with the delayed feedback CSI in [
21]. The adaptive coding schemes for deep space communications over the Ka-band channel were also studied in [
22,
23]. However, little work has been done in optimizing the transmission policy for SINs, especially in the presence of highly time-varying Ka-band channels.
In this paper, by utilizing the delayed feedback CSI, we propose an optimal transmission scheme based on the Partially Observed Markov Decision Process (POMDP), and derive the key thresholds for selecting the optimal transmission actions for the SIN communications.
The rest of this paper is organized as follows. In
Section 2, a two-state GE channel is modeled. We derive the threshold of which we should perform channel sensing before we start the transmission or not in
Section 3, and we also derive the thresholds of choosing data transmission actions from two or three actions in POMDP. In
Section 4, simulation results show that the proposed optimal transmission policy can increase the throughput in SIN communications. Finally,
Section 5 concludes the paper.
2. System Model
According to the previous studies [
24,
25,
26], we can select an appropriate threshold of the noise temperature
to capture the channel capacity that randomly ranges from
good to
bad state. Then the time-varying rain attenuation at the Ka-band channel is modeled to a two-state GE channel according to the noise temperature
T.
If the noise temperature satisfies
, the channel is on
good state, where channel bit error rate (BER) is as low as (
∼
); if the noise temperature satisfies
, the channel is on
bad state, and the channel BER is as high as (
∼
). We denote the transition probability matrix
G of the two-state GE channel as
where
is the probability that the Ka-band channel is holding on
good state,
is the probability that the channel state changes from
bad to
good. Without loss of generality, we assume
.
The transmission time slots can be expressed as
, the duration of a transmission time slot is a constant
D, and and the corresponding states series of the GE channel can be expressed as
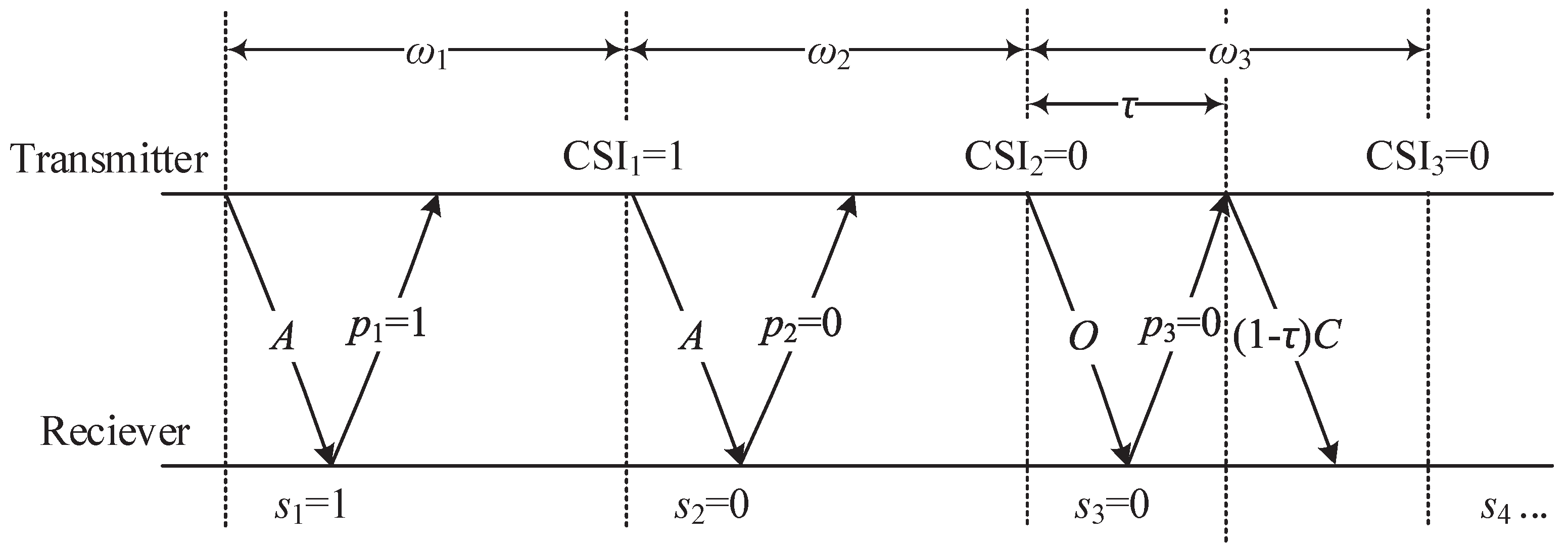
. The proposed POMDP-based transmission scheme with delayed CSI is shown in
Figure 1.
The transmitter can thus obtain the delayed CSI through belief probability p, e.g., if the previous state is in the good state, then the receiver feedback of a single bit information is 1, otherwise 0. Therefore, there are three transmission actions for the transmitter that can be chosen at the beginning of each transmission time slot , and each action is explained in detail as follows.
Betting aggressively (action A): When the transmitter believes that the channel has a high chance in a good state, the transmitter decides to “gamble” and transmits a high number of data bits.
Betting conservatively (action C): When the transmitter believes the channel is in a bad state, and decides to “play safe” and transmits a low number of data bits.
Betting opportunistically (action O): For this action, the transmitter adopts to sense the channel state at the beginning of the slot by sending a control/probing bit. The cost of sensing is a fraction of the slot, which is the time spent sensing the channel, defined as , where is the round trip time, and D is the (constant) duration of a transmission time slot. Then the transmitter selects the appropriate transmission action (A or C) according to the sensing outcome, and data bits will send if the channel was found to be in the good state or data bits if otherwise.
Therefore, at the beginning of i-th transmission time slot , the transmitter needs to decide an optimal action from the three actions above, i.e., to maximize the expected throughput of our proposed POMDP-based transmission scheme. Because the transmitter only can have delayed feedback CSI or even no feedback, this is a POMDP problem.
Let
denote the channel belief, which is the conditional probability that the channel is in the good state at the beginning of the
i-th transmission time slot, from the past channel history of actions and accumulated delay CSI
, thus
. Define a policy
as a map from the belief at a particular time
t to an action in the action space. Hence, by using this belief as the decision variable, let
denote the expected reward, with a discount factor
(
), the maximize expected throughput has the following expression:
where
is the initial value of the belief at the
i-th transmission time slot, and we formulate the optimization problem with
in the next section.
3. Optimal Transmission Policy Based on POMDP
In this section, we derive the optimal policy for the transmitter that knows the CSI feedback at the end of each slot as shown in
Figure 1. The necessary conditions that tell if the action of
betting opportunistically should be used under certain SIN communication scenarios was derived, and then the key thresholds for selecting the optimal transmission actions for the SIN communications are derived.
From the above discussion, we understand that an optimal policy exists for our POMDP problem as shown in Equation (
2), and the expected reward is
; if the aggressive action
A is selected, since the probability of the channel in a good state at the next time is
, then the expected number of successfully transmitted data bits is
; if the conservative action
C is selected,
data bits will be transmitted without error; at last, if opportunistically action
O is selected, the expected transmitted data bits are
. Then, we define the value function
as
, for all
, and
denotes the map from the belief at a particular time to an action in the action space
. The value function
satisfies the Bellman equation
where
is the value acquired by taking action
when the belief is
. By using the delayed feedback belief probability
, the transmitter selects the optimal transmission action
to maximize the throughput with the feedback belief
being given by
where
is the channel belief of the optimal action which selected at the beginning of the next time slot, and
in which
. Then,
can be explained for the three possible actions:
- (1)
Betting aggressively: If aggressive action A is taken, then, the value function evolves as ;
- (2)
Betting conservatively: If the conservative action C is selected, the value function evolves as ;
- (3)
Betting opportunistically: If opportunistic action O is selected, the value function evolves as .
Hence, if the channel belief
is probability of the slot
in a good state, then the channel belief of next slot
is
. Similarly, if the CSI in a bad state is
in
, then the channel belief of
is
, i.e.,
, and then we can rewrite the above equations as follows
Finally, the Bellman equation for our POMDP-based transmission policy over Ka-Band channels for SINs can be expressed as
Moreover, Smallwood et al. [
27] proved that
is convex and nondecreasing, and there exist three thresholds
. Therefore, there are three types of threshold policies accordingly: (1) When
, the optimal policy is a one-threshold policy; (2) When
, the optimal policy is a two-thresholds policy; (3) When
, the optimal policy is a three-thresholds policy. The optimal policy for the three-thresholds policy is illustrated in
Figure 2, and the interval
is separated in four regions by the thresholds
,
and
.
Intuitively, one would think that there should exist only three regions, i.e., if
is small, one should play safe; if
is high, one should gamble, and, somewhere in between, sensing is optimal. However, if the transmitter can not obtain the feedback CSI, for some cases , a three-threshold policy is optimal and an example is shown in [
28].
However, with the help of the delayed feedback CSI, our POMDP-based transmission policy has only three regions, i.e., () = ∅. Therefore, the necessary conditions that tell if action O should be selected under a given SIN communication scenario, with data rate and in good and bad states, respectively, two thresholds , and cost of action O is , are given in the following theorem.
Theorem 1. In terms of the POMDP-based optimal transmission scheme constructed by the Bellman function Equation (6), where is the expected return when the risky action A is taken, bits are transmitted regardless of the channel conditions when action C is selected, and the expected return when the sensing action O is taken is , therefore: If then the optimal policy is a two-thresholds policy, and the optimal action can be selected from ;
Otherwise, if then the optimal policy is a one-threshold ρ policy and the optimal action can be selected from .
Proof of Theorem 1. In our SIN POMDP-based transmission scheme, without loss of generality, assume that the optimal policy has two thresholds
. Note that, since
is the solution of
, and
is the solution of
, it is easy to establish that
From Equation (
5), we have
If the optimal policy has two thresholds then
, and the communication parameters should satisfy
Otherwise, if the optimal policy has one threshold
, then the communication parameters turn to satisfy
☐
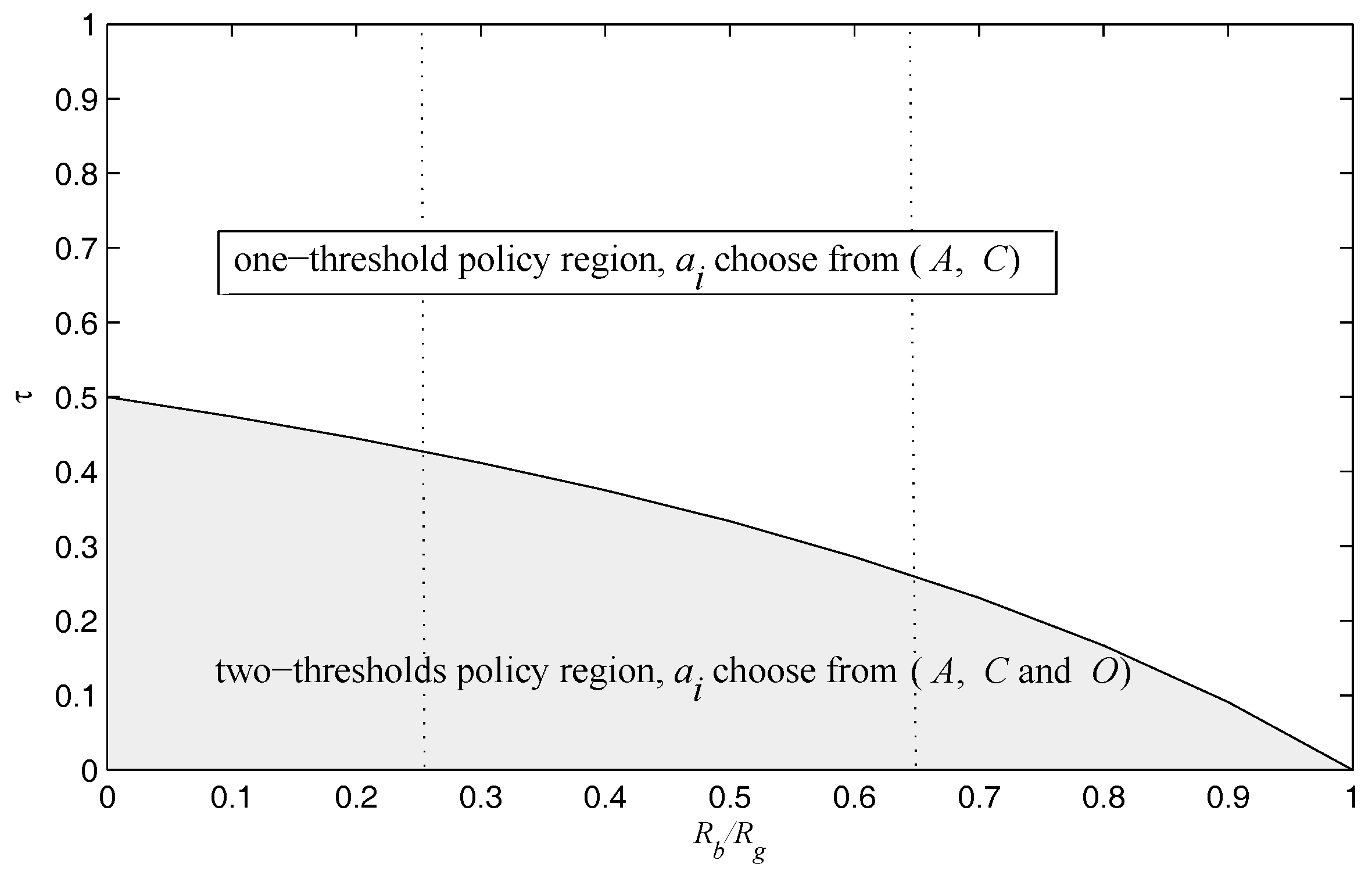
Note that Theorem 1 establishes the structure that tells if action
O should be used, and two types of threshold policies exist depending on the system parameters–in particular, the cost of the sensing action
versus the ratio of
, and the optimal policy space is partitioned into two regions, which is illustrated in
Figure 3.
Figure 3 illustrated that the established two optimal policies regions can be further partitioned into three regions at most. As one should expect, the optimal transmission scheme here is a myopic policy that maximizes the immediate reward. Next, we detailed the optimal transmission action in the one-threshold policy region and the two-thresholds policy region in
Figure 3, and gave a complete characterization of the thresholds for each policy in the following, respectively.
Assume that the one-threshold policy has one threshold , and the transition probability matrix of the two-state GE channel is . Then, the optimal transmission action is introduced in the following Theorem 2.
Theorem 2. Let denote the action space in the one-threshold policy region, and denote the transmitted numbers of data bits that corresponding to the action A and C, respectively, then is determined as follows:
- (1)
If , then the optimal transmission action is regardless of the delayed feedback CSI is or ;
- (2)
If , then the optimal transmission action is regardless of the delayed feedback CSI is or ;
- (3)
Finally if , then the optimal transmission action when the delayed feedback CSI is , and the optimal transmission action is when the delayed feedback CSI is .
Proof of Theorem 2. Recall in our POMDP model that any general value function is convex.
Hence, (1) if
, when the delayed feedback CSI is
, and the channel belief is
, then we have
since
and
. Similarly, when the delayed feedback CSI is
, we still have
since
Hence, the optimal transmission action in this case is .
(2) If
, similar to the previous case, regardless of the delayed feedback CSI is
or
(i.e., the channel belief is
or
, respectively), we have
, therefore, by substituting
into Equations (
11) and (
12) directly. Therefore, the action
is optimal in this case.
(3) If
, the approach here is similar to the previous cases, i.e., when the delayed feedback CSI is
and
, we will have
, therefore by substituting
into Equation (
11), and the action
is the optimal strategy here; otherwise, when the delayed feedback CSI is
and
, we consequently obtain
by substituting
into Equation (
12) and the optimal transmission action in this case is
. ☐
The complete characterization of the optimal transmission action of the one-threshold policy is given in
Table 1.
Furthermore, it is worth noting that Theorem 2 proves that the value function is totally determined by finding and . In order to calculate the expected reward of the optimal action when the belief is or , we start by comparing these value functions established in Theorem 2 to the threshold in Theorem 1. Then, all that remains is solving a system of two linear equations with two unknowns, i.e., and , in three cases: , and .
To illustrate the procedure of determining
and
, we consider the example where
, and the optimal transmission action is
regardless of the delayed feedback CSI in this case, as we have proved in Theorem 2; we have then
Recall that we have
, and solving for
and
leads to
All other cases can be solved similarly, and the closed form computation expressions of the one-threshold policy are given in
Table 2.
Next, assume that in the two-thresholds policy region, the optimal policy has two thresholds , and the transition probability matrix is . Then, the optimal transmission action is given in the following Theorem 3.
Theorem 3. Let denote the action space in the two-thresholds policy region, and and denote the transmitted numbers of data bits that correspond to the actions A and C, respectively. Recall that τ is the sensing cost that is the ratio of the round trip time to the time slot duration D and satisfies as in Theorem 1, and is the channel belief, then is determined as follows:
- (1)
If , then two cases can be distinguished: if , the optimal transmission action is , regardless of the delayed feedback CSI being or ; else, if , the optimal transmission action is , regardless of the delayed feedback CSI being or .
- (2)
If , then two cases can be distinguished: if , the optimal transmission action is , regardless of the delayed feedback CSI being or ; else, if , the optimal transmission action is regardless of the delayed feedback CSI being or .
- (3)
Finally if , when the delayed feedback CSI is and , then the optimal transmission action is ; when the delayed feedback CSI is and , then the optimal transmission action is .
Proof of Theorem 3. The proof here needs to utilize the previous case in Theorem 1; recall in our POMDP model that any general value function
is convex, the interval [0, 1] of
is separate in three regions by the thresholds
and
, all the six possible optimal policy structures of the two-thresholds policy are illustrated in
Figure 4, and, then, we can distinguish them into three possible scenarios.
(1) If , we can distinguish three subcases:
If
as shown in
Figure 4a, then we have that the optimal action is
for
where
and
, and since
Hence, the optimal transmission action in this case is for and .
Else, if
, as is illustrated in
Figure 4b, then we have
for
where
as the above subcase obtained, and
is the optimal action for
where
in
Figure 4b, and
by substituting
into Equation (
17) with
.
Lastly, if
, as is shown in
Figure 4c, we have
for
being the optimal action due to the solution of
and
by substituting
and
into Equation (
17), and we obtain
.
(2) If , similarly, three subcases can be distinguished:
If
, as is shown in
Figure 4c, then we have
and
; thus, we have
where
is the optimal action since
and
by solving the value function Equation (
18).
Else, if
, as is shown in
Figure 4e, then we have
for
where
for
by substituting
into Equation (
18), and
is the optimal action for
where
for
by substituting
into Equation (
18).
Lastly, if
, as is shown in
Figure 4f, we have
being the optimal action regardless if the delayed feedback CSI is
or
, where
and
. Then
and
by substituting
and
into Equation (
18), respectively.
(3) Finally, if
, the computation is similar to the previous cases. For
, as is shown in
Figure 4d, where the optimal action is
for
, by using (
17) to solve
with
, then
. In addition, if
, then
is the optimal action, by solving Equation (
18) with
for
, and then we have
.
☐
Let
and
, and
Table 3 shows the complete characterization of the optimal transmission action in the two-thresholds policy region.
Similar to the previous case, we illustrate mathematical expressions for the
and
of Theorem 3 in
Table 4, in order to calculate the expected reward of the value function of the corresponding optimal action that is given in Theorem 3. Again, once
and
have been computed for the six possible optimal policy structures of the two-thresholds policy region in Theorem 3, we retain the scenario that gives the maximal values.
The procedure to calculate
and
starts by comparing these value functions established in Theorem 3 to the thresholds
and
established in
Figure 4, and all the cases can be solved similarly to the previous example, and the closed form computation expressions of the two-thresholds policy are given in
Table 4.
4. Simulation and Results
To evaluation our proposed POMDP-based optimal transmission policy, we start by comparing the transmission actions with different setups, each leading to a different optimal policy. We choose the parameters below in order to illustrate that, in theory, the optimal policy is determined by the communication scenario parameters, such as data rate , and which is affected by the round trip time and the duration of the transmission time slot as in Theorem 1.
The first set of parameters considered is
,
,
,
,
, and
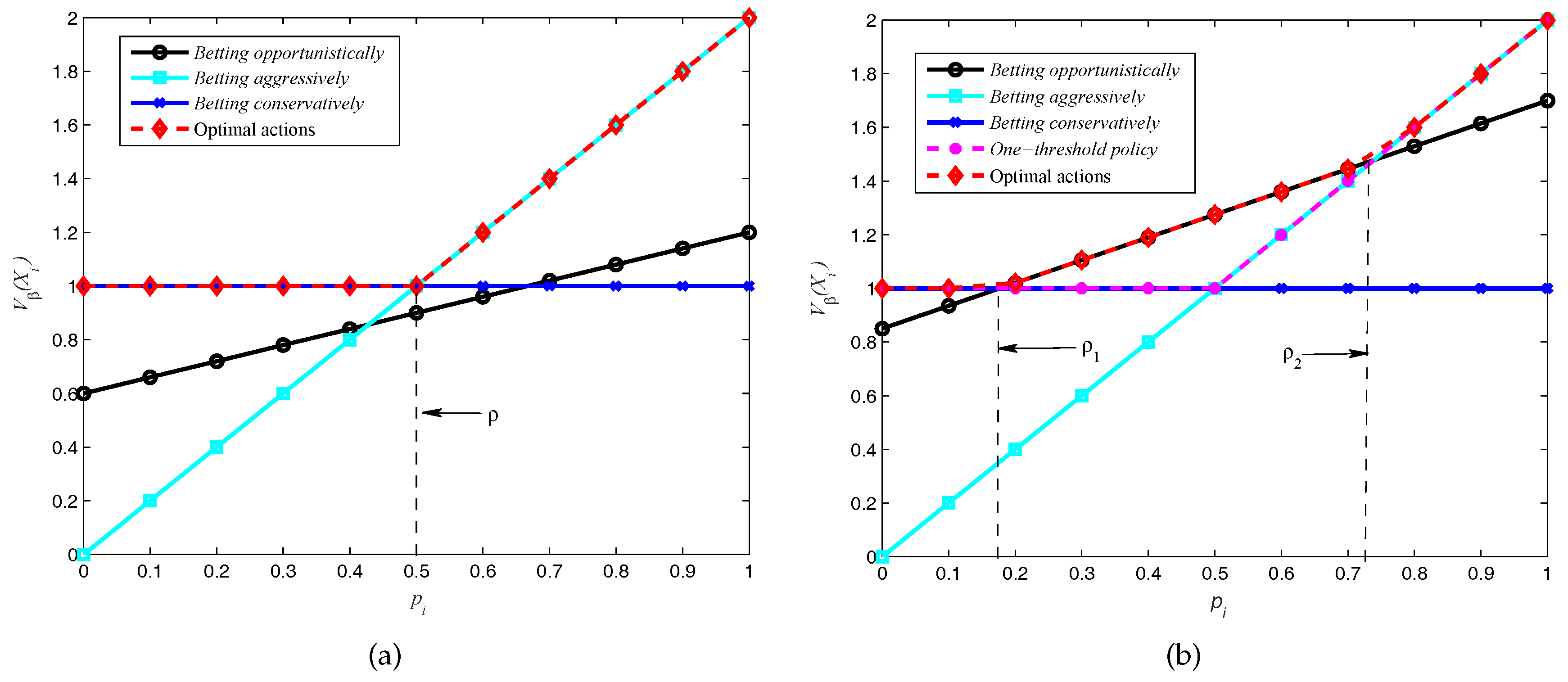
. Note that from Theorem 1,
represents the action of
betting opportunistically, which could not be used under this scenario, thus the one-threshold policy is optimal as the numerical result shows in
Figure 5a. Furthermore, from Theorem 2, the threshold in
Figure 5a is
. Therefore, if
, the optimal action is
, else if
, the optimal action is
, and
betting opportunistically is unfeasible in this scenario.
If we keep all the parameter values fixed and diminish the cost of sensing to
, then from Theorem 1 we can compute that the optimal policy is the two-thresholds policy, shown in
Figure 5b. From
Figure 5b we can see that the one-threshold policy gives suboptimal values, and the two thresholds in this scenario are
and
by using Theorem 3. If
, the optimal transmission action is
betting conservatively (
); else if
, the optimal transmission action is
betting opportunistically (
), which can achieve a better reward than
or
unless
, the optimal action is
betting aggressively (
).
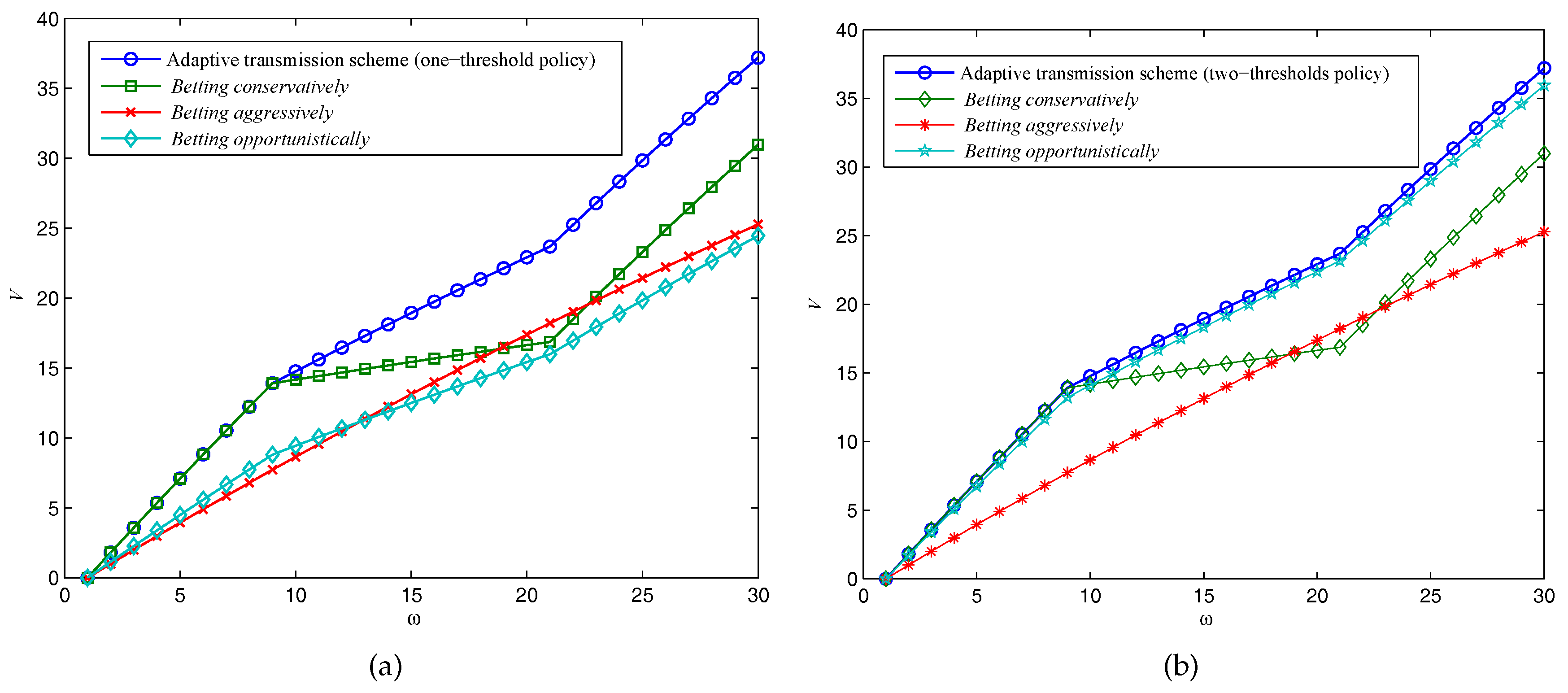
Next, we compare the long-term effect of the expected throughput of our adaptive data transmission scheme with conventional fixed-rate schemes, to validate the optimality of our POMDP-based transmission policy over Ka-band channels for SIN communications. Let
w denote the number of the transmission time slots
, and
denote the accumulated expected values in
Figure 6.
The system parameters in these scenarios are as follows:
,
,
,
, and
. With these parameters, the one-threshold policy is optimal for
, and beyond these critical values, the two-thresholds policy will become optimal. We have
in
Figure 6a, and
in
Figure 6b, respectively. As expected, at the beginning of several transmission time slots,
betting conservatively can archive the same throughput as the adaptive transmission scheme does as is illustrated in
Figure 6a. However, the adaptive transmission scheme can better utilize the channel capacity when the Ka-band channel turns it into a
good state, which leads to a higher throughput in a long-term program. On the other hand, if the two-thresholds policy is optimal as in
Figure 6b,
betting opportunistically is also performed well, but still has a gap remaining compared to our adaptive transmission scheme due to the reward from “gamble”, and “play safe” will be better than sensing the channel sometimes.
So far, we have demonstrated our POMDP-based transmission policy can perform well with different communication setups. In the following, we simulate and compare the adaptive transmission schemes under Ka-band channel communications.
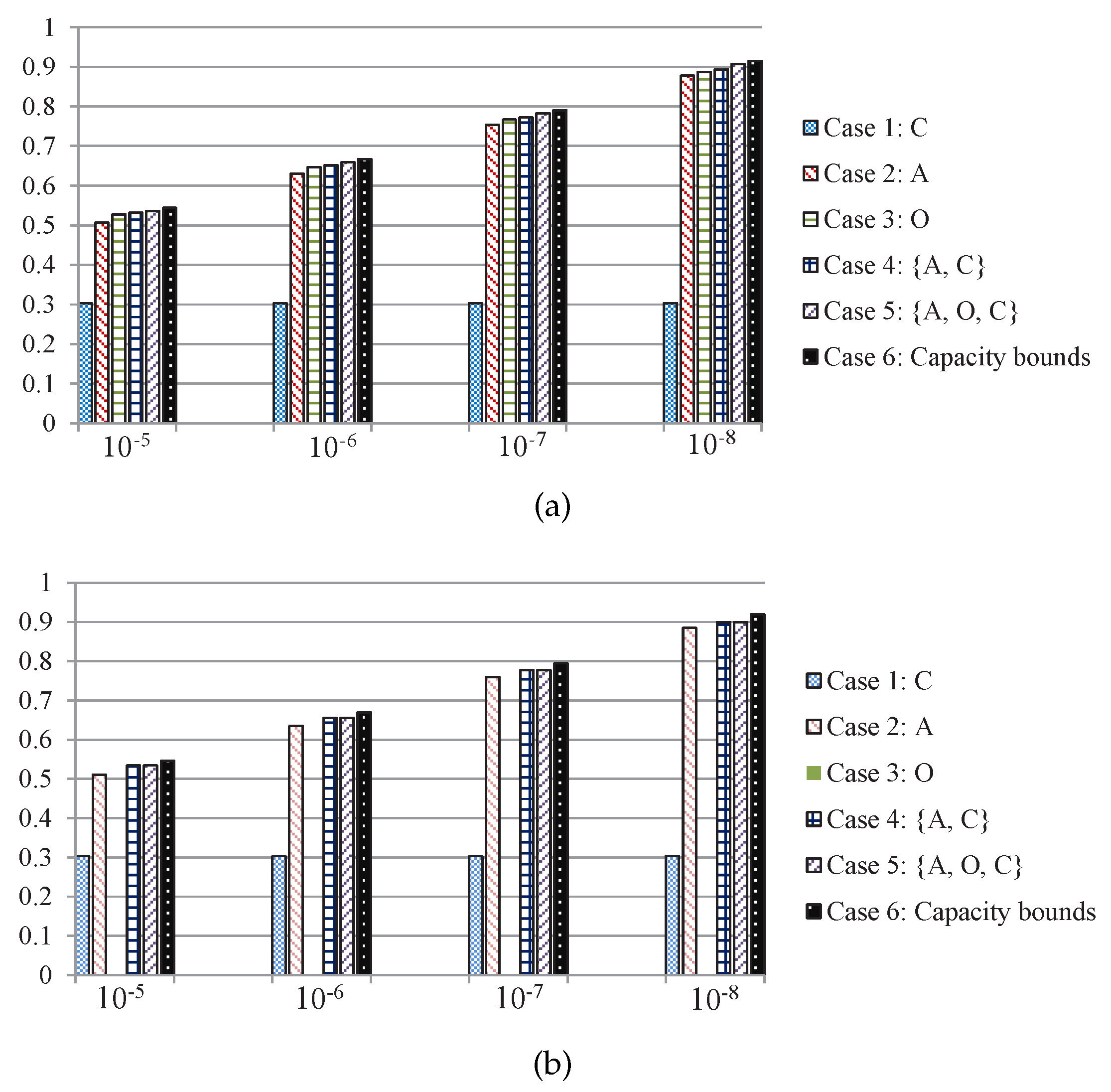
Assume the threshold of the two-state GE channel noise temperature is
K, and the corresponding transition probability of the GE channel is
, according to [
24]. If the channel state is bad, the channel bit error rate (BER) is
, and we select four different BERs
,
,
and
as the channel state is good. Assume normalized the data bit
when BER is
, then we can calculate data bits
and
with other BER values according to the error function [
24]. We simulate the adaptive transmission schemes in two cases, Earth-to-Moon (
), and Earth-to-Mars (
), and the transmission schemes are as follows.
Case 1: The transmitter adopts the action of betting conservatively regardless of the channel state, which can ensure data bits are successfully transmitted.
Case 2: The transmitter only adopts the action of betting aggressively, if the channel state is good, bits are successfully transmitted; else, if the channel state is bad, all data bits are lost.
Case 3: The transmitter only adopts the action of betting opportunistically, if the channel state is good, bits can be received; else, if the channel state is bad, bits can be received successfully.
Case 4: The transmitter chooses optimal action by using delayed feedback CSI and and Theorem 2, the adaptive data transmission action space is a, .
Case 5: The transmitter chooses optimal action by using delayed feedback CSI and Theorem 3, the adaptive data transmission action space is a, .
Case 6: We directly give the outage capacity bounds of the corresponding channels.
The simulation results of throughput performance of the 5 transmission schemes above and the capacity bounds are shown in
Figure 7, and we can see that if the right transmission scheme with certain channel conditions can be selected by using our derived thresholds, it can increase the throughput in Ka-band SIN communications.
Based on the previous analysis, we can expect that the two-thresholds policy is optimal for the Moon-to-Earth scenario in
Figure 7a as the sensing cost is
. Therefore, the transmitter can access the sensing action with little cost. As it can be seen in
Figure 7a, the total number of transmitted bits of
betting opportunistically is substantially augmented and the two-thresholds policy transmission scheme performs close to the capacity bounds.
On the other hand, the round trip time between Mars-to-Earth is about 6–40 min, which is leading to the one-threshold policy being optimal with
, and
betting opportunistically is completely unfeasible as shown in
Figure 7b, there is no data bit that can be transmitted if the transmitter perform channel sensing. And the two-thresholds policy transmission scheme in this scenario is degenerated to the one-threshold policy transmission scheme, where both of the transmission schemes have exactly the same expected total number of transmitted bits.