Active and Purely Dissipative Nambu Systems in General Thermostatistical Settings Described by Nonlinear Partial Differential Equations Involving Generalized Entropy Measures
Abstract
:1. Introduction
2. Stochastic Nambu Systems in General Thermostatistic Settings
2.1. Nambu Dynamics: Deterministic Case
2.2. Nambu Dynamics: Stochastic Case
2.3. Approach to Stationarity and Stationary Solutions
2.4. Active Nambu Systems Exhibit Attractors Defined by Classical Nambu Systems
3. Examples of Active and Purely-Dissipative Systems
3.1. Brownian Motion in a Potential Field
3.2. Charged Particle in a Magnetic Field
3.3. Active Spinning Top Featuring Non-Extensive Statistics: An Approach Involving Thermodynamic State Variables
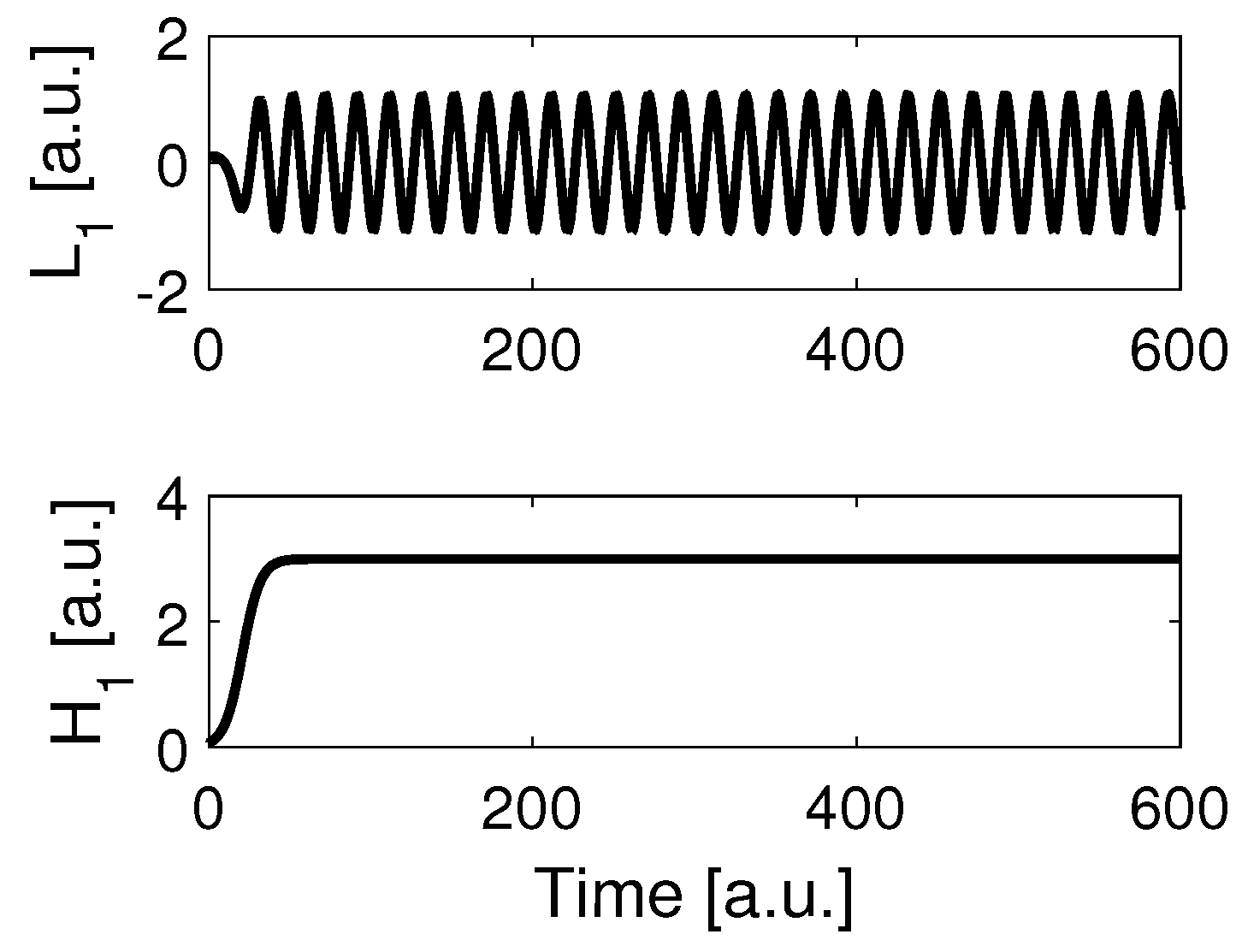
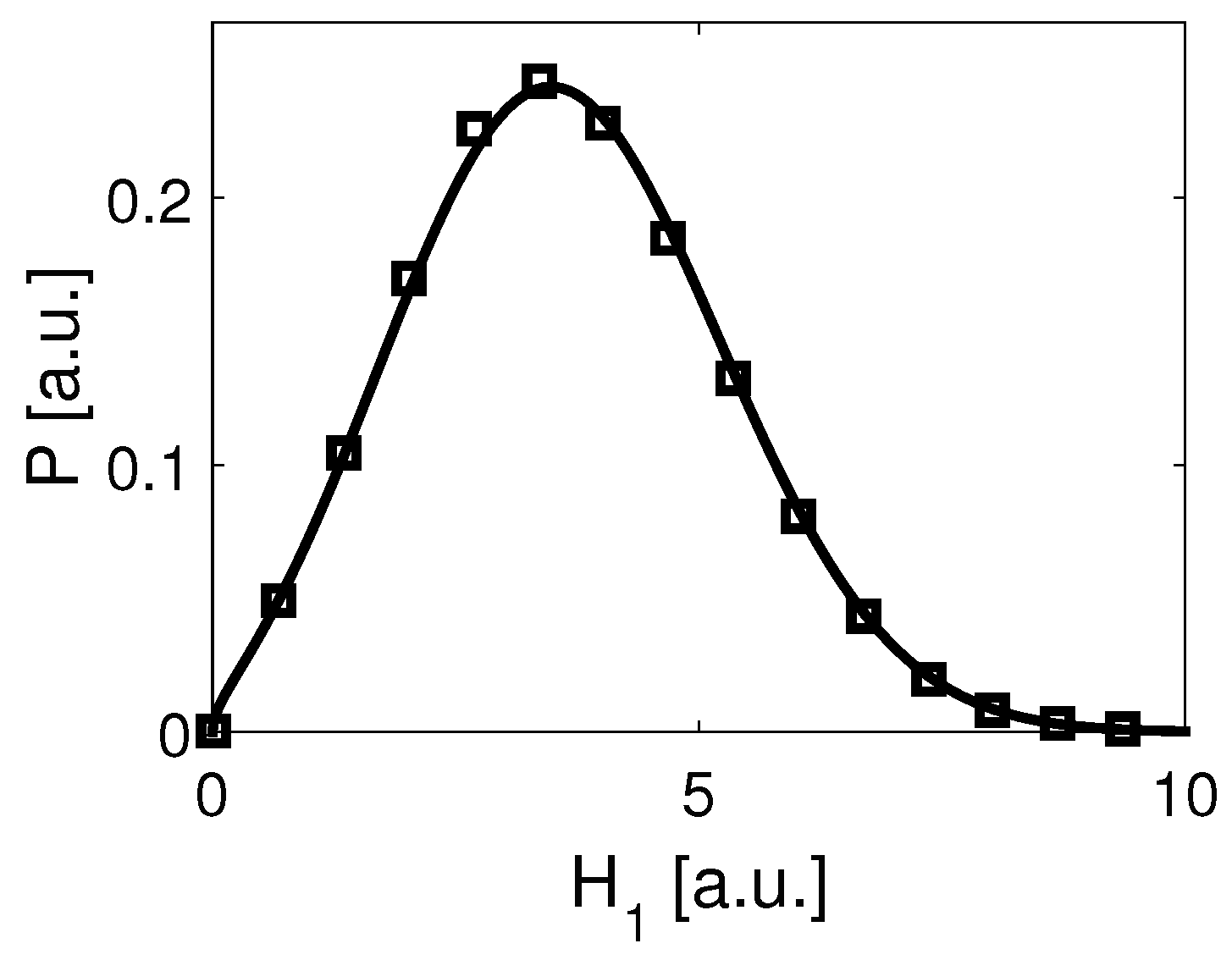
3.4. Numerics
4. Discussion
4.1. Invariants of Nambu Dynamics as Pseudo-Invariants
4.2. Active, Stochastic Systems and Generalized, Non-Extensive Entropic Measures
5. Conclusions
Conflicts of Interest
Appendix A. Derivation of Equations (14) and (15)
References
- Nambu, Y. Generalized Hamiltonian dynamics. Phys. Rev. D 1973, 7, 2405–2412. [Google Scholar] [CrossRef]
- Pandit, S.A.; Gangal, A.D. On generalized Nambu mechanics. J. Phys. A 1998, 31, 2899–2912. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A.; da Silva, L.R.; Casas, M. Dynamic thermostatting, divergenceless phase-space flows, and KBB systems. Physica A 1999, 271, 343–356. [Google Scholar] [CrossRef]
- Roston, G.B.; Plastino, A.R.; Casas, M.; Plastino, A.; da Silva, L.R. Dynamic thermostatting and statistical ensemble. Eur. Phys. J. B 2005, 48, 87–93. [Google Scholar] [CrossRef]
- Steeb, W.H.; Euler, N. A note on Nambu mechanics. Il Nuovo Cim. B 1991, 106, 263–272. [Google Scholar] [CrossRef]
- Tegmen, A. Momentum map and action-angle variables for Nambu mechanics. Czechoslov. J. Phys. 2004, 54, 749–757. [Google Scholar] [CrossRef]
- Frank, T.D. A Fokker-Planck approach to canonical-dissipative Nambu systems: With an application to human motor control during dynamic haptic perception. Phys. Lett. A 2010, 374, 3136–3142. [Google Scholar] [CrossRef]
- Yamaleev, R.M. Generalized Newtonian equations of motion. Ann. Phys. 1999, 277, 1–18. [Google Scholar] [CrossRef]
- Yamaleev, R.M. Relativistic equations of motion within Nambu’s formalism of dynamics. Ann. Phys. 2000, 285, 141–160. [Google Scholar] [CrossRef]
- Molgado, A.; Rodriguez, A. Mapping between the dynamic and mechanical properties of the relativistic oscillator and Euler free rigid body. J. Nonlinear Math. Phys. 2007, 14, 534–547. [Google Scholar] [CrossRef]
- Codriansky, S.; Bernardo, C.A.G.; Aglaee, A.; Carrillo, F.; Castellanos, J.; Pereira, G.; Perez, J. Developments in Nambu mechanics. J. Phys. A 1994, 27, 2565–2578. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Statistical treatment of autonomous systems with divergenceless flow. Physica A 1996, 232, 458–476. [Google Scholar] [CrossRef]
- Chatterjee, R. Dynamical symmetries and Nambu mechanics. Lett. Math. Phys. 1996, 36, 117–126. [Google Scholar] [CrossRef]
- Nutku, Y. Quantization with maximally degenerate Poisson brackets: The harmonic oscillator. J. Phys. A 2003, 36, 7559–7567. [Google Scholar] [CrossRef]
- Baleanu, D. Angular momentum and Killing-Yano tensors. Proc. Inst. Math. NSA Ukraine 2004, 50, 611–616. [Google Scholar] [CrossRef]
- Curtright, T.L.; Zachos, C. Deformation quantization of superintegrable systems and Nambu mechanics. New J. Phys. 2002, 4. [Google Scholar] [CrossRef]
- Curtright, T.L.; Zachos, C. Classic and quantum Nambu mechanics. Phys. Rev. D 2002, 68, 085001. [Google Scholar] [CrossRef]
- Zachos, C. Membranes and consistent quantization of Nambu dynamics. Phys. Lett. B 2003, 570, 82–88. [Google Scholar] [CrossRef]
- Frank, T.D. Active systems with Nambu dynamics: With applications to rod wielding for haptic length perception and self-propagating systems on two-spheres. Eur. Phys. J. B 2010, 74, 195–203. [Google Scholar] [CrossRef]
- Hirayama, M. Realization of Nambu mechanics: A particle interacting with an SU(2) monopole. Phys. Rev. D 1977, 16, 530. [Google Scholar] [CrossRef]
- Yamaleev, R.M. Generalized Lorentz-force equations. Ann. Phys. 2001, 292, 157–178. [Google Scholar] [CrossRef]
- Pletnev, N.G. Fillipov-Nambu n-algebras relevant to physics. Sib. Electron. Math. Rep. 2009, 6, 272–311. [Google Scholar]
- Gonera, C.; Nuktu, Y. Super-integrable Calogero-type systems admit maximal number of Poisson structures. Phys. Lett. A 2001, 285, 301–306. [Google Scholar] [CrossRef]
- Tegmen, A.; Vercin, A. Superintegrable systems, multi-Hamiltonian structures and Nambu mechanics in an arbitrary dimension. Int. J. Mod. Phys. B 2004, 19, 393–409. [Google Scholar] [CrossRef]
- Guha, P. Application of Nambu mechanics to systems of hydrodynamical type II. J. Nonlinear Math. Phys. 2004, 11, 223–232. [Google Scholar] [CrossRef]
- Müller, R.; Nevir, P. A geometric application of Nambu mechanics: The motion of three point vortices in the plane. J. Phys. A 2014, 47, 105201. [Google Scholar] [CrossRef]
- Roupas, Z. Phase space geometry and chaotic attractors in dissipative Nambu mechanics. J. Phys. A 2012, 45, 195101. [Google Scholar] [CrossRef]
- Mathis, W.; Stahl, D.; Mathis, R. Oscillator synthesis based on Nambu mechanics and canonical dissipative damping. In Proceedings of the 21st European Conference on Circuit Theory and Design (ECCTD 2013), Dresden, Germany, 8–12 September 2013.
- Mathis, W.; Mathis, R. Dissipative Nambu systems and oscillator circuit design. Nonlinear Theory Appl. IEICE 2014, 5, 259–271. [Google Scholar] [CrossRef]
- Frank, T.D. Unifying mass-action kinetics and Newtonian mechanics by means of Nambu brackts. J. Biol. Phys. 2011, 37, 375–385. [Google Scholar] [CrossRef] [PubMed]
- Frank, T.D. Nambu brackt formulation of nonlinear biochemical reactions beyond elementary mass action kinetics. J. Nonlinear Math. Phys. 2012, 19, 81–97. [Google Scholar] [CrossRef]
- Mongkolsakulvong, S.; Chaikhan, P.; Frank, T.D. Oscillatory nonequilibrium Nambu systems: The canonical-dissipative Yamaleev oscillator. Eur. Phys. J. B 2012, 85. [Google Scholar] [CrossRef]
- Chaikhan, P.; Frank, T.D.; Mongkolsakulvong, S. In-phase and anti-phase synchronization in an active Nambu mechanics system. Acta Mech. 2016, 10, 2703–2717. [Google Scholar] [CrossRef]
- Gordon, J.M.; Kim, S.; Frank, T.D. Linear non-equilibrium thermodynamics of human voluntary behavior: A canonical-dissipative Fokker-Planck equation approach involving potentials beyond the harmonic case. Condens. Matter Phys. 2016, 19, 1–6. [Google Scholar] [CrossRef]
- Schweitzer, F. Brownian Agents and Active Particles; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Romanczuk, P.; Bär, M.; Ebeling, W.; Lindner, B.; Schimansky-Geier, L. Active Brownian particles: From individual to collective stochastic dynamics. Eur. Phys. J. Spec. Top. 2012, 202, 1–162. [Google Scholar] [CrossRef]
- Haken, H. Synergetics: An Introduction; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Frank, T.D. Nonlinear Fokker-Planck Equations: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Non-extensive thermostatistics: Brief review and comment. Physica A 1995, 221, 227–290. [Google Scholar] [CrossRef]
- Abe, S.; Okamoto, Y. Nonextensive Statistical Mechanics and Its Applications; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Haken, H. Distribution function for classical and quantum systems far from thermal equilibrium. Z. Phys. 1973, 263, 267–282. [Google Scholar] [CrossRef]
- Graham, R. Statistical Theory of Instabilities in Stationary Nonequilibrium Systems with Applications to Lasers and Nonlinear Optics. In Springer Tracts in Modern Physics; Höhler, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1973; Volume 66, pp. 1–97. [Google Scholar]
- Ebeling, W.; Sokolov, I.M. Statistical Thermodynamics and Stochastic Theory of Nonequilibrium Systems; World Scientific: Singapore, 2004. [Google Scholar]
- Plastino, A.R.; Plastino, A. Non-extensive statistical mechanics and generalized Fokker-Planck equation. Physica A 1995, 222, 347–354. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Peletier, L.A. The Porous Media Equation; Applications of Nonlinear Analysis in the Physical Science; Amann, H., Bazley, N., Kirchgässner, K., Eds.; Pitman Advanced Publishing Program: Boston, MA, USA, 1981; pp. 229–241. [Google Scholar]
- Barenblatt, G.I.; Entov, V.M.; Ryzhik, V.M. Theory of Fluid Flows through Natural Rocks; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Risken, H. The Fokker-Planck Equation. Methods of Solution and Applications; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Kaniadakis, G. H-theorem and generalized entropies within the framework of nonlinear kinetics. Phys. Lett. A 2001, 288, 283–291. [Google Scholar] [CrossRef]
- Shiino, M. Free energies based on generalized entropies and H-theorems for nonlinear Fokker-Planck equations. J. Math. Phys. 2001, 42, 2540–2553. [Google Scholar] [CrossRef]
- Frank, T.D.; Daffertshofer, A. H-theorem for nonlinear Fokker-Planck equations related to generalized thermostatistics. Physica A 2001, 295, 455–474. [Google Scholar] [CrossRef]
- Chavanis, P.H. Generalized Fokker-Planck equations and effective thermodynamics. Physica A 2004, 340, 57–65. [Google Scholar] [CrossRef]
- Schwämmle, V.; Nobre, F.D.; Curado, E. Consequences of the H-theorem for nonlinear Fokker-Planck equations. Phys. Rev. E 2007, 76, 041123. [Google Scholar] [CrossRef] [PubMed]
- Frank, T.D. On the boundedness of free energy functionals. Nonlinear Phenom. Complex Syst. 2003, 6, 696–704. [Google Scholar]
- Dotov, D.G.; Frank, T.D. From the W-method to the canonical-dissipative method for studying uni-manual rhythmic behavior. Motor Control 2011, 15, 550–567. [Google Scholar] [CrossRef] [PubMed]
- Dotov, D.G.; Kim, S.; Frank, T.D. Non-equilibrium thermodynamical description of rhythmic motion patterns of active systems: A canonical-dissipative approach. BioSystems 2015, 128, 26–36. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Gordon, J.M.; Frank, T.D. Nonequilibrium thermodynamic state variables of human self-paced rhythmic motions: Canonical-dissipative approach, augmented Langevin equation, and entropy maximization. Open Syst. Inf. Dyn. 2015, 22. [Google Scholar] [CrossRef]
- Mongkolsakulvong, S.; Frank, T.D. Canonical-dissipative limit cycle oscillators with a short-range interaction in phase space. Condens. Matter Phys. 2010, 13, 13001. [Google Scholar] [CrossRef]
- Frank, T.D. On a moment-based data analysis method for canonical-dissipative oscillator systems. Fluct. Noise Lett. 2010, 9, 69–87. [Google Scholar] [CrossRef]
- Frank, T.D.; Kim, S.; Dotov, D.G. Canonical-dissipative nonequilibrium energy distributions: Parameter estimation via implicit moment method, implementation and application. Int. J. Mod. Phys. B 2013, 27. [Google Scholar] [CrossRef]
- Frank, T.D. Virial theorem and non-equilibrium canonical-dissipative distributions characterizing Parkinson tremor. Int. J. Mod. Phys. B 2011, 25, 1465–1469. [Google Scholar] [CrossRef]
- Bödeker, H.U.; Beta, C.; Frank, T.D.; Bodenschatz, E. Quantitative analysis of random ameboid motion. Europhys. Lett. 2010, 90, 28005. [Google Scholar] [CrossRef]
- Frank, T.D. Nonextensive cutoff distributions of postural sway for the old and the young. Physica A 2009, 388, 2503–2510. [Google Scholar] [CrossRef]

© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frank, T.D. Active and Purely Dissipative Nambu Systems in General Thermostatistical Settings Described by Nonlinear Partial Differential Equations Involving Generalized Entropy Measures. Entropy 2017, 19, 8. https://doi.org/10.3390/e19010008
Frank TD. Active and Purely Dissipative Nambu Systems in General Thermostatistical Settings Described by Nonlinear Partial Differential Equations Involving Generalized Entropy Measures. Entropy. 2017; 19(1):8. https://doi.org/10.3390/e19010008
Chicago/Turabian StyleFrank, T. D. 2017. "Active and Purely Dissipative Nambu Systems in General Thermostatistical Settings Described by Nonlinear Partial Differential Equations Involving Generalized Entropy Measures" Entropy 19, no. 1: 8. https://doi.org/10.3390/e19010008
APA StyleFrank, T. D. (2017). Active and Purely Dissipative Nambu Systems in General Thermostatistical Settings Described by Nonlinear Partial Differential Equations Involving Generalized Entropy Measures. Entropy, 19(1), 8. https://doi.org/10.3390/e19010008