A Soft Parameter Function Penalized Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification
Abstract
:1. Introduction
2. Traditional MCC Algorithm and ZA Techniques
2.1. Traditional MCC Algorithm
2.2. Zero Attracting Techniques
3. Proposed Sparse SPF-NMCC Algorithm
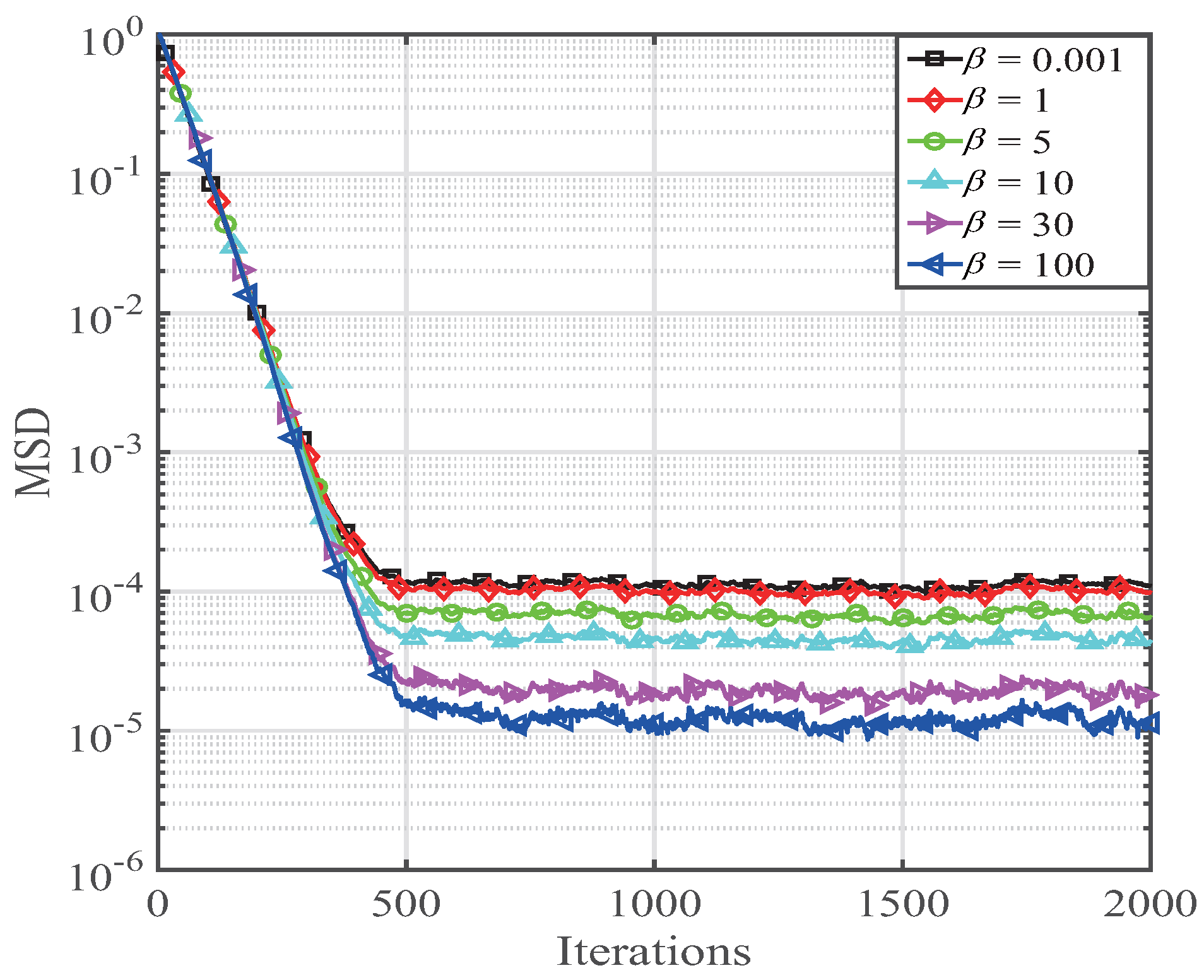
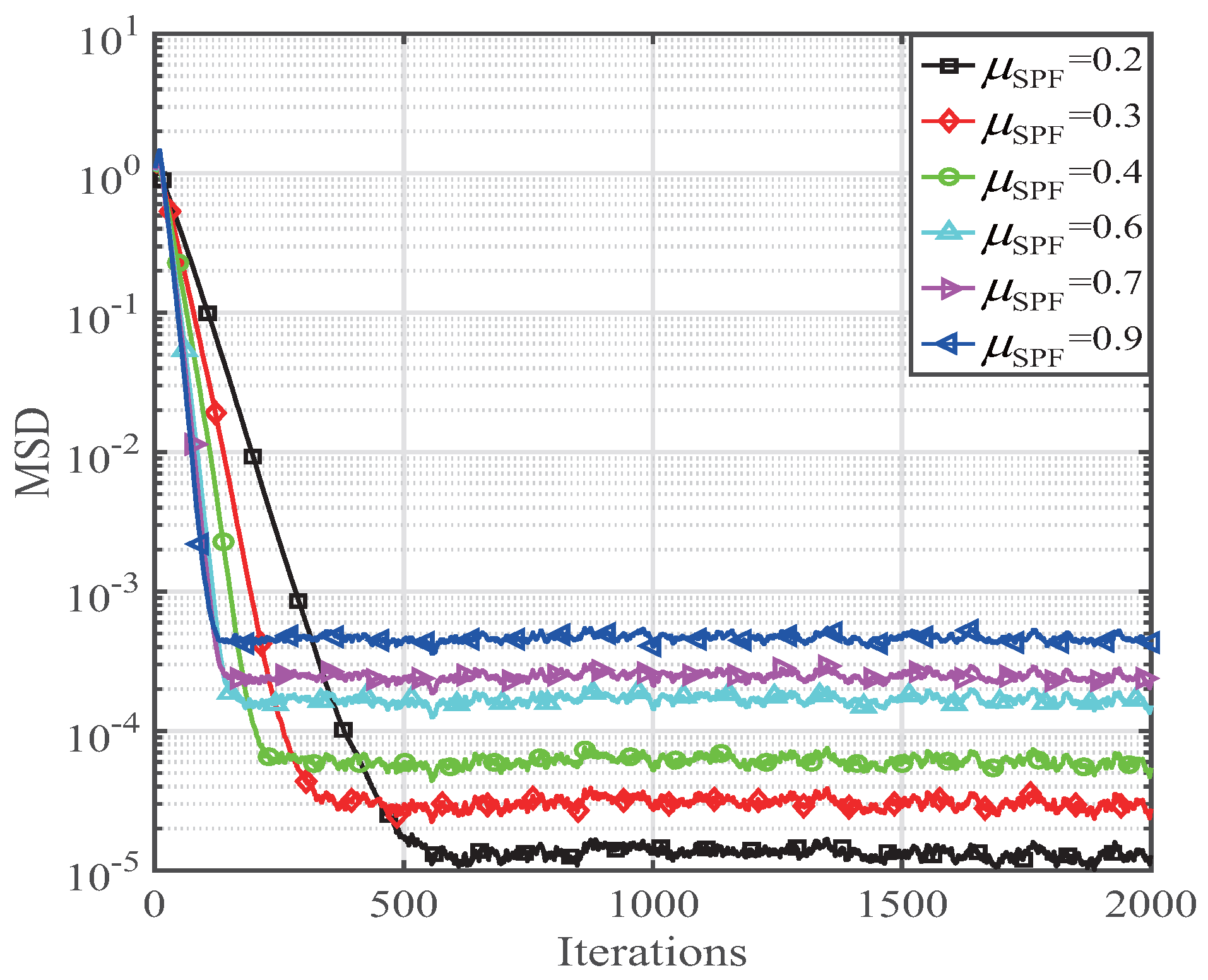
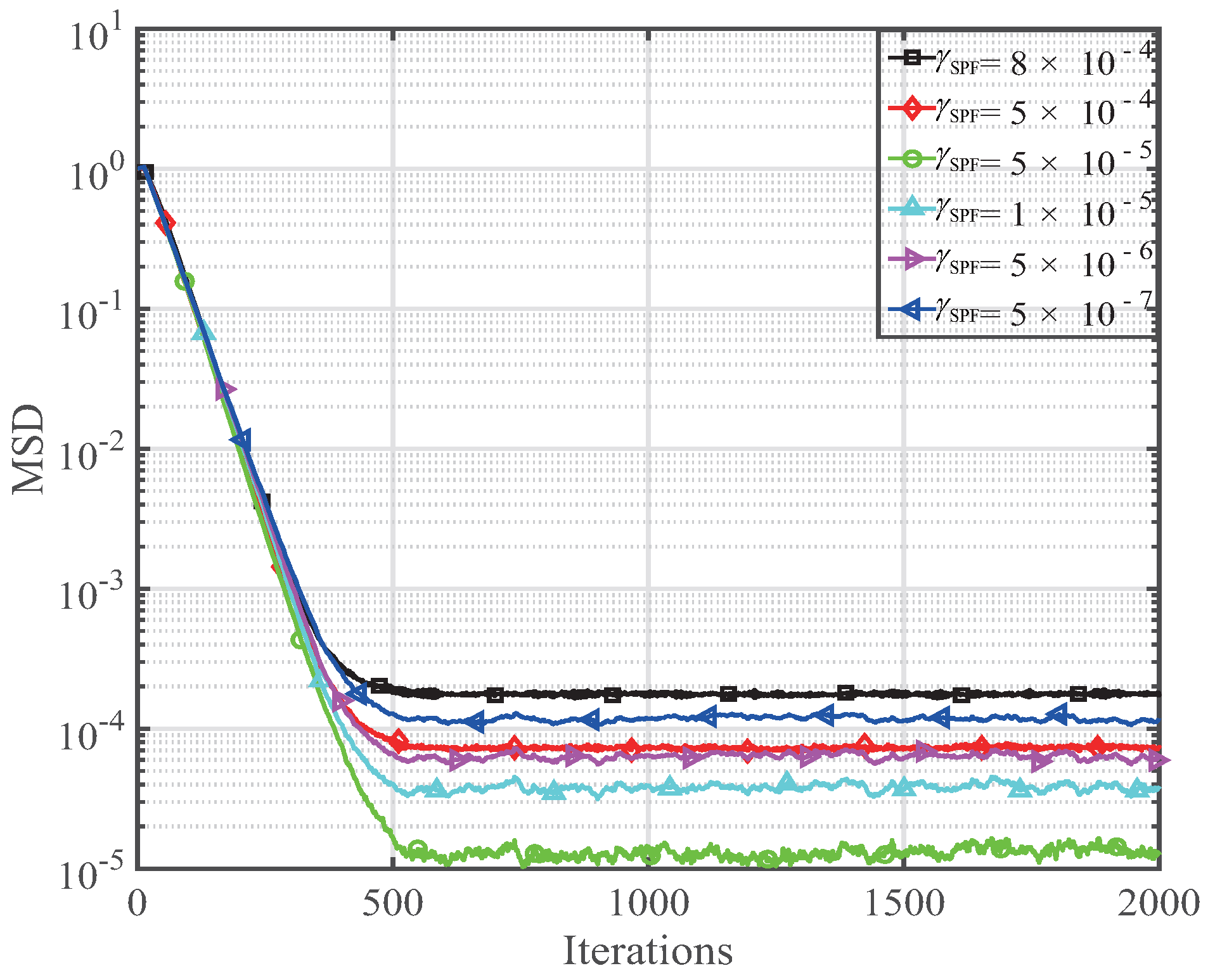
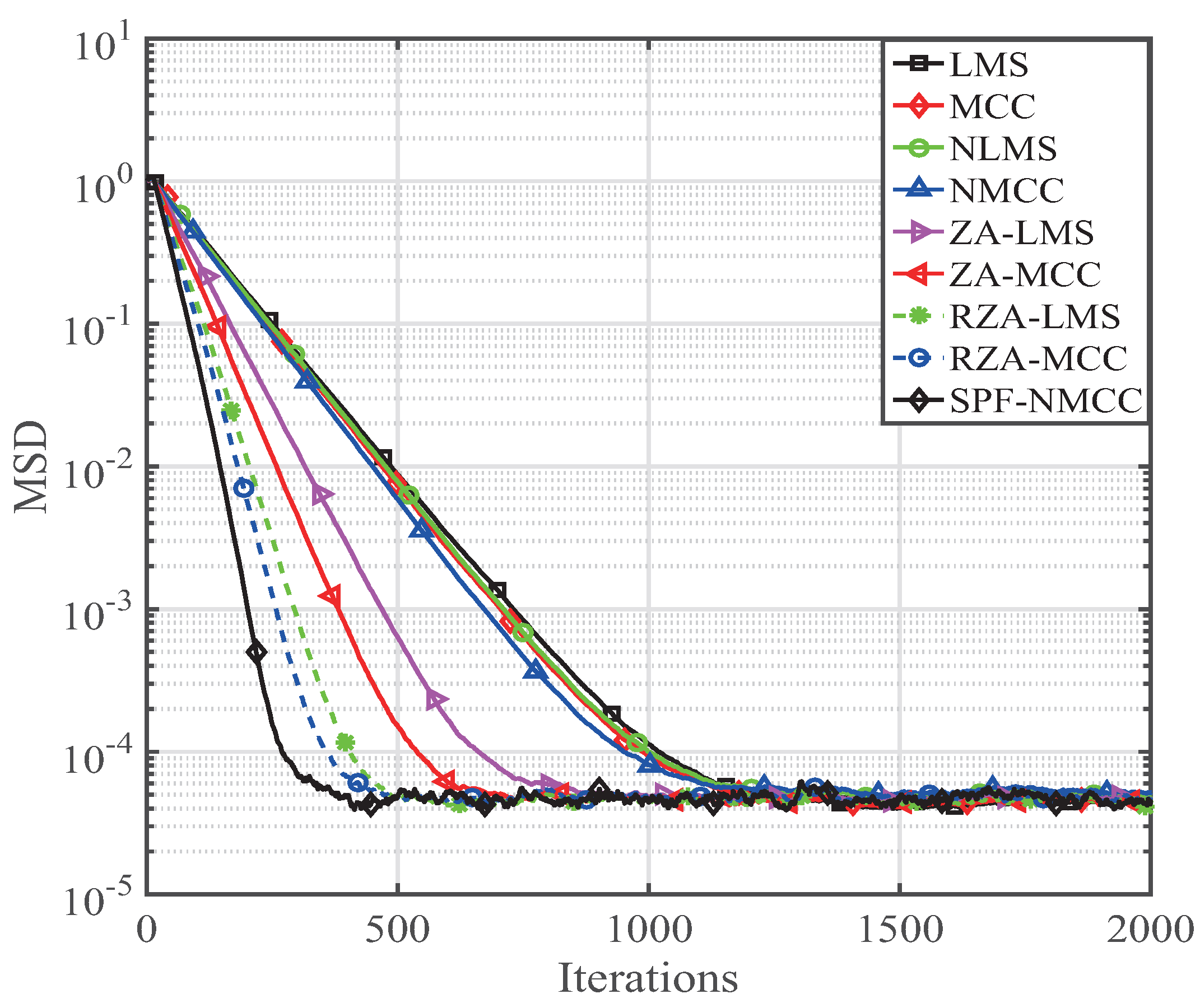
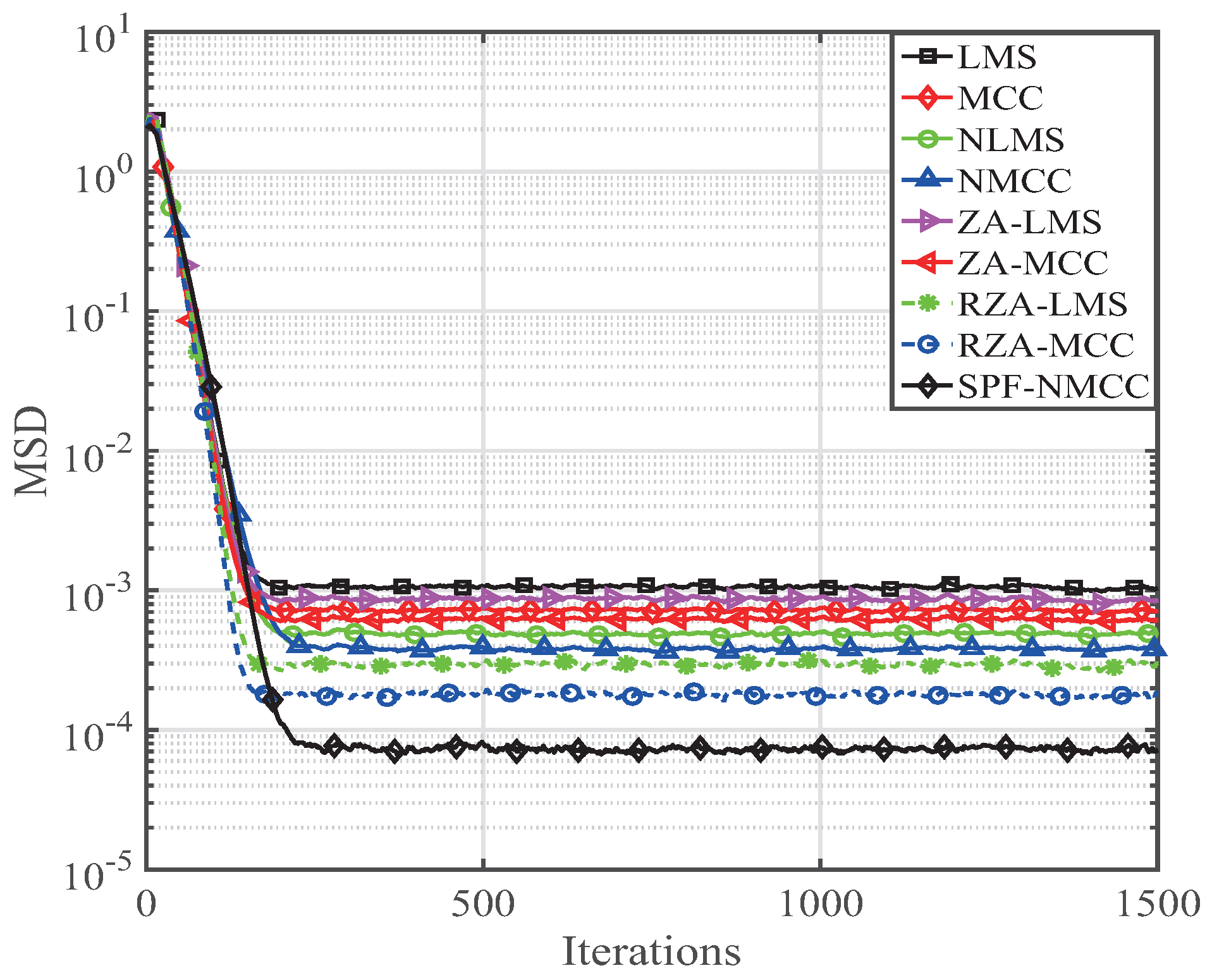
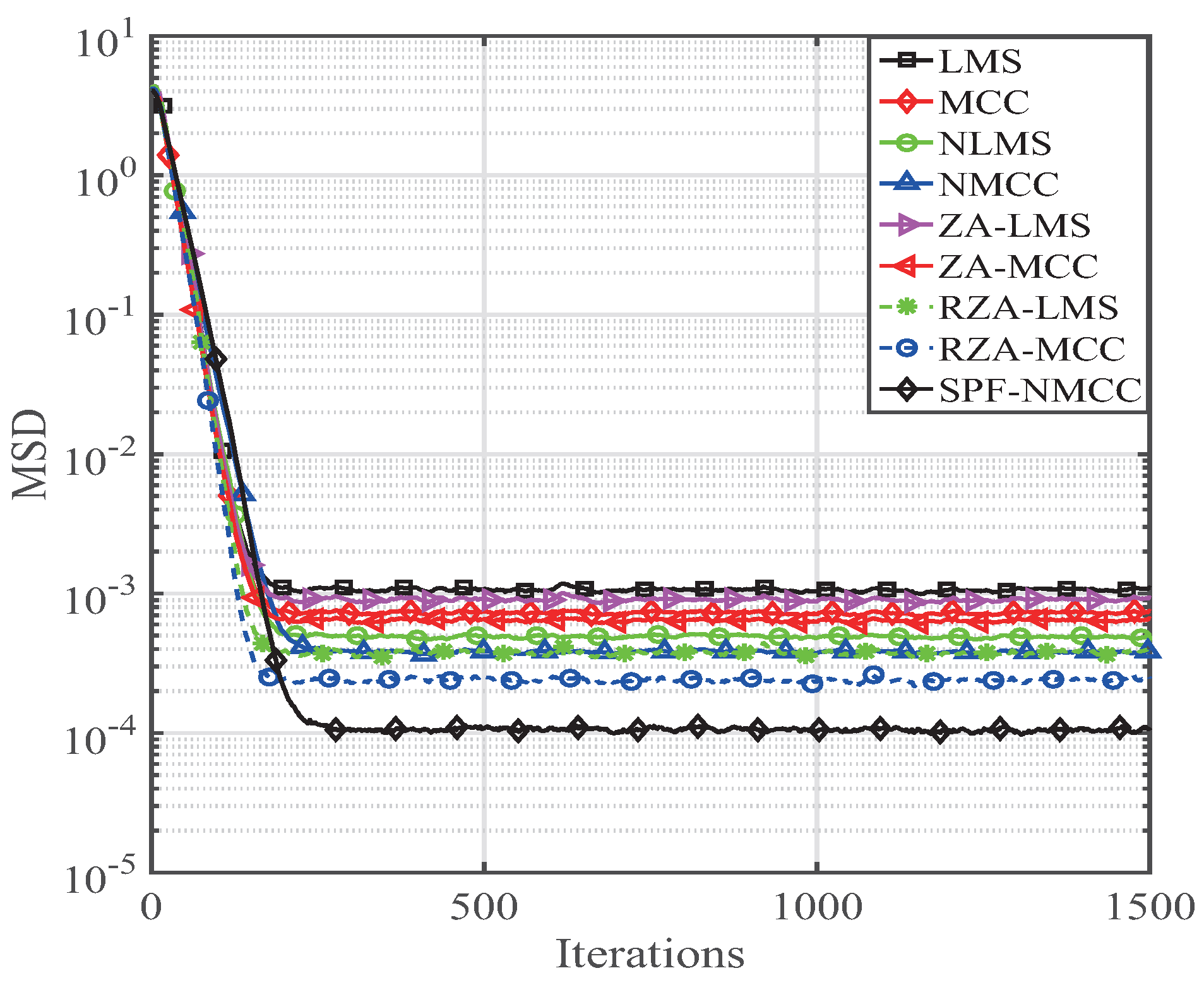
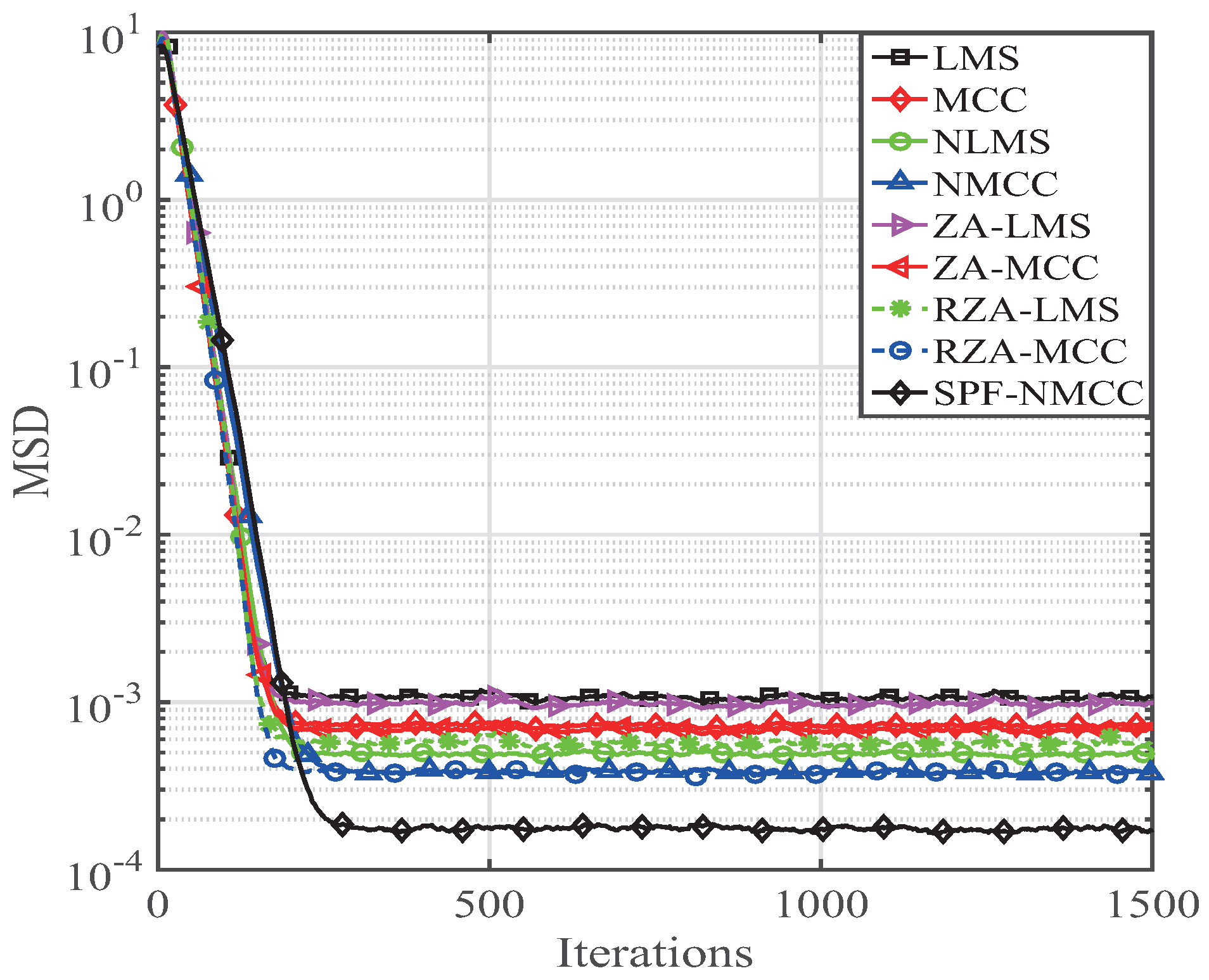
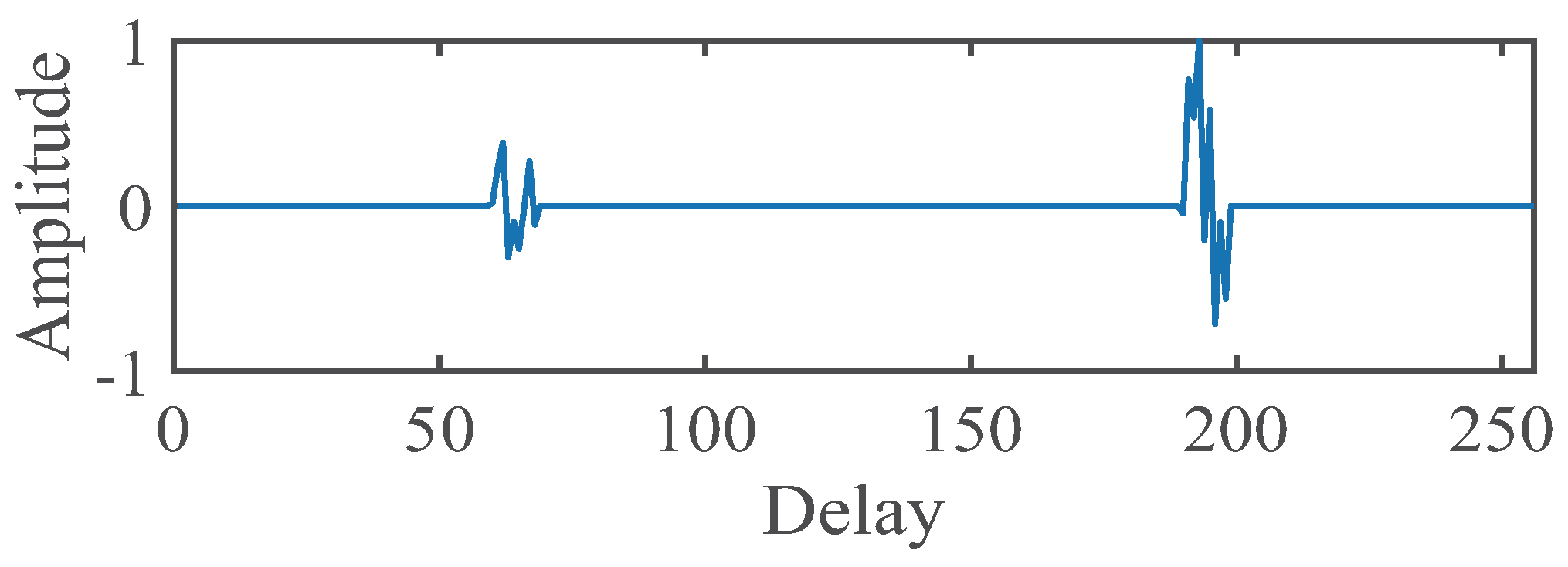
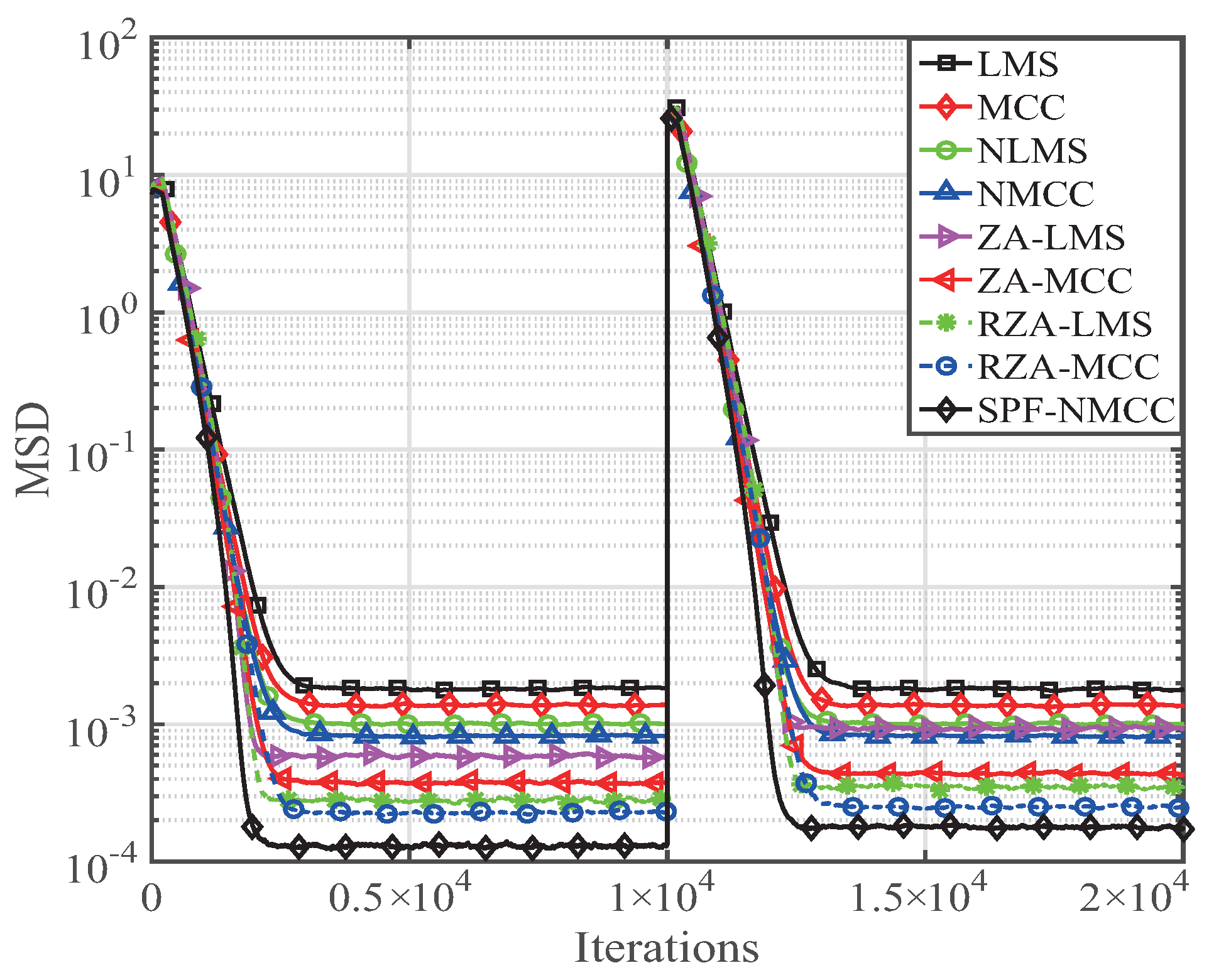
4. Performance of the SPF-NMCC Algorithm
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gui, G.; Kumagai, S.; Mehbodniya, A.; Adachi, F. Two are better than one:adaptive sparse system idenfication using affine aombination of two sparse adaptive filters. In Proceedings of the IEEE 79th Vehicular Technology Conference (VTC2014-Spring), Seoul, Korea, 18–21 May 2014.
- Chen, B.; Xing, L.; Liang, J.; Zheng, N.; Principe, J.C. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 2014, 21, 880–884. [Google Scholar]
- Cotter, S.F.; Rao, B.D. Sparse channel estimation via matching pursuit with application to equalization. IEEE Trans. Commun. 2002, 50, 374–377. [Google Scholar] [CrossRef]
- Kalouptsidis, N.; Mileounis, G.; Babadi, B.; Tarkh, V. Adaptive algorithms for sparse system identification. Signal Process. 2011, 91, 1910–1919. [Google Scholar] [CrossRef]
- Marvasti, F.; Amini, A.; Haddadi, F. A unified approach to sparse signal processing. EURASIP J. Adv. Signal Process. 2012, 2012, 1–45. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Statist. Soc B. 1996, 58, 267–288. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, Y.; Hero, A.O. Sparse LMS for system identification. In Proceedings of the 2009 IEEE International Conference on Acoustic Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 3125–3128.
- Gu, Y.; Jin, J.; Mei, S. L0 norm constraint LMS algorithms for sparse system identification. IEEE Signal Process. Lett. 2009, 16, 774–777. [Google Scholar]
- Taheri, O.; Vorobyov, S.A. Sparse channel estimation with Lp-norm and reweighted L1-norm penalized least mean squares. In Proceedings of the 2011 IEEE International Conference on Acoustic, Speech and Signal Processing, Prague, Czech Republic, 22–27 May 2011; pp. 2864–2867.
- Li, Y.; Wang, Y.; Jiang, T. Sparse channel estimation based on a p-norm-like constrained least mean fourth algorithm. In Proceedings of the 7th International Conference on Wireless Communications and Signal Processing, Nanjing, China, 15–17 October 2015.
- Gui, G.; Adachi, F. Sparse least mean fourth filter with zero-attracting l1-norm constraint. In Proceedings of the 9th International Conference on Information, Communications and Signal Processing (ICICS), Tainan, Taiwan, 10–13 December 2013.
- Li, Y.; Zhang, C.; Wang, S. Low complexity non-uniform penalized affine projection algorithm for sparse system identification. Circuits Syst. Signal Process. 2016, 35, 1611–1624. [Google Scholar] [CrossRef]
- Meng, R.; de Lamare, R.C.; Nascimento, H.V. Sparsity-aware affine projection adaptive algorithms for system identification. In Proceedings of the 2011 Sensor Signal Processing for Defence (SSPD 2011), London, UK, 17–29 September 2011.
- Li, Y.; Li, W.; Yu, W.; Wan, J.; Li, Z. Sparse adaptive channel estimation based on lp-norm-penalized affine projection algorithm. Int. J. Antennas Propag. 2014, 2014, 434659. [Google Scholar] [CrossRef]
- Duttweiler, D.L. Proportionate normalized least-mean-squares adaptation in echo cancelers. IEEE Trans. Speech Audio Process. 2000, 8, 508–518. [Google Scholar] [CrossRef]
- Deng, H.; Doroslovacki, M. Improving convergence of the PNLMS algorithm for sparse impulse response identification. IEEE Signal Process. Lett. 2005, 12, 181–184. [Google Scholar] [CrossRef]
- Li, Y.; Hamamura, M. An improved proportionate normalized least-mean-square algorithm for broadband multipath channel estimation. Sci. World J. 2014, 2014, 572969. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Peng, S.; Chen, B.; Zhao, H.; Principe, J.C. Proportionate minimum error entropy algorithm for sparse system identification. Entropy 2015, 17, 5995–6006. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y. Sparse SM-NLMS algorithm based on correntyopy criterion. Electron. Lett. 2016, 52, 1461–1463. [Google Scholar] [CrossRef]
- Li, Y.; Hamamura, M. Zero-attracting variable-step-size least mean square algorithms for adaptive sparse channel estimation. Int. J. Adapt. Control Signal Process. 2015, 29, 1189–1206. [Google Scholar] [CrossRef]
- Gui, G.; Peng, W.; Adachi, F. Sparse least mean fourth algorithm for adaptive channel estimation in low signal-to-noise ratio region. Int. J. Commun. Syst. 2014, 27, 3147–3157. [Google Scholar] [CrossRef]
- Gui, G.; Xu, L.; Matsushita, S. Improved adaptive sparse channel estimation using mixed square/fourth error criterion. J. Frankl. Inst. 2015, 352, 4579–4594. [Google Scholar] [CrossRef]
- Gui, G.; Mehbodniya, A.; Adachi, F. Least mean square/fourth algorithm for adaptive sparse channel estimation. In Proceedings of the IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 296–300.
- Li, Y.; Wang, Y.; Jiang, T. Norm-adaption penalized least mean square/fourth algorithm for sparse channel estimation. Signal Process. 2016, 128, 243–251. [Google Scholar] [CrossRef]
- Salman, M.S. Sparse leaky-LMS algorithm for system identification and its convergence analysis. Int. J. Adapt. Control Signal Process. 2014, 28, 1065–1072. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Sparse-aware set-membership NLMS algorithms and their application for sparse channel estimation and echo cancelation. AEU Int. J. Electron. Commun. 2016, 70, 895–902. [Google Scholar] [CrossRef]
- Albu, F.; Gully, A.; de Lamare, R.C. Sparsity-aware pseudo affine projection algorithm for active noise control. In Proceedings of the 2014 Annual Summit and Conference on Asia-Pacific Signal and Information Processing Association (APSIPA), Siem Reap, Cambodia, 9–12 December 2014.
- Li, Y.; Jin, Z.; Wang, Y.; Yang, R. A robust sparse adaptive filtering algorithm with a correntropy induced metric constraint for broadband multi-path channel estimation. Entropy 2016, 18, 380. [Google Scholar] [CrossRef]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. C. R. Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Paleologu, C.; Ciochina, S.; Benesty, J. An efficient proportionate affine projection algorithm for echo cancellation. IEEE Signal Process. Lett. 2010, 17, 165–168. [Google Scholar] [CrossRef]
- Walach, E.; Widrow, B. The least mean fourth (LMF) adaptive algorithm and its family. IEEE Trans. Inf. Theory 1984, 30, 275–283. [Google Scholar] [CrossRef]
- Lim, S. Combined LMS/F algorithm. Electron. Lett. 1997, 33, 467–468. [Google Scholar] [CrossRef]
- Chambers, J.A.; Tanrikulu, O.; Constantinides, A.G. Least mean minxed-norm adaptive filtering. Electron. Lett. 1994, 30, 1574–1575. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Albu, F. Sparse channel estimation based on a reweighted least-mean mixed-norm adaptive filter algorithm. In Proceedings of the 2016 European Signal Processing Conference (EUSIPCO 2016), Budapest, Hungary, 29 August–2 September 2016.
- Li, Y.; Wang, Y.; Jiang, T. Sparse least mean mixed-norm adaptive filtering algorithms for sparse channel estimation applications. Int. J. Commun. Syst. 2016. [Google Scholar] [CrossRef]
- Ozeki, K.; Umeda, T. An adaptive filtering algorithm using an orthogonal projection to an affine subspace and its properties. Electron. Commun. Jpn. 1984, 67, 19–27. [Google Scholar] [CrossRef]
- Shin, H.-C.; Sayed, A.H. Mean-square performance of a family of affine projection algorithms. IEEE Trans. Signal Process. 2004, 52, 90–102. [Google Scholar] [CrossRef]
- Haykin, S. Adaptive Filter Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Sayed, A.H. Fundamentals of Adaptive Filtering, 1st ed.; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Gui, G.; Peng, W.; Adachi, F. Improved adaptive sparse channel estimation based on the least mean square algorithm. In Proceedings of the 2013 IEEE wireless communication and neteorking conference, Shanghai, China, 7–10 April 2013; pp. 3105–3109.
- Erdogmus, D.; Principe, J.C. Generalized information potential criterion for adaptive system training. IEEE Trans. Neural Netw. 2002, 13, 1035–1044. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Principe, J.C. Using correntropy as a cost function in linear adaptive filters. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GE, USA, 14–19 June 2009; pp. 2950–2955.
- Haddad, D.B.; petraglia, M.R.; Petraglia, A. A unified approach for sparsity-aware and maximum correntropy adaptive filters. In Proceedings of the 24th European Signal processing Conference (EUSIPCO’16), Budapest, Hungary, 29 August–2 September 2016; pp. 170–174.
- Zhao, S.; Chen, B.; Principe, J.C. Kernel adaptive filtering with maximum correntropy criterion. In Proceedings of the 2011 International Joint Conference on Neural Networks (IJCNN), San Jose, CA, USA, 31 July–5 August 2011.
- Chen, B.; Xing, L.; Zhao, H.; Zheng, N.; Principe, J.C. Generalized correntropy for robust adaptive filtering. IEEE Trans. Signal Process. 2016, 64, 3376–3387. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Zhao, H.; Zheng, N.; Principe, J.C. Convergence of a fixed-point algorithm under maximum correntropy criterion. IEEE Signal Process. Lett. 2015, 22, 1723–1727. [Google Scholar] [CrossRef]
- Ma, W.; Qu, H.; Gui, G.; Xu, L.; Zhao, J.; Chen, B. Maximum correntropy criterion based sparse adaptive filtering algorithms for robust channel estimation under non-Gaussian environments. J. Frankl. Inst. 2015, 352, 2708–2727. [Google Scholar] [CrossRef]

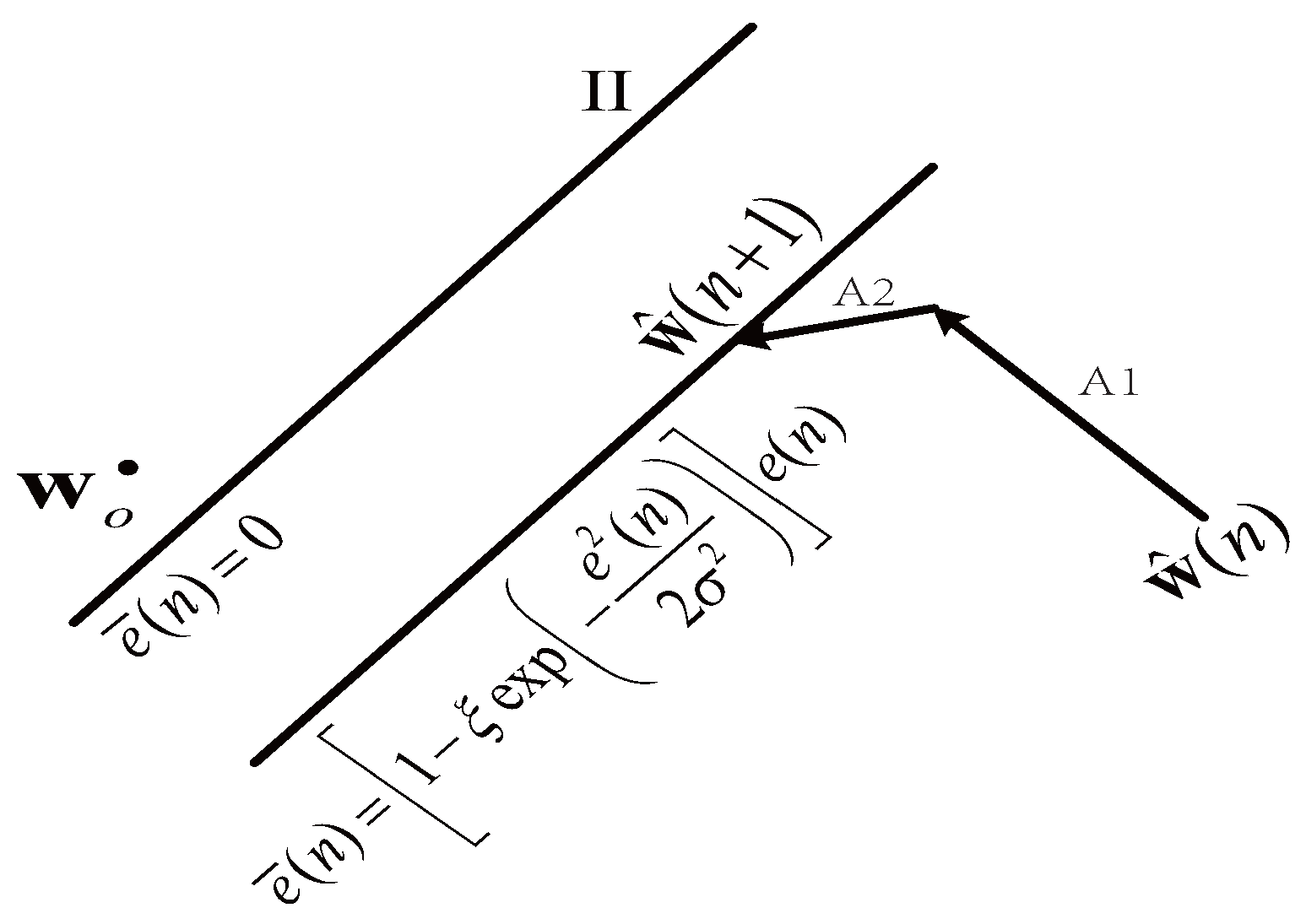
| Algorithms | Additions | Multiplications | Divisions | Exponential Calculation |
|---|---|---|---|---|
| LMS | - | - | ||
| MCC | - | 1 | ||
| NLMS | 1 | - | ||
| NMCC | 1 | 1 | ||
| ZA-LMS | N+ 3K | N+ 3K + 1 | - | - |
| ZA-MCC | N+ 3K | N+ 3K + 2 | - | 1 |
| RZA-LMS | N+ 4K | N+ 4K + 1 | N | - |
| RZA-MCC | N+ 4K | N+ 4K + 2 | N | 1 |
| SPF-NMCC | N+ 4K + 1 | N+ 5K | N | N+ 1 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, Y.; Yang, R.; Albu, F. A Soft Parameter Function Penalized Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification. Entropy 2017, 19, 45. https://doi.org/10.3390/e19010045
Li Y, Wang Y, Yang R, Albu F. A Soft Parameter Function Penalized Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification. Entropy. 2017; 19(1):45. https://doi.org/10.3390/e19010045
Chicago/Turabian StyleLi, Yingsong, Yanyan Wang, Rui Yang, and Felix Albu. 2017. "A Soft Parameter Function Penalized Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification" Entropy 19, no. 1: 45. https://doi.org/10.3390/e19010045
APA StyleLi, Y., Wang, Y., Yang, R., & Albu, F. (2017). A Soft Parameter Function Penalized Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification. Entropy, 19(1), 45. https://doi.org/10.3390/e19010045







