1. Introduction
Cranes, highly risky specialized pieces of equipment, are widely used in industrial and mining enterprises, real estate, ports, railway transportation, and construction [
1]. Due to the risks associated with cranes, their safety problems have received widespread attention [
2,
3]. According to China’s General Administration of Quality Supervision, Inspection and Quarantine, there were 2.1044 million registered cranes in China in 2015 [
4]. Hence, problems influenced by factors such as service life, environmental impact, equipment failure, operator error, and inadequate training constitute a significant threat to human life and property. In 2015, 257 special equipment accidents were reported in China, killing 278 people and injuring 320. Crane accidents represented 30.74% of the total [
4], and were responsible for 41.01% of all deaths [
4], an increase of 27.42% and 16.32%, respectively, on the figures for 2014. Thus, crane safety has become the focus of occupational safety supervision in China, and crane safety assessments are emerging as an important means of preventing accidents and reducing the number of casualties.
There have been a number of studies on crane safety assessments. Xu and Jiang [
5] studied a fuzzy analytic hierarchy process (FAHP) for determining the safety status of cranes, and Hu et al. [
6] evaluated a safety classification for bridges and gantries based on FAHP. Zhao et al. [
7] applied FAHP to evaluate the structural safety of shipbuilding cranes, while Xu and Li [
8] constructed a three-scale analytic hierarchy process for assessing the hazard degree of the hoisting mechanism of a crawler crane. Chen and Zhang [
9] developed a grey model for evaluating the safety of the gantry system in a portal crane. In reality, fuzzy evaluation methods are widely used because their mathematics is easy to understand and calculate. However, the maximum membership principle (MMP) of comprehensive fuzzy evaluations is not suitable for determining safety grades [
10,
11,
12]. To overcome the limitations of MMP, Yang et al. [
13] used unascertained measurement theory (UMT) for crane safety assessments, but their assessment results were affected by the selection of confidence criteria. This is because higher confidence values give more conservative results. If lower confidence intervals are selected, the results may not be reliable. In addition, the above methods often use the analytic hierarchy process to calculate index weights, which cannot clearly reveal the potential information provided by each index value.
Intelligent assessment methods can avoid those shortages above. Intelligent assessment approaches based on machine learning, such as back-propagation artificial neural networks [
14], fuzzy neural networks [
15], and support vector machines [
16], have been applied to crane safety evaluations, but these techniques depend on reliable and typical standard samples, which are often unavailable. Therefore, intelligent risk assessment approaches are rarely used in practice for crane safety assessments.
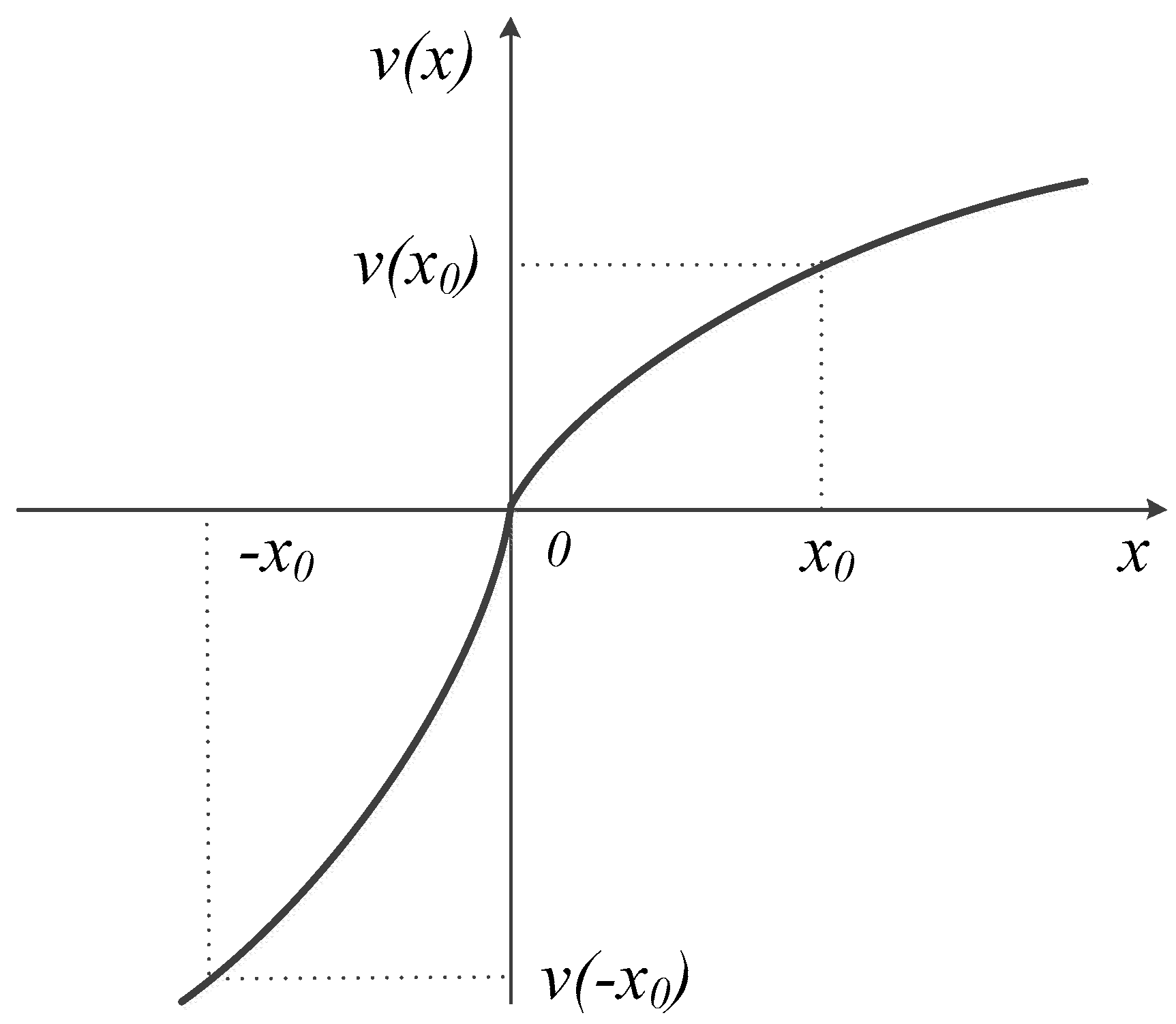
Via a study of the literature, there are three major limitations for crane safety assessment based on fuzzy evaluation approaches: (i) the existing crane safety studies are based on expected utility theory which assumes that people are completely rational. However, this theory has been queried by behavioral economists and psychologists using the Allais paradox and the Ellsberg paradox [
17]. When assessing crane safety, the evaluators are not absolutely rational and the evaluation results are inevitably linked to the subjectivity of the evaluators. The risk attitude of evaluators should not be neglected; (ii) index weights are usually calculated by subjectively weighting method, which cannot sufficiently reflect the index evaluation value information itself; and (iii) crane safety grade is often determined on MMP or confidence criteria which may lead to unreasonable results.
Regarding to the aforementioned limitations, this work aims to propose a crane safety assessment model based on entropy and cumulative prospect theory. Entropy was originally introduced to information theory by Shannon [
18], and has become a popular method for objective weight determination [
19]. Proposed prospect theory [
20] was proposed by Kahneman and Tversky. It later was developed into cumulative prospect theory (CPT) [
21]. CPT states that decision-makers are not perfectly rational, but instead display a limited degree of rationality [
22]. Other descriptive decision theories have been developed, such as disappointment theory [
23,
24], regret theory [
25], and third-generation prospect theory [
26]. However, CPT is regarded as one of the popular of these descriptive decision theories [
27,
28,
29,
30]. Advances by psychologists and behavioral economists mean that CPT provides a well-supported descriptive paradigm for decision-making based on bounded rationality [
22]. Thus, CPT is an attractive alternative for improving the rationality of evaluation results. In this study, on one hand we are using entropy to obtain objective weights about the importance of crane risk factors, and on the other hand we are using cumulative prospect theory to determine the safety grade of the crane.
The remainder of this paper is organized as follows: In
Section 2, the entropy method and CPT are briefly introduced. The proposed method for crane safety assessments, which combines the concepts of entropy and CPT, is presented in
Section 3.
Section 4 presents a case study in which the proposed method is used to assess the safety grade of a general overhead traveling crane. In
Section 5, the results obtained from this case study are discussed and compared with those from other methods. Finally,
Section 6 presents our conclusions.
4. Case Study
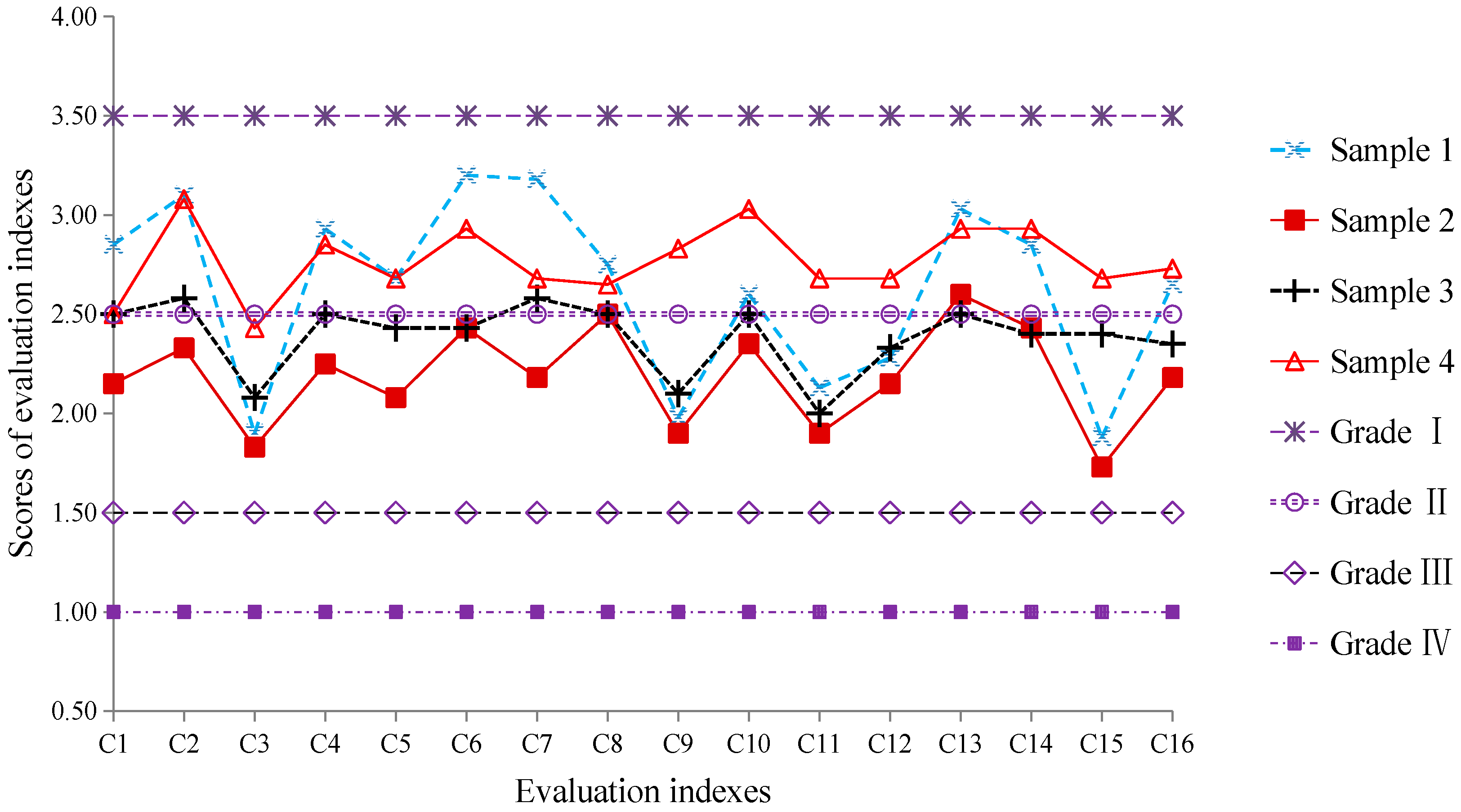
Cranes are widely used in industrial production processes. Crane safety problems are, therefore, a significant concern for numerous enterprises, as well as the Special Equipment Inspection Institute. Of the different types of cranes, general overhead cranes are commonly used and have a high accident rate [
45,
46]. Thus, to illustrate the proposed method, we determined the safety grade of a general overhead traveling crane. For comparison with the proposed model, sample data from four general overhead traveling cranes [
5,
13] are also examined. The index system includes four subsystems: portal frame (B1), hoisting mechanism (B2), operation mechanism (B3), and staff and management factors (B4). A total of 16 key criteria across these four subsystems [
5,
13] are used in the safety assessment of general overhead traveling cranes. These criteria are listed in
Table 1. According to previous studies, the safety grades for general overhead traveling cranes were divided into four categories [
5,
6,
13], i.e., very low, low, medium, and high risk, denoted as I, II, III, and IV, respectively. The grade standard is given in
Table 2.
4.1. Establishing the Evaluation Vector
Ten experts were invited to judge the crane safety status according to
Table 1 and
Table 2. The probability of every index with respect to grade
h (
h = I, II, III, IV) is presented in
Table 3 [
5,
13]. For example, C1 of sample 1 was judged as belonging to grade I by two experts, to grade II by five experts, and to grade III by three experts. None of the experts judged this index as belonging to grade IV. Thus, the evaluation vector for this index can be written as (0.2, 0.5, 0.3, 0) [
5]. The remaining indices were judged in a similar manner.
The judgments given by the experts for four general overhead traveling crane samples were defuzzified according to Equation (9) and
Table 3. For example, the fuzzy assessment results for C1 of sample 1 were defuzzified as follows:
The other fuzzy assessment results were handled similarly. The defuzzified results for the four samples are presented in
Table 4.
4.2. Calculating the Weights of Evaluation Indexes
To reduce the effect of subjective judgments, the proposed model uses an entropy method to calculate the weights of indexes. According to
Table 2, four typical crane samples were established based on the lower limits value of the standard evaluation index score interval. These are denoted by I#, II#, III#, and IV#. The decision matrix based on the evaluation standard and defuzzification values of the four crane samples were then obtained as:
The normalized decision-making matrix was obtained using Equation (2) as:
Equations (3) and (4) were then used to calculate the entropy weight of each index. To analyze the sensitivity of the assessment results to different weights, we also considered 16 subjective weights for general overhead traveling cranes [
5]. The subjective and objective weights of general overhead traveling cranes are listed separately in
Table 5.
4.3. Establishing Positive and Negative Prospect Matrices
According to the normalized decision-making matrix
R, the PIS and NIS were acquired as:
According to Equations (10) and (11), the positive and negative prospect matrices were then calculated as follows:
4.4. Determining the Safety Grade
The overall prospect values of the four crane samples were calculated using Equation (5). Finally, the safety grades were determined according to the overall prospect values
Vi. The assessment results are given in
Table 6.
The safety grade of the crane based on the overall prospect value can be obtained from
Table 6. Using the subjective weight vector
W1, the overall prospect values
Vi for the crane safety grades were found to be as follows:
- Grade I:
Vi ≥ 0.9596.
- Grade II:
−0.2271 ≤ Vi < 0.9596.
- Grade III:
−1.3241 ≤ Vi < −0.2271.
- Grade IV:
−1.89 ≤ Vi < −1.3241.
When we adopted the objective weight vector
W2, the overall prospect values V
i for the crane safety grades were as follows:
- Grade I:
Vi ≥ 0.9596.
- Grade II:
−0.2246 ≤ Vi < 0.9596.
- Grade III:
−1.3072 ≤ Vi < −0.2246.
- Grade IV:
−1.8742 ≤ Vi < −1.3072.
The results in
Table 6 indicate that, regardless of whether we use the subjective weight vector
W1 or the objective weight vector
W2, the safety grades and rankings are consistent. It can be concluded that the assessment results are not particularly sensitive to different weights.
6. Conclusions
Crane safety assessment is a significant issue affecting people’s lives and property. The safety grade of a crane should be reasonably evaluated with respect to different attributes. However, the accuracy of the evaluation results is affected by MMP (FAHP) and confidence criteria (UMT). Therefore, a more scientific and reasonable method is needed for crane safety assessments.
This work proposed a method for crane safety assessments using CPT and entropy. Entropy was used to calculate index weights, and CPT was applied to calculate the overall prospect values. The safety grade was then identified according to the ranking of the overall prospect values. A case study demonstrated that the proposed method is suitable for crane safety assessments. The assessment results can help to identify the safety state of crane equipment, allowing effective measures to be taken to improve its security and reliability. Therefore, the method proposed in this paper has real practical value.
Through a comparative study, it was found that the existing crane safety grades given by FAHP methods may be inaccurate as a result of the improper use of MMP. In addition, the UMT method may exaggerate the risk, which will affect the decision-making process. Compared with the assessment results given by FAHP and UMT, the proposed method generates precise and reasonable evaluations of the crane safety grade. In addition, the proposed method can also compare the safety state of different cranes that have the same safety grade. Thus, the proposed method is superior to both FAHP and UMT methods, and provides an alternative for evaluating crane safety. Compared with VS method, the main advantage of the proposed method is that it considers the evaluators’ behavior factor.
Although the method proposed in this study was applied to a crane safety grade assessment, it could also be used in other fields, such as flood classification, slope stability evaluation, and other risk assessment problems. Since subjective and objective weighting methods have both advantages and disadvantages, an integrated weighting method may provide a more scientific means of assigning weights and highlighting the importance of each index to crane safety. In future work, if an advanced combined weighting model could be coupled with CPT, the reliability and rationality of the crane evaluation results may be further improved. Moreover, measures of crane safety criteria and the weights of the criteria may not be precisely determined by elevators. Thus, applications of fuzzy numbers for describing criteria values and weights can also be considered as part for future research prospects.