Impact of Ambient Conditions of Arab Gulf Countries on the Performance of Gas Turbines Using Energy and Exergy Analysis

Abstract

In this paper, energy and exergy analysis of typical gas turbines is performed using average hourly temperature and relative humidity for selected Gulf cities located in Saudi Arabia, Kuwait, United Arab Emirates, Oman, Bahrain and Qatar. A typical gas turbine unit of 42 MW is considered in this study. The electricity production, thermal efficiency, fuel consumption differences between the ISO conditions and actual conditions are determined for each city. The exergy efficiency and exergy destruction rates for the gas turbine unit and its components are also evaluated taking ISO conditions as reference conditions. The results indicate that the electricity production losses occur in all cities during the year, except in Dammam and Kuwait for the period between November and March. During a typical day, the variation of the power production can reach 4 MW. The rate of exergy destruction under the combined effect of temperature and humidity is significant in hot months reaching a maximum of 12 MW in July. The presented results show also that adding inlet cooling systems to the existing gas turbine units could be justified in hot periods. Other aspects, such as the economic and environmental ones, should also be investigated.

1. Introduction

The power generation sector is one of the most expanding sectors in the Gulf countries mainly due to the rise of the population size, economic and industrial development and the availability of fossil fuels. Several new projects are planned, commissioned or already launched. The power plants are composed mainly of gas turbine units, steam turbines and combined cycle plants. Several questions are arising including the optimum operation of these power plants, the reduction of their energy consumption and the reduction of their environmental impacts. The possible electrical interconnection between the Gulf countries is another important issue.

The Gulf Cooperation Council (GCC) was formed in 1981, consisting of the six Arab Gulf countries, namely the United Arab Emirates, Bahrain, Saudi Arabia, Oman, Qatar and Kuwait [1]. Based on some previous studies, it has been demonstrated that the electrical interconnection among the GCC countries is possible technically and economically. As a result, the GCC Interconnection Authority (GCCIA) was established in July 2001 with headquarters located in Dammam and the control center in Ghunan, Saudi Arabia [1,2,3].

Table 1. Capacity of interconnection of Gulf Cooperation Council (GCC) countries [2,3].

Country	Capacity (MW)
Kuwait	1200
Saudi Arabia (East Region)	1200
Bahrain	600
Qatar	750
UAE	900
Oman	400

presents the electrical capacity of interconnection of each country in GCC. Saudi Arabia contributes with its eastern region having the largest production of electricity in the Kingdom [4].

Gas turbine plants are widely used to generate electricity worldwide, in particular to cover the peak load demand as in Kuwait [5] and to produce electrical power in inland regions, such as in Saudi Arabia. For instance, gas turbine units produced about 50% of the total electrical capacity of the Saudi Kingdom in 2012 [6].

Gas turbines are considered constant volumetric flow rate machines using ambient air as the working fluid [7,8]. Therefore, ambient conditions (temperature, humidity and pressure) are considered as important factors affecting the performance of such power plants. The production capacity of gas turbines is rated by the International Standards Organization (ISO), which specified the following reference air inlet conditions: air temperature 15 °C (59 °F), relative humidity 60% and absolute pressure (sea-level) 101.325 kPa (14.7 psia).

Several studies have discussed the effect of ambient conditions on the performance of gas turbines. Al Ibrahim et al. [9] tested a simple gas cycle in the central Qaseem region of Saudi Arabia. They concluded that high ambient temperatures of mid-day of the summer season cause a 24% decreasing in system capacity [10]. Baakeem et al. [11] studied theoretically the effect of the average hourly temperature and relative humidity on the performance of a typical gas turbine unit used in three Saudi regions: Ad Dammam, Riyadh and Jeddah. The obtained results showed that both ambient temperature and humidity have a significant effect on the gas turbine performance. They reported that due to weather variation, the maximum electricity production losses were 20%, 18% and 17.5% of ISO production in Riyadh, Ad Dammam and Jeddah, respectively. De Sa and Al Zubaidy [12] investigated the gas turbine performance at varying ambient temperatures for specific turbines (SIEMENS SGT 94.2 and SIEMENS SGT 94.3) installed at the Dewa Power Station located at Al Aweer, Phases II and III in Dubai, UAE. Each of these types of gas turbine has a power generation capacity of 160 MW and 265 MW, respectively. De Sa and Al Zubaidy [12] reported that for every 1 °C rise in ambient temperature above ISO conditions, the units lose 0.1% in terms of thermal efficiency and 1.47 MW of its gross (useful) power output. Al-Fahed et al. [8] focused on the effect of ambient air temperature and relative humidity on the performance of a gas turbine cogeneration system under Kuwait summer climate conditions. They concluded that increasing inlet air temperatures have a negative effect on the net power and thermal efficiency of the gas turbine, while increasing relative humidity has a small positive impact on gas turbine cycle net power and thermal efficiency. For an integrated gas turbine and heat recovery steam generator (HRSG), increasing inlet air temperature has a negative impact on the power to heat ratio (PHR), while relative humidity has no effect on PHR. Ameri and Hejazi [13] reported that there are more than 170 gas turbine units in Iran with a combined capacity of 9500 MW. In the summer season, the power output of those units is about 80% of their rated capacity, meaning that around 1900 MW are lost during the hot season. Erdem and Sevilgen [14] analyzed the effect of ambient temperature on electricity production and fuel consumption of two simple gas turbine models. They considered seven climate regions in Turkey using average monthly temperature data corresponding to those regions. They reported that electricity production loss occurs in all regions when the temperature is above 15 °C, and loss rates vary between 1.67% and 7.22% depending on the regions. Electricity generation increases by 0.27% to 10.28% when inlet air is cooled to 10 °C.

The second law of thermodynamics has been frequently used to analyze the performance of such power systems. Ameri et al. [15] evaluated the irreversibility rates occurring in each component of Neka combined cycle power plants using exergy analysis. Khaliq [16] analyzed the performance of a tri-generation system using energy and exergy balances, while Sanjay and Prasad [17] evaluated the energy and exergy efficiencies of an inter-cooled combustion turbine-based combined cycle (ICCT-CC) power plant. Chen et al. [18] investigated the exergy and energy levels of a combined cooling, heating and power system driven by a small-scale gas turbine at off design conditions. The performance of a gas turbine with air bottoming cycle (ABC) was investigated by Ghazikhani et al. [19] using the first and second laws. Working fluid was treated as an ideal gas with variable specific heat, and the fuel was assumed to be pure methane. All components of the system were assumed to operate under adiabatic conditions and with fixed turbine and compressor isentropic efficiencies.

Bhargava et al. [20] conducted thermo-economic analyses of various power augmentation technologies, implemented on a selected gas turbine using selected climatic conditions in order to identify the best techno-economic solution for the considered weather data. Bhargava et al. [21] investigated the gas turbine performance enhancement approaches using wet cycles and hybrid cycles. These high performance cycles consist of modified Brayton cycles with humidification or water/steam injection and with fuel cells. They include an intercooled steam-injected gas turbine cycle, a humidified air turbine cycle, a cascaded humidified advanced turbine cycle, a Brayton cycle with high temperature fuel cells and their combinations with the modified Brayton cycles. The main results of this work show that the cycle efficiency obtained with those high performance systems can be comparable or better than combined cycle efficiency.

In hot climates, the performance of gas turbines can be enhanced by reducing air temperature at the compressor inlet, because cooled air has higher density, giving the turbine a higher mass flow rate and a lower power required by the compressor. Several cooling methods commonly called turbine inlet-air cooling technologies (TIAC) have been proposed and implemented. A good number of works have investigated the effect of inlet air-cooling systems (TIAC) on the performance of gas turbines and combined cycles [7,10,22,23,24,25,26,27]. Al-Ibrahim and Varnham [10] conducted a review on inlet air-cooling technologies for enhancing the performance of combustion turbines in Saudi Arabia. Al-Ansary et al. [7] studied the effect of inlet air cooling systems in gas turbines in Riyadh for every hour of every day during the period from May to September using four technologies. The authors have investigated the prospects of using a hybrid turbine inlet air cooling (TIAC) system consisting of mechanical chilling followed by evaporative cooling. Alhazmy et al. [22] studied the effect of inlet air-cooling on gas turbine power output and efficiency using two different cooling techniques, namely direct mechanical refrigeration and evaporative water spray cooler, under the hot humid conditions of Jeddah, Saudi Arabia. Popli et al. [23] enhanced the gas turbine efficiency by using 17 MW of gas turbine exhaust heat to provide 12.3 MW of cooling to cool compressor inlet air to 10 °C by single-effect water-lithium bromide (H₂O-LiBr) absorption chillers in the United Arab Emirates. The power requirements of several inlet air cooling techniques for the GE Frame 6B gas turbine power plants in two Omani locations, Marmul and Fahud, were evaluated using typical meteorological year (TMY) data by Dawoud et al. [24]. Chakerand Meher-Homji [25] analyzed the impact of the inlet fogging on the performance of simple gas turbines (GE Frame 7EA and GE Frame 9FA gas turbines for 60- and 50-Hz applications). They explained the methodology and data analysis used to derive the cooling potential. The study considered the weather data for 106 major locations over the world.

Based on the above described references, it comes in particular:

• Those references have dealt each and in general with the analysis of the performance of gas turbines for one specific or very few locations. The work of Chaker and Meher-Homji [25] considered however the weather data for a good number of locations.
• The humidity effect on the gas turbines’ performance calculations, particularly the exergy ones, was not systematically investigated.
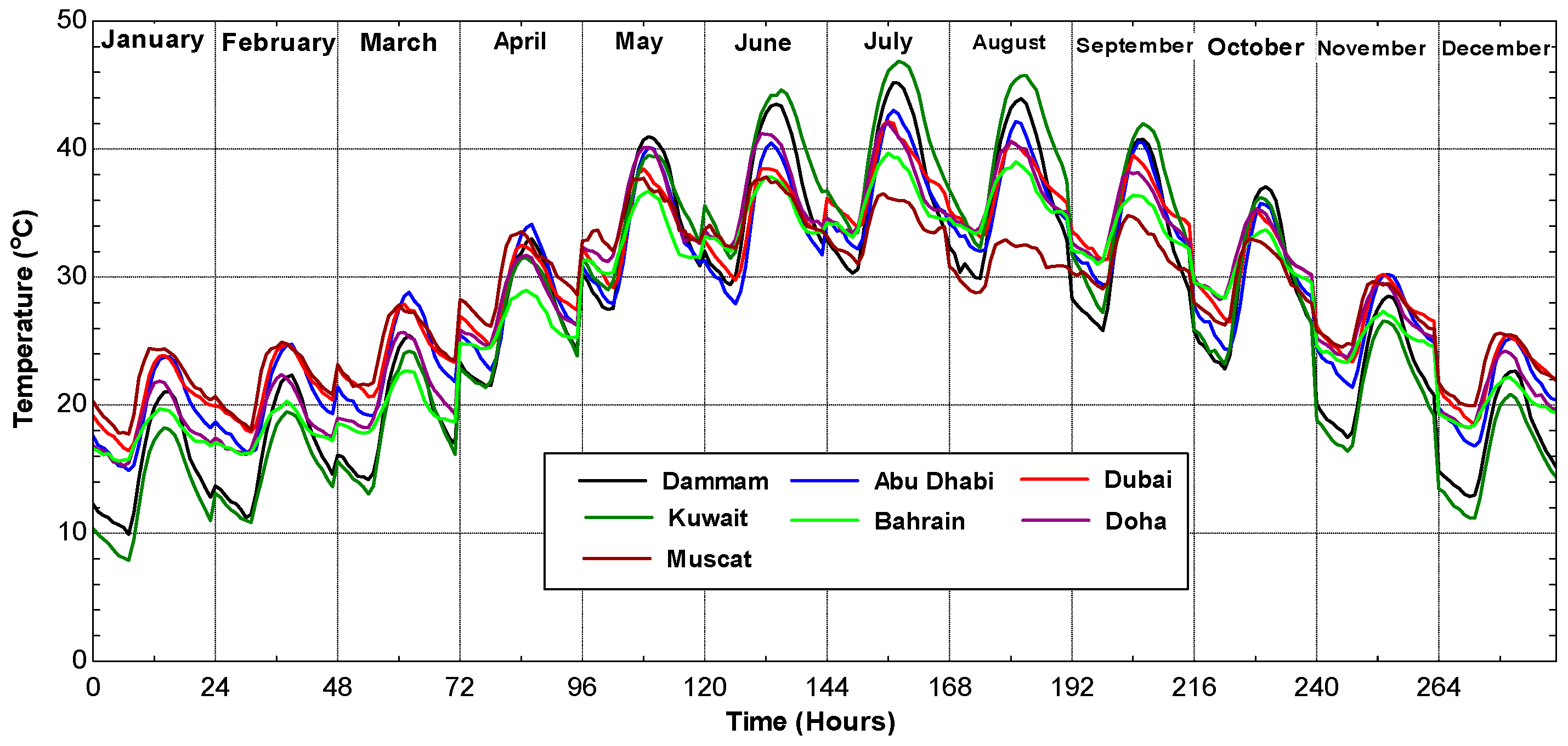
• Very few studies have focused on the analysis of the effect of actual weather conditions using average hourly temperature and relative humidity for several Gulf cities.

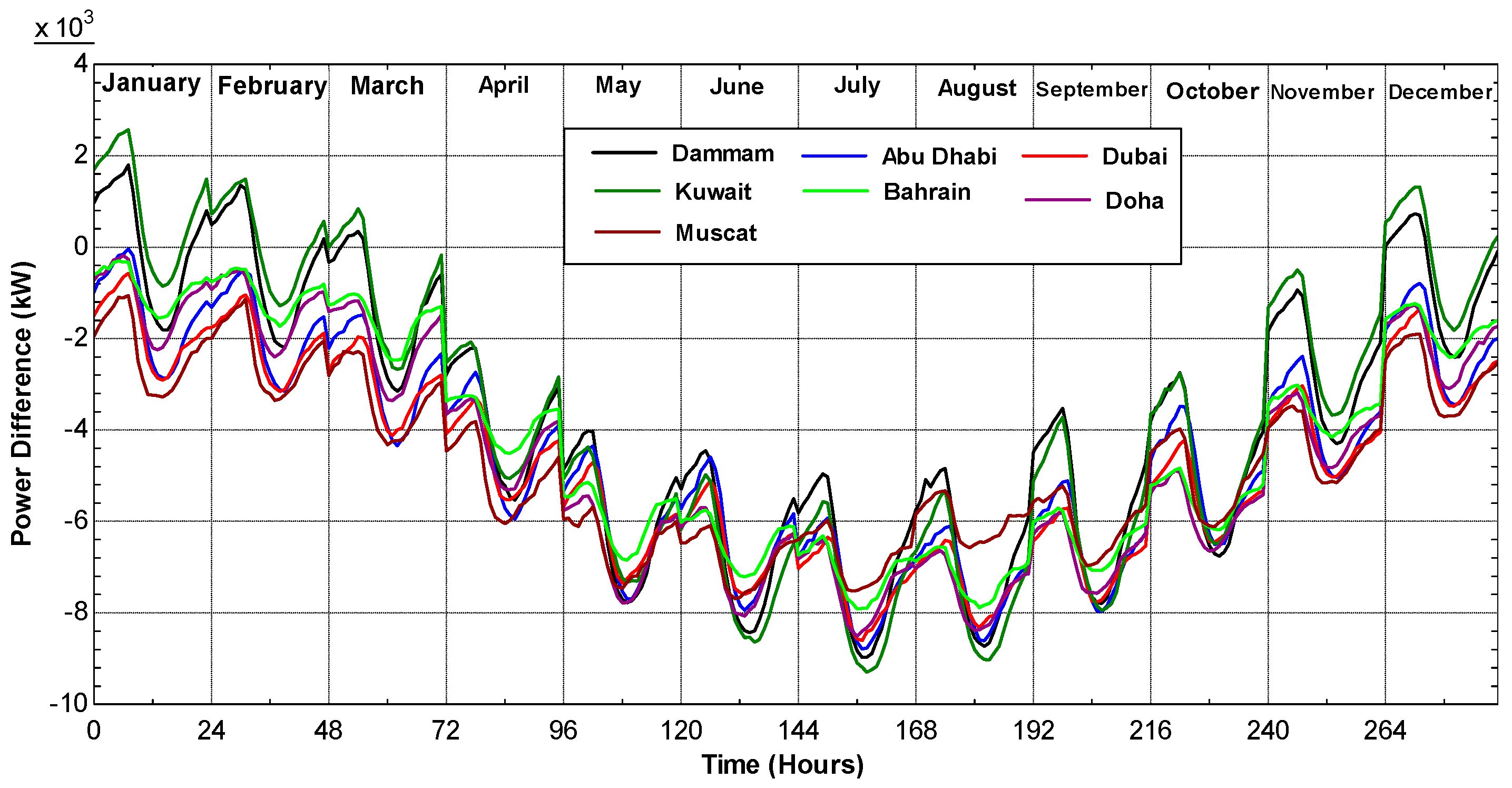
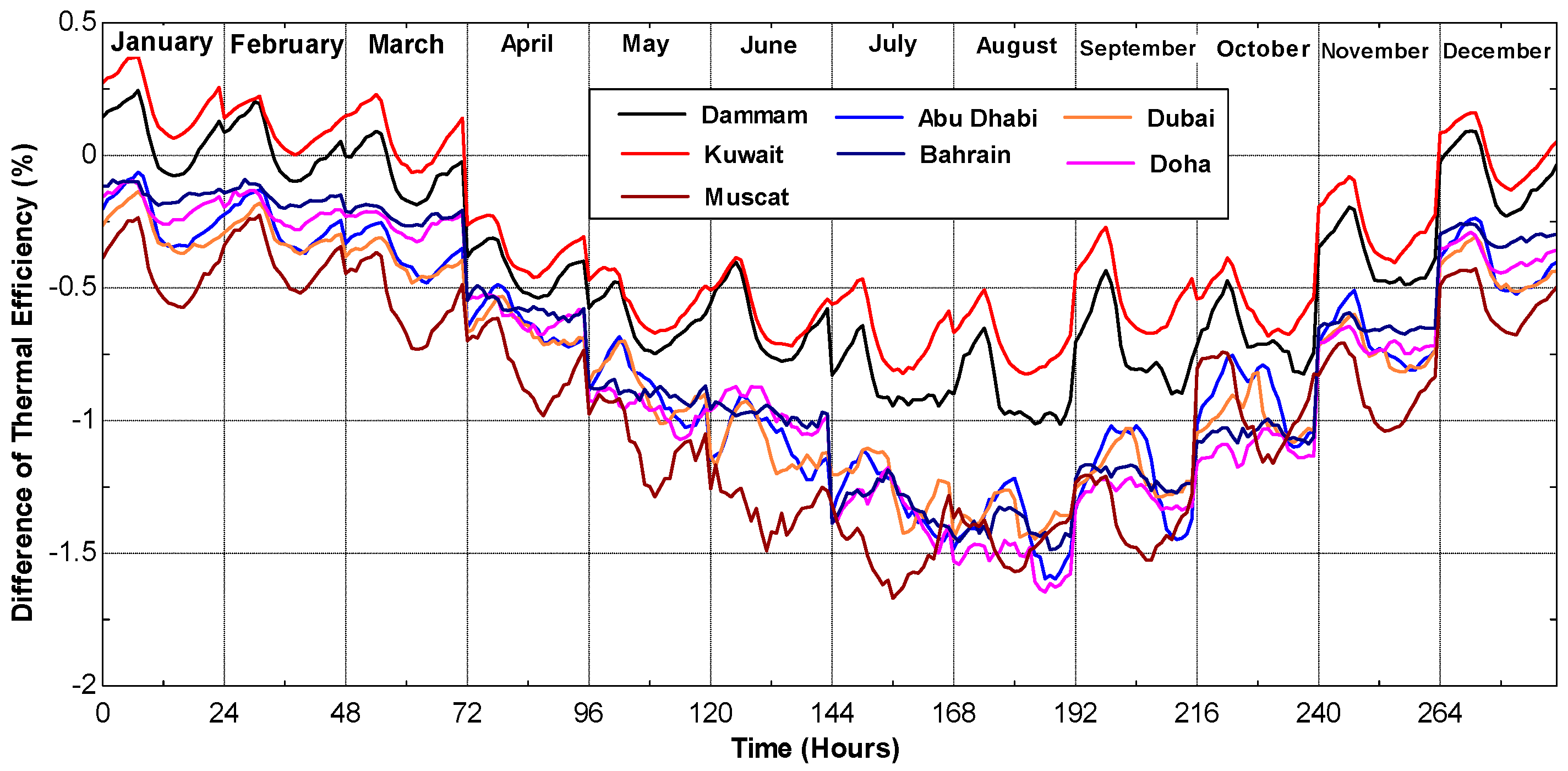
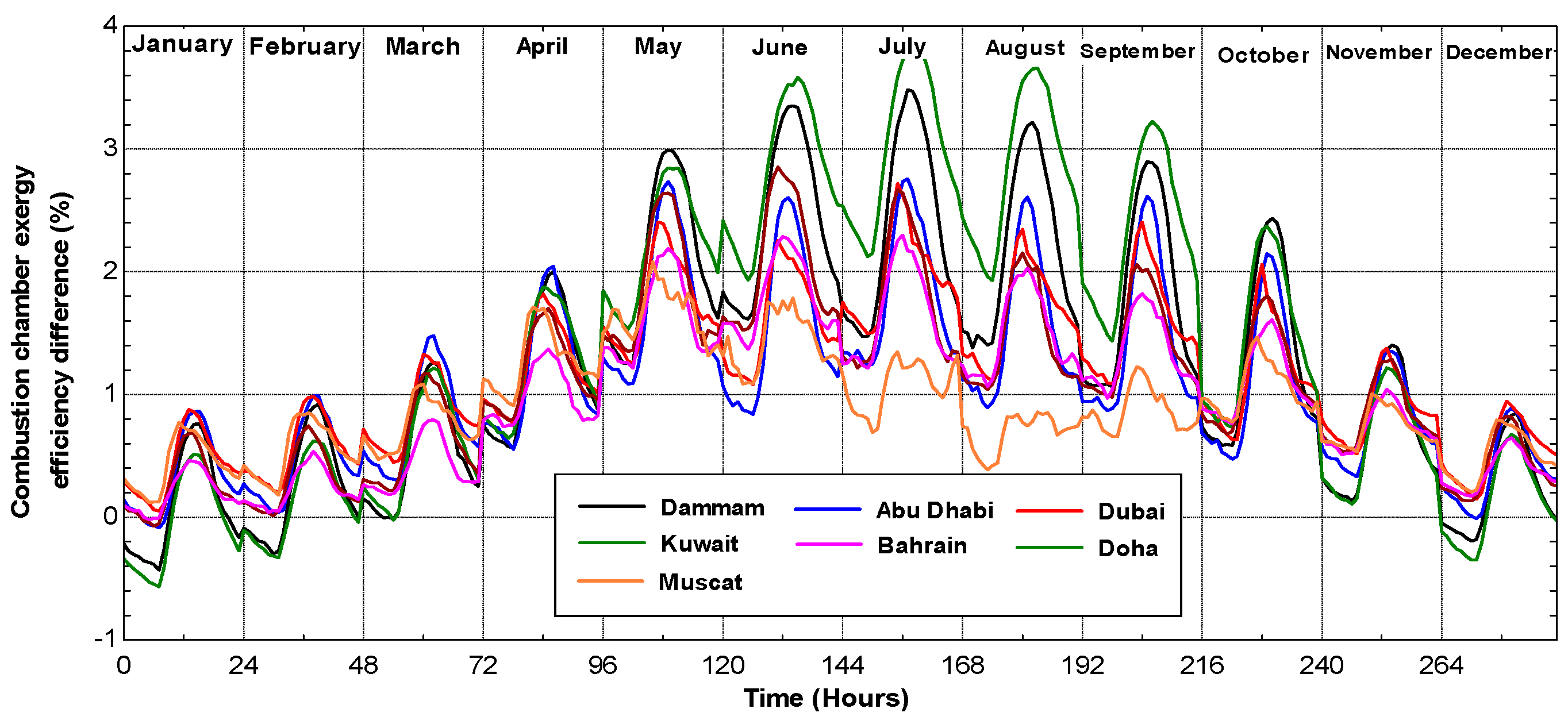
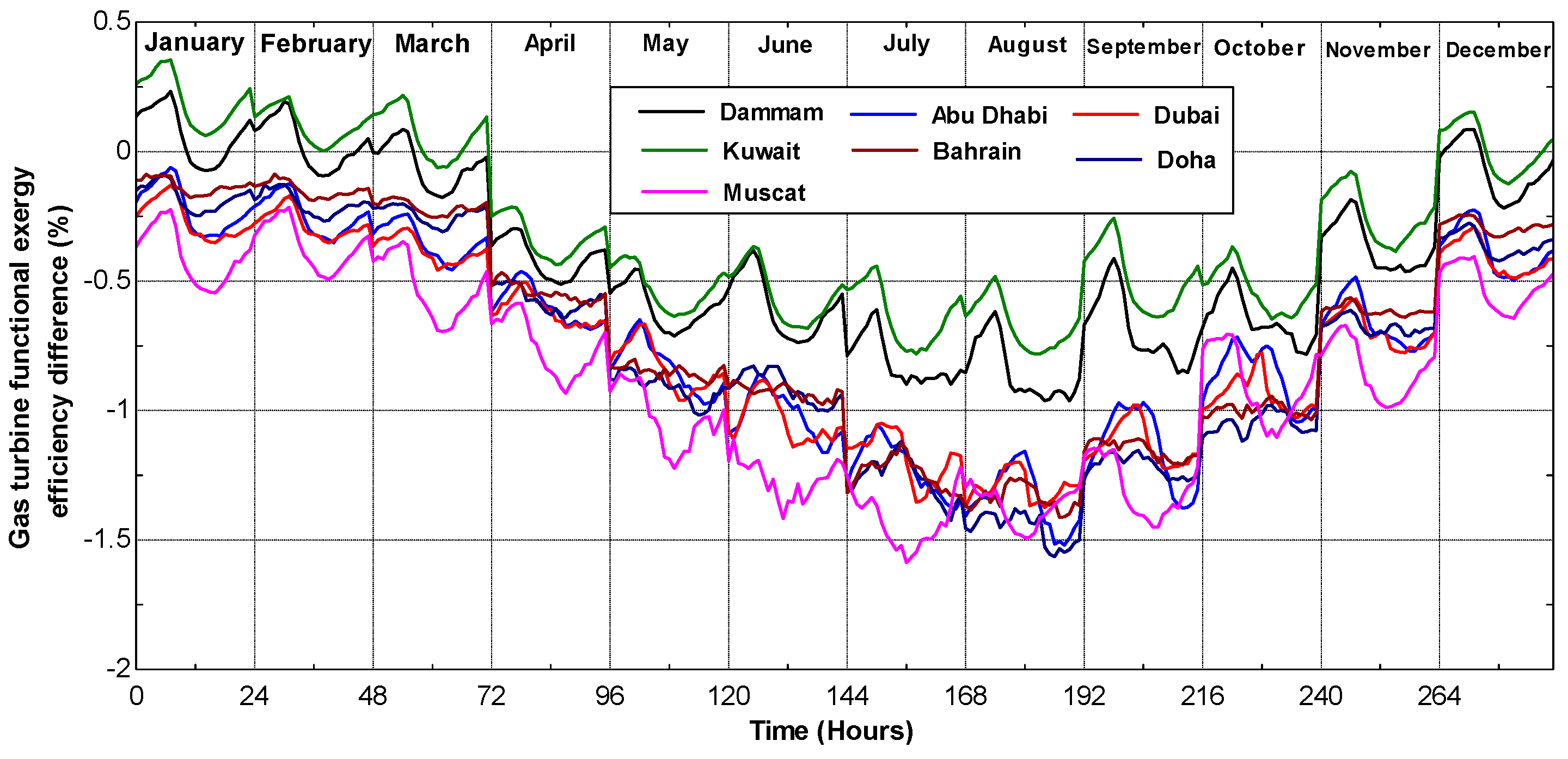
The aim of this paper is to present a theoretical energy and exergy analysis of typical gas turbines using average hourly temperature and relative humidity for selected Arab Gulf cities. The differences between the ISO and actual electricity production and fuel consumption will be evaluated and analyzed. The exergy efficiency of those power systems will be also presented taking ISO conditions as reference conditions.

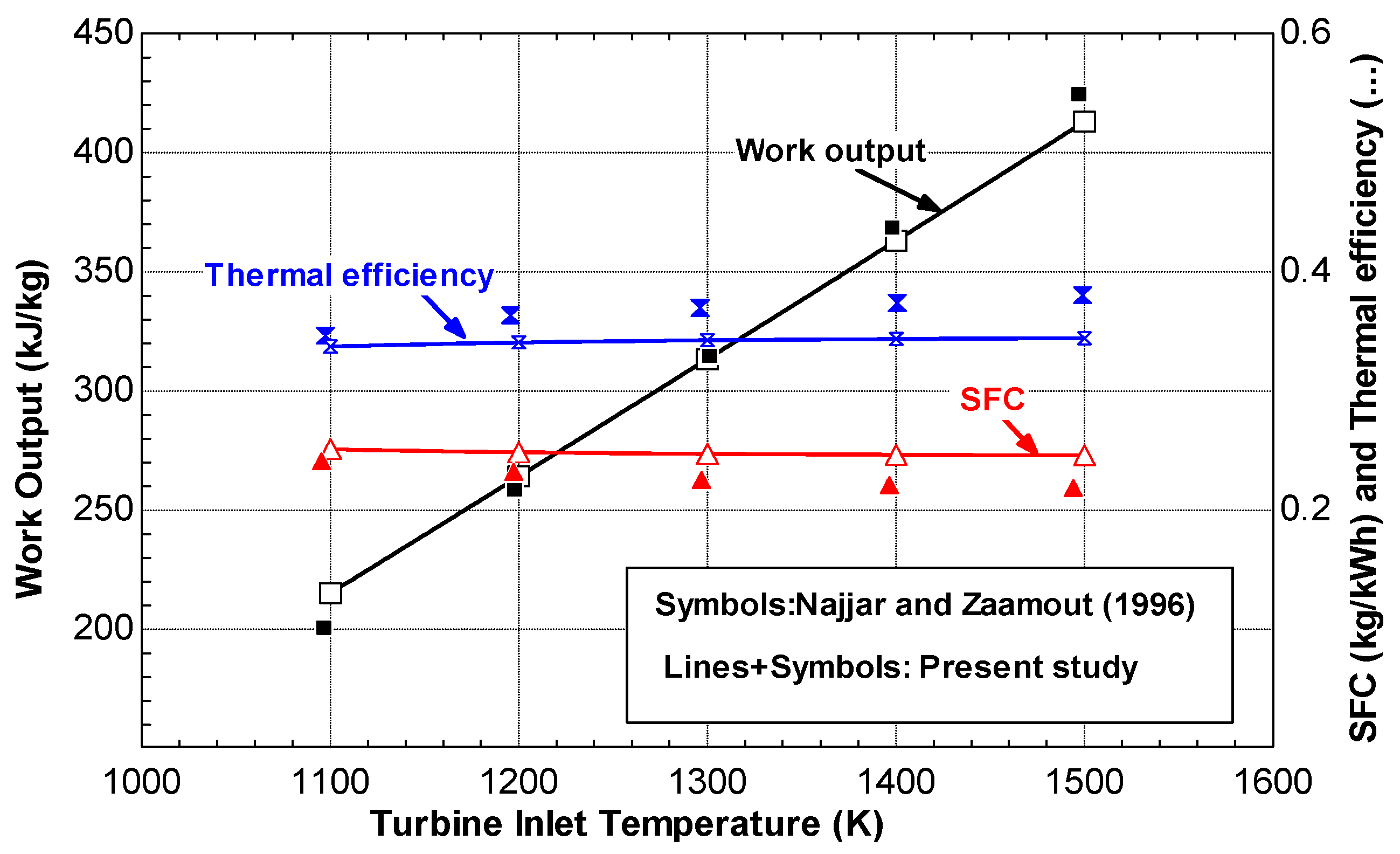
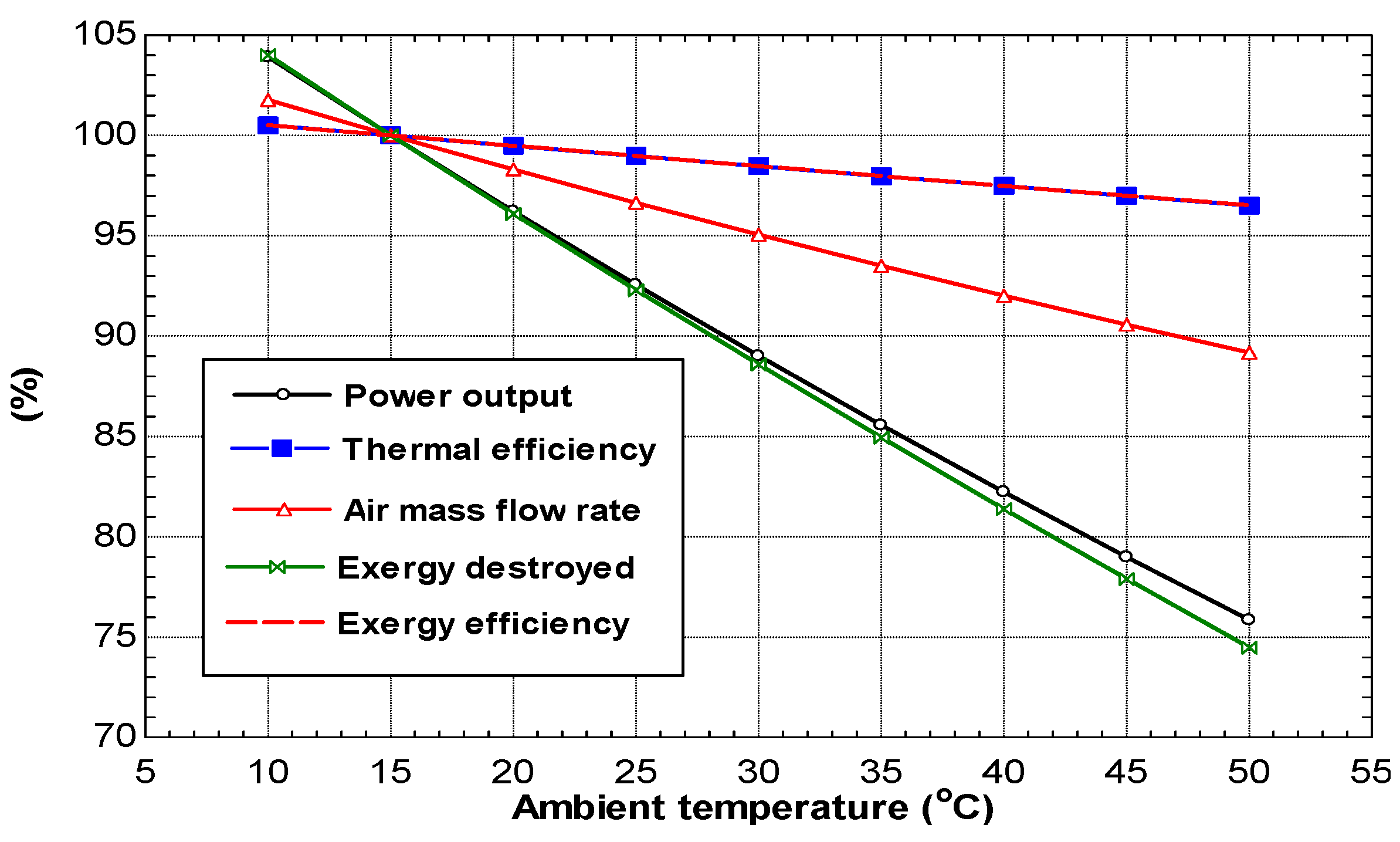
In the following, the theoretical model with the basic assumptions used in this work will be presented first. The model validation tests are outlined in Section 3, while Section 4 includes the results and discussion of the first law and second law analysis.

2. Gas Turbine Cycle

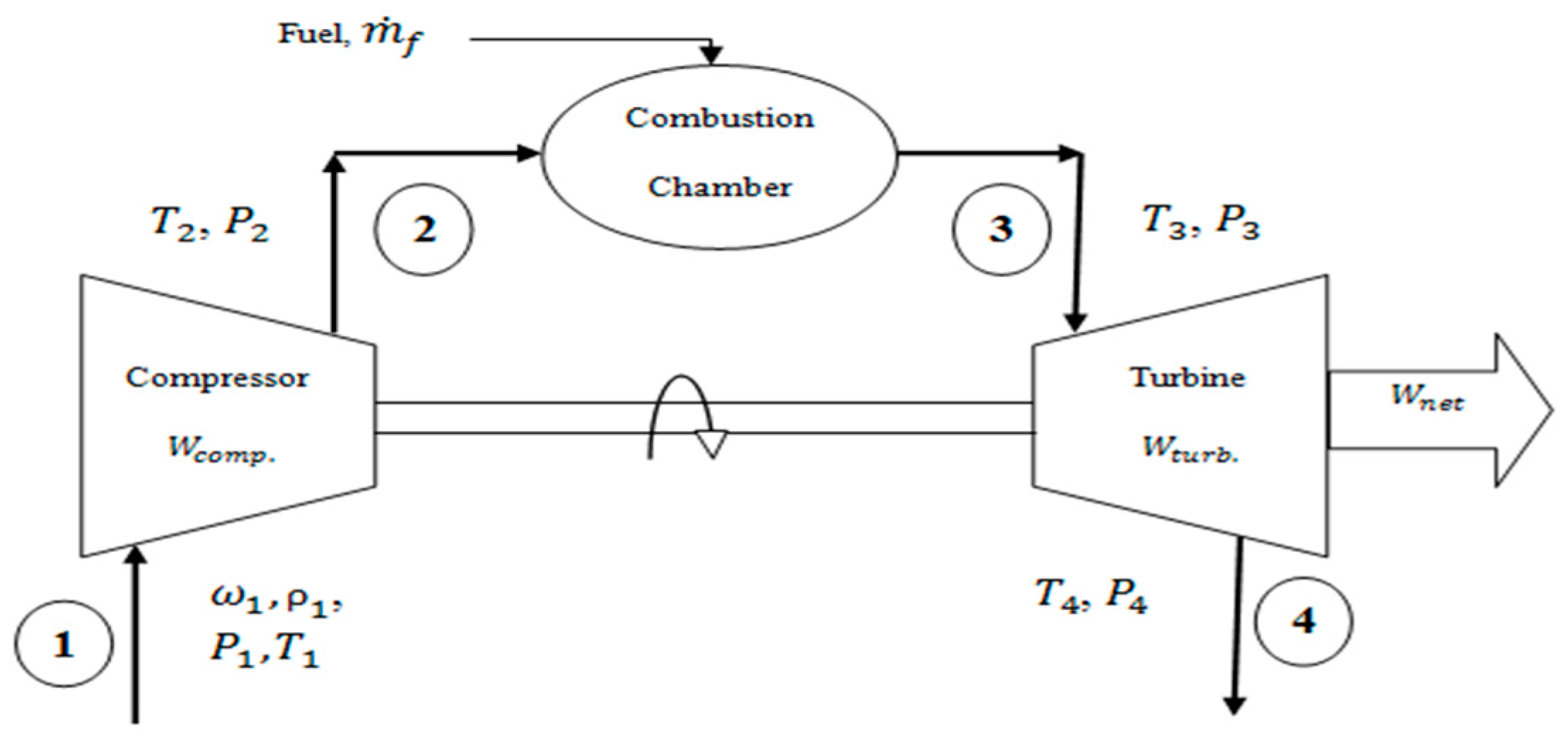
A simple gas turbine operates in the open Brayton thermodynamic cycle, as depicted in Figure 1. As the ambient air enters the gas turbine, it passes through a compressor, which causes its pressure to increase rapidly. Fuel is then injected into the high-pressure air and ignited in the combustion chamber. The combustion products expand into the turbine and produce the work that is used to drive the generator shaft and, so, generating electricity. Part of the generated work is also used to drive the initial stage compressor.

Table 2. Gas turbine operating data and fixed input variables.

Description	Unit	Value
Pressure ratio 1, $r_c$	-	12.2
Turbine inlet temperature 1, $T_3$	K	1362
Volume flow rate of dry air 1, ${\dot{V}}_a$	m3/s	117.302
Air specific heat at constant pressure, $C_{pa}$	kJ/kg·°C	Equation (8)
Gas specific heat at constant pressure 2, $C_{pg}$	kJ/kg·°C	1.147
Combustion chamber specific heat at constant pressure, $C_{pcom}$	kJ/kg·°C	Equation (8)
Air specific ratio 2, ${\gamma }_a$	-	1.4
Gas specific ratio 2, ${\gamma }_g$	-	1.333
Lower calorific value ( LCV) (methane) 3	kJ/kg	50,050
Isentropic efficiency of compressor, ${\eta }_c$	-	Equation (7)
Isentropic efficiency of turbine 4, ${\eta }_{tu}$	-	0.868
Combustion chamber efficiency 2, ${\eta }_{com}$	-	0.98

¹ These values are inferred from the other data provided in [30]; ² these values are selected from [14]; ³ these values are selected from [28]; ⁴ these values are selected from [27].

shows the technical parameters selected for modeling the gas turbine unit. The following basic assumptions are considered:

• Each component of the gas turbine is analyzed as a control volume assumed to be at steady state with neglected pressure drop, except in the combustion chamber.
• Fuel is supposed to be pure methane, and its temperature is constant and equal to the ambient temperature.
• All components of the system are operated under adiabatic conditions. In particular, the combustion chamber is considered as an insulated chamber.
• All fluid thermo-physical properties are modeled as temperature and pressure dependent.
• Kinetic and potential energy and exergy variations in different components of the system and in the pipelines are neglected.
• The ISO conditions are considered as the reference state conditions.

Based on the above assumptions, the general from of the governing equations can be expressed based on the first and second laws of thermodynamics as:

$$\text{Mass balance}, {{\displaystyle \sum }}^{}\dot{m}=0$$

(1)

$$\text{Energy balance}, {{\displaystyle \sum }}^{}Q+{{\displaystyle \sum }}^{}W+{{\displaystyle \sum }}^{}\dot{m}h=0$$

(2)

$$\text{Exergy balance}, {{\displaystyle \sum }}_{in}X-{{\displaystyle \sum }}_{out}X-{{\displaystyle \sum }}_{heat}X-{{\displaystyle \sum }}_{work}X-X_{destroyed}=0$$

(3)

where $\dot{m}$, Q, W and h are the mass flow rate, heat transfer, work and specific enthalpy, respectively. ${{\displaystyle \sum }}_{in}X$, ${{\displaystyle \sum }}_{out}X$, ${{\displaystyle \sum }}_{heat}X$, ${{\displaystyle \sum }}_{work}X$ and $X_{destroyed}$ are the exergy input, exergy output, exergy associated with heat transfer, exergy associated with work and exergy destroyed, respectively. The specific flow exergy at any thermodynamic state is equal to [28]:

$${\psi }_k=\left(h-h_0\right)-T_0\left(s-s_0\right)$$

(4)

$s$ is the specific entropy; the subscript 0 refers to the reference state conditions. The mass flow rate of the moist inlet air is:

$${\dot{m}}_{ma}={\dot{m}}_a+{\dot{m}}_w$$

$${\dot{V}}_{ma}{\rho }_{ma}={\dot{m}}_a\left(1+ {\omega }_1\right)$$

(5)

where ${\rho }_{ma}$ is the moist air density and $\omega$ is the humidity ratio (the ratio of the mass of water vapor to the mass of dry air). Those variables are functions of air inlet conditions (T₁, P₁ and ${\omega }_1$). The moist air density is calculated based on the ambient conditions. The compression work can be estimated as:

$$W_c={\dot{m}}_a\left[C_{pa}\frac{T_1}{{\eta }_c}\left[r_c^{\frac{{\gamma }_a-1}{{\gamma }_a}}-1\right]+{\omega }_1\left(h_{w2}-h_{w1}\right)\right]$$

(6)

where ${\dot{m}}_a$ is the dry air mass flow rate, r_c is the compressor pressure ratio, ${\gamma }_a$ is the ratio of air specific heat, $C_{pa}$ is the air specific heat at constant pressure and ${\eta }_c$ is the compressor is entropic efficiency that can be evaluated as [29]:

$${\eta }_c=1-\left[0.04+\frac{r_c-1}{150}\right]$$

(7)

The air specific heat at constant pressure can be calculated as [26]:

For $200 \mathrm{K}<T<800 \mathrm{K}$:

$$C_{pa}=1.0189134\times {10}^3-1.3783636\times {10}^{-1}T+1.9843397\times {10}^{-4}{T}^2+4.2399242\times {10}^{-7}{T}^3 (\mathrm{J}/\mathrm{kg}·°\mathrm{C})$$

For $800 \mathrm{K}<T<2200 \mathrm{K}$:

$$C_{pa}=7.9865509\times {10}^2+5.3392159\times {10}^{-1}T-2.2881694\times {10}^{-4}{T}^2+3.7420857\times {10}^{-8}{T}^3 (\mathrm{J}/\mathrm{kg}·°\mathrm{C})$$

(8)

$h_{w2}$ and $h_{w1}$ in Equation (6) are the specific enthalpies of the vapor at the inlet and outlet of the compressor, respectively. The saturation pressure ($P_w$) of water vapor depends on the absolute humidity as:

$$\omega =\frac{0.622\times P_{wk}}{P_k-P_{wk}} k \mathrm{refers} \mathrm{to} \mathrm{states} 1, 2 \mathrm{or} 3$$

(9)

The total temperature and pressure of the moist air leaving the compressor can be evaluated as:

$$T_2=T_1+\frac{T_1}{{\eta }_c}\left[r_c^{\frac{{\gamma }_a-1}{{\gamma }_a}}-1\right]$$

(10)

$$P_2=r_c\times P_1$$

(11)

The exergy at the inlet and outlet of the compressor can be calculated as:

$$X_1={\dot{m}}_a\left\{\left[C_{pa}\left(T_1-T_0\right)-T_0\left[C_{pa}\ln \left(\frac{T_1}{T_0}\right)-R_a ln\left(\frac{P_1}{P_0}\right)\right]\right]+{\omega }_1\left[\left(h_w\left(T_1,P_1\right)-h_w\left(T_0,P_0\right)\right)-T_0\left(s_w\left(T_1,P_1\right)-s_w\left(T_0,P_0\right)\right)\right]\right\}$$

(12)

$$X_2={\dot{m}}_a\left\{\left[C_{pa}\left(T_2-T_0\right)-T_0\left[C_{pa}\ln \left(\frac{T_2}{T_0}\right)-R_a ln\left(\frac{P_2}{P_0}\right)\right]\right]+{\omega }_1\left[\left(h_w\left(T_2,P_2\right)-h_w\left(T_0,P_0\right)\right)-T_0\left(s_w\left(T_2,P_2\right)-s_w\left(T_0,P_0\right)\right)\right]\right\}$$

(13)

The exergy destroyed in the compressor can be evaluated as:

$$X_{destroyed,c}=W_c+X_1-X_2$$

(14)

Simplifying Equations (12)–(14), the exergy destroyed in the compressor becomes:

$$X_{destroyed,c}={\dot{m}}_a{T}_0\left[C_{pa}\ln \left\{\frac{1}{{\eta }_c}-\left(\frac{1}{{\eta }_c}-1\right){\left(\frac{P_1}{P_2}\right)}^{({\gamma }_a-1)/{\gamma }_a}\right\}+{\omega }_1\left\{s_w\left(T_2,P_2\right)-s_w\left(T_1,P_1\right)\right\}\right]$$

(15)

The heat added to the combustion chamber is:

$$Q_{in}={\eta }_{com}\times {\dot{m}}_f\times LCV$$

(16)

where ${\dot{m}}_f$ is the fuel mass flow rate, LCV is its lower calorific value and ${\eta }_{com}$ is the combustion chamber efficiency. The fuel consumption rate can be calculated as follows:

$${\dot{m}}_f={\dot{m}}_{a }\left[\frac{C_{pcom}\times T_3+{\omega }_1\times (h_{w3}-h_{w2})- C_{pa}\times T_2}{{\eta }_{com}\times LCV-C_{pcom}\times T_3}\right]$$

(17)

where $C_{pcom}$ is the combustion gases’ specific heat at constant pressure and $h_{w3}$ is the specific enthalpy of vapor at the outlet of the combustion chamber. The combustion chamber discharge pressure $P_3$ can be estimated as:

$$P_3=P_2\times \left(1-\Delta P_{com}\right)$$

(18)

where $\Delta P_{com}$ is the percentage combustion chamber pressure loss.

The specific flow exergy of fuel is given as [18,31,32]:

$${\psi }_f=LCV·A\approx LCV \left(1.033+0.0169\times \frac{\mathrm{b}}{\mathrm{a}}-\frac{0.0698}{\mathrm{a}}\right)$$

(19)

where A is the fuel chemical energy level. The parameters a and b are equal to one and four, respectively, for methane (CH₄) [18]. As the combustion products are assumed to behave as an ideal gas, the exergy rate of the flue gas after the combustion chamber can be calculated as:

$$X_3={\dot{m}}_{tot}\left[C_{pg}\left(T_3-T_o\right)-T_0\left[C_{pg}\ln \left(\frac{T_3}{T_o}\right)-{\mathrm{R}}_{\mathrm{g}} \ln \left(\frac{P_3}{P_o}\right)\right]\right]$$

(20)

${\dot{m}}_{tot}$ is the total mass of working fluid flowing through the turbine and equals:

$${\dot{m}}_{tot}={\dot{m}}_a+{\dot{m}}_w+{\dot{m}}_f$$

$${\dot{m}}_{tot}={\dot{m}}_a\left(1+\omega +f\right)$$

(21)

where $f$ is the fuel to air ratio defined as $f={\dot{m}}_f/{\dot{m}}_a, C_{pg}$ is the gas specific heat at constant pressure and ${\mathrm{R}}_{\mathrm{g}}$is the gas constant. Therefore, the exergy balance of the combustion chamber is:

$$X_{destroyed,com}=X_2+1.0308 {\dot{m}}_{f}LCV -X_3$$

(22)

The total work produced by the turbine can be estimated as:

$$W_{tu}={\dot{m}}_{tot}{C}_{pg}{T}_3{\eta }_{tu}\left[1-{\left(\frac{1}{r_c^{ }}\right)}^{\frac{{\gamma }_g-1}{{\gamma }_g}}\right]$$

(23)

where ${\gamma }_g$ is the gas specific ratio, and ${\eta }_{tu}$ is the turbine isentropic efficiency and can be evaluated as [29]:

$${\eta }_{tu}=1-\left[0.03+\frac{r_c-1}{180}\right]$$

(24)

The exergy rate of the flue gas after the turbine can be estimated as:

$$X_4={\dot{m}}_{tot}\left[C_{pg}\left(T_4-T_0\right)-T_0\left[C_{pg}\ln \left(\frac{T_4}{T_o}\right)-{\mathrm{R}}_{\mathrm{g}} \ln \left(\frac{P_4}{P_o}\right)\right]\right]$$

(25)

The exergy balance for the adiabatic process in the turbine can be evaluated as:

$$X_{destroyed,tu}=X_3-X_4-W_{tu}$$

(26)

Similarly as the compressor, by simplifying Equations (20), (25) and (26) the exergy destroyed in the turbine becomes:

$$X_{destroyed,tu}={\dot{m}}_{tot}{T}_0{C}_{pg} \ln \left\{\left(1-{\eta }_{tu}\right){\left(\frac{P_3}{P_4}\right)}^{({\gamma }_g-1)/{\gamma }_g}+{\eta }_{tu}\right\}$$

(27)

Finally, the net power of the gas turbine can be calculated as:

$$W_{net}=W_{tu}-W_c$$

$$W_{net}={\dot{m}}_a\left[\left(1+f+\omega \right)C_{pg}{T}_3{\eta }_{tu}\left(1-{\left(\frac{1}{r_c}\right)}^{\frac{{\gamma }_g-1}{{\gamma }_g}}\right)-C_{pa}\frac{T_1}{{\eta }_c}\left(r_c^{\frac{{\gamma }_a-1}{{\gamma }_a}}-1\right)-{\omega }_1\left(h_{w2}-h_{w1}\right)\right]$$

(28)

The thermal efficiency of the gas turbine cycle is:

$${\eta }_{th}=\frac{w_{net}}{Q_{in}}$$

(29)

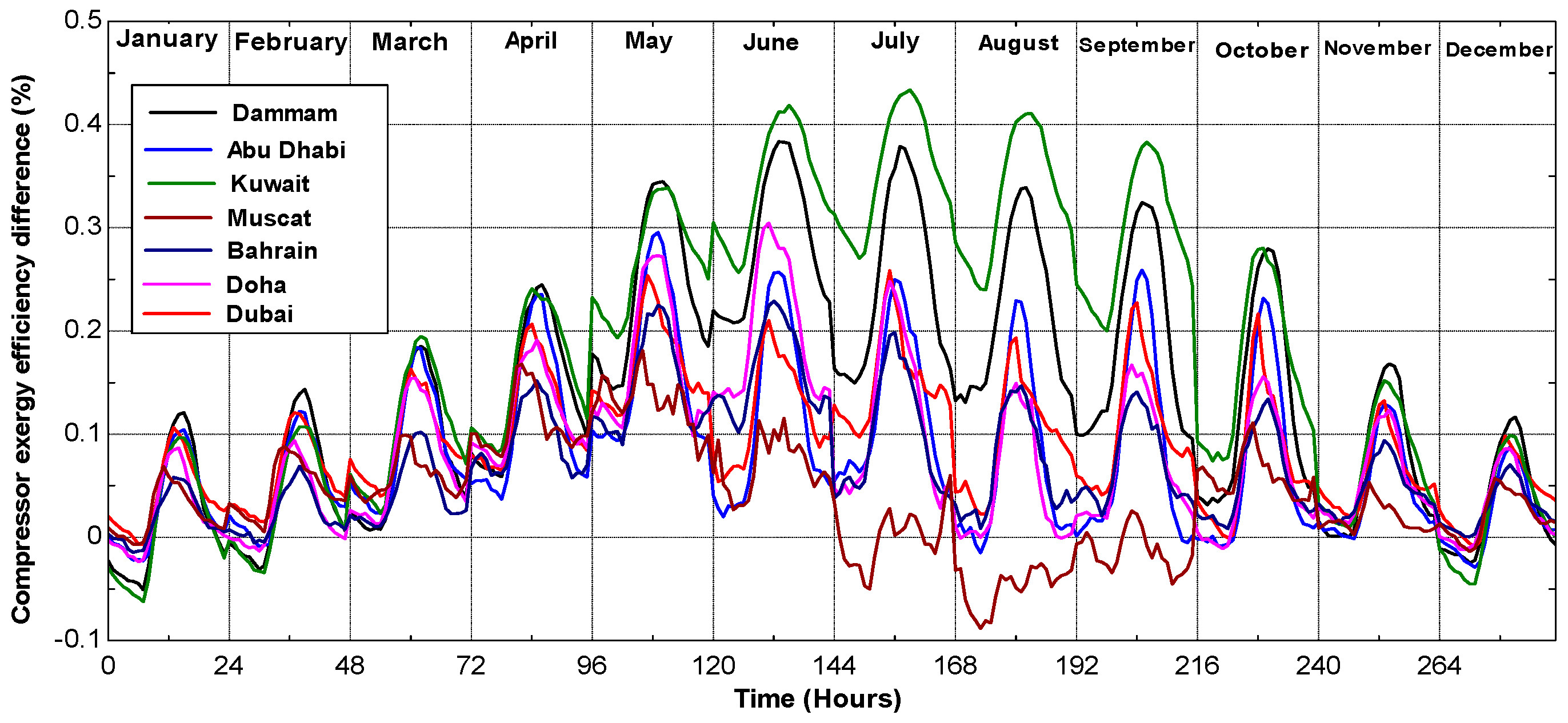
The exergy destroyed of a gas turbine is a summation of the exergies destroyed of the gas turbine components:

$$X_{destroyed}=X_{destroyed,c}+X_{destroyed,com}+X_{destroyed,tu}$$

(30)

The functional exergy efficiency of the gas turbine and those of its components can be expressed as [28]:

$${\eta }_{II,c}=\frac{X_2-X_1}{W_c}=1-\frac{X_{destroyed,c}}{W_c}$$

(31)

$${\eta }_{II,com}=\frac{X_3}{X_2+X_f}=1-\frac{X_{destroyed,com}}{X_2+X_f}$$

(32)

$${\eta }_{II,tu}=\frac{W_{tu}}{X_3-X_4}=1-\frac{X_{destroyed,tu}}{X_3-X_4}$$

(33)

$${\eta }_{II}=\frac{W_{net}}{X_f}$$

(34)

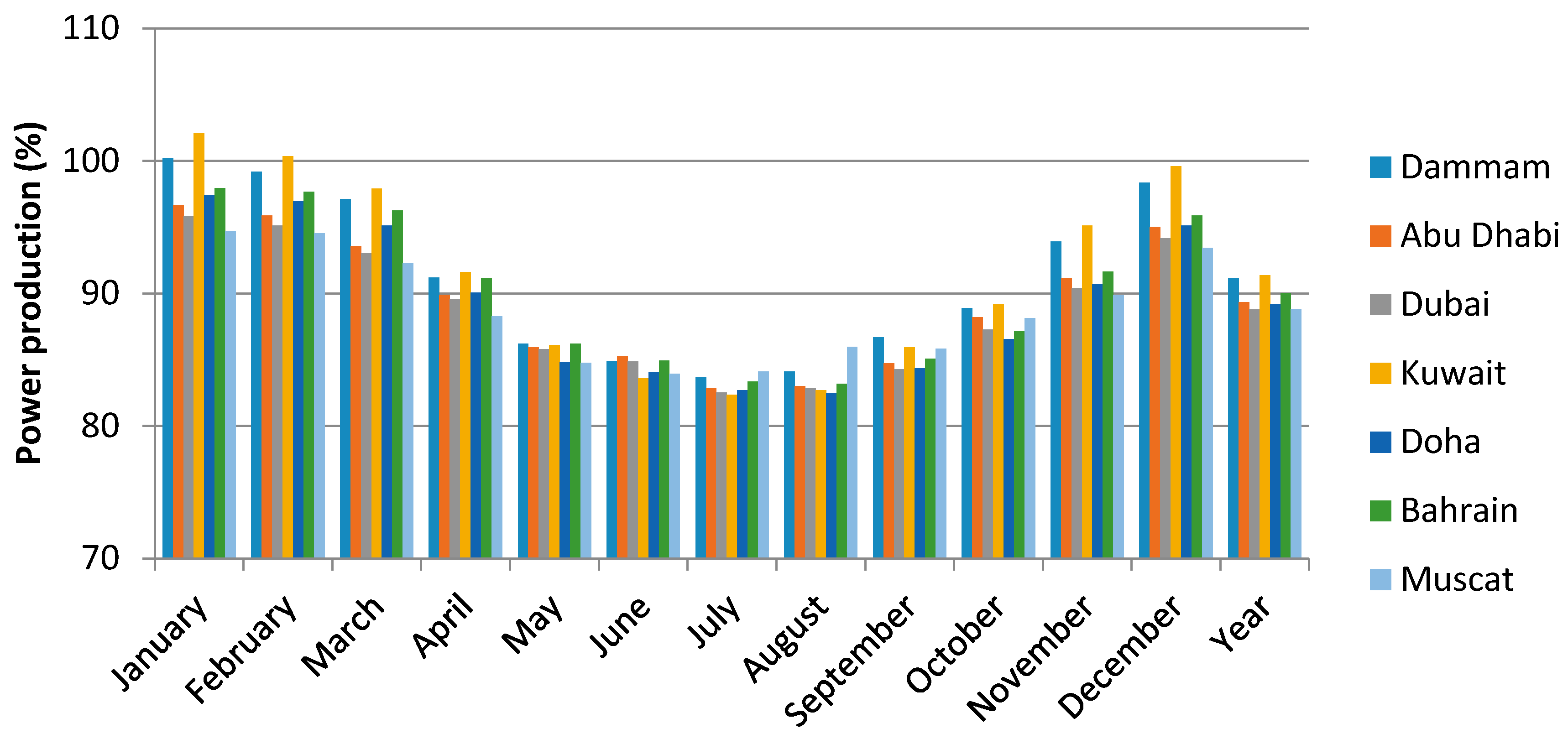
The monthly and annual power production of the gas turbine is:

$$P{r}_m={\displaystyle \sum }_{i=0}^{23}N\times {W_{net}}_i$$

(35)

$$P{r}_{an}={\displaystyle \sum }_{j=1}^{12}P{r}_{m_j}$$

(36)

$P{r}_m$ is the monthly power production; N is the number of days in that month; i refers to the time of the day; $P{r}_{an}$ is the annual power production; and j represents the month. The monthly and annual fuel consumption rates are:

$${{\dot{m}}_f}_m={\displaystyle \sum }_{i=0}^{23}N\times {{\dot{m}}_f}_i$$

(37)

$${{\dot{m}}_f}_{an}={\displaystyle \sum }_{j=1}^{12}{{\dot{m}}_f}_{m_j}$$

(38)

The difference between the actual and ISO performance of a gas turbine can be expressed as:

$$\Delta D_p=D_p-D_{ISO}$$

(39)

D refers to the performance parameters of a gas turbine, and p represents the time of the day or month or year.

It is of interest to mention that the above governing equations are based on mass, energy and exergy balances for the whole gas turbine unit and its main components under steady-state conditions. Such an approach has been widely used in similar previous works (see, for instance, [8,11,12,13,14,19,22,26]). It is assumed the changes in the ambient conditions and their effect on the gas turbine performance and components parameters would not affect the steady-state behavior of the power system.

3. Model Validation

The gas turbine model is developed using Engineering Equation Solver (EES), which has been widely used for these kinds of problems. The model is first validated with the results of Najjar and Zaamout [33] using their operating data. Figure 2 shows the comparison between the results of the present model with those of Najjar and Zaamout [33] for the work output, thermal efficiency and specific fuel consumption (SFC) of a simple gas turbine. The differences between the results are very small, which indicates a good agreement.

The model is also validated using data of a typical gas turbine at the ISO conditions [30] as given in Table 2.

Table 3. Comparison of typical and calculated performance parameters for gas turbine at ISO conditions.

Performance Parameter	Unit	Ref. 1	Calculated 2	Difference 3 (%)
Gas turbine power output, Pr	kW	42,100	42,734	1.5
Hate rate, HR	kJ/kWh	11,223	11,292	0.62
Exhaust flow rate, ${\dot{m}}_{tot}$	kg/s	145.833	145.9	0.05
Turbine outlet temperature, $T_4$	K	816.2	812.7	−0.43

¹ Ref. refers to the performance of a typical gas turbine [30]; ² Calculated refers to the performance calculated using the present model; ³ Difference (%) = (Calculated − Ref.) × 100/Ref.

presents a comparison between the performance of a typical gas turbine [30] and the measured performance parameters obtained from the gas turbine modeling at the ISO conditions. The maximum difference is 1.5% for the gas turbine power output, thereby demonstrating a good agreement.

4. Results and Discussion

Figure 3 presents the performance of a gas turbine unit at the ISO humidity ratio (i.e., $\omega =0.006284\frac{{\mathrm{kg}}_{\mathrm{w}}}{{\mathrm{kg}}_{\mathrm{a}}}$) and as a function of ambient temperature. Because the gas turbines are constant volumetric flow rate machines [7,8], therefore increasing the ambient temperature causes decreasing air density, which impacts their performance, where the hot air is less dense than cold air. This phenomenon is shown in Figure 3. As the temperature of air entering the compressor section increases, all of the power output, thermal efficiency, air mass flow rate, as well as exergy destroyed and exergy efficiency decrease in comparison with ISO-rated values.

4.1. Weather Data of Cities

In this work, the performance of gas turbines is investigated for seven geographic cities in the Arab Gulf. These cities are Dammam in Saudi Arabia, Abu Dhabi and Dubai in the United Arab Emirates, Kuwait, capital of Kuwait, Doha, capital of Qatar, Muharraq in Bahrain and Muscat, capital of Oman. The weather data for those regions are obtained from the Department of Energy’s EnergyPlusProgram [34]. The data include the dry bulb temperature, dew point temperature and barometric pressure. The weather data for Dammam, Abu Dhabi, Dubai, Kuwait, Doha, Muharraq and Muscat are taken from the weather stations at King Fahd International Airport, at Abu Dhabi International Airport, at Dubai International Airport, at Kuwait International airport, at Doha International Airport, at Bahrain International Airport and at Seeb Muscat International Airport, respectively.

Figure 4 and Figure 5 show the average hourly temperature and relative humidity data in the above mentioned cities. Abu Dhabi, Dubai, Doha and Muharraq (Bahrain) have approximately the same temperatures, higher than the ISO temperature, and the same relative humidity values. Muscat has very close temperature and relative humidity values as the previous cities (Abu Dhabi, Dubai, Doha and Muharraq) in the winter season while in the hot season, it has lower temperatures and higher relative humidity values. Dammam and Kuwait have temperatures less than the ISO temperature during the period from the beginning of midnight until dawn in the cold months and have higher temperatures than the other cities during the summer season.

Table 4. Weather data for all cities.

City	Temperature (°C)		Relative Humidity (%)
	Max.	Min.	Max.	Min.
Dammam	45.19	9.9	68.4	7.8
Abu Dhabi	43.02	14.9	78.6	15.9
Dubai	42.13	16.44	72.2	20.5
Kuwait	46.9	7.9	69.8	5.05
Doha	42.02	15.24	73.3	15.3
Bahrain	39.7	15.7	69.4	23.7
Muscat	37.8	17.8	87.3	30.4

summarizes the maximum and minimum values of temperature and relative humidity for all cities.

4.2. First Law Analysis

Erdem and Sevilgen [14] performed an energy analysis on the effect of dry air ambient temperature on the electricity production and fuel consumption of two simple gas turbine models for seven climate regions in Turkey. Average monthly temperature data corresponding to those regions were used. The present study examines the effect of both ambient temperature and humidity. It focuses on the effect of the ambient conditions on the performance of gas turbines using energy and exergy balances. The performance of gas turbines at ISO conditions is calculated and considered as a reference performance.

Table 5. Gas turbine performance indicators at ISO conditions.

Performance	Value
First Law of Thermodynamic
Power output (kW)	42,734
Thermal efficiency (%)	31.882
Heat rate (kJ/kWh)	11292
Specific fuel consumption (kg/kWh)	0.2256
Second Law of Thermodynamic
Compressor exergy destroyed (kW)	2769
Compressor exergy efficiency (%)	94.37
Combustion chamber exergy destroyed (kW)	52,621
Combustion chamber exergy efficiency (%)	71.92
Turbine exergy destroyed (kW)	5089
Turbine exergy efficiency (%)	94.75
Gas turbine exergy destroyed (kW)	60,479
Gas turbine functional exergy efficiency (%)	30.31

presents details on gas turbine performance at ISO conditions. These details include unit thermal and exergy efficiencies, compressor, combustor and turbine exergy efficiencies and exergy destruction rates.

The difference between actual and ISO power production of the gas turbine unit is shown in Figure 6. The negative and positive values refer to the loss and excess in the power output and the thermal efficiency of the gas turbine, respectively.

The general trend shown in Figure 6 indicates that the electricity production losses occur in all cities during the year, except in Dammam and Kuwait, for the period between November and March. During the hot period extended from April to September, the power losses vary between 2 MW to about 9 MW. During a typical day, the variation of the power production can reach 4 MW. When the temperature becomes below the ISO temperature, the power production increases. The maximum power gain ranges from 4% and 6% of the ISO power at temperatures of 9.9 and 7.9 °C in January for Dammam and Kuwait, respectively.

Figure 7 presents the effect of ambient conditions on the hourly thermal efficiency of the gas turbine in all cities. The general picture given in Figure 7 shows some dispersion in the different curves corresponding to the selected cities with two main trends: that of Dammam and Kuwait and that of the remaining cities. The effect of ambient conditions is clear mainly in summer time where we can see losses in thermal efficiency of more than 1.5%. Such losses are reduced in Dammam and Kuwait due to their respective lower relative humidity.

As given in Figure 4 and Table 4, Dammam and Kuwait have lower relative humidity and higher temperature values than the other cities in the hot season. They have approximately the same electrical losses as the other cities. The maximum value for the power loss in those cities reaches around 22% of the ISO production, while it is slightly lower in Dubai with about 20%. For the period from the beginning of midnight until dawn in hot months, Dammam and Kuwait have lower temperature and relative humidity than the remaining cities. This explains why they have lower electricity production losses in that period. In conclusion, the performance of the gas turbine is a function of both ambient temperature and relative humidity. The power output decreases significantly when the air temperature and relative humidity increase.

The annual performance of the gas turbine unit for all cities is shown in

Table 6. Annual performance of gas turbine for all cities. SFC, specific fuel consumption.

	Dammam	Abu Dhabi	Dubai	Kuwait	Doha	Bahrain	Muscat
Pr (GWh)	342.25	335.30	333.29	342.90	334.72	337.86	333.36
$P{r}_{ISO}$ (GWh)	375.38	375.38	375.38	375.38	375.38	375.38	375.38
$\Delta Pr$ (GWh)	−33.13	−40.08	−42.09	−32.47	−40.65	−37.51	−42.02
$\Delta Pr$ (%)	−8.8	−10.7	−11.2	−8.7	−10.8	−10	−11.2
${\dot{m}}_f$ (106 × kg/year)	79.84	79.08	78.65	79.67	78.97	79.58	79.04
${{\dot{m}}_f}_{ISO}$ (106 × kg/year)	86.42	86.42	86.42	86.42	86.42	86.42	86.42
$\Delta {\dot{m}}_f$ (106 × kg/year)	−6.59	−7.34	−7.77	−6.75	−7.45	−6.84	−7.39
$\Delta {\dot{m}}_f$ (%)	−7.62	−8.5	−9	−7.8	−8.6	−7.9	−8.6
SFC (kg/kWh)	0.2333	0.2358	0.2360	0.2323	0.2359	0.2355	0.2371
SFCISO (kg/kWh)	0.2302	0.2302	0.2302	0.2302	0.2302	0.2302	0.2302

. The negative and positive signs stand for the loss and excess in the actual performance of the power unit, respectively. The annual power loss ranges between 8.7% and 11.2% of the ISO annual power, and the maximum annual loss occurs in Dubai and Muscat. The actual specific fuel consumption for all cities is higher than the ISO specific fuel consumption. The relative drop in the fuel consumption ranges between 7.6% and 9%. As the ambient temperature increases and the turbine inlet temperature is kept constant, the heat added in the combustion chamber decreases, which causes a reduction in the fuel consumption. The decreasing rate of fuel consumption is lower than the loss rate in power production. Figure 8 gives a general picture of the monthly and annual electricity production rates for all cities compared to the production rates at ISO conditions. The power production is lower than the ISO production, except for Kuwait city in January, where we can see a gain of about 2%. For the period between May and October, the power production losses are significant, representing more than 15% of the ISO production rate. In this period, adding inlet cooling systems to the existing gas turbine units could be justified.

4.3. Second Law Analysis

Ghazikhani et al. [19] studied the performance of a gas turbine with air bottoming cycle (ABC) using the second law of thermodynamics. By considering the working fluid as dry air and the ambient temperature as dead state temperature, the results show that, as the inlet temperature increases, the exergy destroyed in the compressor and the turbine would increase, while the exergy destroyed in the combustion chamber and in the whole simple gas turbine cycle would decrease. Figure 9, Figure 10, Figure 11 and Figure 12 present the effect of the ambient conditions, i.e., temperature and humidity, on the exergy efficiency parameters of the gas turbine. The actual exergy parameters for all cities are compared to those of the reference conditions given in Table 5. The negative and positive signs in Figure 9, Figure 10, Figure 11 and Figure 12 represent the loss and excess respectively in the performance indicators of the gas turbine unit. The reduction in the exergy destroyed is considered as a benefit, while the reduction in the exergy efficiency as a disadvantage. From a simple look at Equation (15), one can note that the first term is constant and a function of the pressure ratio, compressor isentropic efficiency, air specific heat, air specific heats’ ratio and the reference temperature. The second term varies as the inlet conditions change. Furthermore, as Equations (19), (20) and (25) show, the specific exergy of the fuel and the flue gases at States 3 and 4 are constant. The exergy efficiency difference of the compressor and that of the combustion chamber are presented in Figure 9 and Figure 10, respectively. The actual exergy efficiency of the turbine is constant and equal to that of ISO conditions, since the specific work and exergy in the turbine are constant.

As a general comment, Figure 9 shows that the ambient conditions have a positive impact on the available energy efficiency of the compressor for almost all of the year. Due to the higher relative humidity in hot months in Muscat, the compressor actual exergy efficiency becomes lesser than the ISO efficiency. At higher inlet temperatures, the air mass flow rate decreases, which contribute to the reduction of the exergy destroyed of the compressor. Therefore, the actual exergy efficiency of the compressor increases. This behavior is clearly depicted in Figure 9. For Dammam and Kuwait, the ambient temperature can be lower than the ISO temperature, which results in increasing the exergy destruction in the compressor and decreasing in its exergy efficiency.

As Figure 10 shows, when the ambient temperature increases, the specific exergy at State 2 (Figure 1) rises; this would reduce the amount of fuel added to the combustion chamber, and as mentioned above, the specific exergy of the fuel and the gas at State 3 is constant. Therefore, as the ambient temperature increases, the exergy destroyed in the combustion chamber decreases, causing an increase in its exergy efficiency.

The total exergy destroyed of the gas turbine is the summation of the exergies destroyed of its components. Figure 11 shows the evolution of the destroyed exergy of the power unit in all cities. The rate of exergy destruction under the combined effect of temperature and humidity is significant in hot months, reaching a maximum of 12 MW in July. It decreases as the ambient temperature increases, but increases as the relative humidity increases.

Figure 12 presents the difference between the actual and ISO functional exergy efficiency of the gas turbine in all cities. The gas turbine functional exergy efficiency has the same behavior of its thermal efficiency during the year in all cities: decreasing as the ambient temperature increases. The gas turbine functional exergy efficiency difference between the actual and ISO exergy efficiencies is negative for most of the time in the year, except when the ambient temperature becomes less than the ISO temperature in Dammam and Kuwait. In conclusion, the ambient conditions have a negative effect on the functional exergy efficiency of the gas turbine. The latter decreases with the increase of the ambient temperature and relative humidity.

5. Conclusions

This work investigates the effect of ambient temperature and humidity on the energetic and exergetic performance of a typical gas turbine unit. The analysis is performed using average hourly temperature and relative humidity for selected Arab Gulf cities. For each city, the electricity production and the fuel consumption differences between the ISO conditions and actual conditions are determined over the year. The exergy efficiency of those power systems is also presented taking ISO conditions as reference conditions.

For all considered cities, the daily temperature is higher than the ISO temperature, except sometimes in the cold months in Dammam and Kuwait. The maximum power gain is 4% and 6% of the ISO production at temperatures of 9.9 and 7.9 °C in January for Dammam and Kuwait, respectively. While for the rest of the time, electricity production losses occur in all cities.

The second law analysis shows that, as the ambient temperature increases and the relative humidity decreases, the exergy destroyed of the whole gas turbine decreases.