A Probabilistic Damage Identification Method for Shear Structure Components Based on Cross-Entropy Optimizations
Abstract
:1. Introduction
2. General Cross-Entropy Optimization
- Generate a random set of candidate states of the system according to a specified mechanism.
- Rank the candidate states based on particular performance measures and keep candidate states that perform well and use them for the next iteration. This step usually involves minimization of the cross-entropy measure.
| Algorithm 1 Iterative Procedure of Estimation for |
| , initialize , e.g., . repeat (1) Draw N random samples from . (2) Calculate for all i. Sort from largest to smallest. (3) , where . (4) Calculate by solving . (5) . until . . |
| Algorithm 2 Iterative Procedure of Estimation for in a General Minimization Problem |
| , initialize and γ, e.g., Let and assign γ a large value. repeat (1) Draw N random variables from . (2) Calculate for all i. Sort from smallest to largest. (3) , where . (4) Calculate by solving . (5) , . until convergence is reached. Draw samples from . is estimated by . |
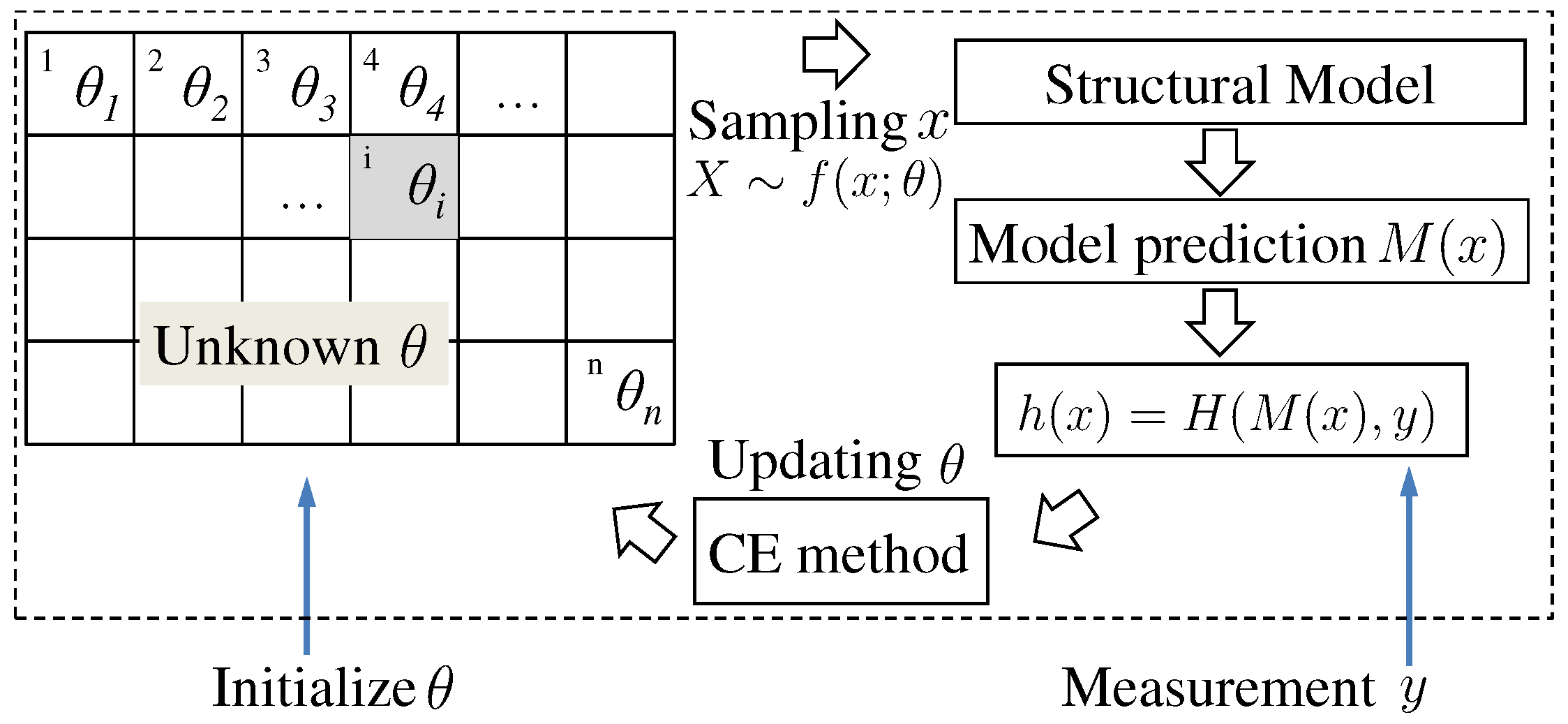
3. Formulation of Structural Component Damage Identification Using Cross-Entropy Optimizations
| Algorithm 3 Probabilistic Identification of Structural Damage |
| Set up a structural model for response prediction, e.g., an FE model. Define a performance function , e.g., , where y is measured response. . Initialize and , e.g., and . repeat (1) Draw N random variables from . (2) Calculate for all and sort from smallest to largest. (3) , where . (4) Calculate using Equation (16). (5) . until θ is converged. Draw samples from . is estimated by . |
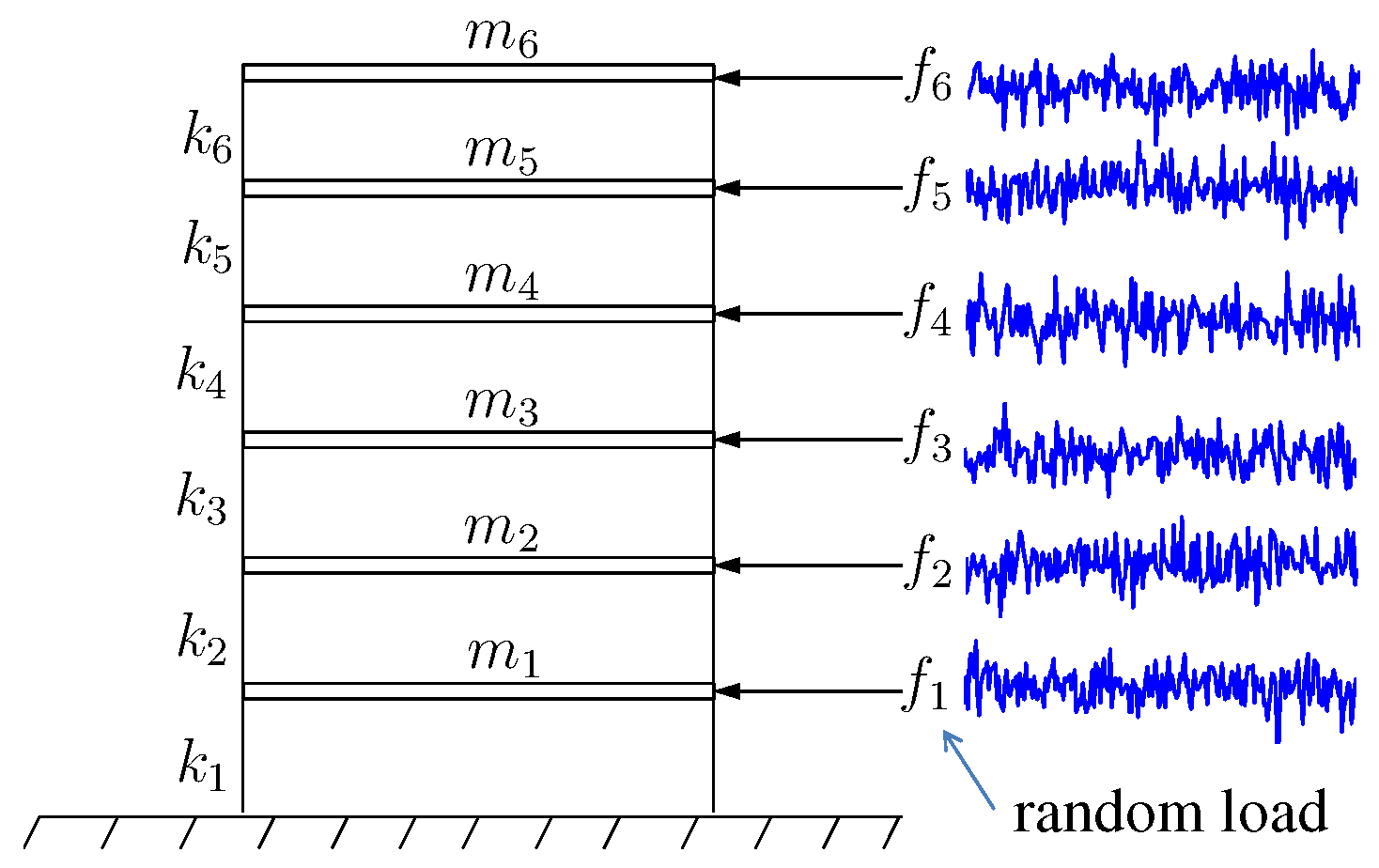
4. Application Example
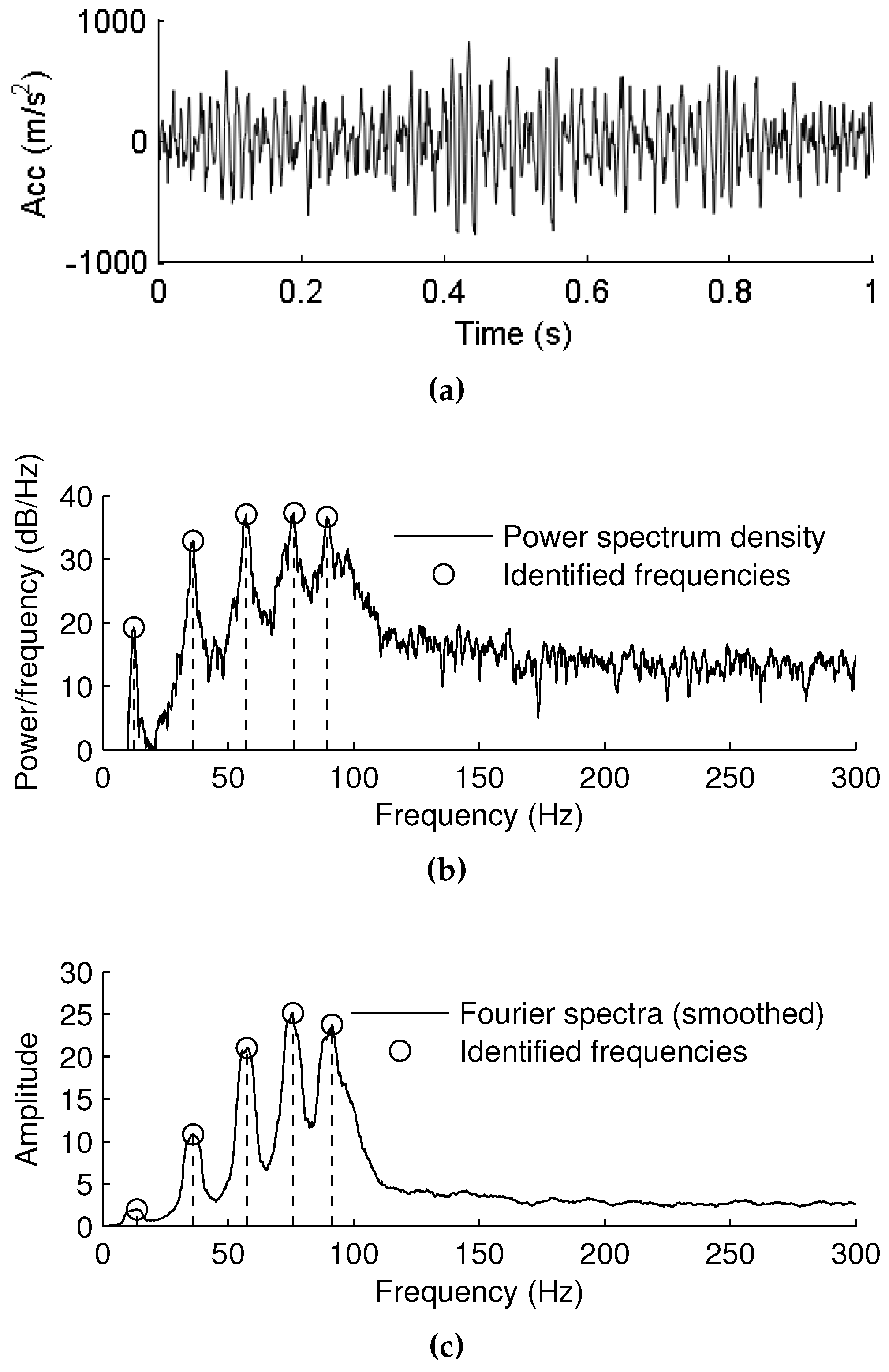
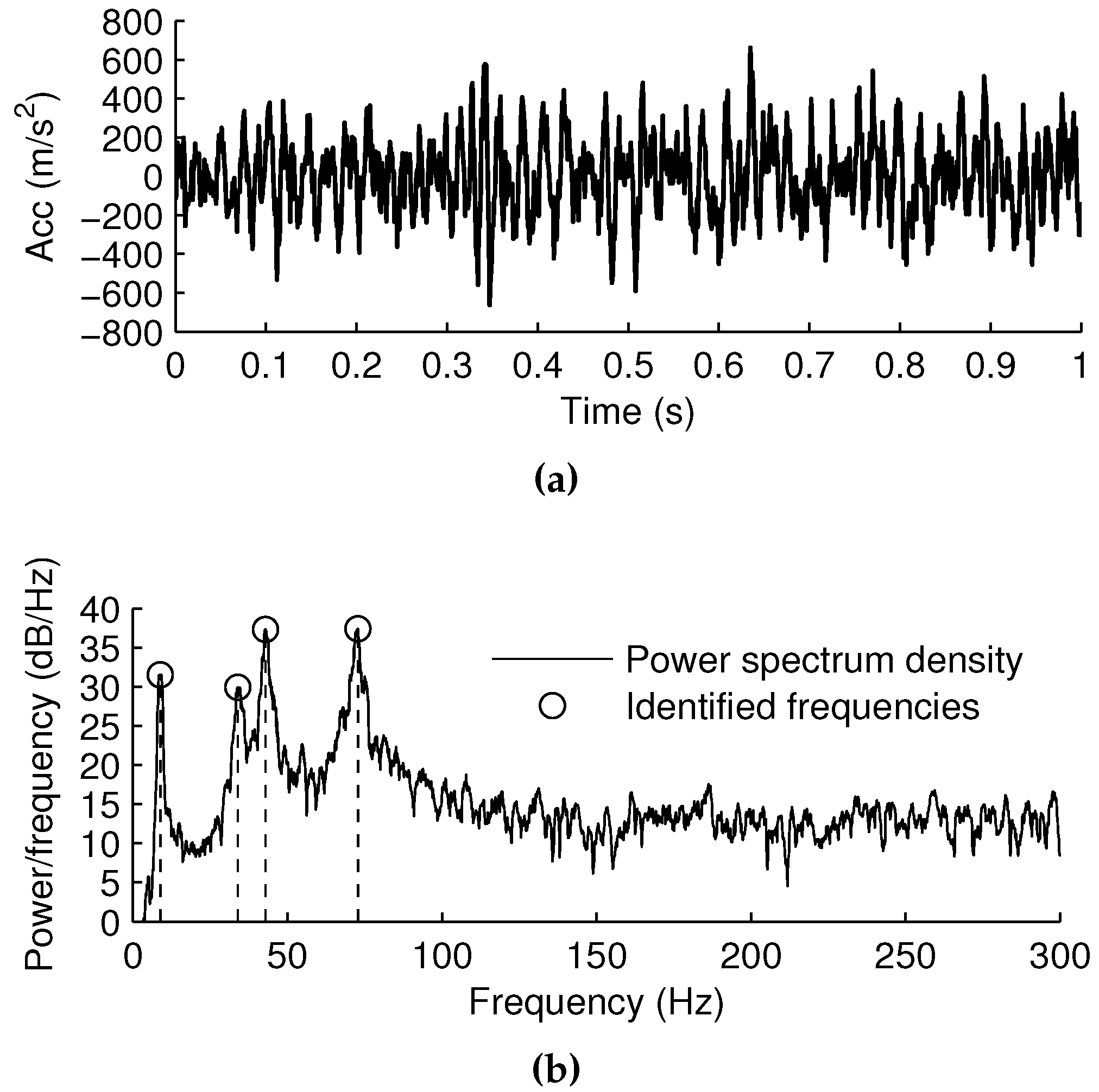
4.1. Measurement of Vibration Data and Extraction of Frequency Components
4.2. Performance Function
4.3. Damage Identification
4.3.1. Case 1
4.3.2. Case 2
4.3.3. Case 3
4.3.4. Case 4
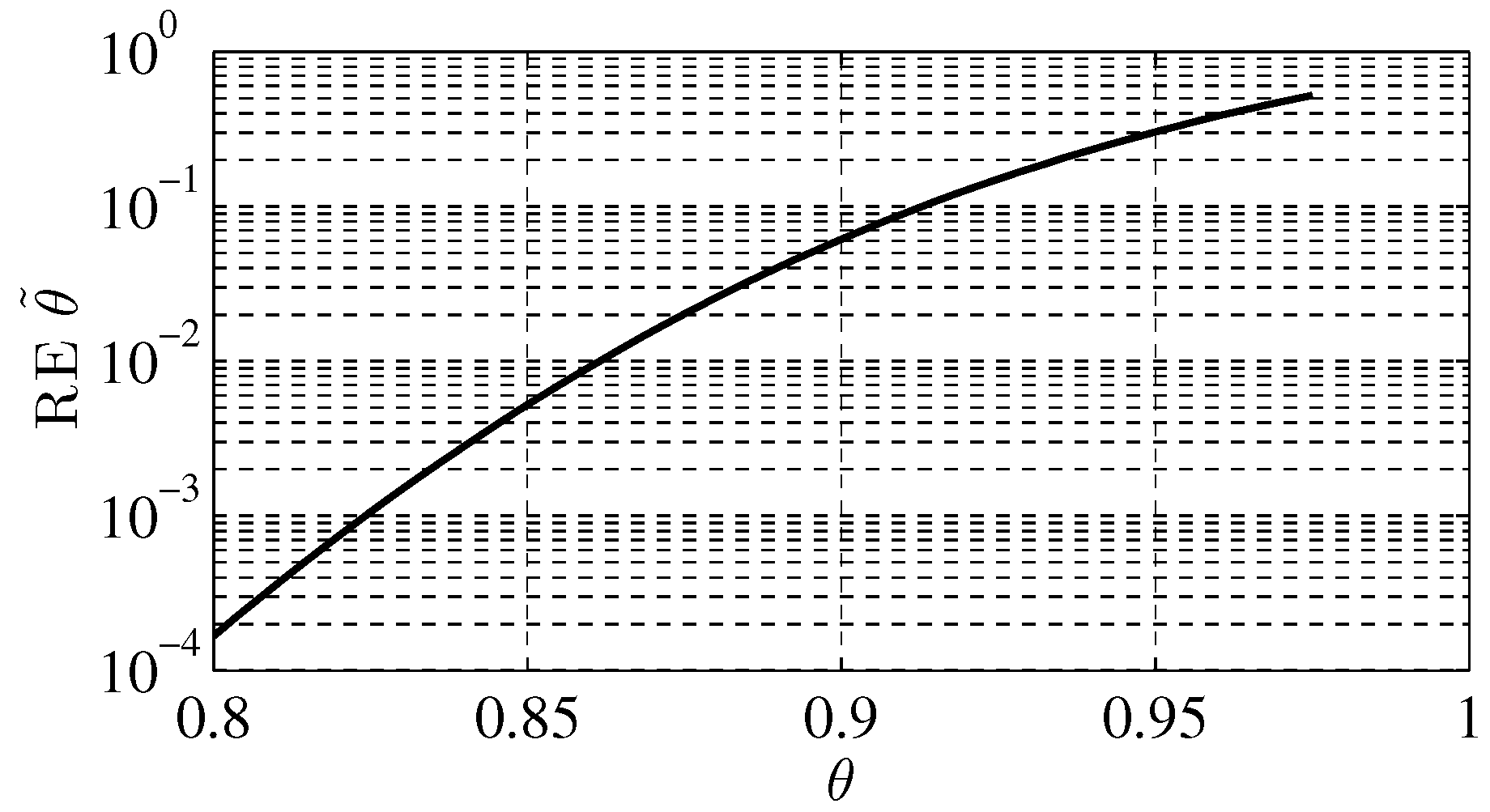
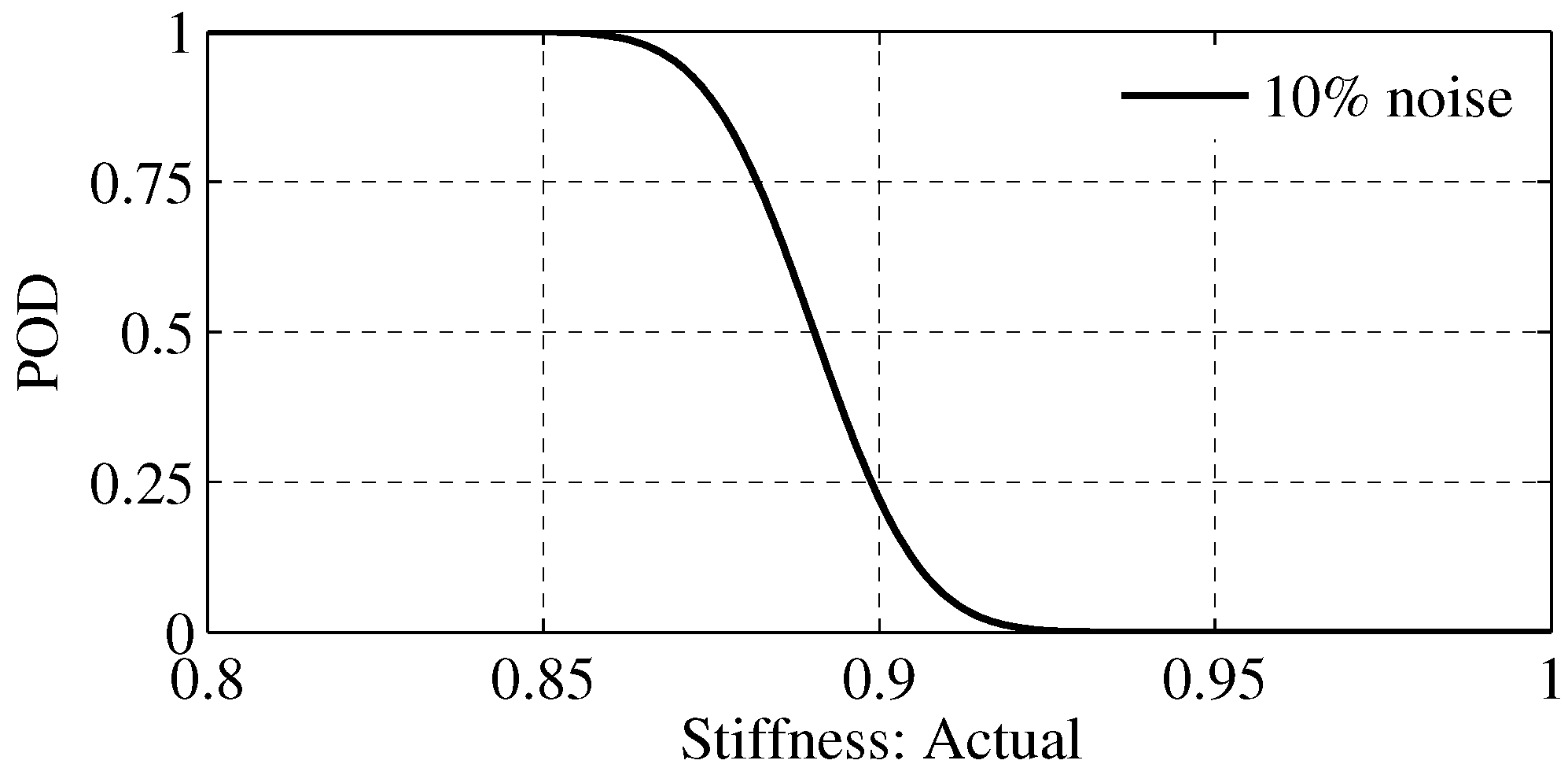
4.4. Probability of Detection
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Doebling, S.; Farrar, C.; Prime, M.; Shevitz, D. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Technical Report LA–13070-MS; Los Alamos National Lab: Los Alamos, NM, USA, May 1996. [Google Scholar]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Dessi, D.; Camerlengo, G. Damage identification techniques via modal curvature analysis: Overview and comparison. Mech. Syst. Signal Process. 2015, 52, 181–205. [Google Scholar] [CrossRef]
- Jardine, A.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Li, H.N.; Li, D.S.; Ren, L.; Yi, T.H.; Jia, Z.G.; LI, K.P. Structural health monitoring of innovative civil engineering structures in Mainland China. Struct. Monit. Maint. 2016, 3, 1–32. [Google Scholar] [CrossRef]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, April 1993. [Google Scholar]
- Blitz, J.; Simpson, G. Ultrasonic Methods of Non-Destructive Testing; Champman & Hall: London, UK, 1996; Volume 2. [Google Scholar]
- Drinkwater, B.; Wilcox, P. Ultrasonic arrays for non-destructive evaluation: A review. NDT & E Int. 2006, 39, 525–541. [Google Scholar]
- Guan, X.; Zhang, J.; Rasselkorde, E.M.; Abbasi, W.A.; Zhou, S.K. Material damage diagnosis and characterization for turbine rotors using three-dimensional adaptive ultrasonic NDE data reconstruction techniques. Ultrasonics 2014, 54, 516–525. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Zhang, J.; Zhou, S.K.; Rasselkorde, E.M.; Abbasi, W. Probabilistic modeling and sizing of embedded flaws in ultrasonic non-destructive inspections for fatigue damage prognostics and structural integrity assessment. NDT & E Int. 2014, 61, 1–9. [Google Scholar]
- Guan, X.; Zhang, J.; Zhou, S.K.; Rasselkorde, E.M.; Abbasi, W.A. Post-processing of phased-array ultrasonic inspection data with parallel computing for nondestructive evaluation. J. Nondestruct. Eval. 2014, 33, 342–351. [Google Scholar] [CrossRef]
- Guan, X.; He, J.; Rasselkorde, E.M. A time-domain synthetic aperture ultrasound imaging method for material flaw quantification with validations on small-scale artificial and natural flaws. Ultrasonics 2015, 56, 487–496. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Rasselkorde, E.M.; Abbasi, W.A.; Zhou, S.K. Turbine fatigue reliability and life assessment using ultrasonic inspection: Data acquisition, interpretation, and probabilistic modeling. In Quality and Reliability Management and Its Applications; Springer: London, UK, 2016; pp. 415–434. [Google Scholar]
- Bowler, J. Eddy-current interaction with an ideal crack. I. The forward problem. J. Appl. Phys. 1994, 75, 8128–8137. [Google Scholar] [CrossRef]
- Takagi, T.; Huang, H.; Fukutomi, H.; Tani, J. Numerical evaluation of correlation between crack size and eddy current testing signal by a very fast simulator. IEEE Trans. Magn. 1998, 34, 2581–2584. [Google Scholar] [CrossRef]
- Kessler, S.; Spearing, S.; Soutis, C. Damage detection in composite materials using Lamb wave methods. Smart Mater. Struct. 2002, 11, 269. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Kudela, P.; Malinowski, P.; Wandowski, T. Damage localisation in plate-like structures based on PZT sensors. Mech. Syst. Signal Process. 2009, 23, 1805–1829. [Google Scholar] [CrossRef]
- He, J.; Guan, X.; Peng, T.; Liu, Y.; Saxena, A.; Celaya, J.; Goebel, K. A multi-feature integration method for fatigue crack detection and crack length estimation in riveted lap joints using Lamb waves. Smart Mater. Struct. 2013, 22, 105007. [Google Scholar] [CrossRef]
- He, J.; Zhou, Y.; Guan, X.; Zhang, W.; Wang, Y.; Zhang, W. An integrated health monitoring method for structural fatigue life evaluation using limited sensor data. Materials 2016, 9, 894. [Google Scholar] [CrossRef]
- Yang, J.; He, J.; Guan, X.; Wang, D.; Chen, H.; Zhang, W.; Liu, Y. A probabilistic crack size quantification method using in-situ Lamb wave test and Bayesian updating. Mech. Syst. Signal Process. 2016, 78, 118–133. [Google Scholar] [CrossRef]
- He, J.; Zhou, Y.; Guan, X.; Zhang, W.; Zhang, W.; Liu, Y. Time domain strain/stress reconstruction based on empirical mode decomposition: numerical study and experimental validation. Sensors 2016, 16, 1290. [Google Scholar] [CrossRef] [PubMed]
- Farrar, C.; Doebling, S.; Nix, D. Vibration-based structural damage identification. Phil. Trans. R. Soc. Lond. A 2001, 359, 131–149. [Google Scholar] [CrossRef]
- Yan, Y.; Cheng, L.; Wu, Z.; Yam, L. Development in vibration-based structural damage detection technique. Mech. Syst. Signal Process. 2007, 21, 2198–2211. [Google Scholar] [CrossRef]
- Salawu, O. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Cawley, P.; Adams, R. A vibration technique for non-destructive testing of fibre composite structures. J. Compos. Mater. 1979, 13, 161. [Google Scholar] [CrossRef]
- Friswell, M.; Penny, J.; Wilson, D. Using vibration data and statistical measures to locate damage in structures. Int. J. Anal. Exp. Modal Anal. 1994, 9, 239–254. [Google Scholar]
- Fritzen, C.; Jennewein, D.; Kiefer, T. Damage detection based on model updating methods. Mech. Syst. Signal Process. 1998, 12, 163–186. [Google Scholar] [CrossRef]
- Bayissa, W.; Haritos, N.; Thelandersson, S. Vibration-based structural damage identification using wavelet transform. Mech. Syst. Signal Process. 2008, 22, 1194–1215. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Reynders, E.; De Roeck, G.; Kullaa, J. Vibration-based structural health monitoring using output-only measurements under changing environment. Mech. Syst. Signal Process. 2008, 22, 34–56. [Google Scholar] [CrossRef]
- Fugate, M.; Sohn, H.; Farrar, C. Vibration-based damage detection using statistical process control. Mech. Syst. Signal Process. 2001, 15, 707–721. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Li, H.; Bao, Y.; Ou, J. Structural damage identification based on integration of information fusion and shannon entropy. Mech. Syst. Signal Process. 2008, 22, 1427–1440. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Beck, J.; Katafygiotis, L. Updating robust reliability using structural test data. Probabilist. Eng. Mech. 2001, 16, 103–113. [Google Scholar] [CrossRef]
- Sohn, H.; Law, K.H. A Bayesian probabilistic approach for structure damage detection. Earthq. Eng. Struct. Dyn. 1997, 26, 1259–1281. [Google Scholar] [CrossRef]
- Worden, K.; Farrar, C.R.; Haywood, J.; Todd, M. A review of nonlinear dynamics applications to structural health monitoring. Struct. Control Health Monit. 2008, 15, 540–567. [Google Scholar] [CrossRef]
- Behmanesh, I.; Moaveni, B.; Lombaert, G.; Papadimitriou, C. Hierarchical Bayesian model updating for structural identification. Mech. Syst. Signal Process. 2015, 64, 360–376. [Google Scholar] [CrossRef]
- Friswell, M.; Mottershead, J.E. Finite Element Model Updating in Structural Dynamics; Springer Science & Business Media: Dordrecht, The Netherlands, 1995; Volume 38. [Google Scholar]
- Mottershead, J.; Friswell, M. Model updating in structural dynamics: A survey. J. Sound Vib. 1993, 167, 347–375. [Google Scholar] [CrossRef]
- Yuen, K.V.; Beck, J.L.; Katafygiotis, L.S. Unified probabilistic approach for model updating and damage detection. J. Appl. Mech. 2006, 73, 555–564. [Google Scholar] [CrossRef]
- Rubinstein, R. The cross-entropy method for combinatorial and continuous optimization. Methodol. Comput. Appl. Probab. 1999, 1, 127–190. [Google Scholar] [CrossRef]
- Rubinstein, R.; Kroese, D. The Cross-Entropy Method: A Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation, and Machine Learning; Springer: New York, NY, USA, 2004. [Google Scholar]
- Kroese, D.P.; Porotsky, S.; Rubinstein, R.Y. The cross-entropy method for continuous multi-extremal optimization. Methodol. Comput. Appl. Probab. 2006, 8, 383–407. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Park, J. Optimal Latin-hypercube designs for computer experiments. J. Stat. Plan. Inference 1994, 39, 95–111. [Google Scholar] [CrossRef]
- Guan, X.; He, J.; Rasselkorde, E.M.; Zhang, J.; Abbasi, W.A.; Zhou, S.K. Probabilistic fatigue life prediction and structural reliability evaluation of turbine rotors integrating an automated ultrasonic inspection system. J. Nondestruct. Eval. 2014, 33, 51–61. [Google Scholar] [CrossRef]

| Case | Damage Component | Measurement Location | Measurement Noise | Stiffness Reduced by |
|---|---|---|---|---|
| 1 | floor 3 | floor 3 | 10% | 0.9 |
| 2 | floor 4 | floor 1 | 5% | 0.8 |
| 3 | floor 6 | floor 4 | 20% | 0.85 |
| 4 | floor 1 | floor 6 | 10% | 0.925 |
| t | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | +∞ |
| 1 | 0.72 | 0.57 | 0.67 | 0.70 | 0.65 | 0.74 | 987.818 |
| 2 | 0.91 | 0.75 | 0.82 | 0.88 | 0.87 | 0.93 | 201.615 |
| 3 | 0.97 | 0.93 | 0.95 | 0.98 | 0.95 | 0.97 | 16.973 |
| 4 | 0.99 | 0.99 | 0.96 | 1.00 | 0.99 | 1.00 | 1.738 |
| * | 1.00 | 1.00 | 0.92 | 1.00 | 1.00 | 1.00 | 0.180 |
| t | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | +∞ |
| 1 | 0.72 | 0.61 | 0.68 | 0.68 | 0.67 | 0.75 | 965.583 |
| 2 | 0.89 | 0.79 | 0.85 | 0.85 | 0.87 | 0.94 | 177.565 |
| 3 | 0.97 | 0.96 | 0.97 | 0.95 | 0.98 | 0.97 | 12.256 |
| 4 | 0.96 | 0.98 | 0.98 | 0.87 | 0.99 | 0.99 | 3.803 |
| * | 0.99 | 1.00 | 0.99 | 0.81 | 0.99 | 1.00 | 0.751 |
| t | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | +∞ |
| 1 | 0.71 | 0.63 | 0.69 | 0.67 | 0.65 | 0.74 | 1068.041 |
| 2 | 0.90 | 0.81 | 0.86 | 0.86 | 0.85 | 0.93 | 194.705 |
| 3 | 0.97 | 0.96 | 0.96 | 0.96 | 0.97 | 0.97 | 12.073 |
| 4 | 0.98 | 0.99 | 0.97 | 0.96 | 0.99 | 0.93 | 3.316 |
| * | 0.98 | 1.00 | 1.00 | 0.99 | 1.00 | 0.86 | 0.399 |
| t | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | +∞ |
| 1 | 0.72 | 0.61 | 0.68 | 0.68 | 0.67 | 0.75 | 1065.796 |
| 2 | 0.89 | 0.79 | 0.85 | 0.85 | 0.87 | 0.94 | 222.107 |
| 3 | 0.97 | 0.95 | 0.96 | 0.97 | 0.97 | 0.97 | 18.414 |
| 4 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 1.00 | 0.986 |
| * | 0.96 | 1.00 | 1.00 | 1.00 | 0.98 | 1.00 | 0.124 |
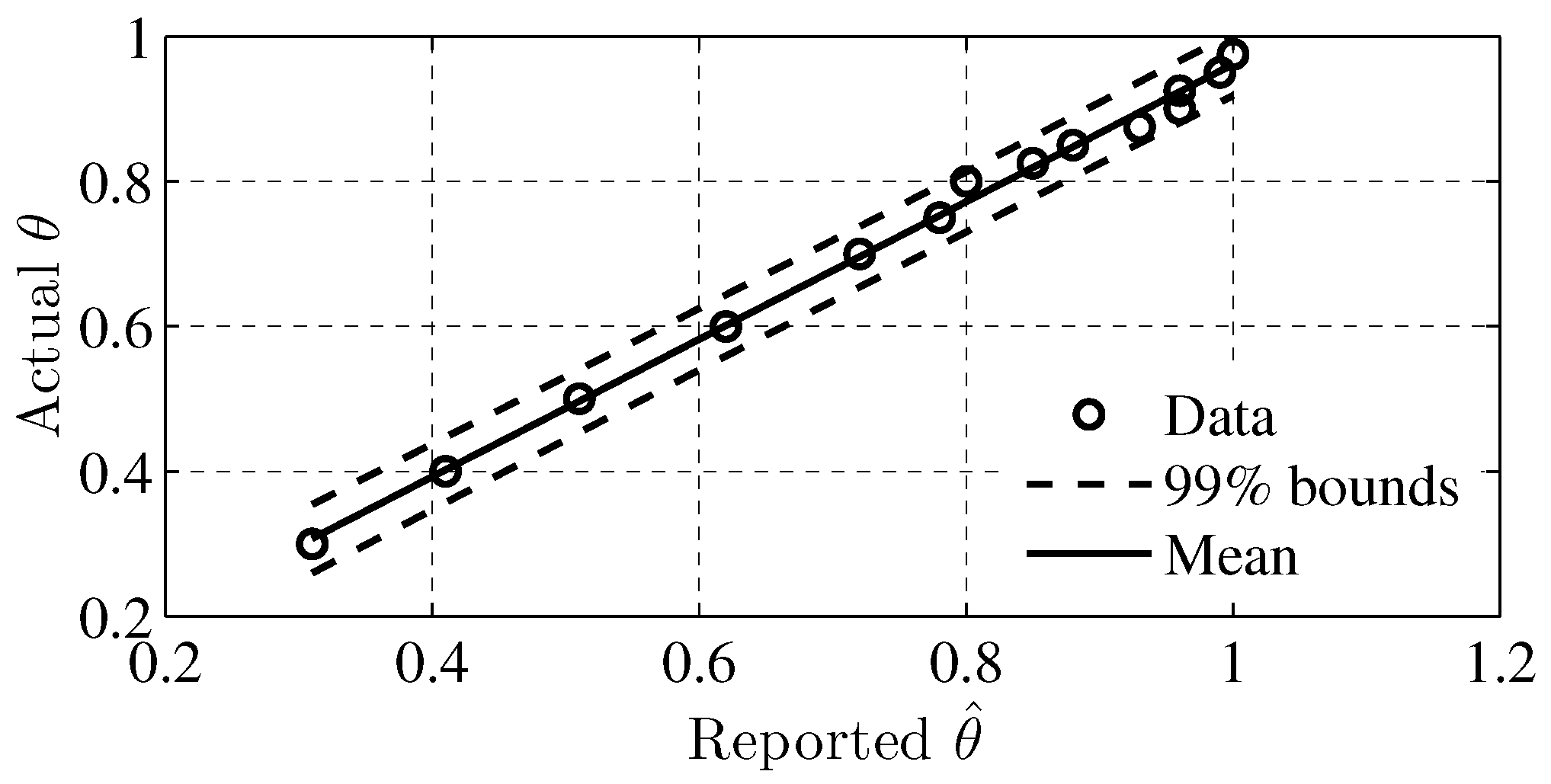
| Actual | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.75 | 0.8 | 0.825 | 0.85 | 0.875 | 0.9 | 0.925 | 0.95 | 0.975 |
| Reported | 0.31 | 0.41 | 0.51 | 0.62 | 0.72 | 0.78 | 0.8 | 0.85 | 0.88 | 0.93 | 0.96 | 0.96 | 0.99 | 1 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Wang, Y.; He, J. A Probabilistic Damage Identification Method for Shear Structure Components Based on Cross-Entropy Optimizations. Entropy 2017, 19, 27. https://doi.org/10.3390/e19010027
Guan X, Wang Y, He J. A Probabilistic Damage Identification Method for Shear Structure Components Based on Cross-Entropy Optimizations. Entropy. 2017; 19(1):27. https://doi.org/10.3390/e19010027
Chicago/Turabian StyleGuan, Xuefei, Yongxiang Wang, and Jingjing He. 2017. "A Probabilistic Damage Identification Method for Shear Structure Components Based on Cross-Entropy Optimizations" Entropy 19, no. 1: 27. https://doi.org/10.3390/e19010027
APA StyleGuan, X., Wang, Y., & He, J. (2017). A Probabilistic Damage Identification Method for Shear Structure Components Based on Cross-Entropy Optimizations. Entropy, 19(1), 27. https://doi.org/10.3390/e19010027






