1. Introduction
At present, as the development of the economy and society as a whole’s quality of life is increasing, human consumption of energy is increasing while variety is becoming more and more diversified. Because coal and oil are not renewable, it is more and more difficult to meet the needs of social development with these resources. Therefore, people are paying more attention to renewable energy, such as hydropower and solar power. Renewable energy can be sustainably developed in a certain range through rational planning, and it can be used to optimize the configuration, which has important significance for the development on national and regional scales. In energy market research, there exists a background of oligopoly competition for example China Petroleum (Beijing, China), China Petrochemical Corporation (Beijing, China), and China National Offshore Oil Corporation (Beijing, China). In addition, there is also much interest in game theory, entropy theory, and nonlinear dynamics theory, which provide facilities to acquire insight into issues about energy markets. There is also an oligopoly competition in the renewable energy market. Therefore, the oligarch competition analysis of the renewable energy market is a topic of concern.
Oligopolistic competition systems, as complex systems, are always difficult to model, or modeled, difficult to solve. Our focus is to determine how to use the limited observational data to infer the dynamic evolutionary process of the system, and analyze the complexity of the analysis system and entropy of systems on this basis. We need to analyze from different sides of the system, such as equilibrium point, the existence of Hopf bifurcation, the stability of the system, and the change of entropy, etc. Because unfair competition in an oligopoly may get out of control, at this time, the system will suffer from stability to chaos. It is well known that a chaotic system is not conducive to normal market competition, and businesses and consumers will be hurt. We use entropy to describe the degree of system chaos. The degree of system chaos affects the degree of the control of chaos. We mainly study the influence of time delay and the natural growth rate of renewable energy on the stability of the system. So, we use an entropy diagram and a power spectrum to demonstrate the evolution of the system’s complexity.
Energy is a foundation of the national development, and it is vital to the national economy. The energy problem is always related to the national and regional stability and security, so it has always been the focus of research. In the research field of energy economy strategy and the environment, Weidou and Johansson [
1] comprehensively researched the energy policy and energy structure of China, and gave some strategies and suggestions about energy consumers and energy supply. The conclusion of the research helped to ensure the sustainable development of energy and economy in China. Nwaobi [
2] took Nigeria as an example, and a general equilibrium model was established. The influence of energy saving and emission reduction policies on economic development were analyzed, and significant results were obtained. Vera et al. [
3] built a national energy index system through analysis of the 3E problem. They studied the formulation of energy policy. The results of the study indicate that the correct energy policy contributes to society, economy, environment, and energy of sustainable development. Omri [
4] analyzed the game relationship between economic growth and energy consumption. Through the statistical calculation of electricity consumption, nuclear consumption, and renewable energy consumption, further validation of the relationship between economic growth and energy consumption was obtained. The research results have good practical significance to the economic development.
Nowadays, in the research field of renewable energy, the oligopoly game has become the frontier research area, analyzing real renewable energy with nonlinear dynamic models, entropy theory, and chaos theory. These theories are beneficial to constructing the game model and measuring the uncertainty of actual processes. Ma et al. [
5] built a closed-loop supply chain (CLSC) based on product recovery, and developed a Stackelberg game model and a peer-to-peer game model. The nonlinear dynamic behavior of the system was studied. The results show that the CLSC system enters chaos more easily with the improvement of the retailer’s competitive position. Batabyal et al. [
6] focused on the trade of renewable resources all over the world, and studied a Stackelberg differential model. The trade policy of new energy sources was proposed. The results show that the policy tool plays an important role in the promotion of energy conservation. Ma et al. [
7] analyzed the dynamic behavior of a duopoly Cournot game model with different adjustment mechanisms and expectations, and studied the local stability and global stability of this game model. Research conclusions are very helpful for the game models with two-stage consideration. In the Markov information structure field, Halkos et al. [
8] established a renewable energy game model and obtained a renewable energy Nash equilibrium. They used the utility function to put forward the strategy of energy game, which has a very good practical significance.
In recent years, according to the entropy theory and non-linear theory, many scholars found some valuable entropy results. There are some studies connecting entropy with management and the economy. Salo et al. [
9] established an equilibrium game model with entropy analysis in the nonrenewable resource markets, where they captured the characters of the system and gained the entropy changes. However, they are not the first to research in this field; Polansky et al. [
10] published their entropy research on oil in 1992. They analyzed an oligopoly model of exhaustible resource extraction and proposed several predictions about producers’ relative extraction patterns. Additionally, Chermak et al. [
11] found natural gas also had this nature when focusing on the cost function and the economics of exhaustible resources. With the deepening of research, entropy theory has been widely used in the research methods of system complexity, and many valuable results have been obtained. Yan et al. [
12] cited the entropy change in a delayed Lokta–Volterra predator–prey system. Meanwhile, Chen et al. [
13] followed the former results and used entropy control to a financial system with time-delayed feedbacks. Furthermore, Ma et al. [
14] established a discrete triopoly dynamical game model. They considered multi-product firms with heterogeneous expectations, and studied the influence of the change of parameters on the levels of sensitivity. The studies show that the adaptive game model is beneficial to the stability of the system. Ma et al. [
15] established a Complexity and Hopf bifurcation fractional-order IS-LM macroeconomic system model, and Ma et al. [
16] established a price game model about triopoly in different decision-making , The research conclusions provide important guidance for market decision making. Benchekroun et al. [
17] combined entropy with game theory, expanding the entropy research field, as they studied the dramatic system on price taking behavior. While Rubio [
18] did the same job, he proposed a dynamic game approach. In the research of Fan et al. [
19], entropy was used to analyze the economy and the supply chain, and they drew the conclusion that financial forecasts of foreign exchange currency in low entropy regions have a slight advantage in trading, and it is very difficult to achieve the predicting time series in high entropy regions. Ma et al. [
20] studied a continuous Bertrand duopoly game model with two-stage delay. The effects of delay parameters on the complex dynamic characteristics and entropy of the system were the main concerns. The study shows that the stability and entropy of the system depends on the variation of time delay parameter.
In reality, renewable energy is a complex dynamic system which is related to many factors. In this paper, we study the problem of oligopoly game in the market of renewable energy by nonlinear theory and complex dynamics theory; we analyze the complex dynamic characteristics of the system and the law of entropy change, and study the effect of the natural growth rate of energy and time delay on the system.
2. Renewable Energy Oligopoly Game Model
In the renewable energy market, we want to find the total economic variables: energy price, market demand, and energy reserves, and the conditions that need to be met when the market reaches equilibrium, and then analyze the complex dynamic characteristics of renewable energy system and the influence of the important parameters to the system.
Hypothesis: there exist
N (
N ≥ 2) oligopolies in the renewable energy market. The inverse demand function for the energy market is
, and
is energy price,
is the demand of energy,
. Due to market competition, international form, and other reasons, and
is the highest price of the energy [
7].
In the energy market,
is the cost function which is related to its own energy reserves
[
8,
9].
is the energy reserve, and
. Obviously,
is the producer’s effective energy reserves; when
, producers will not develop the energy. So, the cost per unit is
. The energy is renewable, and its natural growth rate is
k. For now, the growth rate of renewable energy is mainly related to the installed capacity of the equipment, which is a positive correlation,
. Taking solar and wind energy as an example, in the case of no change on external conditions, the transformation of these energy sources to electricity is mainly related to the number of erected pieces of equipment. In 2013, renewable energy met about 19.1% of the world’s energy consumption; in recent years, renewable energy capacity and power generation continued to maintain steady growth. According to a recent study by Bloomberg New Energy Finance, the annual investment in non-hydro renewable energy projects will increase 2.3 times that of in 2012, to $630 billion. So, the energy reserves should be met
.
To maximize its own profit, each player get its profit as the model below:
So, we can establish the optimization problem to show the game strategy for each oligopoly:
indicates the discount factor,
,
With a Hamilton function, we can solve optimization problem Equation (1):
indicates a co-state variable: ,
There are
N equations of Equation (4), sum and obtained
,
If
N = 2, the renewable energy market is a two-member oligopoly. We can get the following game strategy model:
In the actual operation of the energy market, in order to ensure the sustainable development of energy, as well as the stability of the international energy prices, the energy supply of the market will be fixed in a certain period of time, to ensure that the supply of energy will not be too large, resulting in excessive energy consumption and market price fluctuations. This is also a means of Energy Organization for the regulation of the energy market. Suppose that in a certain period of time, the largest energy supply is a, so positive correlation with , is the change rate of energy supply.
Therefore, integrating Equations (5) and (6) and
, we can obtain a double oligopoly game model for the renewable energy market:
3. Analysis and Numerical Simulation of the Renewable Energy Model
For the renewable energy market, we analyze the system characteristics of the double oligopoly game model Equation (7). In order to facilitate analysis, we analyze its total equation, as follows:
Solving the equilibrium point, there are two equilibrium points of Equation (8): , . is the boundary equilibrium point, and is the Nash equilibrium point.
The Jacobi matrix of Equation (8):
In order to distinguish the stability of the system, the symbol of the system characteristic value is needed, which can be known by the property of the quadratic function:
Make:
,
- (1)
When , , there is system convergence
- (2)
When , the equilibrium point is a saddle point
- (3)
When , , the equilibrium point is a saddle point
- (4)
When , there is system divergence
In order to analyze the influence of the natural growth rate of energy on the operating state of the system, we make a numerical simulation of the system Equation (7), setting the energy market parameters as , and the change rate of energy supply . The initial value of effective energy reserves is , and the initial value of market demand is . Bringing the parameters into the formula above, we can determine that , , and the equilibrium point is a saddle point. At this moment, we can analyze the stability of the system by simulation, and study the impact of the natural growth rate of energy k on the system.
With Matlab software, we can conduct a numerical simulation, as shown in
Figure 1.
As shown in
Figure 1, the market demand of two energy companies will be stable at a fixed value; after a brief rise, the system does not appear chaotic, and the system is stable. So at this point, the entropy of system is 0.
Figure 1a shows that when energy’s natural growth rate is low (
k = 0.35), according to the economic and parameter values, we can know that in a certain period of time, the energy is less, the oligopoly who has a high energy demand can have a greater advantage in the competition, and the final game equilibrium results will be more favorable.
Figure 1a shows stability in (1.471, 0.556).
Adjusting the natural growth rate of energy k—where other parameters are unchanged—setting k = 0.40, 0.45, we find that with the increase of k, the equilibrium point of the system gradually changes, the market demand of oligopoly 1 is gradually reduced, and the market demand of oligopoly 2 is gradually increasing. According to the economic analysis, the increase of the natural growth rate of energy gives the advantage to the initial weak oligopoly. As renewable energy is increased, the initial weak oligopoly is able to use more renewable energy, and due to its larger market demand, the increase in energy regeneration has little effect on the market demand for the initial strong oligopoly, so the share of market demand is gradually occupied by oligopoly 2. The simulation results are consistent with the actual situation. Therefore, in the renewable energy market game process, the oligopoly should pay close attention to the renewable rate of energy, and adjust their own game strategy to ensure their own interests.
4. Time Delay and Hopf Bifurcation of the Model
In the actual operation process of the energy enterprise, it is not only necessary to consider the market demand, but also to consider the market demand of
τ time early, which makes the final decision results more close to the actual situation. In this paper, we assume that oligopoly 1 considered time delay in order to formulate the game strategy, and we assume that oligopoly 2 did not consider the time delay. That is:
and
is the weight of the current period price.
Solving the equilibrium point of the system, the delay decision does not affect the system’s solution, so there are two equilibrium points of the system in Equation (7); one of them is
. Solving the second equilibrium point, when
:
That is: and .
At this point, we can transfer the system’s equilibrium point to the origin of the system by linear transformation, so in this paper, we analyze the delay decision with the equilibrium point of
. Then, the linear part of the delay decision system Equation (7) is:
For the convenience of the model analysis, make
, and Equation (10) can be expressed as:
and
,
.
The characteristic equation of system (11) is:
If
is a root of the Equation (13), according to the Euler equation
, Equation (14) can be expressed as:
Separating real and imaginary parts, Equation (14) can be transformed into
and:
So, when
, and
or
, the system has a unique positive root.
That is, Equation (13) has a pair of pure imaginary roots ±iω.
Therefore, the delay points
of the Hopf bifurcation can be obtained.
Verify the cross section condition of Hopf bifurcation:
Therefore, we can know that when , , the cross-section condition of the Hopf bifurcation is satisfied. At this point, the minimum that makes (17) set up is the time delay of the occurrence of Hopf bifurcation.
Having all the relevant parameters assigned in the numerical simulation, we analyze the influence of the change of delay τ on the operating status of the system. , the initial value of market demand is . The current weight of market demand of oligopoly 1 is μ = 0.45; bringing the corresponding parameters into Equations (14) and (16), we can know that , so when τ = 0, the equilibrium point is local stability, Hopf bifurcation occurs at . When , the system is local asymptotic stable; when i = 0, we can obtain when Hopf bifurcation occurs based on Equation (16). In this time, when the bifurcation appears it triggers the system gradually towards instability, and the entropy becomes larger while the system is transforming. Once the entropy is in the system, it means the system does not operate orderly and may be out of control. To avoid further increases of the entropy, it is necessary to use time-delay by changing τ.
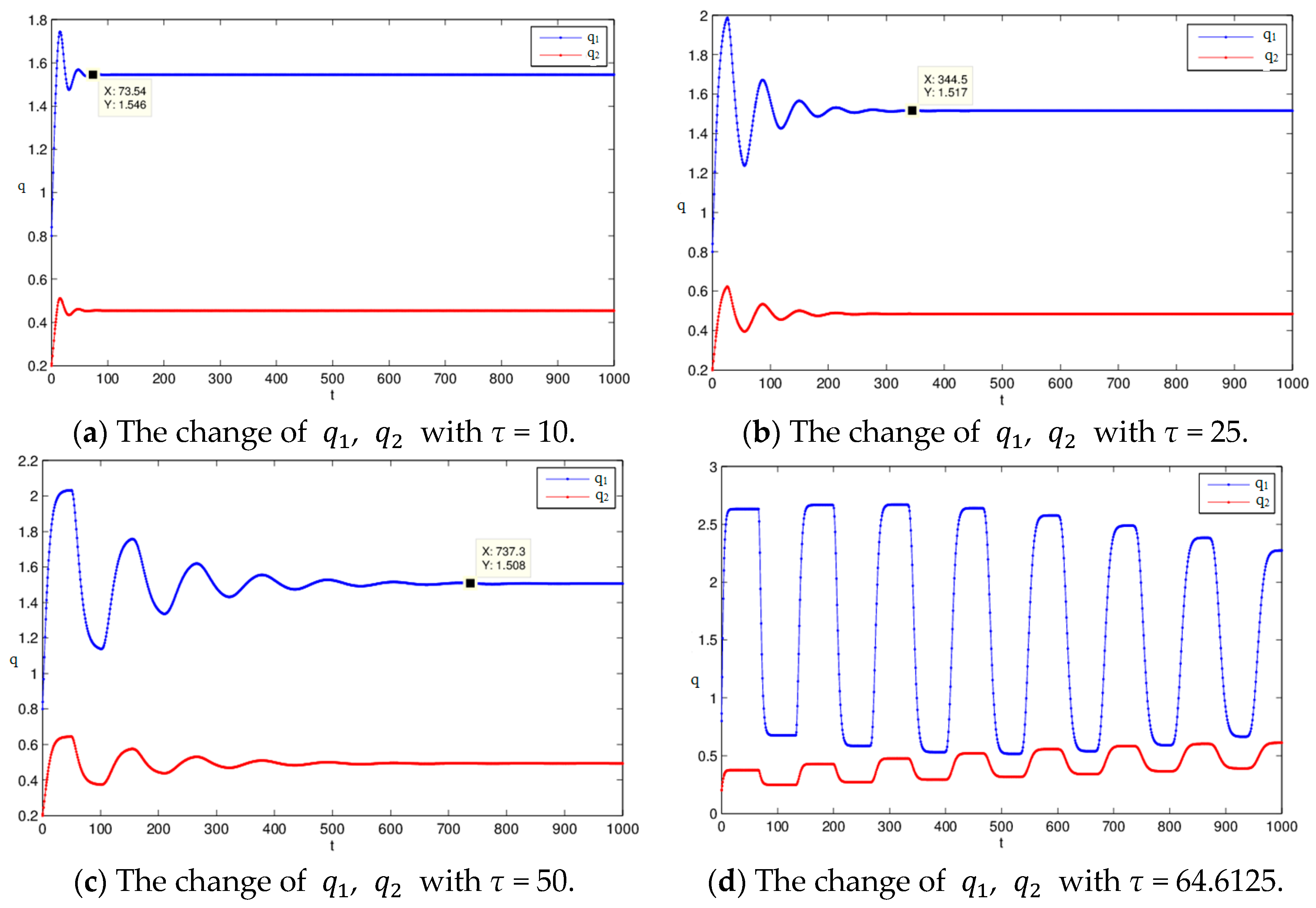
Make
τ = 10, 25, 50, 64.6125, observe the change of the solution of the system under different delay conditions. As shown in
Figure 2:
From
Figure 2, we can clearly see that in the energy market, the oligopoly has a strong mutual influence, and a single oligopoly taking the decision of time delay will affect the stability of both oligopolies; with the increase of delay, the time required to reach the stable state will grow. With the increase of the delay, the system may reach the Hopf bifurcation state, the system presents a periodic solution, and it is very challenging for the oligopoly to grasp the operation of the market, which is unfavorable for the energy market.
When , the time delay game system Equation (10) will eventually reach the stable state, and the time of the system to achieve stability will increase gradually with the increase of τ. This is in line with the actual situation; when the delay is increased, the oligopoly needs to consider the early energy market demand, more factors need to be considered, so the corresponding decision-making process will be long, and ultimately lead to more time for the system to achieve stable state. When , the system has a Hopf bifurcation, and entropy appears; with continually increasing τ, the system will not be stable while the entropy gradually increases.
In the oligopoly game process of the renewable energy market, the market demand of the past period of time will be considered by the oligopoly. However, more time is not better; a long delay decision will lead to a long time for the energy market to reach a stable state. Therefore, in the process of the game, we need to choose a suitable amount of delay τ, which can guarantee a reasonable oligopoly strategy, and the renewable energy market can quickly enter a stable state.
5. Conclusions
This paper established a double oligopoly game model of a renewable energy market based on previous research results. We analyzed the complex dynamic characteristics of game models, such as equilibrium point, system stability, the existence of Hopf bifurcation and entropy change, etc. We studied and simulated the effect of the natural growth rate of energy and the single delay decision on the complexity of the renewable energy system. We reached the following conclusions:
(1) The change of the natural growth rate of the energy k does not affect the stability of the system, but it can affect the equilibrium results of the system. The equilibrium point of the system gradually changes with the gradual increase of k, the market demand of oligopoly 1 gradually decreases, and the market demand of oligopoly 2 gradually increases.
(2) The time delay τ will affect the stability of the system, and lead to the increase of system entropy, and the system becomes more complex. The system will enter into a Hopf bifurcation phenomenon with the gradual increase of τ, and the system will lose stability while the entropy becomes larger.
(3) The system complexity is higher with the increase of entropy. At the same time, the system’s return to stability is more difficult when the system is in a chaotic state.
Therefore, the oligopoly should pay close attention to the natural growth rate of the energy k in the game process of the renewable energy market. It is essential to adjust the game strategy to ensure their interests. Meanwhile, a reasonable choice of delay decision τ is needed to avoid chaos. The research results of this paper have important theoretical and practical value for the renewable energy market.